Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame
Abstract
1. Introduction
2. Infrared Radiation Calculation
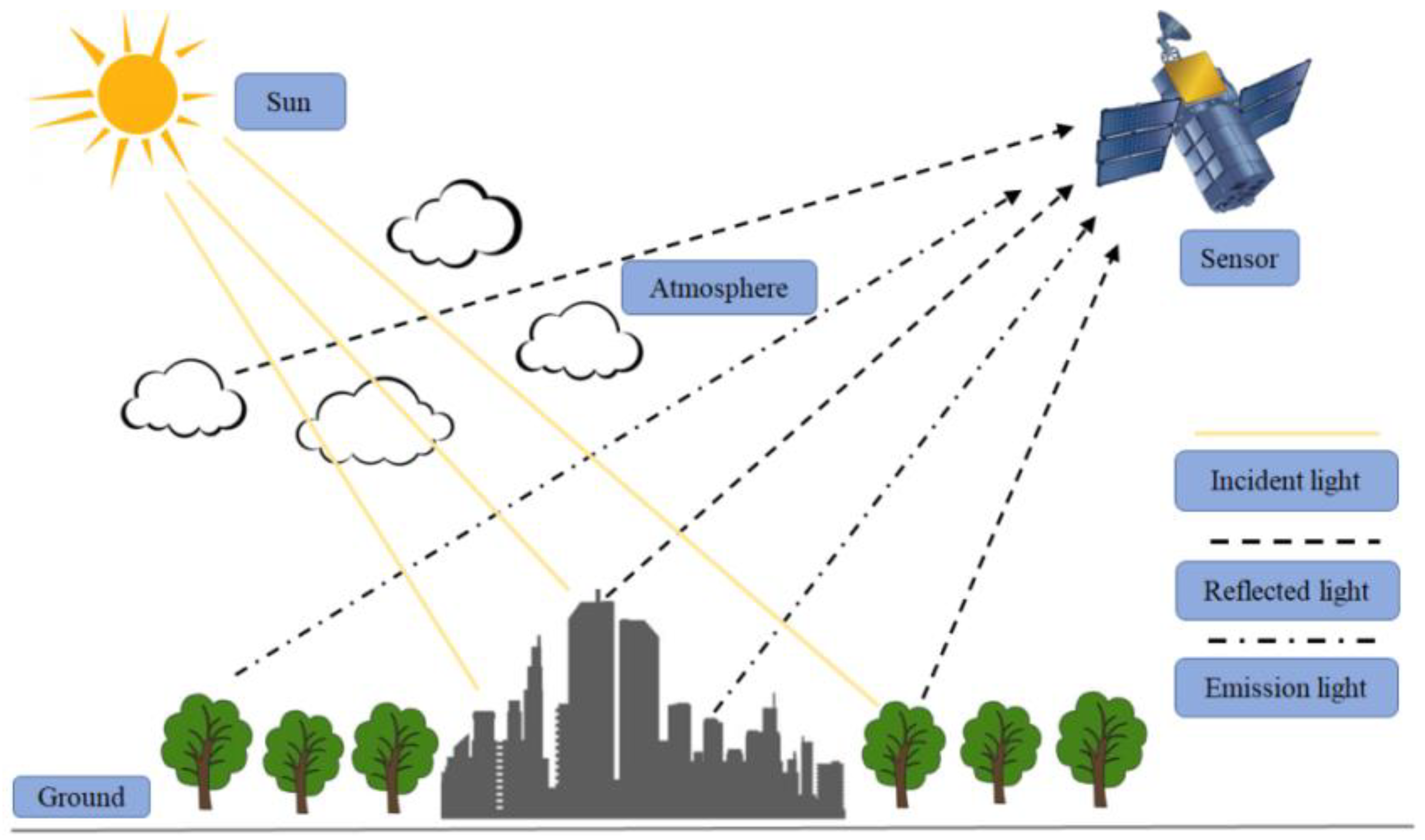
2.1. Earth Background
2.2. Missile Flame
3. Detectability Analysis of Flame Infrared Radiation
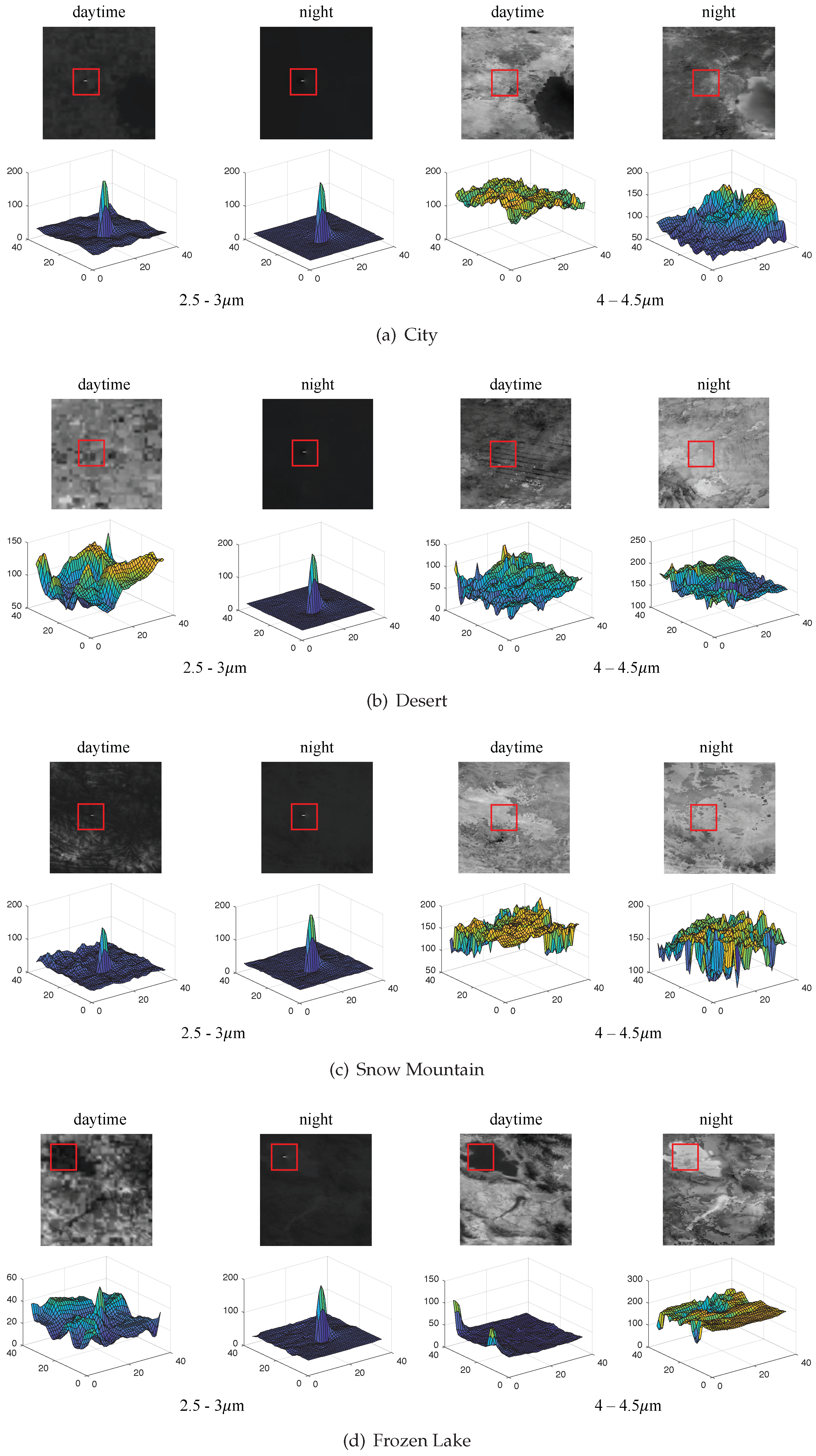
3.1. Generation of Infrared Radiation Data of Flame and Background
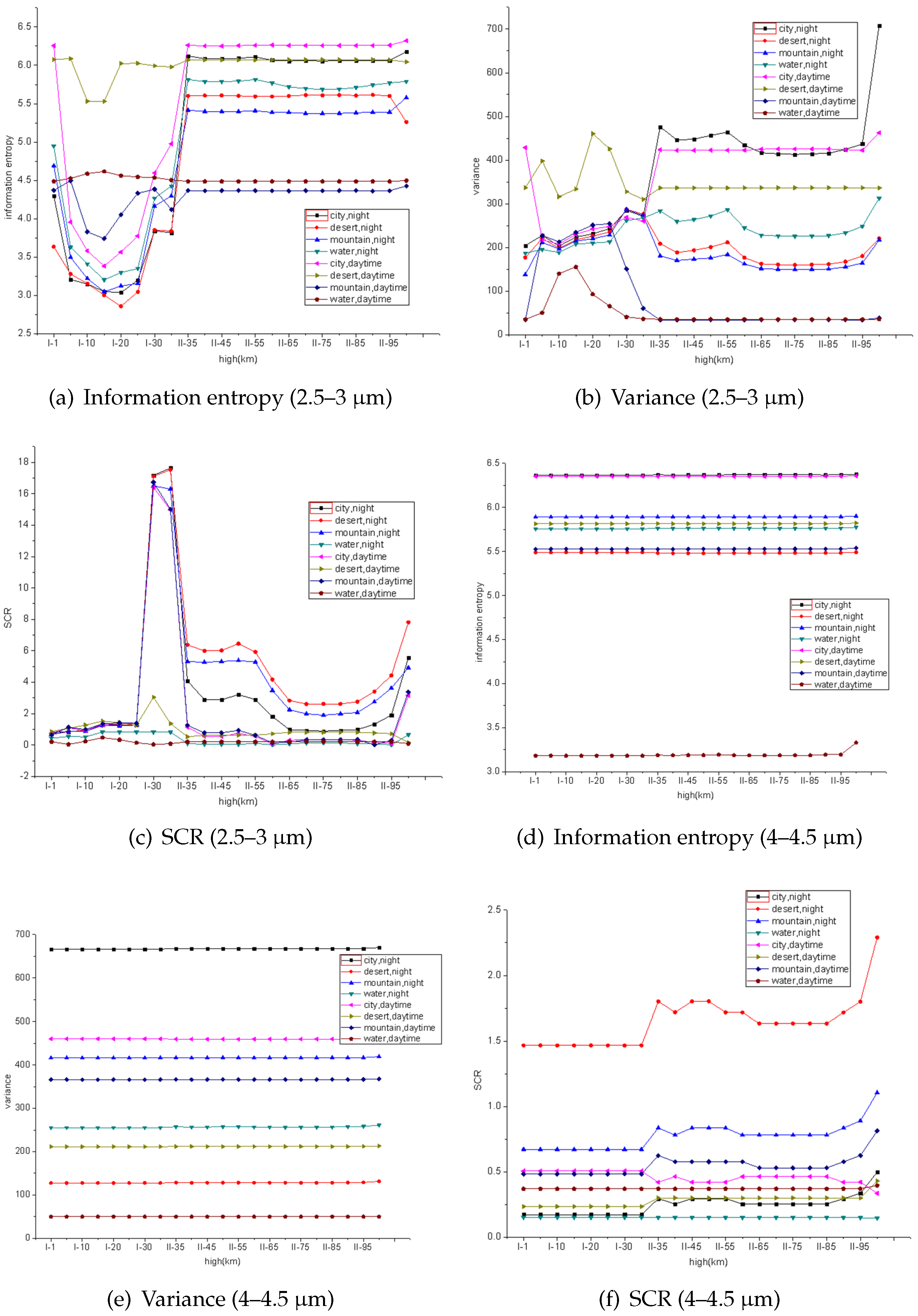
3.2. Detectability Analysis of Flame Radiation
- (1)
- Signal Effectiveness
- Peak signal-to-noise ratioThe calculation of the peak signal-to-noise ratio (PSNR) is based on the mean square error (MSE) and is defined by:where MSE is defined as:where t and b represent the target area and background area, respectively.
- Signal-to-clutter ratioThe signal-to-clutter ratio is defined as:where is the average gray value of target pixels, is the average gray value of the background pixels, is the standard deviation of the gray value of the background area.
- ContrastThe contrast describes the gradual change of image brightness [18]. A larger contrast value represents a richer gray level change of an image. The contrast is defined as:where represents the gray difference between adjacent pixels. represents the distribution probability of pixels whose gray difference is equal to .
- (2)
- Statistical Characteristics
- VarianceImage variance is a measure of gray contrast and a measure of uniformity of sample distribution [19].where z is a random variable representing gray level, is the corresponding histogram distribution, m is the mean of z.
- SkewnessThe skewness of an image is defined by the third-order statistical moments [18]:
- KurtosisThe kurtosis of an image is defined by the fouth-order statistical moments [18]:
- (3)
- Texture
- HomogeneityThe homogeneity describes the variance of pixels within a region. It is defined as follows [18]:where z is a random variable representing gray level, is histogram distribution, L is the number of different gray levels.
- SmoothnessThe smoothness of an image is defined by the second-order statistical moments [18]:where m is the average gray value of an image.
- (4)
- InformationThe image entropy is the average number of bits per pixel in the gray level set of the image. The greater the image entropy, the more uniform the gray distribution of the image. The definition of image information entropy is as follows [20,21,22,23,24]:where z is a random variable representing gray level, is histogram distribution, L is the number of different gray levels.
- (5)
- Structural similarityThe structural similarity index measurement(SSIM)is designed to improve on traditional methods such as PSNR and mean squared error(MSE) and is based on the image light, contrast and structure and is defined as [25]:where is the average gray value of target pixels, is the average gray value of the background pixels, is the standard deviation of the target, is the standard deviation of the background. , and are constants.
4. Simulation Results
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, K.; Mao, X. Detectability of infrared small targets. Infrared Phys. Technol. 2010, 53, 208–217. [Google Scholar] [CrossRef]
- Florez-Ospina, J.F.; Benitez, H.D. From local to global analysis of defect detectability in infrared non-destructive testing. Infrared Phys. Technol. 2014, 63, 211–221. [Google Scholar] [CrossRef]
- Hiasa, S.; Birgul, R.; Catbas, F.N. Effect of defect size on subsurface defect detectability and defect depth estimation for concrete structures by infrared thermography. J. Nondestruct. Eval. 2017, 36, 57. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, L.; Huang, S.; Wang, X.; Wang, Y.; Peng, Z. River detection in high-resolution SAR data using the Frangi filter and shearlet features. Remote Sens. Lett. 2019, 10, 949–958. [Google Scholar] [CrossRef]
- Peng, L.; Zhang, T.; Liu, Y.; Li, M.; Peng, Z. Infrared Dim Target Detection using Shearlet’s Kurtosis Maximization Under Non-Uniform Background. Symmetry 2019, 11, 723. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Z.; Zhang, J.; Huang, Y.; Peng, Z.; Wei, Z.; Guo, H. Dim small target detection based on high-order cumulant of motion estimation. Infrared Phys. Technol. 2019, 99, 86–101. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Z.; Zhang, J.; Huang, Y.; Peng, Z. Infrared Dim and Small Targets Detection Method Based on Local Energy Center of Sequential Image. Math. Probl. Eng. 2017, 4572147, 1–16. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L.; Yang, C.; Peng, Z. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-Norm Constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared small target detection via non-convex rank approximation minimization joint l2,1 norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; He, Y. Infrared dim and small target detection based on stable multi-subspace learning in heterogeneou sscene. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5481–5493. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Zhang, P.; He, Y. Infrared small target detection via nonnegativity-constrained variational mode decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1700–1704. [Google Scholar] [CrossRef]
- Wang, X.; Peng, Z.; Kong, D.; Zhang, P.; He, Y. Infrared Dim Target Detection Based on Total Variation Regularization and Principal Component Pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Dong, Y. Simulation of global infrared background based on remote sensing data. Infrared Laser Eng. 2018, 47, 1104004-1–1104004-7. [Google Scholar]
- Wout, V. Simulation of hyper spectral and direction radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar]
- Liu, Z.; Shao, L.; Wang, Y.; Sun, X. Influence on afterburning on infrared radiation of solid rocket exhaust plume. Acta Opt. Sin. 2013, 33, 1–8. [Google Scholar]
- Ruan, L.; Qi, H.; Wang, S.; Yang, C. Numerical simulation of the infrared characteristic of missile exhaust plume. Infrared Laser Eng. 2008, 37, 59–962. [Google Scholar]
- Gonzalez, R.; Wintz, P. Digital Image Processing; Addison Wesley Publishing Company: Boston, MA, USA, 1977; p. 451. [Google Scholar]
- Huber, S.; Hadar, O.; Rotman, S.; Huber, L.; Evstigneev, S. Improving variance estimation ratio score calculation for slow moving point targets detection in infrared imagery sequences. In Proceedings of the Signal and Data Processing of Small Targets, International Society for Optics and Photonics, San Diego, CA, USA, 28–29 August 2013; p. 885707. [Google Scholar]
- Zhang, X.; Chi, J.; Hu, J.; Liu, L.; Xing, Y. Infrared small target detection using modified order morphology and weighted local entropy. In Proceedings of the International Conference on Computer Engineering, Information Science & Application Technology (ICCIA), Beijing, China, 8–11 September 2017; pp. 368–377. [Google Scholar]
- Mello Román, J.C.; Vázquez Noguera, J.L.; Legal-Ayala, H.; Pinto-Roa, D.P.; Gomez-Guerrero, S.; García Torres, M. Entropy and contrast enhancement of infrared thermal images using the multiscale top-hat transform. Entropy 2019, 21, 244. [Google Scholar] [CrossRef]
- Chi, J.; Fu, P.; Wang, D.; Xu, X. A detection method of infrared image small target based on order morphology transformation and image entropy difference. In Proceedings of the International Conference on Machine Learning and Cybernetics (ICMLC), Providence, Guangzhou, China, 18–21 August 2005; pp. 5111–5116. [Google Scholar]
- Deng, H.; Liu, J.; Chen, Z. Infrared small target detection based on modified local entropy and EMD. Chin. Opt. Lett. 2010, 8, 24–28. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]


| Indicator | PSNR | Contrast | SSIM | En | Hom | Smo | Var | Skew | SCR | Kur | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Altitude | |||||||||||
| Including Flame | 10 km | 43.32 | 36.08 | 0.97 | 4.70 | 7.2 × | 0.40 | 210.20 | 5.9 × | 0.55 | 2.7 × |
| 20 km | 40.04 | 38.00 | 0.95 | 4.71 | 7.0 × | 0.41 | 214.60 | 5.9 × | 1.23 | 2.7 × | |
| 30 km | 39.99 | 64.09 | 0.93 | 4.96 | 6.1 × | 0.63 | 330.90 | 1.1 × | 1.91 | 6.1 × | |
| 40 km | 38.39 | 68.41 | 0.91 | 5.06 | 5.4 × | 0.65 | 345.10 | 1.1 × | 2.14 | 6.2 × | |
| 50 km | 37.91 | 94.92 | 0.88 | 5.08 | 5.5 × | 0.71 | 399.80 | 1.4 × | 3.59 | 8.6 × | |
| 60 km | 36.19 | 150.77 | 0.84 | 5.28 | 4.7 × | 0.85 | 602.10 | 3.2 × | 5.54 | 2.8 × | |
| 70 km | 35.63 | 167.29 | 0.83 | 5.33 | 4.4 × | 0.88 | 704.30 | 4.3 × | 6.38 | 4.2 × | |
| 80 km | 34.86 | 239.91 | 0.81 | 5.53 | 3.6 × | 0.93 | 962.40 | 8.1 × | 8.11 | 1.0 × | |
| 90 km | 34.96 | 224.68 | 0.81 | 5.52 | 3.8 × | 0.93 | 900.70 | 7.0 × | 7.61 | 8.4 × | |
| 100 km | 33.01 | 213.19 | 0.77 | 5.66 | 3.1 × | 0.96 | 1.2 × | 1.1 × | 10.21 | 1.4 × | |
| Without Flame | 10 km | 38.11 | 43.95 | 0.93 | 5.56 | 2.6 × | 0.29 | 161.90 | −1.9 × | 1.74 | 1.2 × |
| 20 km | 37.54 | 46.07 | 0.92 | 5.61 | 2.6 × | 0.31 | 171.20 | −1.7 × | 2.46 | 1.3 × | |
| 30 km | 37.80 | 56.53 | 0.90 | 5.63 | 2.6 × | 0.35 | 188.30 | −841.50 | 3.74 | 1.8 × | |
| 40 km | 36.99 | 60.16 | 0.89 | 5.66 | 2.5 × | 0.41 | 211.70 | 290.90 | 4.14 | 2.5 × | |
| 50 km | 36.54 | 87.18 | 0.87 | 5.70 | 2.4 × | 0.56 | 288.60 | 6.7 × | 6.47 | 8.4 × | |
| 60 km | 35.36 | 119.96 | 0.84 | 5.74 | 2.4 × | 0.78 | 476.30 | 2.4 × | 8.15 | 2.7 × | |
| 70 km | 34.91 | 121.29 | 0.83 | 5.79 | 2.3 × | 0.81 | 533.50 | 2.8 × | 8.07 | 3.0 × | |
| 80 km | 34.03 | 140.35 | 0.82 | 5.83 | 2.2 × | 0.85 | 600.80 | 3.4 × | 7.99 | 3.7 × | |
| 90 km | 34.18 | 139.90 | 0.82 | 5.83 | 2.2 × | 0.85 | 597.80 | 3.3 × | 8.15 | 3.6 × | |
| 100 km | 32.53 | 153.77 | 0.79 | 5.75 | 2.4 × | 0.92 | 856.80 | 6.4 × | 11.19 | 7.1 × |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, J.; Li, M.; Peng, Z.; Liu, X. Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame. Entropy 2019, 21, 946. https://doi.org/10.3390/e21100946
Li X, Wang J, Li M, Peng Z, Liu X. Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame. Entropy. 2019; 21(10):946. https://doi.org/10.3390/e21100946
Chicago/Turabian StyleLi, Xia, Jun Wang, Meihui Li, Zhenming Peng, and Xingrun Liu. 2019. "Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame" Entropy 21, no. 10: 946. https://doi.org/10.3390/e21100946
APA StyleLi, X., Wang, J., Li, M., Peng, Z., & Liu, X. (2019). Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame. Entropy, 21(10), 946. https://doi.org/10.3390/e21100946





