On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules
Abstract
1. Introduction
2. Materials and Methods
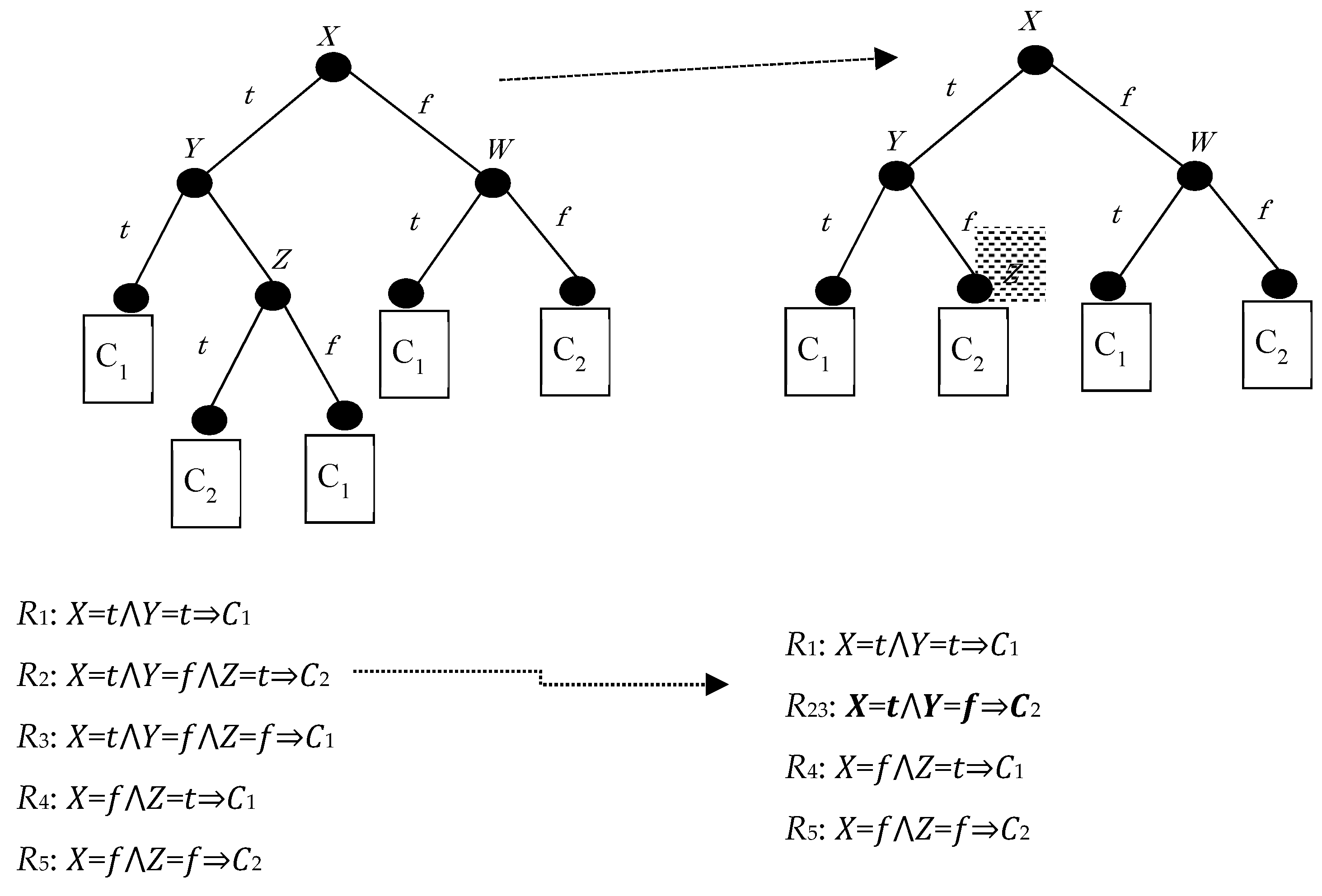
2.1. Adding Instances to Preserve the Class Balance Using Linear Diophantine Equations: A Proof of Concept and an Indicative Example
2.2. Fully Specifying Instances
2.3. Hiding in Parallel: Grouping of Hiding Requests
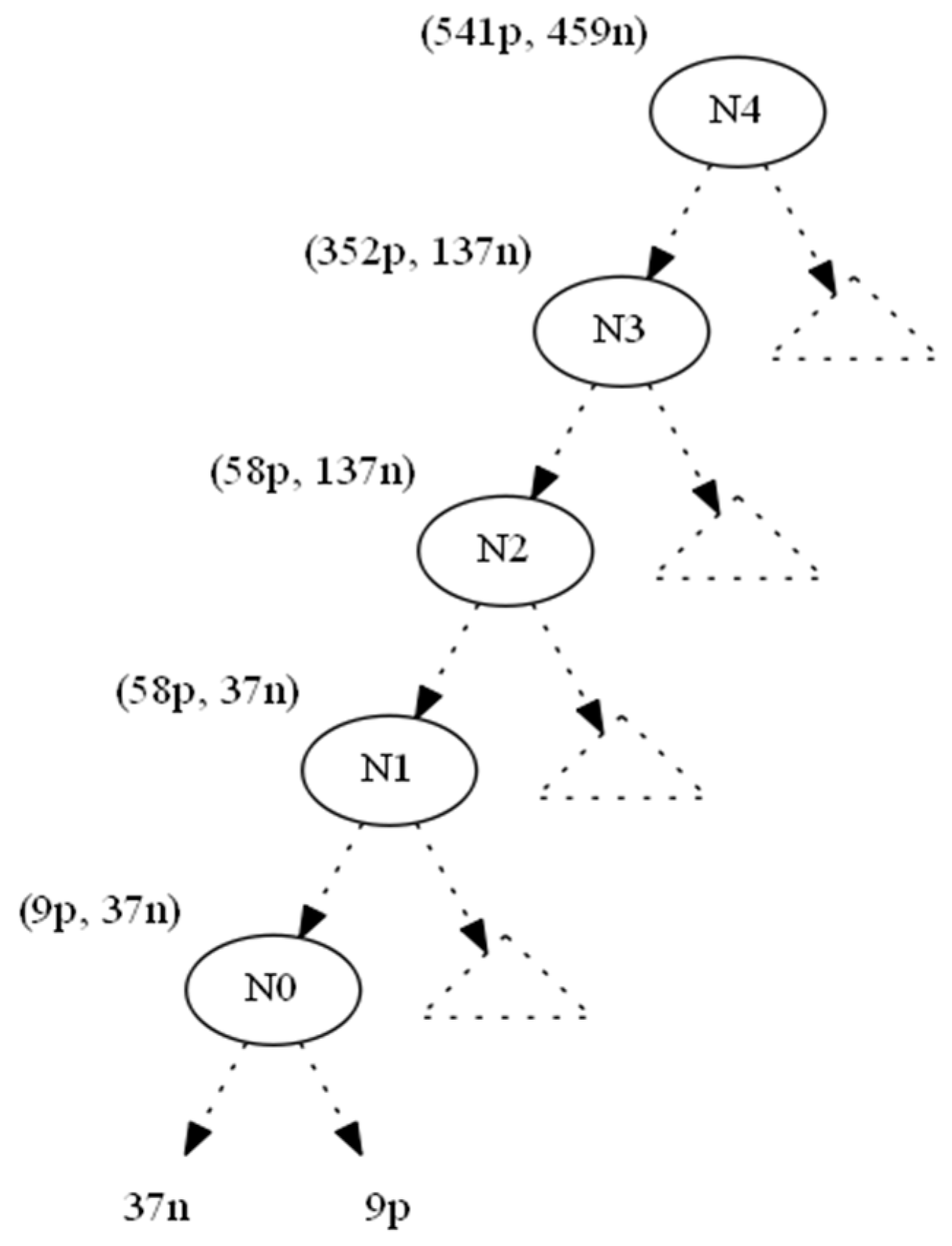
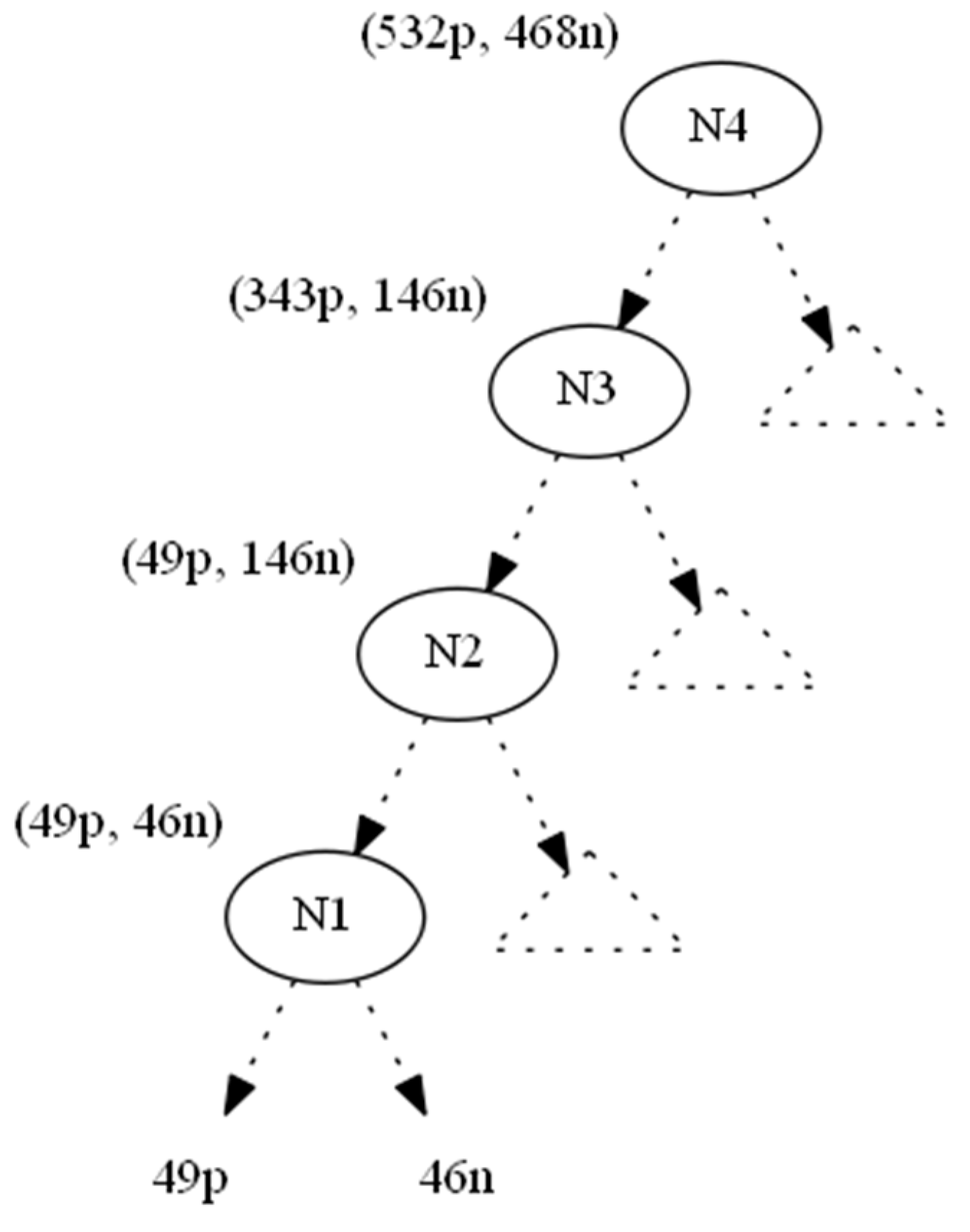
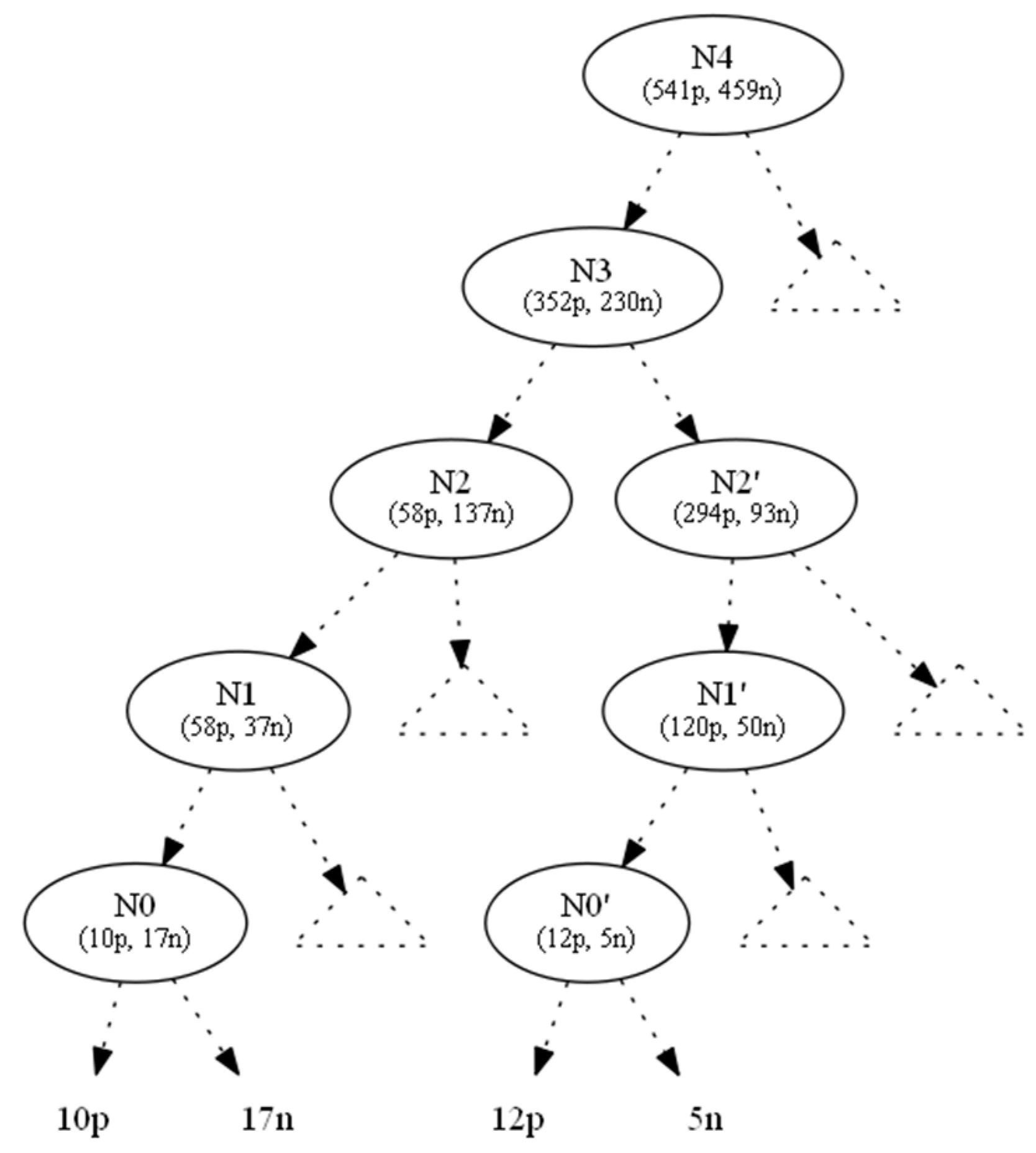
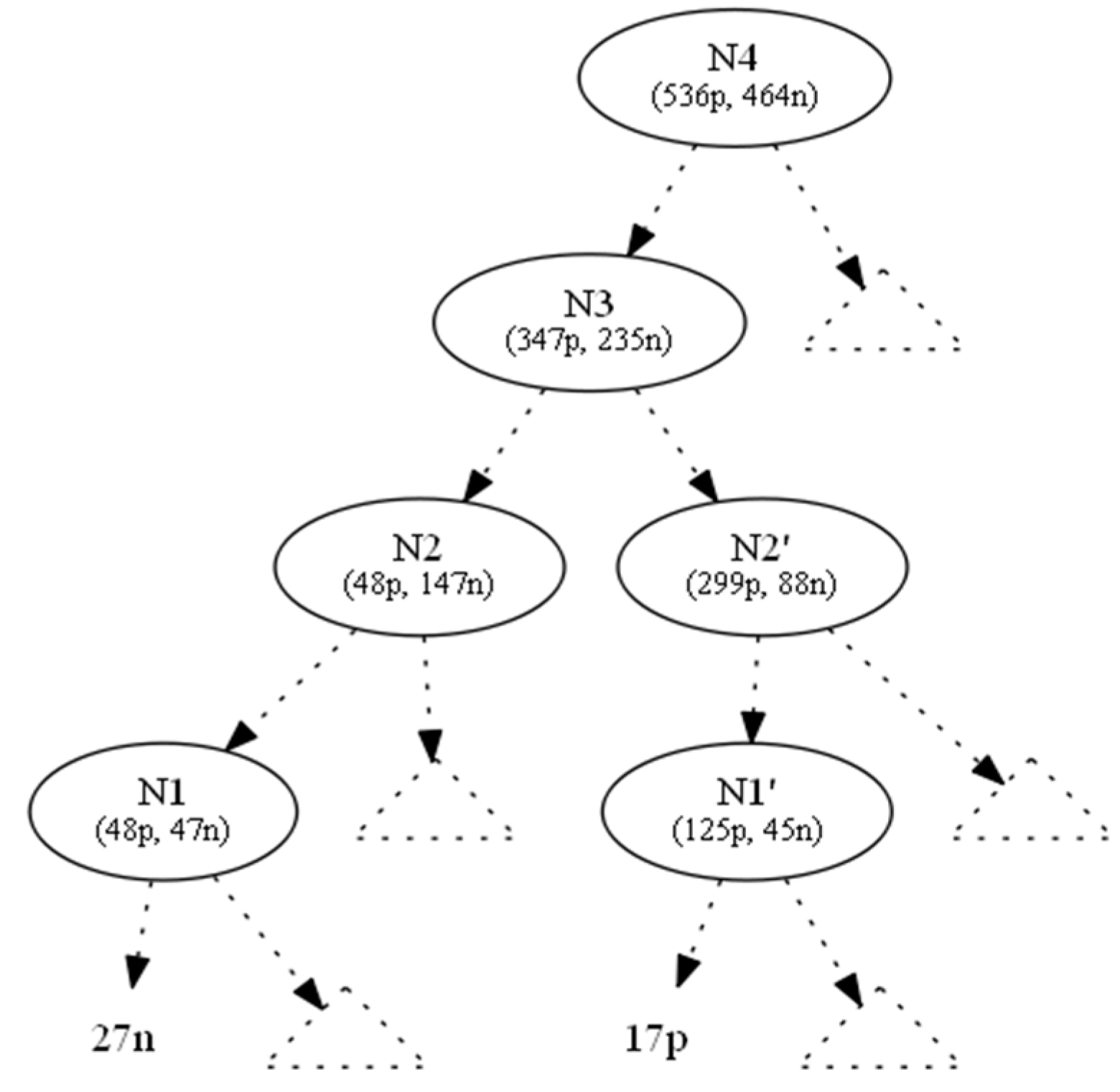
3. Results
4. Brief Discussion and Conclusions
Author Contributions
Conflicts of Interest
Appendix A
| Parallel | Serially |
|---|---|
- Case (I-1):
- Case (I-2):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option , we would have case (II-2).From (*), (**) above, we have Q.E.D.
- Case (I-3):If , then this case is impossible because all terms in the left-hand side in the above equation are positive.If then we have Q.E.D.
- Case (I-4):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option , we would have case (II-4), for which it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (I-5):This case is impossible because all the terms in the left-hand side in the above equation are positive.
- Case (I-6):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (IV-6),From (*), (**) above, we have Q.E.D.
- Case (I-7):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (I-8):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (II-8), for which it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (II-1):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have the case (I-1), and for that it had been proven thatFrom (*), (**) above, we have Q.E.D.
- Case (II-2):
- Case (II-3):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have the case (I-3), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (II-4):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (II-5):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (III-5), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (II-6):This case is impossible because all the terms in the left-hand side in the above equation are positive.
- Case (II-7):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have the case (I-7), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (II-8):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (III-1):This case is impossible because all the terms in the left-hand side in the above equation are positive.
- Case (III-2):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (II-2), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (III-3):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (III-4):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (I-4), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (III-5):
- Case (III-6):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, meaning that If we had selected option we would have the case (IV-6), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (III-7):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (III-8):The reason that we selected option , is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, meaning that If we had selected option we would have case (II-8), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (IV-1):The reason that we selected option , is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, meaning that If we had selected option we would have case (II-1), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (IV-2):This case is impossible because all the terms in the left-hand side in the above equation are positive.
- Case (IV-3):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore,, meaning that If we had selected option we would have case (I-3), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (IV-4):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
- Case (IV-5):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, meaning that If we had selected option we would have case (III-5), and for that it had been proved thatFrom (*), (**) above, we have Q.E.D.
- Case (IV-6):
- Case (IV-7):The reason that we selected option is that is the minimum number of instances to add in order to maintain the ratio in the parent node.Therefore, , meaning that If we had selected option we would have case (I-7), and for that it had been proven thatFrom (*), (**) above, we have Q.E.D.
- Case (IV-8):If then this case is impossible, since the left-hand side in the above equation is positive.If then we have Q.E.D.
Appendix B
process (node X)
begin
if (X.affected != DO_NOTHING) then
// X has been selected for hiding
if X.is-leaf() then
X.parent.affected = MAKE_LEAF
else
// X is an internal node
if (X.parent != null) then
// set X’s parent to be affected
X.parent.affected = ADJUST_RATIO
if (X.affected == MAKE_LEAF) then
// if X is the parent of a leaf
make-leaf (X)
elseif (X.affected == ADJUST_RATIO) then
// if X is a node on the path
adjust-ratio (X)
end-if
end-if
end-if
end-if
end
make-leaf (node X)
begin
// calculate required local changes
// modify local instance population
if (X.parent != null) then
// propagate change to parent
end-if
// turn X into a leaf if you can
if (X.left.is-leaf() && X.right.is-leaf()) then
X.left = null
X.right = null
end-if
end
adjust-ratio (node Y)
begin
// calculate ratio to be preserved
// absorb changes from children
if (Y.parent != null) then
// propagate changes to parent
end-if
// calculate LDE pairs
// select minimum pair to accommodate nodes below
end
References
- Verykios, V.S.; Bertino, E.; Fovino, I.; Provenza, L.; Saygin, Y.; Theodoridis, Y. State-of-the-art in privacy preserving data mining. ACM SIGMOD Rec. 2004, 33, 50–57. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data—SIGMOD’00, Dallas, TX, USA, 16–18 May 2000. [Google Scholar] [CrossRef]
- Gkoulalas-Divanis, A.; Verykios, V.S. Privacy Preserving Data Mining: How Far Can We Go? In Data Mining in Public and Private Sectors:Organizational and Government ApplicationsInformation Science Reference; IGI Global: Hershey, PA, USA, 2010. [Google Scholar] [CrossRef]
- Estivill-Castro, V.; Brankovic, L. Data swapping: Balancing privacy against precision in mining for logic rules. In Proceedings of the First International Conference on Data Warehousing and Knowledge Discovery, Florence, Italy, 30 August–1 September 1999. [Google Scholar]
- Chang, L.; Moskowitz, I. Parsimonious downgrading and decision trees applied to the inference problem. In Proceedings of the 1998 Workshop on New Security Paradigms—NSPW’98, Charlottesville, VA, USA, 22–26 September 1998. [Google Scholar] [CrossRef]
- Natwichai, J.; Li, X.; Orlowska, M. Hiding Classification Rules for Data Sharing with Privacy Preservation. In Proceedings of the 7th International Conference on Data Warehousing and Knowledge Discovery, Copenhagen, Denmark, 22–26 August 2005; pp. 468–477. [Google Scholar]
- Natwichai, J.; Li, X.; Orlowska, M. A Reconstruction-based Algorithm for Classification Rules Hiding. In Proceedings of the 17th Australasian Database Conference, Hobart, Australia, 16–19 January 2006; pp. 49–58. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: Burlington, MA, USA, 1993. [Google Scholar]
- Cohen, W.W. Fast, effective rule induction. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 2–9 July 1995. [Google Scholar] [CrossRef]
- Katsarou, A.; Gkouvalas-Divanis, A.; Verykios, V.S. Reconstruction-based Classification Rule Hiding through Controlled Data Modification. In IFIP International Federation for Information Processing 296; Springer: Boston, MA, USA, 2009; pp. 449–458. [Google Scholar] [CrossRef]
- Natwichai, J.; Sun, X.; Li, X. Data Reduction Approach for Sensitive Associative Classification Rule Hiding. In Proceedings of the 19th Australian Database Conference, Wollongong, Australia, 22–25 January 2008. [Google Scholar]
- Wang, K.; Fung, B.; Yu, P. Template-Based Privacy Preservation in Classification Problems. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005. [Google Scholar] [CrossRef]
- Delis, A.; Verykios, V.; Tsitsonis, A. A data perturbation approach to sensitive classification rule hiding. In Proceedings of the 2010 ACM Symposium on Applied Computing—SAC’10, Sierre, Switzerland, 22–26 March 2010. [Google Scholar] [CrossRef]
- Bost, R.; Popa, R.; Tu, S.; Goldwasser, S. Machine Learning Classification over Encrypted Data. In Proceedings of the 2015 Network and Distributed System Security Symposium, San Diego, CA, USA, 8–11 February 2015. [Google Scholar] [CrossRef]
- Tai, R.; Ma, J.; Zhao, Y.; Chow, S. Privacy-Preserving Decision Trees Evaluation via Linear Functions. In Proceedings of the Computer Security—ESORICS 2017, Oslo, Norway, 11–15 September 2017; pp. 494–512. [Google Scholar] [CrossRef]
- Kalles, D.; Verykios, V.S.; Feretzakis, G.; Papagelis, A. Data set operations to hide decision tree rules. In Proceedings of the Twenty-second European Conference on Artificial Intelligence, The Hague, The Netherlands, 29 August–2 September 2016. [Google Scholar] [CrossRef]
- Kalles, D.; Verykios, V.; Feretzakis, G.; Papagelis, A. Data set operations to hide decision tree rules. In Proceedings of the 1st International Workshop on AI for Privacy and Security—Praise’16, The Hague, The Netherlands, 29–30 August 2016. [Google Scholar] [CrossRef]
- Li, R.; de Vries, D.; Roddick, J. Bands of Privacy Preserving Objectives: Classification of PPDM Strategies. In Proceedings of the 9th Australasian Data Mining Conference, Ballarat, Australia, 1–2 December 2011; pp. 137–151. [Google Scholar]
- Kalles, D.; Morris, T. Efficient incremental induction of decision trees. Mach. Learn. 1996, 24, 231–242. [Google Scholar] [CrossRef]
- Kalles, D.; Papagelis, A. Stable decision trees: Using local anarchy for efficient incremental learning. Int. J. Artif. Intell. Tools 2000, 9, 79–95. [Google Scholar] [CrossRef]
- Kalles, D.; Papagelis, A. Lossless fitness inheritance in genetic algorithms for decision trees. Soft Comput. 2009, 14, 973–993. [Google Scholar] [CrossRef]
- Feretzakis, G. Full Look Ahead Calculator for “On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules”. Available online: www.learningalgorithm.eu (accessed on 1 January 2019).
- Zantema, H.; Bodlaender, H.L. Finding Small Equivalent Decision Trees is Hard. Int. J. Found. Comput. Sci. 2000, 11, 343–354. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feretzakis, G.; Kalles, D.; Verykios, V.S. On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules. Entropy 2019, 21, 66. https://doi.org/10.3390/e21010066
Feretzakis G, Kalles D, Verykios VS. On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules. Entropy. 2019; 21(1):66. https://doi.org/10.3390/e21010066
Chicago/Turabian StyleFeretzakis, Georgios, Dimitris Kalles, and Vassilios S. Verykios. 2019. "On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules" Entropy 21, no. 1: 66. https://doi.org/10.3390/e21010066
APA StyleFeretzakis, G., Kalles, D., & Verykios, V. S. (2019). On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules. Entropy, 21(1), 66. https://doi.org/10.3390/e21010066







