Analog Circuit Fault Diagnosis via Joint Cross-Wavelet Singular Entropy and Parametric t-SNE
Abstract
1. Introduction
2. Related Works
3. Feature Extraction
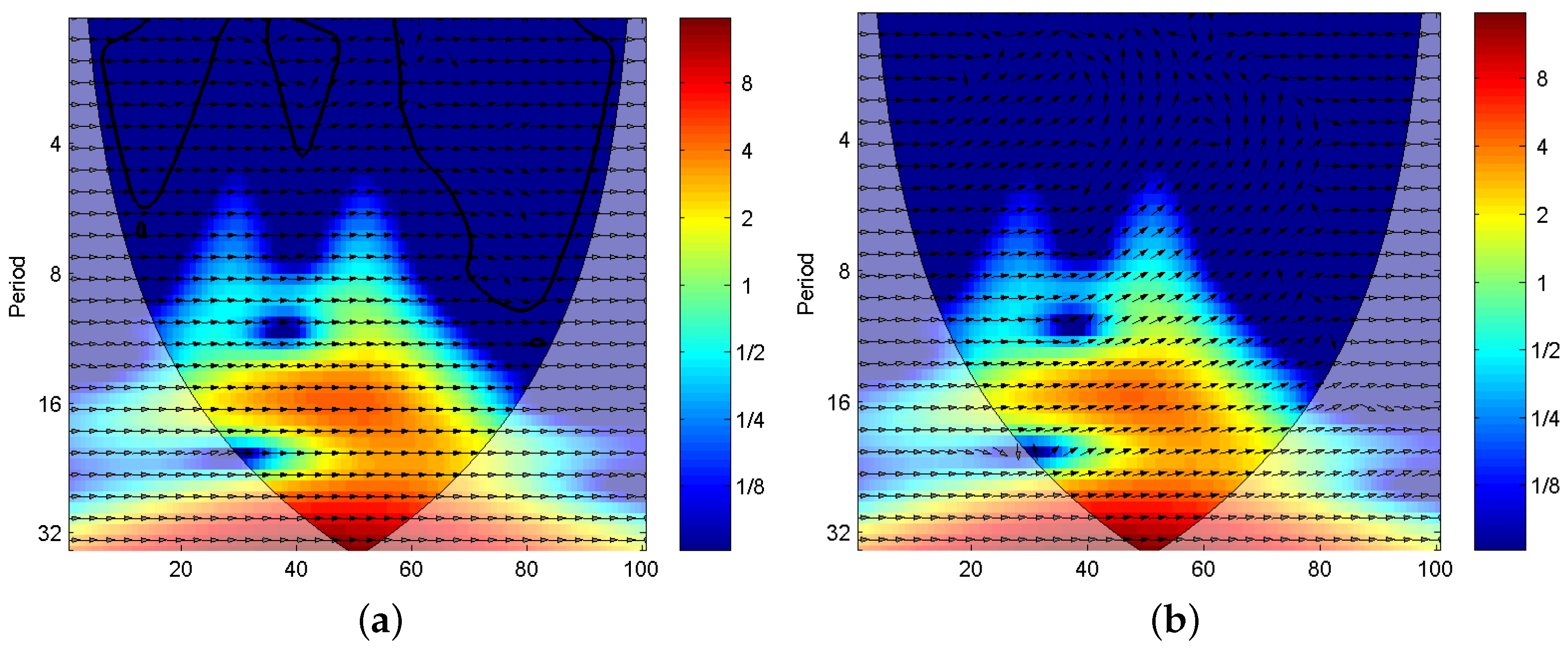
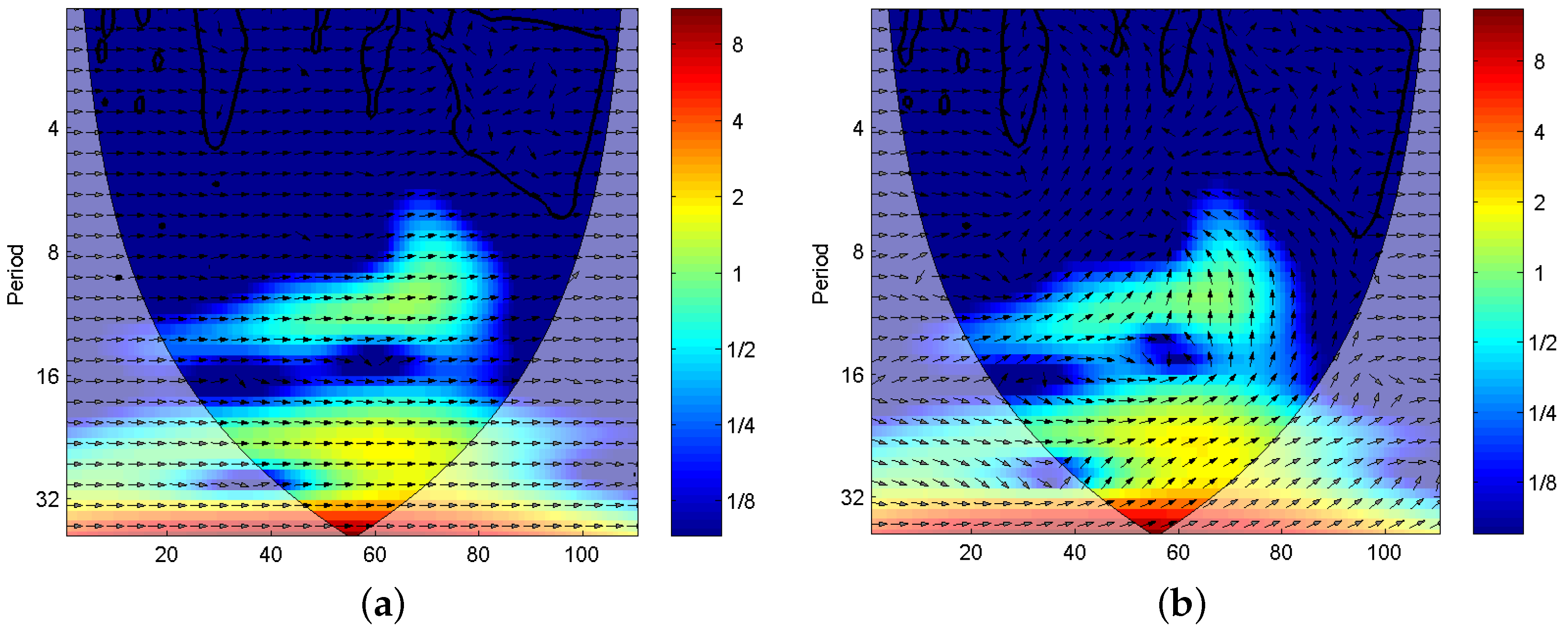
3.1. Cross Wavelet Transform
3.2. Singular Value Decomposition (SVD)
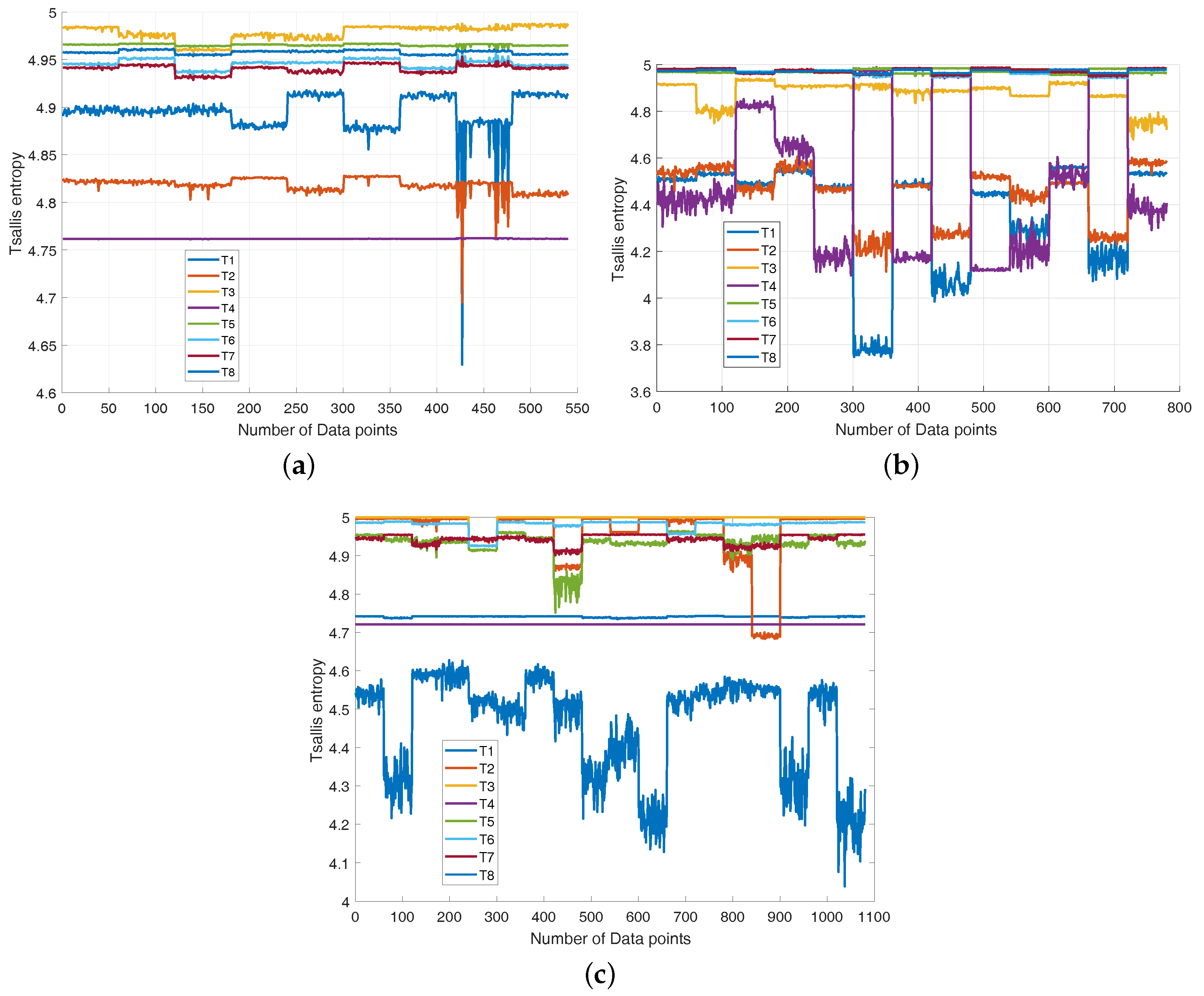
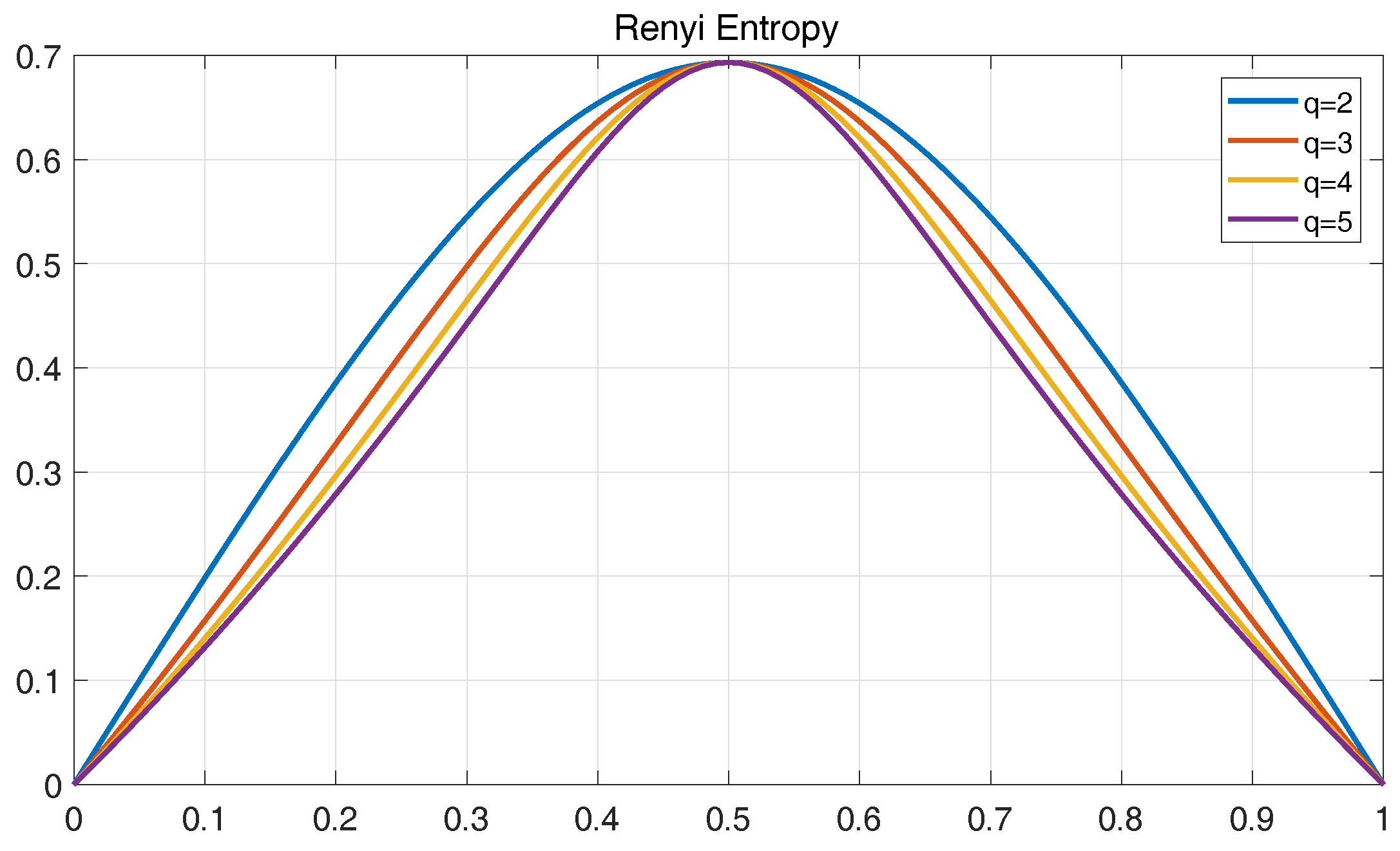
3.3. Tsallis Entropy
3.4. Definition of XWSE
- Second, the matrix A is divided into eight blocks with the same size as follows:
- Third, decompose the block with SVD, and a singular-value sequence for each block can be obtained as where r is the rank of the diagonal matrix .
- Finally, the XWSE of the block is defined bywhere the probability associated with is defined as . Thus, the XWSE features of fault signal can be expressed as
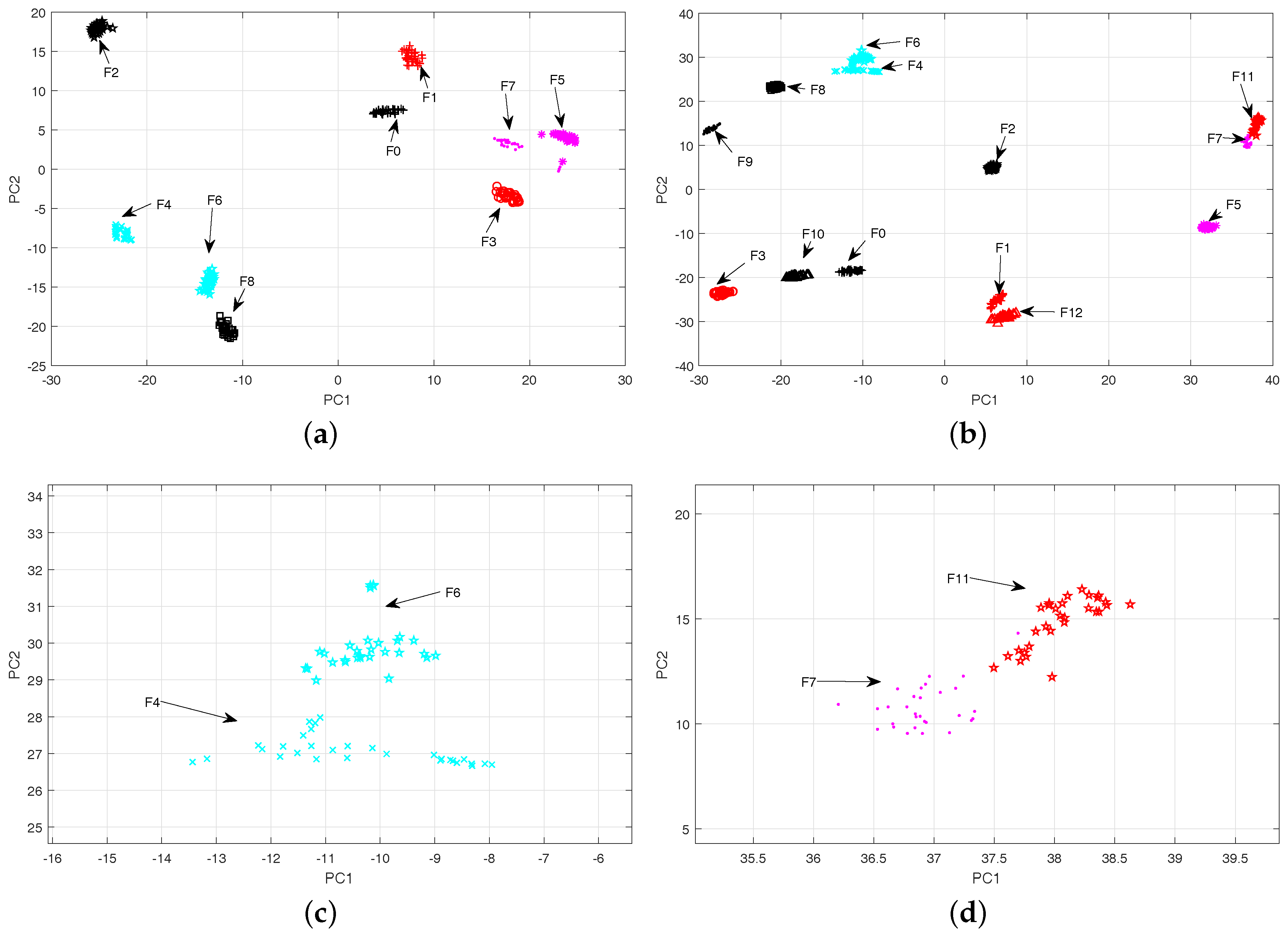
3.5. Parametric t-Stochastic Neighbor Embedding (Parametric t-SNE)
4. SVM and QPSO
4.1. Support Vector Machine (SVM)
4.2. Quantum-Behaved Particle Swarm Optimization (QPSO)
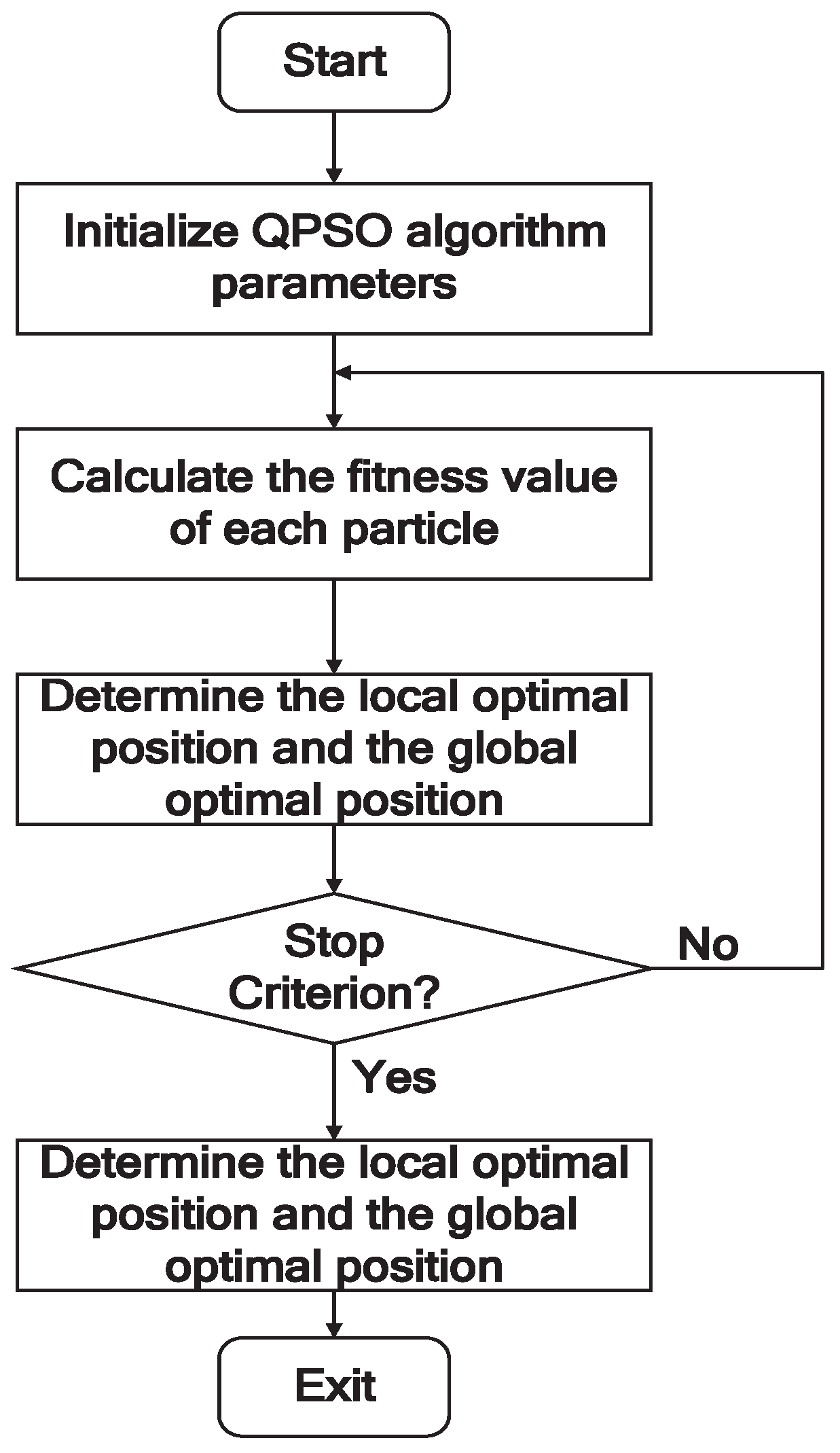
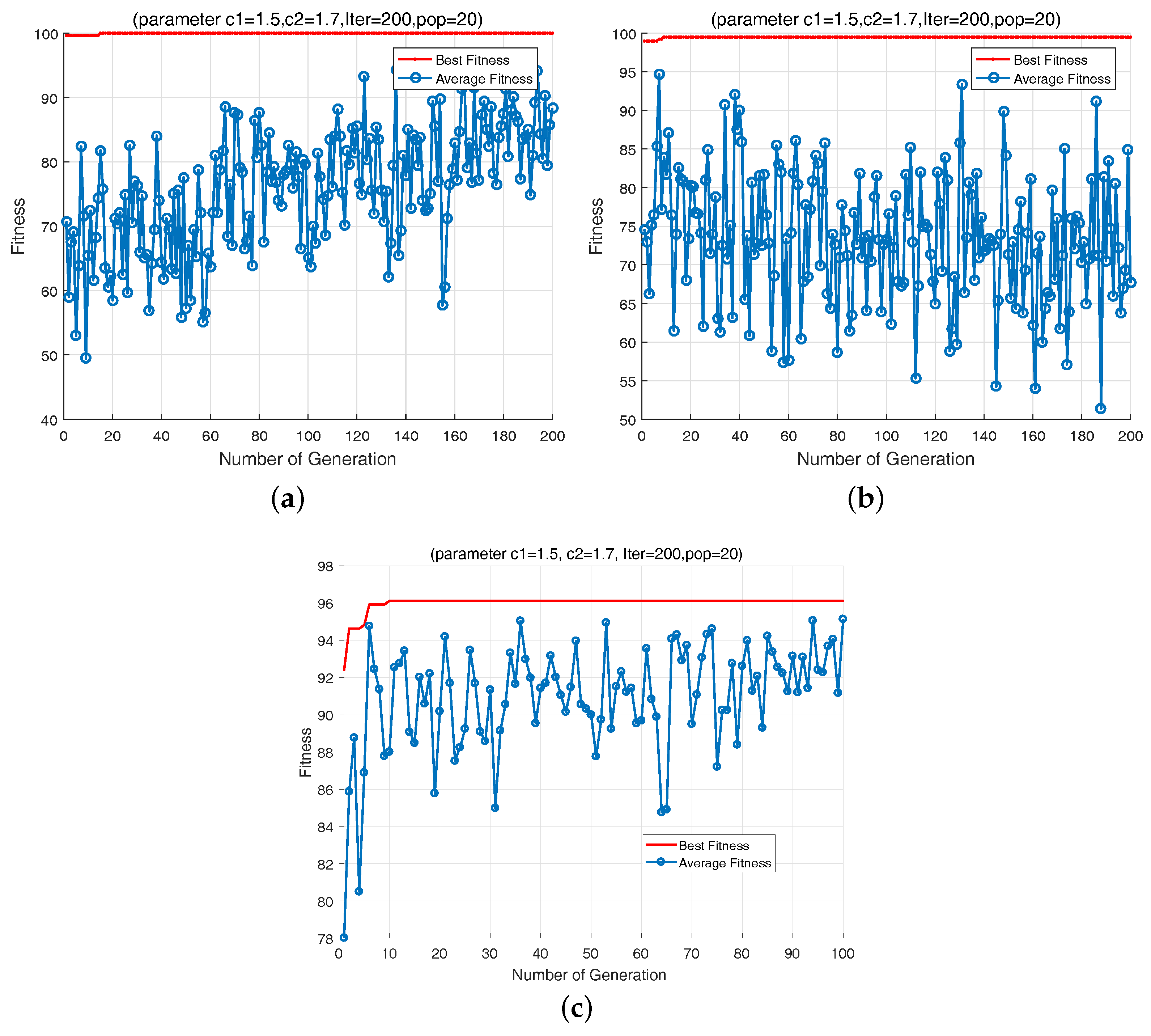
4.3. The Procedure of Parameters Optimization
5. Experimental Results and Analysis
5.1. Example Circuits
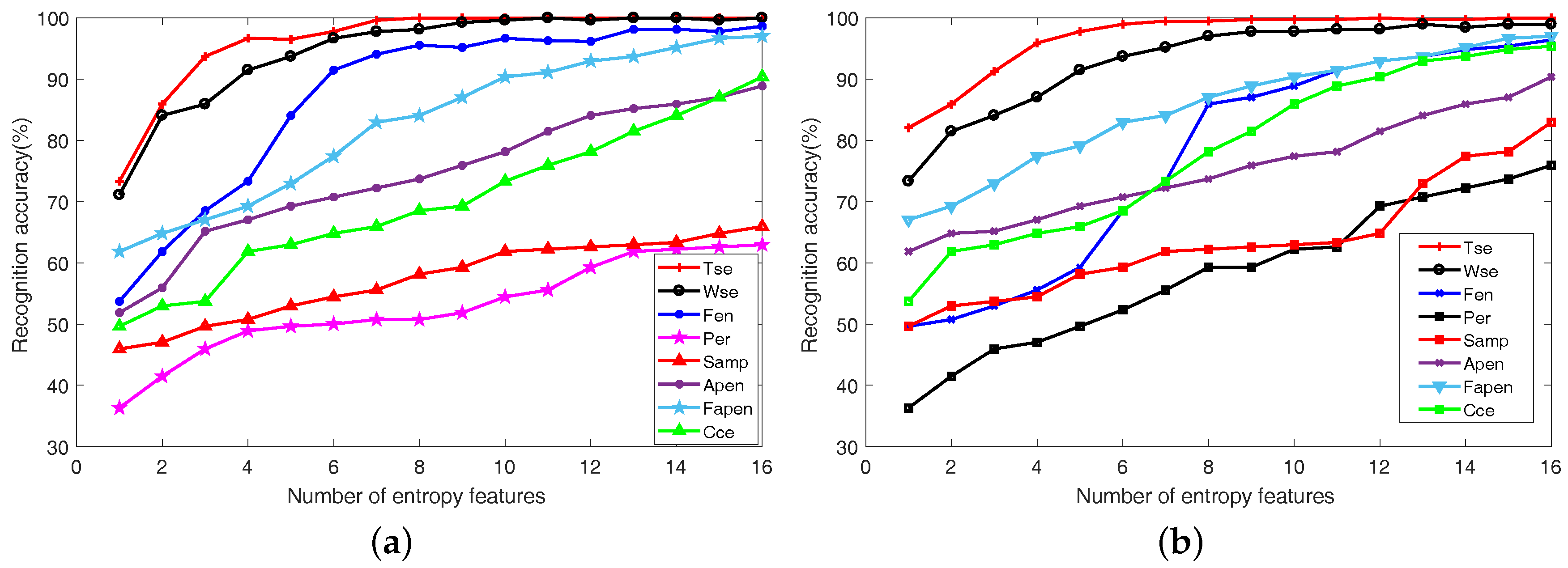
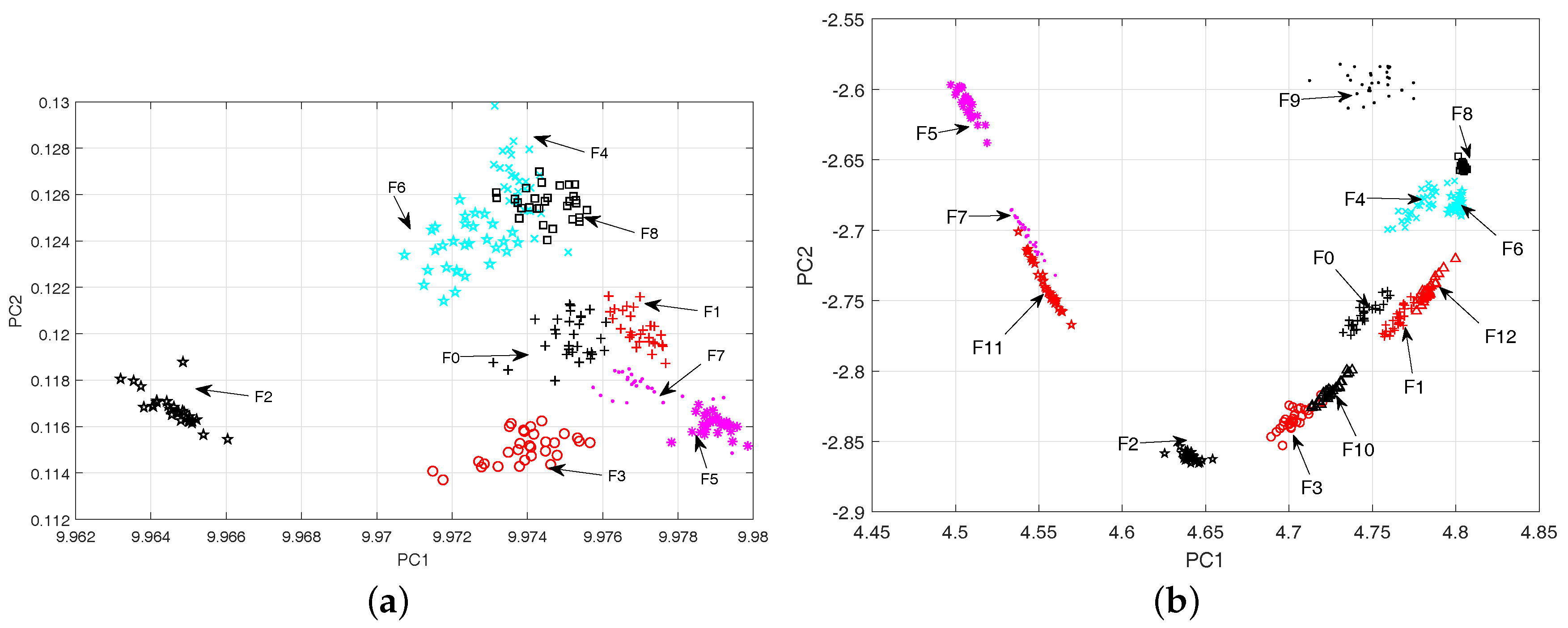
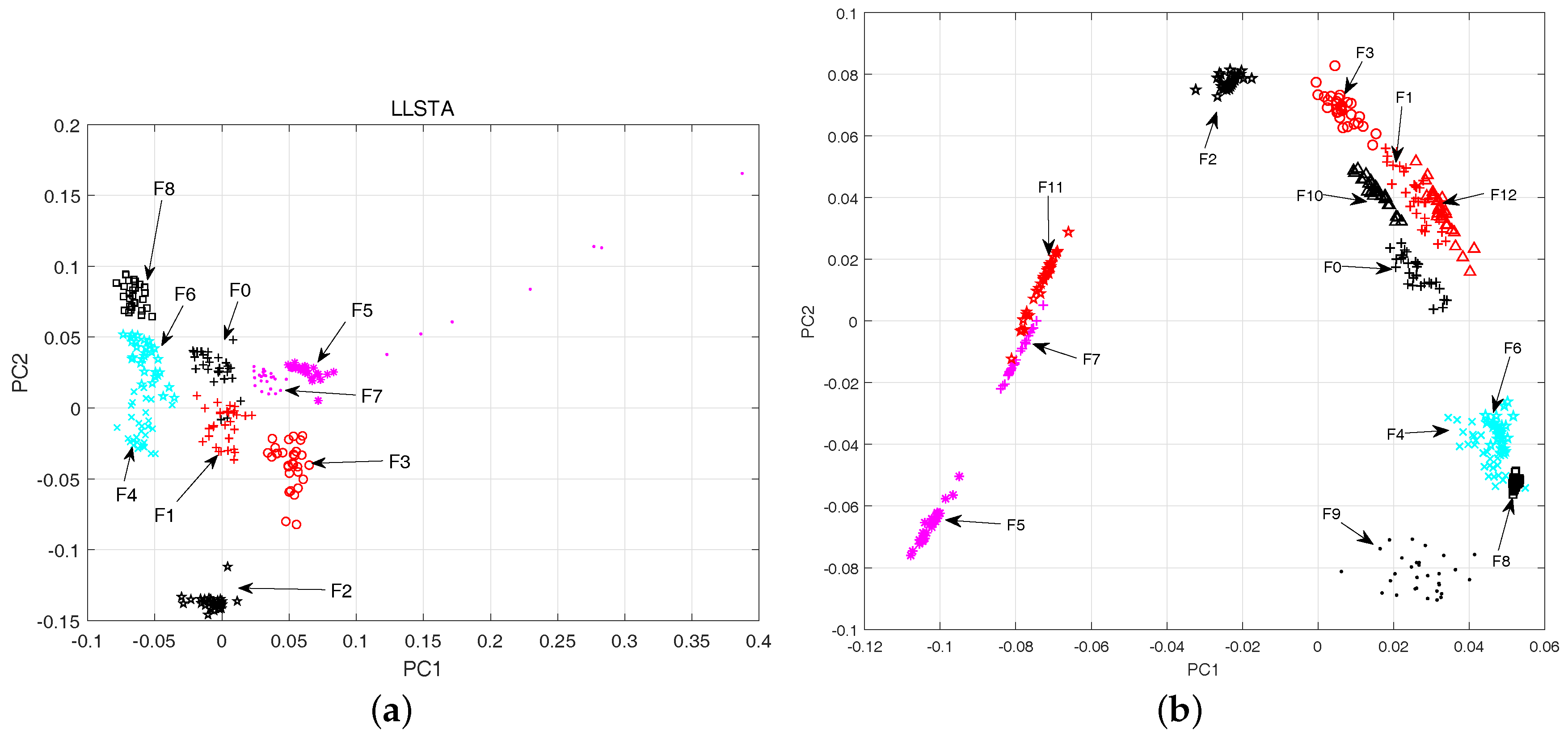
5.2. The Results Analysis of Feature Extraction
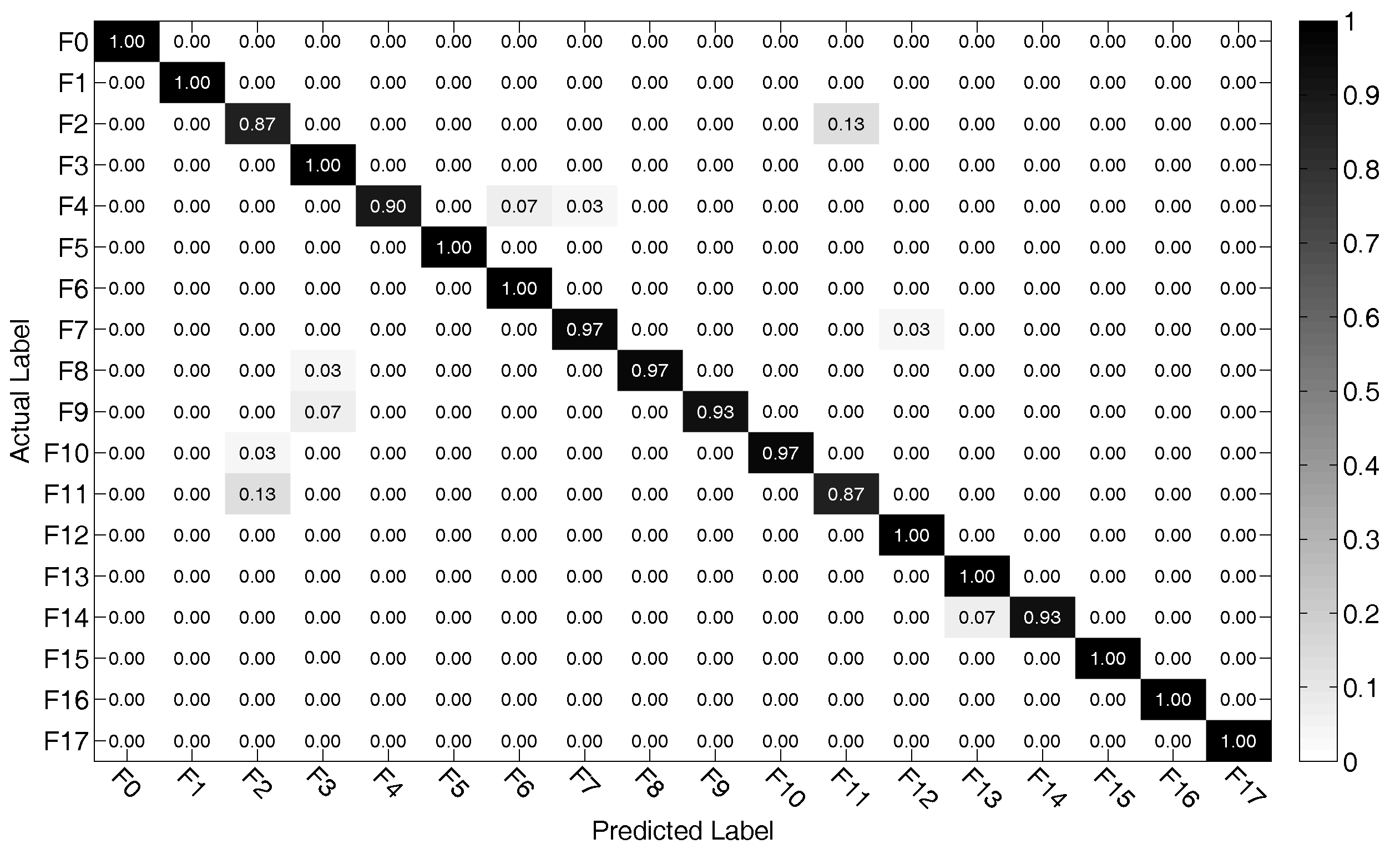
5.3. Classification Result by Using QPSO-SVM Model
6. Discussion
7. Conclusions
- Via making full use of the time-frequency distribution characteristics and entropy description, the XWSE method has a better ability to effectively extract essential features of the analyzed fault signals, and the experimental results lead us to believe that the proposed algorithm offers great potential in revealing the difference between different fault classes.
- For the sake of eliminating useless information, the parametric t-SNE is implemented to provide a nonlinear projection from the input space to the reduced space for enhancing the feature separation degree of the fault classes. The comparisons with other dimensionality reduction methods have demonstrated its feasibility and effectiveness.
- Moreover, this work also proposes a promising means for the optimization of SVM classifier by using QPSO, which is an bionic heuristic algorithm that shows faster and better convergence rate than other methods. Simulation tests have been conducted to validate that the presented QPSO-SVM model can achieve a desirable classification performance in linear circuits as well as nonlinear circuits.
Author Contributions
Funding
Conflicts of Interest
References
- Aminian, F.; Member, S.; Aminian, M.; Collins, H.W. Analog Fault Diagnosis of Actual Circuits Using Neural Networks. IEEE Trans. Instrum. Meas. 2002, 51, 544–550. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, T.; Han, J.; Bu, S.; Tang, X.; Pecht, M. Signal Model-based Fault Coding for Diagnostics and Prognostics of Analog Electronic Circuits. IEEE Trans. Ind. Electron. 2016, 46, 605–614. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, A.P. Fuzzy classifier for fault diagnosis in analog electronic circuits. ISA Trans. 2013, 52, 816–824. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Feng, L. A novel linear ridgelet network approach for analog fault diagnosis using wavelet-based fractal analysis and kernel PCA as preprocessors. Measurement 2012, 45, 297–310. [Google Scholar] [CrossRef]
- Liu, Z.; Jia, Z.; Vong, C.M.; Member, S.; Bu, S. Capturing High-Discriminative Fault Features for Electronics-Rich Analog System via Deep Learning. IEEE Trans. Ind. Inf. 2017, 13, 1213–1226. [Google Scholar] [CrossRef]
- Binu, D.; Kariyappa, B. A survey on fault diagnosis of analog circuits: Taxonomy and state of the art. AEU Int. J. Electron. Commun. 2017, 73, 68–83. [Google Scholar] [CrossRef]
- Catelani, M.; Fort, A. Soft fault detection and isolation in analog circuits: Some results and a comparison between a fuzzy approach and radial basis function networks. IEEE Trans. Instrum. Meas. 2002, 51, 196–202. [Google Scholar] [CrossRef]
- Tian, S.; Yang, C.; Chen, F.; Liu, Z. Circle Equation-Based Fault Modeling Method for Linear Analog Circuits. IEEE Trans. Instrum. Meas. 2014, 63, 2145–2159. [Google Scholar] [CrossRef]
- Yuan, L.; He, Y.; Huang, J.; Sun, Y. A new neural-network-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor. IEEE Trans. Instrum. Meas. 2010, 59, 586–595. [Google Scholar] [CrossRef]
- Vasan, A.S.S.; Long, B.; Pecht, M. Diagnostics and Prognostics Method for Analog Electronic Circuits. IEEE Trans. Ind. Electron. 2013, 60, 5277–5291. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Zhao, Z.; Wang, R. A Novel Method for Multi-Fault Feature Extraction of a Gearbox under Strong Background Noise. Entropy 2018, 20, 10. [Google Scholar] [CrossRef]
- Cui, Y.; Shi, J.; Wang, Z. Analog circuits fault diagnosis using multi-valued Fisher’ s fuzzy decision tree (MFFDT). Int. J. Circuit Theory Appl. 2016, 44, 240–260. [Google Scholar] [CrossRef]
- Kumar, S.; Chow, T.W.S.; Pecht, M. Approach to Fault Identification for Electronic Products Using Mahalanobis Distance. IEEE Trans. Instrum. Meas. 2010, 59, 2055–2064. [Google Scholar] [CrossRef]
- Kang, H.J.; Van, M. Bearing-fault diagnosis using non-local means algorithm and empirical mode decomposition-based feature extraction and two-stage feature selection. IET Sci. Meas. Technol. 2015, 9, 671–680. [Google Scholar]
- Roh, J.; Abraham, J.A. Subband filtering for time and frequency analysis of mixed-signal circuit testing. IEEE Trans. Instrum. Meas. 2004, 53, 602–611. [Google Scholar] [CrossRef]
- Dey, D.; Chatterjee, B.; Chakravorti, S.; Munshi, S. Cross-wavelet transform as a new paradigm for feature extraction from noisy partial discharge pulses. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 157–166. [Google Scholar] [CrossRef]
- Banerjee, S.; Member, S.; Mitra, M. Application of Cross Wavelet Transform for ECG Pattern Analysis and Classification. IEEE Trans. Instrum. Meas. 2014, 63, 326–333. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J. Multi-Level Wavelet Shannon Entropy-Based Method for Single-Sensor Fault Location. Entropy 2015, 17, 7101–7117. [Google Scholar] [CrossRef]
- Widodo, A.; Shim, M.C.; Caesarendra, W.; Yang, B.S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Zhang, Z.; Duan, Z.; Long, Y.; Yuan, L. A new swarm-SVM-based fault diagnosis approach for switched current circuit by using kurtosis and entropy as a preprocessor. Analog Integr. Circuits Signal Process. 2014, 81, 289–297. [Google Scholar] [CrossRef]
- Han, M.; Pan, J. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Zhao, H.; Huang, W. Hierarchical fuzzy entropy and improved support vector machine based binary tree approach for rolling bearing fault diagnosis. Mech. Mach. Theory 2016, 98, 114–132. [Google Scholar] [CrossRef]
- Li, X.; Xie, Y. Analog circuits fault detection using cross-entropy approach. J. Electron. Test. Theory Appl. 2013, 29, 115–120. [Google Scholar] [CrossRef]
- Xie, X.; Li, X.; Bi, D.; Zhou, Q.; Xie, S.; Xie, Y. Analog Circuits Soft Fault Diagnosis Using Rényi’s Entropy. J. Electron. Test. 2015, 31, 217–224. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using continuous wavelet transform. Appl. Soft Comput. J. 2011, 11, 2300–2312. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Optimal Multi-Level Thresholding Based on Maximum Tsallis Entropy via an Artificial Bee Colony Approach. Entropy 2011, 13, 841–859. [Google Scholar] [CrossRef]
- Dong, S.; Tang, B.; Chen, R. Bearing running state recognition based on non-extensive wavelet feature scale entropy and support vector machine. Measurement 2013, 46, 4189–4199. [Google Scholar] [CrossRef]
- Maaten, L.V.D. Learning a Parametric Embedding by Preserving Local Structure. J. Mach. Learn. Res. 2009, 5, 384–391. [Google Scholar]
- Boser, E.; Vapnik, N.; Guyon, I.M.; Laboratories, T.B. A Training Algorithm Margin for Optimal Classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Saitta, L. Support-Vector Networks. Mach. Learn. 1995, 297, 273–297. [Google Scholar]
- Soliman, M.M.; Hassanien, A.E.; Onsi, H.M. An adaptive watermarking approach based on weighted quantum particle swarm optimization. Neural Comput. Appl. 2016, 27, 469–481. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S.; Grinsted, A.; Moore, J.C.; Application, S.J. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Coco, G.; Ranasinghe, R.; Turner, I.L. A cross-wavelet study of alongshore nonuniform nearshore sandbar behavior. In Proceedings of the 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 16–21 July 2006; pp. 4310–4317. [Google Scholar]
- Series, H.; Algebra, L. Singular Value Decomposition and Least Squares Solutions. Numer. Math. 1970, 14, 403–420. [Google Scholar]
- Physics, S.; November, R. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Pan, M.; Jiang, J.; Kong, Q.; Shi, J.; Sheng, Q.; Zhou, T. Radar HRRP Target Recognition Based on t-SNE Segmentation and Discriminant Deep Belief Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1609–1613. [Google Scholar] [CrossRef]
- Li, M.; Luo, X.; Yang, J. Extracting the nonlinear features of motor imagery EEG using parametric t-SNE. Neurocomputing 2016, 218, 371–381. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium on International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Sun, J. Quantum-Behaved Particle Swarm Optimization: Analysis of Individual Particle Behavior and Parameter Selection. Evol. Comput. 2012, 20, 349–393. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.Y.; Wang, L.; Yan, R.Q. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Decomposition and Multi-Scale Permutation Entropy. Entropy 2015, 17, 6447–6461. [Google Scholar] [CrossRef]
- Pang, Q.; Liu, X.; Sun, B.; Ling, Q. Approximate Entropy Based Fault Localization and Fault Type Recognition for Non-solidly Earthed Network. Meas. Sci. Rev. 2012, 12, 309–313. [Google Scholar] [CrossRef]
- Su, Z.; Tang, B.; Liu, Z.; Qin, Y. Multi-fault diagnosis for rotating machinery based on orthogonal supervised linear local tangent space alignment and least square support vector machine. Neurocomputing 2015, 157, 208–222. [Google Scholar] [CrossRef]
- Tang, G.; Wang, X.; He, Y. A Novel Method of Fault Diagnosis for Rolling Bearing Based on Dual Tree Complex Wavelet Packet Transform and Improved Multiscale Permutation Entropy. Math. Probl. Eng. 2016, 2016, 5432648. [Google Scholar] [CrossRef]
- Song, P.; He, Y.; Cui, W. Statistical property feature extraction based on FRFT for fault diagnosis of analog circuits. Analog Integr. Circuits Signal Process. 2016, 87, 427–436. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, L.; He, Y.; Luo, S. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis. Neurocomputing 2016, 211, 202–211. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Zabkowski, T.; Orlowski, A. Comparison of decision trees with Rényi and Tsallis entropy applied for imbalanced churn dataset. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems, Lodz, Poland, 13–16 September 2015; pp. 39–44. [Google Scholar]
- Chen, J.; Dou, Y.; Wang, Z.; Li, G. A novel method for PD feature extraction of power cable with Rényi entropy. Entropy 2015, 17, 7698–7712. [Google Scholar] [CrossRef]
- Johal, R.S.; Tirnakli, U. Tsallis versus Rényi entropic form for systems with q-exponential behaviour: The case of dissipative map. Phys. A Stat. Mech. Appl. 2004, 331, 487–496. [Google Scholar] [CrossRef]
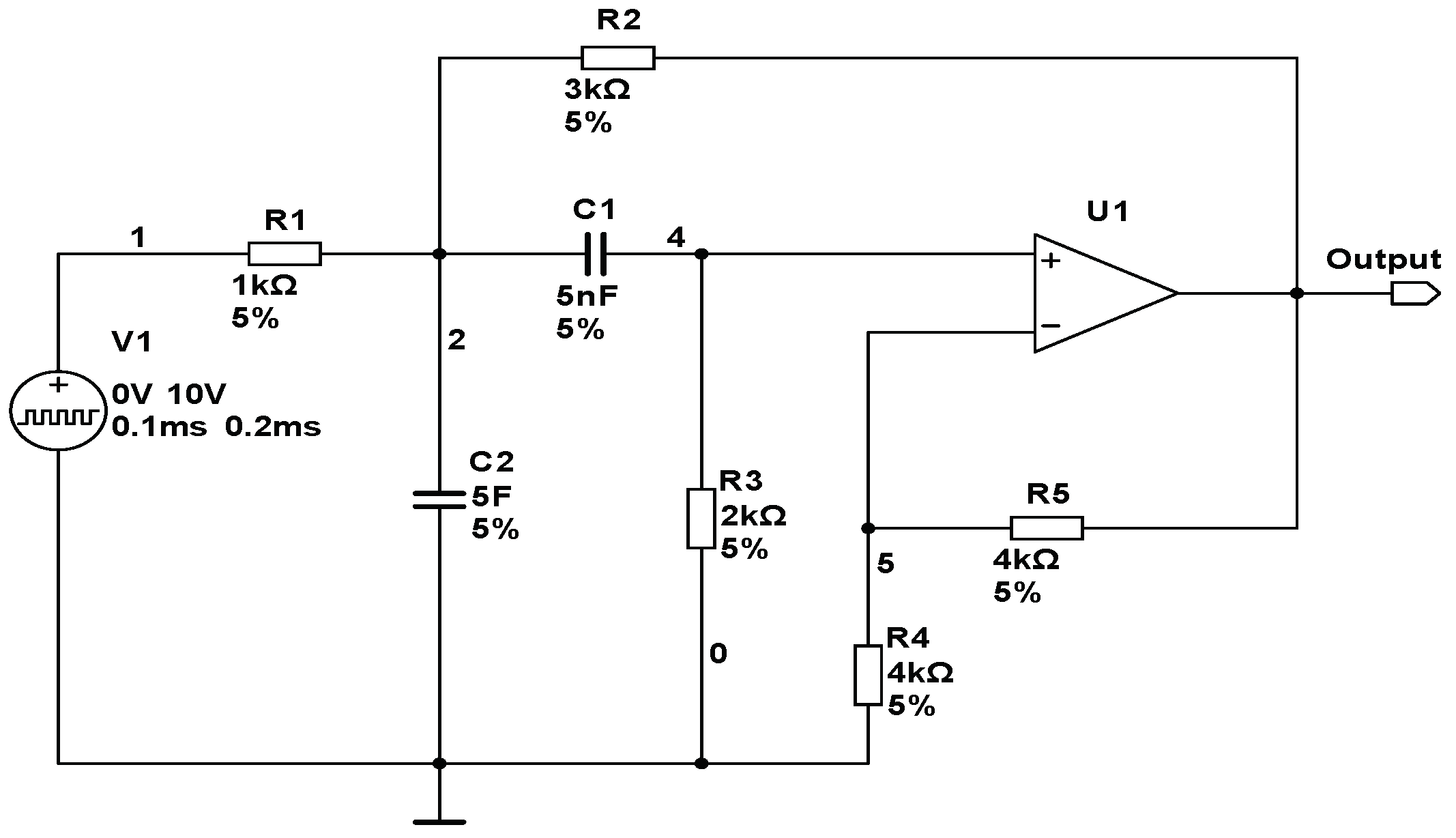

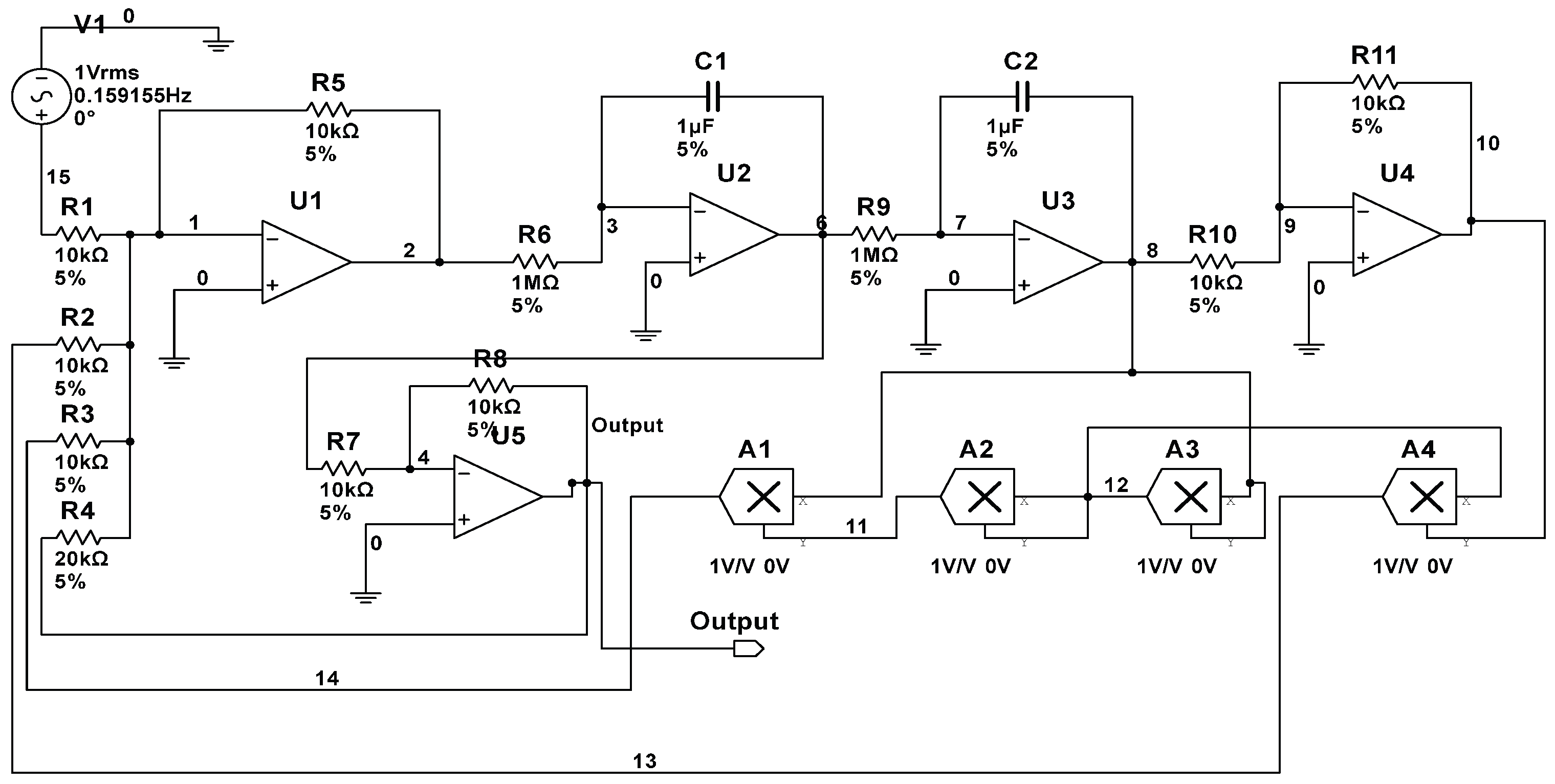

| Fault Code | Fault Class | Nominal Value | Faulty Value |
|---|---|---|---|
| F0 | NF | - | - |
| F1 | R2↓ | 3 kΩ | 2.2 kΩ |
| F2 | R2↑ | 3 kΩ | 3.6 kΩ |
| F3 | R3↓ | 2 kΩ | 1.6 kΩ |
| F4 | R3↑ | 2 kΩ | 2.4 kΩ |
| F5 | C1↓ | 5 nF | 4 nF |
| F6 | C1↑ | 5 nF | 6.5 nF |
| F7 | C2↓ | 5 nF | 4 nF |
| F8 | C2↑ | 5 nF | 6.5 nF |
| Fault Code | Fault Class | Nominal Value | Faulty Value |
|---|---|---|---|
| F0 | NF | - | - |
| F1 | R1↓ | 6.2 kΩ | 3 kΩ |
| F2 | R1↑ | 6.2 kΩ | 15 kΩ |
| F3 | R2↓ | 6.2 kΩ | 2 kΩ |
| F4 | R2↑ | 6.2 kΩ | 18 kΩ |
| F5 | R3↓ | 6.2 kΩ | 2.7 kΩ |
| F6 | R3↑ | 6.2 kΩ | 12 kΩ |
| F7 | R4↓ | 6.2 kΩ | 0.5 kΩ |
| F8 | R4↑ | 6.2 kΩ | 2.5 kΩ |
| F9 | C1↓ | 5 nF | 2.5 nF |
| F10 | C1↑ | 5 nF | 10 nF |
| F11 | C2↓ | 5 nF | 1.5 nF |
| F12 | C2↑ | 5 nF | 15 nF |
| Fault Code | Fault Class | Fault Value |
|---|---|---|
| F0 | - | - |
| F1 | R1↓ | 7 kΩ |
| F2 | R1↑ | 13 kΩ |
| F3 | R2↓ | 7 kΩ |
| F4 | R2↑ | 13 kΩ |
| F5 | R3↓ | 7 kΩ |
| F6 | R3↑ | 13 kΩ |
| F7 | R4↓ | 14 kΩ |
| F8 | R4↑ | 26 kΩ |
| F9 | R8↓ | 7 kΩ |
| F10 | R9↓ | 0.7 MΩ |
| F11 | R10↑ | 13 kΩ |
| F12 | C1↓ | 0.7 µF |
| F13 | C2↑ | 1.3 µF |
| F14 | R1↑R2↑ | (13 kΩ) (13 kΩ) |
| F15 | R1↓R3↓ | (7 kΩ) (7 kΩ) |
| F16 | R5↑C1↑ | (7 kΩ) (1.3 µF) |
| F17 | R6↓C2↓ | (0.7 MΩ) (0.7 µF) |
| Works | Approach | Accuracy (%) | |
|---|---|---|---|
| CUT 1 | CUT 2 | ||
| Aminian et al. [1] | WT + PCA + NN | 97 | 95 |
| Xiao et al. [4] | FrWT + KPCA + Ridgelet−NN | 100 | 98.52 |
| Yuan et al. [9] | Entropy + Kurtosis + NN | 100 | 99 |
| Vasan et al. [10] | WT + entropy, Kurtosis + SVM | 99.70 | 95.69 |
| Song et al. [46] | FrFT statistical feature + SVM | 98.41 | 95.12 |
| Chen et al. [47] | WPT + DCQGA−SVM | 97.41 | 98.72 |
| Proposed | XWSE + Pt−SNE + QPSO-SVM | 99.26 | 99.74 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; He, Y.; Li, B.; Zhang, C. Analog Circuit Fault Diagnosis via Joint Cross-Wavelet Singular Entropy and Parametric t-SNE. Entropy 2018, 20, 604. https://doi.org/10.3390/e20080604
He W, He Y, Li B, Zhang C. Analog Circuit Fault Diagnosis via Joint Cross-Wavelet Singular Entropy and Parametric t-SNE. Entropy. 2018; 20(8):604. https://doi.org/10.3390/e20080604
Chicago/Turabian StyleHe, Wei, Yigang He, Bing Li, and Chaolong Zhang. 2018. "Analog Circuit Fault Diagnosis via Joint Cross-Wavelet Singular Entropy and Parametric t-SNE" Entropy 20, no. 8: 604. https://doi.org/10.3390/e20080604
APA StyleHe, W., He, Y., Li, B., & Zhang, C. (2018). Analog Circuit Fault Diagnosis via Joint Cross-Wavelet Singular Entropy and Parametric t-SNE. Entropy, 20(8), 604. https://doi.org/10.3390/e20080604






