1. Introduction
There is increasing interest in a metric on probability from theoretical and practical considerations, with different metrics proposed depending on the question of interest (e.g., [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10] and further references therein). Theoretically, the assignment of an appropriate metric to probability enables us to mathematically quantify the difference among different Probability Density Functions (PDFs), providing a beautiful conceptual link between a stochastic process and geometry. At a practical level, it can be utilized for optimising various desired outcomes. For instance, the Wasserstein metric has been extensively studied for the optimal transport problem to minimize transport cost, typically taken to increase quadratically with distance between two locations [
1]. The Fisher (also called Fisher-Rao) metric has recently been used for optimization, including the minimization of entropy production [
11], parameter estimation [
12], controlling population [
13], understanding the arrow of time [
14], and analysing the convexity of the relative entropy [
15].
However, compared with the Wasserstein metric, whose application has established itself as a branch of applied mathematics, the geometric structure associated with the information change in the Fisher metric and its utility have been explored much less. Unlike the Wasserstein distance, the Fisher metric yields a hyperbolic geometry in the upper half-plane (e.g., [
9,
10]) where the distance is measured in units of the width of the PDF. That is, the distance in the Fisher metric is dimensionless and represents the number of different statistical states. Consequently, for a Gaussian PDF, statistically distinguishable states are determined by the standard deviation; two PDFs that have the same standard deviation and differ in peak positions by less than one standard deviation are statistically indistinguishable (e.g., [
11,
16,
17,
18,
19,
20,
21,
22]).
By extending the Fisher metric to time-dependent problems, we recently introduced a system-independent way of quantifying information change associated with time-evolution of PDFs [
13,
23,
24,
25,
26,
27,
28,
29,
30]. (Note that we use information for statistically different states, refraining from the debate on the exact definition of information, e.g., [
5,
31].) The key idea is to define an infinitesimal distance at any time by comparing two PDFs at adjacent times and sum these distances. The total distance gives us the number of statistically different states that a system passes through in time, and is called information length
. While the detailed derivation of
is given in [
5,
13,
16,
23,
24,
25,
26,
27,
28,
29,
30], it is useful to highlight that
is a measure of the total elapsed time in units of a dynamical timescale for information change. To show this, we define the dynamical time
as follows:
Here,
is the characteristic timescale over which the information changes. Having units of time,
quantifies the correlation time of a PDF. Alternatively,
quantifies the (average) rate of change of information in time. A particular path which gives a constant valued
is a geodesic along which the information propagates at the same speed [
13].
is then defined by measuring the total elapsed time
t in units of
as:
is a Lagrangian quantity (unlike entropy or relative entropy), uniquely defined as a function of time
t for a given initial PDF, and represents the total number of statistically distinguishable states that a system evolves through. It thus provides a very convenient methodology for measuring the distance between
and
continuously in time for a given
. One of the utilities of
is to quantify the proximity of any initial PDF to a final attractor of a dynamical system. We note that for a linear process, we can express the information length in terms of a metric tensor
using the two parameters
and
(e.g., [
13]). However, even in the case where the control parameters are not known, we can still define
as long as we can compute time-dependent PDFs (e.g., from data [
24]).
Traditionally, concepts such as bifurcations, Lyapunov exponent or a distance to an equilibrium point are commonly used to understand dynamical systems (e.g., see [
32]). An intriguing question arises as to how to define a distance between a point, say
x, and an equilibrium which is not a point but a limit cycle, or chaotic attractor. One interesting possibility is to consider a narrow initial PDF around
x and to measure the total information length
as the initial PDF evolves toward the equilibrium PDF.
offers a Lagrangian distance that depends on the trajectory/history of the system (e.g., time-dependent PDF), being uniquely defined as a function of time for a given initial PDF. This enables us to map out the attractor structure by measuring
for different locations of a narrow initial PDF. In a chaotic system,
changes abruptly when a different initial PDF is used, as shown in Figure 4 in [
24], where the very spiky curve represents a sensitive dependence of
on
, the location of a very narrow initial PDF. This sensitive dependence of
on
means that a small change in the initial condition causes a large difference in a path that a system evolves through and thus
. This is quite similar to the sensitive dependence of the Lyapunov exponent on the initial condition. That is, our
provides a new methodology to test chaos. Furthermore, Figure 4 in [
24] shows small
for unstable points, demonstrating that unstable points are more similar to chaotic attractors.
The purpose of this paper is to consider the effect of different orders of nonlinear interaction on the geometric structure by considering the case when the equilibrium is a stable point [
26,
33]. The remainder of this paper is organised as follows:
Section 2 introduces the basic model.
Section 3 derives exact analytic solutions in the absence of stochastic noise, as well as asymptotic scalings for the timescales, peak amplitudes and widths once noise plays a role.
Section 4 presents numerical results, and shows how they compare with the analytic scalings.
Section 5 summarizes the results.
4. Numerical Solutions
For
, an exact analytic solution to the Fokker–Planck Equation (
6) only exists for the linear case
[
33]. For the nonlinear cases
that are the focus of this paper, we must resort to numerical solutions. Without loss of generality, we set
. The interval in
x is fixed to be
, rather than the original
. This may seem drastic, but actually involves no real loss of generality either, since any finite interval can always be mapped to
by suitably rescaling
x,
t and
D. As long as the initial condition (and
D) are chosen such that
p would be negligible outside
anyway, solving the FP equation only on
, and with
boundary conditions is then equivalent in all essentials to the original infinite interval.
The numerical solution is done by second-order finite-differencing in x, with up to grid points. The time-stepping is also second-order accurate, with increments as small as . Both M and were varied to check the accuracy of the solutions. In the later stages, when the PDFs are evolving to increasingly broad profiles, M can also be decreased, and increased, while still preserving accuracy. Regridding the solutions in this way is indeed crucial, since the final adjustment timescale is extremely long for small D, and could not be reached if M and were kept fixed at their initial values.
In [
33], we considered the initial condition
and then compared numerical solutions for
and
to
with the corresponding analytical solutions for
. That is, the initial peak was extremely narrow, and diffusion was greater than what we consider here. As a result of these choices, the peaks only became broader but never narrower; the nondiffusive regime in
Section 3.1 simply does not exist in this case.
In contrast, in this work, we take the initial condition
and
to
. By starting with broader peaks and having smaller
D, we do have an initial nondiffusive regime here, and are able to observe the narrowing of the peaks predicted by Equations (
13) and (
14). We begin by fixing the initial peak position
; below, we also consider the range
.
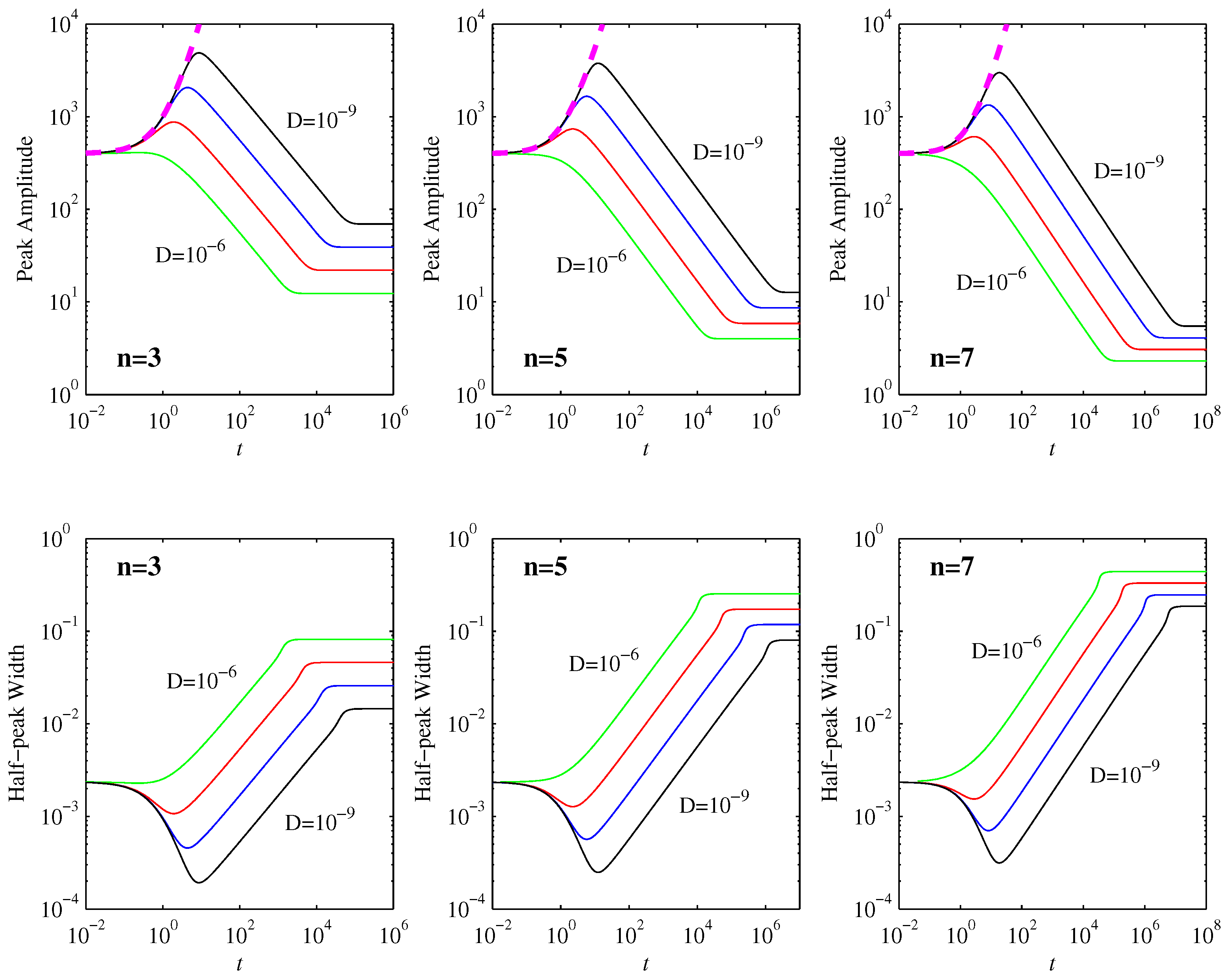
Figure 1 shows how the peak amplitudes evolve in time. We can clearly see the three regimes deduced in
Section 3: the peaks initially increase, in excellent agreement with Equation (
15), then they decrease in agreement with Equation (
28), and finally they equilibrate to Equation (
31). To more quantitatively compare the overall peak amplitudes
and the corresponding times
at which they occur with the analytic predictions given by Equations (
26) and (
29), we note first that
is clearly not yet sufficiently small for there to be an initial nondiffusive regime at all (for this particular width of the initial condition). Even
only follows the nondiffusive Equation (
15) for a very brief time, not yet long enough to be in the
regime where Equations (
26) and (
29) are expected to apply.
Table 1 therefore compares the
and
cases, and uses them to extract scaling exponents of the form
. We see that the agreement of
with Equation (
29) is virtually perfect. The corresponding times
are close to the expected scaling
, but are not fully in the asymptotic limit yet. This is hardly surprising, since even for
the
values in
Table 1 only have
(for all three
n values).
To similarly test the scalings that are predicted for
, further runs were done with fixed
, and
and
. As
Table 2 shows, the extracted exponents are again in very good (
) and perfect (
) agreement with the predicted asymptotic scalings. The interesting feature that larger initial positions
have smaller times to reach the maximum peak amplitude is certainly very well reproduced. Note finally that the two
values used to extract these exponents in
Table 2 differ by less than a factor of two even, and would thus certainly not be enough to extract reliable scaling exponents if we did not already have robust analytic predictions. As we also show in more detail below, in principle, it would be possible to have the analytic predictions extend over an arbitrarily large range in
, but that would require increasingly small
D as well, which becomes numerically too time-consuming.
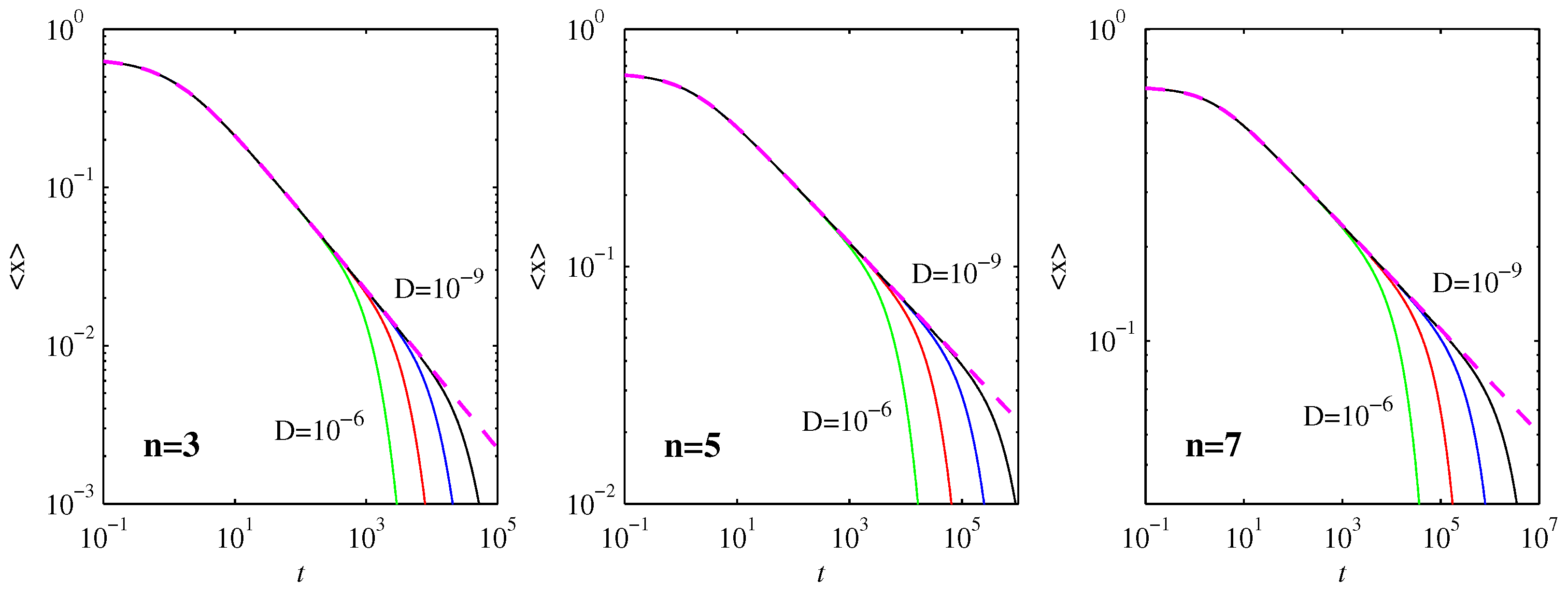
Returning to the
runs in
Figure 1 and
Figure 2 shows the expectation values
, and how they compare with the nondiffusive result (Equation (
5)). The agreement is close to perfect even after the first timescale
is reached. It is only once the very long second timescale
is reached that
approaches 0 exponentially, far more rapidly than the
power law scaling in (
5).
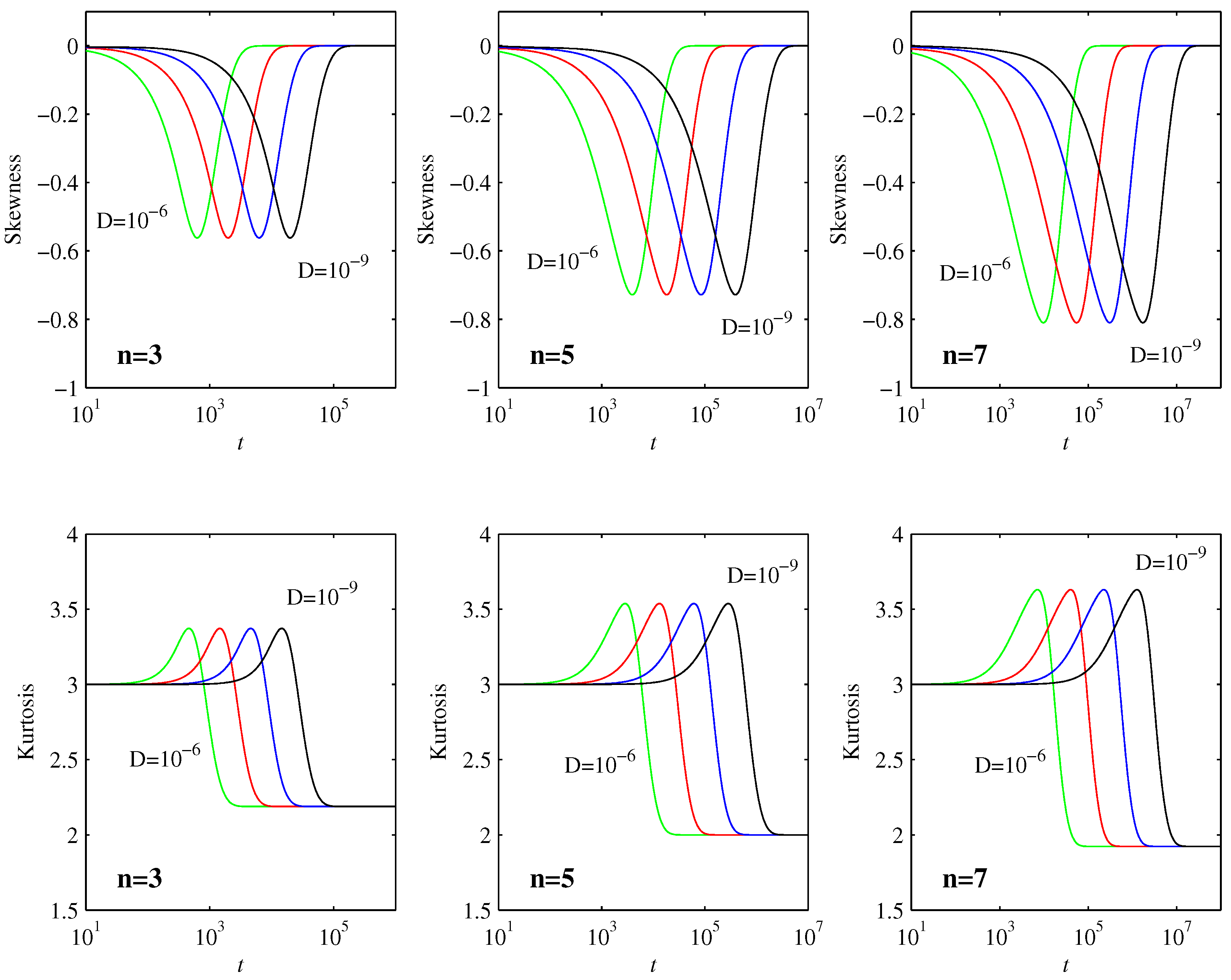
Figure 3 shows two commonly used diagnostic quantities, the skewness
and the kurtosis
, where
is the standard deviation. Skewness is a measure of how asymmetric a PDF is about its peak, with a value of 0 indicating a symmetric peak. Kurtosis measures the flatness of a PDF, especially in comparison with a Gaussian, which has
. We see that
and
is maintained all the way until the final equilibration timescale
is reached, indicating that the PDFs remain largely Gaussian up to this time, as predicted in
Section 3.2. For the final equilibrated profiles in Equation (
30), the skewness is again 0, whereas the kurtosis has values that depend on
n (the precise values can be evaluated analytically in terms of
functions, but are not particularly insightful). It is interesting though to note in
Figure 3 that both skewness and kurtosis exhibit non-monotonic behavior during the final adjustment process, where the PDFs transition from being largely Gaussian to their final form. Note also how the maxima reached during this transition process are independent of
D, and even broadly similar for the different values of
n.
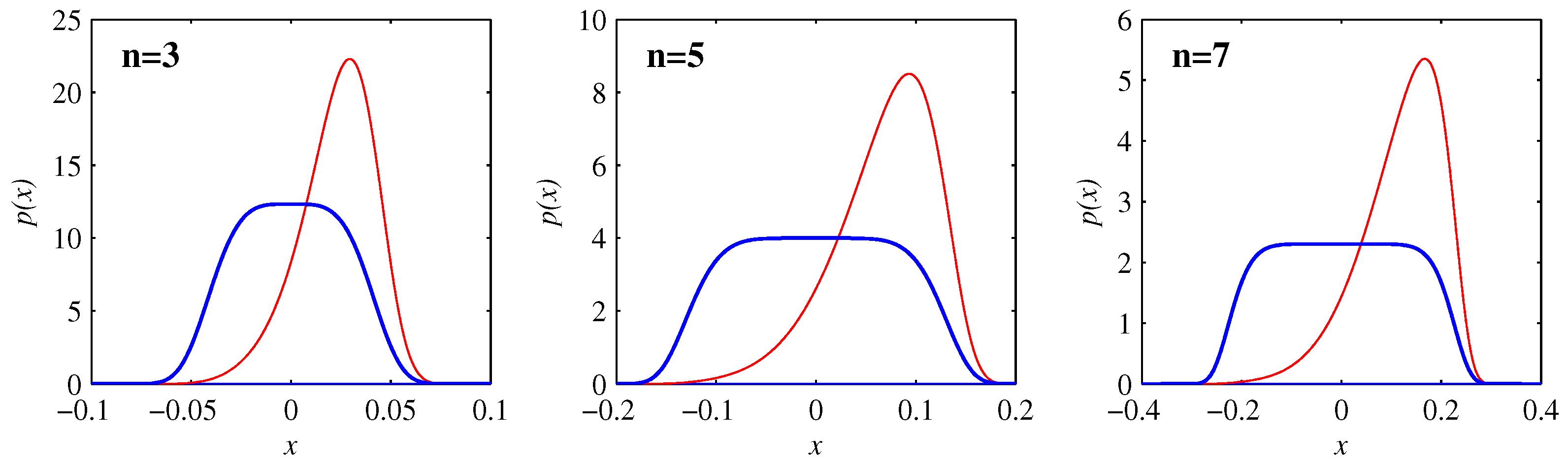
Figure 4 compares the PDFs at the times when the skewness reaches its maximum (negative) value with the final equilibrated profiles in Equation (
30). The entire evolution is then clear: as long as the PDFs are well outside their final profiles, they remain essentially Gaussian, with widths as in
Figure 1 and positions as in
Figure 2. The skewness and kurtosis start to deviate significantly from their Gaussian values when the PDFs start to reach their final positions, with the maximum skewness as in
Figure 4. The final rearrangement for
then merely adjusts to the final profiles (
30), but with relatively little further movement of the PDFs.
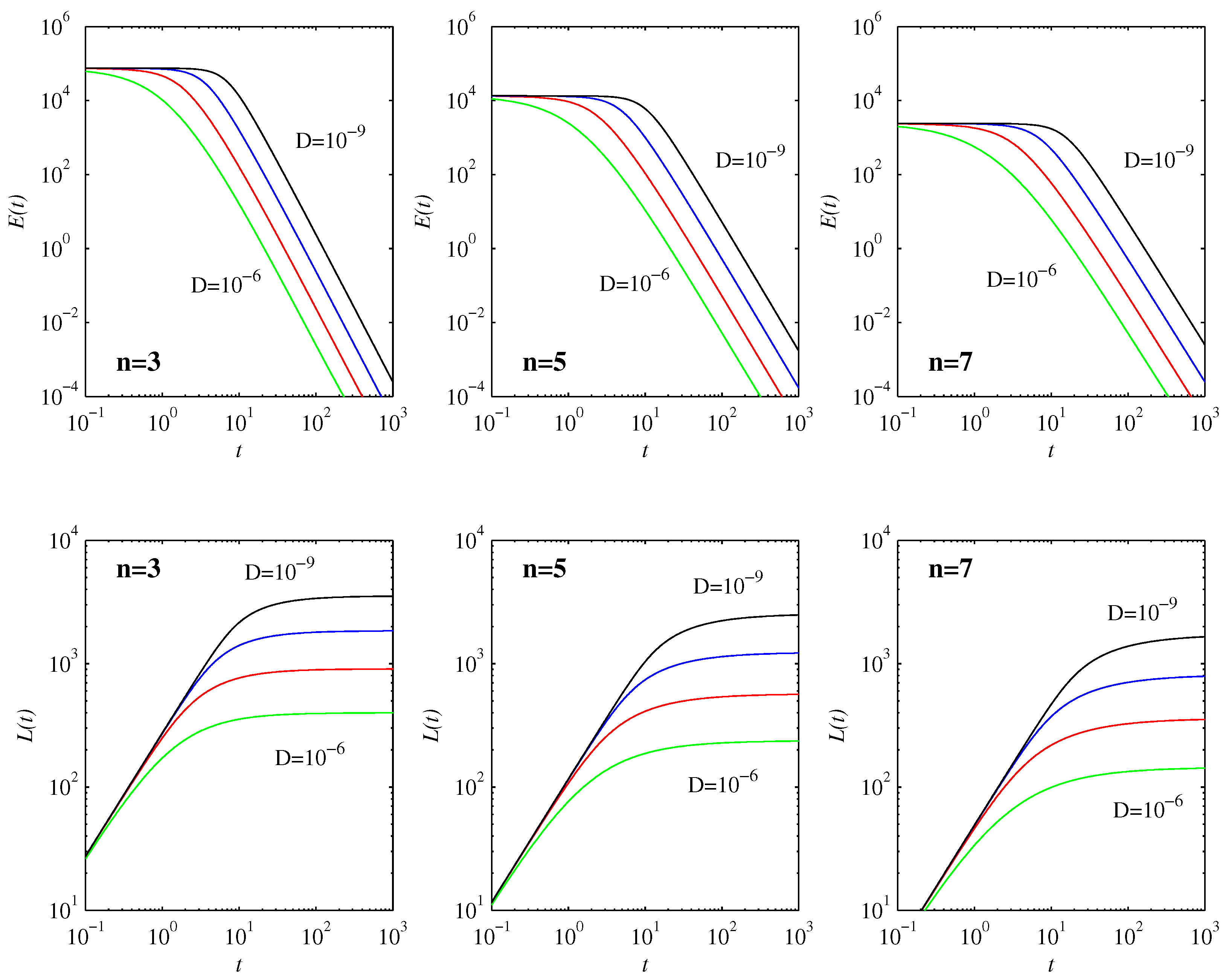
Figure 5 shows the diagnostic quantities
and
. As predicted by Equation (
17),
remains constant in the initial nondiffusive phase. Once the first timescale
is reached,
decreases as
. Once the second timescale
is reached,
decreases exponentially. (This is not included in
Figure 5, however, as
at that point, and is thus already negligibly small.) The behavior of
is as expected: while
is constant,
increases linearly in time, and, once
starts decreasing,
levels off to its final value
.
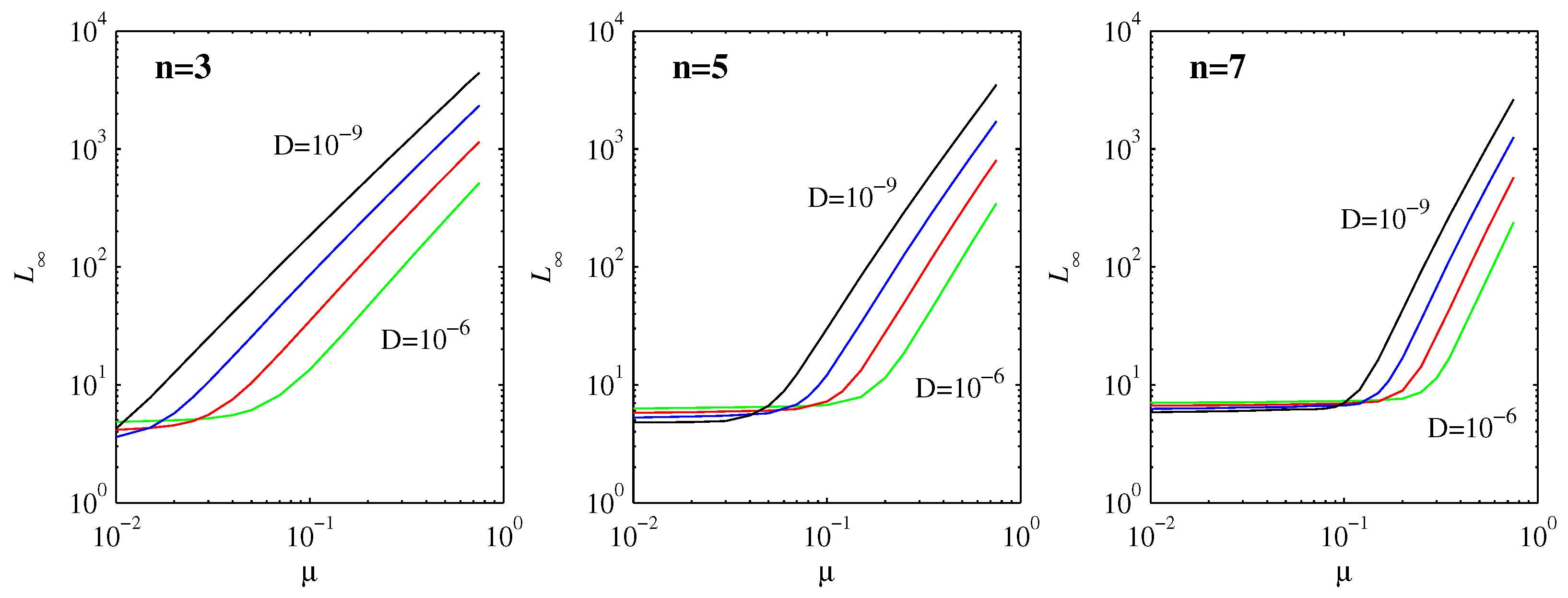
Based on the scaling for
, namely that
initially, and the range
for which this applies, we expect at least a lowest-order estimate for
to be given simply by
Figure 6 shows numerically computed results, for the same
to
range considered throughout, and
. At least for sufficiently large
, we do indeed see clear evidence of power-law behavior, with a negative exponent for
D and a positive one for
. Concentrating on the variation with
, for
, the slopes vary between
for
and
for
; for
, they vary between
and
; and for
, they vary between
and
. By comparison, according to Equation (
35), the exponent should be
, which yields 1.5, 2.1, 2.8 for
, respectively. The agreement is thus quite good, especially when we recall (
Table 1 and
Table 2) that even
was not quite small enough yet to obtain precise agreement with the asymptotic formula for
, which in turn affects Equation (
35) as well.
as a function of
provides a mapping from the physical distance
(the distance between the peak position
of an initial PDF and the final equilibrium point 0) to the information length (the total number of statistically different states of a system reaching a final stationary PDF from an initial PDF). From Equation (
35), this mapping is linear for a linear force; that is,
is linearly proportional to the physical distance. This linear relation breaks down for nonlinear forces as
depends nonlinearly on the physical distance
. Specifically, for
,
; for
,
; and, for
,
. Thus, we can envision that nonlinear forces affect the information geometry, changing a linear (flat) coordinate to a power-law (curved) coordinate. This is reminiscent of gravity changing a flat to a curved space-time. Furthermore, interestingly, Equation (
35) shows that
is independent of
D for the linear force, manifesting the information geometry as independent of the resolution (set by
D). In contrast,
decreases with
as
, suggesting that the information geometry is fractal, depending on the resolution. This would be equivalent to the
I theorem of [
14].
Finally, what about the small
limit in
Figure 6, which clearly does not follow the expected scaling (
35)? The explanation is that the initial position
is already within the
width of the final distribution in Equation (
30). In this limit, the behavior is different, and the peak merely spreads out, resulting in a small and relatively uniform
. For any given
,
D must therefore satisfy
to be in the regime where Equation (
35) is expected to apply. That is, in principle, it would be possible to have Equation (
35) apply over several orders of magnitude in
, but
D would have to be far smaller than is numerically feasible.