Entropy-Based Feature Extraction for Electromagnetic Discharges Classification in High-Voltage Power Generation
Abstract
1. Introduction
2. EMI Monitoring
3. Description of Employed Algorithms
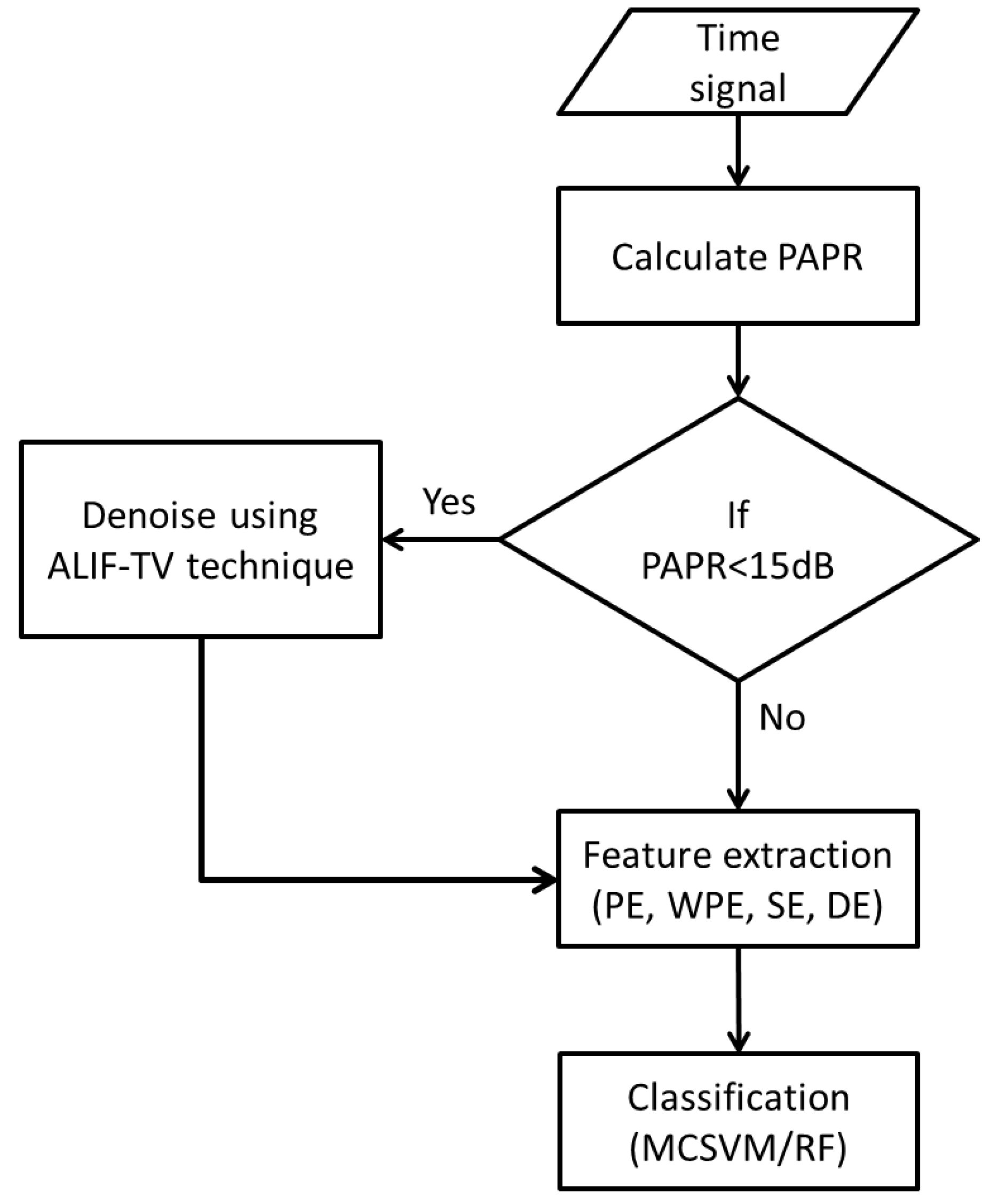
3.1. Signal Denoising
3.2. Entropy Measures
3.2.1. Permutation Entropy (PE)
3.2.2. Weighted Permutation Entropy (WPE)
3.2.3. Sample Entropy (SE)
3.2.4. Dispersion Entropy (DE)
3.3. Classification Algorithms
3.3.1. Support Vector Machine (SVM) and Multi-Class SVM (MCSVM)
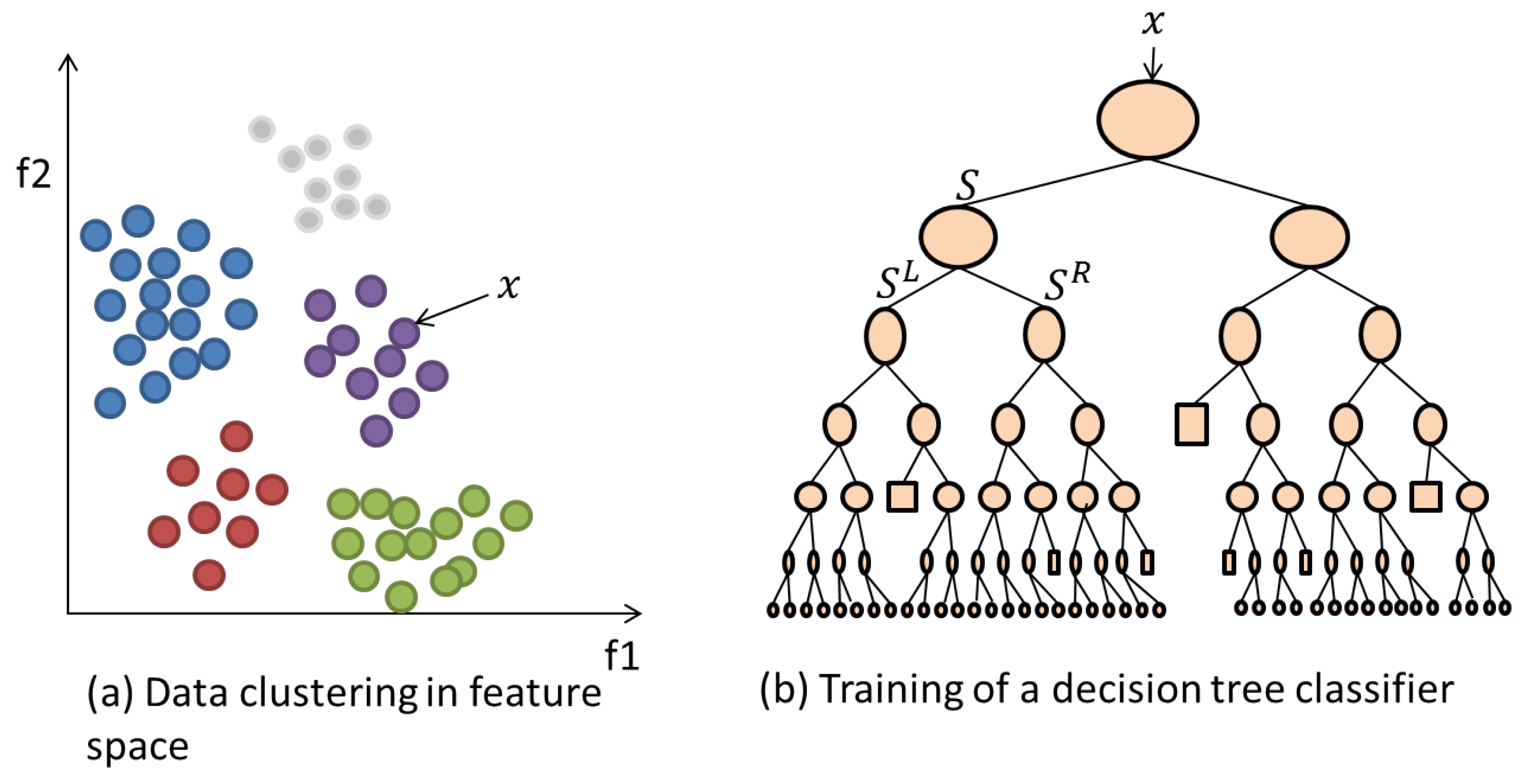
3.3.2. Random Forests (RF)
- At an initial node, randomly choose feature instances from the overall instances presented to the classifier, where is much smaller than .
- Calculate the best split point using Information Gain defined as:where is the Shannon Entropy [26] of the node and is the child node.
- Using the best split point, divide the main node into daughter nodes and reduce the number of feature instances along the nodes.
- Repeat steps 1 to 3 until a maximum depth is reached.
- Repeat steps 1 to 4 for trees of the model. The more trees that are employed then the higher the achieved performance.
4. Experimental Set-Up
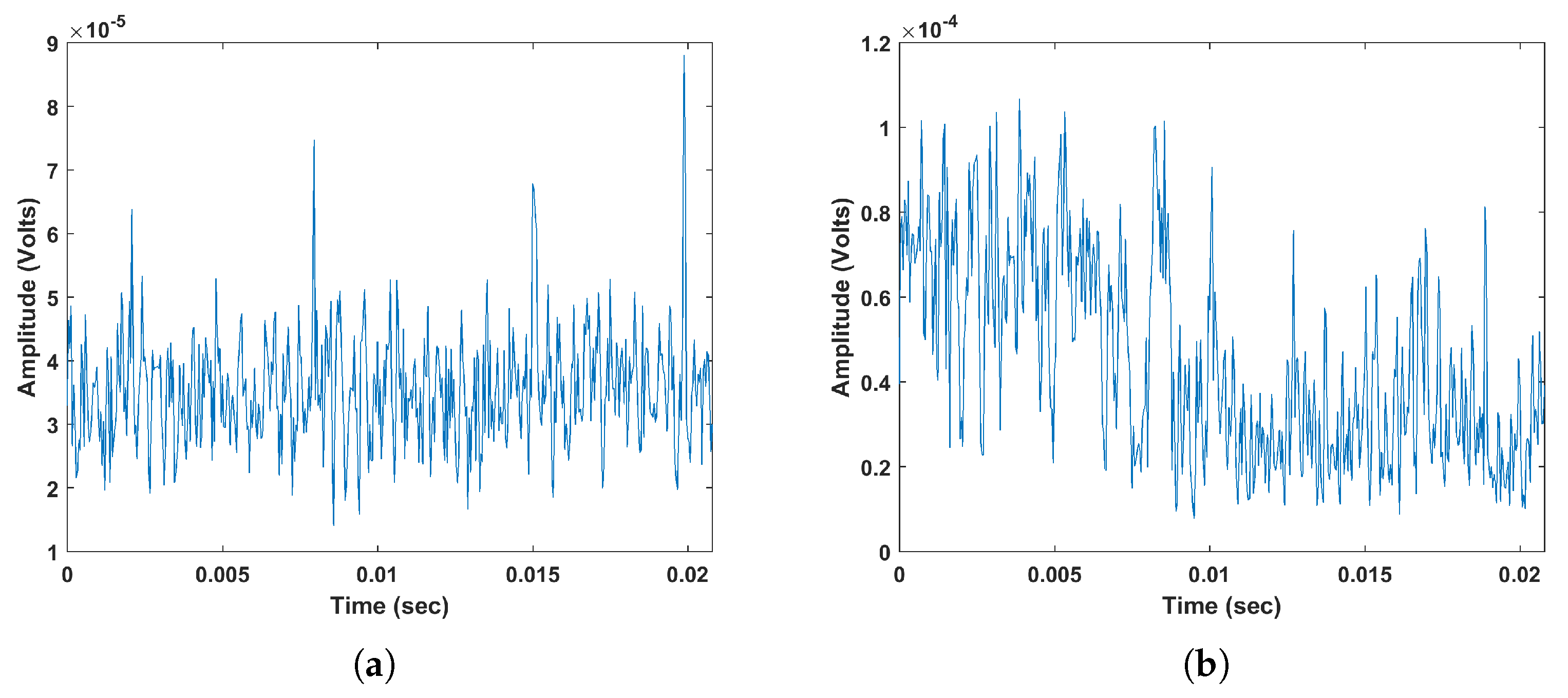
4.1. EMI Signals Measurement
4.2. Application of Feature Extraction and Classification
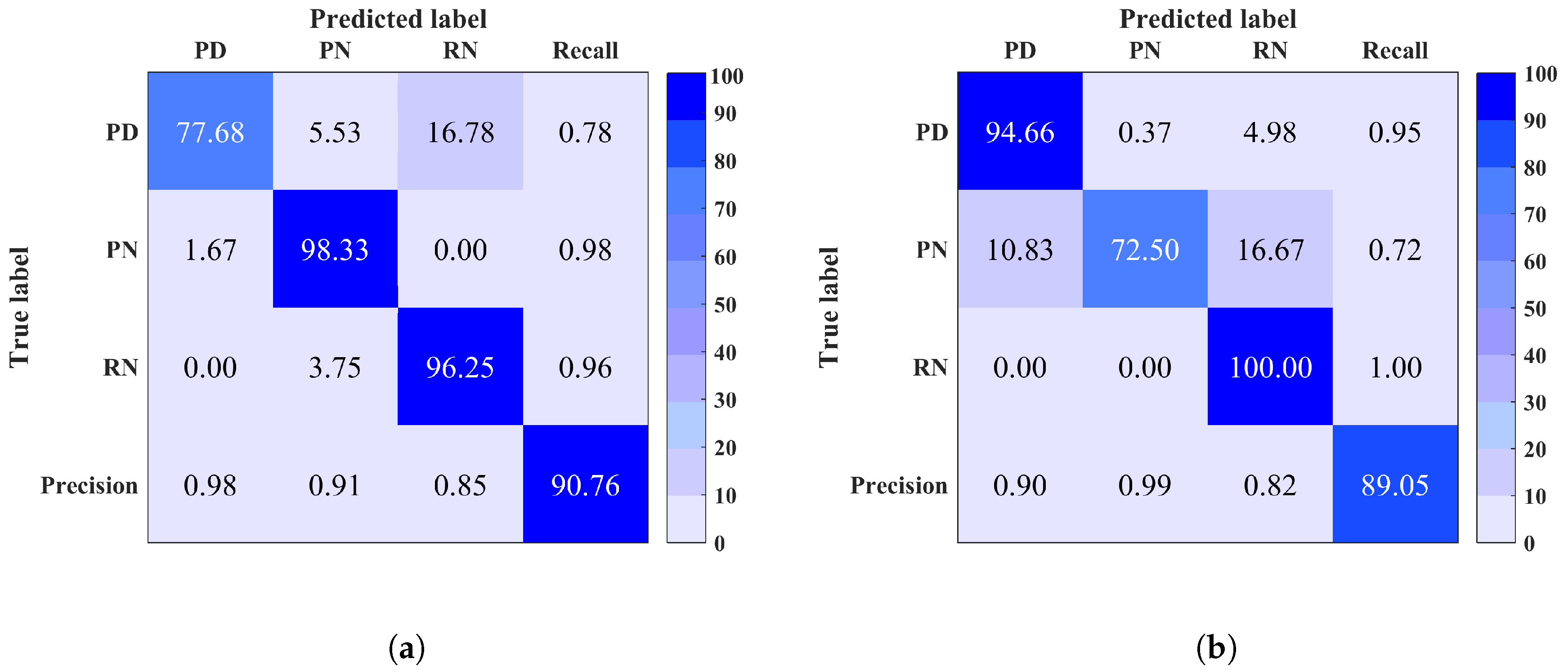
5. Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kuffel, E.; Zaengl, W.S.; Kuffel, J. High Voltage Engineering Fundamentals, 2nd ed.; Newnes: Oxford, UK, 2000; pp. 8–76. [Google Scholar]
- Kreuger, F.H. Industrial High Voltage: 4. Coordinating, 5. Testing, 6. Measuring; Delft University Press: Delft, The Netherlands, 1992; pp. 117–129. [Google Scholar]
- Bodega, R.; Morshuis, P.H.F.; Lazzaroni, M.; Wester, F.J. PD Recurrence in Cavities at Different Energizing Methods. IEEE Trans. Instrum. Meas. 2004, 53, 251–258. [Google Scholar] [CrossRef]
- Robles, G.; Parrado-Hernandez, E.; Ardila-Rey, J.; Martinez-Tarifa, J.M. Multiple partial discharge source discrimination with multiclass support vector machines. Expert Syst. Appl. 2016, 55, 417–428. [Google Scholar] [CrossRef]
- Spyker, R.; Schweickart, D.L.; Horwath, J.C.; Walko, L.C.; Grosjean, D. An evaluation of diagnostic techniques relevant to arcing fault current interrupters for direct current power systems in future aircraft. In Proceedings of the Electrical Insulation Conference and Electrical Manufacturing Expo (EICEME’05), Indianapolis, IN, USA, 23–26 October 2005; pp. 146–150. [Google Scholar]
- Tang, W.H.; Wu, Q.H. Condition Monitoring and Assessment of Power Transformers Using Computational Intelligence; Springer-Verlag: Liverpool, UK, 1992; pp. 1–13. [Google Scholar]
- Sureshjani, S.A.; Kayal, M. A Novel Technique for Online Partial Discharge Pattern Recognition in Large Electrical Motors. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (SIE’14), Istanbul, Turkey, 1–4 June 2014; pp. 721–726. [Google Scholar]
- Hunter, J.A.; Lewin, P.L.; Hao, L.; Walton, C.; Michel, M. Autonomous classification of PD sources within three-phase 11 kV PILC cables. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2117–2124. [Google Scholar] [CrossRef]
- Majidi, M.; Fadali, M.S.; Etezadi-Amoli, M.; Oskuoee, M. Partial discharge pattern recognition via sparse representation and ANN. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1061–1070. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Wang, K.; Li, J.; Liao, R.; Zhou, T.; Zhang, Y. Improving recognition accuracy of partial discharge patterns by image-oriented feature extraction and selection technique. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1076–1087. [Google Scholar] [CrossRef]
- Karthikeyan, B.; Gopal, S.; Vimala, M. Conception of complex probabilistic neural network system for classification of partial discharge patterns using multifarious inputs. Expert Syst. Appl. 2005, 29, 953–963. [Google Scholar] [CrossRef]
- Hunter, J.A.; Hao, L.; Lewin, P.L.; Evagorou, D.; Kyprianou, A.; Georghiou, G.E. Comparison of two partial discharge classification methods. In Proceedings of the IEEE International Symposium on Electrical Insulation Conference (ISEI’10), San Diego, CA, USA, 6–9 June 2010; pp. 1–5. [Google Scholar]
- Timperley, J.E. Comparison of PDA and EMI diagnostic measurements [for machine insulation]. In Proceedings of the Conference Record of the 2002 IEEE International Symposium on Electrical Insulation, Boston, MA, USA, 7–10 April 2002; pp. 575–578. [Google Scholar]
- Timperley, J.E.; Vallejo, J.M. Condition Assessment of Electrical Apparatus With EMI Diagnostics. IEEE Trans. Ind. Appl. 2017, 53, 693–699. [Google Scholar] [CrossRef]
- Timperley, J.E. Audio spectrum analysis of EMI patterns. In Proceedings of the 2007 Electrical Insulation Conference and Electrical Manufacturing Expo, Nashville, TN, USA, 22–24 October 2007; pp. 39–41. [Google Scholar]
- Internation Special Committee on Radio Interference. IEC CISPR 1-6-1-1:2015; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- Timperley, J.E.; Vallejo, J.M.; Nesbitt, A. Trending of EMI data over years and overnight. In Proceedings of the 2014 IEEE Electrical Insulation Conference (EIC), Philadelphia, PA, USA, 8–11 June 2014; pp. 176–179. [Google Scholar]
- Feher, K. Telecommunications Measurements, Analysis, and Instrumentation; SciTech Publishing: Stevenage, UK, 1997; p. 188. [Google Scholar]
- Mitiche, I.; Morison, G.; Nesbitt, A.; Hughes-Narborough, M.; Boreham, P.; Stewart, B.J. An Evaluation of Total Variation Signal Denoising Methods for Partial Discharge Signals. In Proceedings of the 13th International Electrical Insulation Conference (INSUCON), Birmingham, UK, 16–18 May 2017; pp. 1–5. [Google Scholar]
- Ding, Y.; Selesnick, I.W. Artifact-Free Wavelet Denoising: Non-convex Sparse Regularization, Convex Optimization. IEEE Signal Process. Lett. 2015, 22, 1364–1368. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Afonso, M.; Bioucas-Dias, J.; Figueiredo, M.T. Fast Image Recovering Using Variable Splitting and Constrained Optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef] [PubMed]
- Eckstein, J.; Bertsekas, D. On the Douglas Rachford Splitting Method and the Proximal Point Algorithm for Maximal Monotone Operators. Math. Program. 1992, 5, 293–318. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Amigo, J.M.; Keller, K. Permutation Entropy: One Concept, two Approaches. Eur. Phys. J. Spec. Top. 2013, 222, 263–273. [Google Scholar] [CrossRef]
- Rathie, P.; Da Silva, S. Shannon, Levy, and Tsallis: A note. Appl. Math. Sci. 2008, 2, 1359–1363. [Google Scholar]
- Riedl, M.; Müller, A.; Wessel, N. Practical Considerations of Permutation Entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Yan, R.; Liu, Y.; Gao, R.X. Permutation Entropy: A nonlinear Statistical Measure for Status Characterization of Rotary Machines. Mech. Syst. Signal Process. 2012, 29, 474–484. [Google Scholar] [CrossRef]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-Permutation Entropy: A Complexity Measure for Time Series Incorporating Amplitude Information. Phys. Rev. E 2013, 87, 022911. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Shang, P.; Wang, J.; Shi, W. Permutation and Weighted-Permutation Entropy Analysis for the Complexity of Nonlinear Time Series. Commun. Nonlinear Sci. Numer. Simul. 2016, 31, 60–68. [Google Scholar] [CrossRef]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample Entropy. In Numerical Computer Methods, Part E; Academic Press: San Diego, CA, USA, 2004; pp. 172–184. [Google Scholar]
- Ahmed, M.U.; Mandic, D.P. Multivariate Multiscale Entropy: A tool for Complexity Analysis of Multichannel Data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Proc. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Massimiliano, Z.; Luciano, Z.; Osvaldo, R.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1961. [Google Scholar]
- Boardman, M.; Trappenberg, T. A Heuristic for Free Parameter Optimization with Support Vector Machines. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 16–21 July 2006; pp. 1337–1344. [Google Scholar]
- Widodo, A.; Yang, B.-S. Support Vector Machine in Machine Condition Monitoring and Fault Diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Criminisi, A.; Konukoglu, E.; Shotton, J. Decision Forests for Classification, Regression, Density Estimation, Manifold Learning and Semi-Supervised Learning; Microsoft Technical Report; Microsoft Research: Washington, DC, USA, 2011; pp. 5–19. [Google Scholar]
- Timperley, J.E. Generator condition assessment through EMI diagnostics. In Proceedings of the ASME 2008 Power Conference, Lake Buena Vista, FL, USA, 22–24 July 2008; pp. 349–354. [Google Scholar]


| Site | Discharge Source |
|---|---|
| 1 | PD, RN, PN |
| 2 | mS, DM, RN, PD, A |
| 3 | PD, E |
| 4 | PD, E |
| 5 | RN, DM, PD |
| 6 | RN, DM, E, PD, mS |
| 7 | PN, E, PD |
| 8 | PD, E |
| 9 | PN, E, PD |
| 10 | PD, E |
| Site | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy % | MCSVM | 91 | 75 | 91 | 100 | 96 | 99 | 100 | 99 | 100 | 100 |
| RF | 89 | 79 | 92 | 100 | 97 | 98 | 72 | 100 | 99 | 100 |
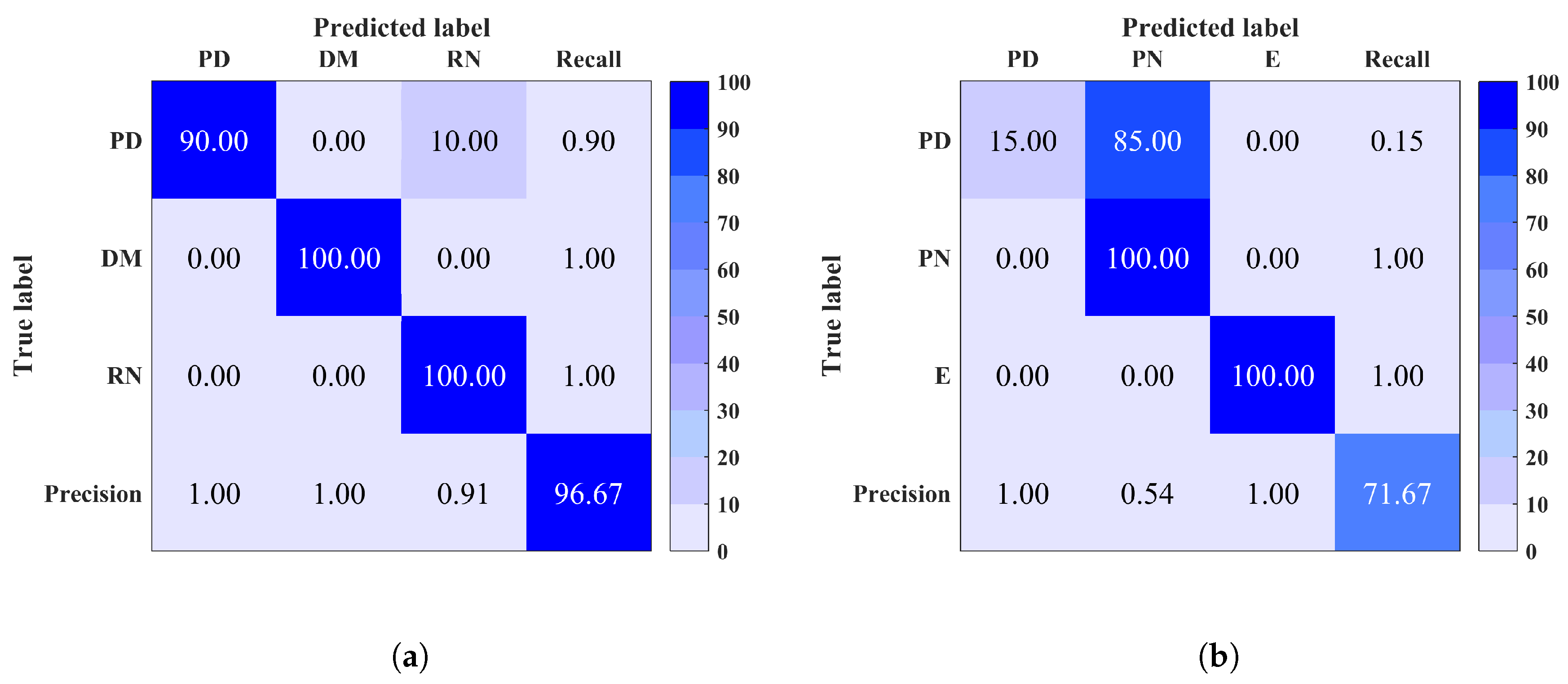
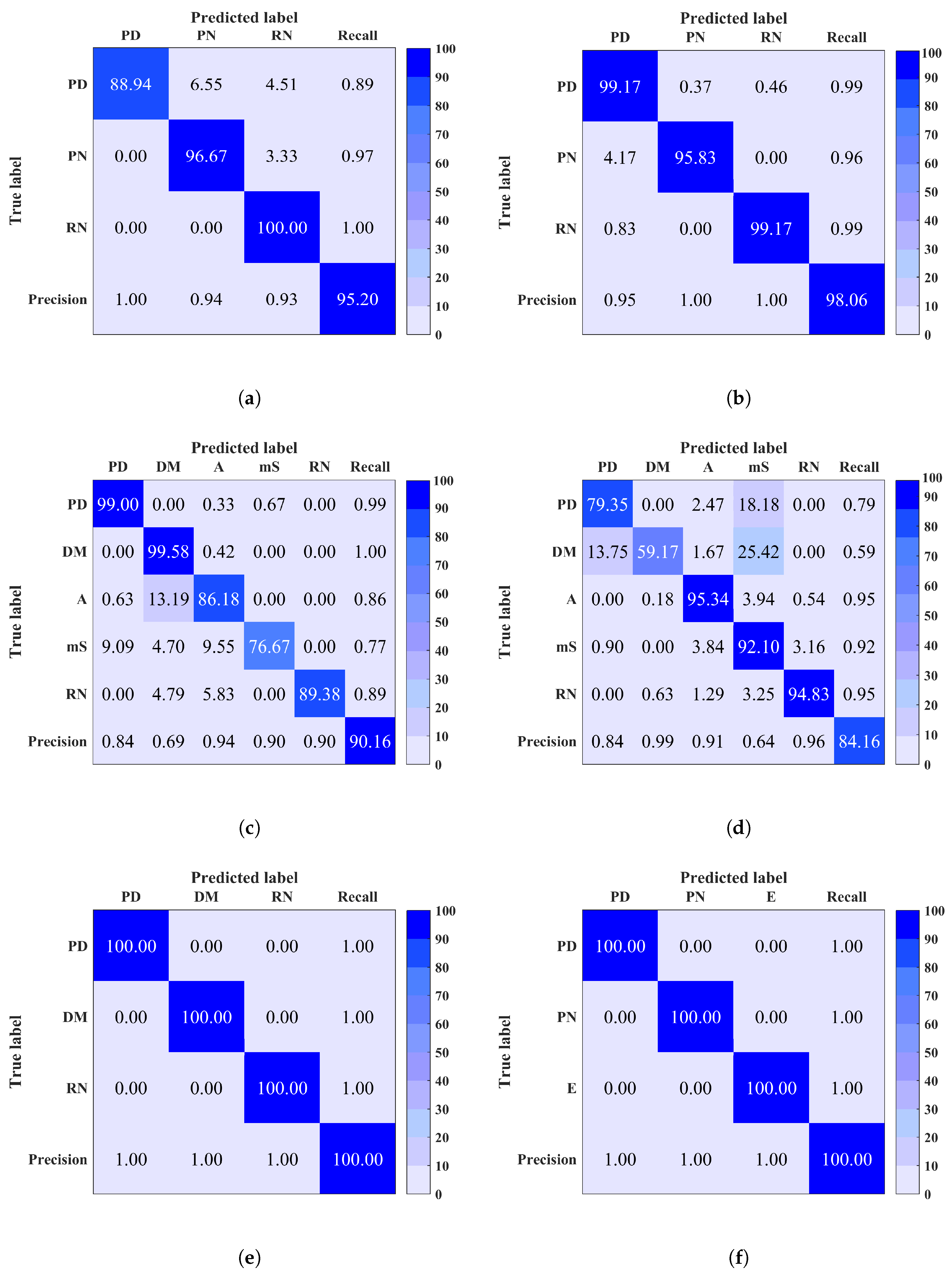
| Before Denoising | |||||
|---|---|---|---|---|---|
| Site | 1 | 2 | 5 | 7 | |
| Accuracy % | 91/89 | 75/79 | 96/97 | 100/72 | |
| Precision | 0.91/0.90 | 0.72/0.84 | 0.96/0.97 | 1/0.85 | |
| Recall | 0.91/0.89 | 0.76/0.79 | 0.97/0.96 | 1/0.72 | |
| F-measure | 0.91/0.90 | 0.74/0.81 | 0.96/0.96 | 1/0.78 | |
| After denoising | |||||
| Accuracy % | 95/98 | 90/84 | 100/100 | 100/100 | |
| Precision | 0.96/0.98 | 0.85/0.87 | 1/1 | 1/1 | |
| Recall | 0.98/0.98 | 0.90/0.84 | 1/1 | 1/1 | |
| F-measure | 0.97/0.98 | 0.87/0.85 | 1/1 | 1/1 |
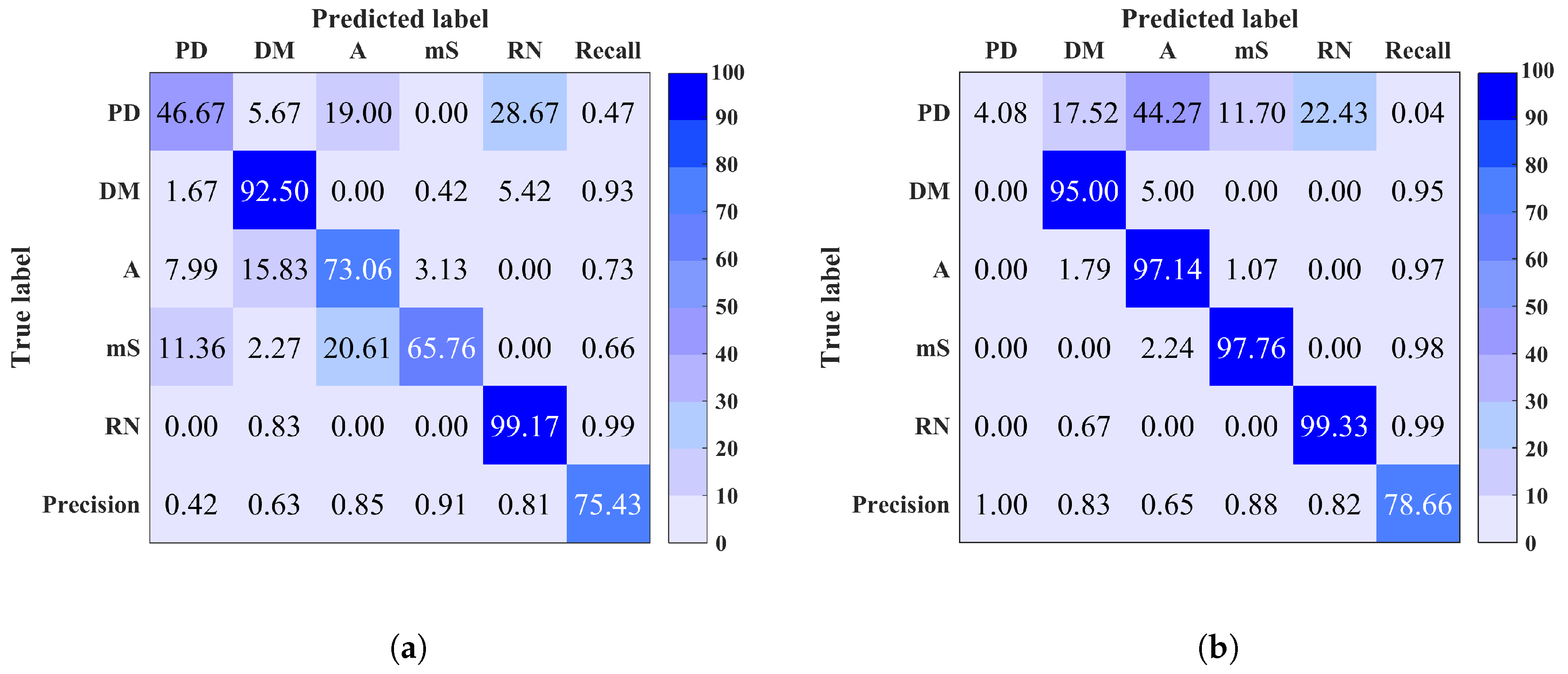
| Before Denoising | Accuracy % | Precision | Recall | F-Measure |
|---|---|---|---|---|
| 77/73 | 0.83/0.77 | 0.77/0.73 | 0.78/0.72 | |
| After denoising | ||||
| 91/66 | 0.91/0.79 | 0.91/0.66 | 0.91/0.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitiche, I.; Morison, G.; Nesbitt, A.; Stewart, B.G.; Boreham, P. Entropy-Based Feature Extraction for Electromagnetic Discharges Classification in High-Voltage Power Generation. Entropy 2018, 20, 549. https://doi.org/10.3390/e20080549
Mitiche I, Morison G, Nesbitt A, Stewart BG, Boreham P. Entropy-Based Feature Extraction for Electromagnetic Discharges Classification in High-Voltage Power Generation. Entropy. 2018; 20(8):549. https://doi.org/10.3390/e20080549
Chicago/Turabian StyleMitiche, Imene, Gordon Morison, Alan Nesbitt, Brian G. Stewart, and Philip Boreham. 2018. "Entropy-Based Feature Extraction for Electromagnetic Discharges Classification in High-Voltage Power Generation" Entropy 20, no. 8: 549. https://doi.org/10.3390/e20080549
APA StyleMitiche, I., Morison, G., Nesbitt, A., Stewart, B. G., & Boreham, P. (2018). Entropy-Based Feature Extraction for Electromagnetic Discharges Classification in High-Voltage Power Generation. Entropy, 20(8), 549. https://doi.org/10.3390/e20080549






