Rate-Distortion Region of a Gray–Wyner Model with Side Information
Abstract
:1. Introduction
1.1. Main Contributions
1.2. Related Works
1.3. Outline
Notation
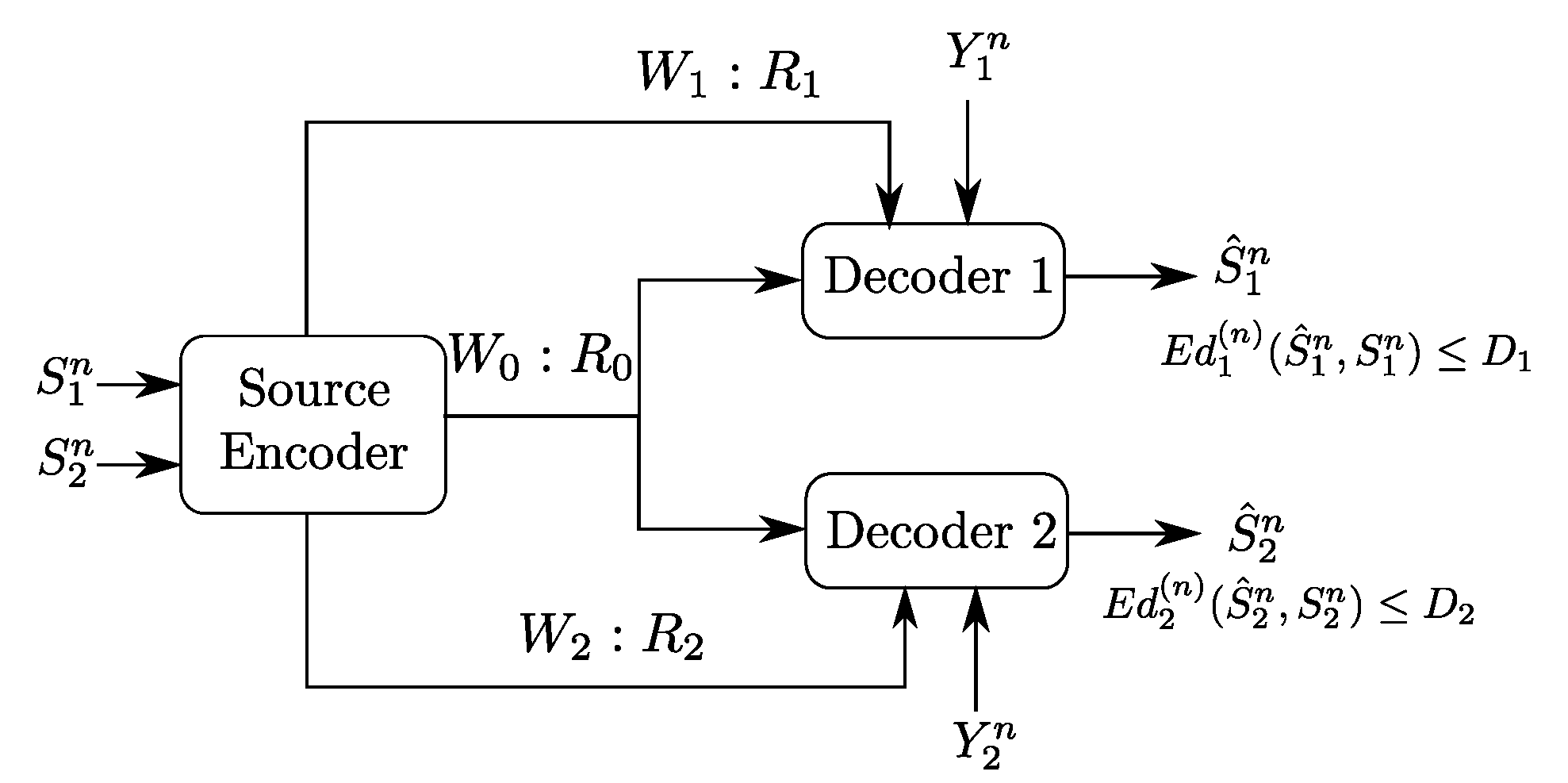
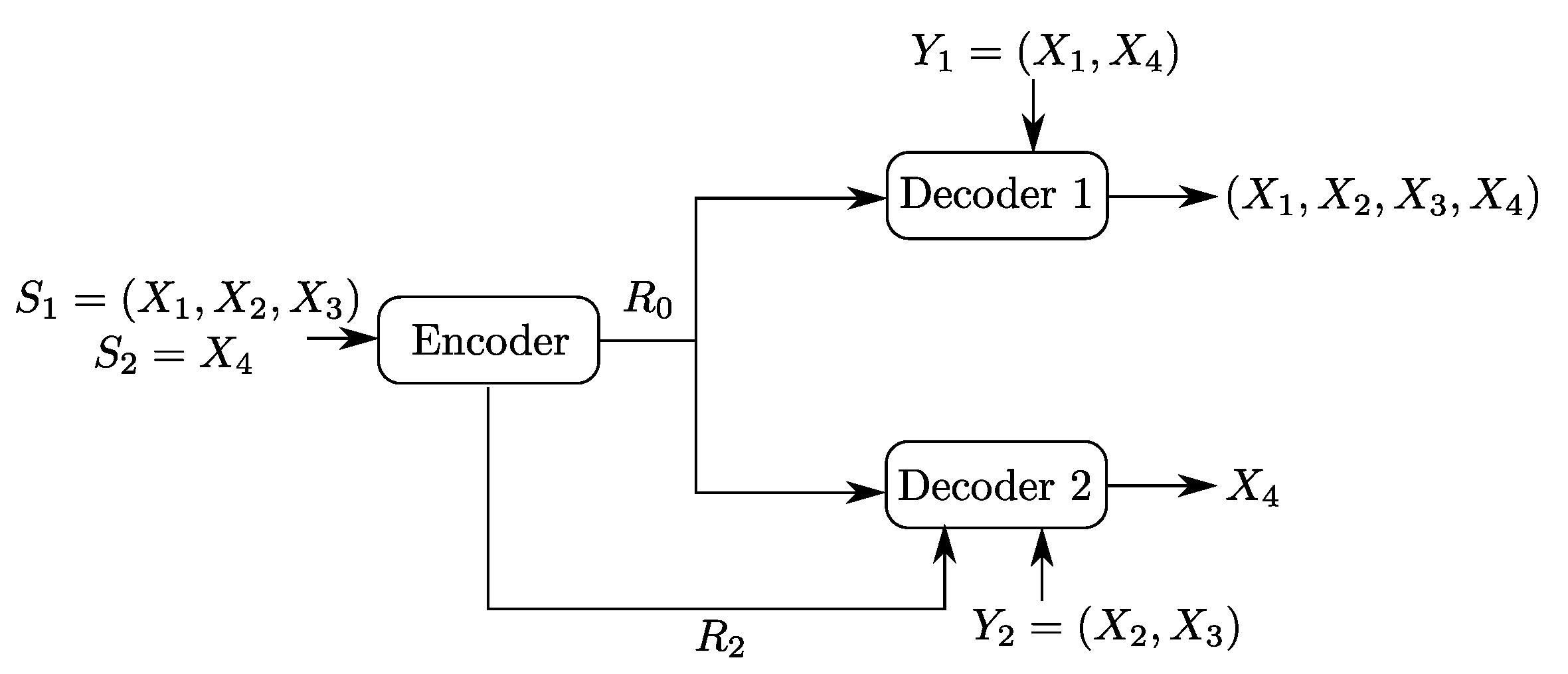
2. Problem Setup and Formal Definitions
- -
- Three sets of messages , , and .
- -
- Three encoding functions, , and defined, for as
- -
- Two decoding functions and , one at each user:andThe expected distortion of this code is given byThe probability of error is defined as
3. Gray–Wyner Model with Side Information and Degraded Reconstruction Sets
- (1)
- The following Markov chain is valid:
- (2)
- There exists a function such that:
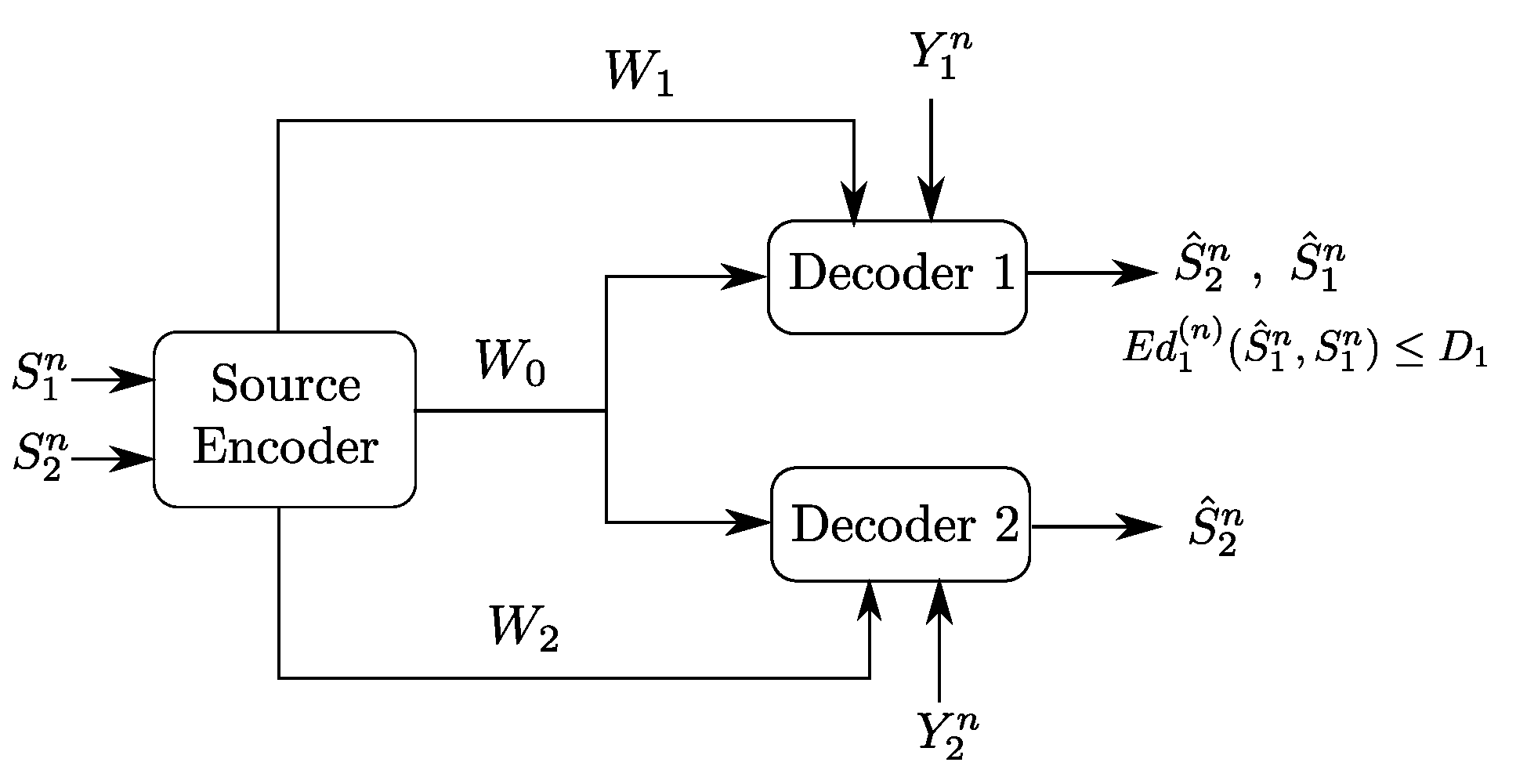
4. The Heegard–Berger Problem with Successive Refinement
4.1. Rate-Distortion Region
- (1)
- The following Markov chain is valid:
- (2)
- There exists a function such that:
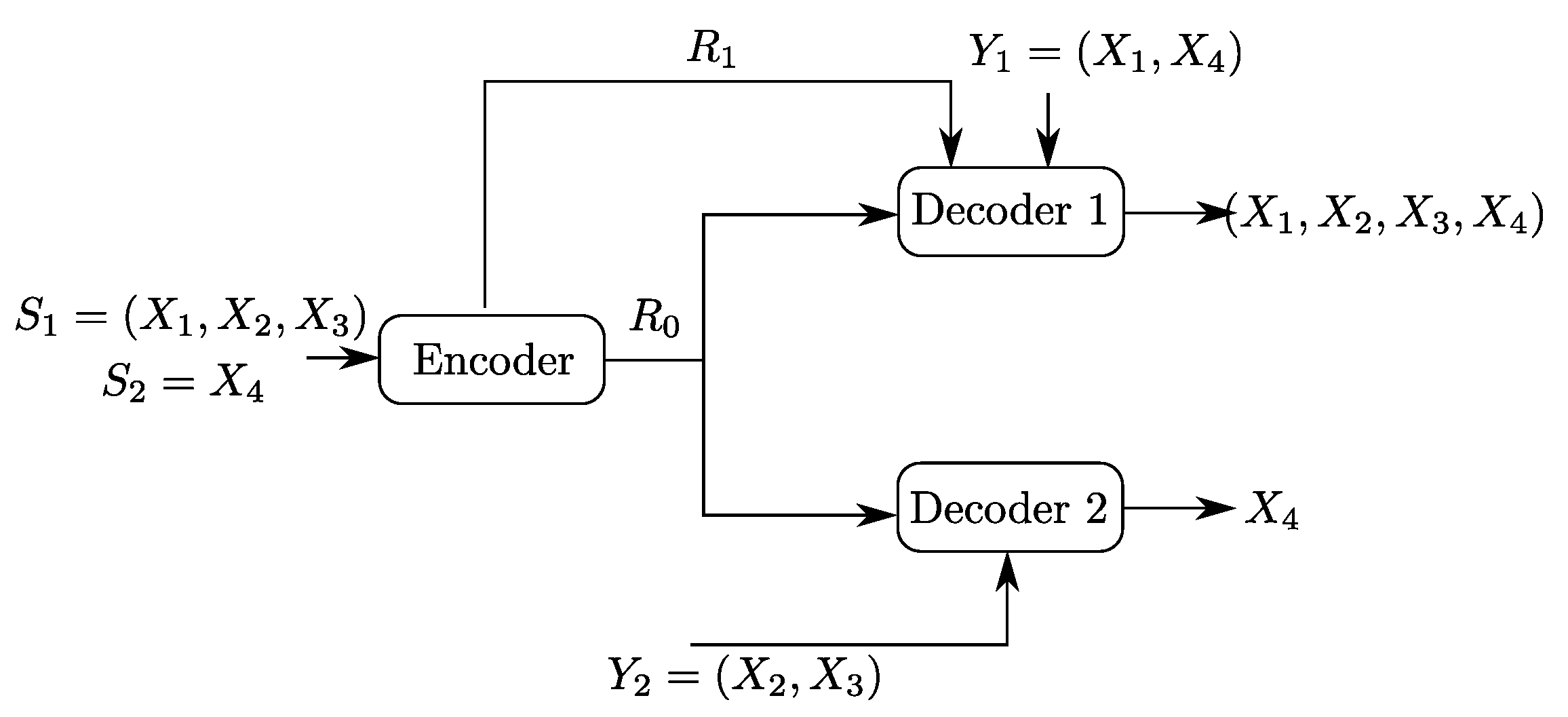
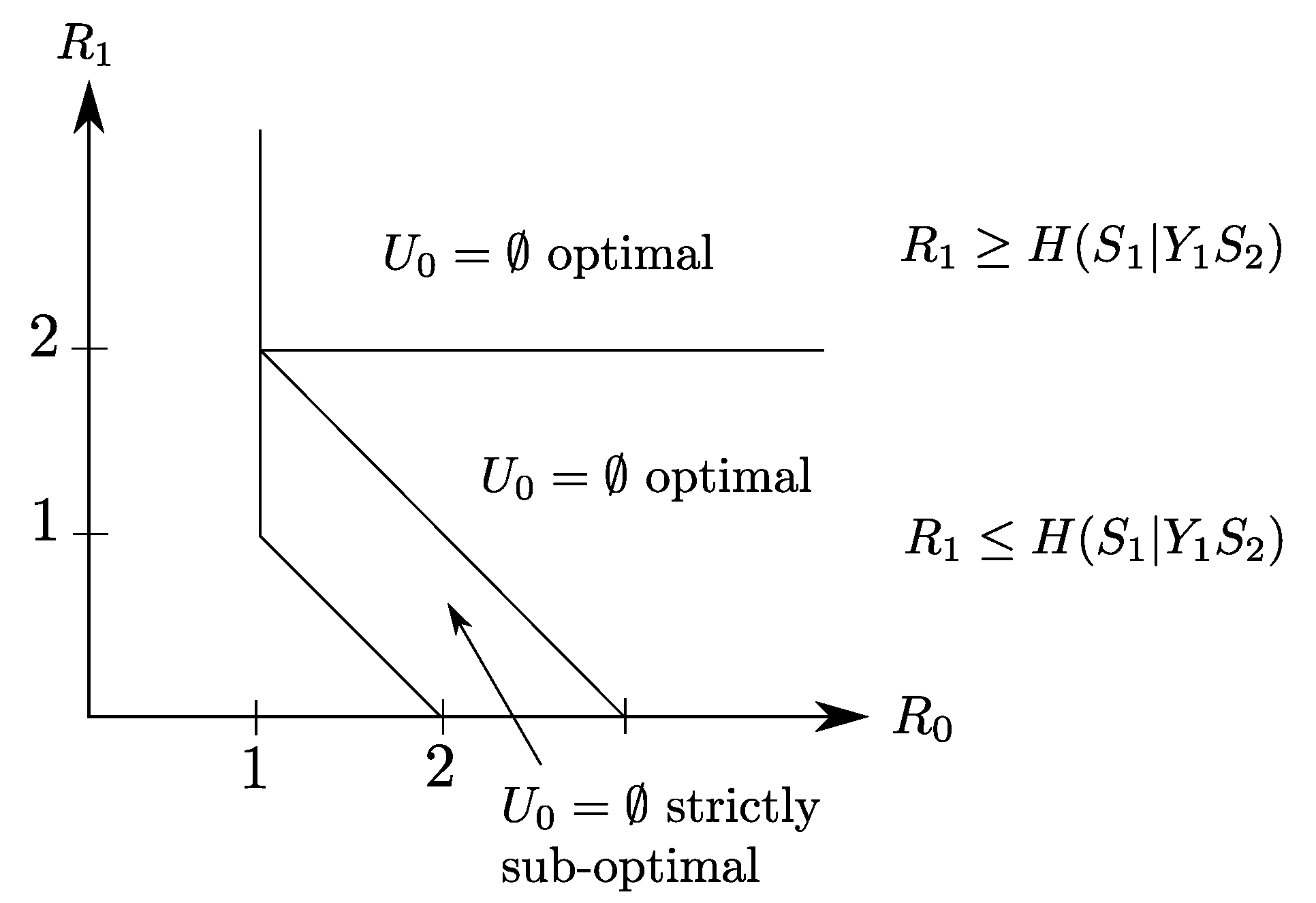
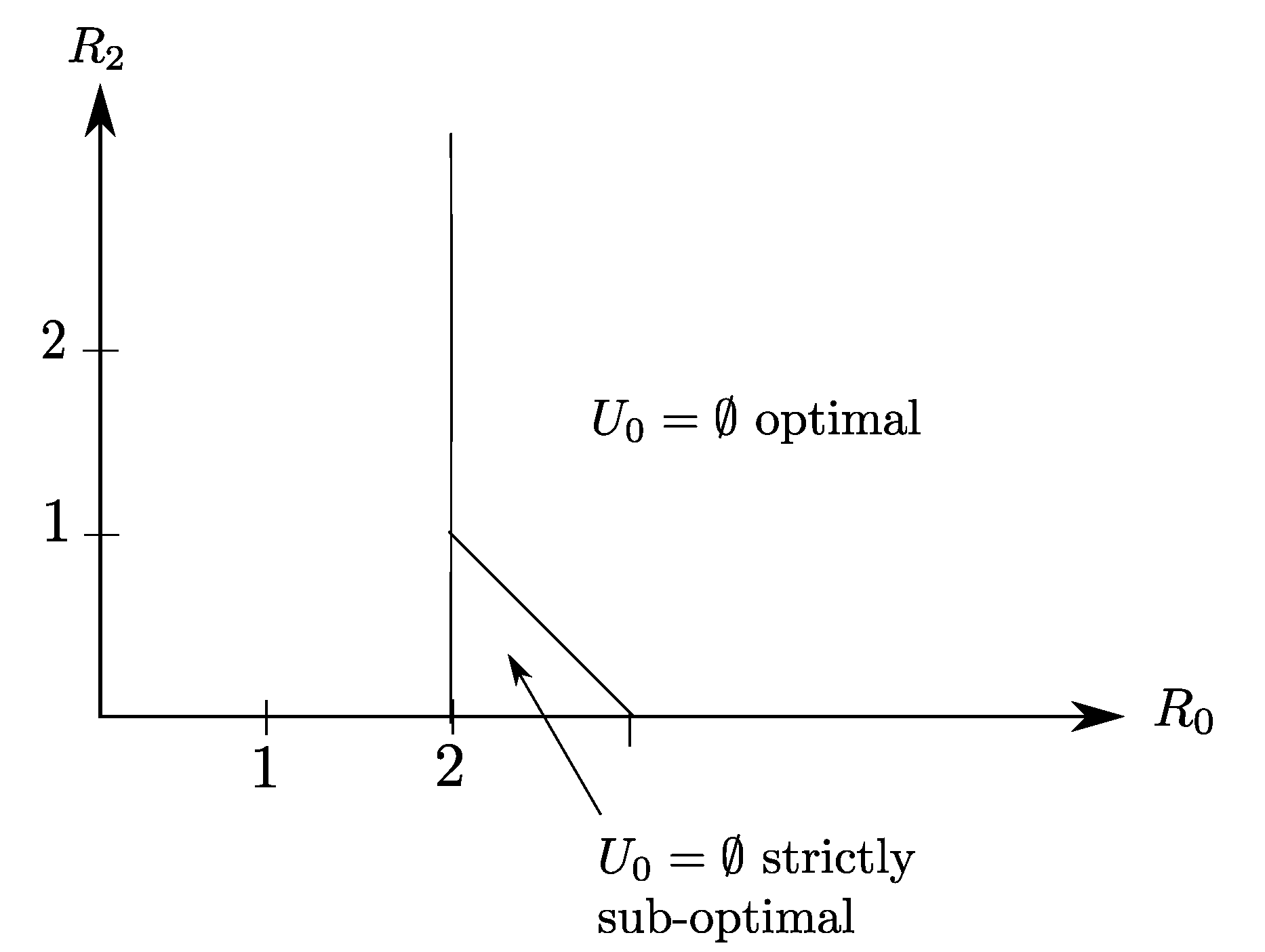
4.2. Binary Example
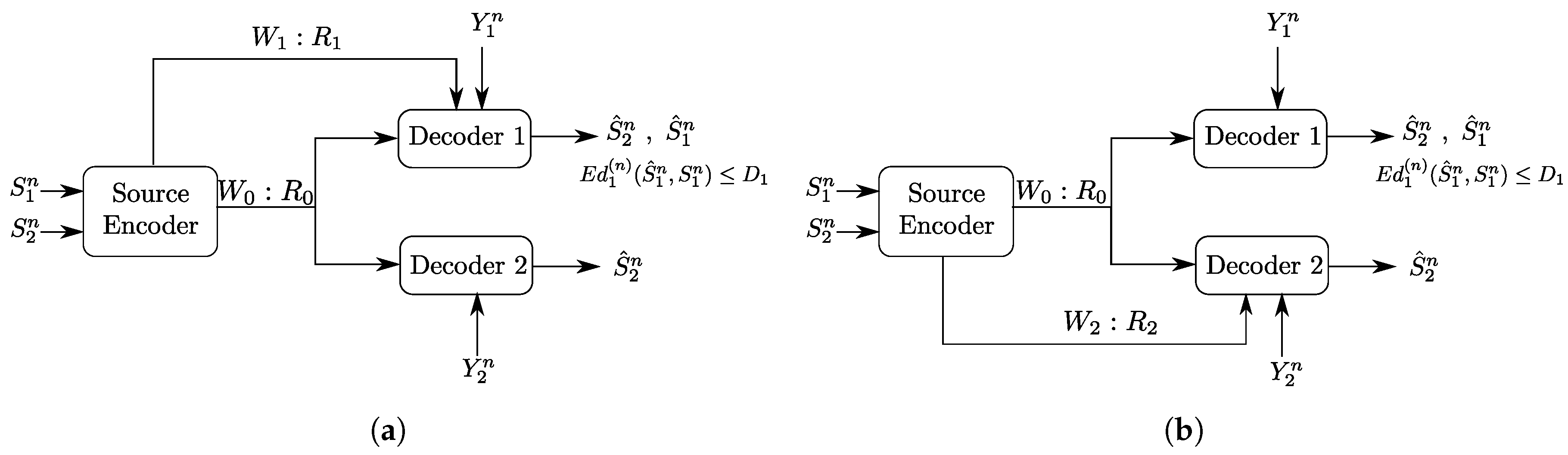
5. The Heegard–Berger Problem with Scalable Coding
5.1. Rate-Distortion Region
- (1)
- The following Markov chain is valid:
- (2)
- There exists a function such that:
5.2. Binary Example
6. Proof of Theorem 1
6.1. Proof of Converse Part
6.2. Proof of Direct Part
6.2.1. Codebook Generation
- (1)
- Randomly and independently generate length-n codewords indexed with the pair of indices , where and . Each codeword has i.i.d. entries drawn according to . The codewords are partitioned into superbins whose indices will be relevant for both receivers; and each superbin is partitioned int two different ways, each into subbins whose indices will be relevant for a distinct receiver (i.e., double-binning). This is obtained by partitioning the indices as follows. We partition the indices into bins by randomly and independently assigning each index to an index according to a uniform pmf over . We refer to each subset of indices with the same index as a bin , . In addition, we make two distinct partitions of the indices , each relevant for a distinct receiver. In the first partition, which is relevant for Receiver 1, the indices are assigned randomly and independently each to an index according to a uniform pmf over . We refer to each subset of indices with the same index as a bin , . Similarly, in the second partition, which is relevant for Receiver 2, the indices are assigned randomly and independently each to an index according to a uniform pmf over ; and refer to each subset of indices with the same index as a bin , .
- (2)
- For each , randomly and independently generate length-n codewords indexed with the pair of indices , where and . Each codeword is with i.i.d. elements drawn according to . We partition the indices into bins by randomly and independently assigning each index to an index according to a uniform pmf over . We refer to each subset of indices with the same index as a bin , . Similarly, we partition the indices into bins by randomly and independently assigning each index to an index according to a uniform pmf over ; and refer to each subset of indices with the same index as a bin , .
- (3)
- Reveal all codebooks and their partitions to the encoder, the codebook of and its partitions to both receivers, and the codebook of and its partitions to only Receiver 1.
6.2.2 Encoding
6.2.3 Decoding
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gray, R.; Wyner, A. Source coding for a simple network. Bell Syst. Tech. J. 1974, 53, 1681–1721. [Google Scholar] [CrossRef]
- Heegard, C.; Berger, T. Rate distortion when side information may be absent. IEEE Trans. Inf. Theory 1985, 31, 727–734. [Google Scholar] [CrossRef]
- Tian, C.; Diggavi, S.N. Side-information scalable source coding. Inf. Theory IEEE Trans. 2008, 54, 5591–5608. [Google Scholar] [CrossRef]
- Shayevitz, O.; Wigger, M. On the capacity of the discrete memoryless broadcast channel with feedback. IEEE Trans. Inf. Theory 2013, 59, 1329–1345. [Google Scholar] [CrossRef]
- Kaspi, A.H. Rate distortion function when side information may be present at the decoder. IEEE Trans. Inf. Theory 1994, 40, 2031–2034. [Google Scholar] [CrossRef]
- Sgarro, A. Source coding with side information at several decoders. Inf. Theory IEEE Trans. 1977, 23, 179–182. [Google Scholar] [CrossRef]
- Tian, C.; Diggavi, S.N. On multistage successive refinement for Wyner–Ziv source coding with degraded side informations. Inf. Theory IEEE Trans. 2007, 53, 2946–2960. [Google Scholar] [CrossRef]
- Timo, R.; Oechtering, T.; Wigger, M. Source Coding Problems With Conditionally Less Noisy Side Information. Inf. Theory IEEE Trans. 2014, 60, 5516–5532. [Google Scholar] [CrossRef]
- Benammar, M.; Zaidi, A. Rate-distortion function for a heegard-berger problem with two sources and degraded reconstruction sets. IEEE Trans. Inf. Theory 2016, 62, 5080–5092. [Google Scholar] [CrossRef]
- Timo, R.; Grant, A.; Kramer, G. Rate-distortion functions for source coding with complementary side information. In Proceedings of the 2011 IEEE International Symposium on Information Theory (ISIT), St. Petersburg, Russia, 31 July–5 August 2011; pp. 2934–2938. [Google Scholar]
- Unal, S.; Wagner, A. An LP bound for rate distortion with variable side information. In Proceedings of the Data Compression Conference (DCC), Snowbird, UT, USA, 4–7 April 2017. [Google Scholar]
- Equitz, W.H.; Cover, T.M. Successive refinement of information. IEEE Trans. Inf. Theory 1991, 37, 269–275. [Google Scholar] [CrossRef]
- Steinberg, Y.; Merhav, N. On successive refinement for the Wyner-Ziv problem. IEEE Trans. Inf. Theory 2004, 50, 1636–1654. [Google Scholar] [CrossRef]
- Timo, R.; Chan, T.; Grant, A. Rate distortion with side-information at many decoders. Inf. Theory IEEE Trans. 2011, 57, 5240–5257. [Google Scholar] [CrossRef]
- Timo, R.; Grant, A.; Chan, T.; Kramer, G. Source coding for a simple network with receiver side information. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Toronto, ON, Canada, 6–11 July 2008; pp. 2307–2311. [Google Scholar]
- Gamal, A.E.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]

| ∅ | ∅ | ||
| ∅ | |||
| ∅ | ∅ | ||
| ∅ | ∅ | ∅ | |
| ∅ | ∅ | ∅ | |
| ∅ | ∅ | ∅ |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benammar, M.; Zaidi, A. Rate-Distortion Region of a Gray–Wyner Model with Side Information. Entropy 2018, 20, 2. https://doi.org/10.3390/e20010002
Benammar M, Zaidi A. Rate-Distortion Region of a Gray–Wyner Model with Side Information. Entropy. 2018; 20(1):2. https://doi.org/10.3390/e20010002
Chicago/Turabian StyleBenammar, Meryem, and Abdellatif Zaidi. 2018. "Rate-Distortion Region of a Gray–Wyner Model with Side Information" Entropy 20, no. 1: 2. https://doi.org/10.3390/e20010002
APA StyleBenammar, M., & Zaidi, A. (2018). Rate-Distortion Region of a Gray–Wyner Model with Side Information. Entropy, 20(1), 2. https://doi.org/10.3390/e20010002




