Abstract
In this work we relax the usual separability assumption made in rate-distortion literature and propose -separable distortion measures, which are well suited to model non-linear penalties. The main insight behind -separable distortion measures is to define an n-letter distortion measure to be an -mean of single-letter distortions. We prove a rate-distortion coding theorem for stationary ergodic sources with -separable distortion measures, and provide some illustrative examples of the resulting rate-distortion functions. Finally, we discuss connections between -separable distortion measures, and the subadditive distortion measure previously proposed in literature.
1. Introduction
Rate-distortion theory, a branch of information theory that studies models for lossy data compression, was introduced by Claude Shannon in [1]. The approach of [1] is to model the information source with distribution on , a reconstruction alphabet , and a distortion measure . When the information source produces a sequence of n realizations, the source is defined on with reconstruction alphabet , where and are n-fold Cartesian products of and . In that case, [1] extended the notion of a single-letter distortion measure to the n-letter distortion measure, , by taking an arithmetic average of single-letter distortions,
Distortion measures that satisfy (1) are referred to as separable (also additive, per-letter, averaging); the separability assumption has been ubiquitous throughout rate-distortion literature ever since its inception in [1].
On the one hand, the separability assumption is quite natural and allows for a tractable characterization of the fundamental trade-off between the rate of compression and the average distortion. For example, in the case when is a stationary and memoryless source the rate-distortion function, which captures this trade-off, admits a simple characterization:
On the other hand, the separability assumption is very restrictive as it only models distortion penalties that are linear functions of the per-letter distortions in the source reproduction. Real-world distortion measures, however, may be highly non-linear; it is desirable to have a theory that also accommodates non-linear distortion measures. To this end, we propose the following definition:
Definition 1 (f-separable distortion measure).
Let be a continuous, increasing function on . An n-letter distortion measure is -separable with respect to a single-letter distortion if it can be written as
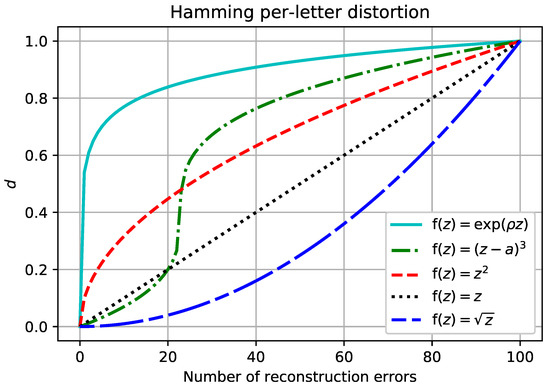
For this is the classical separable distortion set up. By selecting appropriately, it is possible to model a large class of non-linear distortion measures, see Figure 1 for illustrative examples.

Figure 1.
The number of reconstruction errors for an information source with 100 bits vs. the penalty assessed by -separable distortion measures based on the Hamming single-letter distortion. The plot corresponds to the separable distortion. The -separable assumption accommodates all of the other plots, and many more, with the appropriate choice of the function .
In this work, we characterize the rate-distortion function for stationary and ergodic information sources with -separable distortion measures. In the special case of memoryless and stationary sources we obtain the following intuitive result:
A pleasing implication of this result is that much of rate-distortion theory (e.g., the Blahut-Arimoto algorithm) developed since [1] can be leveraged to work under the far more general -separable assumption.
The rest of this paper is structured as follows. The remainder of Section 1 overviews related work: Section 1.1 provides the intuition behind Definition 1, Section 1.2 reviews related work in other compression problems, and Section 1.3 connects -separable distortion measures with sub-additive distortion measures. Section 2 formally sets up the problem and demonstrates why convexity of the rate-distortion function does not always hold under the -separable assumption. Section 3 presents our main result, Theorem 1, as well as some illustrative examples. Additional discussion about problem formulation and sub-additive distortion measures is given in Section 4. We conclude the paper in Section 5.
1.1. Generalized -Mean and Rényi Entropy
To understand the intuition behind Definition 1, consider aggregating n numbers by defining a sequence of functions (indexed by n)
where is a continuous, increasing function on , , and . It is easy to see that (5) satisfies the following properties:
- is continuous and monotonically increasing in each ,
- is a symmetric function of each ,
- If for all i, then ,
- For any
Moreover, it is shown in [2] that any sequence of functions that satisfies these properties must have the form of Equation (5) for some continuous, increasing . The function is referred to as “Kolmogorov mean”, “quasi-arithmetic mean”, or “generalized -mean”. The most prominent examples are the geometric mean, , and the root-mean-square, .
The main insight behind Definition 1 is to define an n-letter distortion measure to be an -mean of single-letter distortions. The -separable distortion measures include all n-letter distortion measures that satisfy the above properties, with the last property saying that the non-linear “shape” of distortion measure (cf. Figure 1) is independent of n.
Finally, we note that Rényi also arrived at his well-known family of entropies [3] by taking an -mean of the information random variable:
where the information at x is
Rényi [3] limited his consideration to functions of the form in order to ensure that entropy is additive for independent random variables.
1.2. Compression with Non-Linear Cost
Source coding with non-linear cost has already been explored in the variable-length lossless compression setting. Let denote the length of the encoding of x by a given variable length code. Campbell [4,5] proposed minimizing a cost function of the form
instead of the usual expected length. The main result of [4,5] is that for
the fundamental limit of such setup is Rényi entropy of order . For more general , this problem was handled by Kieffer [6], who showed that (9) has a fundamental limit for a large class of functions . That limit is Rényi entropy of order with
More recently, a number of works [7,8,9] studied related source coding paradigms, such as guessing and task encoding. These works also focused on the exponential functions given in (10); in [7,8] Rényi entropy is shown to be a fundamental limit yet again.
1.3. Sub-Additive Distortion Measures
A notable departure from the separability assumption in rate-distortion theory is sub-additive distortion measures discussed in [10]. Namely, a distortion measure is sub-additive if
In the present setting, an -separable distortion measure is sub-additive if is concave:
Thus, the results for sub-additive distortion measures, such as the convexity of the rate-distortion function, are applicable to -separable distortion measures when is concave.
2. Preliminaries
Let X be a random variable defined on with distribution , with reconstruction alphabet , and a distortion measure . Let be the message set.
Definition 2 (Lossy source code).
A lossy source code is a pair of mappings,
A lossy source-code is an -lossy source code on if
A lossy source code is an -lossy source code on if
Definition 3.
An information source is a stochastic process
If is an -lossy source code for on , we say is an -lossy source code. Likewise, an -lossy source code for on is an -lossy source code.
2.1. Rate-Distortion Function (Average Distortion)
Definition 4.
Let a sequence of distortion measures be given. The rate-distortion pair is achievable if there exists a sequence of -lossy source codes such that
Our main object of study is the following rate-distortion function with respect to -separable distortion measures.
Definition 5.
Let be a sequence of -separable distortion measures. Then,
If is the identity, then we omit the subscript and simply write .
2.2. Rate-Distortion Function (Excess Distortion)
It is useful to consider the rate-distortion function for -separable distortion measures under the excess distortion paradigm.
Definition 6.
Let a sequence of distortion measures be given. The rate-distortion pair is (excess distortion) achievable if for any there exists a sequence of -lossy source codes such that
Definition 7.
Let be a sequence of -separable distortion measures. Then,
Characterizing the -separable rate-distortion function is particularly simple under the excess distortion paradigm, as shown in the following lemma.
Lemma 1.
Let the single-letter distortion and an increasing, continuous function be given. Then,
where is computed with respect to .
Proof.
Let be a sequence of -separable distortions based on and let be a sequence of separable distortion measures based on .
Since is increasing and continuous at d, then for any there exists such that
The reverse is also true by continuity of : for any there exists such that (22) is satisfied.
Any source code is an -lossless code under -separable distortion if and only if is also an -lossless code under separable distortion . Indeed,
where . It follows that is (excess distortion) achievable with respect to if and only if is (excess distortion) achievable with respect to . The lemma statement follows from this observation and Definition 6. ☐
2.3. -Separable Rate-Distortion Functions and Convexity
While it is a well-established result in rate-distortion theory that all separable rate-distortion functions are convex ([11], Lemma 10.4.1), this need not hold for -separable rate-distortion functions.
The convexity argument for separable distortion measures is based on the idea of time sharing; that is, suppose there exists an -lossy source code of blocklength and an -lossy source code of blocklength . Then, there exists an -lossy source code of blocklength n with and : such a code is just a concatenation of codes over blocklengths and . The distortion d is achievable since
and letting ,
Time sharing between the two schemes gives
However, this bound on the distortion need not hold for -separable distortions. Consider which is strictly convex and suppose
We can write
Thus, concatinating the two schemes together does not guarantee that the distortion assigned by the -separable distortion measure is bounded by d.
3. Main Result
In this section we make the following standard assumptions, see [12].
- is a stationary and ergodic source.
- The single-letter distortion function and the continuous and increasing function are such that
- For each , there exists a countable subset of and a countable measurable partition of such that , for each , and
Theorem 1.
Under the stated assumptions, the rate-distortion function is given by
where
is the rate-distortion function computed with respect to the separable distortion measure given by .
For stationary memoryless sources (34) particularizes to
Proof.
Equations (35) and (36) are widely known in literature (see, for example, [10,11,13]); it remains to show (34). Under the stated assumptions,
where (a) follows from assumption (2) and Theorem A1 in the Appendix A, (b) is shown in Lemma 1, and (c) is due to [14] (see also ([13], Theorem 5.9.1)). The other direction,
is a consequence of the strong converse by Kieffer [12], see Lemma A1 in the Appendix A. ☐
An immediate application of Theorem 1 gives the -separable rate-distortion function for several well-known binary memoryless sources (BMS).
Example 1 (BMS, Hamming distortion).
Let be the binary memoryless source. That is, , is a Bernoulli random variable, and is the usual Hamming distortion measure. Then, for any continuous increasing and ,
where
is the binary entropy function. The result follows from a series of obvious equalities,
The rate-distortion function given in Example 1 is plotted in Figure 2 for different functions . The simple derivation in Example 1 could be applied to any source for which the single-letter distortion measure can take on only two values, as is shown in the next example.

Figure 2.
for the binary memoryless source with . Compare these to the -separable distortion measures plotted for the binary source with Hamming distortion in Figure 1.
Example 2 (BMS, Erasure distortion).
Let be the binary memoryless source and let the reconstruction alphabet have the erasure option. That is, , , and is a Bernoulli random variable. Let be the usual erasure distortion measure:
The separable rate-distortion function for the erasure distortion is given by
see ([11], Problem 10.7). Then, for any continuous increasing ,
The rate-distortion function given in Example 2 is plotted in Figure 3 for different functions . Observe that for concave (i.e., subadditive distortion) the resulting rate-distortion function is convex, which is consistent with [10]. However, for that are not concave, the rate-distortion function is not always convex. Unlike in the conventional separable distortion measure, an -separable distortion measure is not convex in general.
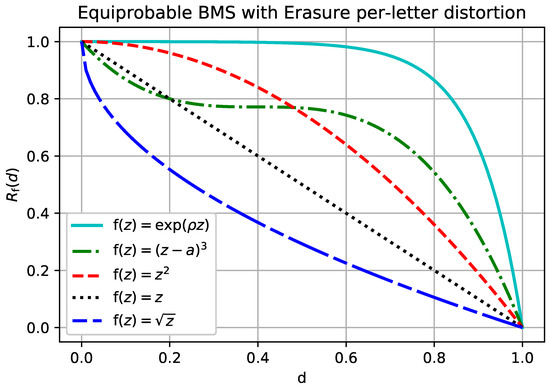
Figure 3.
for the binary memoryless source with and erasure per-letter distortion.
Having a closed-form analytic expression for a separable distortion measure does not always mean that we could easily derive such an expression for an -separable distortion measure with the same per-letter distortion. For example, consider the Gaussian source with the mean-square-error (MSE) per-letter distortion. According to Theorem 1, letting recovers the Gaussian source with the absolute value per-letter distortion. This setting, and variations on it, is a difficult problem in general [15]. However, we can recover the -separable rate-distortion function whenever the per-letter distortion composed with reconstructs the MSE distortion, see Figure 4.
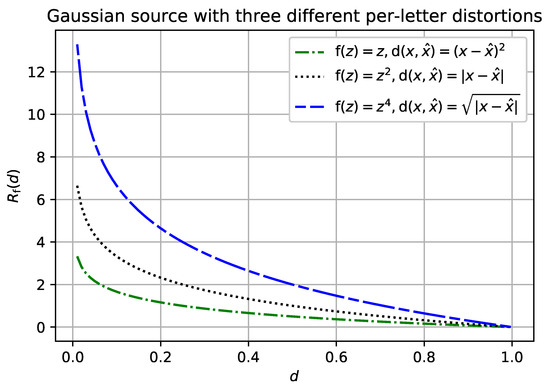
Figure 4.
for the Gaussian memoryless source with mean zero and unit variance.
Theorem 1 shows that for well-behaved stationary ergodic sources, admits a simple characterization. According to Lemma 1, the same characterization holds for the excess distortion paradigm without stationary and ergodic assumptions. The next example shows that, in general, within the average distortion paradigm. Thus, assumption (1) is necessary for Theorem 1 to hold.
Example 3 (Mixed Source).
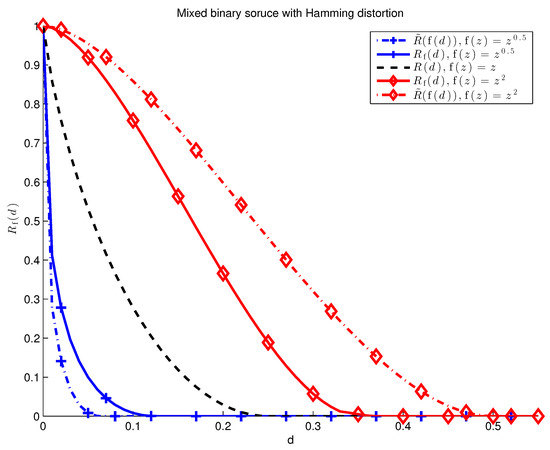
Fix and let the source be a mixture of two i.i.d. sources,
We can alternatively express as
where Z is a Bernoulli(λ) random variable. Then, the rate-distortion function for the mixture source (45) and continuous increasing is given in Lemma A2 in the Appendix B. Namely,
where and are the rate-distortion functions for discrete memoryless soruces given by and , respectively. Likewise,

Figure 5.
Mixed binary source with , , and . Three examples of -separable rate-distortion functions are given. For , the relation follows immediately. When is not the identity, in general for non-ergodic sources.
4. Discussion
4.1. Sub-Additive Distortion Measures
Recall that an -separable distortion measure is sub-additive if is concave (cf. Section 1.3). Clearly, not all -separable distortion measures are sub-additive, and not all sub-additive distortion measures are -separable. An examplar of a sub-additive distortion measure (which is not -separable) given in ([10], Chapter 5.2) is
The sub-additivity of (49) follows from the Minkowski inequality. Comparing (49) to a sub-additive, -separable distortion measure given by
we see that the discrepancy between (49) and (50) has to do not only with the different ranges of q but with the scaling factor as a function of n.
Consider a binary source with Hamming distortion and let . Rewriting (49) we obtain
and
In the binary example, the limiting distortion of (49) is zero even when the reconstruction of gets every single symbol wrong. It is easy to observe that example (49) is similarly degenerate in many cases of interest. The distortion measure given by (50), on the other hand, is an example of a non-trivial sub-additive distortion measure, as can be seen in Figure 2 and Figure 3 for .
4.2. A Consequence of Theorem 1
In light of the discussion in Section 1.1, an alert reader may consider modifying (16) to
and studying the -lossy source codes under this new paradigm. Call the corresponding rate-distortion function and assume that n-letter distortion measures are separable. Thus, at block length n the constraint (55) is
where . This is equivalent to the following constraints:
where is an -separable distortion measure. Putting these observations together with Theorem 1 yields
A consequence of Theorem 1 is that the rate distortion function remains unchanged under this new paradigm.
5. Conclusions
This paper proposes -separable distortion measures as a good model for non-linear distortion penalties. The rate-distortion function for -separable distortion measures is characterized in terms of separable rate-distortion function with respect to a new single-letter distortion measure, . This characterization is straightforward for the excess distortion paradigm, as seen in Lemma 1. The proof is more involved for the average distortion paradigm, as seen in Theorem 1. An important implication of Theorem 1 is that many prominant results in rate-distortion literature (e.g., Blahut-Arimoto algorithm) can be leveraged to work for -separable distortion measures.
Finally, we mention that a similar generalization is well-suited for channels with non-linear costs. That is, we say that is an -separable cost function if it can be written as
With this generalization we can state the following result which is out of the scope of this special issue.
Theorem 2 (Channels with cost).
The capacity of a stationary memoryless channel given by and -separable cost function based on single-letter function is
Author Contributions
Authors had equal contributions in the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Lemmas for Theorem 1
Theorem A1 can be distilled from several proofs in literature. We state it here, with proof, for completeness; it is given in its present form in [16]. The condition of Theorem A1 applies when the source satisfies assumptions (1)–(3) in Section 3. This is a consequence of the ergodic theorem and continuity of .
Theorem A1.
Suppose that the source and distortion measure are such that for any there exists and a sequence such that
If a rate-distortion pair is achievable under the excess distortion criterion, it is achievable under the average distortion criterion.
Proof.
Choose . Suppose there is a code with M codewords that achieves
We construct a new code with codewords:
Then
For brevity denote,
Then,
☐
The following theorem is shown in ([12], Theorem 1).
Theorem A2 (Kieffer).
Let be an information source satisfying conditions (1)–(3) in Section 3, with being the identity. Let be separable. Given an arbitrary sequence of -lossy source codes, if
then
An important implication of Theorem A2 for -separable rate-distortion functions is given in the following lemma.
Lemma A1.
Let be an information source satisfying conditions (1)–(3) in Section 3. Then,
Proof.
If , we are done. Suppose . Assume there exists a sequence of -lossy source codes (under -separable distortion) with
and
Since is continuous and decreasing, there exists some such that
For every n, the lossy source code is also an -lossy source code for some and -separable . It is also an -lossy source code with respect to separable distortion . We can therefore apply Theorem A2 to obtain
Thus,
where (A22) holds for all sufficiently large n. The result follows since we obtained a contradiction with (A18). ☐
Appendix B. Rate-Distortion Function for a Mixed Source
Lemma A2.
The rate-distortion function with respect to -separable distortion for the mixture source (45) is given by
where and are the rate-distortion functions with respect to -separable distortion for stationary memoryless sources given by and , respectively.
Proof.
Observe that,
where
and are the non-asymptotic limits for and , respectively. Indeed, the upper bound follows by designing optimal codes for and separately, and then combining them to give
The lower bound follows by the following argument. Fix an -lossy source code (-separable distortion), . Define
Clearly, . It also follows that
since is an -lossy source code (-separable distortion) code for . Likewise,
which proves the lower bound. The result follows directly from (A25). ☐
References
- Shannon, C.E. Coding Theorems for a Discrete Source with a Fidelity Criterion Institute of Radio Engineers, International Convention Record, vol. 7, 1959. In Claude E. Shannon: Collected Papers; Wiley-IEEE Press: Hoboken, NJ, USA, 1993. [Google Scholar]
- Tikhomirov, V. On the Notion of Mean. In Selected Works of A. N. Kolmogorov; Tikhomirov, V., Ed.; Springer: Dordrecht, The Netherlands, 1991; Volume 25, pp. 144–146. [Google Scholar]
- Rényi, A. On Measures of Entropy and Information; Contributions to the Theory of Statistics. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Campbell, L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Campbell, L. Definition of entropy by means of a coding problem. Z. Wahrscheinlichkeitstheorie Verwandte Gebiete 1966, 6, 113–118. [Google Scholar] [CrossRef]
- Kieffer, J. Variable-length source coding with a cost depending only on the code word length. Inf. Control 1979, 41, 136–146. [Google Scholar] [CrossRef]
- Arikan, E. An inequality on guessing and its application to sequential decoding. IEEE Trans. Inf. Theory 1996, 42, 99–105. [Google Scholar] [CrossRef]
- Bunte, C.; Lapidoth, A. Encoding Tasks and Rényi Entropy. IEEE Trans. Inf. Theory 2014, 60, 5065–5076. [Google Scholar] [CrossRef]
- Arikan, E.; Merhav, N. Guessing subject to distortion. IEEE Trans. Inf. Theory 1998, 44, 1041–1056. [Google Scholar] [CrossRef]
- Gray, R.M. Entropy and Information Theory, 2nd ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kieffer, J. Strong converses in source coding relative to a fidelity criterion. IEEE Trans. Inf. Theory 1991, 37, 257–262. [Google Scholar] [CrossRef]
- Han, T.S. Information-Spectrum Methods in Information Theory; Springer: Berlin, Germany, 2003. [Google Scholar]
- Steinberg, Y.; Verdú, S. Simulation of random processes and rate-distortion theory. IEEE Trans. Inf. Theory 1996, 42, 63–86. [Google Scholar] [CrossRef]
- Dytso, A.; Bustin, R.; Poor, H.V.; Shitz, S.S. On additive channels with generalized Gaussian noise. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 426–430. [Google Scholar]
- Verdú, S. ELE528: Information Theory Lecture Notes; Princeton University: Princeton, NJ, USA, 2015. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).