Abstract
Information processing performed by any system can be conceptually decomposed into the transfer, storage and modification of information—an idea dating all the way back to the work of Alan Turing. However, formal information theoretic definitions until very recently were only available for information transfer and storage, not for modification. This has changed with the extension of Shannon information theory via the decomposition of the mutual information between inputs to and the output of a process into unique, shared and synergistic contributions from the inputs, called a partial information decomposition (PID). The synergistic contribution in particular has been identified as the basis for a definition of information modification. We here review the requirements for a functional definition of information modification in neuroscience, and apply a recently proposed measure of information modification to investigate the developmental trajectory of information modification in a culture of neurons vitro, using partial information decomposition. We found that modification rose with maturation, but ultimately collapsed when redundant information among neurons took over. This indicates that this particular developing neural system initially developed intricate processing capabilities, but ultimately displayed information processing that was highly similar across neurons, possibly due to a lack of external inputs. We close by pointing out the enormous promise PID and the analysis of information modification hold for the understanding of neural systems.
1. Introduction
Shannon’s quantitative description of information and its transmission through a communication channel via the entropy and the channel capacity, respectively, has drawn considerable interest from the field of neuroscience from the very beginning. This is because information processing in neural systems is typically performed in a highly distributed way by many communicating processing elements, the neurons.
However, in contrast to a channel in Shannon’s sense, the purpose of dendritic connections in a neural system is not to simply relay information for the sake of reliable communication. Instead, communication between neurons serves the purpose of collecting multiple streams of information at a neural processing element that modifies this information, i.e., that synthesizes the incoming streams into output information that is not available from any of these streams in isolation. This becomes immediately clear when looking at the meshed structure of nervous systems, where multiple communication streams converge on single neurons, and where neural output signals are sent in a divergent manner to many different receiving neurons. This structure differs dramatically from a structure solely focused on the reliable transmission of information where many parallel, but non-interacting streams would suffice. Thus, the meshed architecture seems to have evolved to “fuse” information from different input sources (including a neuron’s recent spiking history and its current state) in a nontrivial way, e.g., other than simply multiplexing it in the output. In other words, the distributed computation in neural systems may heavily rely on information modification [1].
Attempts at formally defining information modification have presented a considerable challenge, however, in contrast to the well established measures of information transfer [2,3,4,5,6] and active information storage [7,8,9]. This is because identifying the “modified” information in the output of a processing element amounts to distinguishing it from the information from any input that survives the passage through the processor in unmodified form. These unmodified parts, in turn, may either come uniquely from one of the inputs, uniquely from another input (unique mutual information between an input and the output), or may be provided by multiple inputs simultaneously (shared mutual information between several inputs and the output). A decomposition of the mutual information between the inputs and the output of this kind is called a partial information decomposition (PID) [10] (Some authors prefer the simpler term “information decomposition”, also in this special issue.).
In a PID, the problem of identifying modified information is equivalent to identifying the part of the (joint) mutual information that is not unique mutual information from one or another input, and that is also not shared mutual information from multiple inputs. This remaining part has been termed synergistic mutual information in the work of Williams and Beer [10], and has been identified with information modification in [11] for the reasons given above.
The recent pioneering work by Williams and Beer [10] revealed that the standard axioms of information theory do not uniquely define the unique, shared and synergistic contributions to the mutual information, and that additional axioms must be chosen for its meaningful decomposition. Among several possible choices of additional axioms or assumptions available at the time of this study (see Section 4.1) we here adhere to the definition given independently by Bertschinger, Rauh, Olbrich, Jost, and Ay (“BROJA-measure”, [12]) and Griffith and Koch [13]. Our decision is based on two properties of the BROJA measure that seem necessary for an application to the problem of information modification as described above: first, in their definition, the presence of non-zero synergistic mutual information for the case of two inputs and one output cannot be deduced from the (two) marginal distributions of one input and one output variable. This property distinguishes the BROJA measure from the others available at the time; Bertschinger et al. [12] referred to it as Assumption (), and showed that the BROJA measure is the only measure that satisfies both Assumption (*) and (), where Assumption (*) indicates that the existence of unique information only depends on the pairwise marginal distributions between the individual inputs and the output. The measures from Williams and Beer [10] and Harder et al. [14] only satisfy Assumption (*), but not ()—see [12] for details. Second, the BROJA measure is placed on a rigorous mathematical footing, being derived directly from the aforementioned Assumption (*) rather than postulated ad hoc; furthermore, it has an operational interpretation in terms of expected utilities from the output based on knowledge of only each input, and many mathematical properties proven.
In our proof-of-principle study, we apply the BROJA decomposition of mutual information to the analysis of the emergent information processing in self-organizing neural cultures, and show that these novel information theoretic concepts indeed provide a meaningful contribution to our understanding of neural computation in this system.
2. Methods
In the following, we consider the neural data produced by two neurons as coming from two stationary random processes , , composed of random variables and , , with realizations , . The corresponding embedding or state space vectors are given in bold font, e.g., . The state space vector is constructed such that it renders the variable conditionally independent of all random variables with , i.e., .
2.1. Definition and Estimation of Unique, Shared and Synergistic Mutual Information
For two input random variables , and an output random variable Y (Figure 1), Bertschinger et al. [12] defined the four unique, shared and synergistic contributions to the joint mutual information as:
where I is the standard mutual or conditional mutual information [15,16], is the unique, the shared, and the synergistic mutual information. In our notation, the comma separates variables within a set that are considered jointly, the colon separates the (sets of) random variables between which the mutual information is computed, while the semicolon or backslash separates sets of random variables that we are decomposing such mutual information across. For the latter, the semicolon is used for measures where the sets of random variables are considered symmetrically (i.e., shared and synergistic information), while the backslash is used for asymmetric cases (i.e., unique information in one but not the other). in the above definitions is the space of probability distributions Q that have the same pairwise marginal distributions between each input and the output as the original joint distribution P of , , Y, i.e.:
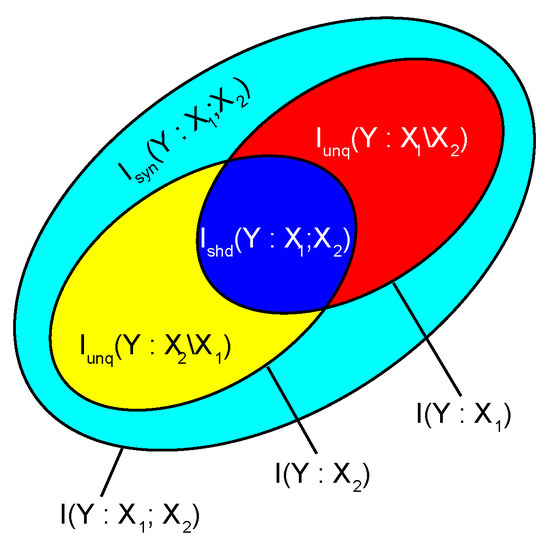
Figure 1.
Decomposition of the joint mutual information between two input variables , and the output variable Y. Modified from [17], CC-BY license.
2.2. Mapping of Neural Recordings to Input and Output Variables for PID, and Definition of Information Modification
In our application to developing neural cultures, we always consider two spike trains (A,B) at a time: the past state of the spike train A, , is one of the input variables and the past state of a spike train B, , is considered as the other input variable. Empirically, these states are usually constructed using the aforementioned embedding or state space vectors of length l. The output variable is simply spike train A’s current spiking behavior (spiking or not).
This output variable is computed from external inputs ( ) as well as the output variable’s own history . When analyzing this computation, one wishes to focus on the operations of information storage, transfer and modification, in alignment with established views of distributed information processing in complex systems [18,19]. In this study, specifically, we will focus on information modification, yet we first need to decompose the output variable in terms of information storage and information transfer, where the latter will also contain the information modification (see [11] and Figure 2):
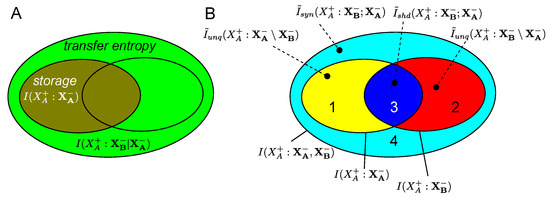
Figure 2.
Mapping between the decomposition into storage and transfer (A) and individual or joint mutual information terms, and PID components (B). Numbers in (B) refer to the enumeration of components given in Section 2.2. Number “4” is the modified information.
Here, is the active information storage [7], the predictive information from the past state of the variable to its next value. Then, is the transfer entropy [2], the predictive information from the past of the other source B to the next value of A, in the context of the past of A.
In order to identify information modification, we need to take this decomposition further to reveal two sub-components of each of these information storage and transfer terms. These sub-components result from a partial information decomposition of into four parts (see Figure 2):
- The unique mutual information of the output spike train’s own past —this can be considered as information uniquely stored in the past output of the spike train that reappears at the present sample.
- The unique information from the other spike train —this is the information that is transferred unmodified from the input to the output of the receiving spike train (also known as the state independent transfer entropy [20]).
- The shared mutual information about the output of spike train A that can be obtained both from the past states of spike train A and of spike train B, —this is information that is redundantly stored in the past of both spike trains and that reappears at the present sample.
- The synergistic mutual information , i.e., the information in the output of spike train A, , that can only be obtained when having knowledge about both the past state of the external input, , and the past state of the receiving spike train, . (This is also known as the state dependent transfer entropy [20]).
We see that Components 1 and 3 above form the active information storage in Equation (6), while Components 2 and 4 form the transfer entropy term. Component 4, as the synergistic mutual information contributed by the storage and the transfer source, is what we consider to be the modified information (following [11]). The same underlying definition of information modification from [11] was used by Timme et al. [21] in an earlier study of dynamics of spiking activity of neural cultures, yet with another PID measure and considering multiple external inputs to a neuron (see discussion for further details).
2.3. PID Estimation
PID terms were estimated by minimizing the conditional mutual information as indicated in the first equation of the system 1. To perform the minimization, we used a stochastic approach where alternative trial distributions in are created by swapping probability mass between the symbols of the current distribution such that the constraints defining are satisfied. If this swap of probability mass leads to a reduction in the conditional mutual information, the trial distribution is made the current distribution, and a new trial distribution is created. If the trial distribution fails to reduce the conditional mutual information, then a new trial distribution is created from the current distribution. This latter process is repeated for a maximum of n unsuccessful swaps in a row (here n = 20,000), with a reset of the counter in case of a successful swap. If after these trials no reduction is reached, then we assume that we have found the optimum possible with the current increment in probability mass and that a finer resolution is needed. Hence, the increment is halved: . This process starts with an initial equal to the largest probability mass assigned to any symbol in the distribution P, and is repeated until the numerical precision of the machine or programming language is exhausted (here, we performed 63 divisions of the original by a factor of 2, using Numpy 1.11.2 under Python 3.4.3 and 128-bit floating point numbers). The algorithm is available in the open source toolbox IDT [22]. We note that better solutions based on convex optimization exist (see Makkeh et al. [23] in this special issue) and that these are implemented in newer versions of IDT; at the time of performing this study, however, these implementations were not available to us yet.
2.4. Statistical Testing
Results obtained for the joint mutual information, and for the four PID measures normalized by the joint mutual information, were subjected to pairwise statistical tests for differences in the median between recordings days (see Section 2.5) by means of permutation tests. An uncorrected p-value of , corresponding to p-value of with Bonferroni correction for multiple comparisons across five measures, and 20 pairs of recording days, was considered significant.
We normalized the PID values to remove influences from changes in the overall activity of the culture (that change the entropy of the inputs) and to abstract from changes in the overall joint mutual information. Note that we did not test these normalized PID values for significance against surrogate data, as the focus here was on changes with development of the culture. Moreover, the four normalized PID terms analyzed here are not independent from each other, but instead sum up to a value of 1, making the construction of a meaningful statistical test difficult.
2.5. Electrophysiological Data—Acquisition and Preprocessing
The spike recordings were obtained by Wagenaar et al. [24] from a single in vitro culture of 50,000 cortical neurons. The data are available online at [25]; of the data provided in this repository, we used culture/experiment “2-1”, days 7, 14, 21, 28, and 34. Details on the preparation, maintenance and recording setting can be found in the original publication. In brief, cultures were prepared from embryonic E18 rat cortical tissue. Recordings lasted more than 30 min. The recording system comprised an array of 59 titanium nitride electrodes with 30 m diameter and 200 m inter-electrode spacing, manufactured by Multichannel Systems (Reutlingen, Germany). As described in the original publication, spikes were detected online using a threshold based detector as upward or downward excursions beyond 4.5 times the estimated root mean squared (RMS) noise [26]. Spike waveforms were stored, and used to remove duplicate detections of multiphasic spikes. Spike sorting was not employed, and thus spike data represent multi-unit activity. To obtain a tractable amount of data, we randomly picked spike time series from the dataset, and of these only selected those that developed at least a moderate level of activity with maturation of the culture (channels 01, 02, 03, 04, 05, 07, 11, 13, 14, 16, 19, 50, 53, 57, 58, 60), to guarantee a certain level of (Shannon) information to be present. In total, our analyses comprise 16 spike time series, i.e., 240 pairs of spike time series.
From these spike time series, the realizations of the random variable were constructed by applying bins of 8 ms length; empty bins were denoted by zeros, whereas bins that contained at least one spike were denoted with ones. The corresponding approximate past state vectors were constructed with finite past length , and to balance the need for low dimensionality for an unbiased estimate and a coverage of as much past history as possible, three past bins of size 8 ms, 32 ms and 32 ms were defined, where the shortest bin was the bin closest to i, and where both the 8 ms and the two 32 ms bins were set to one or zero depending on whether or not a spike occurred anywhere within these bins. This approach to cover a longer history at a low dimensionality amounts to a compressing of the information in the history of the process, aiming to retain what we perceive to be the most relevant information. This approach is similar to the one used by Timme et al. [27], except for the use of nonuniform binwidths in our case. Alternative approaches to large bin widths exist that are either based (i) on nonuniform embedding, picking the most informative past samples (or bins with a small width on the order of the inverse sampling rate) from a collection of candidates (e.g., [28,29,30]), and the IDT toolbox [22]; or (ii) on varying the lag between an a vector of evenly spaced past bins and the current sample [4,31,32], but both of these approaches might be less suitable for relatively sparse binary data, such as spike trains.
3. Results
3.1. PID of Information Processing in Neural Cultures
From the original report by Wagenaar et al. [26], the following aspects of the development of the “dense” culture analyzed here can be observed: (i) by preparation, neurons were unconnected and mostly silent at first; then (ii) show spontaneous activity and begin to be connected (compare the increase of mutual information between inputs and outputs in Figure 3); later, they (iii) become densely connected and thereby strongly responsive to each other’s spiking activity (Quote from [26]: “We … found that functional projections grew rapidly during the first week in vitro in dense cultures, reaching across the entire array within 15 days (Figure 9)”); while, in a last stage, (iv) connectivity often leads to activity pattern where all neurons become simultaneously active in large, culture spanning bursts of activity. This can, for example, be seen for data used here in the development of large, system spanning neural avalanches with maturation of the culture (see Figure 4 in [33] and Figure 13 in the corresponding preprint [34]; for the definition of neural avalanches as used here, see [35]). The number of such system spanning avalanches was [0, 0, 7, 50, 73] for the five recording weeks. At the same time, the mean avalanche sizes (defined in [35]) also increased as (1.05, 1.31, 1.81, 4.39, 3.42)—note the jump from week 2 to 3 in both measures, and compare to the normalized shared information in Figure 4.
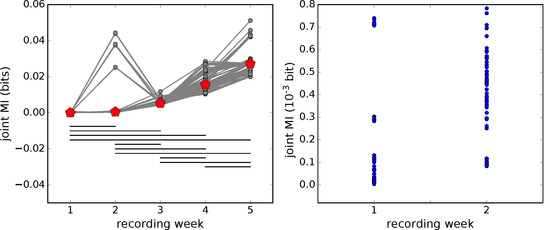
Figure 3.
Left: development of the joint mutual information with network maturation. Grey symbols and lines—joint mutual information (MI) from individual pairs of spike time series, red symbols—median over all pairs. Horizontal black lines connect significantly different pairs of median values (, permutation test, Bonferroni corrected for multiple comparisons); Right: magnification of the joint mutual information estimates in the first two recording weeks. Note that the three large outliers from week 2 have been omitted from the plot. These tiny, but non-zero, values form the basis for the normalized non-zero PID terms presented in Figure 4—also leading to considerable variance there.
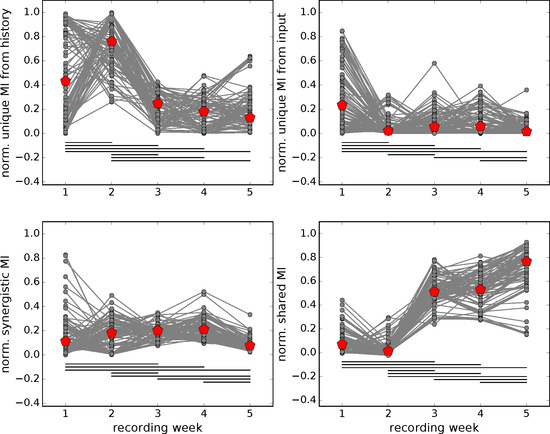
Figure 4.
Development of normalized PID contributions (i.e., PID terms normalized by the joint mutual information) with network maturation. Grey symbols and lines—PID values from individual pairs of spike time series, red symbols—median over all pairs. Horizontal black lines connect significantly different pairs of median values (, permutation test, Bonferroni corrected for multiple comparisons). On the lower right, note the sudden increase in normalized shared mutual information from week 2 to 3 that coincides with the onset of system spanning neural avalanches (see text).
From the viewpoint of partial information decomposition, we hypothesized that stages (i) and (ii) should be characterized by a high fraction of unique information from a neuron’s own history because neurons that do not yet receive sufficient input to trigger their firing can only have unique mutual information with their own history.
Unique information from other neuron’s inputs, and also synergy between both neurons’ past states should be visible in stage (iii) because we assume that neurons, even in vitro are wired to fuse information from multiple sources with their the information of their own state. Thus, we expected non-trivial computation in the form of synergy to be visible as long as the input distributions are sufficiently different from a neuron’s own history.
In the last stage (iv), partial information decomposition should then be dominated by shared mutual information because when all input distributions are more or less identical and highly correlated, then there can only be shared information (at least when using the BROJA measure).
From preliminary investigations [36], we also expected the joint mutual information between both inputs and the output to rise. Given the caveat that we analyzed multi-unit activity here, instead of single units (i.e., single neurons) obtained by spike sorting, our results comply with these hypotheses: the initial two recording weeks were dominated by unique information from a spike time series’ own history, while, in intermediate recording weeks, synergistic and shared information were dominant, and shared information finally prevailed in the last two recordings (Figure 3 shows the joint mutual information, with the normalized PID contributions to this shown in Figure 4 and raw PID contributions in Figure 5).
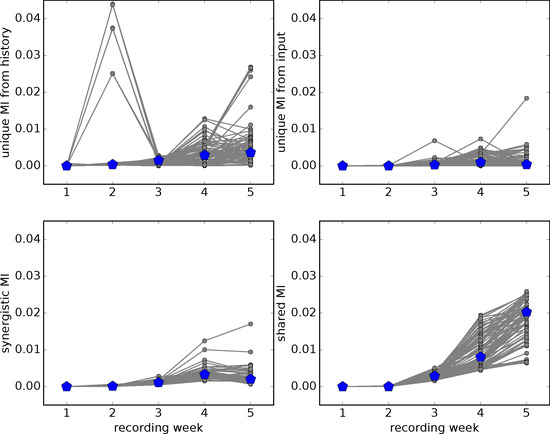
Figure 5.
Development of raw PID contributions with network maturation. Grey symbols and lines—PID values from individual pairs of spike time series, blue symbols—median over all pairs. Note that we do not provide statistical tests here as the visible differences are heavily influenced by the corresponding differences in the joint mutual information (see Figure 3).
4. Discussion
We here applied PID to neural spike recordings with the objective to compute a measure of information modification, and, for the first time, to assess its face validity given what is already known about information processing in developing neural cultures. Our analyses of the synergistic part of the mutual information between information storage and transfer sources, which we see as a promising candidate measure of information modification, complied with our intuition on how information modification should rise with development as neurons get connected and their synaptic weights adapt to the environment of the culture (i.e., with a lack of external input to the culture). The end of this rise in (relative) information modification and a final drop caused by a jump in the (relative) shared part in the mutual information was also expected given that a computation must always be understood as the composition of a mechanism and an input distribution. This input distribution is well known to get more and more similar over neurons as the culture approaches the typical bursting behavior that synchronizes all activity. With all input distributions being similar in this way, there is reduced scope for modifying information—hence the observed drop in the last recording week. In summary, the partial information decomposition used here and the results for its synergistic part capture well our intuition of what should happen in this simple neural system. This increases confidence in the usefulness and interpretability of PID measures in the analysis of neural data from more complex neural systems.
Two additional aspects seem important here: first, our analyses underline one of the key theoretical advances of PID, that all four PID terms, and especially shared and synergistic ones, can coexist simultaneously—a fact overlooked in early attempts to define shared (or `redundant’) and synergistic contributions to the mutual information (see references in [10]); second, no knowledge on the typical development of neural cultures was necessary to arrive at our PID results; in other words, the development of computation in the culture could have been derived from our PID analysis alone. This makes PID of neural activity a useful first step when investigating the computational architecture of a neural system.
In the sections below, we discuss some caveats to consider with this relatively young analysis technique, where several competing definitions of a PID coexist, not all of them equally suitable for computing information modification [11]. We also expand on the aforementioned relation between measures of information transfer and modification. Moreover, we would like to highlight and expand on the fact that a computation is a composition of an input distribution and a mechanism working on these inputs. Neglecting the importance of the input distribution and understanding a PID as directly describing a computational mechanism is a frequent misunderstanding that we would like to clarify here. We close by highlighting potential uses of PID in neuroscience.
4.1. Which Definition of Synergistic Mutual Information to Use?
In contrast to earlier studies of synergy or information modification in neural data [21,37], we here used the definition of unique, shared and synergistic mutual information as given by Bertschinger et al. [12] and by Griffith and Koch [13] (BROJA-decomposition). As initially outlined, in our view, this definition was the only published one at the time of experiment that had the properties necessary for a mapping between information modification and the synergistic part of the mutual information, and is sufficiently easy to compute because of the convexity of the underlying optimization.
However, the BROJA definition has also been criticized because a decomposition is only possible for the case of two inputs (although these inputs themselves can be arbitrarily large groups of variables). We consider this an acceptable restriction for some purposes in neuroscience as it seems to map well to the properties of cortical neurons; for example, the pyramidal neurons of the neocortex keep exactly two classes of inputs separate via their apical and basal dendrites (see [17,38,39] and references therein). In addition, as long as one is only interested in the computations performed by a neuron based on its own history and all its inputs considered together as one (vector-valued) input variable, this framework is sufficient (see, for example, the treatment of this case in the theoretical study presented in [17]).
In contrast to the BROJA-decomposition, Williams and Beer suggested in their original work [10] an alternative definition that allowed the decomposition of the mutual information between multiple inputs (considered separately, not as a group) and an output into a partial order (a mathematical “lattice”) of shared information terms. While this decomposition into a lattice of terms clearly is desirable, the measure of shared information given by Williams and Beer [10] (known as ) also has several properties that have been questioned. First, it does not respect the locality of information, i.e., point-wise interpretations of this shared information are not continuous with respect to the underlying probability distribution functions [11]. Second, it suggests the presence of shared information in situations where in each realization only a single source ever holds non-zero information about a target [40]. We note that the latter is an issue for the BROJA-decomposition as well.
Third, several authors have questioned the presence of non-zero shared mutual information under when there is no pairwise mutual information between the inputs themselves while the output is a simple collection of these inputs (known as “two bit copy”). A desire for zero shared mutual information in this case was formalized in a so-called identity axiom by Harder et al. [14]. This axiom suggests that if two inputs , with no mutual information between them () are combined into an output that is simply their collection, i.e., then the shared part of the joint mutual information must be zero. However there are significant arguments against the inclusion of such an axiom, and in support of the presence of shared information in the two bit copy problem; see, e.g., Bertschinger et al. [41], and, in this issue, by Ince [42] and Finn et al. [40]. For example, there can be no measure of redundant information that simultaneously satisfies the original three PID axioms, has non-negative PI atoms, and possesses the identity property [43].
Debates continue on this aspect, and, in the future, it will be interesting to check the consistency of results reported here with respect to alternative decompositions, such as those presented by Finn et al. [40] or Ince [42] in this issue.
In summary, the BROJA measure used in this study has several appealing properties, yet it lacks the ability to decompose the information of more than two input variables into a lattice. Several contributions to this special issue present progress on lattice-compatible distributions [40,42] and also investigate the consequences of the symmetrical, or asymmetrical treatment of information sources and targets [44] (also see the work of Olbrich et al. [45] on this topic).
4.2. Previous Studies of Information Modification in Neural Data
Timme et al. [21] studied information modification in the dynamics of spiking activity of neural cultures with a focus on the relation between information modification at a neuron and its position in the underling (effective) network structure. They report, for example, that neurons which modify “large amounts of information tended to receive connections from high out-degree neurons”. Both their study and ours have in common the same underlying definition of information modification [11]. Their study differs slightly from ours in examining synergy between two external inputs to a neuron, conditional on that neuron’s past, whereas we examine synergy between one external input and the receiving neuron’s past. A more important difference between their study and ours, however, is the choice of PID measure (see above). Specifically, they used the Williams and Beer [10] measure, in contrast to the BROJA measure used here—see Section 4.1 for details on the consequences of these choices.
Another important difference is the use of multi unit activity in our study, while Timme et al. [21] used spike sorted data that represents the activity of single neurons. However, for the data-set we used, spike extraction was relatively conservative, using a high threshold and removing events with spurious waveforms [26]. This resulted in a relatively low average multi-unit activity of less than 3.5 Hz. This is comparable to the mean rate of 2.1 Hz reported by Timme et al. [21]. From this, we estimate that only one or two close by neurons typically contribute to the recorded multi-unit activity. Thus, this difference may be relatively minor in practice. Conceptually, however, the information contained in single and multi-unit activity clearly differs in interpretation—see the next section for the more details.
We also note that there are earlier applications of the concept of synergy (meant as synergistic mutual information) to neural data (e.g., [46,47,48,49]) that relied on the computation of interaction information. However, when interpreting these studies, it should be kept in mind that these report the difference between shared information and synergistic information—as detailed by Williams and Beer [10]. If both are present in the data (a possibility that may simply have been overlooked by most researchers before Williams and Beer [10]), then this view of a `net-synergy’ only gives a partial view of the coding principles involved.
4.3. Information Represented by Multi and Single Unit Data
As detailed in the methods section, we performed our analyses on multi unit activity, i.e., we considered all spiking activity picked up by a recording electrode—potentially coming from multiple neurons. Thus, the information processing analyzed here is that of a cluster of neurons close to the recording electrodes, but not that of individual neurons, limiting the direct interpretation of our results. This problem can be alleviated by using spike sorting algorithms, e.g., based on the individual waveforms to assign each spike to an individual neuron, and then analyzing only the spikes of individual neurons. This has indeed been done in the study by Timme et al. [21] and improves the interpretation of the results in terms of neural coding. Ideally, it should be included in follow-up studies on information modification via PID as well. However, as the multi-unit activity reported here most likely contained only one or two single units (see previous section), we expect very similar results for an analysis of single units.
4.4. Measured Information Modification versus the Capacity of a Mechanism for Modifying Information
To appreciate the findings of the current study, it is important to realize that any computation is a composition of (i) a mechanism and (ii) an input distribution. As an extreme example, take an “exclusive or” (XOR)-gate, which has only one bit of synergy when fed by two uniformly distributed random bit inputs. However, when we clamp one of these inputs, for example , to producing just ’0s, then all the information (still one bit of joint mutual information) is unique information from the other input . This result must hold for all PID measures by virtue of the equations linking classic mutual information terms and PID terms (Equations (1)–(3) in [12], also consult Figure 1), and due to the fact that the mutual information of the clamped input and the output must be equal to or smaller than the entropy of that input, which is zero. Feeding the XOR gate with an alternative input distribution of the form , , yields bits of synergy and of unique information from , using the BROJA PID.
Another simple example would be a logical conjunction (AND)–gate fed by two different input distributions: when fed by two independent streams of input bits with uniform probabilities of zeros and ones, the BROJA PID results in bit of synergy and bit of shared information [12]. Feeding the same mechanism with an alternative input distribution of the following form: , , results in approximately bit of synergy and bit of shared information as measured by the BROJA PID.
This dependence of the PID on the input distribution means that describing a computation in terms of information modification via the synergistic information describes the joint operation of input distribution and mechanism (with the consequences related to bursting activity in neural cultures that were noted above). Indeed, this is the correct information theoretic description of how the system modified information in the specific computation reflected in the data. This description does not, however, inform us about how much information modification the mechanism performing the computation is capable of in principle. This is analogous to the situation of a communication channel in Shannon’s theory where the mutual information between the input X and the output Y of a channel informs us about how much information is actually communicated across the channel when it is fed by the input distribution . However, will not inform us about how much information we could in principle communicate across the channel, i.e., the capacity of the channel defined by:
Thus, for describing the potential of a mechanism to modify information, we must define an information modification capacity in analogy to the definition of an information transmission capacity (Equation (7)) by maximizing the synergistic mutual information over all input distributions as:
How tractable the double optimization process implied in Equation (8) is in practice and whether analytical simplifications can be derived remains the topic of future work. However, other measures of PID that do not rely on an optimization over the space of probability distributions (such as the one by Finn et al. [40] in this special issue) may allow for the computation of a capacity for information modification—given the mechanism is known.
We would like to emphasize that maximizing synergy, or any other PID term, over possible input distributions is different from maximizing the same PID term via changes to the mechanism that yields the output, while keeping the input distributions fixed. This latter approach is considered in detail by the contribution of Rauh et al. [50] in this special issue.
4.5. On the Distinction between Information Modification and Noise
We emphasize that the definition of information modification used here (and first put forward in [11]) will not count information that is created de novo in an information processing element and then appears in its output. This is because modified information in the output has to be explained ultimately by the input to a processing element and the state (or history) of that element, taken together. This clearly does not hold for information just created independently of the processor’s history. In other words, the information created de novo is counted as output noise instead of as modified information by our definition of information modification—a property that we consider desirable for any measure of information modification.
4.6. On the Relation between Transfer Entropy and Information Modification
As introduced in Section 2.2, the transfer entropy between two processes , , where the variables , carry the current values of the processes and the variables , carry the past state information is defined as [2]:
As first noted by Williams and Beer [20], the (conditional) mutual information on the right-hand side can be decomposed using a PID as well. As shown in Section 2.2, this conditional mutual information is composed of both a unique contribution from the source, and a synergistic contribution where the current value is determined jointly—and not explainable in any simpler way—by the combination of past states and , i.e., the input from to and ’s own history. (Of course, either component could be zero for a given distribution). Williams and Beer [10] suggested to call this synergistic part of the transfer entropy the (receiver) state dependent transfer entropy (SDTE) to highlight the interplay between sender and receiver in modifying the information. Obviously, such a subdivision of transfer is highly useful where computable. Naturally, the overlaps between the concepts of information modification and (multivariate) transfer entropy become more involved if receives more than one external input. What we label as information modification in this case would comprise the SDTE above, but perhaps not all of it, and also have additional contributions (see below and Figure 6).
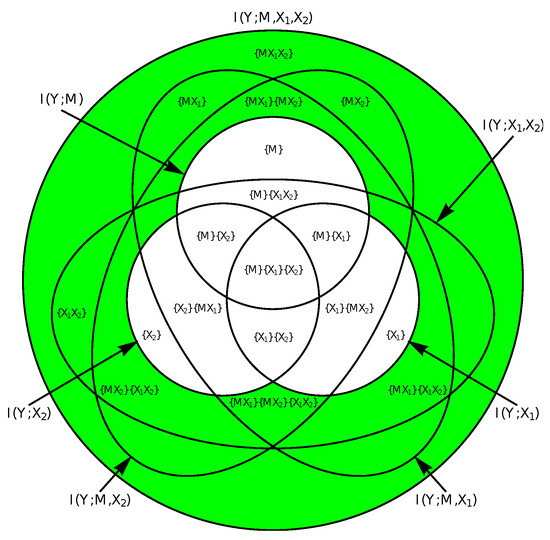
Figure 6.
PID diagram for three input variables—two of them external inputs (, ), and one representing the past state of the receiving system (). The parts of the diagram highlighted in green would be considered information modification. These parts represent the information in the receiver that can only be explained by two or more input variables considered jointly.
This is a special case of the general effect that the synergistic components of a PID may change if additional inputs are considered, e.g., when the additional input on its own brings in information that is itself redundant with the information seen as synergistic between the other inputs. See, for example, the component labeled with in Figure 6, which is synergistic when not considering , but redundantly also provided by alone. In more detail, a PID may decompose the information provided by a larger set of sources into many different shared (redundant), unique and synergistic components between subsets of these inputs. These components are placed onto a lattice (a partial order) by some variants of PID measures (see Section 4.1).
4.7. New Research Perspectives in Neuroscience Based on PID and Information Modification
In closing, we would like to highlight the vast potential that PID and the analysis of information modification have both in understanding biological neural systems, and in designing artificial ones.
As detailed in [1], the comparison of shared vs. synergistic mutual information in the output of a neuron or neural network allows us to address directly issues of robust coding vs. maximizing coding capacity, and thereby helps us to understand fundamental design principles of biological networks.
Conversely, PID can also be used to define information theoretic goal functions and to derive local learning rules for neurons in artificial neural networks with unprecedented detail and precision as explicated in [17], extending popular information theoretic goal functions like infomax [51], or coherent infomax (see [52] and references therein). In particular, the formulation of novel PID estimators that no longer rely on an optimization step (see the work of Finn et al. [40] in this special issue) has seemingly removed remaining difficulties with an analytical treatment of this approach.
Moreover, the PID formalism lends itself easily to the analysis of both neural and behavioral data, enabling a direct comparison of the two. This will take our understanding of the relationship between neural activity and behavior beyond the level of an analysis of mere representations, i.e., beyond decoding representations of objects and intentions, to finding the loci of particular aspects of neural computation. For example, in a human performing a task requiring an XOR computation, one may look for hot-spots of synergistic mutual information in the system.
Ultimately, the ability to obtain a complete fingerprint of a neural computation in terms of active information storage, information transfer and, now, information modification makes it possible to identify algorithms implemented by a neural system—or at least strongly confines the search space. This finally allows to fully address the algorithmic level of understanding neural systems as formulated more than 30 years ago by David Marr ([53], also see [1]).
5. Conclusions
We used a recent extension of information theory here to measure where and when in a neural network information is not simply communicated through a channel but modified. The definition of information modification here builds on the concept of synergistic mutual information as introduced by Williams and Beer [10], and the measure defined by Bertschinger et al. [12]. We show that, in the developing neural culture analyzed here, the contribution of synergistic mutual information rose as the network became more connected with development but ultimately dropped again as the activity became largely synchronized in bursts across the whole neural culture such that most mutual information was shared mutual information.
Acknowledgments
This project was supported through a Universities Australia/German Academic Exchange Service (DAAD) Australia–Germany Joint Research Cooperation Scheme grant (2016-17): “Measuring neural information synthesis and its impairment”. Joseph T. Lizier was also supported through the Australian Research Council DECRA grant DE160100630, and a Faculty of Engineering and IT Early Career Researcher and Newly Appointed Staff Development Scheme 2016 grant. Viola Priesemann received financial support from the Max Planck Society, and from the German Ministry for Education and Research (BMBF) via the Bernstein Center for Computational Neuroscience (BCCN) Göttingen under Grant No. 01GQ1005B. The authors would like to thank all participants of the 2016 Workshop on Partial Information Decomposition held by the Frankfurt Institute for Advanced Studies (FIAS) and the Goethe University for their inspiring discussions on PID.
Author Contributions
Michael Wibral and Viola Priesemann conceived of the study; Michael Wibral and Viola Priesemann analyzed the data; Conor Finn, Joseph T. Lizier, Patricia Wollstadt and Michael Wibral wrote the code for PID computation in the IDT toolbox; Michael Wibral, Viola Priesemann, and Joseph T. Lizier wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from Brains for Biologically Inspired Computing. Front. Robot. AI 2015, 2, 5. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhühner, F.; Seiwert, H.; Lindner, M.; Lizier, J.T.; Vicente, R. Measuring information-transfer delays. PLoS ONE 2013, 8, e55809. [Google Scholar] [CrossRef] [PubMed]
- Wollstadt, P.; Martínez-Zarzuela, M.; Vicente, R.; Díaz-Pernas, F.J.; Wibral, M. Efficient transfer entropy analysis of non-stationary neural time series. PLoS ONE 2014, 9, e102833. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inf. Sci. 2012, 208, 39–54. [Google Scholar] [CrossRef]
- Wibral, M.; Lizier, J.T.; Vögler, S.; Priesemann, V.; Galuske, R. Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinf. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Gomez, C.; Lizier, J.T.; Schaum, M.; Wollstadt, P.; Grützner, C.; Uhlhaas, P.; Freitag, C.M.; Schlitt, S.; Bölte, S.; Hornero, R.; et al. Reduced Predictable Information in Brain Signals in Autism Spectrum Disorder. Front. Neuroinf. 2014, 8, 9. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Lizier, J.T.; Flecker, B.; Williams, P.L. Towards a synergy-based approach to measuring information modification. In Proceedings of the 2013 IEEE Symposium on Artificial Life (ALIFE), Singapore, 16–19 April 2013; pp. 43–51. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin, Germany, 2014; Volume 9, pp. 159–190. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Fano, R. Transmission of Information; The MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Wibral, M.; Priesemann, V.; Kay, J.W.; Lizier, J.T.; Phillips, W.A. Partial information decomposition as a unified approach to the specification of neural goal functions. Brain Cognit. 2017, 112, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Langton, C.G. Computation at the edge of chaos: Phase transitions and emergent computation. Phys. D Nonlinear Phenom. 1990, 42, 12–37. [Google Scholar] [CrossRef]
- Mitchell, M. Computation in Cellular Automata: A Selected Review. In Non-Standard Computation; Gramß, T., Bornholdt, S., Groß, M., Mitchell, M., Pellizzari, T., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 1998; pp. 95–140. [Google Scholar]
- Williams, P.L.; Beer, R.D. Generalized Measures of Information Transfer. arXiv, 2011; arXiv:1102.1507. [Google Scholar]
- Timme, N.M.; Ito, S.; Myroshnychenko, M.; Nigam, S.; Shimono, M.; Yeh, F.C.; Hottowy, P.; Litke, A.M.; Beggs, J.M. High-Degree Neurons Feed Cortical Computations. PLoS Comput. Biol. 2016, 12, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Wollstadt, P.; Lizier, J.T.; Finn, C.; Martinz-Zarzuela, M.; Vicente, R.; Lindner, M.; Martinez-Mediano, P.; Wibral, M. The Information Dynamics Toolkit, IDTxl. Available online: https://github.com/pwollstadt/IDTxl (accessed on 25 August 2017).
- Makkeh, A.; Theis, D.O.; Vicente Zafra, R. Bivariate Partial Information Decomposition: The Optimization Perspective. 2017. under review. [Google Scholar]
- Wagenaar, D.A.; Pine, J.; Potter, S.M. An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci. 2006, 7, 11. [Google Scholar] [CrossRef] [PubMed]
- Wagenaar, D.A. Network Activity of Developing Cortical Cultures In Vitro. Available online: http://neurodatasharing.bme.gatech.edu/development-data/html/index.html (accessed on 25 August 2017).
- Wagenaar, D.; DeMarse, T.B.; Potter, S.M. MeaBench: A toolset for multi-electrode data acquisition and on-line analysis. In Proceedings of the 2nd International IEEE EMBS Conference on Neural Engineering, Arlington, VA, USA, 16–20 March 2005; pp. 518–521. [Google Scholar]
- Timme, N.; Shinya, I.; Maxym, M.; Fang-Chin, Y.; Emma, H.; Pawel, H.; Beggs, J.M. Multiplex Networks of Cortical and Hippocampal Neurons Revealed at Different Timescales. PLoS ONE 2014, 9, 1–43. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Marinazzo, D.; Montalto, A.; Nollo, G. Lag-specific transfer entropy as a tool to assess cardiovascular and cardiorespiratory information transfer. IEEE Trans. Biomed. Eng. 2014, 61, 2556–2568. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Rubinov, M. Inferring effective computational connectivity using incrementally conditioned multivariate transfer entropy. BMC Neurosci. 2013, 14, P337. [Google Scholar] [CrossRef]
- Montalto, A.; Faes, L.; Marinazzo, D. MuTE: A MATLAB Toolbox to Compare Established and Novel Estimators of the Multivariate Transfer Entropy. PLoS ONE 2014, 9, e109462. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Vicente, R.; Priesemann, V.; Wibral, M. TRENTOOL: A Matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011, 12, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Wollstadt, P.; Meyer, U.; Wibral, M. A Graph Algorithmic Approach to Separate Direct from Indirect Neural Interactions. PLoS ONE 2015, 10, e0140530. [Google Scholar] [CrossRef] [PubMed]
- Levina, A.; Priesemann, V. Subsampling scaling. Nat. Commun. 2017, 8, 15140. [Google Scholar] [CrossRef] [PubMed]
- Levina, A.; Priesemann, V. Subsampling Scaling: A Theory about Inference from Partly Observed Systems. arXiv, 2017; arXiv:1701.04277. [Google Scholar]
- Priesemann, V.; Wibral, M.; Valderrama, M.; Pröpper, R.; le van Quyen, M.; Geisel, T.; Triesch, J.; Nikolić, D.; Munk, M.H.J. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 2014, 8, 108. [Google Scholar] [CrossRef] [PubMed]
- Priesemann, V.; Lizier, J.; Wibral, M.; Bullmore, E.; Paulsen, O.; Charlesworth, P.; Schröter, M. Self-organization of information processing in developing neuronal networks. BMC Neurosci. 2015, 16, P221. [Google Scholar] [CrossRef]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: an experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Phillips, W.A. Cognitive functions of intracellular mechanisms for contextual amplification. Brain Cognit. 2017, 112, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Larkum, M. A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends Neurosci. 2013, 36, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Finn, C.; Prokopenko, M.; Lizier, J.T. Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices. 2017. under review. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer International Publishing: Cham, Vietnam, 2013; pp. 251–269. [Google Scholar]
- Ince, R.A.A. Measuring Multivariate Redundant Information with Pointwise Common Change in Surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2232–2236. [Google Scholar]
- Pica, G.; Piasini, E.; Chicharro, D.; Panzeri, S. Invariant Components of Synergy, Redundancy, and Unique Information among Three Variables. Entropy 2017, 19, 451. [Google Scholar] [CrossRef]
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information Decomposition and Synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Schneidman, E.; Puchalla, J.L.; Segev, R.; Harris, R.A.; Bialek, W.; Berry, M.J. Synergy from Silence in a Combinatorial Neural Code. J. Neurosci. 2011, 31, 15732–15741. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Wu, G.R.; Pellicoro, M.; Marinazzo, D. Expanding the transfer entropy to identify information circuits in complex systems. Phys. Rev. E 2012, 86, 066211. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Stramaglia, S.; Angelini, L.; Wu, G.; Cortes, J.M.; Faes, L.; Marinazzo, D. Synergetic and redundant information flow detected by unnormalized Granger causality: Application to resting state fMRI. IEEE Trans. Biomed. Eng. 2016, 63, 2518–2524. [Google Scholar] [CrossRef] [PubMed]
- Rauh, J.; Banerjee, P.; Olbrich, E.; Jost, J.; Bertschinger, N. On Extractable Shared Information. Entropy 2017, 19, 328. [Google Scholar] [CrossRef]
- Linsker, R. Self-organisation in a perceptual network. IEEE Comput. 1988, 21, 105–117. [Google Scholar] [CrossRef]
- Kay, J.W.; Phillips, W.A. Coherent Infomax as a computational goal for neural systems. Bull. Math. Biol. 2011, 73, 344–372. [Google Scholar] [CrossRef] [PubMed]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; Henry Holt and Co., Inc.: New York, NY, USA, 1982. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).