Novel Early EEG Measures Predicting Brain Recovery after Cardiac Arrest
Abstract
:1. Introduction
2. Quantitative EEG Predicting Long-Term Brain Injury after CA
2.1. Review of Shannon Entropy Based qEEG Measures
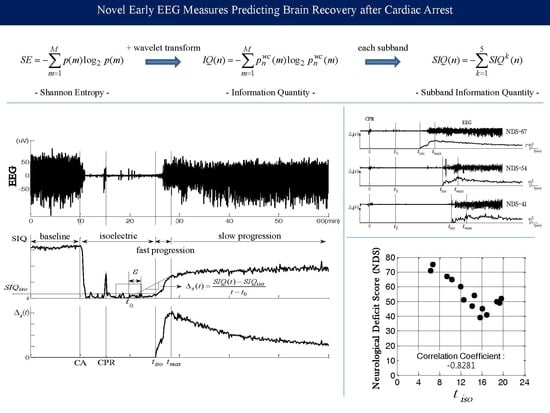
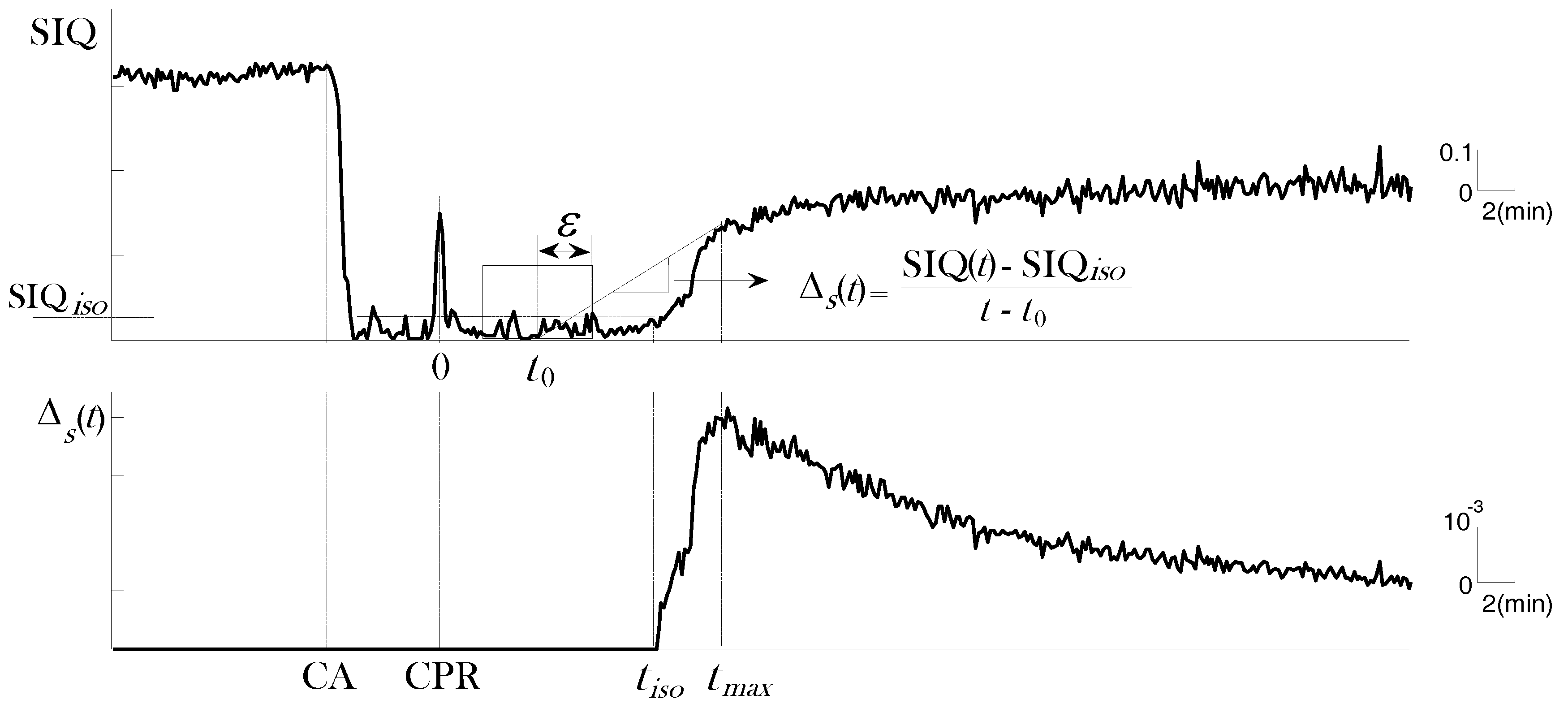
2.2. Novel qEEG Measures Exploiting Critical Transition in EEG
3. Experimental Methods
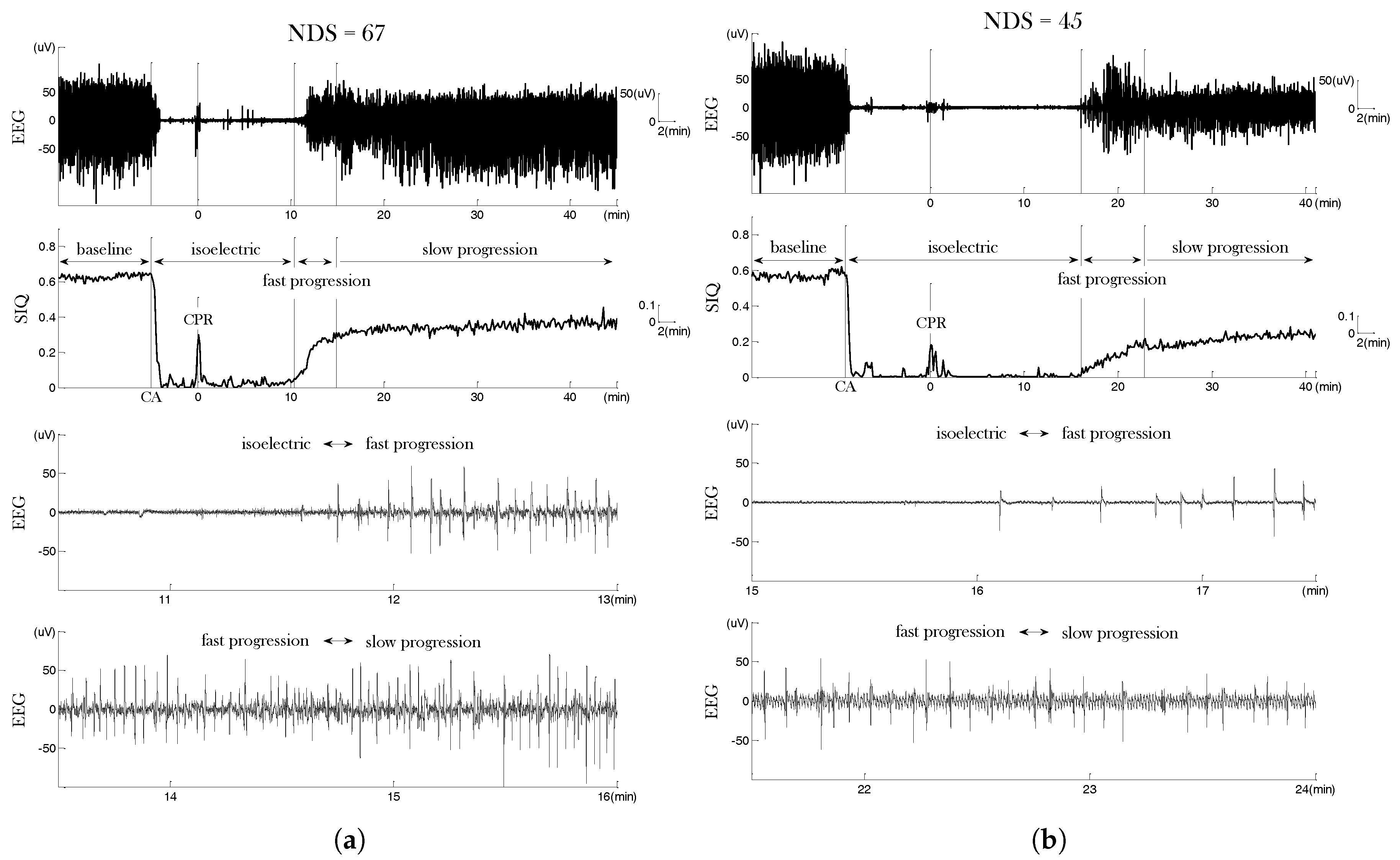
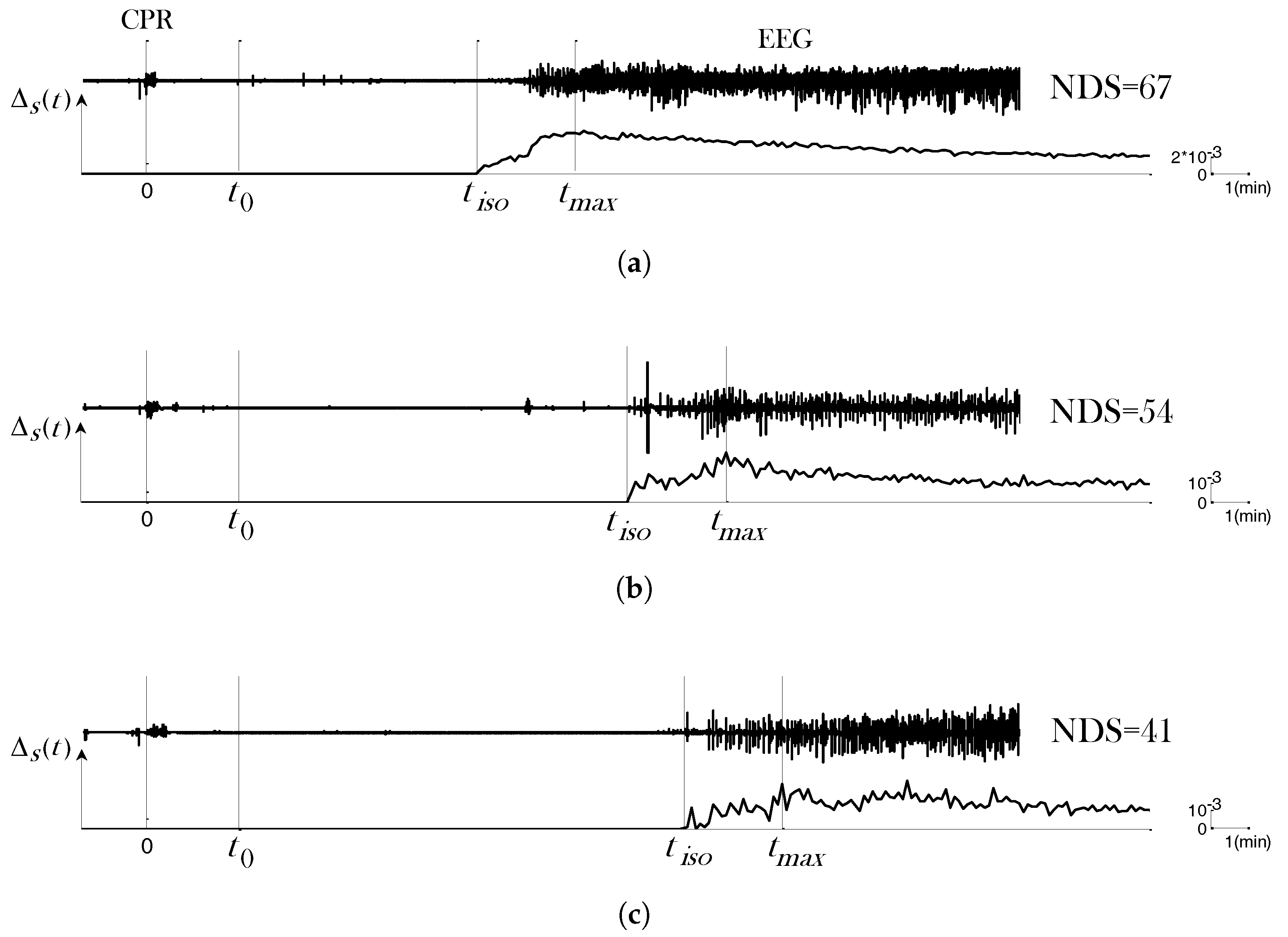
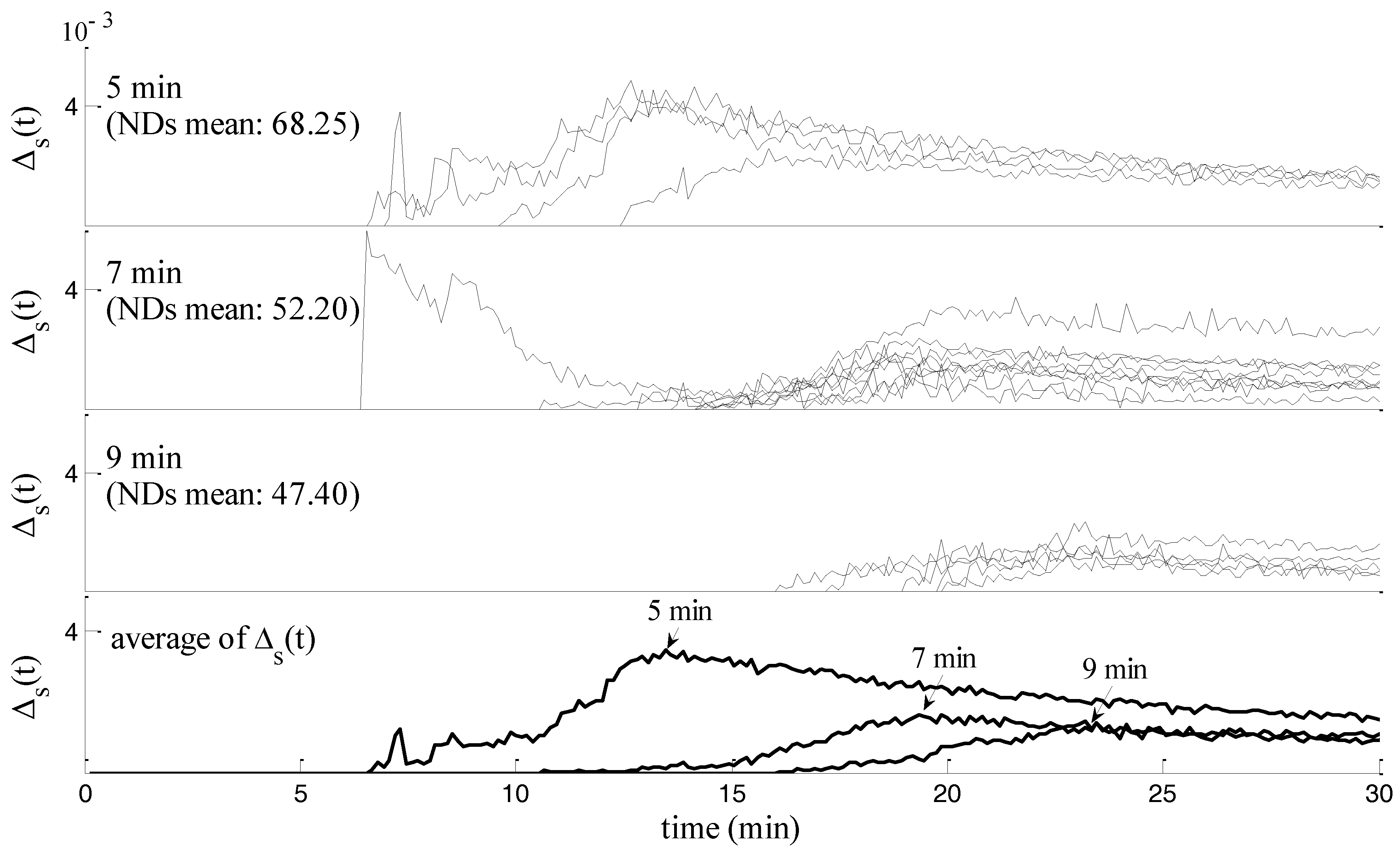
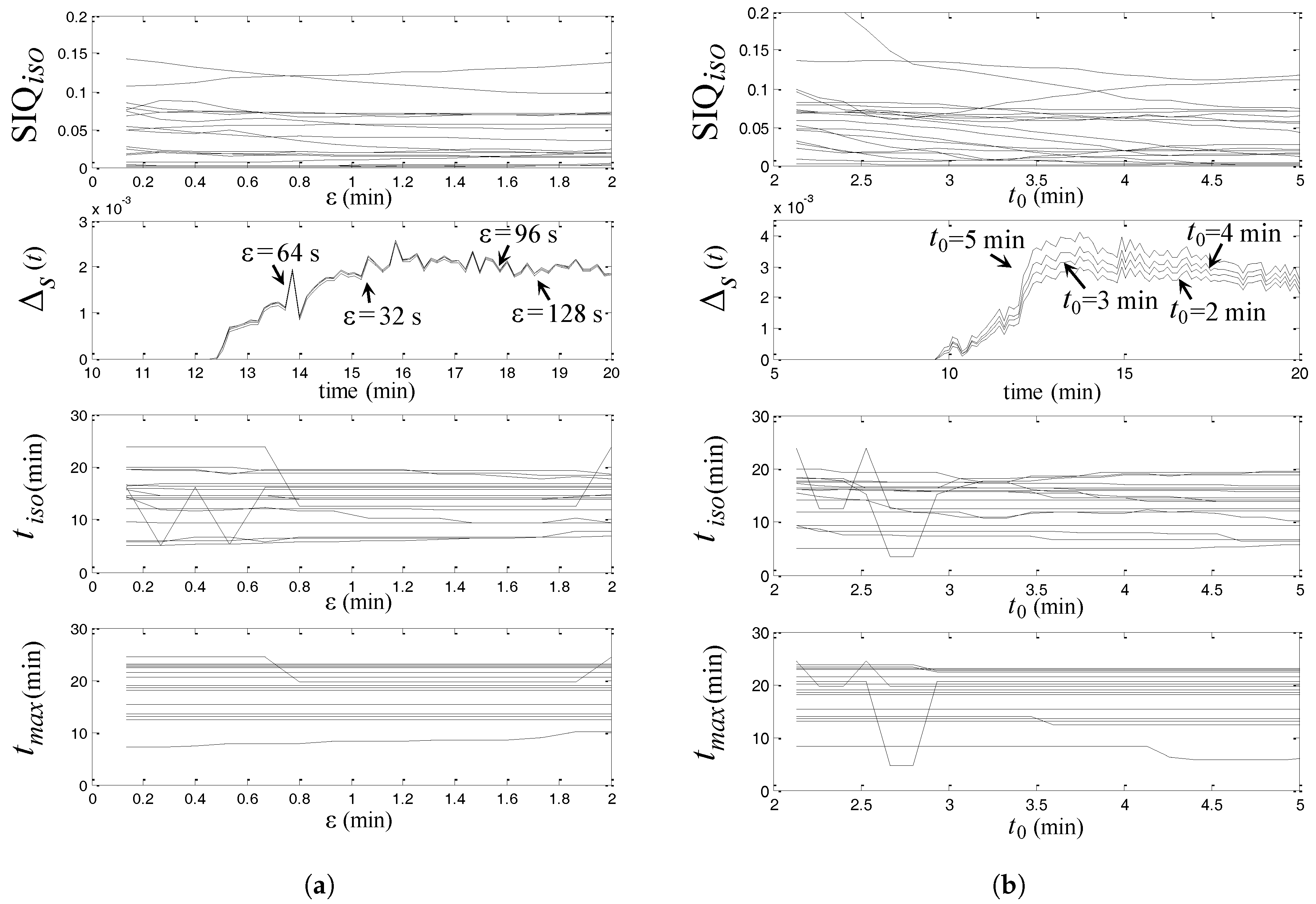
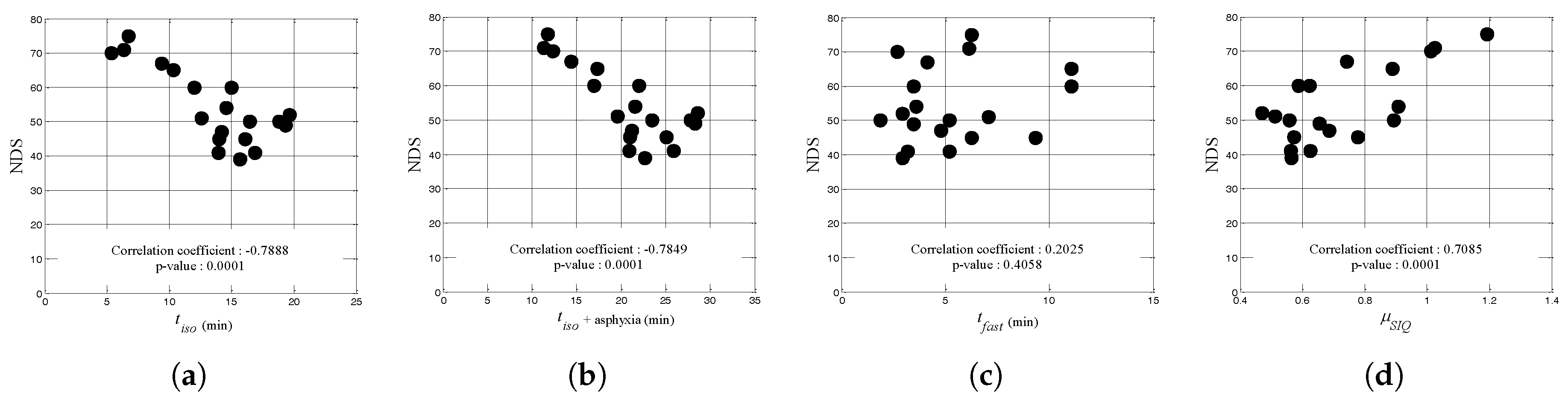
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bedell, S.E.; Delbanco, T.L.; Cook, E.F.; Epstein, F.H. Survival after cardiopulmonary resuscitation in the hospital. N. Engl. J. Med. 1983, 309, 569–576. [Google Scholar] [CrossRef] [PubMed]
- Longstreth, W.T.; Diehr, P.; Inui, T.S. Prediction of awakening after out of hospital cardiac arrest. N. Engl. J. Med. 1983, 308, 1378–1382. [Google Scholar] [CrossRef] [PubMed]
- Berek, K.; Jeschow, M.; Aichner, F. The prognostication of cerebral hypoxia after out of hospital cardiac arrest in adults. Eur. Neurol. 1997, 37, 135–145. [Google Scholar] [CrossRef] [PubMed]
- Safar, P. Cerebral resuscitation after cardiac arrest: A review. Circulation 1986, 74, IV138–IV153. [Google Scholar] [PubMed]
- Vaagenes, P.; Ginsberg, M.; Ebmeyer, U.; Ernster, L.; Fischer, M.; Gisvold, S.E.; Gurvitch, A.; Hossmann, K.A.; Nemoto, E.M.; Radovsky, A.; et al. Cerebral resuscitation from cardiac arrest: Pathophysiologic mechanisms. Crit. Care Med. 1996, 24, S57–S68. [Google Scholar] [CrossRef] [PubMed]
- American Heart Association in Collaboration; International Liaison Committee on Resuscitation (IL-COR). Guidelines 2000 for cardiopulmonary resuscitation and emergency cardiovascular care—An international consensus on science. Circulation 2000, 102, I-1–I-11. [Google Scholar]
- Nolan, J.P.; Morley, P.T.; Hoek, T.L.; Hickey, R.W.; Advancement Life Support Task Force of the International Liaison Committee on Resuscitation. Therapeutic hypothermia after cardiac arrest. An advisory statement by the advancement life support task force of the international liaison committee on resuscitation. Circulation 2003, 57, 231–235. [Google Scholar]
- Bezerianos, A.; Tong, S.; Thakor, N.V. Time-dependent entropy estimation of EEG rhythm changes following brain ischemia. Ann. Biomed. Eng. 2003, 31, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Thakor, N.V.; Tong, S. Advances in quantitative electroencephalogram analysis methods. Annu. Rev. Biomed. Eng. 2004, 6, 453–495. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.C.; Tong, S.; Yamashita, S.; Jia, X.; Geocadin, R.G.; Thakor, N.V. Quantitative EEG and Effect of Hypothermia on Brain Recovery after Cardiac Arrest. IEEE Trans. Biomed. Eng. 2006, 53, 1016–1023. [Google Scholar] [CrossRef] [PubMed]
- Thakor, N.V.; Shin, H.C.; Tong, S.; Geocadin, R. Quantitative EEG Assessment. IEEE Eng. Med. Biol. Mag. 2006, 25, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.C.; Jia, X.; Nickl, R.; Geocadin, R.G.; Thakor, N.V. A Subband-based Information measure of EEG during Brain Injury and Recovery After Cardiac Arrest. IEEE Trans. Biomed. Eng. 2008, 55, 1985–1990. [Google Scholar] [CrossRef] [PubMed]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Basar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Yordanova, J.; Kolev, V.; Rosso, O.A.; Schürmann, M.; Sakowitz, O.W.; Özgören, M.; Basar, E. Wavelet entropy analysis of event-related potentials indicates modality-independent theta dominance. J. Neurosci. Methods 2002, 117, 99–109. [Google Scholar] [CrossRef]
- Edgren, E.; Hedstrand, U.; Kelsey, S.; Sutton-Tyrrell, K.; Safar, P.; BRCTI Study Group. Assessment of neurological prognosis in comatose survivors of cardiac arrest. Lancet 1994, 343, 1055–1059. [Google Scholar] [CrossRef]
- Bernard, S.A.; Gray, T.; Buist, M.; Jones, B.; Silvestar, W.; Gutteridge, G.; Smith, K. Treatment of comatose survivors of out-of-hospital cardiac arrest with induced hypothermia. N. Engl. J. Med. 2002, 346, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Geocardin, R.G.; Ghodadra, R.; Kimura, T.; Lei, H.; Sherman, D.L.; Hanley, D.F.; Thakor, N.V. A novel quantitative EEG injury measure of global cerebral ischemia. Clin. Neurophysiol. 2000, 111, 1779–1787. [Google Scholar] [CrossRef]
- Katz, L.; Ebmeyer, U.; Safar, P.; Radovsky, A.; Neumar, R. Outcome model of asphyxia cardiac arrest in rats. J. Cereb. Blood Flow Metab. 1995, 15, 1032–1039. [Google Scholar] [CrossRef] [PubMed]
| Rat Num. | Asphyxia (min) | NDS | (min) | + Asphyxia | (min) | |
|---|---|---|---|---|---|---|
| 1 | 5 | 75 | 6.73 | 11.73 | 6.27 | 1.1920 |
| 2 | 5 | 71 | 6.33 | 11.33 | 6.14 | 1.0245 |
| 3 | 5 | 67 | 9.40 | 14.40 | 4.13 | 0.7412 |
| 4 | 5 | 60 | 11.98 | 16.98 | 3.47 | 0.6222 |
| correlation coefficient | 0.9358 | 0.9622 | ||||
| p-value | 0.0530 | 0.0530 | 0.0642 | 0.0378 | ||
| 5 | 7 | 70 | 5.35 | 12.35 | 2.67 | 1.0121 |
| 6 | 7 | 65 | 10.33 | 17.33 | 11.07 | 0.8879 |
| 7 | 7 | 60 | 14.97 | 21.97 | 11.06 | 0.5869 |
| 8 | 7 | 54 | 14.58 | 21.58 | 3.60 | 0.9063 |
| 9 | 7 | 51 | 12.60 | 19.60 | 7.07 | 0.5117 |
| 10 | 7 | 50 | 16.47 | 23.47 | 5.20 | 0.8929 |
| 11 | 7 | 47 | 14.20 | 21.20 | 4.80 | 0.6859 |
| 12 | 7 | 45 | 13.98 | 20.98 | 9.34 | 0.5716 |
| 13 | 7 | 41 | 13.93 | 20.93 | 5.20 | 0.5619 |
| 14 | 7 | 39 | 15.67 | 22.67 | 2.93 | 0.5647 |
| correlation coefficient | 0.2497 | 0.6806 | ||||
| p-value | 0.0149 | 0.0149 | 0.4866 | 0.0303 | ||
| 15 | 9 | 52 | 19.62 | 28.62 | 2.93 | 0.4707 |
| 16 | 9 | 50 | 18.80 | 27.80 | 1.87 | 0.5584 |
| 17 | 9 | 49 | 19.32 | 28.32 | 3.46 | 0.6547 |
| 18 | 9 | 45 | 16.10 | 25.10 | 6.27 | 0.7770 |
| 19 | 9 | 41 | 16.87 | 25.87 | 3.20 | 0.6253 |
| correlation coefficient | 0.8524 | 0.8524 | ||||
| p-value | 0.0666 | 0.0666 | 0.4991 | 0.2843 | ||
| Total | ||||||
| correlation coefficient | 0.2025 | 0.7085 | ||||
| p-value | 0.0001 | 0.0001 | 0.4058 | 0.001 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cha, K.-M.; Thakor, N.V.; Shin, H.-C. Novel Early EEG Measures Predicting Brain Recovery after Cardiac Arrest. Entropy 2017, 19, 466. https://doi.org/10.3390/e19090466
Cha K-M, Thakor NV, Shin H-C. Novel Early EEG Measures Predicting Brain Recovery after Cardiac Arrest. Entropy. 2017; 19(9):466. https://doi.org/10.3390/e19090466
Chicago/Turabian StyleCha, Kab-Mun, Nitish V. Thakor, and Hyun-Chool Shin. 2017. "Novel Early EEG Measures Predicting Brain Recovery after Cardiac Arrest" Entropy 19, no. 9: 466. https://doi.org/10.3390/e19090466
APA StyleCha, K.-M., Thakor, N. V., & Shin, H.-C. (2017). Novel Early EEG Measures Predicting Brain Recovery after Cardiac Arrest. Entropy, 19(9), 466. https://doi.org/10.3390/e19090466