Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability
Abstract
1. Introduction
2. Materials and Methods
2.1. Linear and Nonlinear Parameters
2.2. The Surrogate Data Tests
2.3. Statistical Methods
3. Results
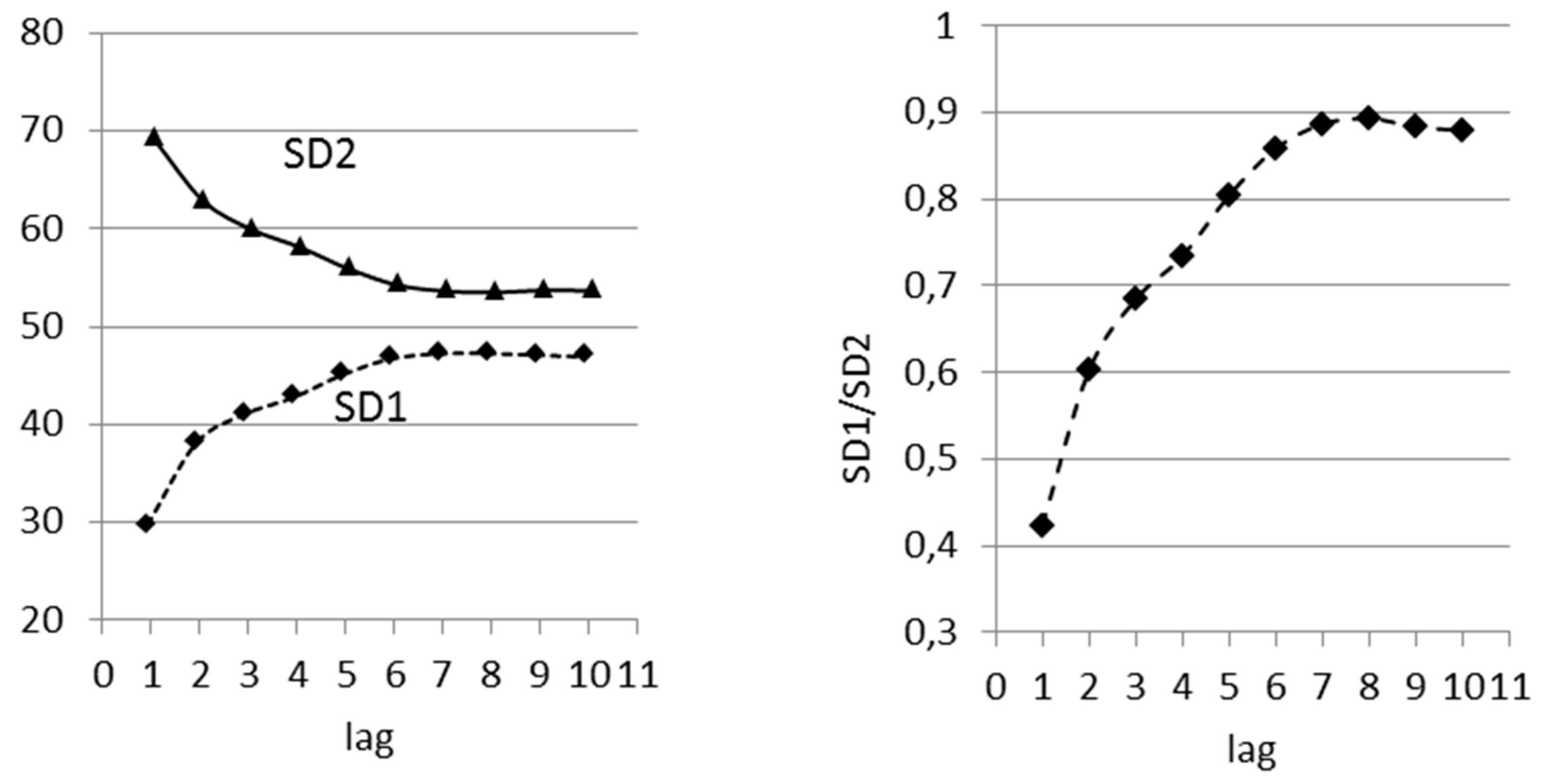
3.1. Influence of Time Lag on Poincaré Plot Indices
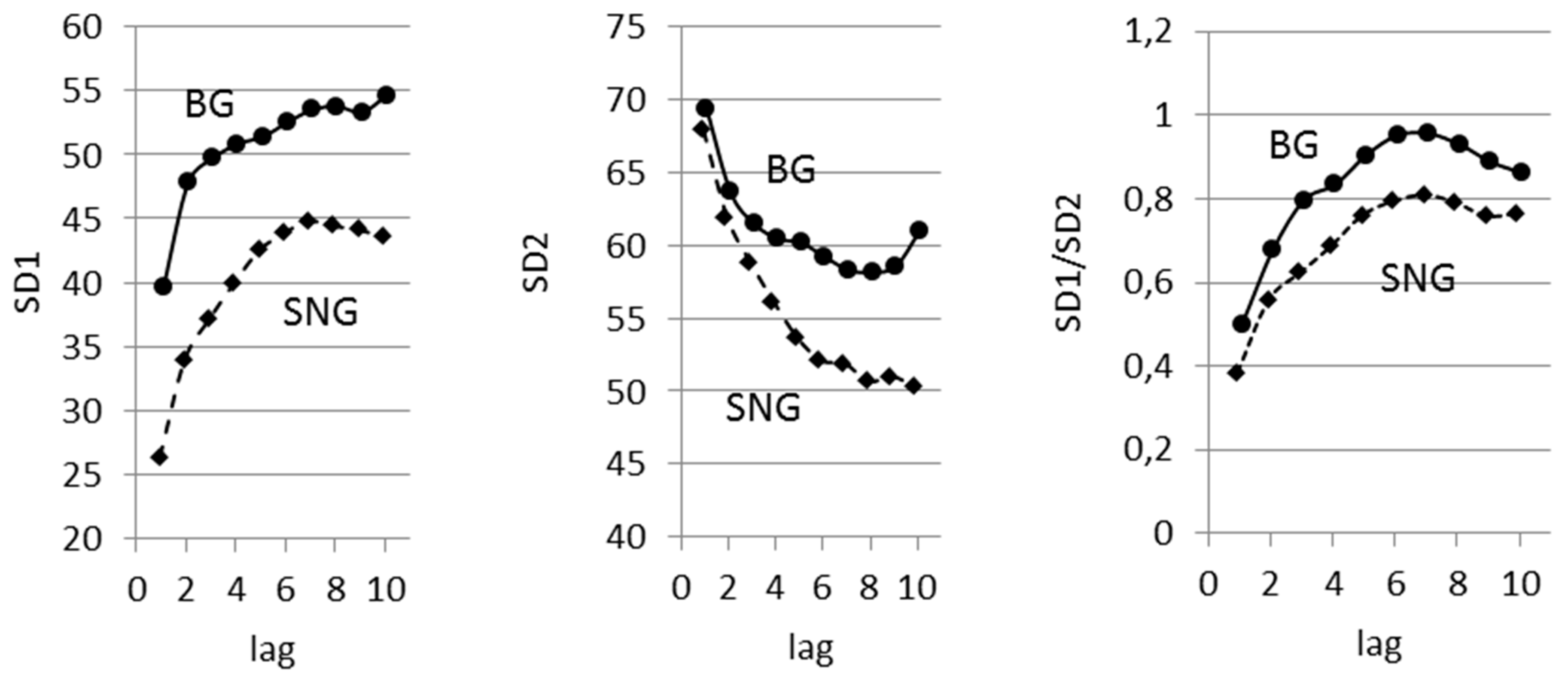
3.2. Lagged Poincaré Plot in Persons with Different Balancing of Autonomic Nervous System
3.3. The Analysis of Age-Related Differences
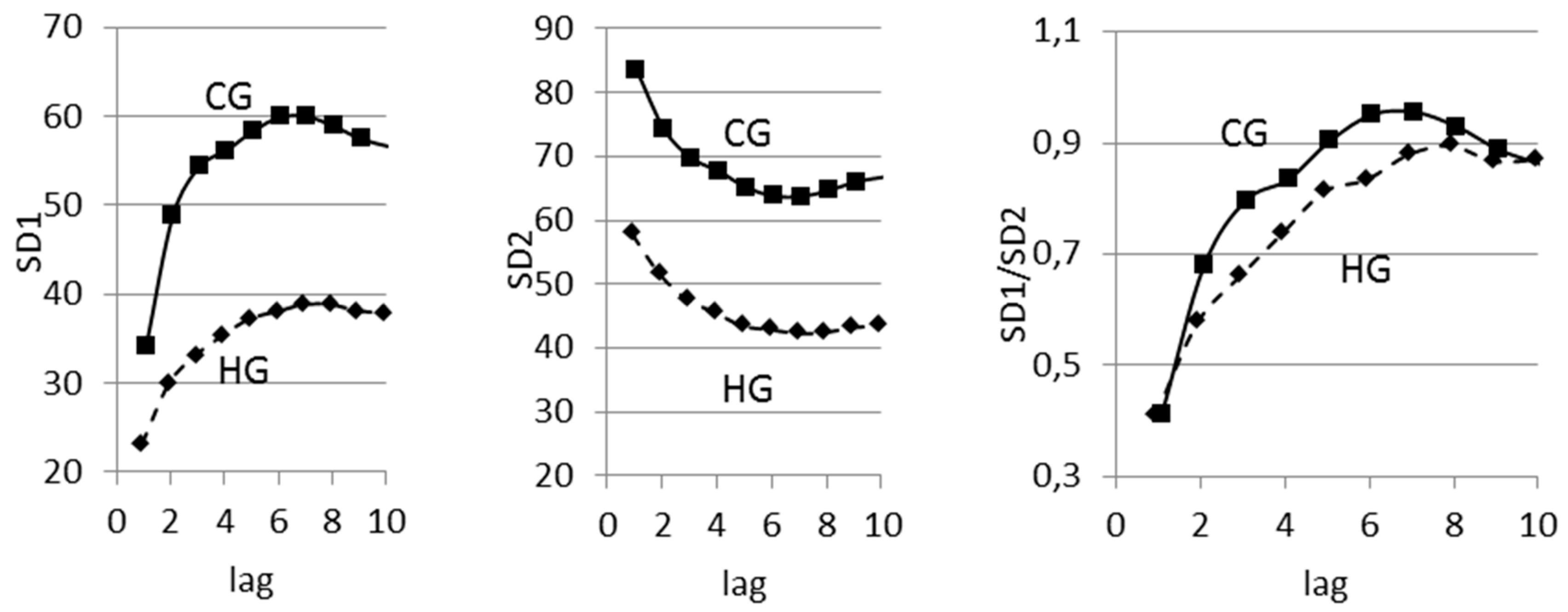
3.4. Lagged Poincaré Plot in Hypertension
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heart Rate Variability. Standards of Measurement, Physiological Interpretation and Clinical Use. Available online: http://circ.ahajournals.org/content/93/5/1043.long (accessed on 28 September 2017).
- Schumacher, J.M. Linear and Nonlinear Approaches to the Analysis of RR Interval Variability. Biol. Res. Nurs. 2004, 5, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Buccelletti, F.; Bocci, M.G.; Gilardi, E.; Fiore, V.; Calcinaro, S.; Fragnoli, C.; Maviglia, R.; Franceschi, F. Linear and Nonlinear Heart Rate Variability Indexes in Clinical Practice. Comput. Math. Methods Med. 2012, 2012, 219080. [Google Scholar]
- Narin, A.; Isler, Y.; Ozer, M. Investigating the Performance Improvement of HRV Indices in CHF Using Feature Selection Methods Based on Backward Elimination and Statistical Significance. Comput. Biol. Med. 2014, 45, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Shi, P.; Hu, S.; Yu, H. Recovery of Heart Rate Variability after Treadmill Exercise Analyzed by Lagged Poincaré Plot and Spectral Characteristics. Med. Biol. Eng. Comput. 2017, 1–11. [Google Scholar] [CrossRef] [PubMed]
- La Rovere, M.T.; Pinna, G.D.; Maestri, R.; Barlera, S.; Bernardinangeli, M.; Veniani, M.; Nicolosi, G.L.; Marchioli, R.; Tavazzi, L. Autonomic Markers and Cardiovascular and Arrhythmic Events in Heart Failure Patients: Still a Place in Prognostication? Data from the GISSI-HF Trial. Eur. J. Heart Fail. 2012, 14, 1410–1419. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Schroeder, R.; Vallverdú, M.; Schulz, S.; Cygankiewicz, I.; Vázquez, R.; de Luna, A.B.; Caminal, P. Short-Term vs. Long-Term Heart Rate Variability in Ischemic Cardiomyopathy Risk Stratification. Front. Physiol. 2013, 4, 364. [Google Scholar] [CrossRef] [PubMed]
- Behbahani, S.; Dabanloo, N.J.; Nasrabadi, A.M.; Teixeira, C.A.; Dourado, A. Pre-ictal heart rate variability assessment of epileptic seizures by means of linear and non-linear analyses. Anadolu Kardiyol. Derg. 2013, 13, 797–803. [Google Scholar] [CrossRef] [PubMed]
- Neves, V.R.; Takahashi, A.C.; do Santos-Hiss, M.D.; Kiviniemi, A.M.; Tulppo, M.P.; de Moura, S.C.; Karsten, M.; Borghi-Silva, A.; Porta, A.; Montano, N.; et al. Linear and nonlinear analysis of heart rate variability in coronary disease. Clin. Auton. Res. 2012, 22, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Linear and Nonlinear Analysis of Heart Rate Variability in Coronary Disease. Available online: https://link.springer.com/article/10.1007/s10286-012-0160-z (accessed on 28 September 2017).
- Kunz, V.C.; Borges, E.N.; Coelho, R.C.; Gubolino, L.A.; Martins, L.E.; Silva, E. Linear and nonlinear analysis of heart rate variability in healthy subjects and after acute myocardial infarction in patients. Braz. J. Med. Biol. Res. 2012, 45, 450–458. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.G.; Kim, W.-S.; Noh, K.Y.; Shin, J.-H.; Yun, U.; Ryu, K.H. Coronary artery disease prediction method using linear and nonlinear feature of heart rate variability in three recumbent postures. Inf. Syst. Front. 2009, 11, 419–431. [Google Scholar] [CrossRef]
- Voss, A.; Kurths, J.; Kleiner, H.J.; Witt, A.; Wessel, N.; Saparin, P.; Osterziel, K.J.; Schurath, R.; Dietz, R. The application of methods of non-linear dynamics for the improved and predictive recognition of patients threatened by sudden cardiac death. Cardiovasc. Res. 1996, 31, 419–433. [Google Scholar] [CrossRef]
- Maestri, R.; Pinna, G.D.; Accardo, A.; Allegrini, P.; Balocchi, R.; D’Addio, G.; Ferrario, M.; Menicucci, D.; Porta, A.; Sassi, R.; et al. Nonlinear indices of heart rate variability in chronic heart failure patients: Redundancy and comparative clinical value. J. Cardiovasc. Electrophysiol. 2007, 18, 425–433. [Google Scholar] [CrossRef] [PubMed]
- Makikallio, T.H.; Huikuri, H.V.; Makikallio, A.; Sourander, L.B.; Mitrani, R.D.; Castellanos, A.; Myerburg, R.J. Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. J. Am. Coll. Cardiol. 2001, 37, 1395–1402. [Google Scholar] [CrossRef]
- Huikuri, H.V.; Makikallio, T.H.; Airaksinen, K.E.J.; Seppänen, T.; Puukka, P.; Räihä, I.J.; Sourander, L.B. Power-law relationship of heart rate variability as a predictor of mortality in the elderly. Circulation 1998, 97, 2031–2036. [Google Scholar] [CrossRef] [PubMed]
- Stein, P.K.; Barzilay, J.I.; Chaves, P.H.; Mistretta, S.Q.; Domitrovich, P.P.; Gottdiener, J.S.; Rich, M.W.; Kleiger, R.E. Novel measures of heart rate variability predict cardiovascular mortality in older adults independent of traditional cardiovascular risk factors: the cardiovascular health study (CHS). J. Cardiovasc. Electrophysiol. 2008, 19, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Vikman, S.; Makikallio, T.H.; Yli-Mayry, S.; Pikkujamsa, S.; Koivisto, A.-M.; Reinikainen, P.; Airaksinen, K.E.; Huikuri, H.V. Altered complexity and correlation properties of RR interval dynamics before the spontaneous onset of paroxysmal atrial fibrillation. Circulation 1999, 100, 2079–2084. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2002, 283, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Ryan, S.M.; Goldberger, A.L.; Pincus, S.M.; Mietus, J.; Lipsitz, L.A. Gender-and age-related differences in heart rate: Are women more complex than men? J. Am. Coll. Cardiol. 1994, 24, 1700–1707. [Google Scholar] [CrossRef]
- Yamasaki, Y.; Kodama, M.; Matsuhisa, M. Diurnal heart rate variability in healthy subjects: Effects of aging and sex differences. Am. J. Physiol. 1996, 271, 303–310. [Google Scholar]
- Beckers, F.; Verheyden, B.T.; Aubert, A.E. Aging and nonlinear heart rate control in a healthy population. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, 2560–2570. [Google Scholar] [CrossRef] [PubMed]
- Owis, M.I.; Abou-Zied, A.H.; Youssef, A.B.M.; Kadah, Y.M. Study of features on nonlinear dynamical modeling in ECG arrhythmia detection and classification. IEEE Trans. Biomed. Eng. 2002, 9, 733–736. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Chan, K.L.; Krishnan, S.M. Arrhythmia detection and recognition in ECG signals using nonlinear techniques. Ann. Biomed. Eng. 2000, 28, 37. [Google Scholar]
- Cohen, M.; Hudson, D.L.; Deedwania, P.C. Heart rate variability and cardiovascular mortality. IEEE Eng. Med. Biol. Mag. 1996, 15, 97–102. [Google Scholar] [CrossRef]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.K.; Schmidt, G.; Yamamoto, Y. Advances in heart rate variability signal analysis: Joint position statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association co-endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence. Lect. Notes Math. 1981, 898, 366–372. [Google Scholar]
- Kamen, P.W.; Krum, H.; Tonkin, A.W. The Correlation Dimension of Heart Rate Variability Reflects Cardiac Autonomic Activity. Ann. Noninvasive Electrocardiol. 1997, 2, 206–212. [Google Scholar] [CrossRef]
- Kamen, P.W.; Tonkin, A.M. Application of the Poincaré plot to heart rate variability: A new measure of functional status in heart failure. Aust. N. Z. J. Med. 1995, 25, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Tulppo, M.; Makikallio, T.H.; Takala, T.E. Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am. J. Physiol. 1996, 71, 244–252. [Google Scholar]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincaré plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef] [PubMed]
- Toichi, M.; Sugiura, T.; Murai, T.; Sengoku, A. A new method of assessing cardiac autonomic function and its comparison with spectral analysis and coefficient of variation of RR interval. J. Auton. Nerv. Syst. 1997, 62, 79–84. [Google Scholar] [CrossRef]
- Hayano, J.; Takahashi, H.; Toriyama, T.; Mukai, S.; Okada, A.; Sakata, S.; Yamada, A.; Ohte, N.; Kawahara, H. Prognostic value of heart rate variability during long-term follow-up in chronic haemodialysis patients with end-stage renal disease. Nephrol. Dial. Transplant. 1999, 14, 1480–1488. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Joseph, K.P.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef] [PubMed]
- Woo, M.A.; Stevenson, W.G.; Moser, D.K.; Trelease, R.B.; Harper, R.M. Patterns of beat-to-beat heart rate variability in advanced heart failure. Am. Heart J. 1992, 123, 704–710. [Google Scholar] [CrossRef]
- Schechtman, V.L.; Lee, M.Y.; Wilson, A.J.; Harper, R.M. Dynamics of respiratory patterning in normal infants and infants who subsequently died of the sudden infant death syndrome. Pediatr. Res. 1996, 40, 571–577. [Google Scholar] [CrossRef] [PubMed]
- Makikallio, T.H.; Seppanen, T.; Airaksinen, K.E.; Koistinen, J.; Tulppo, M.P.; Peng, C.K.; Goldberger, A.L.; Huikuri, H.V. Dynamic analysis of heart rate may predict subsequent ventricular tachycardia after myocardial infarction. Am. J. Cardiol. 1997, 80, 779–783. [Google Scholar] [CrossRef]
- Lerma, C.; Infante, O.; Perez-Grovas, H. Poincaré plot indexes of heart rate variability capture dynamic adaptations after haemodialysis in chronic renal failure patients. Clin. Physiol. Funct. Imaging 2003, 23, 72–80. [Google Scholar] [PubMed]
- Goshvarpour, A.; Goshvarpour, A.; Rahati, S. Analysis of Lagged Poincare Plots in Heart Rate Signals during Meditation. Digit. Signal Process. 2011, 21, 208–214. [Google Scholar] [CrossRef]
- Bhaskar, R.; Sobhendu, G. Nonlinear Methods to Assess Changes in Heart Rate Variability in Type 2 Diabetic Patients. Arq. Bras. Cardiol. 2013, 101, 317–327. [Google Scholar]
- Contreras, P.; Canetti, R.; Migliaro, R. Correlations between frequency-domain HRV indices and lagged Poincaré plot width in healthy and diabetic subjects. Physiol. Meas. 2007, 28, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Thakre, T.P.; Smith, M.L. Loss of lag-response curvilinearity of indices of heart rate variability in congestive heart failure. BMC Cardiovasc. Disord. 2006, 6, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Martini, G.; Rabbia, F.; Gastaldi, L.; Riva, P.; Sibona, M.P.; Morra di Cella, S.; Chiandussi, L.; Veglio, F. Heart rate variability and left ventricular diastolic function in patients with borderline hypertension with and without left ventricular hypertrophy. Clin. Exp. Hypertens. 2001, 23, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Garcia, A.; Gomez-Marcos, M.A.; Recio-Rodriguez, J.I.; Patino-Alonso, M.C.; Rodríguez-Sánchez, E.; Agudo-Conde, C.; García-Ortiz, L.; Vaso-risk group. Office and 24-hour heart rate and target organ damage in hypertensive patients. BMC Cardiovasc. Disord. 2012, 12, 19. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Heitmann, A.; Schroeder, R.; Peters, A.; Perz, S. Short-term heart rate variability—Age dependence in healthy subjects. Physiol. Meas. 2012, 33, 1289–1311. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Tarvainen, M.P.; Niskanen, J.-P.; Lipponen, J.A.; Ranta-aho, P.O.; Karjalainen, P.A. Kubios HRV—A Software for Advanced Heart Rate Variability Analysis. In Proceedings of the 4th European Conference of the International Federation for Medical and Biological Engineering, Antwerp, Belgium, 23–27 November 2008; pp. 1022–1025. [Google Scholar]
- Heart Rate Variability. Available online: https://www.amazon.com/Heart-Rate-Variability-Marek-Malik/dp/087993607X (accessed on 28 September 2017).
- Tarvainen, M.P.; Ranta-Aho, P.O.; Karjalainen, P.A. An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 49, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Theiler, J.; Eubank, S.; Longtin, A. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Some Methods for Classification and Analysis of Multivariate Observations. Available online: https://projecteuclid.org/download/pdf_1/euclid.bsmsp/1200512992 (accessed on 28 September 2017).
- Kaplan, D.; Glass, L. Time-Series Analysis Understanding Nonlinear Dynamics; Kaplan, D., Glass, L., Eds.; Springer: New York, NY, USA, 1995. [Google Scholar]
- Otzenberger, H.; Gronfier, C.; Simon, C.; Charloux, A.; Ehrhart, J.; Piquard, F.; Brandenberger, G. Dynamic heart rate variability: A tool for exploring sympathovagal balance continuously during sleep in men. Am. J. Physiol. 1998, 275, 946–950. [Google Scholar]
- De Vito, G.; Galloway, S.D.R.; Nimmo, M.A.; Maas, P.; McMurray, J.J.V. Efects of central sympathetic inhibition on heart rate variability during steady-state exercise in healthy humans. Clin. Physiol. Funct. Imaging 2002, 22, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Hayano, J.; Coleman, E.R.; Hanson, M.W.; Frid, D.J.; O’Connor, C.; Thurber, D.; Waugh, R.A.; Blumenthal, J.A. Relation of cardiovascular responses to mental stress and cardiac vagal activity in coronary artery disease. Am. J. Cardiol. 1993, 72, 551–554. [Google Scholar] [CrossRef]
- Akselrod, S.; Gordon, D.; Ubel, F.A.; Shannon, D.C.; Berger, A.C.; Cohen, R.J. Power spectrum analysis of heart rate fluctuation: A quantitive probe of beat-to-beat cardiovascular control. Science 1981, 213, 220–222. [Google Scholar] [CrossRef] [PubMed]
- Bolis, L.; Licinio, J.; Govoni, S. Handbook of the Autonomic Nervous System in Health and Disease; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Amenta, F. Aging of the Autonomic Nervous System; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Julius, S. Autonomic nervous system dysregulation in human hypertension. Am. J. Cardiol. 1991, 67, 3B–7B. [Google Scholar] [CrossRef]
- Kaplan, N.M. Primary hypertension: Pathogenesis. In Clinical Hypertension; Kaplan, N.M., Ed.; Williams & Wilkins: Baltimore, MD, USA, 1990; pp. 55–111. [Google Scholar]
- Bhaskar, R.; Raghabendra, C.; Ambarish, P.; Sajal, B.; Sasmit, S.; Sobhendu, K.G. Effect of rotating acoustic stimulus on heart rate variability in healthy adults. Open Neurol. J. 2012, 6, 71–77. [Google Scholar]
- Manzano, B.M.; Vanderlei, L.C.; Ramos, E.M.; Ramos, D. Acute effects of smoking on autonomic modulation: Analysis by Poincaré plot. Arq. Bras. Cardiol. 2011, 96, 154–160. [Google Scholar] [CrossRef] [PubMed]
- Tulppo, M.P.; Makikallio, T.H.; Seppanen, T. Heart rate dynamics during accentuated sympathovagal interaction. Am. J. Physiol. Heart Circ. Physiol. 1998, 274, 810–816. [Google Scholar]
- Yamamoto, Y.; Nakamura, Y.; Sato, H. On the fractal nature of heart rate variability in humans: Effects of vagal blockade. Am. J. Physiol. Regul. Integr. Comp. Physiol. 1995, 269, 830–837. [Google Scholar]
- Hagerman, I.; Berglund, M.; Lorin, M. Chaos-related deterministic regulation of heart rate variability in time- and frequency domains: Effects of autonomic blockade and exercise. Cardiovasc. Res. 1996, 31, 410–418. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Hausdorff, J.M. Fractal mechanisms and heart rate dynamics. Long-range correlations and their breakdown with disease. J. Electrocardiol. 1995, 28, 59–65. [Google Scholar] [CrossRef]
- Otsuka, K.; Cornellssent, G.; Halbergt, F. Age, gender and fractal scaling in heart rate variability. Clin. Sci. 1997, 93, 299–308. [Google Scholar] [CrossRef] [PubMed]
- Heart Rate Analysis in Normal Subjects of Various Age Groups. Available online: https://biomedical-engineering-online.biomedcentral.com/articles/10.1186/1475-925X-3-24 (accessed on 28 September 2017).
- Kagiyama, S.; Tsukashima, A.; Abe, I.; Fujishima, S.; Ohmori, S.; Onaka, U.; Ohya, Y.; Fujii, K.; Tsuchihashi, T.; Fujishima, M. Chaos and spectral analyses of heart rate variability during head-up tilting in essential hypertension. J. Auton. Nerv. Syst. 1999, 76, 153–158. [Google Scholar] [CrossRef]
- Shi, P.; Yu, H. Heart Rate Variability in Essential Hypertension Patients with Different Stages by Nonlinear Analysis: A Preliminary Study. Adv. Biomed. Eng. Res. 2013, 1, 33. [Google Scholar]
- Poddar, M.G.; Vinod, K.; Yash, P.S. Heart rate variability based classification of normal and hypertension cases by linear–nonlinear method. Def. Sci. J. 2014, 64, 542–548. [Google Scholar] [CrossRef]
- Moga, V.D.; Kurcalte, I.; Moga, M.; Vidu, F.; Rezus, C.; Cotet, I.; Avram, R. Dynamics of heart rate and blood pressure in hypertensive patients. J. Exp. Med. Surg. Res. Cercet. Exp. Med. Chir. 2013, 2, 11–16. [Google Scholar]
- Mäkikallio, T.H.; Tulppo, M.P.; Seppänen, T.; Huikuri, H.V. Analysis of nonlinear heart rate dynamics in cardiac arrhythmias. Herzschrittmachertherapie Elektrophys. 2000, 11, 131–138. [Google Scholar] [CrossRef]

| Title | Sex | N | Age | Height, cm | Weight, kg | BMI | SBP, mmHg | DBP, mmHg |
|---|---|---|---|---|---|---|---|---|
| Healthy | f | 15 | 8–10 | 132.4 ± 5.5 | 28.0 ± 5.8 | 16.2 ± 3.1 | 107.4 ± 10.2 | 70.5 ± 8.8 |
| 20 | 19–21 | 162.2 ± 6.2 | 65.4 ± 16.4 | 24.3 ± 5.8 | 110 ± 13.5 | 73.6 ± 10.8 | ||
| 18 | 35–55 | 160.4 ± 6.4 | 69.5 ± 14.3 | 26.6 ± 5.3 | 118 ± 14.3 | 78.4 ± 11.3 | ||
| m | 20 | 8–10 | 129.6 ± 4.2 | 25.6 ± 6.6 | 15.3 ± 4.1 | 115.3 ± 11.6 | 75.2 ± 7.5 | |
| 8 | 19–21 | 174.7 ± 7.1 | 73.0 ± 14.5 | 23.8 ± 4.1 | 118 ± 12.2 | 79.5 ± 9.9 | ||
| 14 | 35–55 | 173.4 ± 7.11 | 81.5 ± 14.7 | 26.8 ± 4.3 | 124 ± 12.9 | 84.6 ± 12.2 | ||
| Hypertension | f | 4 | 35–55 | 156.8 ± 6.3 | 74 ± 15.0 | 30.1 ± 5.6 | 137.3 ± 20.3 | 86.5 ± 12.0 |
| m | 10 | 35–55 | 168.1 ± 6.7 | 78 ± 16.0 | 27.6 ± 5.2 | 140.5 ± 23.8 | 86.7 ± 13.3 |
| Lag | Title | SDNN | p-Level | RMSSD | p-Level | SDSD | p-Level |
|---|---|---|---|---|---|---|---|
| 1 | SD1 | 0.94 | <0.05 | 1.00 | <0.05 | 1.00 | <0.05 |
| SD2 | 0.97 | <0.05 | 0.84 | <0.05 | 0.84 | <0.05 | |
| SD1/SD2 | 0.63 | <0.05 | 0.80 | <0.05 | 0.80 | <0.05 | |
| 2 | SD1 | 0.97 | <0.05 | 0.98 | <0.05 | 0.98 | <0.05 |
| SD2 | 0.97 | <0.05 | 0.85 | <0.05 | 0.85 | <0.05 | |
| SD1/SD2 | 0.62 | <0.05 | 0.73 | <0.05 | 0.73 | <0.05 | |
| 3 | SD1 | 0.98 | <0.05 | 0.95 | <0.05 | 0.95 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.91 | <0.05 | 0.91 | <0.05 | |
| SD1/SD2 | 0.50 | <0.05 | 0.54 | <0.05 | 0.54 | <0.05 | |
| 4 | SD1 | 0.98 | <0.05 | 0.93 | <0.05 | 0.93 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.91 | <0.05 | 0.91 | <0.05 | |
| SD1/SD2 | 0.42 | <0.05 | 0.44 | <0.05 | 0.44 | <0.05 | |
| 5 | SD1 | 0.98 | <0.05 | 0.95 | <0.05 | 0.95 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.90 | <0.05 | 0.90 | <0.05 | |
| SD1/SD2 | 0.44 | <0.05 | 0.47 | <0.05 | 0.47 | <0.05 | |
| 6 | SD1 | 0.98 | <0.05 | 0.94 | <0.05 | 0.94 | <0.05 |
| SD2 | 0.98 | <0.05 | 0.91 | <0.05 | 0.91 | <0.05 | |
| SD1/SD2 | 0.31 | <0.05 | 0.33 | <0.05 | 0.33 | <0.05 | |
| 7 | SD1 | 0.98 | <0.05 | 0.93 | <0.05 | 0.93 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.92 | <0.05 | 0.92 | <0.05 | |
| SD1/SD2 | 0.07 | NS † | 0.09 | NS † | 0.09 | NS † | |
| 8 | SD1 | 0.98 | <0.05 | 0.93 | <0.05 | 0.93 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.91 | <0.05 | 0.91 | <0.05 | |
| SD1/SD2 | 0.02 | NS † | 0.06 | NS † | 0.06 | NS † | |
| 9 | SD1 | 0.98 | <0.05 | 0.95 | <0.05 | 0.95 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.90 | <0.05 | 0.90 | <0.05 | |
| SD1/SD2 | 0.06 | NS † | 0.15 | NS † | 0.15 | NS † | |
| 10 | SD1 | 0.98 | <0.05 | 0.95 | <0.05 | 0.95 | <0.05 |
| SD2 | 0.99 | <0.05 | 0.90 | <0.05 | 0.90 | <0.05 | |
| SD1/SD2 | 0.05 | NS † | 0.16 | NS † | 0.16 | NS † |
| Lag | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | 0.000 † | 0.022 † | 0.001 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † |
| 2 | 0.000 † | - | 0.065 | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † |
| 3 | 0.022 | 0.065 | - | 1.000 | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.000 † |
| 4 | 0.001 † | 0.000 † | 1.000 | - | 0.011 † | 0.005 † | 0.024 † | 0.003 † | 0.009 † | 0.012 † |
| 5 | 0.000 † | 0.000 † | 0.000 † | 0.011 † | - | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 6 | 0.000 † | 0.000 † | 0.000 † | 0.005 † | 1.000 | - | 1.000 | 1.000 | 1.000 | 1.000 |
| 7 | 0.000 † | 0.000 † | 0.000 † | 0.024 † | 1.000 | 1.000 | - | 1.000 | 1.000 | 1.000 |
| 8 | 0.000 † | 0.000 † | 0.000 † | 0.003 † | 1.000 | 1.000 | 1.000 | - | 1.000 | 1.000 |
| 9 | 0.000 † | 0.000 † | 0.000 † | 0.009 † | 1.000 | 1.000 | 1.000 | 1.000 | - | 1.000 |
| 10 | 0.000 † | 0.000 † | 0.000 † | 0.012 † | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | - |
| Lag | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| % | 82 | 78 | 76 | 81 | 78 | 82 | 69 | 74 | 79 | 72 |
| Title | Group 1 | Group 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| N | Me | Q25 | Q75 | N | Me | Q25 | Q75 | p-Level | |
| HR | 57 | 69.03 | 63.18 | 74.32 | 38 | 76.91 | 68.43 | 82.60 | 0.003 † |
| SDNN | 57 | 60.57 | 41.40 | 80.00 | 38 | 53.69 | 41.57 | 67.08 | 0.242 |
| SDSD | 57 | 57.45 | 37.70 | 83.12 | 38 | 40.59 | 24.90 | 53.93 | 0.004 † |
| RMSSD | 57 | 57.35 | 37.65 | 82.99 | 38 | 40.54 | 24.87 | 53.85 | 0.004 † |
| TP | 57 | 5196.89 | 2418.43 | 9369.49 | 38 | 3887.35 | 2540.30 | 8025.33 | 0.455 |
| HFn.u. | 57 | 36.89 | 26.83 | 54.16 | 38 | 24.43 | 17.39 | 35.67 | 0.002 † |
| LFn.u. | 57 | 29.22 | 21.33 | 37.22 | 38 | 42.25 | 31.88 | 50.72 | 0.000 † |
| LF/HF | 57 | 0.86 | 0.44 | 1.23 | 38 | 1.56 | 1.10 | 2.69 | 0.000 † |
| Lag | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| SD1 | 0.043 † | 0.026 † | 0.032 † | 0.139 | 0.219 | 0.275 | 0.384 | 0.205 | 0.205 | 0.182 |
| SD2 | 0.982 | 0.699 | 0.767 | 0.946 | 0.927 | 0.820 | 0.974 | 0.783 | 0.683 | 0.635 |
| SD1/SD2 | 0.000 † | 0.000 † | 0.000 † | 0.000 † | 0.016 † | 0.015 † | 0.008 † | 0.001 † | 0.001 † | 0.003 † |
| Lag | Group | ChG | YG | AG |
|---|---|---|---|---|
| l = 1 | ChG | - | 0.465 | 0.000 † |
| YG | 0.465 | - | 0.563 | |
| AG | 0.000 † | 0.563 | - | |
| l = 2 | ChG | - | 1.000 | 0.002 † |
| YG | 1.000 | - | 0.014 † | |
| AG | 0.002 † | 0.014 † | - | |
| l = 3 | ChG | - | 0.168 | 0.329 |
| YG | 0.168 | - | 0.005 † | |
| AG | 0.329 | 0.005 † | - | |
| l = 4 | ChG | - | 0.000 † | 0.145 |
| YG | 0.000 † | - | 0.030 † | |
| AG | 0.145 | 0.030 † | - | |
| l = 5 | ChG | - | 0.000 † | 0.003 † |
| YG | 0.000 † | - | 0.048 † | |
| AG | 0.003 † | 0.048 † | - | |
| l = 6 | ChG | - | 0.000 † | 0.005 † |
| YG | 0.000 † | - | 0.047 † | |
| AG | 0.005 † | 0.047 † | - | |
| l = 7 | ChG | - | 0.001 † | 0.010 † |
| YG | 0.001 † | - | 0.264 | |
| AG | 0.010 † | 0.264 | - | |
| l = 8 | ChG | - | 0.058 | 0.007 † |
| YG | 0.058 | - | 1.000 | |
| AG | 0.007 † | 1.000 | - | |
| l = 9 | ChG | - | 0.401 | 0.007 † |
| YG | 0.401 | - | 1.000 | |
| AG | 0.007 † | 1.000 | - | |
| l = 10 | ChG | - | 1.000 | 0.014 † |
| YG | 1.000 | - | 0.590 | |
| AG | 0.014 † | 0.590 | - |
| Lag | Age Group | N | SD1 Me (Q25; Q75) | SD2 Me (Q25; Q75) | SD1/SD2 Me (Q25; Q75) |
|---|---|---|---|---|---|
| 5 | ChG | 35 | 44.0 (36.3; 54.1) | 59.2 (47.9; 72.9) | 0.75 (0.66; 0.83) |
| YG | 28 | 56.4 (42.8; 68.9) | 65.6 (49.4; 71.6) | 0.92 (0.82; 1.05) | |
| AG | 32 | 35.1 (23.2; 56.1) | 43.1 (30.8; 61.3) | 0.82 (0.71; 0.96) | |
| 6 | ChG | 35 | 46.4 (37.7; 57.5) | 57.7 (45.8; 69.9) | 0.81 (0.73; 0.89) |
| YG | 28 | 57.8 (46.7; 68.4) | 64.3 (46.2; 70.7) | 0.99 (0.89; 1.05) | |
| AG | 32 | 36.4 (24.3; 57.1) | 41.6 (29.6; 60.3) | 0.90 (0.77; 1.00) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koichubekov, B.; Riklefs, V.; Sorokina, M.; Korshukov, I.; Turgunova, L.; Laryushina, Y.; Bakirova, R.; Muldaeva, G.; Bekov, E.; Kultenova, M. Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability. Entropy 2017, 19, 523. https://doi.org/10.3390/e19100523
Koichubekov B, Riklefs V, Sorokina M, Korshukov I, Turgunova L, Laryushina Y, Bakirova R, Muldaeva G, Bekov E, Kultenova M. Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability. Entropy. 2017; 19(10):523. https://doi.org/10.3390/e19100523
Chicago/Turabian StyleKoichubekov, Berik, Viktor Riklefs, Marina Sorokina, Ilya Korshukov, Lyudmila Turgunova, Yelena Laryushina, Riszhan Bakirova, Gulmira Muldaeva, Ernur Bekov, and Makhabbat Kultenova. 2017. "Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability" Entropy 19, no. 10: 523. https://doi.org/10.3390/e19100523
APA StyleKoichubekov, B., Riklefs, V., Sorokina, M., Korshukov, I., Turgunova, L., Laryushina, Y., Bakirova, R., Muldaeva, G., Bekov, E., & Kultenova, M. (2017). Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability. Entropy, 19(10), 523. https://doi.org/10.3390/e19100523





