Abstract
This paper analyzes the energetic and exergy performance of an active magnetic regenerative refrigerator using water-based Al2O3 nanofluids as heat transfer fluids. A 1D numerical model has been extensively used to quantify the exergy performance of a system composed of a parallel-plate regenerator, magnetic source, pump, heat exchangers and control valves. Al2O3-water based nanofluids are tested thanks to CoolProp library, accounting for temperature-dependent properties, and appropriate correlations. The results are discussed in terms of the coefficient of performance, the exergy efficiency, and the cooling power as a function of the nanoparticle volume fraction and blowing time for a given geometrical configuration. It is shown that while the heat transfer between the fluid and solid is enhanced, it is accompanied by smaller temperature gradients within the fluid and larger pressure drops when increasing the nanoparticle concentration. It leads in all configurations to lower performance compared to the base case with pure liquid water.
1. Introduction
Refrigeration and air conditioning demand has continuously grown during the last decades. Environmental requirements and current ecological standards limit conventional technologies, such as vapor compression cycles. Research on future technologies of refrigeration turned to other principles. Around room temperature, magnetic refrigeration suggests many industrial applications: domestic or industrial cold production for food storage or air conditioning of buildings as few examples. It offers economic, ecological and environmental benefits and a high potential to develop higher efficiencies and lower noise production than current refrigeration systems. The operating principle is based on the magnetocaloric effect (MCE), which is related to a change of entropy in the magnetocaloric material (MCM) due to a variation of the applied magnetic field. This generates a quasi-instantaneous temperature change, typically about 2 K·T−1 for gadolinium at room temperature [1]. A heat transfer fluid, typically water, is then used as a heat transfer medium to remove heat. This process (Brayton cycle) produces cold and reaches steady-state conditions after a number of repeated cycles.
Researches in magnetic refrigeration focus mainly on three specific axes: magnetocaloric materials, magnets, and regenerators. The reader can refer to [2] for a complete review about magnetic refrigeration and to [3] for some recent perspectives. Recently, Trevizoli et al. [4] reviewed different design of Active Magnetic Regenerator (AMR) and proposed an extended optimization methodology based on the minimization of the generated entropy.
One of the main remaining concerns in magnetic refrigeration remains indeed to find the best architecture for the regenerator, which can be composed or parallel-plates, packed-bed media or wires [5]. For this purpose, constant researches have been conducted over the last decades to develop efficient AMR systems. Tusek et al. [6] compared experimentally six AMRs with gadolinium, namely three parallel-plate AMRs and three packed-bed AMRs. Their results showed that the parallel-plate AMR with the smallest porosity and a magnetic field parallel to the plates offers the best overall performance in terms of temperature span, cooling capacity and COP (Coefficient of Performance). Trevizoli et al. [7] compared three different regenerator geometries (parallel-plate, pin array and packed bed of spheres) having the same porosity and interstitial area. Thus, they could quantify the thermal, viscous and magnetic losses individually. The pin array offered the highest COP and second-law efficiency, while the parallel-plate AMR exhibited the lower performance.
Numerical 1D or 2D models appeared also as valuable tools to design new active magnetic regenerative refrigeration (AMRR) systems [8,9,10,11,12,13,14,15,16]. Tagliafico et al. [8] considered a reciprocating AMR with powder of gadolinium and investigated the influences of both the utilization factor UF (within the range [0.5, 3.5]) and the cycle frequency (within the range [0.1, 0.6] Hz). They showed that, for the optimal value of UF that maximizes the cooling power, the cycle frequency has only a weak influence on the COP of the system contrary to the effect the ambient temperature has on the system. Tura et al. [9] included the demagnetization effect in their 2D model, for which the velocity of water varies with the distance to the plates. They obtained a good agreement between their 2D model and experimental data, and showed that very thin plates and channels are required to get performances comparable to those of a packed-bed regenerator. Wu et al. [10] developed a 2D porous model to investigate the influence of the heat transfer fluid on the performance of the AMRR. For example, mercury offers a 600% enhancement of the cooling capacity. A detailed review about the numerical strategies to model magnetic regenerators up to 2011 may be found in [11].
Recently, Trevizoli et al. [12] quantified the internal (axial conduction, demagnetization, viscous losses) and external (heat transfer through the casing, dead volume, non-uniform applied magnetic field) losses in an AMR device using a 1D model. Losses to the surroundings and dead volumes are shown to have the largest impact on the AMR performance. The 1D model proposed by Niknia et al. [13] has been validated against experimental data for a packed bed regenerator with gadolinium spheres. These authors showed that the step change model for the applied magnetic field is a valid assumption for 1D models and that accounting for loss mechanisms like external heat leaks and demagnetization effects is necessary in the simulations not to overestimate the performance of the machine. Numerically, they introduced a sinusoidal meshing technique, which enables to save about 70% of computational time compared to uniform meshes. Roy et al. [14] compared several heat transfer fluid mixtures with temperature and pressure dependent properties using the same 1D numerical model as the one presented in Section 2. Pure liquid water clearly appeared to offer the best performance compared to mixtures with ethanol, ethylene-glycol, glycerol, ammonia or sodium chloride. They also investigated the effects of the mass flow rate along with the thicknesses of the plates and fluid channels on the COP, exergy efficiency and cooling load. The optimum configuration regarding the prescribed constraints requires a very low mass flow rate as well as low values of the fluid and plate thicknesses to increase the exchange surfaces. This way, conduction losses in the solid are also reduced because of a lower cross section of MCM. Finally, these last authors used a genetic algorithm to propose an optimized active regenerator. Mugica et al. [15] improved the previous 1D code to model a parallel-plate regenerator with insulator layers. Results showed higher temperature spans at zero cooling power, higher cooling load and COP with the same amount of MCM and applied magnetic field. The authors suggested to find a compromise between reducing the entropy generation by heat conduction, and increasing the magnetocaloric work when introducing insulator layers. Lei et al. [16] published a parametric study about the influence of the cycle frequency, hydraulic diameter and mass flow rate on the COP and generated entropy of an AMR for five geometrical configurations using a 1D model. They recommended the use of the packed screen bed or of a similar matrix structure.
The objectives of the present paper are in three folds: (1) to test the potentiality of enhancing the heat transfer between the magnetocaloric material and the heat transfer fluid by the means of nanofluids; (2) to better understand the influence of each transfer mechanism on the performance of the system; (3) to perform a parametric study and qualify the influences of the nanoparticle volume fraction and the blowing time (through UF) on the COP, exergy efficiency and cooling power. To the best of the author’s knowledge, these three objectives have not been considered yet in the literature.
In this article, the description of the thermodynamical model is first presented in Section 2. The assumptions are stated and the main parameters are introduced. The results are discussed in Section 3. Emphasis is made on the influence of the nanoparticle volume fraction and blowing time on the COP, exergy efficiency and cooling power of the system. Finally, conclusions are drawn in Section 4 about the relevance of using nanofluids in magnetic refrigeration to enhance the thermal exchanges between the magnetocaloric material and the heat transfer fluid.
2. One-Dimensional Numerical Method
2.1. Description of the System
The considered model is schematically depicted in Figure 1. This device is made from two heat exchangers at each end, a source of magnetic field that can be removed with the help of an actuator, a pump that drives the heat transfer fluid and a regenerator which consists of parallel-plates composed of a magnetocaloric material (gadolinium). The valves allow the fluid inside the heat exchangers to flow only when the temperature gradient is sufficient. When steady state is reached, heat is absorbed at the cold end (CS) and rejected at the hot source (HS). This configuration is similar to the experimental reciprocating prototype constructed by Roudaut [17].
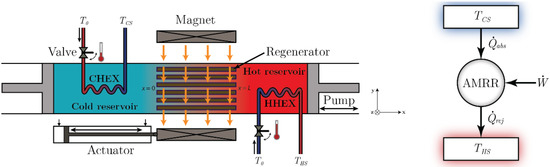
Figure 1.
Simplified scheme of the active magnetic regenerative refrigeration (AMRR) and its power balance.
This system can be emulated into four steps following the Brayton cycle [2]. First, the magnetization occurs when the magnetic field is on. Due to the MCE, the temperature of the MCM rises. Second, the refrigerant flows from the cold to the hot reservoir, absorbing heat while passing through the regenerator. During this process which is referred as a cold blow, the temperature of the hot reservoir increases. When it reaches a specific limit (THHEX), the valve opens to keep the temperature constant. Third, the magnetic field is removed and the magnetic entropy increases. As a result of the demagnetization, the temperature of the MCM goes down below its original value. For the last step, the refrigerant is pumped from the hot to the cold end, referred as a hot blow. It follows that the temperature in the cold reservoir decreases. In a similar way to the cold blow, the valve now opens if the temperature drops below TCHEX. Hence, heat is absorbed to maintain the same temperature level.
2.2. Numerical Modeling
2.2.1. Assumptions
- The system operating near room temperature, adiabatic conditions may be assumed. It has been carefully checked that including losses to the surroundings leads to similar results.
- The plates are made of gadolinium (Gd), which is the most common material used in magnetic refrigeration near room temperature. To model the magnetocaloric effect (MCE), the experimental data of Dankov et al. [18] are used showing better results compared to the Weiss-Debye-Sommerfeld model. The properties of Gd are temperature- and pressure-dependent thanks to Coolprop library.
- The magnetic field is applied in the y-direction (Figure 1). As a first step, the demagnetization is neglected. The reader can refer to the works of Nielsen et al. [19], Engelbrecht et al. [20] and Mugica et al. [15] for details on the impact of the demagnetization effect on the performance of the AMR.
- The magnetic field is assumed equally applied throughout the entire length of the regenerator. The parasitic losses are neglected. Their influence on the AMR performance has been discussed in [20].
- The time for magnetization or demagnetization is fixed to tmag = tdemag = 0.01 s and no idle time between each step of the cycle is considered.
- The flow is supposed to be laminar, fully-developed and steady-state with only one uniform velocity component V in the streamwise direction. The impact of flow maldistribution discussed in [20] is not taken into account here.
- Nanofluids are assumed to be single-phase fluids with constant volumetric concentration in nanoparticles throughout the domain. Their thermophysical properties depend on the fluid and nanoparticle properties, and the local temperature T.
2.2.2. Energy Equations
The equations that govern the temperature distributions in the fluid and solid parts during blows are obtained from the energy conservation law applied to a differential control volume inside the regenerator [2]:
where the indexes f and s refer to the (nano) fluid and the solid (gadolinium) respectively. V is the mean axial fluid velocity (in the x direction) and t is time. ρ, CP (or c) and λ represent the density (kg·m−3), the heat capacity (J·kg−1·K−1) and thermal conductivity (W·m−1·K−1) of the materials respectively. Note that the solid is subjected to an instantaneous increase in temperature due to magnetization since the magnetic work term is neglected in Equation (2). The heat capacity of the solid depends also on the applied magnetic field.
The convective heat transfer coefficient h (W·m−2·K−1) is evaluated through: h = Nu Dh/λf, where Dh is the hydraulic diameter defined by Dh = 4 ef l/(2ef + l), for a parallel-plate regenerator. As the flow between two plates is symmetric, ef is half the fluid thickness only and l represents the width of one plate. The heat transfer coefficient h is evaluated using the Nusselt number for constant laminar flow in rectangular ducts (see in [21]):
where α = 3.95 × 10−3 is the aspect ratio of the duct leading to Nu = 8.2831. The maximum value of the Reynolds number is obtained here for pure liquid flow: Re = ρf V Dh/μf ~ 40 confirming the laminar nature of the flow. During the magnetization and demagnetization phases, Nu = 4 as suggested in [17].
The pressure drop for laminar fully developed flows between infinite parallel plates or in a rectangular duct of high aspect ratio is evaluated through the Darcy-Weisbach Equation (see in [22]):
where p represents the pressure, f the friction factor and L the length of the regenerator.
2.2.3. Heat Transfer Fluid Properties
Water-based Al2O3 nanofluids are used in Section 3. The main advantages of alumina nanoparticles are their very low price and the absence of corrosion in thermal systems. Their properties are evaluated using the common relations for the density ρ and heat capacity Cp [23] as follows:
where the index np refers to the nanoparticles, bf to the base fluid and f to the nanofluid. For Al2O3-water-based nanofluids with a mean particle diameter of 47 nm, Equations (8) and (9) provided by Maïga et al. [24] then used by Mintsa et al. [25] have proven to be accurate in most configurations as shown by Sekrani et al. [26] for laminar flows in an uniformly heated pipe. Equations for the dynamic viscosity μ and the thermal conductivity λ of the nanofluid write:
The base fluid properties are temperature- and pressure-dependent thanks to Coolprop library. The properties of alumina at 20 °C are fixed to: ρnp = 3900 kg·m−3, Cp,np = 775 J·kg−1·K−1 and λnp = 40 W·m−1·K−1.
The ratio Cμ/Cλ was introduced as a kind of merit function by Prasher et al. [27] to recommend or not a given nanofluid. In the present case, this ratio, which slightly varies both with temperature and nanoparticle concentration, remains close to 3.537 ± 0.1%. It means that the increase in viscosity is always larger than the increase in thermal conductivity when the nanoparticle concentration increases but as Cμ/Cλ remains lower than 4, it can be recommended as a heat transfer fluid after [27].
2.2.4. Numerical Method and Parameters
Equations (1) and (2) are solved simultaneously using 2nd order finite-difference explicit schemes. The regenerator is discretized into 50 nodes and the maximum CFL is fixed to 0.30. This proved to be a good compromise between computational effort and accuracy. Steady-state is reached when the maximum discrepancy on work for two consecutive cycles is less than 0.005 J.
The boundary conditions for the fluid and solid domains are fully given in Roy et al. [14]. For hot and cold blows, adiabatic conditions are imposed for the fluid at the end of the regenerator assuming that the volume of each reservoir is large compared to the one of the regenerator. The temperatures of the reservoirs are calculated considering a perfect mixing and the displacement of the entire fluid contained within. Adiabatic conditions are imposed at each end of the solid. It is assumed that the heat exchangers absorb or reject all possible heat in order to keep a uniform temperature.
The present model has been validated for the parallel-plate regenerator of Roudaut [17]. It leads to very similar results compared to their experiments with less than 1% error on the hot and cold source temperatures and on the number of cycles to reach a steady-state and about 2% error on the temperature span under steady-state conditions.
2.3. Thermodynamic Analysis
The magnetization/demagnetization processes regarding the solid are associated with the heat absorption/rejection for the heat exchangers. In steady state, the work required to drive the AMRR is related to the actuator (magnetic work) and the pump (viscous dissipation). The overall efficiency must take into account several losses, such as the ones from the actuator, Foucault currents and magnetic hysteresis. Those coefficients given from Kitanovski and Egolf [28] are respectively: ηmot = 0.90, ηFou = 0.95, ηhys = 0.97. The formula to evaluate work power (W) is:
where the pump efficiency s fixed to ηp = 0.95, F is the flow rate (m3·s−1) and tblow the blowing time (s).
The Carnot efficiencies are related to the ambient (T0) and the source temperatures (THS and TCS). The exergy (Ex) produced at each end is the product of the Carnot efficiency (Ɵ) with the heat transfer rate ():
with ΔTHX = THS − T0 = T0 − TCS (Figure 1). Finally, COP and exergy efficiency ηex are defined as:
A detailed review on the thermodynamics of active magnetic regenerators has been proposed by Rowe [29,30].
3. Results and Discussion
Table 1 reports the default parameters used for all simulations chosen according to the optimization study of Roy et al. [14]. The applied magnetic field B is fixed to 1.5 T. Ambient conditions are set to T0 = 293 K and P0 = 105 Pa. The parameter L and es represent the length and half the thickness of one plate, respectively.

Table 1.
Fixed parameters used in the simulations.
The results will be discussed also as a function of the utilization factor UF ρf F . It is a dimensionless parameter classically used to characterize the conditioning of the system [2], which depends on the volumetric flow rate F and the blowing time among other parameters. The cycle frequency is given by f = 1/[2(tblow + tmag)] and will be varied between 0.125 Hz and 0.495 Hz. The fluid and solid properties are averaged values over the temperature range. Rowe [29,30] introduced also the parameter R defined as: R = 1 + UF, which is the ratio of total thermal mass to the solid thermal mass. As it will be shown in the following sections, UF remains relatively small in the present study such that R ≈ 1.
3.1. Influence of the Nanoparticle Concentration
When increasing the thermal conductivity of the heat transfer fluid by adding nanoparticles to liquid water, one expects to increase the heat transfer by convection between the fluid and the plates (positive effect on the performance of the system) but also to increase both the heat transfer by conduction within the fluid and the viscous losses (detrimental effects). The objective is first to qualify the influence of the nanoparticle volume fraction on the overall performance of the system.
The influence of the nanoparticle volume fraction on the COP, exergy efficiency and cooling power of the AMRR is displayed in Figure 2 for tblow = 1 s (f = 0.495 Hz) and F = 10−6 m3·s−1. Note that, on this figure, UF slightly varies from one nanoparticle concentration to another, from UF = 0.0473 at = 0% to UF = 0.0467 at = 5%. The COP and the exergy efficiency decreases quadratically with , while the absorbed power decreases linearly with the volume fraction in nanoparticles . For examples, for pure water: COP = 4.87, ηex = 16.81% and = 55.29 W and for = 5%, COP = 1.88, ηex = 6.93% and = 49.44 W. Introducing nanoparticles increases rapidly the pressure drop and as a consequence, the pumping power required to operate the system. It increases then the total work power and then decreases the COP (Equation (11)). At the same time, the presence of nanoparticles leads to an increase of the cold source temperature. Though the weak increase of the mass flow rate, it is accompanied by a global decrease of the absorbed power and so of the exergy efficiency ηex (Equation (11)).
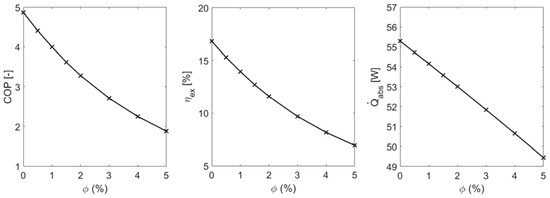
Figure 2.
Influence of the nanoparticle concentration on the Coefficient of Performance (COP), exergy efficiency and absorbed power . Results obtained for UF around 0.047 (tblow = 1 s or f = 0.495 Hz and F = 10−6 m3·s−1).
To better understand how the nanofluids affect the efficiency of the system, one needs to look at the heat transfer mechanisms responsible for the entropy generation within the regenerator. The local rate of entropy generation per unit volume is given by [31]:
where the first term on the right is the entropy generation rate per unit volume due to interphase heat transfer by convection , the other terms are the entropy generation rates due to conduction within the fluid , due to conduction within the solid and due to the viscous losses , respectively. The coefficient β is the surface area density (m2/m3), i.e., the ratio between the heat transfer area and the total volume of the regenerator.
Figure 3 displays the evolution of the generated entropy as a function of the nanoparticle concentration. The different contributions to Equation (12) have been integrated both along the regenerator and over a cycle after the system reached a steady-state regime. For = 0%, convection Sconv contributes to 87.71% of the total generated entropy Sgen. It may be attributed to the particularly high surface area density of the present regenerator. The other contributions come from the viscous losses Sviscous (10.12%), the conduction within the MCM SScond (2.05%) and the conduction within the fluid SFcond (0.12%).
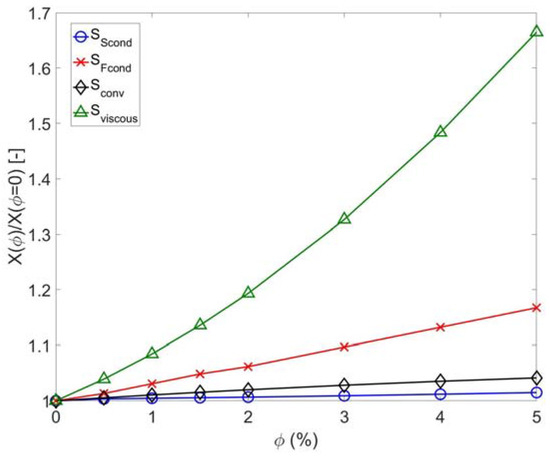
Figure 3.
Evolution of the generated entropy according to the nanoparticle concentration for utilization factor (UF) around 0.047 (tblow = 1 s or f = 0.495 Hz, F = 10−6 m3·s−1). The results are normalized by their values for = 0% (Sconv = 16.95 J·m−2·K−1, SFcond = 0.023 J·m−2·K−1, SScond = 0.396 J·m−2·K−1, Sviscous = 1.956 J·m−2·K−1).
Figure 3 confirms the detrimental effect that moderate fractions of Al2O3 nanoparticles dispersed in water have on the system. It does not only increase the viscous losses greatly, but the entropy generated by conduction within the fluid domain increases more rapidly than the one associated to convection. In this case, an increase of Sconv means a higher heat transfer between the fluid and solid domains. This result was expected as the thermal conductivity of the fluid increased by adding the nanoparticles. This increase is regarded as a positive effect, as Sconv can be lowered by shifting to a hybrid Brayton-Ericsson cycle by lowering F and increasing tblow at the same time (see for example the work of Plaznik et al. [32]). Nonetheless, the increase of SFcond points out that more heat is travelling in the longitudinal direction of the regenerator, destroying to some extent the temperature difference attained in the case with pure water.
3.2. Influence of the Blowing Time
As already mentioned, the utilization factor UF is a key parameter to describe the heat exchange in magnetic refrigeration as it appears as a prefactor in the advection term when one normalized adequately the fluid energy equation. Nevertheless, the temperature profile will change slightly if F and tblow are modified, even if UF is kept constant. Thus, the objective of the present section is quantify the influence of the blowing time tblow (or cycle frequency f) both at a constant volumetric flow rate (such UF will vary) and at constant UF (such that F is changed accordingly to the blowing time variations). Changing the blowing time is expected to enable the nanofluid to catch more or less thermal energy from the MCM.
Figure 4a,c,e display the evolution of the COP, exergy efficiency and cooling power as a function of the utilization factor UF for blowing time (resp. frequency) varying between 1 s (resp. 0.495 Hz) and 4 s (resp. 0.125 Hz) and a constant volumetric flow rate F = 10−6 m3·s−1. The variations of UF directly represent the variations of tblow. The absorbed power increases almost linearly with the blowing time up to a maximum value at tblow = 3 s, while the COP and the exergy efficiency decrease at the same time. It confirms the results of Rowe [30] at R ≈ 1, which obtained also a decrease of the efficiency and an increase of the cooling power when UF increases. The main result here is that, for this range of utilization factor (UF = [0.0467, 0.187]), introducing nanoparticles into the base fluid leads to lower overall performance of the system, whatever the value of .
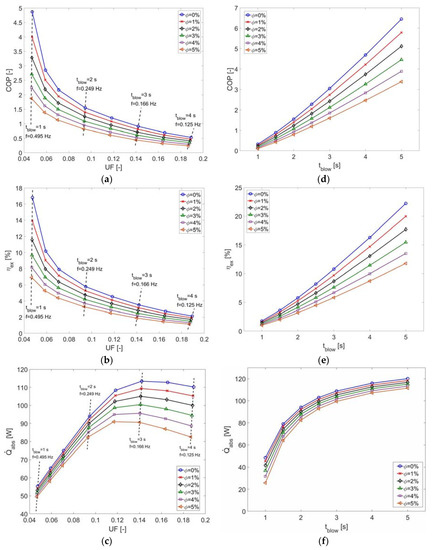
Figure 4.
Variations of the COP, exergy efficiency ηex and absorbed power (a, b, c) as a function of the utilization factor UF (at constant flow rate F = 10−6 m3·s−1) and (d, e, f) as a function of the blowing time (at constant utilization factor UF = 0.095).
In the present case, increasing UF is associated with a small increase of the pumping work as the pressure drop increases faster than the blowing time. At the same time, the absolute value of the rejected heat increases 1.25 faster than the absorbed heat leading to an increase also of the magnetic power. All in all, the total work power increases 2.5 faster than the absorbed heat, which induces a decrease of the COP. It is accompanied for the same reasons by a decrease of the exergy efficiency ηex. The linear increase of the absorbed power up to UF ≈ 0.14 (tblow = 3 s or f = 0.166 Hz) is directly connected to a linear decrease of the cold source temperature when UF is increased.
The present results confirm the former ones of Rowe [30] at R = 1 (small values of UF). For UF varying between 0.1 and 0.5, he also obtained an increase of the cooling power up to a maximum value before a decrease with increasing values of UF. It was attributed to the regenerative temperature change, which starts to limit the net temperature change through the cold heat exchanger. Li et al. [33] applied a simpler model based on the Willmott’s model for the blowing processes to the case of a packed-bed regenerator with 300 μm spheres of Gadolinium and pure water as the heat transfer fluid. They showed also that the total work increases with UF. At the same time, the cooling power increases also linearly with UF up to a critical value around UF = 1 before decreasing when increasing further UF.
Figure 4b,d,f present the variations of the COP, exergy efficiency and absorbed power as a function of the blowing time for a given utilization factor fixed to UF = 0.095. To the best of the author’s knowledge, no work has been published regarding the influence of the blowing time or cycle frequency at constant utilization factor making comparisons difficult. In the present case, COP, ηex and exhibit the same profile and increase when the blowing time is increased. The rejected heat exhibits a non monotonous profile for all cases (not shown here), with a decrease (in magnitude) up to tblow = 1.5 s and then it increases up to tblow = 5 s. Tagliafico et al. [8] obtained a decrease of the COP for increasing values of the cycle frequency for a gadolinium AMR (m = 395 g, B = 1.7 T) for an utilization factor that maximizes the refrigeration capacity. However, the amplitude of its decrease was lower for f = [0.1–0.6] Hz in their case. The results of Lei et al. [16] confirmed this trend whatever the geometry considered (packed bed spheres, parallel plates or pack screen bed). However, they showed also that COP could also increase with the cycle frequency for large aspect ratios depending on the geometry and hydraulic parameter.
To conclude, the operating parameters have been varied as: tblow = [1, 5] s, f = [0.1, 0.495] Hz, F = [0.4, 2.03] × 10−6 m3·s−1 and UF = [0.0467, 0.189]. These ranges do not correspond to any marketable AMR device but have been considered in the literature. The main result obtained here is that whatever the nanoparticle concentrations and the operating conditions, adding alumina nanoparticles to water lead to lower performance in terms of COP, exergy efficiency and cooling power compared to pure water.
4. Conclusions
This paper is focused on the thermodynamic performance of an active magnetic parallel-plate regenerator composed of gadolinium. An attested 1D numerical model coupled with Coolprop database has been used to qualify the influence of the nanoparticle volume fraction and the blowing time on the thermal performance of the system. Adding nanoparticles to the base fluid leads to a decrease of the COP, exergy efficiency and cooling power of the system whatever the operating conditions considered here. As expected, the increase of the thermal conductivity of the fluid due to the alumina nanoparticles is accompanied by a large increase of the pressure drop. At the same time, the generated entropy by conduction within the fluid increases faster than the one due to convection, which is detrimental to the temperature gradient within the machine. The influence of the blowing time on the thermodynamic performance of the system has also been qualified for variable or constant utilization factor. At fixed flowrate, a blowing time equal to 1 s enables to maximize both the COP and exergy efficiency. At the same time, larger blowing times would lead to a higher absorbed power for tblow = 3 s. At constant utilization factor, COP, exergy efficiency and cooling power are found to increase with the blowing time.
Acknowledgments
This project is part of the research program of the NSERC Chair on Industrial Energy Efficiency, established at Université de Sherbrooke in 2014, with the support of Hydro-Québec, Ressources Naturelles Canada (CanmetEnergy in Varennes), Rio Tinto Alcan, and the Natural Sciences and Engineering Research Council of Canada.
Author Contributions
Ibai Mugica and Steven Roy conceived the 1D numerical code; Sébastien Poncet performed the calculations. All authors analyzed the data and contributed to the writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouchekara, H. Recherche sur les Systèmes de Réfrigération Magnétique: Modélisation Numérique, Conception et Optimisation. Ph.D. Thesis, Institut National Polytechnique de Grenoble, Grenoble, France, 2008. (In French). [Google Scholar]
- Kitanovski, A.; Tušek, J.; Tomc, U.; Plaznik, U.; Ožbolt, M.; Poredoš, A. Magnetocaloric Energy Conversion: From Theory to Applications, Green Energy and Technology; Springer: New York, NY, USA, 2015. [Google Scholar]
- Pecharsky, V.V.; Cui, J.; Johnson, D.D. (Magneto) caloric refrigeration: Is there light at the end of the tunnel? Philos. Trans. R. Soc. A 2016, 374. [Google Scholar] [CrossRef] [PubMed]
- Trevizoli, P.V.; Christiaanse, T.V.; Govindappa, P.; Niknia, I.; Teyber, R.; Barbosa, J.R., Jr.; Rowe, A. Magnetic heat pumps: An overview of design principles and challenges. Sci. Technol. Built Environ. 2016, 22, 507–519. [Google Scholar] [CrossRef]
- Yu, B.; Liu, M.; Egolf, P.W.; Kitanovski, A. A review of magnetic refrigerator and heat pump prototypes built before the year 2010. Int. J. Refrig. 2010, 33, 1029–1060. [Google Scholar] [CrossRef]
- Tusek, J.; Kitanovsky, A.; Zupan, S.; Prebil, I.; Poredos, A. A comprehensive experimental analysis of gadolinium active magnetic regenerators. Appl. Therm. Eng. 2013, 53, 57–66. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Nakashima, A.T.; Peixer, G.F.; Barbosa, J.R., Jr. Performance assessment of different porous matrix for active regenerators. Appl. Energy 2017, 187, 847–861. [Google Scholar] [CrossRef]
- Tagliafico, G.; Scarpa, F.; Canepa, F. A dynamic 1-D model for a reciprocating active magnetic regenerator; influence of the main working parameters. Int. J. Refrig. 2010, 33, 286–293. [Google Scholar] [CrossRef]
- Tura, A.; Nielsen, K.K.; Rowe, A. Experimental and modeling results of a parallel plate-based active magnetic regenerator. Int. J. Refrig. 2012, 35, 1518–1527. [Google Scholar] [CrossRef]
- Wu, J.; Liu, C.; Hou, P.; Huang, Y.; Ouyang, G.; Chen, Y. Fluid choice and test standardization for magnetic regenerators operating at near room temperature. Int. J. Refrig. 2014, 37, 135–146. [Google Scholar] [CrossRef]
- Nielsen, K.; Tušek, J.; Engelbrecht, K.; Schopfer, S.; Kitanovski, A.; Bahl, C.; Smith, A.; Pryds, N.; Poredoš, A. Review on numerical modeling of active magnetic regenerators for room temperature applications. Int. J. Refrig. 2011, 34, 603–616. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Nakashima, A.T.; Barbosa, J.R., Jr. Performance evaluation of an active magnetic regenerator for cooling applications—Part II: Mathematical modeling and thermal losses. Int. J. Refrig. 2016, 72, 206–217. [Google Scholar] [CrossRef]
- Niknia, I.; Campbell, O.; Christiaanse, T.V.; Govindappa, P.; Teyber, R.; Trevizoli, P.V.; Rowe, A. Impacts of configuration losses on active magnetic regenerator device performance. Appl. Therm. Eng. 2016, 106, 601–612. [Google Scholar] [CrossRef]
- Roy, S.; Poncet, S.; Sorin, M. Sensitivity analysis and multiobjective optimization of a parallel-plate active magnetic regenerator using a genetic algorithm. Int. J. Refrig. 2017, 75, 276–285. [Google Scholar] [CrossRef]
- Mugica, I.; Poncet, S.; Bouchard, J. Entropy generation in a parallel-plate active magnetic regenerator with insulator layers. J. Appl. Phys. 2017, 121, 074901. [Google Scholar] [CrossRef]
- Lei, T.; Engelbrecht, K.; Nielsen, K.K.; Veje, C.T. Study of geometries of active magnetic regenerators for room temperature magnetocaloric refrigeration. Appl. Therm. Eng. 2017, 111, 1232–1243. [Google Scholar] [CrossRef]
- Roudaut, J. Modélisation et Conception de Systèmes de Réfrigération Magnétique autour de la Température Ambiante. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2012. (In French). [Google Scholar]
- Dankov, S.Y.; Tishin, A.; Pecharsky, V.; Gschneidner, K. Magnetic phase transitions and the magnetothermal properties of gadolinium. Phys. Rev. B 1998, 57, 1–13. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Smith, A.; Bahl, C.R.H.; Olsen, U.L. The influence of demagnetizing effects on the performance of active magnetic regenerators. J. Appl. Phys. 2012, 112, 094905. [Google Scholar] [CrossRef]
- Engelbrecht, K.; Tusek, J.; Nielsen, K.K.; Kitanovski, A.; Bahl, C.R.H.; Poredos, A. Improved modelling of a parallel plate active magnetic regenerator. J. Phys. D 2013, 46, 255002. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P.; Cho, Y.L. Handbook of Heat Transfer; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Garby, L.; Larsen, P.S. Bioenergetics: Its Thermodynamic Foundations; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Bianco, V.; Manca, O.; Nardini, S.; Vafai, K. Heat Transfer Enhancement with Nanofluids; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Maïga, S.E.B.; Palm, S.M.; Nguyen, C.T.; Roy, G.; Galanis, N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow 2005, 26, 530–546. [Google Scholar] [CrossRef]
- Mintsa, H.A.; Roy, G.; Nguyen, C.T.; Doucet, D. New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 2009, 48, 363–371. [Google Scholar] [CrossRef]
- Sekrani, G.; Poncet, S. Further investigation on Laminar forced convection of nanofluid flows in a uniformly heated pipe using direct numerical simulations. Appl. Sci. 2016, 6, 1–24. [Google Scholar] [CrossRef]
- Prasher, R.; Song, D.; Phelan, J.W. Measurements of nanofluid viscosity and its implications for thermal applications. Appl. Phys. Lett. 2006, 89, 133108. [Google Scholar] [CrossRef]
- Kitanovski, A.; Egolf, P.W. Application of magnetic refrigeration and its assessment. J. Magn. Magn. Mater. 2009, 321, 777–781. [Google Scholar] [CrossRef]
- Rowe, A. Thermodynamics of active magnetic regenerators: Part I. Cryogenics 2012, 52, 111–118. [Google Scholar] [CrossRef]
- Rowe, A. Thermodynamics of active magnetic regenerators: Part II. Cryogenics 2012, 52, 119–128. [Google Scholar] [CrossRef]
- Trevizoli, P.V.; Barbosa, J.R., Jr. Entropy generation minimization analysis of oscillating-flow regenerators. Int. J. Heat Mass Transf. 2015, 87, 347–358. [Google Scholar] [CrossRef]
- Plaznik, U.; Tusek, J.; Kitanovski, A.; Poredos, A. Numerical and experimental analyses of different magnetic thermodynamic cycles with an active magnetic regenerator. Appl. Therm. Eng. 2013, 59, 52–59. [Google Scholar] [CrossRef]
- Li, P.; Gong, M.; Yao, G.; Wu, J. A practical model for analysis of active magnetic regenerative refrigerators for room temperature applications. Int. J. Refrig. 2006, 29, 1259–1266. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).