Economics and Finance: q-Statistical Stylized Features Galore
Abstract
:1. Introduction
2. Applications in Economics and Finance
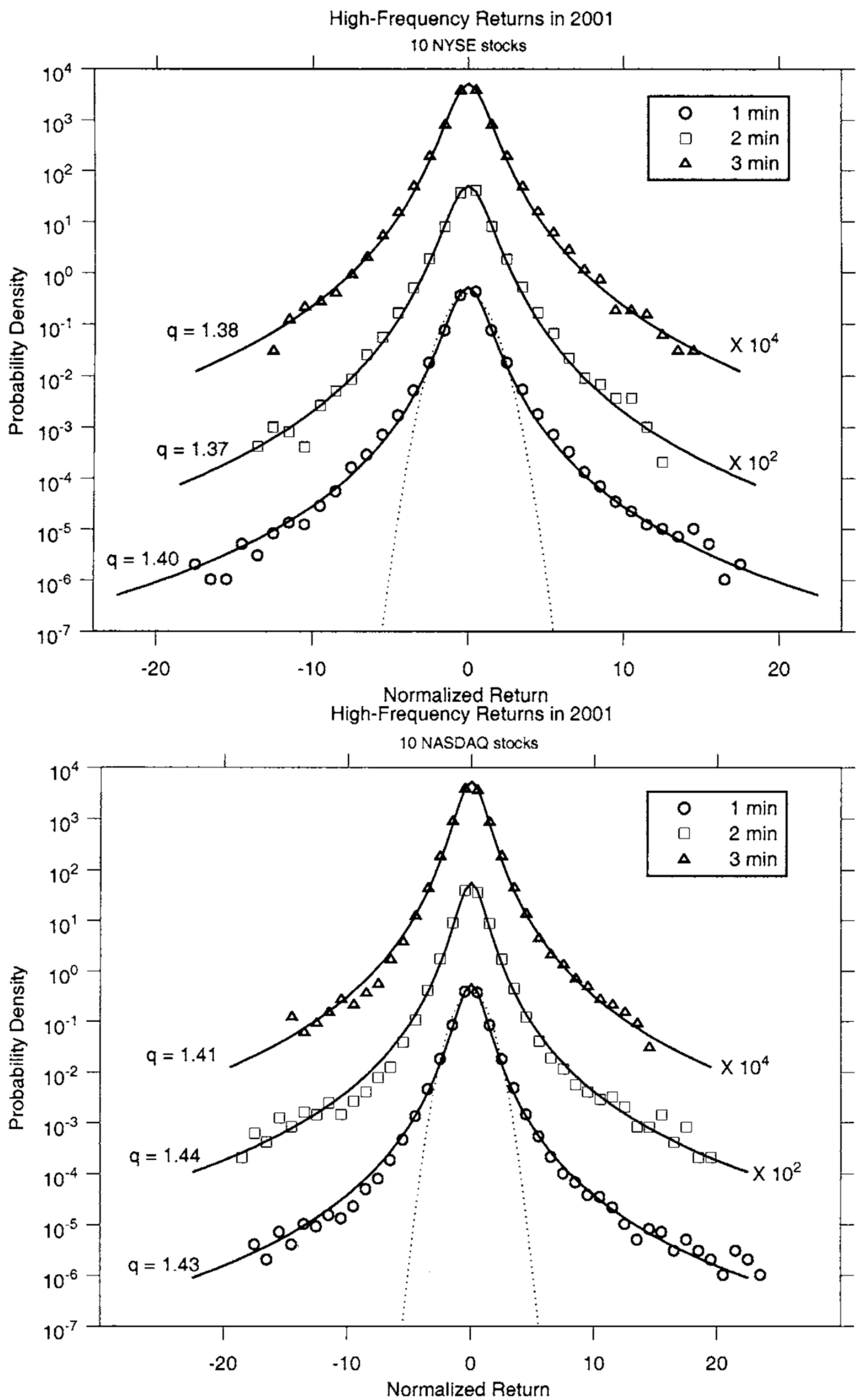
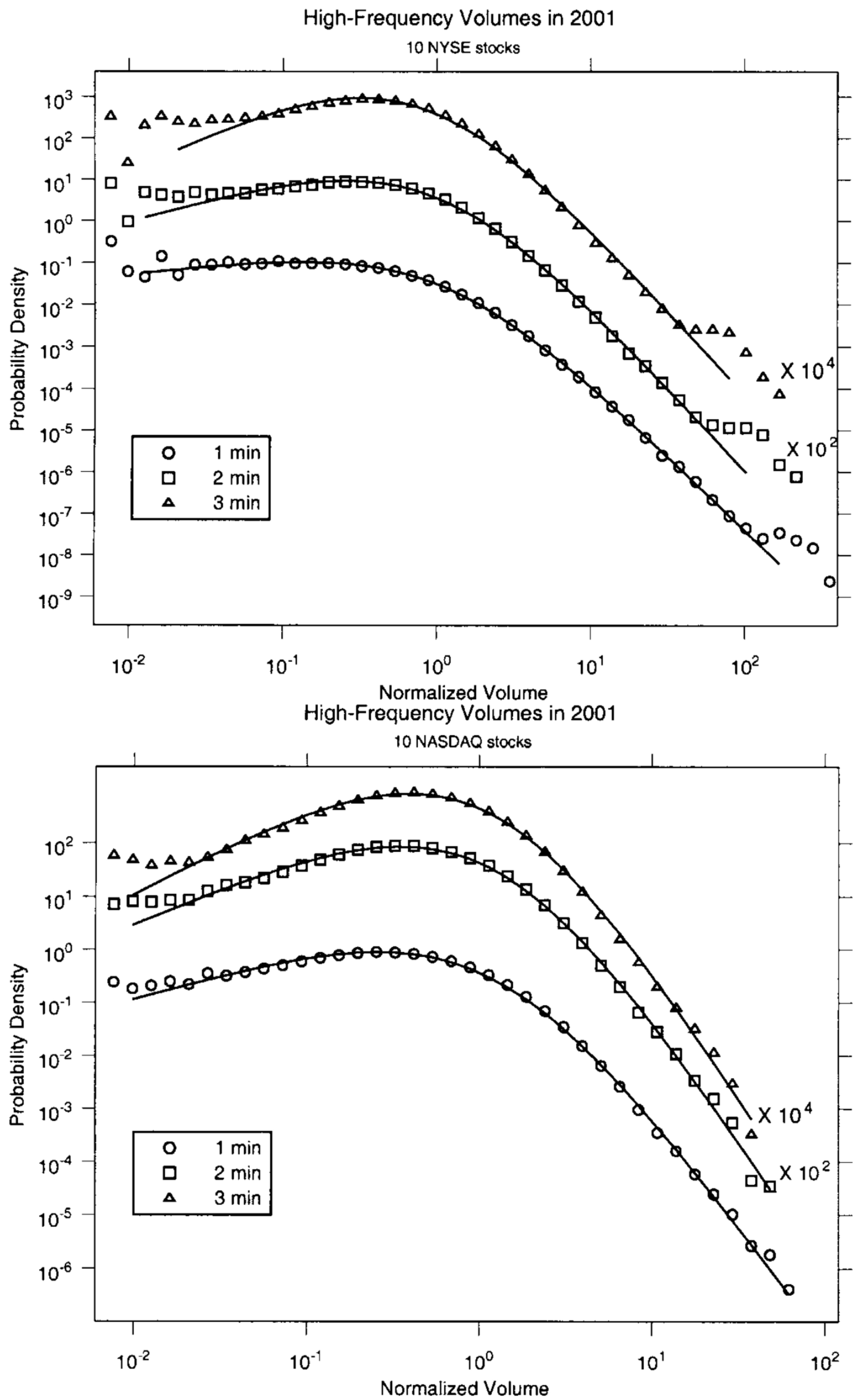
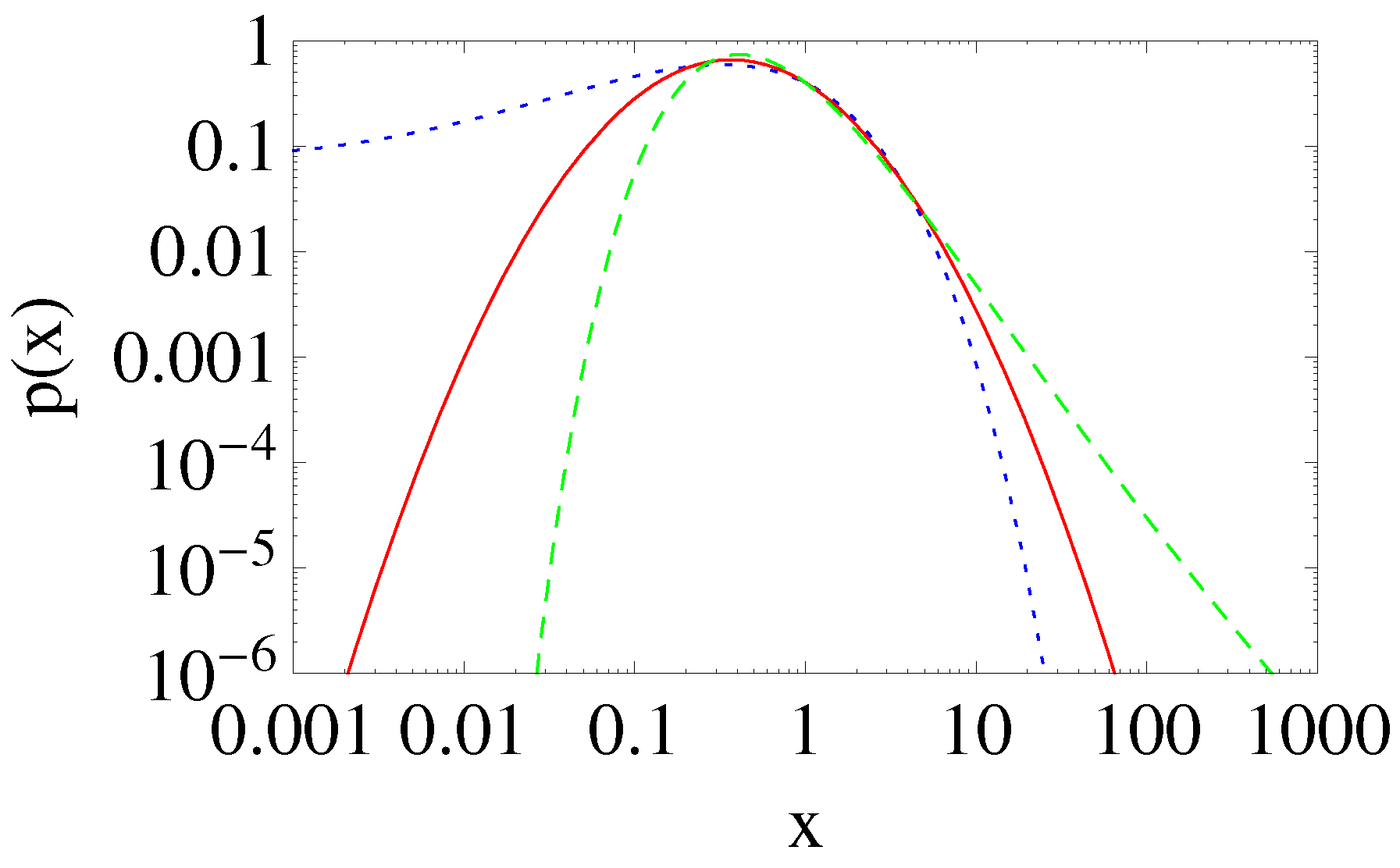
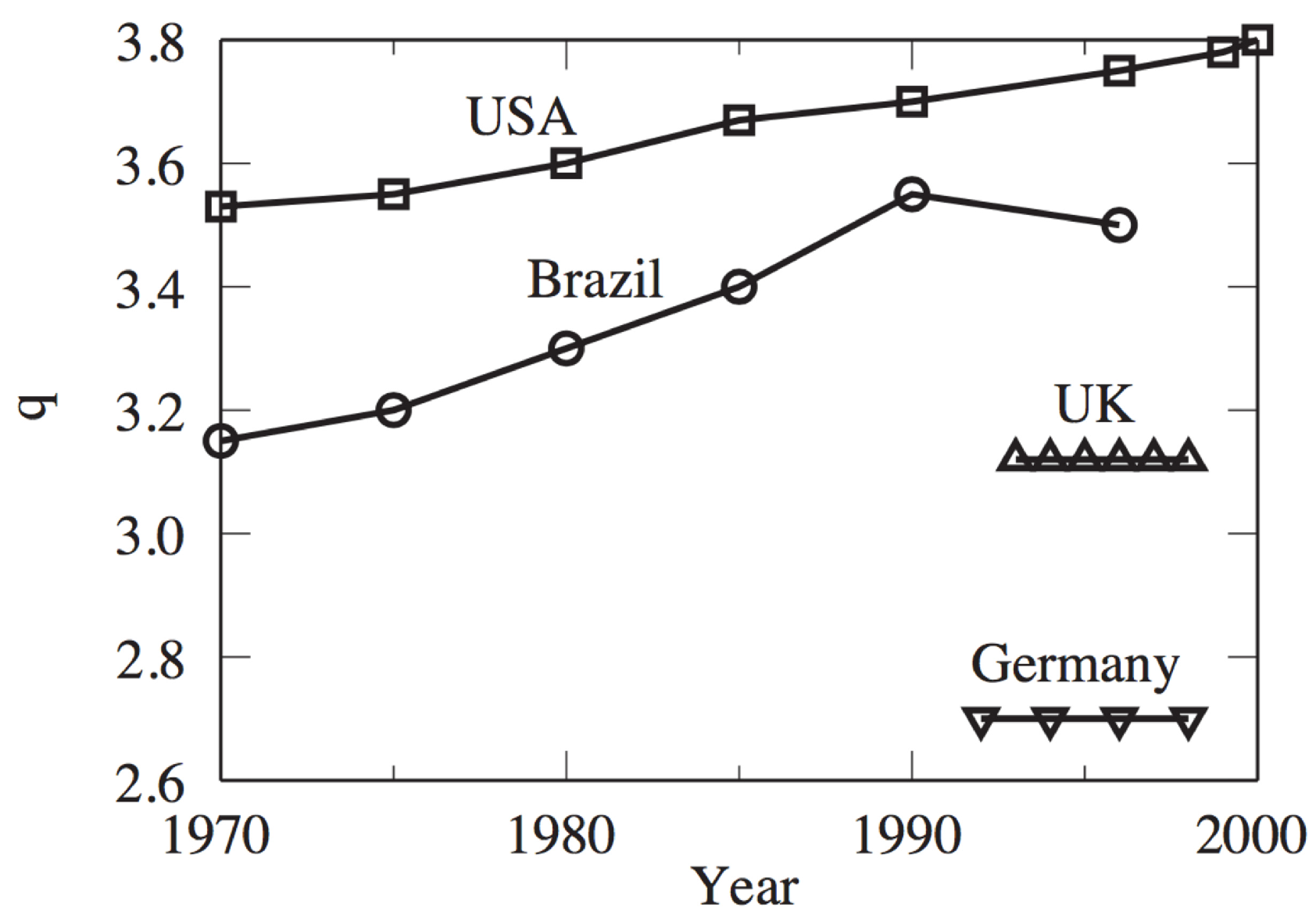
2.1. Prices and Volumes
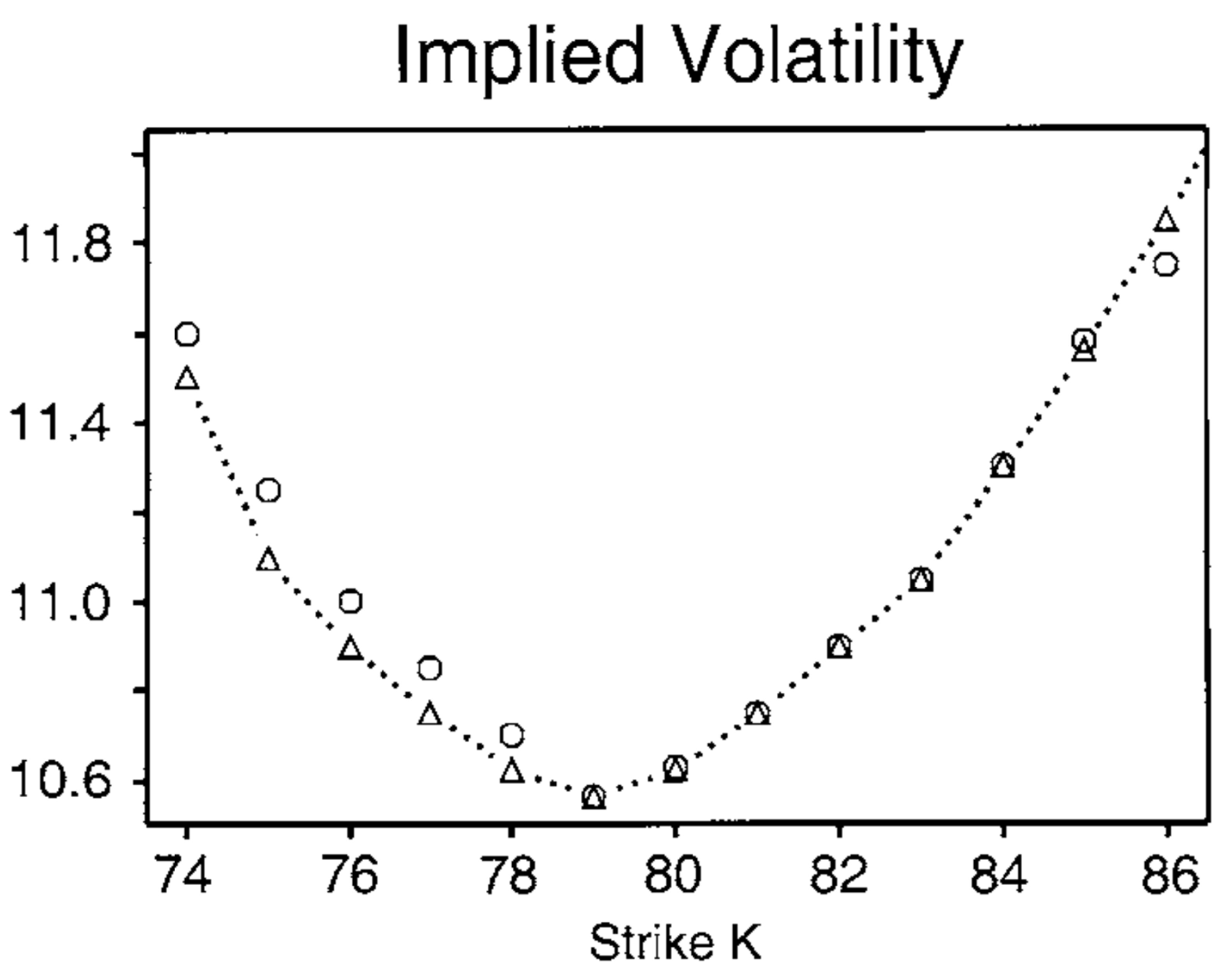
2.2. Volatilities
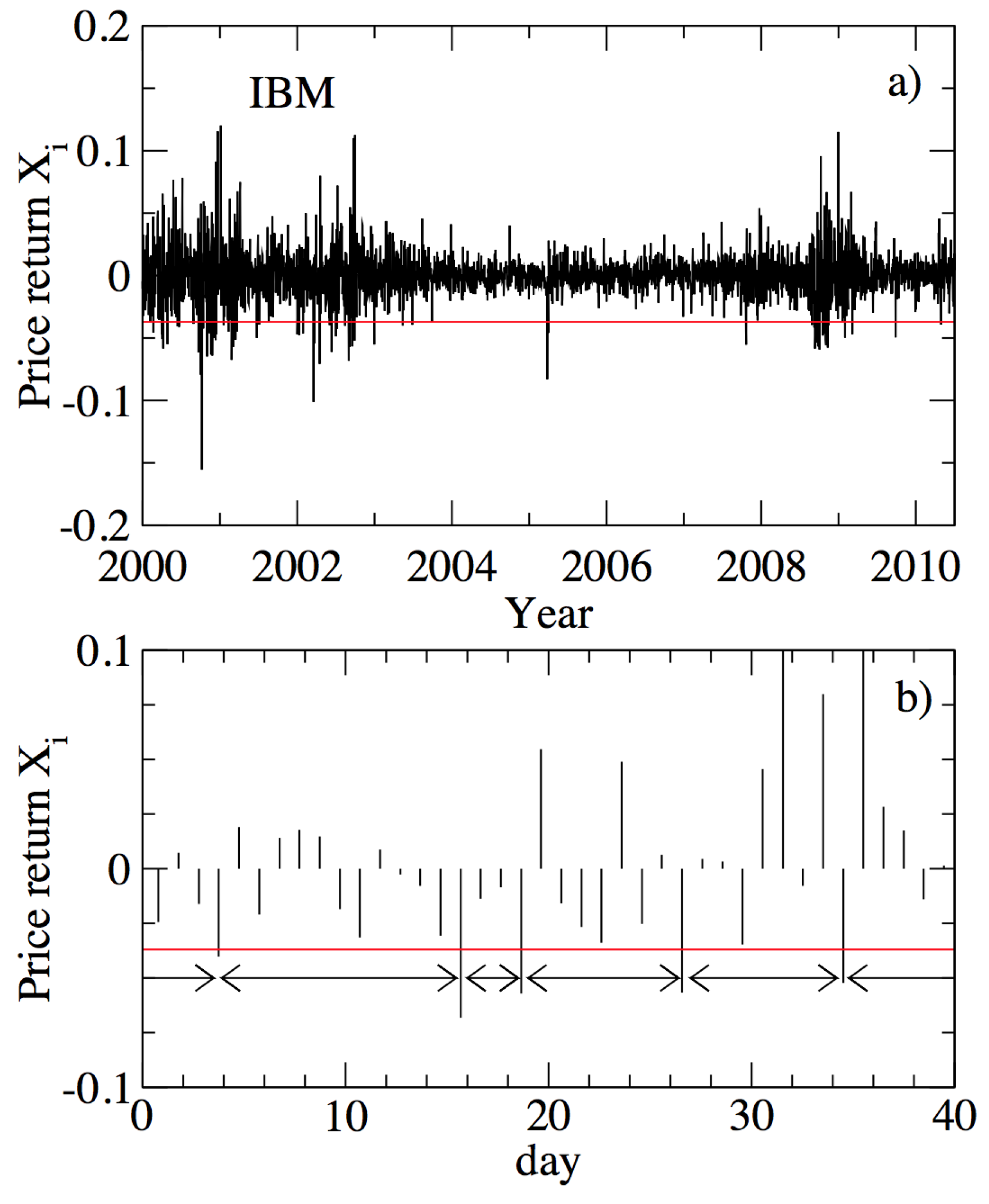
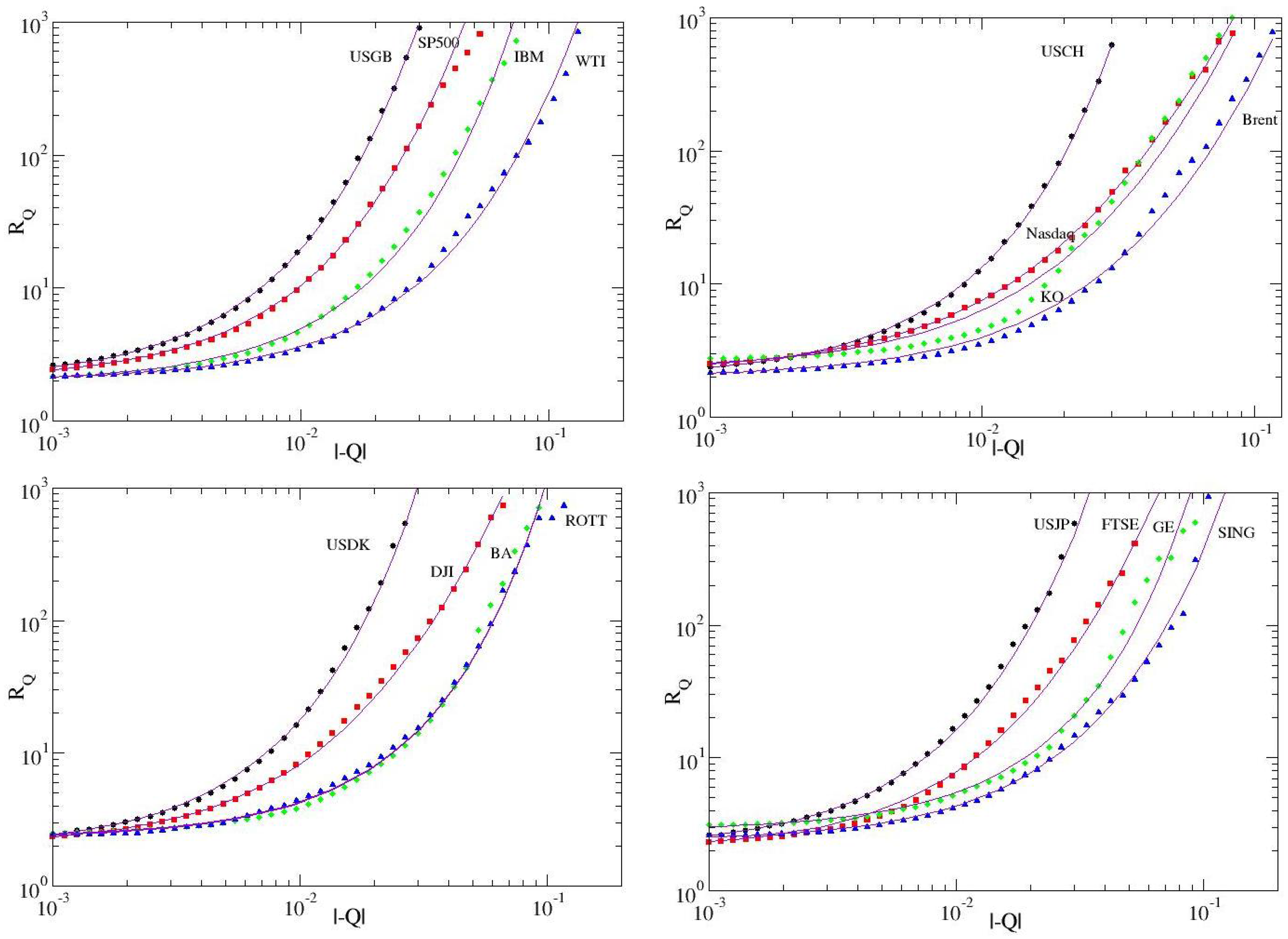
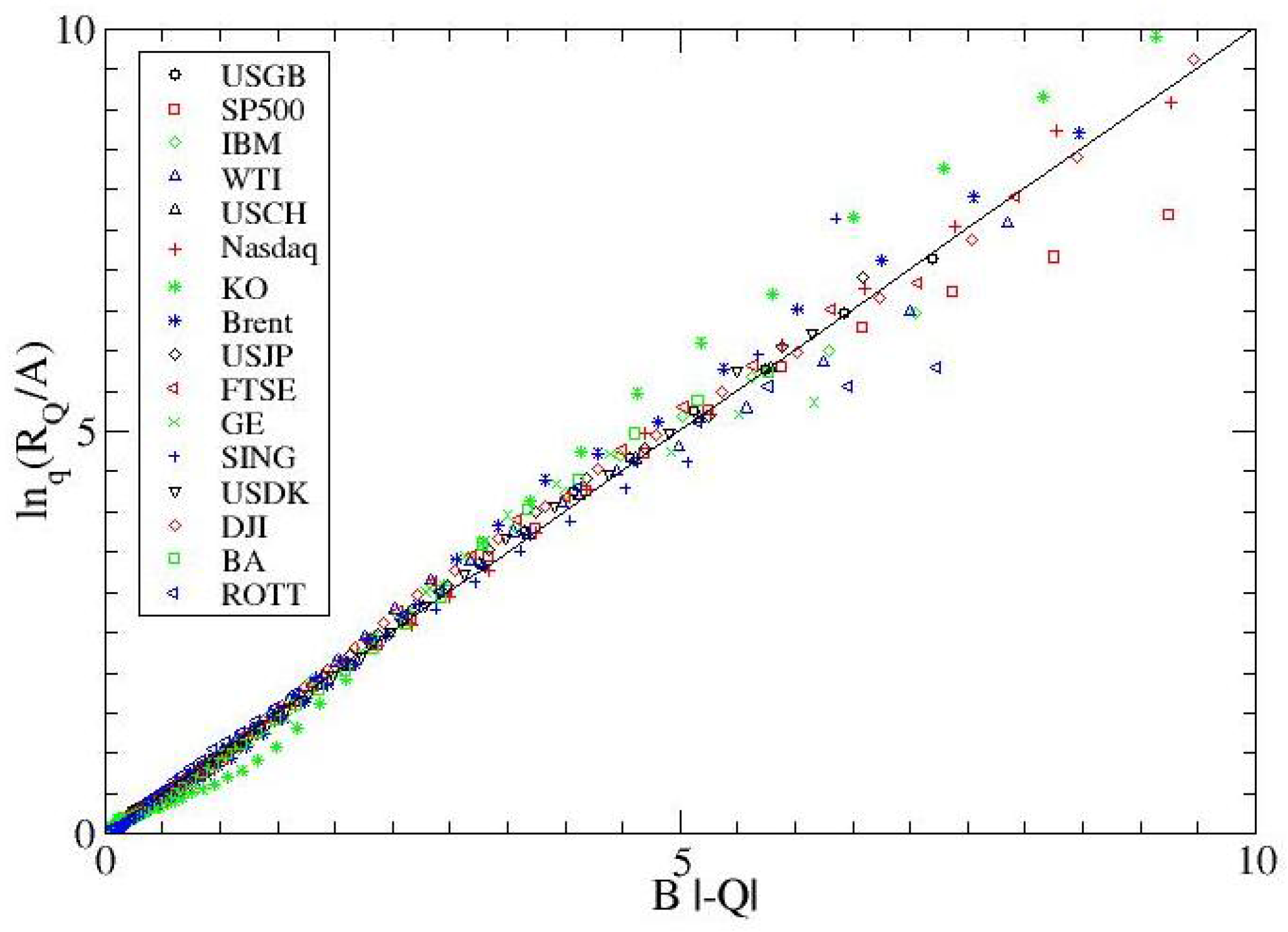
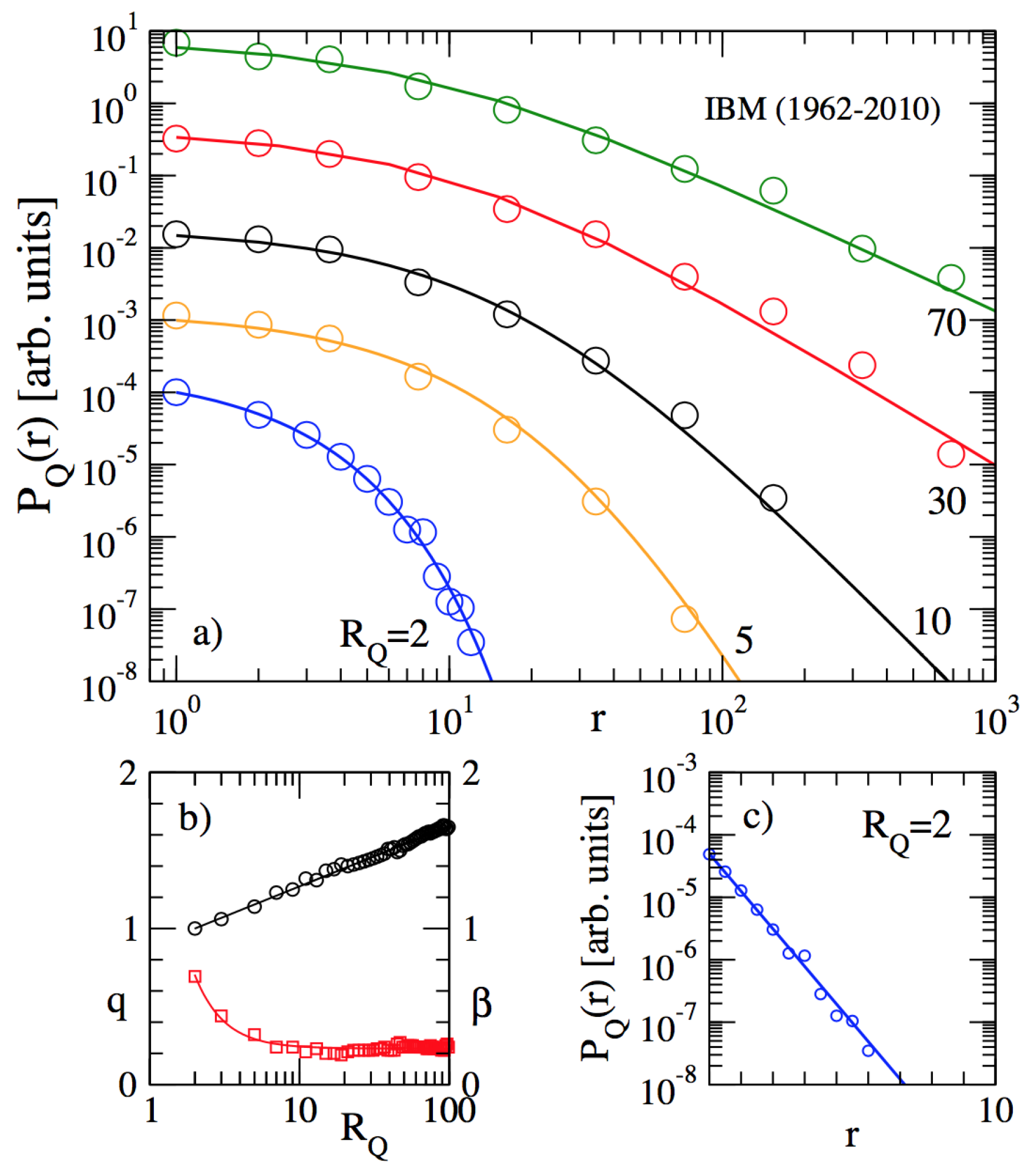
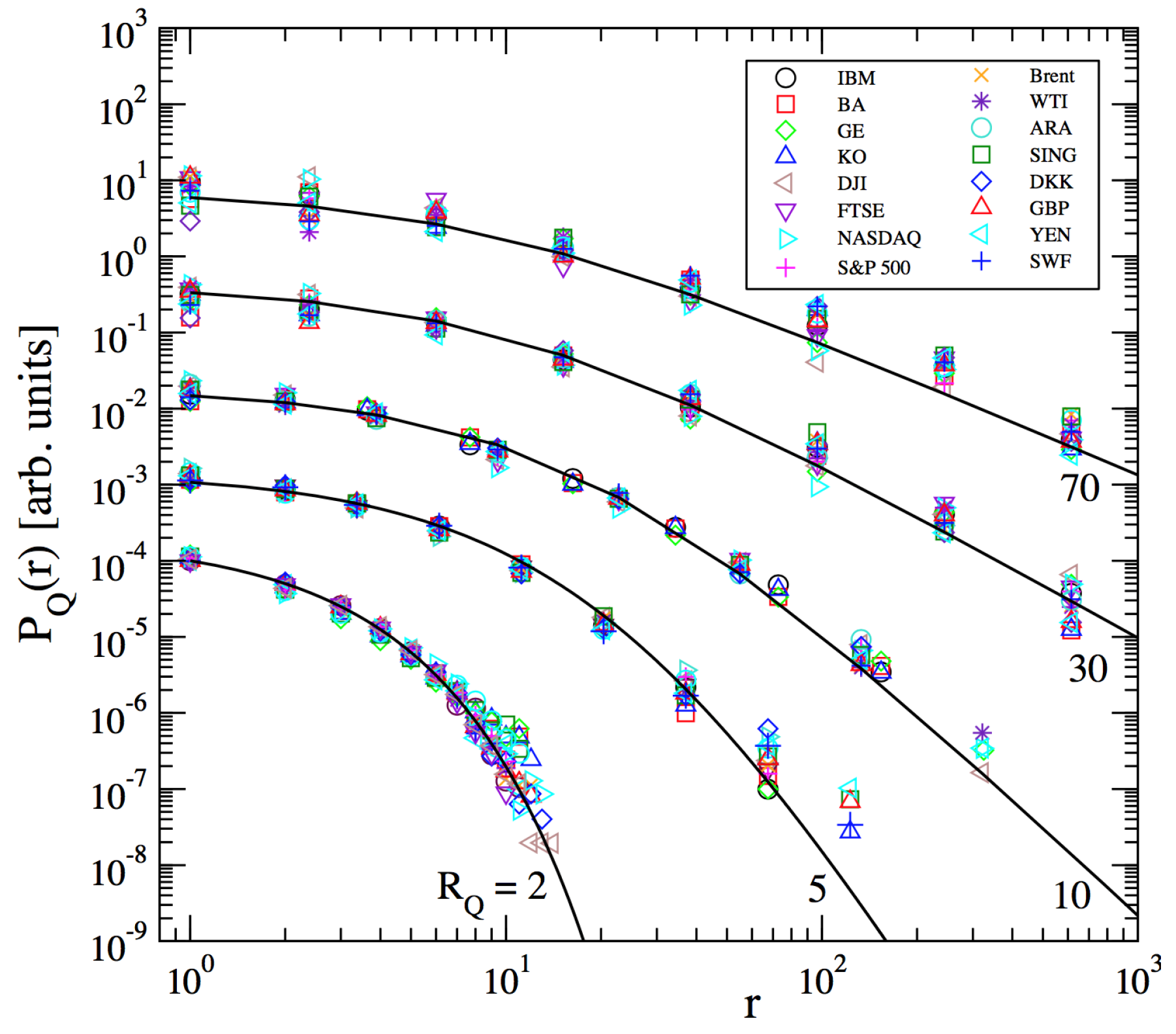
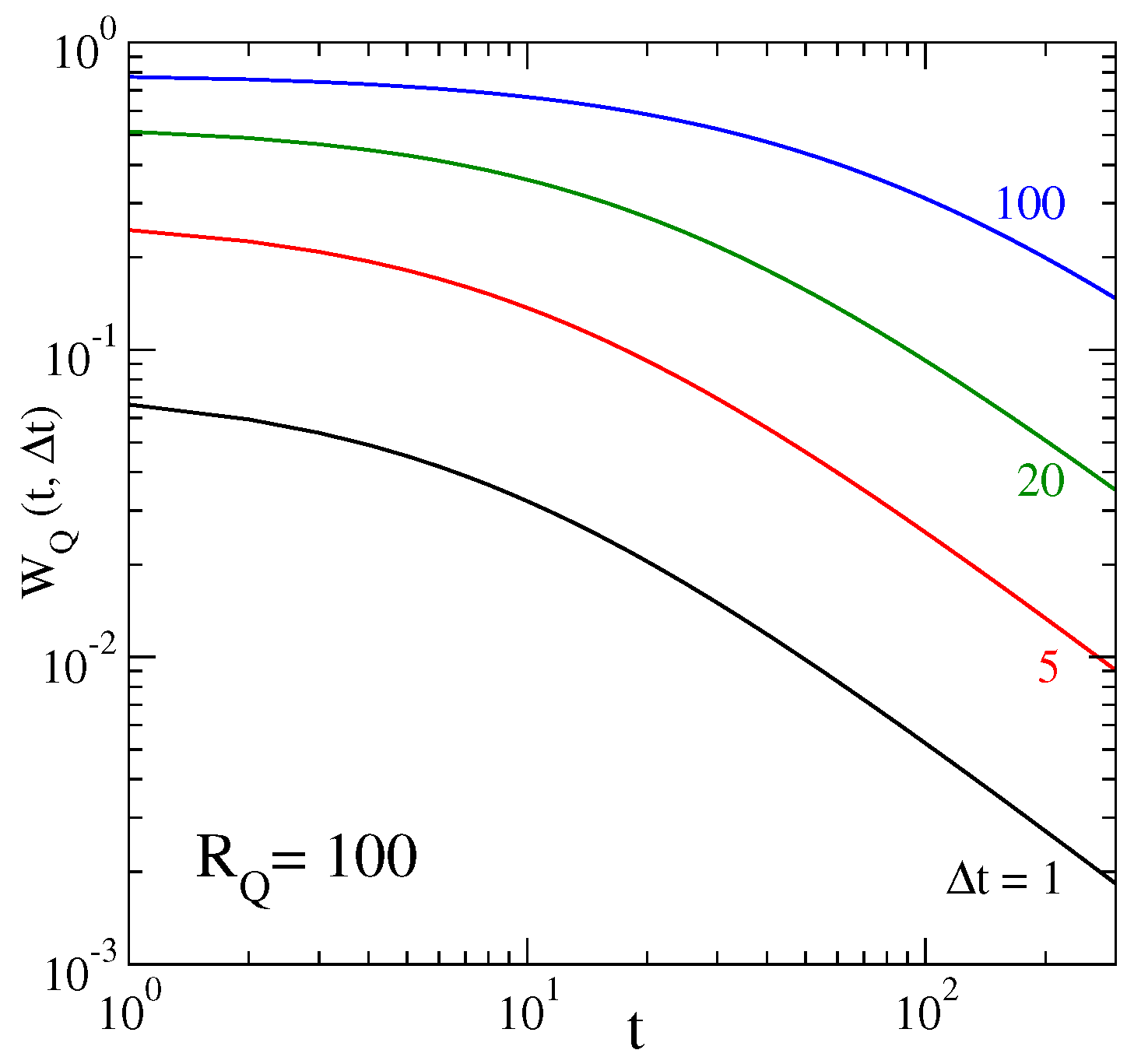
2.3. Inter-Occurrence Times
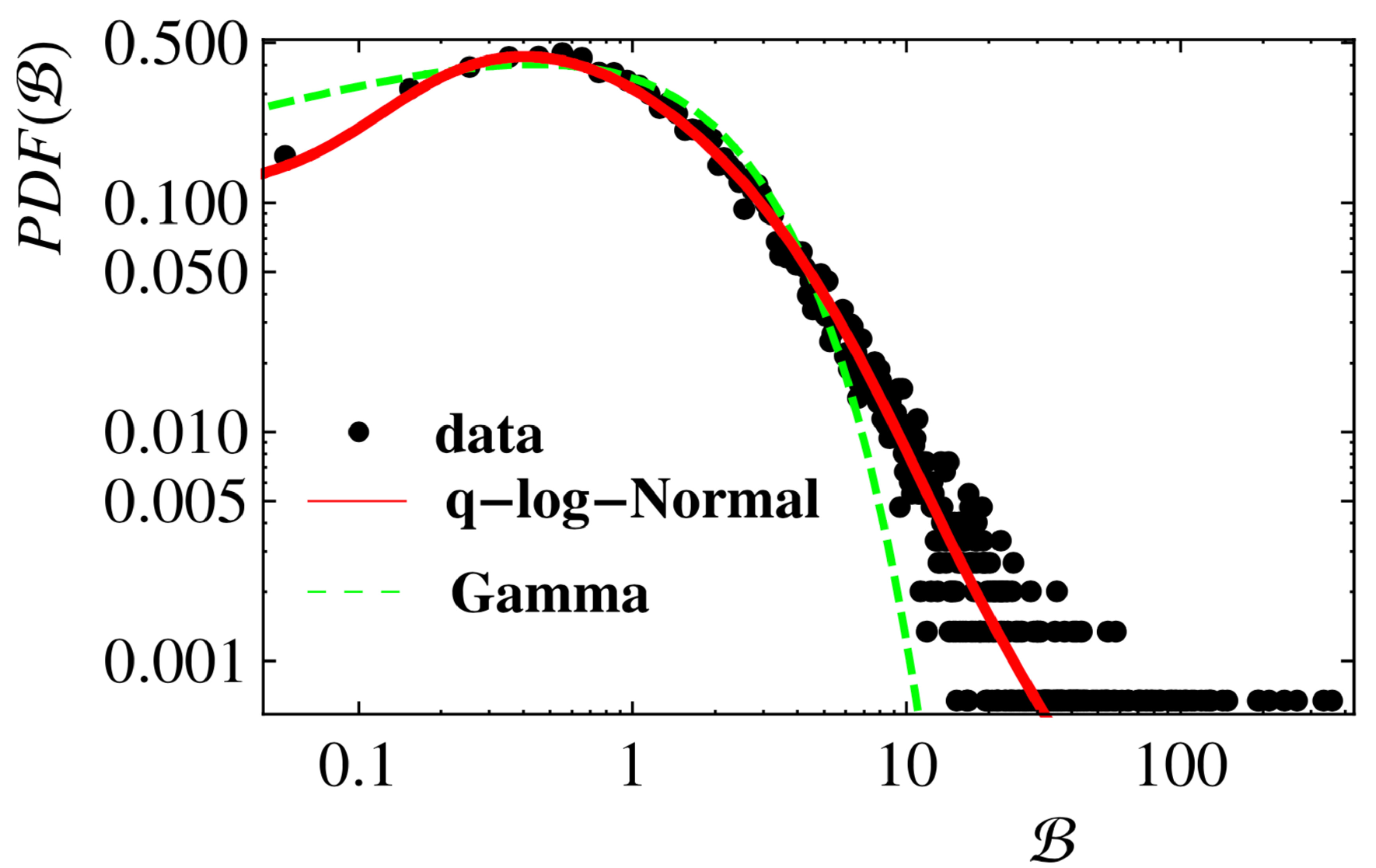
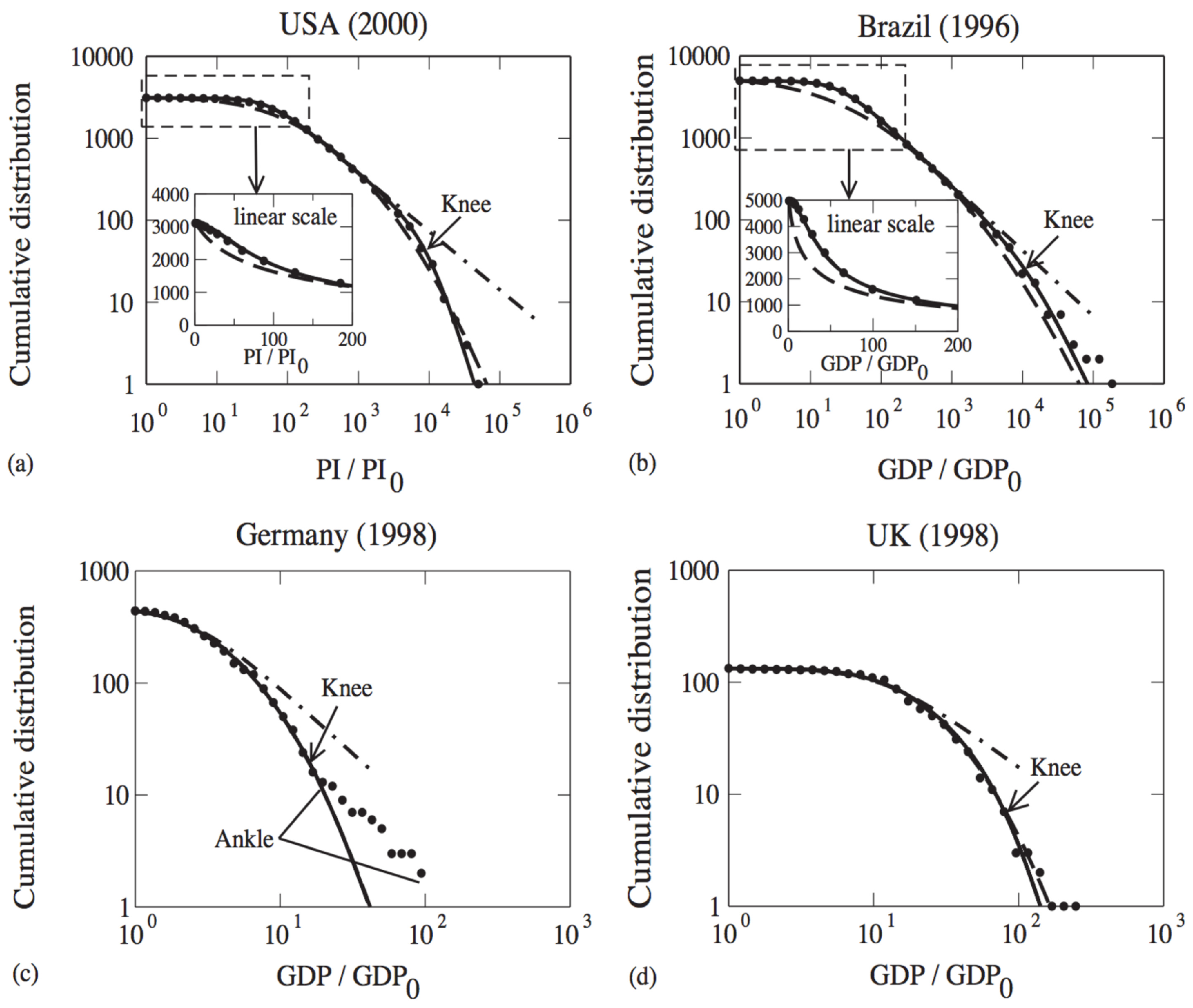
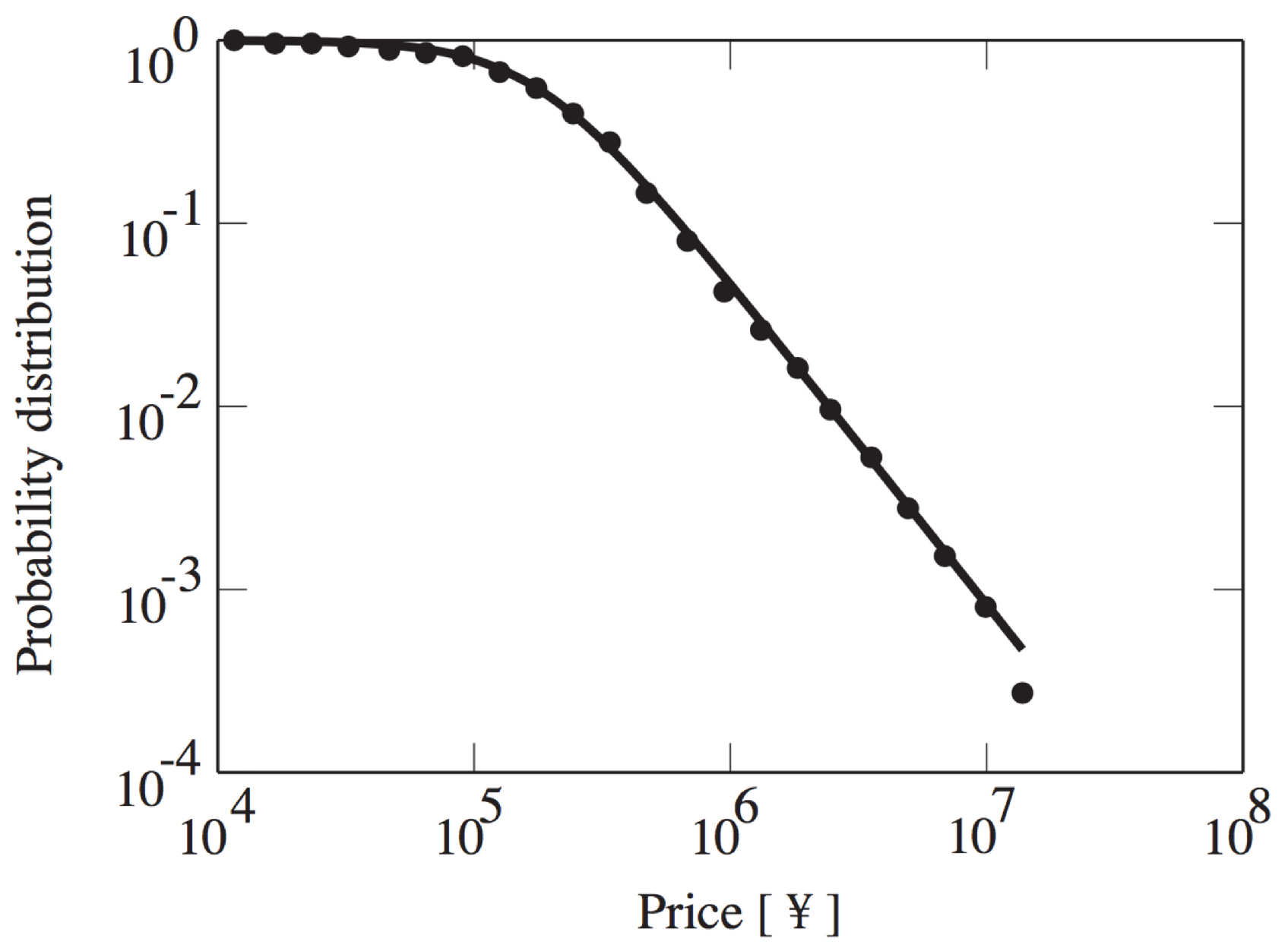
2.4. Wealth
3. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Penrose, O. Foundations of Statistical Mechanics: A Deductive Treatment; Pergamon: Oxford, UK, 1970; p. 167. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 53, 479–487. [Google Scholar]
- Curado, E.M.F.; Tsallis, C. Generalized statistical mechanics: Connection with thermodynamics. J. Phys. A 1991, 24, L69–L72. [Google Scholar]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534–554. [Google Scholar]
- Gell-Mann, M.; Tsallis, C. (Eds.) Nonextensive Entropy-Interdisciplinary Applications; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics-Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; McGraw-Hill: New York, NY, USA, 1937. [Google Scholar]
- Frank, T.D. Nonlinear Fokker–Planck Equations: Fundamentals and Applications; Series Synergetics; Springer: Berlin, Germany, 2005. [Google Scholar]
- Tsallis, C.; Bukman, D.J. Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 1996, 54, R2197–R2200. [Google Scholar]
- Combe, G.; Richefeu, V.; Stasiak, M.; Atman, A.P.F. Experimental validation of nonextensive scaling law in confined granular media. Phys. Rev. Lett. 2015, 115, 238301. [Google Scholar]
- Plastino, A.R.; Plastino, A. Non-extensive statistical mechanics and generalized Fokker–Planck equation. Physica A 1995, 222, 347–354. [Google Scholar]
- Nonextensive Statistical Mechanics and Thermodynamics. Available online: http://tsallis.cat.cbpf.br/biblio.htm (accessed on 29 August 2017).
- Anteneodo, C.; Tsallis, C. Breakdown of exponential sensitivity to initial conditions: Role of the range of interactions. Phys. Rev. Lett. 1998, 80, 5313–5316. [Google Scholar]
- Rapisarda, A.; Pluchino, A. Nonextensive thermodynamics and glassy behavior. Europhys. News 2005, 36, 202–206. [Google Scholar]
- Chavanis, P.-H.; Campa, A. Inhomogeneous Tsallis distributions in the HMF model. Eur. Phys. J. B 2010, 76, 581–611. [Google Scholar]
- Cirto, L.J.L.; Assis, V.R.V.; Tsallis, C. Influence of the interaction range on the thermostatistics of a classical many-body system. Physica A 2014, 393, 286–296. [Google Scholar]
- Christodoulidi, H.; Tsallis, C.; Bountis, T. Fermi–Pasta–Ulam model with long-range interactions: Dynamics and thermostatistics. EPL 2014, 108, 40006. [Google Scholar]
- Christodoulidi, H.; Bountis, T.; Tsallis, C.; Drossos, L. Dynamics and Statistics of the Fermi–Pasta–Ulam β–model with different ranges of particle interactions. JSTAT 2016, 123206. [Google Scholar]
- Bagchi, D.; Tsallis, C. Sensitivity to initial conditions of d-dimensional long-range-interacting quartic Fermi–Pasta–Ulam model: Universal scaling. Phys. Rev. E 2016, 93, 062213. [Google Scholar]
- Bagchi, D.; Tsallis, C. Long-ranged Fermi–Pasta–Ulam systems in thermal contact: Crossover from q-statistics to Boltzmann–Gibbs statistics. Phys. Lett. A 2017, 381, 1123–1128. [Google Scholar]
- Lucena, L.S.; da Silva, L.R.; Tsallis, C. Departure from Boltzmann–Gibbs statistics makes the hydrogen-atom specific heat a computable quantity. Phys. Rev. E 1995, 51, 6247–6249. [Google Scholar]
- Nobre, F.D.; Tsallis, C. Infinite-range Ising ferromagnet-thermodynamic limit within generalized statistical mechanics. Physica A 1995, 213, 337–356. [Google Scholar]
- Caride, A.O.; Tsallis, C.; Zanette, S.I. Criticality of the anisotropic quantum Heisenberg model on a self-dual hierarchical lattice. Phys. Rev. Lett. 1983, 51, 145–147. [Google Scholar]
- Miritello, G.; Pluchino, A.; Rapisarda, A. Central limit behavior in the Kuramoto model at the ‘edge of chaos’. Physica A 2009, 388, 4818–4826. [Google Scholar]
- Tirnakli, U.; Tsallis, C.; Lyra, M.L. Circular-like maps: sensitivity to the initial conditions, multifractality and nonextensivity. Eur. Phys. J. B 1999, 11, 309–315. [Google Scholar]
- Baldovin, F.; Robledo, A. Universal renormalization-group dynamics at the onset of chaos in logistic maps and nonextensive statistical mechanics. Phys. Rev. E 2002, 66, R045104. [Google Scholar]
- Baldovin, F.; Robledo, A. Nonextensive Pesin identity. Exact renormalization group analytical results for the dynamics at the edge of chaos of the logistic map. Phys. Rev. E 2004, 69, R045202. [Google Scholar]
- Mayoral, E.; Robledo, A. Tsallis’ q index and Mori’s q phase transitions at edge of chaos. Phys. Rev. E 2005, 72, 026209. [Google Scholar]
- Tirnakli, U.; Tsallis, C.; Beck, C. A closer look at time averages of the logistic map at the edge of chaos. Phys. Rev. E 2009, 79, 056209. [Google Scholar]
- Luque, B.; Lacasa, L.; Robledo, A. Feigenbaum graphs at the onset of chaos. Phys. Lett. A 2012, 376, 3625. [Google Scholar] [CrossRef]
- Tirnakli, U.; Borges, E.P. The standard map: From Boltzmann–Gibbs statistics to Tsallis statistics. Nat. Sci. Rep. 2016, 6, 23644. [Google Scholar]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis Distributions in Dissipative Optical Lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar]
- Bagci, G.B.; Tirnakli, U. Self-organization in dissipative optical lattices. Chaos 2009, 19, 033113. [Google Scholar]
- Lutz, E.; Renzoni, F. Beyond Boltzmann–Gibbs statistical mechanics in optical lattices. Nat. Phys. 2013, 9, 615–619. [Google Scholar]
- Liu, B.; Goree, J. Superdiffusion and non-Gaussian statistics in a driven-dissipative 2D dusty plasma. Phys. Rev. Lett. 2008, 100, 055003. [Google Scholar]
- Bouzit, O.; Gougam, L.A.; Tribeche, M. Screening and sheath formation in a nonequilibrium mixed Cairns-Tsallis electron distribution. Phys. Plasmas 2015, 22, 052112. [Google Scholar]
- DeVoe, R.G. Power-law distributions for a trapped ion interacting with a classical buffer gas. Phys. Rev. Lett. 2009, 102, 063001. [Google Scholar]
- Pickup, R.M.; Cywinski, R.; Pappas, C.; Farago, B.; Fouquet, P. Generalized spin glass relaxation. Phys. Rev. Lett. 2009, 102, 097202. [Google Scholar]
- Tsallis, C.; de Souza, A.M.C.; Maynard, R. Derivation of Lévy-type anomalous superdiffusion from generalized statistical mechanics. In Lévy Flights and Related Topics in Physics; Shlesinger, M.F., Zaslavsky, G.M., Frisch, U., Eds.; Springer: Berlin, Germany, 1995; p. 269. [Google Scholar]
- Tsallis, C.; Levy, S.V.F.; de Souza, A.M.C.; Maynard, R. Statistical-mechanical foundation of the ubiquity of Levy distributions in nature. Phys. Rev. Lett. 1995, 75, 3589–3593. [Google Scholar]
- CMS Collaboration. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at and 2.36 TeV. J. High Energy Phys. 2010, 2, 41. [Google Scholar] [CrossRef]
- CMS Collaboration. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar]
- Marques, L.; Andrade, E., II; Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 2013, 87, 114022. [Google Scholar]
- Marques, L.; Cleymans, J.; Deppman, A. Description of high-energy pp collisions using Tsallis thermodynamics: Transverse momentum and rapidity distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar]
- Tsallis, C.; Arenas, Z.G. Nonextensive statistical mechanics and high energy physics. EPJ 2014, 71, 00132. [Google Scholar]
- ALICE Collaboration. K*(892)0 and Φ(1020) meson production at high transverse momentum in pp and Pb-Pb collisions at TeV. Phys. Rev. C 2017, 95, 064606. [Google Scholar]
- Oliveira, H.P.; Soares, I.D. Dynamics of black hole formation: Evidence for nonextensivity. Phys. Rev. D 2005, 71, 124034. [Google Scholar]
- Komatsu, N.; Kimura, S. Entropic cosmology for a generalized black-hole entropy. Phys. Rev. D 2013, 88, 083534. [Google Scholar]
- Silva, V.H.C.; Aquilanti, V.; de Oliveira, H.C.B.; Mundim, K.C. Uniform description of non-Arrhenius temperature dependence of reaction rates, and a heuristic criterion for quantum tunneling vs. classical non-extensive distribution. Chem. Phys. Lett. 2013, 590, 201–207. [Google Scholar]
- Antonopoulos, C.G.; Michas, G.; Vallianatos, F.; Bountis, T. Evidence of q-exponential statistics in Greek seismicity. Physica A 2014, 409, 71–77. [Google Scholar]
- Upadhyaya, A.; Rieu, J.-P.; Glazier, J.A.; Sawada, Y. Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates. Physica A 2001, 293, 549–558. [Google Scholar]
- Bogachev, M.I.; Kayumov, A.R.; Bunde, A. Universal internucleotide statistics in full genomes: A footprint of the DNA structure and packaging? PLoS ONE 2014, 9, e112534. [Google Scholar]
- Burlaga, L.F.; Vinas, A.F. Triangle for the entropic index q of non-extensive statistical mechanics observed by Voyager 1 in the distant heliosphere. Physica A 2005, 356, 375–384. [Google Scholar]
- Burlaga, L.F.; Ness, N.F. Magnetic field strength fluctuations and the q-triplet in the heliosheath: Voyager 2 observations from 91.0 to 94.2 AU at latitude 30° S. Astrophys. J. 2013, 765, 35. [Google Scholar]
- Moyano, L.G.; Tsallis, C.; Gell-Mann, M. Numerical indications of a q-generalised central limit theorem. Europhys. Lett. 2006, 73, 813–819. [Google Scholar]
- Thistleton, W.J.; Marsh, J.A.; Nelson, K.P.; Tsallis, C. q-Gaussian approximants mimic non-extensive statistical-mechanical expectation for many-body probabilistic model with long-range correlations. Cent. Eur. J. Phys. 2009, 7, 387–394. [Google Scholar]
- Chavanis, P.-H. Nonlinear mean field Fokker–Planck equations. Application to the chemotaxis of biological population. Eur. Phys. J. B 2008, 62, 179–208. [Google Scholar]
- Umarov, S.; Tsallis, C.; Steinberg, S. On a q-central limit theorem consistent with nonextensive statistical mechanics. J. Math. 2008, 76, 307–328. [Google Scholar]
- Umarov, S.; Tsallis, C.; Gell-Mann, M.; Steinberg, S. Generalization of symmetric α-stable Lévy distributions for q > 1. Math. Phys. 2010, 51, 033502. [Google Scholar]
- Nelson, K.P.; Umarov, S. Nonlinear statistical coupling. Physica A 2010, 389, 2157–2163. [Google Scholar]
- Hanel, R.; Thurner, S.; Tsallis, C. Limit distributions of scale-invariant probabilistic models of correlated random variables with the q-Gaussian as an explicit example. Eur. Phys. J. B 2009, 72, 263–268. [Google Scholar]
- Umarov, S.; Tsallis, C. The limit distribution in the q-CLT for q ≥ 1 is unique and can not have a compact support. J. Phys. A 2016, 49, 415204. [Google Scholar]
- Andrade, J.S., Jr.; da Silva, G.F.T.; Moreira, A.A.; Nobre, F.D.; Curado, E.M.F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett. 2010, 105, 260601. [Google Scholar]
- Vieira, C.M.; Carmona, H.A.; Andrade, J.S., Jr.; Moreira, A.A. General continuum approach for dissipative systems of repulsive particles. Phys. Rev. E 2016, 93, 060103(R). [Google Scholar]
- Caruso, F.; Tsallis, C. Nonadditive entropy reconciles the area law in quantum systems with classical thermodynamics. Phys. Rev. E 2008, 78, 021102. [Google Scholar]
- Carrasco, J.A.; Finkel, F.; Gonzalez-Lopez, A.; Rodriguez, M.A.; Tempesta, P. Generalized isotropic Lipkin-Meshkov-Glick models: Ground state entanglement and quantum entropies. J. Stat. Mech. 2016, 2016, 033114. [Google Scholar]
- Weinstein, Y.S.; Lloyd, S.; Tsallis, C. Border between between regular and chaotic quantum dynamics. Phys. Rev. Lett. 2002, 89, 214101. [Google Scholar]
- Betzler, A.S.; Borges, E.P. Nonextensive distributions of asteroid rotation periods and diameters. Astron. Astrophys. 2012, 539, A158. [Google Scholar] [CrossRef]
- Betzler, A.S.; Borges, E.P. Nonextensive statistical analysis of meteor showers and lunar flashes. Mon. Not. R. Astron. Soc. 2015, 447, 765–771. [Google Scholar]
- Li, Y.; Li, N.; Tirnakli, U.; Li, B.; Tsallis, C. Thermal conductance of the coupled-rotator chain: Influence of temperature and size. EPL 2017, 117, 60004. [Google Scholar]
- Nivanen, L.; Le Mehaute, A.; Wang, Q.A. Generalized algebra within a nonextensive statistics. Rep. Math. Phys. 2003, 54, 437–444. [Google Scholar]
- Borges, E.P. A possible deformed algebra and calculus inspired in nonextensive thermostatistics. Physica A 2004, 340, 95–101. [Google Scholar]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121. [Google Scholar]
- Ruiz, G.; Tsallis, C. Reply to comment on “towards a large deviation theory for strongly correlated systems”. Phys. Lett. A 2013, 377, 491–495. [Google Scholar]
- Jauregui, M.; Tsallis, C. New representations of π and Dirac delta using the nonextensive- statistical-mechanics q-exponential function. Math. Phys. 2010, 51, 063304. [Google Scholar]
- Sicuro, G.; Tsallis, C. q-Generalized representation of the d-dimensional Dirac delta and q-Fourier transform. Phys. Lett. A 2017, 381, 2583–2587. [Google Scholar]
- Nobre, F.D.; Rego-Monteiro, M.A.; Tsallis, C. Nonlinear relativistic and quantum equations with a common type of solution. Phys. Rev. Lett. 2011, 106, 140601. [Google Scholar]
- Costa Filho, R.N.; Almeida, M.P.; Farias, G.A.; Andrade, J.S., Jr. Displacement operator for quantum systems with position-dependent mass. Phys. Rev. A 2011, 84, 050102(R). [Google Scholar]
- Mazharimousavi, S.H. Revisiting the displacement operator for quantum systems with position-dependent mass. Phys. Rev. A 2010, 85, 034102. [Google Scholar]
- Nobre, F.D.; Rego-Monteiro, M.A.; Tsallis, C. A generalized nonlinear Schroedinger equation: Classical field-theoretic approach. Europhys. Lett. 2012, 97, 41001. [Google Scholar]
- Rego-Monteiro, M.A.; Nobre, F.D. Nonlinear quantum equations: Classical field theory. J. Math. Phys. 2013, 54, 103302. [Google Scholar]
- Rego-Monteiro, M.A.; Nobre, F.D. Classical field theory for a non-Hermitian Schroedinger equation with position-dependent masses. Phys. Rev. A 2013, 88, 032105. [Google Scholar]
- Costa Filho, R.N.; Alencar, G.; Skagerstam, B.-S.; Andrade, J.S., Jr. Morse potential derived from first principles. Europhys. Lett. 2013, 101, 10009. [Google Scholar]
- Toranzo, I.V.; Plastino, A.R.; Dehesa, J.S.; Plastino, A. Quasi-stationary states of the NRT nonlinear Schroedinger equation. Physica A 2013, 392, 3945–3951. [Google Scholar]
- Curilef, S.; Plastino, A.R.; Plastino, A. Tsallis’ maximum entropy ansatz leading to exact analytical time dependent wave packet solutions of a nonlinear Schroedinger equation. Physica A 2013, 392, 2631–2642. [Google Scholar]
- Plastino, A.R.; Tsallis, C. Nonlinear Schroedinger equation in the presence of uniform acceleration. J. Math. Phys. 2013, 54, 041505. [Google Scholar]
- Plastino, A.R.; Souza, A.M.C.; Nobre, F.D.; Tsallis, C. Stationary and uniformly accelerated states in nonlinear quantum mechanics. Phys. Rev. A 2014, 90, 062134. [Google Scholar]
- Pennini, F.; Plastino, A.R.; Plastino, A. Pilot wave approach to the NRT nonlinear Schroedinger equation. Physica A 2014, 403, 195–205. [Google Scholar]
- Da Costa, B.G.; Borges, E.P. Generalized space and linear momentum operators in quantum mechanics. J. Math. Phys. 2014, 55, 062105. [Google Scholar]
- Nobre, F.D.; Rego-Monteiro, M.A. Non-Hermitian PT symmetric Hamiltonian with position-dependent masses: Associated Schroedinger equation and finite-norm solutions. Braz. J. Phys. 2015, 45, 79–88. [Google Scholar]
- Plastino, A.; Rocca, M.C. From the hypergeometric differential equation to a non-linear Schroedinger one. Phys. Lett. A 2015, 379, 2690–2693. [Google Scholar]
- Alves, L.G.A.; Ribeiro, H.V.; Santos, M.A.F.; Mendes, R.S.; Lenzi, E.K. Solutions for a q-generalized Schroedinger equation of entangled interacting particles. Physica A 2015, 429, 35–44. [Google Scholar]
- Plastino, A.R.; Tsallis, C. Dissipative effects in nonlinear Klein–Gordon dynamics. EPL 2016, 113, 50005. [Google Scholar]
- Plastino, A.; Rocca, M.C. Hypergeometric connotations of quantum equations. Physica A 2016, 450, 435–443. [Google Scholar]
- Bountis, T.; Nobre, F.D. Travelling-wave and separated variable solutions of a nonlinear Schroedinger equation. J. Math. Phys. 2016, 57, 082106. [Google Scholar]
- Nobre, F.D.; Plastino, A.R. A family of nonlinear Schroedinger equations admitting q-plane wave. Phys. Lett. A 2017, 381, 2457–2462. [Google Scholar]
- Capurro, A.; Diambra, L.; Lorenzo, D.; Macadar, O.; Martin, M.T.; Mostaccio, C.; Plastino, A.; Rofman, E.; Torres, M.E.; Velluti, J. Tsallis entropy and cortical dynamics: The analysis of EEG signals. Physica A 1998, 257, 149–155. [Google Scholar]
- Mohanalin, J.; Beenamol; Kalra, P.K.; Kumar, N. A novel automatic microcalcification detection technique using Tsallis entropy and a type II fuzzy index. Comput. Math. Appl. 2010, 60, 2426–2432. [Google Scholar]
- Soares, D.J.B.; Tsallis, C.; Mariz, A.M.; Silva, L.R. Preferential attachment growth model and nonextensive statistical mechanics. EPL 2005, 70, 70–76. [Google Scholar]
- Thurner, S.; Tsallis, C. Nonextensive aspects of self-organized scale-free gas-like networks. Europhys. Lett. 2005, 72, 197–203. [Google Scholar]
- Brito, S.G.A.; da Silva, L.R.; Tsallis, C. Role of dimensionality in complex networks. Nat. Sci. Rep. 2016, 6, 27992. [Google Scholar]
- Borland, L. Closed form option pricing formulas based on a non-Gaussian stock price model with statistical feedback. Phys. Rev. Lett. 2002, 89, 098701. [Google Scholar]
- Tsallis, C.; Anteneodo, C.; Borland, L.; Osorio, R. Nonextensive statistical mechanics and economics. Physica A 2003, 324, 89–100. [Google Scholar]
- Osorio, R.; Borland, L.; Tsallis, C. Distributions of high-frequency stock-market observables. In Nonextensive Entropy-Interdisciplinary Applications; Gell-Mann, M., Tsallis, C., Eds.; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Borges, E.P. Empirical nonextensive laws for the county distribution of total personal income and gross domestic product. Physica A 2004, 334, 255–266. [Google Scholar]
- Ludescher, J.; Tsallis, C.; Bunde, A. Universal behaviour of inter-occurrence times between losses in financial markets: An analytical description. Europhys. Lett. 2011, 95, 68002. [Google Scholar]
- Ludescher, J.; Institut fur Theoretische Physik, Justus-Liebig-Universitat, Giessen, Germany; Tsallis, C.; Centro Brasileiro de Pesquisas Físicas and National Institute of Science and Technology for Complex Systems, Rio de Janeiro, Brazil. Private Communications, 2011.
- Queiros, S.M.D. On generalisations of the log-Normal distribution by means of a new product definition in the Kapteyn process. Physica A 2012, 391, 3594–3606. [Google Scholar]
- Bogachev, M.I.; Eichner, J.F.; Bunde, A. Effect of nonlinear correlations on the statistics of return intervals in multifractal data sets. Phys. Rev. Lett. 2007, 99, 240601. [Google Scholar]
- Ludescher, J.; Bunde, A. Universal behavior of the inter-occurrence times between losses in financial markets: Independence of the time resolution. Phys. Rev. 2014, 90, 062809. [Google Scholar]
- Perello, J.; Gutierrez-Roig, M.; Masoliver, J. Scaling properties and universality of first-passage-time probabilities in financial markets. Phys. Rev. E 2011, 84, 066110. [Google Scholar]
- Ruseckas, J.; Kaulakys, B.; Gontis, V. Herding model and 1/f noise. EPL 2011, 96, 60007. [Google Scholar]
- Ruseckas, J.; Gontis, V.; Kaulakys, B. Nonextensive statistical mechanics distributions and dynamics of financial observables from the nonlinear stochastic differential equations. Adv. Complex Syst. 2012, 15, 1250073. [Google Scholar]
- Gontis, V.; Kononovicius, A. A consentaneous agent based and stochastic model of the financial markets. PLoS ONE 2014, 9, e102201. [Google Scholar]
- Biondo, A.E.; Pluchino, A.; Rapisarda, A. Modeling financial markets by self-organized criticality. Phys. Rev. E 2015, 92, 042814. [Google Scholar]
- Biondo, A.E.; Pluchino, A.; Rapisarda, A. Order book, financial markets, and self-organized criticality. Chaos Solitons Fractals 2016, 88, 196–208. [Google Scholar]
- Biondo, A.E.; Pluchino, A.; Rapisarda, A. A multilayer approach for price dynamics in financial markets. Eur. Phys. J. Spec. Top. 2017, 226, 477–488. [Google Scholar]
- Ruiz, G.; Fernandez, A. Evidence for criticality in financial data. arXiv, 2017; arXiv:1702.06191. [Google Scholar]
- Tsallis, C.; Gell-Mann, M.; Sato, Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc. Natl. Acad. Sci. USA 2005, 102, 15377–15382. [Google Scholar]
- Tsallis, C. Generalization of the possible algebraic basis of q-triplets. Eur. Phys. J. Spec. Top. 2017, 226, 455–466. [Google Scholar]
- Tsallis, C. Statistical mechanics for complex systems: On the structure of q-triplets. In Proceedings of the 31st International Colloquium on Group Theoretical Methods in Physics, Rio de Janeiro, Brazil, 20–24 July 2016. [Google Scholar]
- Tsallis, C. Dynamical scenario for nonextensive statistical mechanics. Physica A 2004, 340, 1–10. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsallis, C. Economics and Finance: q-Statistical Stylized Features Galore. Entropy 2017, 19, 457. https://doi.org/10.3390/e19090457
Tsallis C. Economics and Finance: q-Statistical Stylized Features Galore. Entropy. 2017; 19(9):457. https://doi.org/10.3390/e19090457
Chicago/Turabian StyleTsallis, Constantino. 2017. "Economics and Finance: q-Statistical Stylized Features Galore" Entropy 19, no. 9: 457. https://doi.org/10.3390/e19090457
APA StyleTsallis, C. (2017). Economics and Finance: q-Statistical Stylized Features Galore. Entropy, 19(9), 457. https://doi.org/10.3390/e19090457



