1. Introduction
Adam Smith [
1] (using the term stock to denote what we now call capital) describes the process by which the competition of individual capitals brings about the emergence of a general (average) rate of profit as an unintended consequence in these terms:
The whole of the advantages and disadvantages of the different employments of labour and stock must, in the same neighbourhood, be either perfectly equal or continually tending to equality. If in the same neighbourhood, there was any employment evidently either more or less advantageous than the rest, so many people would crowd into it in the one case, and so many would desert it in the other, that its advantages would soon return to the level of other employments. This at least would be the case in a society where things were left to follow their natural course, where there was perfect liberty, and where every man was perfectly free both to choose what occupation he thought proper, and to change it as often as he thought proper. Every man’s interest would prompt him to seek the advantageous, and to shun the disadvantageous employment.
(Smith, 1937, Book I, ch 10)
When the stocks of many rich merchants are turned into the same trade, their mutual competition naturally tends to lower its profit...
(Smith, 1937, Book I, ch 9)
Two points are central to Smith’s conception of competition among capitals. First, individual owners of capital are aware of differences in the rate of profit in different “trades” and react to them by moving capital from trades with lower rates of profit to trades with higher rates of profit. Second, the individual capital owner’s action of moving capital out of a trade increases the rate of profit in that trade, and the action of moving capital into a trade reduces the rate of profit in that trade. Together, these mechanisms constitute a negative feedback that can stabilize the distribution of the rate of profit around a central (average) value. In this paper we will use the term market to denote what Smith calls a trade, that is, a site which capitals can enter or exit and in which they can compete.
Social science addresses systems of this general type in which the individual actions of participants interacting in complex, non-additive ways through institutional structures determine social outcomes. In the classical theory of competition, the distribution of the rate of profit is an outcome of a large number of independent decisions of individual owners of capital to enter or exit particular markets, given the institutions of private property and free entry. The profit rate distribution is an unintended consequence of individual capitals seeking higher profit rates that give rise to observed statistical regularities such as a general rate of profit and, we will argue, regular fluctuations of individual rates of profit around the general rate.
The general model we consider represents this type of social interaction in terms of some economic outcome variable such as the profit rate, , which is the result of individual quantal actions, , in some institutional setting. In the simplest binary action case the set of quantal actions consists of just two complementary actions, which we write as .
We write sums over outcomes,
x, as integrals with the understanding that in theoretical applications
x is treated as real valued. In real-world applications, however, measurements will inevitably be coarse-grained in a finite number of bins. We generally omit the limits on integrals with the understanding that the sums are over the range of
x. A model of this interaction is a joint distribution of
, which we write as
, with the marginal and conditional frequencies,
:
We regard conditional distributions, which control for the conditioning variable, as conveying the explanatory content of the model. The accompanying marginal and joint distributions represent the statistical equilibrium resulting from the interaction of individual actions through the relevant social institutions.
The determinants of individual actions (for example, seeking higher profit rates through entry and exit in the profit rate case) determines the dependence of the action
a on
x, which is represented by the conditional frequency distribution:
This conditional distribution expresses the response probability of a quantal action given the outcome x, which quantifies the impact of x on the individual action frequencies.
The chain that links the quantal actions of the individuals to the outcome variable (the impact of entry and exit decisions on the profit rate in some particular market in the profit rate case) determines the other conditional frequency:
The two conditional distributions represent a theory of the interaction through the mutual dependency of the quantal actions and the outcome variable in the particular institutional context.
The statistical equilibrium of this type of model is a joint distribution
, that determines these two conditional distributions:
The statistical equilibrium can be expressed either directly by specifying the joint distribution itself or indirectly by specifying one conditional distribution and the corresponding marginal distribution, because
2. A Quantal Response Statistical Equilibrium Model Example: Adam Smith’s Theory
In the classical Smithian theory of competition, firms make entry and exit decisions that are conditional on the expected rate of return in particular markets. The process of competition is defined by a negative feedback mechanism whereby profit maximizing firms seeking out markets with above average profit rates will relocate capital to these markets, increasing competition and, as an unintended consequence, reducing profit rates (for example, by raising output and lowering prices). As capital is relocated away from markets realizing below average rates of profit this exit process will raise profit rates in those markets (for example, by reducing output and consequently raising prices). The behavioral assumption is that owners of capital make entry and exit decisions in an effort to increase their individual profit rates.
We can model the typical competitive capitalist as making a decision either to add capital to a sector (enter) or withdraw capital from the sector (exit). In this case, the quantal response variable a is a binary choice . The outcome variable in this model is the observed profit rate , which represents both the outcome for an individual observed firm and for the market in which it operates. The marginal distribution is the result of the interaction of exit and entry decisions through a complex mechanism of competition and is the statistical equilibrium of profit rates. The conditional distribution represents a behavioral theory of capitalist firms. Likewise, the impact of the action a on the observed level of x describes the dependency of profit rates on the entry and exit behavior of firms and thus the conditional distribution represents a theory of competition.
2.1. Logit Quantal Response
In modeling the quantal behavior of agents in this framework, relevant theory often suggests that the typical agent responds to a payoff function . Adam Smith tells us that the payoff function of a typical owner of capital is the profit rate.
If the typical agent chooses a mixed strategy,
over actions
to maximize the expected payoff,
, subject to a constraint on the entropy of the mixed strategy, the resulting Gibbs function,
, is the familiar logit quantal response. The agent’s expected payoff maximization program and associated Lagrangian are:
The Lagrange multiplier
T is analogous to temperature variables in statistical mechanical models of thermodynamic systems, and in this context could be regarded as a behavior temperature for the typical actor. The lower
T the more alert the actor is to differences in payoff, and the more closely the action approximates the unconstrained payoff-maximizing outcome. (This approach is similar to the idea of rational inattention [
2]).
The introduction of the informational constraint recovers the logit quantal response distribution without imposing a distributional constraint on the errors that affect decision making, for example, that they follow an extreme value distribution [
3,
4,
5]. Rather than treating the distribution over the individual’s mixed strategy as arising from random error of noisy players or uncertain payoffs, the informational entropy constrained model interprets the observed frequency of actions in terms of their relative payoff.
An important insight is that this Lagrangian is mathematically equivalent to the Lagrangian that arises from maximizing the entropy of the mixed strategy subject to a constraint on the expected payoff:
In this case we are imposing a constraint on our uncertainty of the distribution of actions conditional on the social variable for an ensemble of agents. As the most probable distribution of actions (the one with the maximum informational entropy) is the logit quantal response distribution, these problems are dual to one another [
6,
7]. The shadow prices are related, since
.
In the profit rate context, a reasonable first approximation is that the payoff perceived by competing capitalists to investment in a given sector is the profit rate in that sector, possibly shifted by an amount , so that . In this case the quantal response is
These quantal response functions are plotted in
Figure 1 for increasing values of
T.
The behavioral temperature, T, contributes to the determination of the endogenous fluctuations of the aggregate outcome x. For , becomes “flat” implying a weak dependence of the action variable a on the aggregate variable x. Consequently, fluctuations and our uncertainty of x would be large. When the dependence of a on x becomes unboundedly strong. As aggregate fluctuations and our uncertainty of x goes to zero, as long as there is the smallest impact of entry and exit on market profit rates, will become a Heaviside step function implying that an infinitesimal deviation of x from will result in a uniform response of actors choosing the action variable to eliminate the deviation.
Because this model explains the marginal outcome frequencies as the statistical equilibrium of a system in which agents respond to outcome incentives with quantal responses that in turn stabilize the outcome distribution subject to a constraint on the mean outcome, we refer to this class of models as Quantal Response Statistical Equilibrium (QRSE) models.
2.2. Impact of Actions on Outcomes
Because firms tend to enter markets with higher than average profit rates, if there were no impact of entry and exit on market profit rates, the expectation of the profit rate conditional on entry would tend to be higher than the expectation of the profit rate conditional on exit. However, the act of entry itself tends to lower profit rates in a market and, symmetrically, the action of exit tends to raise the market profit rate. The effectiveness of the competitive process can be represented by the difference between expected profit rates conditional on entry and exit.
Equivalently, we can measure the effectiveness of competition as the difference in the conditional expectations weighted by the frequency of the actions:
The parameter represents the extent to which feedback from the action to the outcome limits the outcomes conditional on actions. The lower is , the higher is the implicit impact of entry and exit decisions on market profit rates. A very large represents a very weak impact of entry and exit decisions on market profit rates.
2.3. Smithian Models of Competition
A Smithian model of competition can be formulated as a parameterized family of functions,
, such as Equation (
10), together with a parameter
specifying the difference between expected profit rates conditional on entry and exit.
The conditional action functions represent the theory of the behavior of owners of capital in responding to differences in market profit rates, and the difference in conditional expected profit rates represent the theory of competition in markets. However, even these strong assumptions are not sufficient to determine the joint distribution . There are many joint distributions that satisfy these constraints.
2.4. Maximum Entropy and Statistical Equilibrium
One powerful approach to underdetermined problems of this type is the maximum entropy method championed particularly by E. T. Jaynes [
8]. Jaynes’ very general idea is to maximize the entropy of the unknown and underdetermined distribution subject to constraints expressing whatever information from observation or theory are relevant. Due to the strict concavity of the entropy function, as long as the constraints describing the available information describe a non-empty convex set in the space of distributions, the maximum entropy program will define some maximizing distribution that is a candidate statistical equilibrium of the model. The substantive interest of the resulting maximum entropy distribution depends on the information expressed by the constraints.
It is due to Jaynes’ demonstration that the statistical mechanical equilibrium distributions of physical systems, such as a perfect gas, can be derived from constrained maximum entropy problems that we refer to the social science generalizations proposed here as statistical equilibria. Shannon’s famous theorems in information theory guarantee that constrained maximum entropy distributions contain no information that is not explicit in the constraints.
For example, if we maximize the entropy of the joint distribution subject only to constraints on the marginal distribution, where
are known marginal frequencies, the maximum entropy problem is:
The Lagrangian associated with this programming problem is:
The first order conditions require
. Plugging this result into the constraint
we find that entropy is maximized when
x and
a are independent, and the marginal distribution of
a is uniform with
and
. This results in the degenerate and uninformative maxent joint distribution
, which just returns the information already known through the observation of
[
9]. The corresponding conditional distributions are
and
, implying that the aggregate outcome has no impact on individual quantal behavior, and
, implying that the aggregate outcome is independent of individual quantal decisions, which shed no light on the behavior of individual actors or on the process through which their actions determine the aggregate outcome.
While the results of this maxent exercise are uninformative for our modeling purposes, they highlight a very important characteristic of maximum entropy problems in general. They tell us that the content of the maxent statistical equilibrium depends on the information in the constraints. In this case, no further information beyond the observed marginal distribution appears in the constraints, and the maxent formalism dutifully reports this by refusing to draw any conclusions about the causal mechanisms shaping the statistical equilibrium.
When we add further constraints, however, either from observation or on the basis of prior theoretical considerations, for example, involving the conditional expectations , the maximum entropy joint distribution will in general (except in the case where the constraint is not binding) convey useful information. The maxent program will produce meaningful conditional frequencies, and , and, as a result, tell us what we can infer from our limited information as to the impact of the outcome variable on the quantal behavior of individuals and the mechanism through which the quantal behavior of individuals shapes the distribution of outcomes. In some cases, such as profit rate equalization, even a small amount of further information can shed light on the statistical equilibrium of the model.
The specification of further constraints of this type and the interpretation of the resulting statistical equilibrium depend critically on the theoretical framework in which a researcher situates the analysis of data. In general, different constraints correspond to different substantive assumptions about the behavior of individuals and their interaction through social institutions. These substantive questions cannot be avoided purely through the invocation of the maxent formalism.
2.5. Statistical Equilibrium in Smithian Competition
In this section we use constrained maximum entropy to derive the statistical equilibrium of the Smithian model of competition. The mathematical programming problem chooses marginal frequencies,
, so as to maximize the Shannon entropy of the implied joint distribution,
, subject to a constraint on the mean value of the outcome,
, the constraint Equation (
12), and the assumption that the conditional action function belongs to the class of logit functions with parameters
. This model is a QRSE model because capitalist firms entering or exiting subsectors in response to profit rate differentials lower or raise the profit rates in those sectors resulting in the emergence of an average rate of profit and a statistical equilibrium distribution of profit rate differences.
The conditional action constraint can be written
, or
. The constraint on the difference between the weighted conditional expected outcomes with this conditional action constraint takes a compact form:
Decomposing the joint entropy into the entropy of the marginal distribution plus the average entropy of the conditional distribution allows us to maximize the joint entropy with respect to marginal frequencies
:
where
is the binary entropy function:
The maximum entropy program that determines
given
T,
and
,
is:
The constraint in Equation (
19) has the sense it does because the conditional action frequencies are given as constraints, so the maxent program will seek to make the marginal outcome frequency as uniform as possible, which results in widening the difference between the weighted conditional outcome expectations. In order to represent the impact of the action on the outcome the constraint must put an upper bound on the difference between the expected outcomes conditional on the actions. (Because the entropy is a strictly concave function, the maxent program exactly satisfies the constraint with equality to avoid wasting degrees of freedom.) Note that the statistical equilibrium is sustained only if individual entry and exit decisions have a finite (even if small) impact on profit rates through competition, in contrast to theories of “perfect” competition in which the typical firm’s investment and production decisions are assumed to have no impact on prices or profitability.
The associated Lagrangian to Equation (
19) is:
The first-order conditions for maximizing entropy of the joint frequencies and conditional frequency require
Solving for we get maximum entropy marginal frequencies
Using the constraint
, we find the normalizing factor:
The marginal distribution
becomes:
The constraints , determine , given T, , , :
The conditional outcome frequencies are then:
Letting the partition function be
, the expected outcomes conditional on the action are:
Given the parameters , and , the maxent program predicts the marginal frequencies . These predicted frequencies represent a statistical model of profit rate equalization that can be compared to the observed frequencies in order see whether or not the maximum entropy model can reproduce important features of capitalist competition.
In many contexts it is more convenient to express the statistical equilibrium distribution in terms of the Lagrange multipliers
and
as in Equation (
24). The resulting statistical equilibrium marginal frequency can then be written directly as a function of the parameters
T,
,
, and
. In this form the statistical equilibrium is a class of parameterized models that predict possible observed outcomes, for example, of profit rate distributions. Given assumed prior probabilities over the parameters
T,
,
, and
, Bayesian statistics can be used to infer posterior probabilities over the parameter space as a method for estimating the parameters given observed data.
2.6. QRSE and Quantal Response Equilibrium
The QRSE model shares certain fundamental features with Quantal Response Equilibrium (QRE) in games [
4,
5,
10] but also has significant differences from that framework.
Both QRSE and QRE regard behavior as inherently stochastic, and represent decisions in the form of quantal responses that assign a positive frequency to every action available to the decision-maker. As a result, both frameworks imply endogenous fluctuations in outcomes arising from the indeterminacy of individual actions. Furthermore, both frameworks specialize to logit quantal responses to describe individual actions, primarily because of the widespread evidence that real-world behavior so often reflects logit quantal response patterns.
There are, however, important differences between the approaches and models. QRE centers on the idea of a strategic interaction among the participants in a game to determine the distribution of outcomes. In QRSE, by contrast, the typical individual actors respond to the actions of others only through the statistical distribution describing those actions. In the case of the QRSE model we develop in this paper, this difference is underlined by the closure of the model through the constraint Equation (
16), which has no parallel in QRE generalizations of Cournot-Nash equilibrium. The implication of this constraint is that each action has a (possibly small, but non-zero) impact on the outcome, which is reflected in the equilibrium joint distribution of actions and outcomes. Traditional game theory formulations of this problem would depend on some explicit model of the strategic interactions underlying this impact (for example, of the competitive strategies through which entry and exit affect profit rates).
The QRSE framework derives from the maximum entropy research program of E. T. Jaynes, while QRE is a generalization of the concept of Nash equilibrium. QRSE characterizes the equilibrium distribution as the maximum entropy distribution consistent with constraints representing knowledge about the system being modeled. QRSE improves on other maximum entropy modeling of social outcomes like the profit rate distribution by deriving the equilibrium distribution from theoretically meaningful behavioral constraints. QRE characterizes equilibrium distributions in terms of reciprocal best responses. A deeper understanding of the relationship between the two approaches awaits further analytical advances.
3. Application to Profit Rate Data
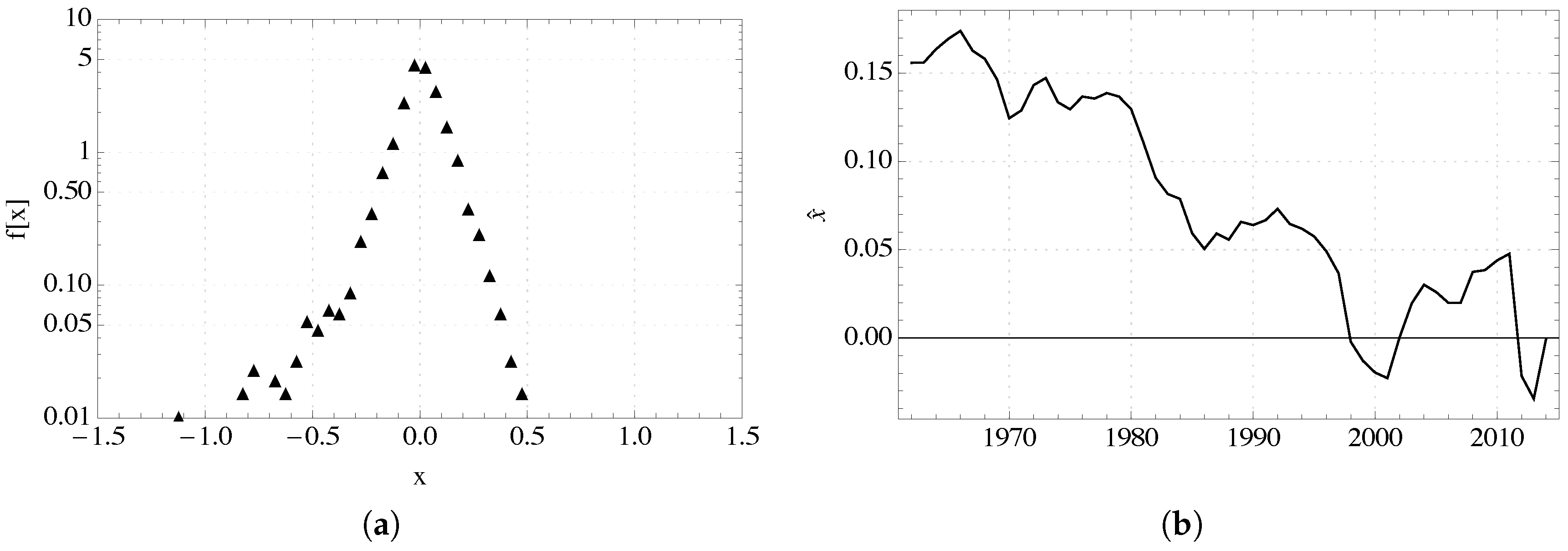
Using data gathered from the Compustat Annual Northern American Fundamentals database (See
Appendix A for details.), we calculate the rate of profit as the ratio of the difference between total revenue and operating costs to total assets which have been shown to approximate a statistical equilibrium distribution [
11,
12,
13]. The marginal frequency distribution of profit rates deviations for a sample year 1975 is plotted in
Figure 2.
Given only the empirical frequency data for and a qualitative theory of the dependency of x on a (and a on x), we are interested in inferring a quantitative model of competition (and capitalist behavior) in the form of a joint probability distribution over the action a and the observed level of profit rate deviations x by using the maximum entropy approach outlined above.
Model Inference
The model of
Section 2.5 assumes that the action frequencies conditional on outcome are logit functions with parameters
T and
. This assumption, as we have seen, together with a constraint on the expectation of the outcome and a constraint on the difference between the expected profit rates conditional on entry and exit, as in Equation (
12), are sufficient to determine the maxent joint frequency and hence the marginal frequency, which can be used as a theory in the Bayesian sense of the observed marginal frequency data.
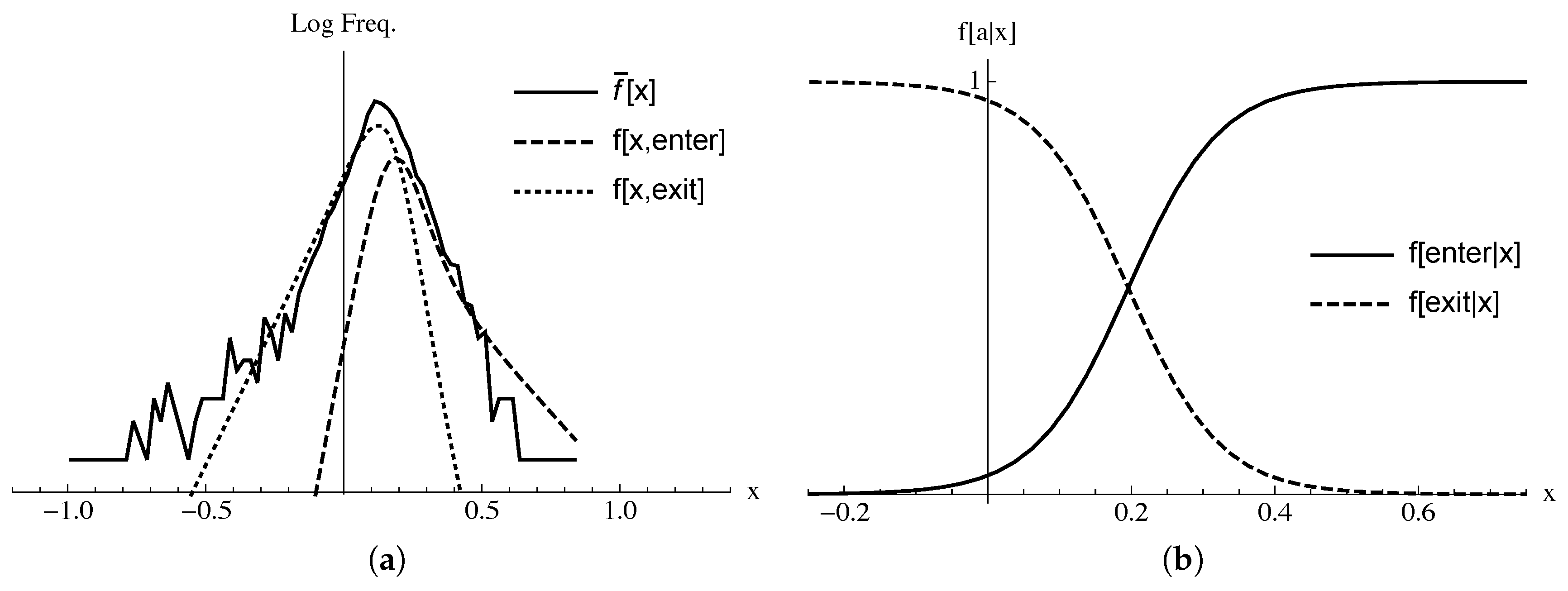
Figure 3 plots the solution to Equation (
19). The tent-shaped marginal frequency of profit rates that appears is the direct result of the maximum entropy program subject to the constraints on the conditional action frequencies and the intensity of competition, and required no direct constraint on, for example, the expectation of the absolute value of the profit rate deviations. These results have significant implications for the widely observed equilibrium distribution of firm growth rates [
14] which are typically modeled using a Laplace or Subbotin distribution [
15,
16]. While the Subbotin distribution is a maximum entropy distribution, the constraints that give rise to it are not specified from clear theoretical priors. In contrast, the QRSE model has clear theoretical foundations and also approximates many well-known symmetric and skew distributions similar to the Subbotin distribution. Effectively, this maxent program shows that the observed distribution of profit rates can be explained as the statistical equilibrium produced by the interaction of capitalists entering and exiting subsectors in response to profit rate deviations according to a logit quantal response and a given effectiveness of entry and exit in changing profit rates through competition.
In
Figure 4 we also show the corresponding maximum entropy conditional outcome, and conditional action frequencies that emerge from the solution to Equation (
19). It is evident that the maximum entropy program, given an appropriate
T and
and
and
, generates marginal outcome frequencies,
, that, from an information theoretic perspective, are nearly indistinguishable from the actual observed frequencies,
.
We estimate
T and
and
and
jointly by minimizing the Kullback-Leibler divergence between the observed marginal frequencies,
, and the inferred marginal frequencies,
, obtained from the output of Equation (
24). (In principle, this problem may be underidentified for higher dimensional problems or multimodal data). Formally, we minimize the functional,
and find
,
,
, and
. Using the information distinguishability (
) statistic [
17], we calculate the informational performance of the fitted distribution,
, as capturing approximately 97 percent of the informational content of the observed frequency distribution
.
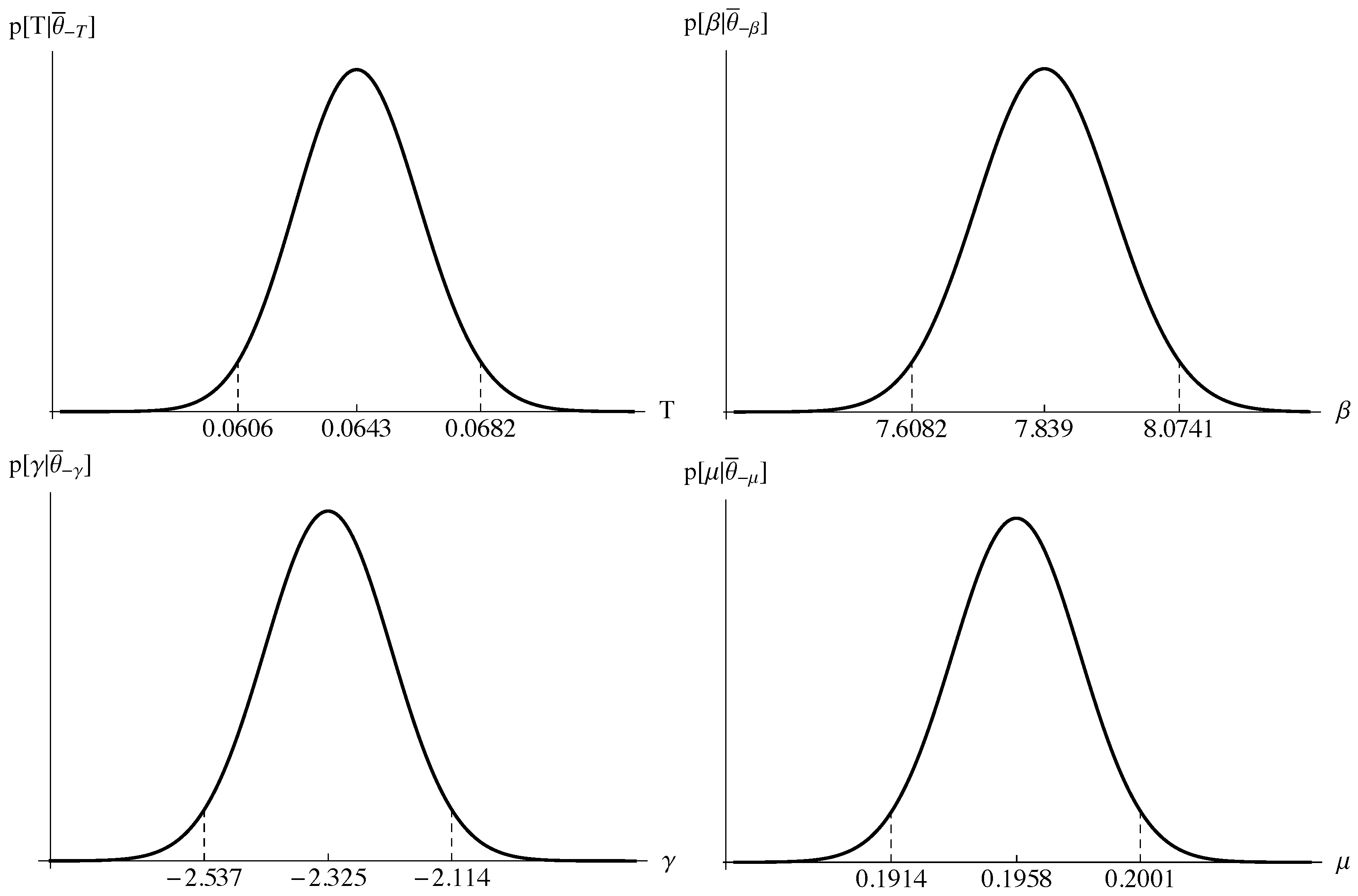
The Kullback-Leibler divergence is a good approximation to the log posterior probability for the multinomial model for any parameters allowing us to make posterior inferences about parameter estimates. (See
Appendix B for proof). Let the vector of the model parameters be
. In order to make posterior inferences about the model parameters we can plot the conditional distributions of each parameter holding all others at their maximum posterior probability estimate
as we do in
Figure 5.
The logit parameter T has at least two behavioral implications. First, it measures the responsiveness of the action frequency to changes in outcome at the average outcome because the derivative of the conditional action function at is . With the profit rate data in our example, indicates that a rise of one basis point in the profit rate in the region near the average profit rate would raise the frequency of entry by . Second, T also defines the region in which the action is sensitive to the outcome, since the value of x for which the conditional action frequency is P, with is . For example, with the profit rate data in our example indicates that the region of profit rate deviations in which the frequency of entry lies between and is .
4. Discussion
Statistical equilibrium depends on individual agent behavior but not on the details of any particular individual agent’s actions. What matters for systems in statistical equilibrium is only the statistical average frequency of behavior. A QRSE model can be thought of as representing a large class of dynamic models based on individual behavior that share the same behavioral averages. While the constraints that define a QRSE model do not determine any unique individual dynamics, they do ensure that the estimated statistical equilibrium will be in the high probability manifold of the state space. For example, if a dynamic model based on individual behavior implies significant deviations from the averages identified in a parallel QRSE model, that dynamic model will have a very low—if not vanishingly small—probability of having generated the QRES predicted statistical equilibrium.
It would be a mistake, however, to interpret the QRSE in concrete terms as the assumption that all agents in reality are identical and behave like the typical agent in the QRSE. This is the fallacy of Milton Friedman’s “only predictions matter” claim [
18]. The QRSE model provides a complete dynamic description of all individual behavior through the ensemble averages. These tell us which dynamics are most likely given the configuration of the state space, not the deterministic time path of a representative agent that can be aggregated over to provide macroscopic properties of the system.
Many economic phenomena can be understood as representing slowly-changing statistical equilibria, analogous to the thermodynamic concept of “adiabatic” changes, where the changes in parameters are sufficiently slow relative to the dynamics that sustain the equilibrium. QRSE will not work (without modification) on data from non-equilibrium systems or data that mixes observations from several equilibria. One important insight from the QRSE method is that in social contexts, purposeful, goal-oriented behavior has the same analytic role in statistical modeling as theoretical laws such as the conservation of energy in physical systems: both give rise to constraints in the maximum entropy mathematical programming problem. This provides a powerful method for testing for the importance of conjectured behavior in specific social phenomena. The key to success in applying maximum entropy methods to underdetermined quantal response social interaction problems is careful attention to the specification of appropriate constraints on the conditional frequency distributions , . When constraints are appropriate, the resulting estimates can be interpreted as quantitative measures of theoretical effects.