1. Introduction
Computations, understood as realized through Turing machines, billiard or ballistic computers [
1], circuits, lists of computer instructions, or otherwise, are often designed to have a linear (i.e., causal) time flow: After a fundamental operation is carried out, the program counter moves to the next operation, and so forth. Surely, this is in agreement with our everyday experience; after you finish to read this sentence, you continue to the next (hopefully), or do something else (in that case: goodbye!).
What sorts of computation become admissible if one drops the assumption of a linear time flow and reduces it to mere logical consistency? One could imagine that a linear time flow restricts computation strictly
beyond what would be allowed for the purely logical point of view. Indeed, we show this to be true. If the assumption of a linear time flow is dropped, a variable of the computational device could depend on “past” as well as “future” computation steps. Such a dependence can be interpreted as
loops in the time flow, e.g., generated by a closed timelike curve [
2]. There are two fundamental issues that might make loops logically inconsistent. One is the liability to the
grandfather antinomy. In a loop-like information flow, multiple contradicting values could potentially be assigned to a variable—the variable is
overdetermined. The other issue is
underdetermination: a variable could take multiple consistent values, yet the model of computation
cannot predict which actual value it takes. This underdetermination is also known as the
information antinomy. To overcome both issues, we restrict ourselves to models of computation where the assumption of a linear time flow is dropped and replaced by the assumption of
logical consistency: All variables are neither overdetermined nor underdetermined. We call such models of computation
non-causal. Our main result is that non-causal models of computation are
strictly more powerful than the traditional causal ones. Therefore, causality is a stronger assumption than logical consistency in the context of computation. Similar results are also known with respect to
quantum computation [
3,
4,
5,
6,
7], correlations [
5,
8,
9,
10,
11] as well as communication [
12]. As we will show later, such circuits are “programmed” by introducing a
contradiction if an
undesired result is found. This is like guessing the solution to a problem and killing the own grandfather in the event that the guess was wrong (similar to “quantum suicide” [
13] or “anthropic computing” [
14]).
The article is structured as follows. First, we discuss the assumption of logical consistency in more depth, then we describe a non-causal circuit model of computation and give a few examples of problems that can be solved more efficiently. We continue by describing other non-causal models of computations: the non-causal Turing machine and non-causal billiard computer. We conclude by showing how to efficiently find a satisfying assignment to a SAT formula if the number of satisfying assignments is previously known.
3. Non-Causal Circuit Model
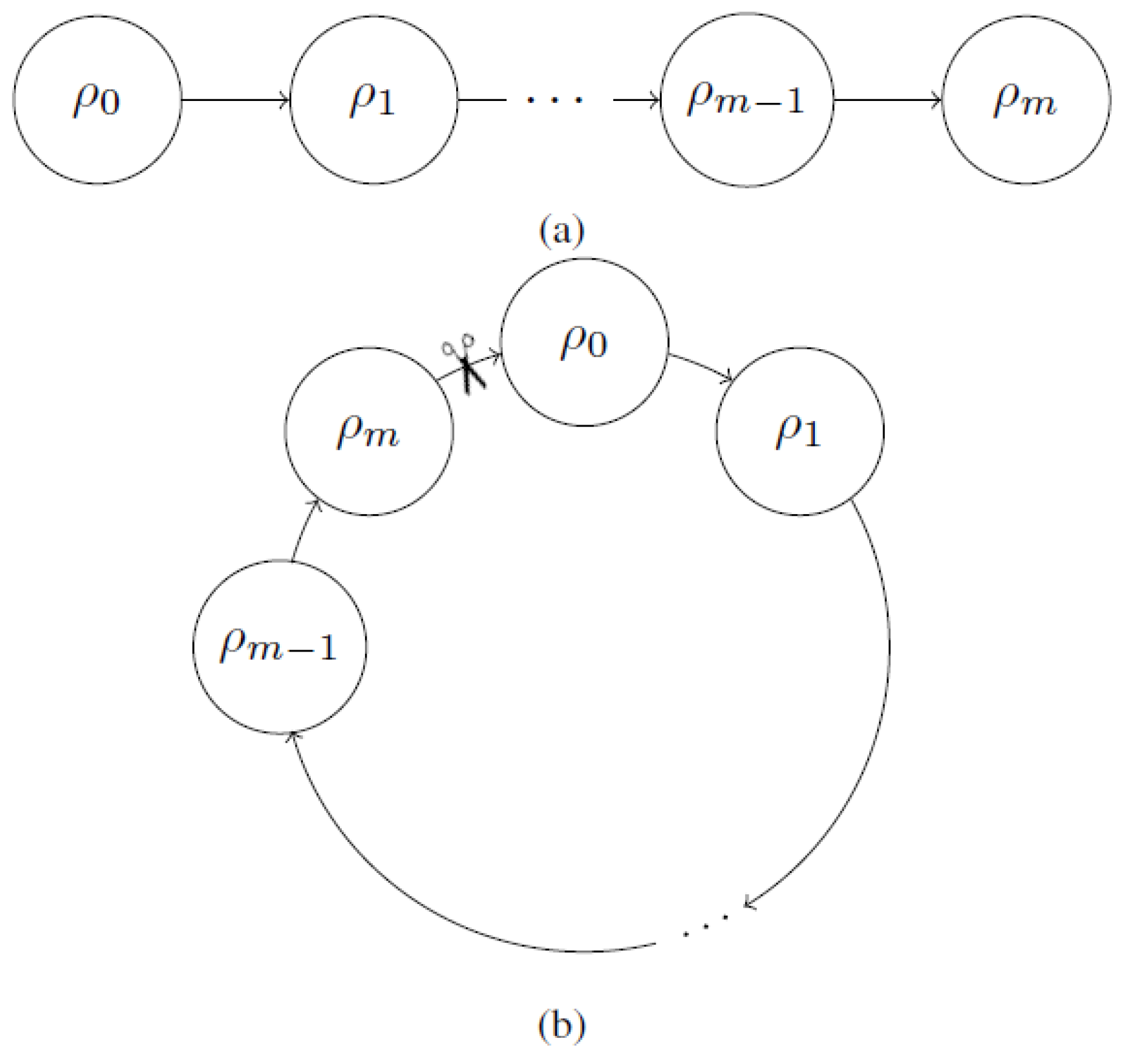
A circuit consists of gates that are interconnected with wires. In the traditional circuit model, back-connections (i.e., a cyclic path through a graph where gates are identified with nodes and wires are identified with edges) are either forbidden or interpreted as
feedback channels. An example of a feedback channel is an autopilot system in an aircraft that, depending on the measured altitude, adjusts the rudder and the power setting to maintain the desired altitude, at the same time avoiding a stall. Here, we interpret back-connections or loops differently. Whilst in the above scenario the feedback gets introduced at a
later point in the computation, the back-action in a non-causal circuit effects the system at an
earlier point. Such a back-action can be interpreted as acting into the past. Another interpretation is that every gate has its own time (clock), but no global time is assumed—this interpretation stems from the studies of correlations without causal order [
5,
8]. Such an interpretation might be more pleasing: Here, “earlier” is understood
logically, and the assumption of a global causal order is simply replaced by logical consistency.
A
non-causal circuit consists of gates that can be interconnected arbitrarily by wires, as long as the circuit as a whole remains logically consistent. An example of a circuit that is overdetermined and an example of a circuit that leads to the information antinomy (under-determined) are given in
Figure 2.
We model a gate
G by a Markov matrix
with 0–1 entries. Without loss of generality, assume that the input and output dimensions of a gate are equal. The Markov matrix of the
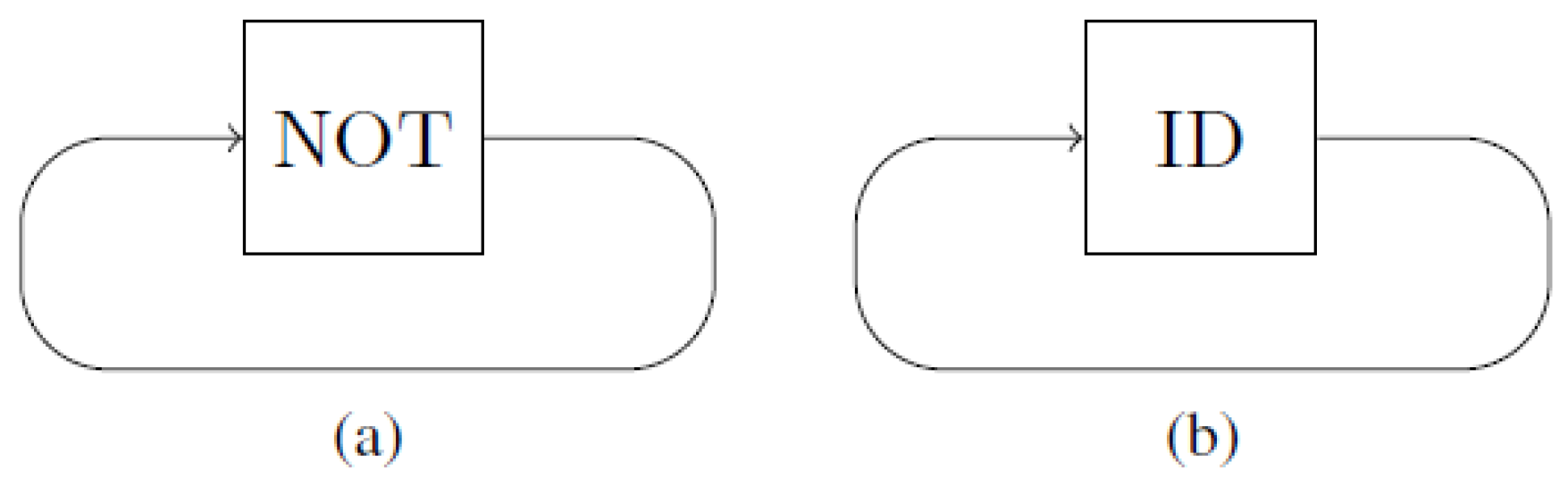
gate on a single bit (see
Figure 2b) is
and the Markov matrix of the
gate on a single bit (see
Figure 2a) is
Values are modeled by vectors; e.g., in a binary setting, the value 0 is represented by the vector
and the value 1 is represented by the vector
. In general, an
n-dimensional variable with value
i is modeled by the
n-dimensional vector
with a 1 at position
i, and where all other entries are 0. A gate is applied to a value via the matrix-vector multiplication; i.e., the output of
G on input
a is
. Let
F and
G be two gates. The Markov matrix of the parallel composition of both gates is
. They are composed sequentially with a wire that takes the
d-dimensional output of
F and forwards it as input to
G. By this, we obtain a new gate
which represents the sequential composition. The sequentially composed gate is
By using these rules of composition, a
causal circuit can always be modeled by a single gate. A
closed circuit is a circuit where all wires are connected to gates on both sides. Let
H be the gate that describes the composition of all gates for a given causal circuit. We can transform any such circuit into a closed non-causal circuit by connecting all outputs from
H with all inputs to
H. A
logically consistent closed circuit is thus a circuit where a
unique assignment of a value
c to the looping wire exists:
In other words, the described closed circuit is logically consistent if and only if the diagonal of
consists of 0’s with a single 1. The position of the 1-entry represents the fixed point and the value
c on the looping wire. Note that for a given closed circuit, the gate
H is not unique, but might depend on where the “cut” is introduced. An
open circuit is a circuit where some wires are not connected to a gate on one side. Thus, such a circuit has either an input
a, an output
x, or both. A logically consistent open circuit, therefore, is a circuit where for
any choice of input
a, a
unique assignment of a value
c to the looping wire and to the output
x exists, such that
where the second output from
H is looped to the second input to
H.
Let
be the value on the looping wire of a logically consistent open circuit
with input
a. We can transform
into a family
of logically consistent
closed circuits such that the value on the same looping wire of
is
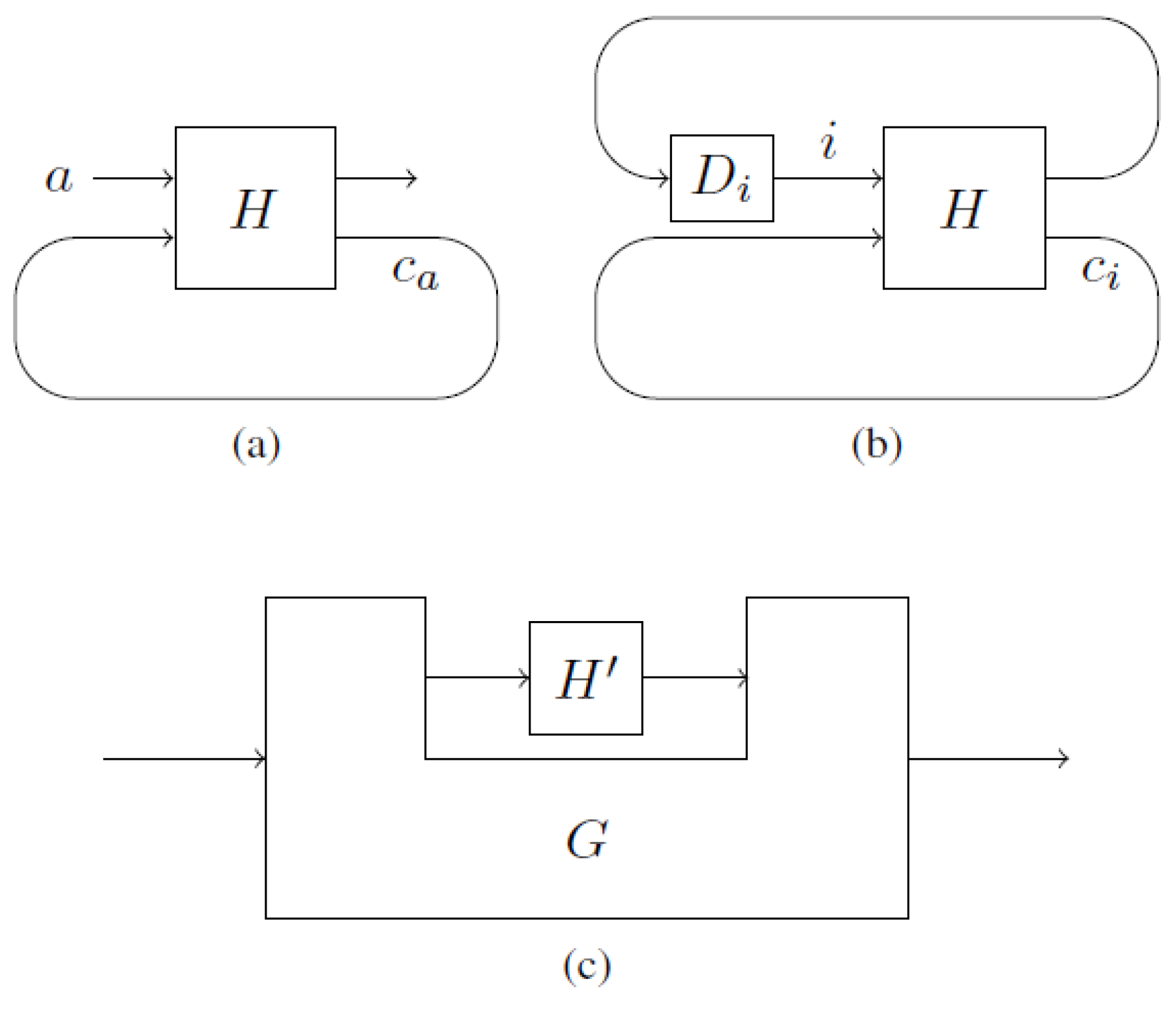
. The circuit
is constructed by attaching the gate
to the input and output wires of
(see
Figure 3a,b). The gate
unconditionally outputs the value
i.
There is an ambiguity on which wires are regarded as “looping”. We show that two different representations
H and
of the same closed non-causal circuit
yield the same computation (the difference between
H and
is the identification of the looping wires). Different
H and
that represent the
same non-causal circuit
can be written as
and
. For
H, the looping wires are those that exit
Q and enter
R, and for
, vice versa. From Equation (
1), we have
Since
R is deterministic, the value of
e is uniquely determined. Thus, we obtain
where
is the specific value on the wire exiting
R and entering
Q. Conversely,
holds. The only way
H and
each have a
unique fixed point is with the identification
. Therefore, both representations
H and
assign the same values to the wires. By the above translation from
open to
closed circuits, we see that the same reasoning can be applied to open circuits.
Above, we considered
deterministic Markov processes. It is natural to extend this model to probabilistic processes (i.e., stochastic matrices). The logical consistency condition in that case—as studied in Ref. [
15]—is
that is, the diagonal of
consists of non-negative numbers (probabilities) that add up to 1. Equation (
2) can be interpreted as “the average number of fixed points is 1”. To see this, we decompose
H as a convex combination of
deterministic matrices
where for all
i,
is deterministic. Then, Equation (
2) states
For an arbitrary deterministic matrix , the expression represents the number of fixed points, with which we arrive at the stated interpretation.
An open non-causal circuit can be represented by a non-causal comb [
5]
G which is a higher-order transformation—
G transforms the gate
to a new gate (see
Figure 3c). The non-causal comb
G, for instance, could connect the output from
with the input of
, as long as the composition remains logically consistent.
4. Computational Advantage
The logical consistency requirement forces the value on a looping wire to be the unique fixed point of the transformation. This can be exploited for
finding fixed points of a black box, which yields an advantage in higher-order computation. Suppose we are given a black box
B that takes (produces) a
d-dimensional input (output) and has a
unique fixed point
x previously unknown to us. As a Markov matrix,
B is
Our task is to find the fixed point
x in as few queries as possible. If we solve this task with a causal circuit, then, in the worst case,
queries are needed. In contrast, with a non-causal circuit, a
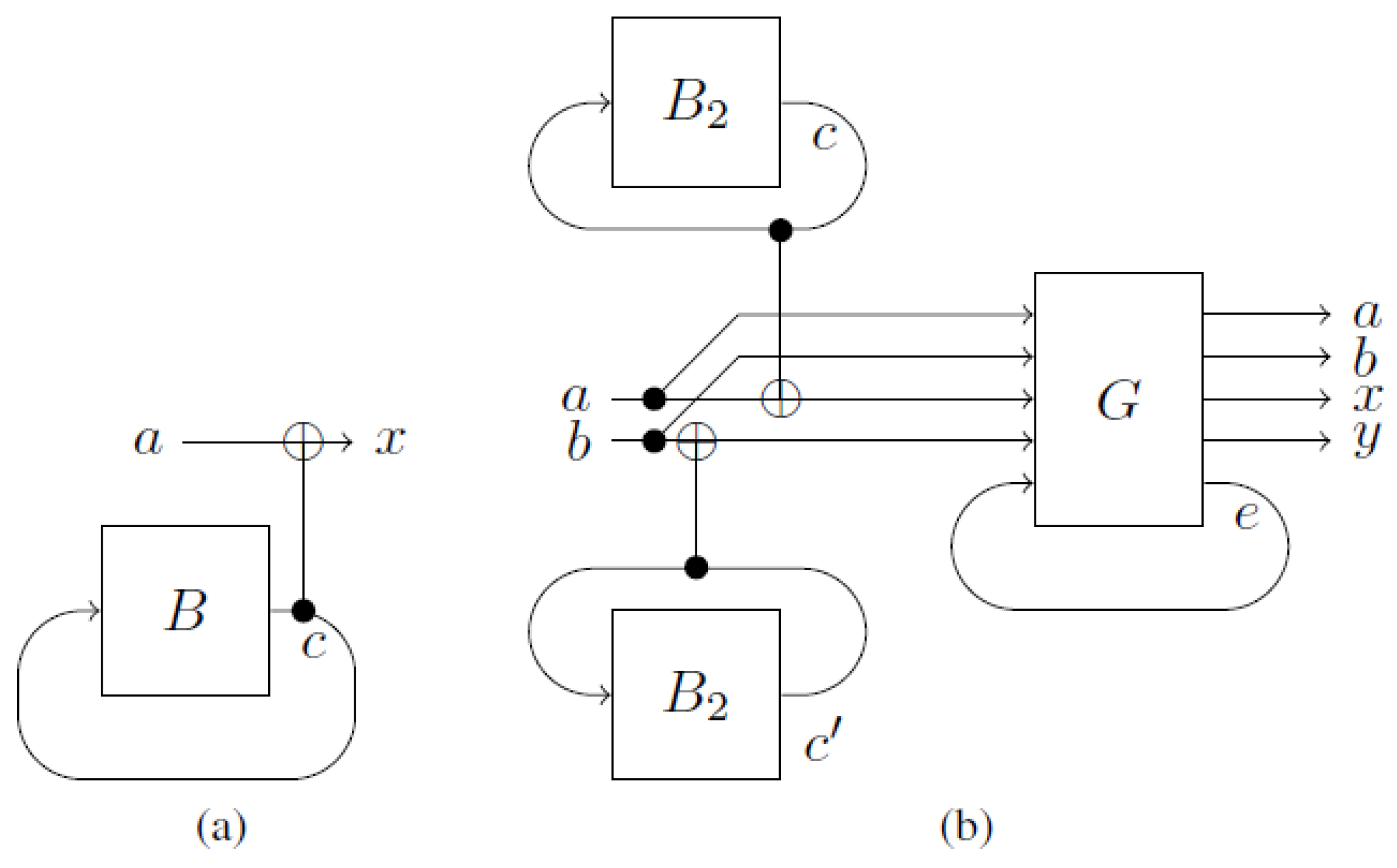
single query suffices. The reason for this is that the black box is queried with the fixed point only. Any other query would lead to a logical contradiction, and therefore does not occur. For that purpose, we just connect the output of
B with the input of
B and use a second wire to read out the value (see
Figure 4a). This circuit is logically consistent because
where
is the CNOT gate and
is the identity. However, this construction only works if
B has a
unique fixed point. Suppose
has
two fixed points. In that case, the circuit from
Figure 4b can be used to find both fixed points with two queries. In addition to short-cutting the black boxes, we need to introduce a gate
G that ensures a
unique fixed point of the whole circuit. The gate
G works in the following way:
where
e is binary,
, the addition is carried out modulo 2, and
is a 2-dimensional vector representing the value 0. In words, if the value
c on the upper wire is less than the value on the lower wire
, and
e is 0, then we get a fixed point on the third wire of
G (variable
e in
Figure 4b). Otherwise, the bit on the third wire gets flipped—no fixed point. This guarantees that all loops together have a
unique fixed point. Ironically, the gate
G suppresses certain fixed points on the previous loops by introducing a logical
inconsistency at a later point in the circuit. This resembles “anthropic computing” [
14], where one guesses the solution to a problem and commits suicide if the guess was wrong—a recipe to solve NP-complete problems in the relative-state interpretation of quantum mechanics [
16] and where consciousness follows only those branches where the programmer remains alive. Such a construction can be used to find the fixed points of a black box with a
few fixed points and where the number of fixed points is
known. For a large number
n of fixed points (e.g.,
), we can use the probabilistic approach to non-causal circuits. Let
be a black box with
n fixed points and input and output spaces of dimension
d. The Markov matrix of
is
We construct a randomized gate where the average number of fixed points is one:
with
The gate
can be understood as a
d-dimensional generalization of the
gate for bits: The input is increased by one modulo
d. Such an
has
no fixed points. The mixture
is logically consistent, because
This means that we can use the circuit from
Figure 4a to find a random fixed point of
.
We apply these tools to find solutions to instances of search problems with a
known number of solutions, and where a guess for a solution can be verified efficiently by a verifier
V. In other words, we can find solutions to NP search problems, yet where the number of solutions to an instance must be known to us in advance. Note that the following construction does not solve a decision problem, but rather
finds the solution. Suppose an instance
I to a problem
has a
unique solution. We replace the gate
B of
Figure 4a with a new gate
that acts in the following way: it takes a guess
c for a solution to
as input, and runs
V to verify
c. If
V accepts
c, then
outputs
c, and otherwise,
outputs
, where the addition is carried out modulo
d. Such a circuit has a unique fixed point
c which equals the solution of
. This, for instance, could be applied to a
formula, where a
unique assignment of values to variables exist which make the formula true. Note that this approach does not prove an advantage in finding satisfying assignments for SAT formulas, even if the number of these satisfying assignments is previously known; currently, we do not know how difficult or easy it is to solve such instances
causally.
5. Other Non-Causal Computational Models
We briefly discuss non-causal Turing machines and non-causal billiard computers. A Turing machine
T has a tape, a read/write head, and an internal state machine. After every read instruction, the state machine moves to the next internal state, and thereby decides what to write and where to move the head to. A non-causal Turing machine is a machine where parts of the tape are not “within time”: “Future” (from the head’s point of view)
write instructions influence “past”
read instructions. A symbol that is written at time
t to position
j could be read at time
form position
j; i.e., symbols can be read “before” they are written. As with other self-referential systems, this leads to problems that can be solved if we enforce the condition of logical consistency, as discussed above. Another issue is that multiple
write instructions could
overwrite the value on position
j. This leaves open the question of what value is read. We can overcome this issue by running the Turing machine in a reversible fashion and by generating a history tape [
17], where
no memory position gets overwritten. An example of a non-causal Turing machine is where the
history tape is non-causal in the sense that symbols can be read “before” they are written.
The billiard computer is a model of computation on a billiard table [
1]. Before the computation starts, obstacles are placed on the table in such a way that the induced reflections of the balls and the collisions among the balls result in the desired computation. A non-causal version of a billiard computer is a billiard table where the holes are connected with closed timelike curves (CTCs) [
2] that are logically consistent. Now, a billiard ball could also collide with its younger self; this introduces a non-causal effect. Echeverria, Klinkhammer, and Thorne [
2] showed that solutions to CTC-dynamics that are not overdetermined exist. However, all solutions that they found are underdetermined. The non-causal circuits presented in this work indicate that logically consistent non-causal billiard computers are also admissible.
6. Conclusions and Open Questions
We show that models of computation where parts of the output of a computation are (re)used as input to the
same computation are logically possible. Furthermore, such a model of computation helps to solve certain tasks more efficiently. The question is how much more powerful this new model of computation is, and whether uncomputable tasks become computable when compared to the standard circuit model. A strong restriction of the model is that before one can find a fixed point, one needs to know the number of fixed points. For instance, if we want to find a satisfying assignment for a SAT formula
F with variables
, we first need to know the number of satisfying assignments—otherwise, we do not know how to construct the circuit. Ironically, this means that to solve a SAT problem without any promise, we first need to solve a problem that is believed to be much harder: a #SAT problem. One might want to apply the Valiant–Vazirani [
18] method to
to reduce the number of satisfying assignments to 1 (the reason why we modify
F to
is to guarantee satisfiability). The problem that we are left with is that we do
not know whether the output
of the Valiant–Vazirani method has a unique satisfying assignment or not—the reduction is probabilistic. Therefore, we cannot plug
into a circuit like the one shown in
Figure 4a to find the fixed point.
A model of computation similar to but more general than ours is based on Deutsch’s [
19] CTCs. Aaronson and Watrous [
20] showed that the classical special case of Deutsch’s model can solve problems in PSPACE efficiently. However, in Deutsch’s model, in contrast to ours, the information antinomy arises. Deutsch mitigates this issue by defining that the value on the looping wire is the uniform mixture of all solutions. This introduces a non-linearity into Deutsch’s model: the output of a circuit depends non-linearly on the input. A consequence of this is that—in the quantum version—quantum states can be cloned [
21]. As it is linear, the model studied here is not exposed to such consequences.