Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths
Abstract
:1. Introduction
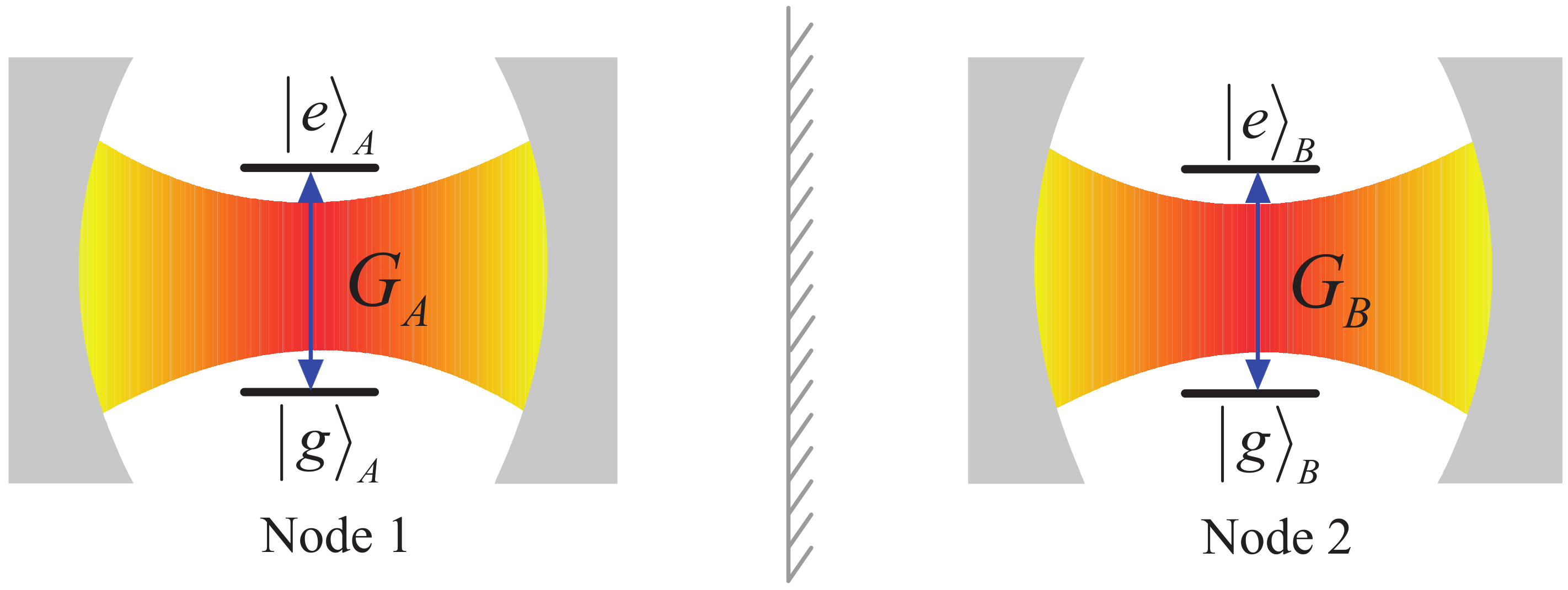
2. Separate Jaynes–Cummings Nodes
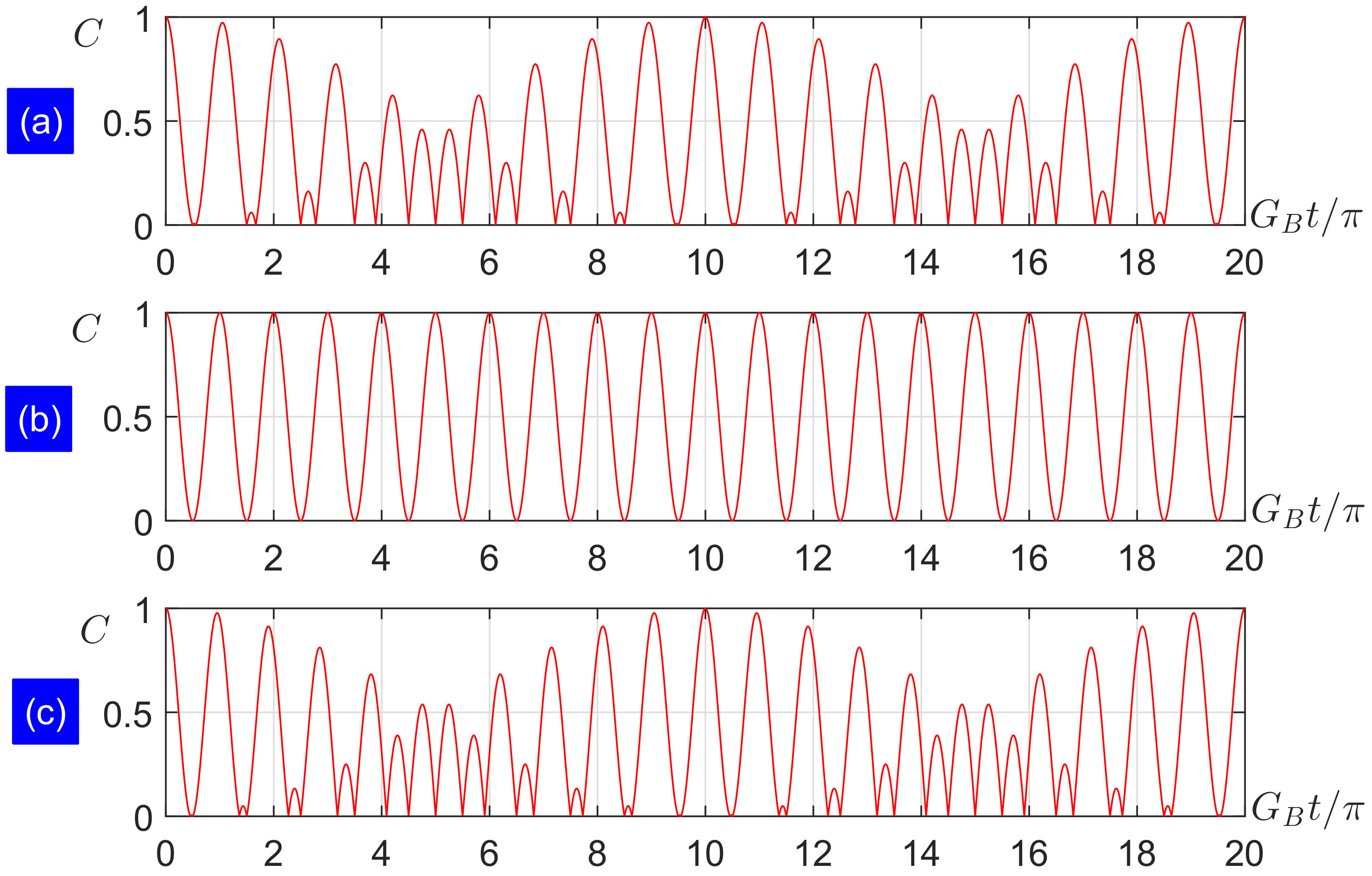
2.1. Vacuum-State Field
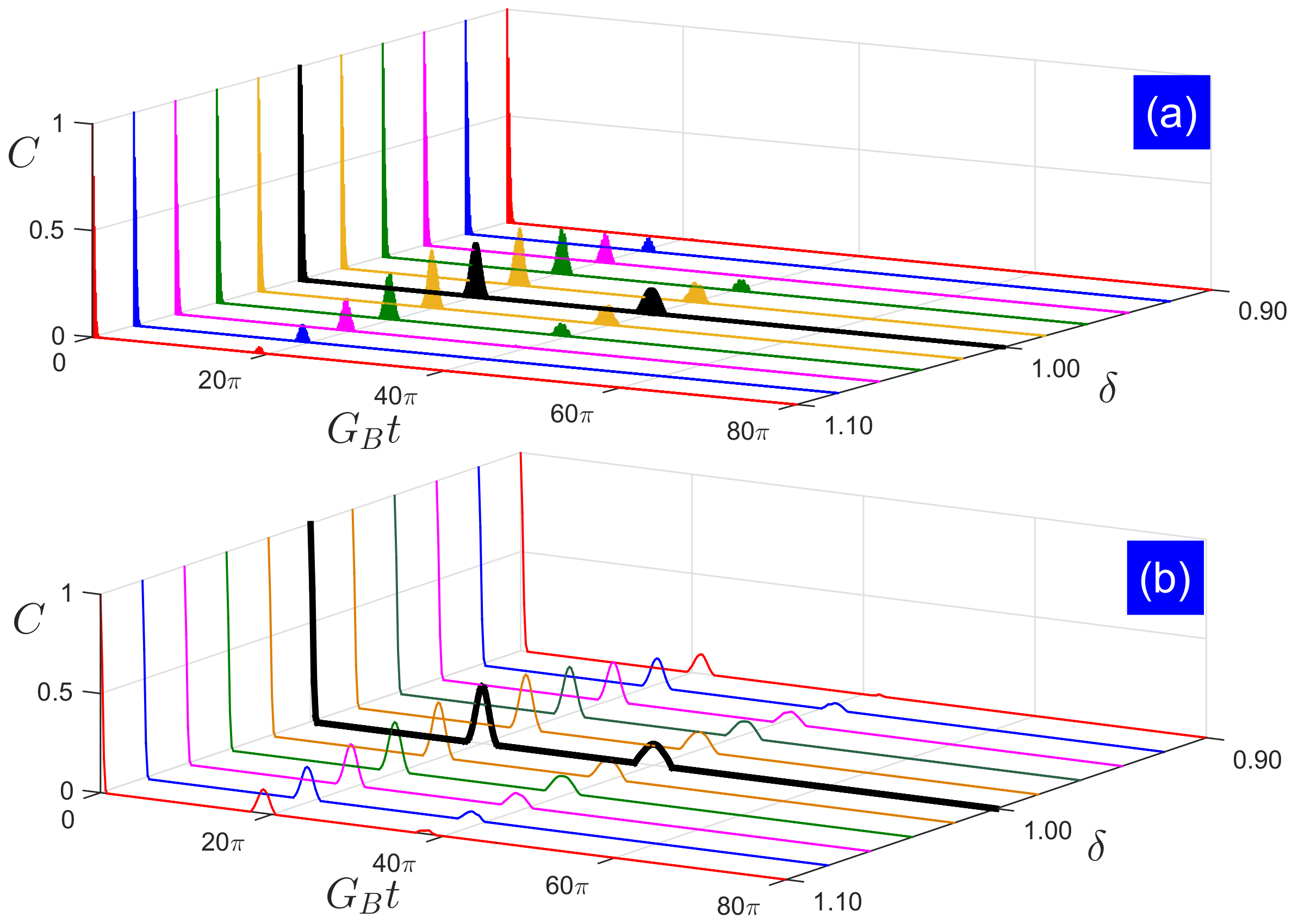
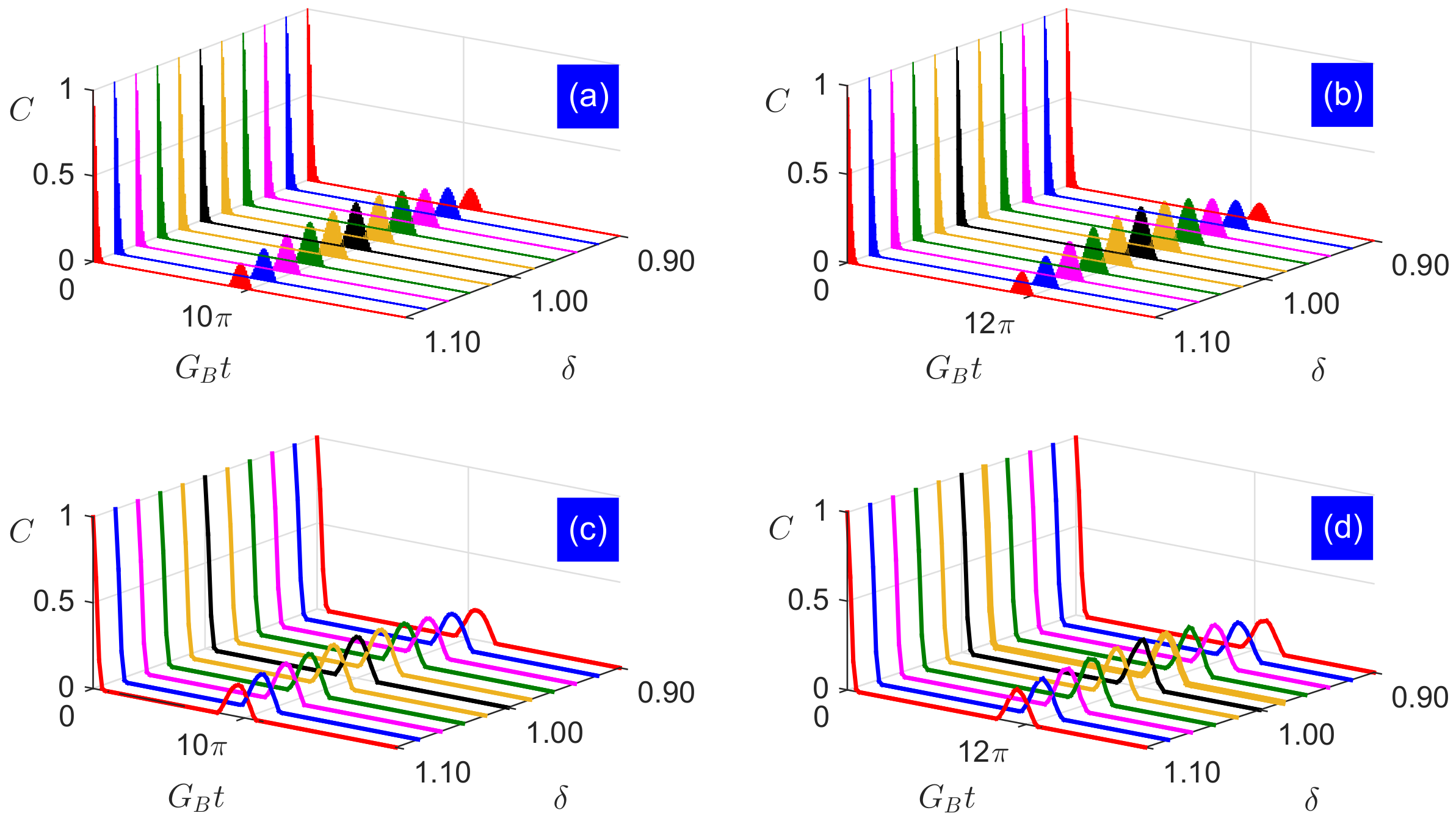
2.2. Coherent-State Field
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Raimond, J.M.; Brune, M.; Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 2001, 73, 565–582. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Zheng, S.B.; Guo, G.C. Efficient scheme for two-atom entanglement and quantum information processing in cavity QED. Phys. Rev. Lett. 2000, 85, 2392–2395. [Google Scholar] [CrossRef] [PubMed]
- Van Enk, S.J.; Cirac, J.I.; Zoller, P. Ideal quantum communication over noisy channels: A quantum optical implementation. Phys. Rev. Lett. 1997, 78, 4293–4296. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Buluta, I.; Ashhab, S.; Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 2011, 74, 104401. [Google Scholar] [CrossRef]
- Ashhab, S.; Niskanen, A.O.; Harrabi, K.; Nakamura, Y.; Picot, T.; de Groot, P.C.; Harmans, C.J.P.M.; Mooij, J.E.; Nori, F. Interqubit coupling mediated by a high-excitation-energy quantum object. Phys. Rev. B 2008, 77, 014510. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Mortezapour, A.; Borji, M.A.; lo Franco, R. Protecting entanglement by adjusting the velocities of moving qubits inside non-Markovian environments. Laser Phys. Lett. 2017, 14, 055201. [Google Scholar] [CrossRef]
- Mortezapour, A.; Borji, M.A.; lo Franco, R. Non-Markovianity and coherence of a moving qubit inside a leaky cavity. arXiv, 2017; arXiv:1705.00887. [Google Scholar]
- Lo Franco, R.; d’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Spin-echo entanglement protection from random telegraph noise. Phys. Scr. 2013, 153, 014043. [Google Scholar] [CrossRef]
- Aolita, L.; de Melo, F.; Davidovich, L. Open-system dynamics of entanglement: A key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef] [PubMed]
- Lo Franco, R.; Bellomo, B.; Maniscalco, S.; Compagno, G. Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 2013, 27, 1345053. [Google Scholar] [CrossRef]
- De Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Lo Franco, R.; Compagno, G. Overview on the phenomenon of two-qubit entanglement revivals in classical environments. arXiv, 2016; arXiv:1608.05970. [Google Scholar]
- D’Arrigo, A.; lo Franco, R.; Benenti, G.; Paladino, E.; Falci, G. Recovering entanglement by local operations. Ann. Phys. 2014, 350, 211–224. [Google Scholar] [CrossRef]
- Leggio, B.; lo Franco, R.; Soares-Pinto, D.O.; Horodecki, P.; Compagno, G. Distributed correlations and information flows within a hybrid multipartite quantum-classical system. Phys. Rev. A 2015, 92, 032311. [Google Scholar] [CrossRef]
- González-Gutiérrez, C.A.; Román-Ancheyta, R.; Espitia, D.; lo Franco, R. Relations between entanglement and purity in non-Markovian dynamics. Int. J. Quantum Inform. 2016, 14, 1650031. [Google Scholar] [CrossRef]
- Sciara, S.; lo Franco, R.; Compagno, G. Universality of Schmidt decomposition and particle identity. Sci. Rep. 2017, 7, 44675. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; lo Franco, R.; Compagno, G. N identical particles and one particle to entangle them all. arXiv, 2017; arXiv:1704.06359. [Google Scholar]
- Lo Franco, R.; d’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Preserving entanglement and nonlocality in solid-state qubits by dynamical decoupling. Phys. Rev. B 2014, 90, 054304. [Google Scholar] [CrossRef]
- D’Arrigo, A.; Benenti, G.; lo Franco, R.; Falci, G.; Paladino, E. Hidden entanglement, system-environment information flow and non-Markovianity. Int. J. Quantum Inform. 2014, 12, 1461005. [Google Scholar] [CrossRef]
- Trapani, J.; Bina, M.; Maniscalco, S.; Paris, M.G. Collapse and revival of quantum coherence for a harmonic oscillator interacting with a classical fluctuating environment. Phys. Rev. A 2015, 91, 022113. [Google Scholar] [CrossRef]
- D’Arrigo, A.; lo Franco, R.; Benenti, G.; Paladino, E.; Falci, G. Hidden entanglement in the presence of random telegraph dephasing noise. Phys. Scr. 2013, 153, 014014. [Google Scholar] [CrossRef]
- Lo Franco, R.; d’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Entanglement dynamics in superconducting qubits affected by local bistable impurities. Phys. Scr. 2012, 147, 014019. [Google Scholar] [CrossRef]
- Bellomo, B.; Compagno, G.; lo Franco, R.; Ridolfo, A.; Savasta, S. Entanglement dynamics of two independent cavity-embedded quantum dots. Phys. Scr. 2011, 143, 014004. [Google Scholar] [CrossRef]
- Dijkstra, A.G.; Tanimura, Y. Non-Markovian entanglement dynamics in the presence of system-bath coherence. Phys. Rev. Lett. 2010, 104, 250401. [Google Scholar] [CrossRef] [PubMed]
- Lo Franco, R.; Compagno, G. Quantum entanglement of identical particles by standard information-theoretic notions. Sci. Rep. 2016, 6, 20603. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; lo Franco, R.; Andersson, E.; Cresser, J.D.; Compagno, G. Dynamics of correlations due to a phase-noisy laser. Sci. Rep. 2012, 147, 014004. [Google Scholar] [CrossRef]
- Maniscalco, S.; Francica, F.; Zaffino, R.L.; Gullo, N.L.; Plastina, F. Protecting entanglement via the quantum Zeno effect. Phys. Rev. Lett. 2008, 100, 090503. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, B.; lo Franco, R.; Maniscalco, S.; Compagno, G. Two-qubit entanglement dynamics for two different non-Markovian environments. Phys. Scr. 2010, T140, 014014. [Google Scholar] [CrossRef]
- Bellomo, B.; Compagno, G.; lo Franco, R.; Ridolfo, A.; Savasta, S. Dynamics and extraction of quantum discord in a multipartite open system. Int. J. Quantum Inform. 2011, 9, 1665–1676. [Google Scholar] [CrossRef]
- Lo Franco, R. Nonlocality threshold for entanglement under general dephasing evolutions: A case study. Quantum Inform. Process. 2016, 15, 2393–2404. [Google Scholar] [CrossRef]
- Silva, I.A.; Souza, A.M.; Bromley, T.R.; Cianciaruso, M.; Marx, R.; Sarthour, R.S.; Oliveira, I.S.; lo Franco, R.; Glaser, S.J.; Deazevedo, E.R.; et al. Observation of time-invariant coherence in a nuclear magnetic resonance quantum simulator. Phys. Rev. Lett. 2016, 117, 160402. [Google Scholar] [CrossRef] [PubMed]
- Orieux, A.; D’Arrigo, A.; Ferranti, G.; lo Franco, R.; Benenti, G.; Paladino, E.; Falci, G.; Sciarrino, F.; Mataloni, P. Experimental on-demand recovery of entanglement by local operations within non-Markovian dynamics. Sci. Rep. 2015, 5, 8575. [Google Scholar] [CrossRef] [PubMed]
- Man, Z.X.; Xia, Y.J.; lo Franco, R. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef] [PubMed]
- Rendell, R.W.; Rajagopal, A.K. Revivals and entanglement from initially entangled mixed states of a damped Jaynes–Cummings model. Phys. Rev. A 2003, 67, 062110. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Brune, M.; Schmidt-Kaler, F.; Maali, A.; Dreyer, J.; Hagley, E.; Raimond, J.M.; Haroche, S. Quantum Rabi oscillation: A direct test of field quantization in a cavity. Phys. Rev. Lett. 1996, 76, 1800–1803. [Google Scholar] [CrossRef] [PubMed]
- Meekhof, D.M.; Monroe, C.; King, B.E.; Itano, W.M.; Wineland, D.J. Generation of nonclassical motional states of a trapped atom. Phys. Rev. Lett. 1996, 76, 1796–1799. [Google Scholar] [CrossRef] [PubMed]
- Boca, A.; Miller, R.; Birnbaum, K.M.; Boozer, A.D.; McKeever, J.; Kimble, H.J. Observation of the vacuum Rabi spectrum for one trapped atom. Phys. Rev. Lett. 2004, 93, 233603. [Google Scholar] [CrossRef] [PubMed]
- Gea-Banacloche, J. Collapse and revival of the state vector in the Jaynes–Cummings model: An example of state preparation by a quantum apparatus. Phys. Rev. Lett. 1990, 65, 3385–3388. [Google Scholar] [CrossRef] [PubMed]
- Phoenix, S.J.D.; Knight, P.L. Establishment of an entangled atom-field state in the Jaynes–Cummings model. Phys. Rev. A 1991, 44, 6023–6029. [Google Scholar] [CrossRef] [PubMed]
- Sainz, I.; Björk, G. Quantum error correction may delay, but also cause, entanglement sudden death. Phys. Rev. A 2008, 77, 052307. [Google Scholar] [CrossRef]
- Chan, S.; Reid, M.D.; Ficek, Z. Entanglement evolution of two remote and non-identical Jaynes–Cummings atoms. J. Phys. B 2009, 42, 065507. [Google Scholar] [CrossRef]
- Agarwal, G.S. Vacuum-field Rabi splittings in microwave absorption by Rydberg atoms in a cavity. Phys. Rev. Lett. 1984, 53, 1732–1734. [Google Scholar] [CrossRef]
- Shen, L.T.; Chen, R.X.; Wu, H.Z.; Yang, Z.B. Distributed manipulation of two-qubit entanglement with coupled continuous variables. J. Opt. Soc. Am. B 2015, 32, 297–302. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden death of entanglement. Science 2009, 323, 598–601. [Google Scholar] [CrossRef] [PubMed]
- Kraus, B.; Cirac, J.I. Discrete entanglement distribution with squeezed light. Phys. Rev. Lett. 2004, 92, 013602. [Google Scholar] [CrossRef] [PubMed]
- Sornborger, A.T.; Cleland, A.N.; Geller, M.R. Superconducting phase qubit coupled to a nanomechanical resonator: Beyond the rotating-wave approximation. Phys. Rev. A 2004, 70, 052315. [Google Scholar] [CrossRef]
- Paternostro, M.; Son, W.; Kim, M.S.; Falci, G.; Palma, G.M. Dynamical entanglement transfer for quantum-information networks. Phys. Rev. A 2004, 70, 022320. [Google Scholar] [CrossRef]
- Paternostro, M.; Son, W.; Kim, M.S. Complete conditions for entanglement transfer. Phys. Rev. Lett. 2004, 92, 197901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Yang, G.H. Entanglement reciprocation between atomic qubits and an entangled coherent state. J. Phys. B 2006, 39, 5143–5150. [Google Scholar] [CrossRef]
- Hu, Y.H.; Tan, Y.G. Delaying disappearance of entanglement by the linear modulation of atom-field coupling. Phys. Scr. 2014, 89, 075103. [Google Scholar] [CrossRef]
- Xu, J.S.; Li, C.F.; Gong, M.; Zou, X.B.; Shi, C.H.; Chen, G.; Guo, G.C. Experimental demonstration of photonic entanglement collapse and revival. Phys. Rev. Lett. 2010, 104, 100502. [Google Scholar] [CrossRef] [PubMed]
- Eleuch, H.; Bennaceur, R. An optical soliton pair among absorbing three-level atoms. J. Opt. A 2003, 5, 528–533. [Google Scholar] [CrossRef]
- Eleuch, H. Autocorrelation function of microcavity-emitting field in the linear regime. Eur. Phys. J. D 2008, 48, 139–143. [Google Scholar] [CrossRef]
- Eleuch, H. Entanglement and autocorrelation function in semiconductor microcavities. Int. J. Mod. Phys. B 2010, 24, 5653–5662. [Google Scholar] [CrossRef]
- Sete, E.A.; Eleuch, H.; Ooi, C.R. Light-to-matter entanglement transfer in optomechanics. J. Opt. Soc. Am. B 2014, 31, 2821–2828. [Google Scholar] [CrossRef]
- Rafsanjani, S.M.H.; Eberly, J.H. Coherent control of multipartite entanglement. Phys. Rev. A 2015, 91, 012313. [Google Scholar] [CrossRef]
- Lawrence, J. Mermin inequalities for perfect correlations in many-qutrit systems. Phys. Rev. A 2017, 95, 042123. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Braunstein, S.L.; van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 2005, 77, 513–577. [Google Scholar] [CrossRef]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: Recent advances and current perspectives. J. Phys. A 2007, 40, 7821–7880. [Google Scholar] [CrossRef]
- Casagrande, F.; Lulli, A.; Paris, M.G. Improving the entanglement transfer from continuous-variable systems to localized qubits using non-Gaussian states. Phys. Rev. A 2007, 75, 032336. [Google Scholar] [CrossRef]
- Blanco, P.; Mundarain, D. Faithful entanglement transference from qubits to continuous variable systems. J. Phys. B 2011, 44, 105501. [Google Scholar] [CrossRef]
- Ballester, D. Entanglement accumulation, retrieval, and concentration in cavity QED. Phys. Rev. A 2009, 79, 062317. [Google Scholar] [CrossRef]
- Lee, J.; Paternostro, M.; Kim, M.S.; Bose, S. Entanglement reciprocation between qubits and continuous variables. Phys. Rev. Lett. 2006, 96, 080501. [Google Scholar] [CrossRef] [PubMed]
- Paternostro, M.; Kim, M.S.; Palma, G.M. Accumulation of entanglement in a continuous variable memory. Phys. Rev. Lett. 2007, 98, 140504. [Google Scholar] [CrossRef] [PubMed]
- Yönaç, M.; Eberly, J.H. Qubit entanglement driven by remote optical fields. Opt. Lett. 2008, 33, 270–272. [Google Scholar] [CrossRef] [PubMed]
- Yönaç, M.; Eberly, J.H. Coherent-state control of noninteracting quantum entanglement. Phys. Rev. A 2010, 82, 022321. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Evolution from entanglement to decoherence of bipartite mixed X states. Quantum Inf. Comput. 2007, 7, 459–468. [Google Scholar]
- Sete, E.A.; Svidzinsky, A.A.; Eleuch, H.; Yang, Z.; Nevels, R.D.; Scully, M.O. Correlated spontaneous emission on the Danube. J. Mod. Opt. 2010, 57, 1311–1330. [Google Scholar] [CrossRef]
- Sete, E.A.; Svidzinsky, A.A.; Rostovtsev, Y.V.; Eleuch, H.; Jha, P.K.; Suckewer, S.; Scully, M.O. Using Quantum Coherence to Generate Gain in the XUV and X-ray: Gain-Swept Superradiance and Lasing without Inversion. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 541–553. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.-T.; Shi, Z.-C.; Wu, H.-Z.; Yang, Z.-B. Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths. Entropy 2017, 19, 331. https://doi.org/10.3390/e19070331
Shen L-T, Shi Z-C, Wu H-Z, Yang Z-B. Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths. Entropy. 2017; 19(7):331. https://doi.org/10.3390/e19070331
Chicago/Turabian StyleShen, Li-Tuo, Zhi-Cheng Shi, Huai-Zhi Wu, and Zhen-Biao Yang. 2017. "Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths" Entropy 19, no. 7: 331. https://doi.org/10.3390/e19070331
APA StyleShen, L.-T., Shi, Z.-C., Wu, H.-Z., & Yang, Z.-B. (2017). Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths. Entropy, 19(7), 331. https://doi.org/10.3390/e19070331




