3.1. Entropy
Entropy, in the statistical sense pioneered by Boltzmann, may be understood very generally in terms of the distinguishability of objects described at two different levels of detail, one regarded as fine, and the other regarded as coarse. The prototypical application of this idea occurs in statistical thermodynamics, in which the fine level of detail for a system, such as a fixed quantity of ideal gas, is described in terms of microscopic data, such as the positions and momenta of individual molecules, while the coarse level of detail is described in terms of macroscopic data, such as pressure, volume, and temperature. Each possible choice of macroscopic data defines a coarse description of the system, called a macrostate, while each possible choice of microscopic data defines a fine description, called a microstate. Each macrostate generally corresponds to many different microstates, since many different choices of microscopic data may be approximated by identical macroscopic data. The entropy of a macrostate measures the quantity of corresponding microstates in a manner that is additive for composite systems. In more general terms, objects distinguishable at some fine level of detail may be indistinguishable at some coarser level, and a notion of entropy may be associated with the two levels to quantify this difference in distinguishability. In particular, generalizations of Boltzmann entropy such as Gibbs, Shannon, and Rényi entropies fall under the same conceptual umbrella. Measures of entropy familiar in ordinary quantum theory, such as von Neumann entropy, are less relevant, since they depend on specific algebraic apparatus less general than the path summation approach.
In statistical thermodynamics, the
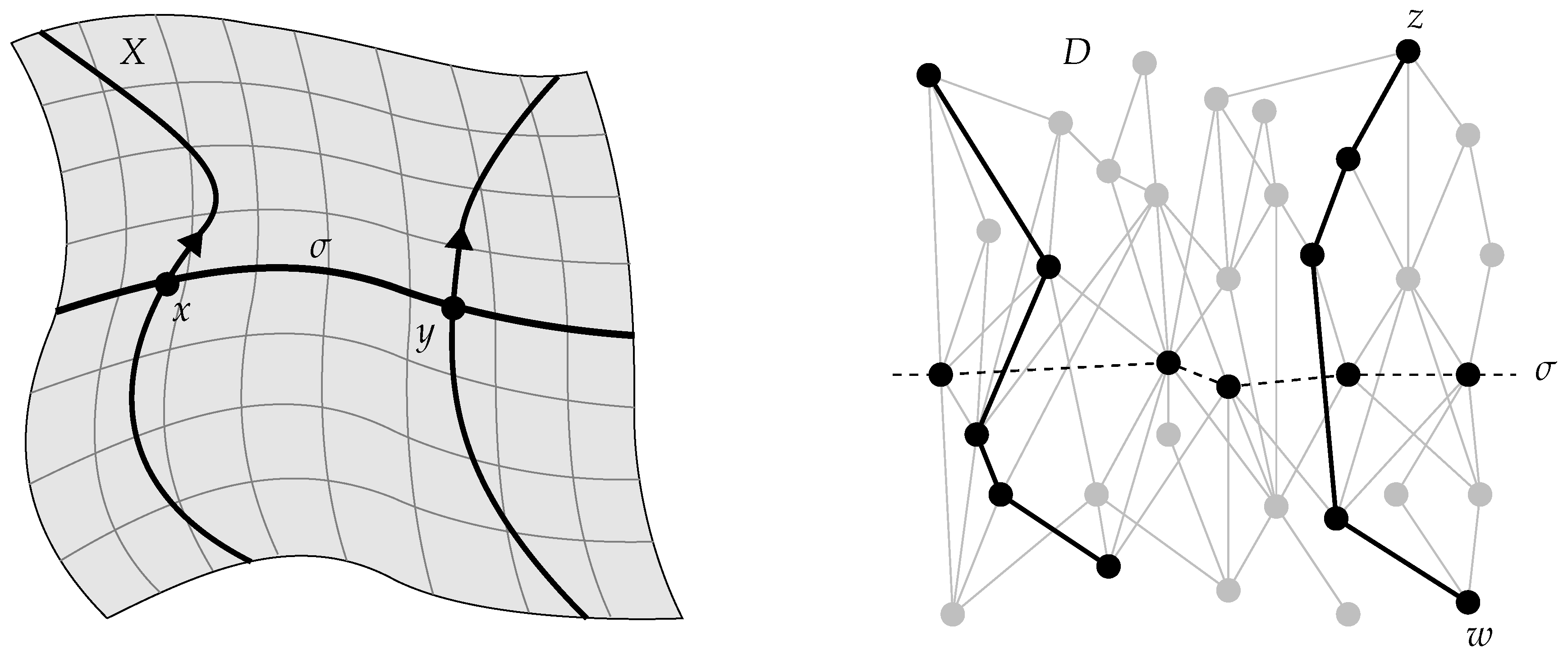
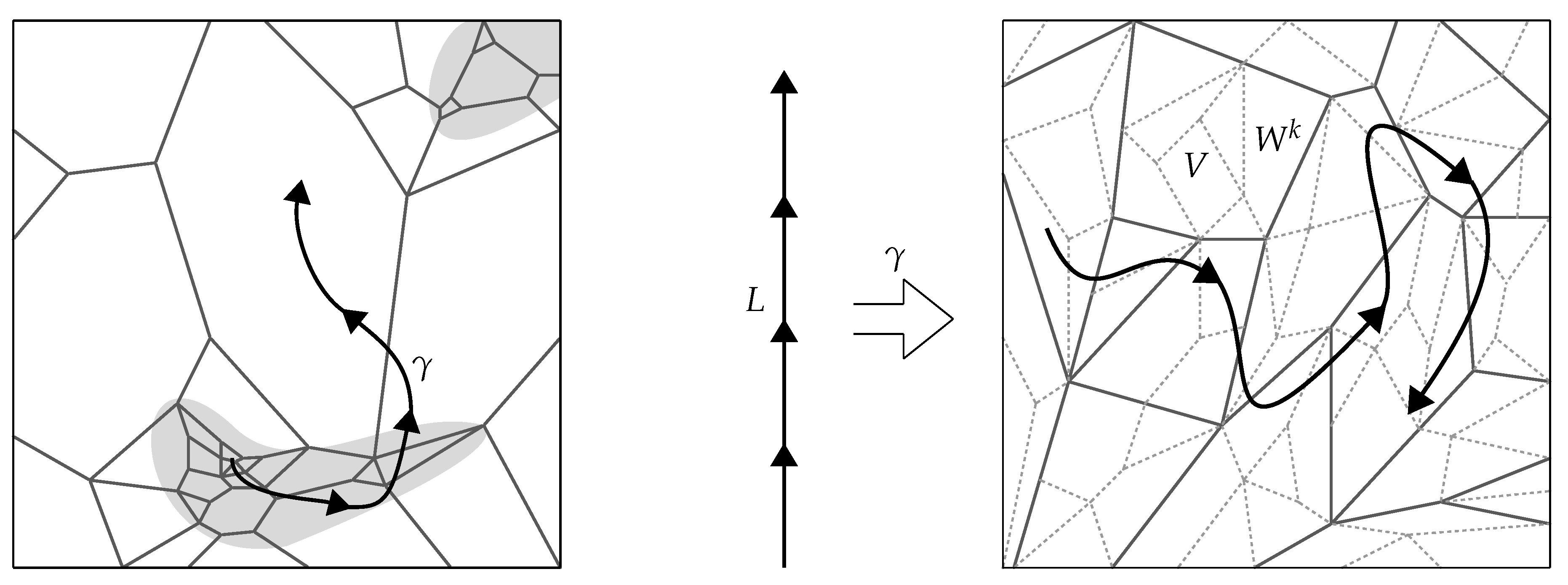
state space for a system is an abstract space parameterizing the set of possible microstates of the system for some choice of fine detail. A choice of coarse detail partitions state space into a family of subsets representing the possible macrostates of the system, where the points of each subset parameterize the microstates associated with the corresponding macrostate. Such a partition is called a
coarse-graining of the state space. The left-hand diagram in
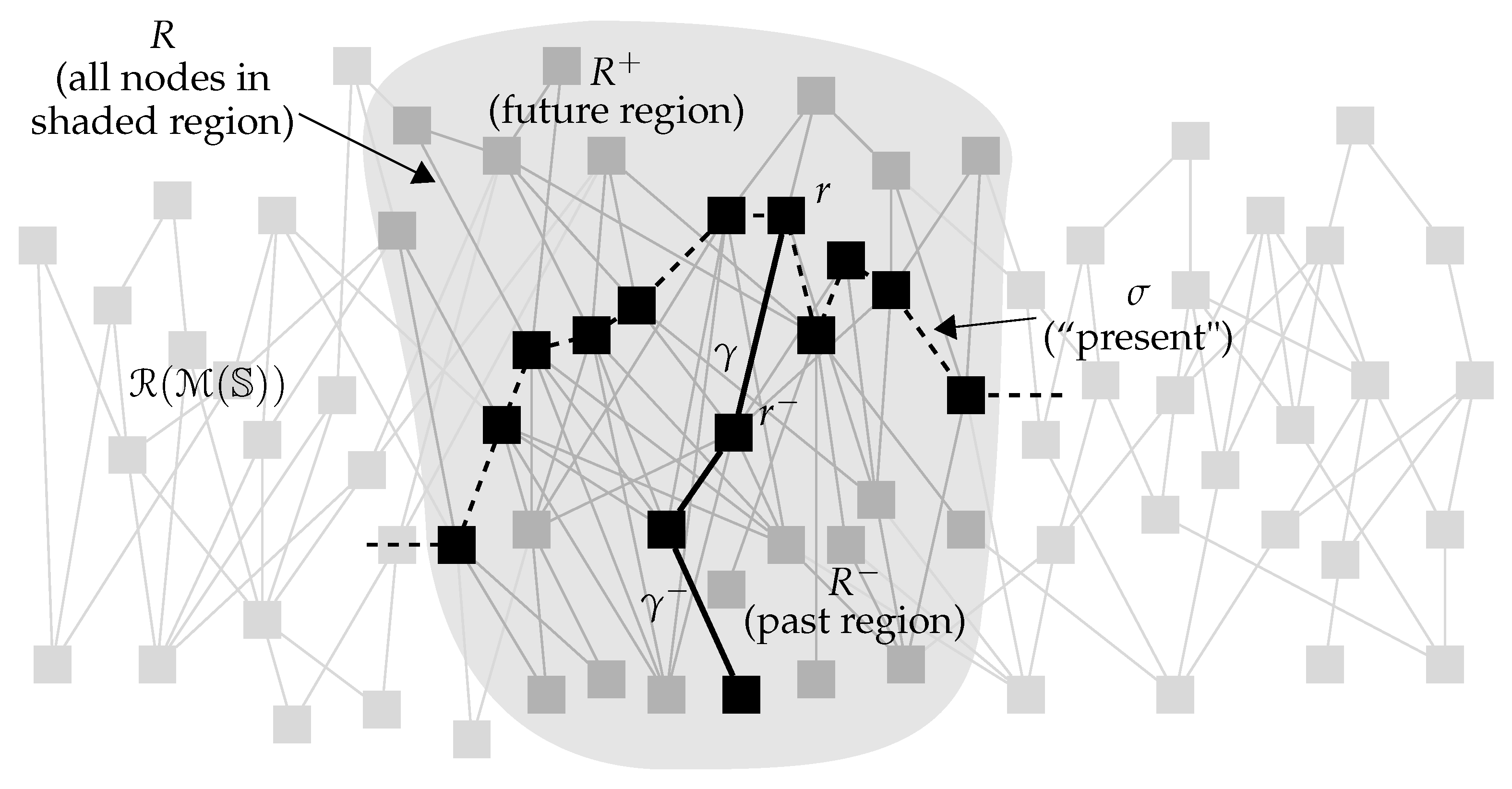
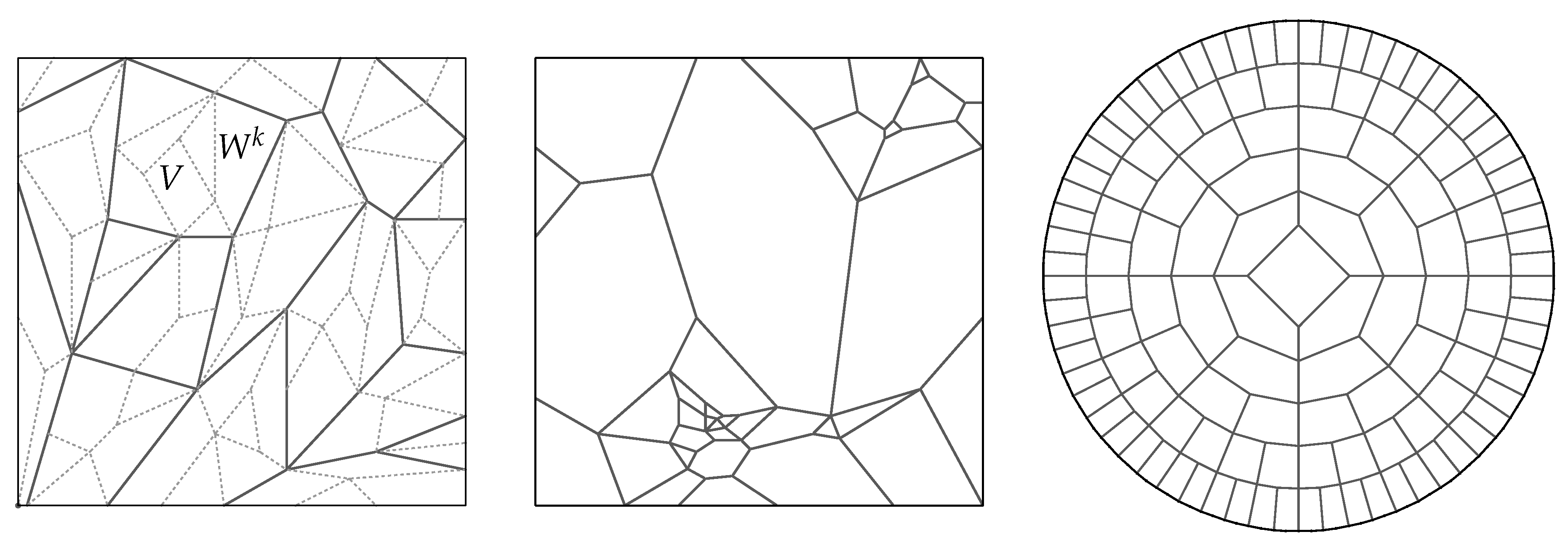
Figure 11 illustrates such a coarse-graining, where the
cells representing macrostates are separated by solid lines. Dotted lines and labels are explained below. Such a planar diagram could be interpreted literally as encoding the possible position and momentum of a single particle moving in one real dimension, but all such diagrams in this paper are schematic. Conventional state spaces are real manifolds, and therefore exhibit notions of proximity, volume, and other topological and metric structure. However, their dimensions are typically quite large, and this implies properties that are not well-represented by planar diagrams; for example, each region typically has very many neighbors. Even in 24-dimensional Euclidean space, each sphere in the regular packing induced by the Leech lattice is tangent to
neighbors; one may imagine the situation in
-dimensional space. Abstract metric-related ideas remain useful for describing the properties of discrete causal state spaces, but planar diagrams only roughly represent these notions.
Generalizing the thermodynamic picture, any set
S of objects may be partitioned into a family of subsets
P, where the objects belonging to each subset are regarded as equivalent at a coarse level of detail. More generally still, one may consider a strictly partially ordered family
of partitions
of
S for some index set
A, where by definition
if
and if every member of
is a union of members of
. In this case,
is called a
refinement of
. Here, ≺ does
not represent causal structure, and superscript indices are used to distinguish information filtering from mere enumeration. One may define equivalence relations
on
S for each
in
A, where
if
s and
belong to the same subset under
. If
, then
induces a
quotient partition of the quotient set
in an obvious way. Any such choice of
and
may be used to define notions of coarse and fine detail. Returning to
Figure 11 in this more abstract setting, the large regions bordered by solid lines in the left-hand diagram represent a choice
of coarse detail for a set
S, while the small regions bordered by dotted lines represent a choice
of fine detail. Here,
and
each partition
S into subsets of roughly equal size, but a typical coarse-graining in conventional thermodynamics exhibits vast differences in the sizes of regions, and correlations exist involving proximity and size. The middle diagram in
Figure 11 illustrates such a coarse-graining. As emphasized by Penrose [
44], such details are crucial for understanding whether a typical system can be expected to exhibit a systematic increase in entropy. For example, the right-hand diagram in
Figure 11 illustrates a state space that induces an “inverse second law of thermodynamics”, in the sense that a typical path in this space moves from larger to smaller cells. If
, and if each member of
is a
finite union of members of
, then one may define multiplicities and entropies via counting: if
is a member of
, and if
for members
of
, then the multiplicity
of
V is
K, and the entropy
of
V is
. The choice of notation for
and
is intended to emphasize the relative viewpoint: multiplicities and entropies are properly understood in terms of
natural relationships between levels of detail, not in terms of any specific level of detail. For the set
V shown in the left-hand diagram in
Figure 11, the entropy is
, since
subdivides
V into seven regions. In more general settings, it may be necessary to measure the sizes of members of
via some measure
other than the counting measure.
Definition 11. An entropy system consists of a set S, a set of partitions of S for some index set A, strictly partially ordered by refinement, and a family μ of measures on the quotient sets , one for each relation in Π. Each such relation induces an entropy quadruple . The entropy of a member V of is , where is the image of V under the quotient map , and where is understood to mean ∞.
It is often convenient to denote an entropy quadruple by just
S, or to write
to indicate that a set
S is equipped with such a structure. The functions
are taken to be measures here for simplicity, but the situation could be generalized further. In particular, the target object of
need only be a totally ordered set. One may also abstain from using logarithms to “rescale”
. However, it suffices here to consider only the counting measure on a finite set or the Lebesgue measure on a finite-dimensional real manifold, and logarithms are useful for producing quantities that are additive for composite systems. The reason for using “
e” instead of the familiar “
h” for entropy is because “
h” is used here to represent co-relative histories.
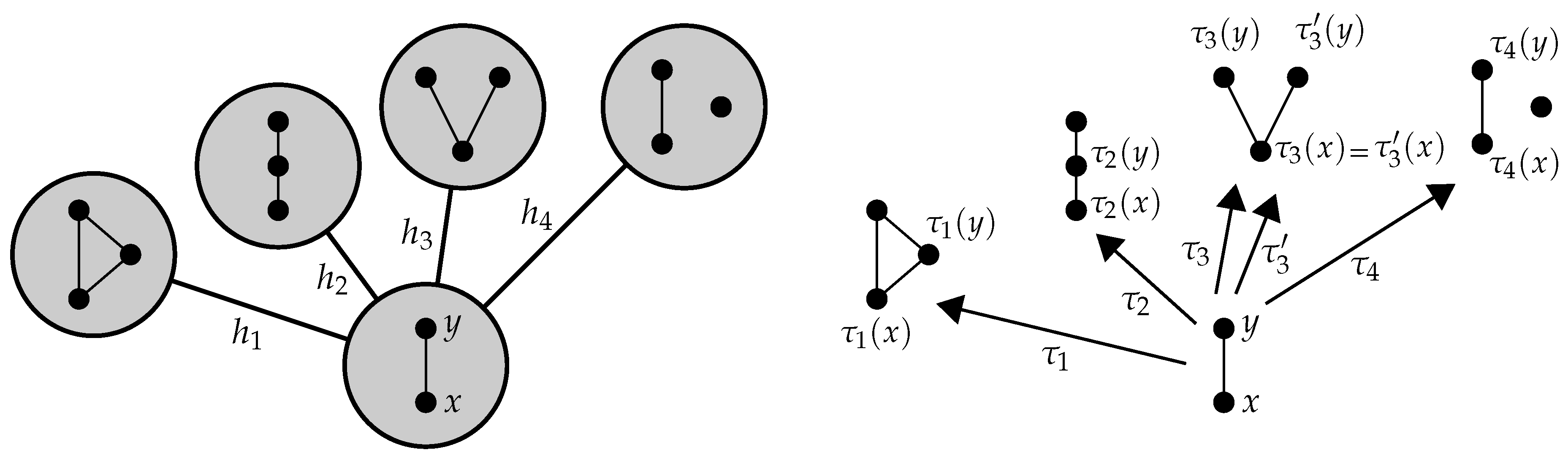
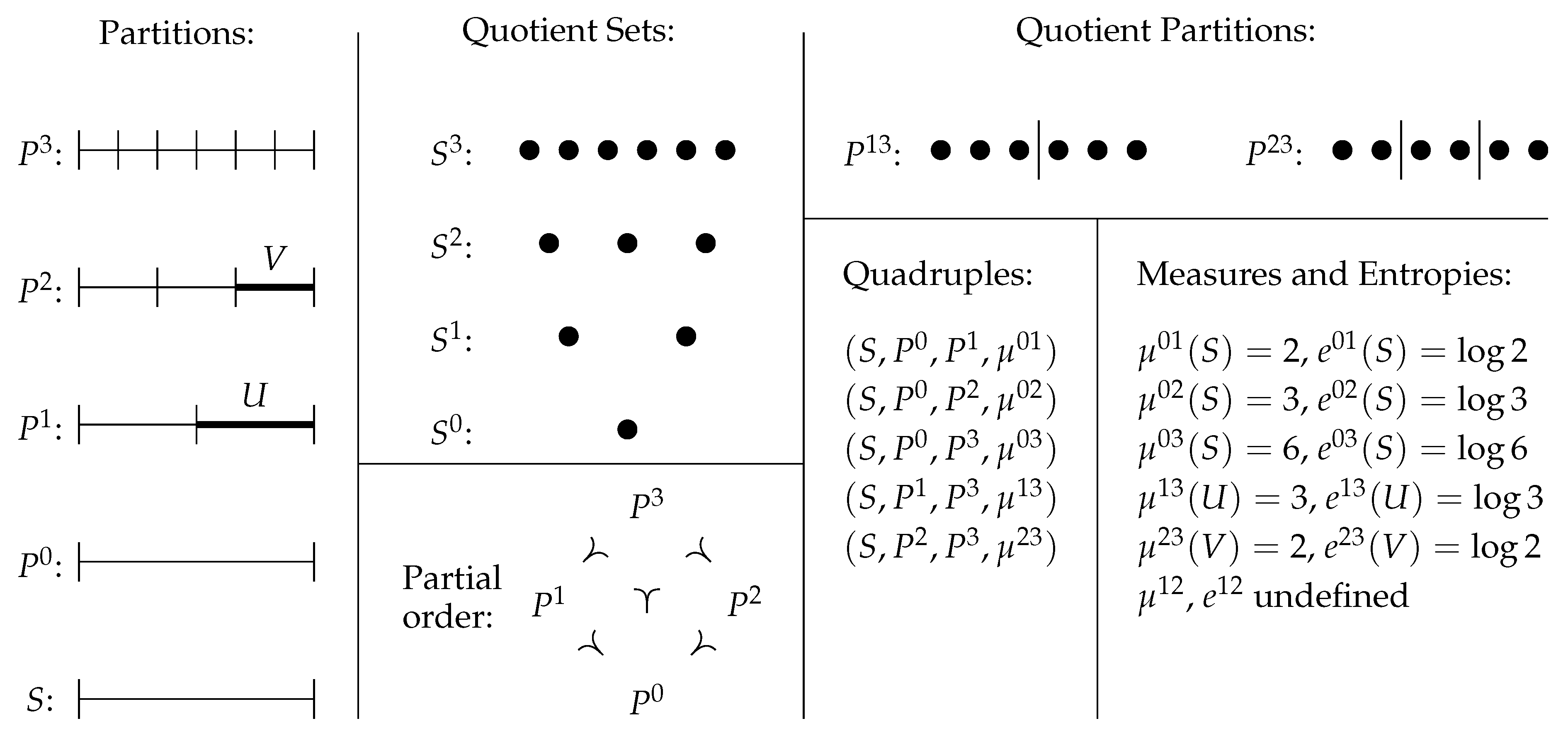
Figure 12 illustrates a simple entropy system
whose underlying set
S is the unit interval
in
. The set
of partitions of
S has members
,
,
, and
, which subdivide
S into segments of equal lengths 1,
,
, and
, respectively.
is the trivial partition, under which
S represents a single macrostate. The strict partial order ≺ on
consists of five individual relations
,
,
,
, and
, each of which induces an entropy quadruple. The quotient sets
,
,
, and
have 1, 2, 3 and 6 elements, respectively. There are two nontrivial quotient partitions,
and
, which subdivide the quotient set
into equal-sized subsets with 3 and 2 elements, respectively. Multiplicities and entropies of some representative subsets of
S with respect to different entropy quadruples are also listed. For example, the subset
of
S has measure
and entropy
with respect to the entropy quadruple
.
The motivation for adopting such a general viewpoint is that multiple “levels” of entropy are evident in discrete causal theory. An important example involves the
nth-degree terminal states
mentioned in
Section 2.4 and formally introduced in Definition 13. Given two directed sets
D and
, it may be the case that
and
are isomorphic, while
and
differ. In this case,
D and
are indistinguishable at the level of detail specified by the index value
n, but become distinguishable at the finer level of detail specified by the index value
. On the level of individual elements, two elements
x and
y belonging to a subobject
of a directed set
D may be “locally indistinguishable”, in the sense that they are interchanged by an automorphism of
, but may be “globally distinguishable”, in the sense that no such automorphism extends to an automorphism of
D. More generally, one may consider chains of subobjects
containing
x and
y, some of which possess automorphism groups interchanging
x and
y, and some of which do not. Of obvious interest is the case in which
is a low-order terminal state of a history, and
for
are progressive “thickenings” of
.
While entropy is defined by associating entire families of “fine” states with individual “coarse” states, it is sometimes interesting to compare the amount of detail encoded by specific pairs of states. It is then natural to relate such “local comparisons” to the “global comparisons” leading to entropy systems. In this context, one need not distinguish a priori between macrostates and microstates; states are defined individually by specifying varying degrees and types information about an object or system, and are then compared and categorized. Given two such states and , it is sometimes possible to unambiguously identify as more detailed than , or vice versa. In other cases, and are incomparable, in the sense that contains more of one type of information, while contains more of another. In this setting, one may recognize a natural partial order ≺ on the family of states under consideration, where if and only if is unambiguously more detailed than . This type of partial order is different from the partial orders on sets of partitions in Definition 11, but the two types of structure are related. For example, given an entropy quadruple , the set is a subset of the power set of all subsets of S. The relation means that every member V of is a union of members W of . One may define an induced relation on , also denoted by ≺, where if and only if V is a proper superset of W. Hence, a single relation between two partitions induces a partial order on a corresponding family of subsets. This partial order is of a special type, with maximal chain length 1, because its only relations are those of the form for and such that . However, one may easily define partially ordered sets with longer chains by considering sequences of partitions
Working in the opposite direction, one may begin with a partial order ≺ on an arbitrary set
. Here,
is viewed as an abstract analogue of a family of states encoding various types and quantities of detail, while ≺ is viewed as an abstract analogue of the partial order relating pairs of states
and
whenever
is unambiguously more detailed than
. One may partition
into a family of antichains
with respect to ≺. There are generally many different choices of partition, each analogous to a frame of reference in relativity. In the entropic setting, elements of a given antichain
are viewed as abstract analogues of states sharing an equal level of detail. In the simplest case, the antichains
“foliate”
, in the sense that each nonextremal antichain
has an unambiguous maximal predecessor
and minimal successor
. More generally, the antichains
form a partially ordered family. In either case, the partition defines an
atomic decomposition of
with respect to ≺, an idea revisited in a different context in
Section 3.3. In many cases, detail may be quantified in a variety of different ways, and this leads to the consideration of families
of partial orders on
. Such families are themselves partially ordered via the order-theoretic version of refinement, under which
precedes
if and only if
whenever
. An antichain with respect to
is then automatically an antichain with respect to
, so any partition of
induced by
refines at least one such partition induced by
. In this manner, the partial ordering by refinement of the family of partitions induced by
respects the partial ordering on
itself. Hence, entropy systems defined in terms of such partitions automatically respect the order-theoretic structure of
.
3.3. Discrete Causal State Spaces
In statistical thermodynamics, microstates are determined by information up to first order, e.g., by positions and momenta of individual molecules. Such information, together with the dynamical laws of classical mechanics, is sufficient to recover higher-order information; one may uniquely evolve a given state “backward in time”. Hence, if two states are indistinguishable up to first order, then they are
absolutely indistinguishable. In discrete causal theory, the situation is different. The analogue of information up to first order in a finite acyclic directed set
D is its first-degree terminal state
, which consists of all maximal elements of
D, all relations terminating at these elements, and all initial elements of these relations. Knowledge of
generally does not enable recovery of
D. One may propose a choice of classical dynamics implying such a relationship for very special classes of directed sets, for example, by abstracting the Einstein–Hilbert action from general relativity, which takes the form
in the simple vacuum case with zero cosmological constant. Here,
g is a Lorentzian metric on a 4-dimensional manifold
X,
R is the curvature scalar arising from the metric connection,
G is Newton’s gravitational constant, and
c is the speed of light. Yet despite interesting efforts in this direction, for example, in causal set theory [
45,
46,
47], such a strategy is dubious due to the amount of geometric structure taken for granted in relativity. Geometric data such as metrics and curvature, and even “pre-geometric” data such as dimension and topology, are emergent notions in discrete causal theory. Action functionals in this context must be defined more fundamentally, and cannot be expected to produce straightforward analogues of deterministic, time-symmetric Euler–Lagrange-type equations that uniquely determine classical dynamics via information up to first order. In particular, elements of a directed set
D that are indistinguishable up to first order, i.e., permuted by an automorphism of
, may be
distinguishable when one considers higher-order information. It is therefore necessary to consider higher-degree terminal states in what follows. The form of Equation (
4) does assume that first-order information suffices at the level of kinematic schemes, in the sense that the phase of an arbitrary co-relative kinematics is the product of the phases of its individual co-relative histories. This picture may be generalized without leaving the general framework of path summation, but such generalization is not undertaken here. In any case, the latter phases do generally depend nontrivially on information above first order in the corresponding cobases and targets.
The simplest discrete causal analogues of familiar thermodynamic state spaces are
nth-order state spaces , whose elements represent isomorphism classes of countable star finite acyclic directed sets
with maximal chain length
n. Equivalently,
is a nonempty antichain. It is useful to preface formal definitions involving
with some informal remarks. First, while the notion of order identifying a state
as a member of
is intrinsic to
itself, the desired interpretation of
is as a terminal state of a history
D, containing information encoded by chains of length at most
n terminating at maximal elements of
D. Second, it is usually impossible to choose a member of
that includes
all such information for
, because chains of length at most
n terminating at different maximal elements of
D may intersect to produce longer chains, thereby defining a higher-order state. One might consider re-defining
to include such states, requiring only that each element be connected to a maximal element by at least one chain of length at most
n. In physical terms, such states are still composed of elements exerting “recent influence”, but may contain chains of arbitrary length. However, such a definition would not be ideal for the desired applications. For example, it would allow any countable star finite acyclic directed set in which all chains are bounded above to be converted to a member of
or
by adding new relations terminating at new maximal elements, thereby flouting the intuition that low-order states should be “causally simple”. It is preferable to define a separate notion called
degree, which facilitates the definition of terminal states containing all information up to a given order in a particular history. Following this idea, Definition 13 introduces special states
, called
nth-degree terminal states, which include all information encoded in chains of length at most
n terminating at a maximal element in
D. Third, as mentioned in
Section 2.4, the distinction between order and degree does not arise for
; the first-degree terminal state
of
D automatically belongs to
. Fourth, the
nth
superset microstates introduced in Definition 18 are constructed by adding
n “prehistorical” elements to a state, which may not increase its maximal chain length at all. These subtleties reflect the fact that more than one natural-number grading is useful in studying discrete causal state spaces.
It is useful to define terminal states in terms of transitions between pairs of histories, using the relative viewpoint. Though the ultimate goal is to use information encoded in terminal states to assign phases to sequences of co-relative histories, i.e., co-relative kinematics, the states of principal interest in studying a given co-relative history are typically not those induced by transitions representing h. This is because the “physically new” structure associated with and is more meaningful than whatever structure h “adds to” to produce . For example, each co-relative history in adds only one element to , so most of the physically new structure in is typically already present in . Yet what one is really interested in is whether or not the physically new structure in is “more favorable” than the physically new structure in ; i.e., one wishes to compare terminal states of and . These may be defined in terms of auxiliary transitions that are determined by h, but do not represent h under Definition 9. First, however, one must define terminal states associated with arbitrary transitions.
Definition 12. Let be a transition of acyclic directed sets. The subobject of consisting of all elements of , all relations terminating at such elements, and all initial elements of such relations, is called the terminal state of τ. If is a nonempty antichain, then the order of is n.
Despite the relative nature of Definition 12, it is convenient to refer to as a terminal state of the target set in many cases. does not include relations between elements of ; it includes only relations that are “new” with respect to . If the context is expanded to include cycles, a different definition of order is necessary. For example, one may define to be the maximal length of non-self-intersecting chains in . Here, however, I focus almost exclusively on the acyclic case. Any directed set is itself the terminal state of the unique transition . This transition may be denoted by when the choice of target set is obvious. As mentioned above, is useful to define special terminal states that encode all information up to order n in a given history.
Definition 13. Let D be an acyclic directed set in which every chain is bounded above.
- 1.
The nth-degree terminal state of D is the subobject of D consisting of all elements connected to a maximal element of D by a chain of length at most n, together with all relations in such chains.
- 2.
The nth-degree initial state of D is the subobject of D constructed by deleting all non-minimal elements of from D, together with all relations in D terminating at such elements.
- 3.
The nth-degree transition associated with D is the inclusion map .
The boundedness hypothesis in Definition 13 is included to rule out situations in which D has maximal elements but also has chains “extending to infinity”, since it is awkward to exclude such chains from consideration when studying terminal behavior. Such histories are not considered here.
Definition 14. The nth-order state space is the set of all isomorphism classes of countable star finite acyclic directed sets Δ such that is a nonempty antichain. The finite-order state space is the disjoint union , and the (total, countable, acyclic) state space is the set of all isomorphism classes of countable acyclic directed sets, which may be viewed as limits of sequences in .
Since the elements and relations in a member
of
are assumed to possess no internal structure, one might expect
to be treated as a microstate. However, since discrete causal theory does not rule out the dynamical relevance of information above order
n at the level of individual histories, data describing how
might fit into a larger history can be important in determining future behavior influenced by
. Such data defines an even finer level of detail than
itself, permitting
to be viewed as a macrostate. Ambiguity regarding the status of
is not surprising, due to the relative nature of entropy.
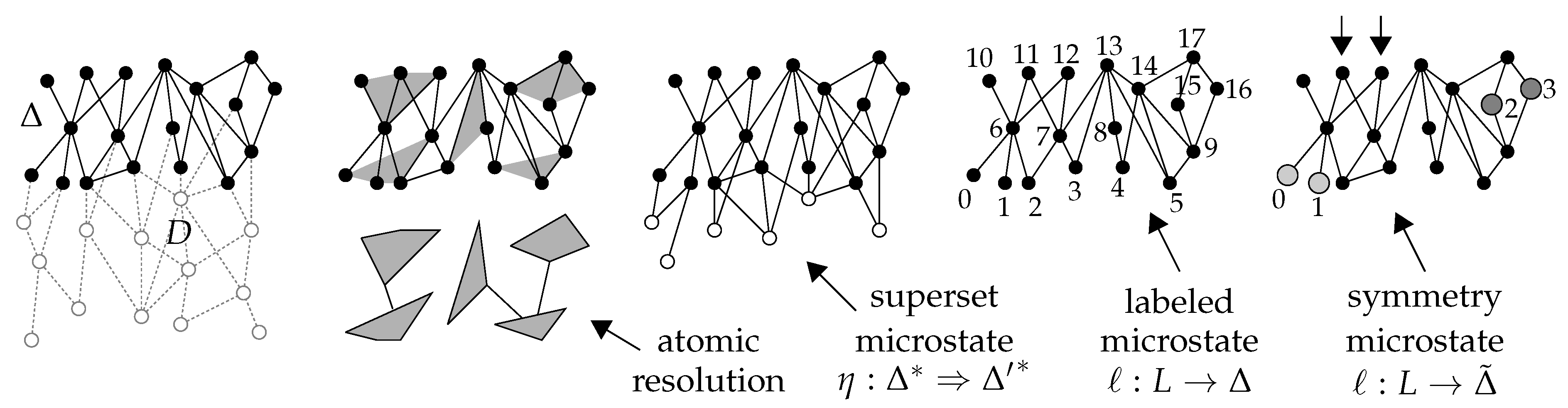
Figure 14 illustrates four different methods of defining coarse and fine levels of detail using
. Informal discussion of these methods then precedes formal treatment in Definition 15. The first diagram shows a third-order state
embedded in a history
D. In this case,
does not contain all the third-order information in
D; in particular, it is
not the third-degree terminal state
of
D. The second diagram illustrates one way to treat
as a microstate, called a
resolution microstate, by approximating its structure via the method of
causal atomic resolution, introduced in [
14]. This method involves choosing special subsets of
, called
causal atoms, which serve as individual elements of a coarser directed set. Such a choice defines a
causal atomic decomposition of
. A sequence of such decompositions is a causal atomic resolution, with each subsequence defining “initial” and “terminal” levels of detail, and hence a notion of entropy. More generally, one may define partially ordered families of decompositions, also called resolutions, which induce entropy systems. The resolution in the figure involves a single decomposition, and hence just two levels of detail. Causal atomic resolution provides perhaps the most obvious discrete causal analogue of conventional coarse-graining. In particular, it involves actual approximation, meaning that the information contained in a causal atomic decomposition is not only incomplete, but also imprecise. However, there is generally no canonical choice of resolution for a given state, and different resolutions may be very dissimilar. Further, resolutions reaching far above the fundamental scale can produce objects that are obviously “too granular” to resemble physical spacetime. Members of
are usually treated as macrostates in this paper, but methods such as causal atomic resolution remain worthy of further study in more general entropic settings.
The third diagram in
Figure 14 illustrates the most obvious way to treat a member
of
as a macrostate, by adding “prehistory” to define larger states called
superset microstates. Different superset microstates of
impose different constraints on the family of histories of which
could be a terminal state. In particular, the superset
of
shown in the diagram is induced by the history
D. At a higher level of detail,
may itself be viewed as a macrostate, with its own superset microstates adding more prehistory. One may imagine “flipping over” this diagram to obtain a co-relative history
between the causal duals
and
of
and
, and this is how superset microstates are formalized in Definition 15. Hence, the convenient term “superset” is not quite precise, because co-relative histories involve equivalence classes. Naïve amalgamation of superset microstates produces a state space with an infinite number of elements in each cell, since one may always add more prehistory to a directed set. This leads a priori to infinite multiplicities and entropies for finite states. However, supersets adding “recent” data are expected to dominate dynamically, and families of superset microstates may be filtered to reflect this expectation. In the case of finite states, one may work with finite families of microstates defined in terms of numbers of elements and relations, lengths of chains, sizes of antichains, and similar quantities. Here, I focus on families defined via the number of prehistorical elements added to
. The quantity of superset microstates of a given type is decreased by symmetries of
, which render equivalent different subsets of
. This meshes with the intuition that high-entropy states should be “disordered”. For example, if
is an antichain of cardinality
K with automorphism group
, then there is only one way to add a single prehistorical element and
k relations to
for any
, since the terminal elements of these relations in
may be exchanged for any other
k elements of
under
. By contrast, there are
ways to add such an element and relations to
if
is trivial.
The fourth and fifth diagrams in
Figure 14 illustrate contrasting ways to treat a member
of
as a macrostate by focusing on its symmetries directly. Under the method illustrated in the fourth diagram, a microstate of
is simply a copy of
labeled via a map
, where
L is a set of consecutive natural numbers starting with zero, and where two labelings are regarded as equivalent if they are related by an automorphism of
. Such a microstate is called a
labeled microstate. The number of labeled microstates associated with a state
of cardinality
K ranges from 1 if
to
if
is trivial. This method agrees qualitatively with the superset approach in the sense that high-entropy states are those for which
is small. The method illustrated in the fifth diagram essentially reverses this relationship. Here, one begins with an arbitrary labeling
, where
is the subset of
not fixed by
. Automorphisms of
convert
ℓ to other labelings, each of which represents a
symmetry microstate. Such a microstate may be viewed as a “mode of symmetry breaking”, since it breaks the symmetries of
in a specific way. For a finite state
, the number of symmetry microstates is just
, so high-entropy states are those for which
is large. More generally, one may work with non-surjective
partial labelings that leave a subgroup of
unbroken. The labeling in the figure is of this type, since there remains an automorphism of
interchanging the elements indicated by arrows. The set of such partial labelings is partially ordered by extension, which is interesting from the perspective of state-specific detail discussed at the end of
Section 3.1. While it is counterintuitive to associate high entropy with symmetry, there are arguments for entertaining such possibilities. Symmetry is central to the theory of “elementary” particles, so certain special structures that are locally symmetric, at least at measurable scales, are favored by the actual dynamics of the physical universe. Such structures may be “attached” to underlying causal structure via auxiliary algebraic information, but the strong interpretation of the causal metric hypothesis demands an emergent description of both spacetime symmetries and internal symmetries. The most obvious way to satisfy this demand is to incorporate some type of symmetry data directly into Equation (
4). Notions of entropy associated with superset microstates and/or labeled microstates might accomplish a similar purpose, since their enumeration depends largely on symmetry considerations. Regardless of the type of entropy chosen, an attractive though speculative idea is that elementary particles might arise via
local entropic traps, whereby certain regular structures that are small by conventional measures but large compared to the fundamental scale might be very stable from an entropic perspective.
A mathematical result important in the study of superset microstates, labeled microstates, and symmetry microstates is Bender and Robinson’s proof [
37] that a typical acyclic directed set
D has trivial automorphism group, i.e., is
rigid. This result applies asymptotically under modest assumptions about the number of relations in
D. However, these assumptions fail to hold for a typical low-order terminal state
, since such a state has unusually large “spatial size” and small “causal size”, and typically lacks enough relations to “bind elements in place”. Hence,
is often nontrivial for such a state. The extreme case is a zeroth-order state, whose automorphism group is the entire symmetric group permuting its elements transitively. However, states tend to become increasingly rigid as their order increases. Bender and Robinson’s result enables rough enumerations of the number of high-order superset microstates and labeled microstates for a state
of a given cardinality. It also suggests a novel explanation for
why the details of the distant past seem to be irrelevant to future dynamics, namely, because relatively few additional generations of elements must be added to a typical low-order state to break most of its symmetries.
Definition 15. , , and may be used to define finer state spaces, for which their members are macrostates.
- 1.
The nth-order superset state space is the set of full, originary co-relative histories . where Δ is a member of and is a member of . Its elements are called superset microstates. The corresponding finite-order superset state space and (total, countable, acyclic) superset state space are defined in the obvious ways.
- 2.
The nth-order labeled state space is the set of complete labelings of members Δ of , where two labelings of Δ are considered to be equivalent if they are related by an element of . Its elements are called labeled microstates. The corresponding finite-order labeled state space and (total, countable, acyclic) labeled state space are defined in the obvious ways.
- 3.
The nth-order symmetry state space is the set of partial labelings of members Δ of induced by applying elements of to arbitrary initial labelings of the subsets of Δ not fixed by . Its elements are called symmetry microstates. The corresponding finite-order symmetry state space and (total, countable, acyclic) symmetry state space are defined in the obvious ways.
The spaces
,
, and
, together with their larger counterparts, offer many alternative notions of states at many different levels of detail, and induce a variety of entropy systems. The reason why the co-relative history
in the definition of
is not assumed to be proper is because it is sometimes convenient to view a state
as a superset microstate of itself, i.e., to take
to be the co-relative history represented by the identity morphism
. The “full” and “originary” conditions on
merely formalize the idea that
adds “prehistory” to
. It is sometimes convenient to refer to a superset
of
as a superset microstate of
if the choice of co-relative history
is clear from context, for example, if there is only one such co-relative history. Using this convention,
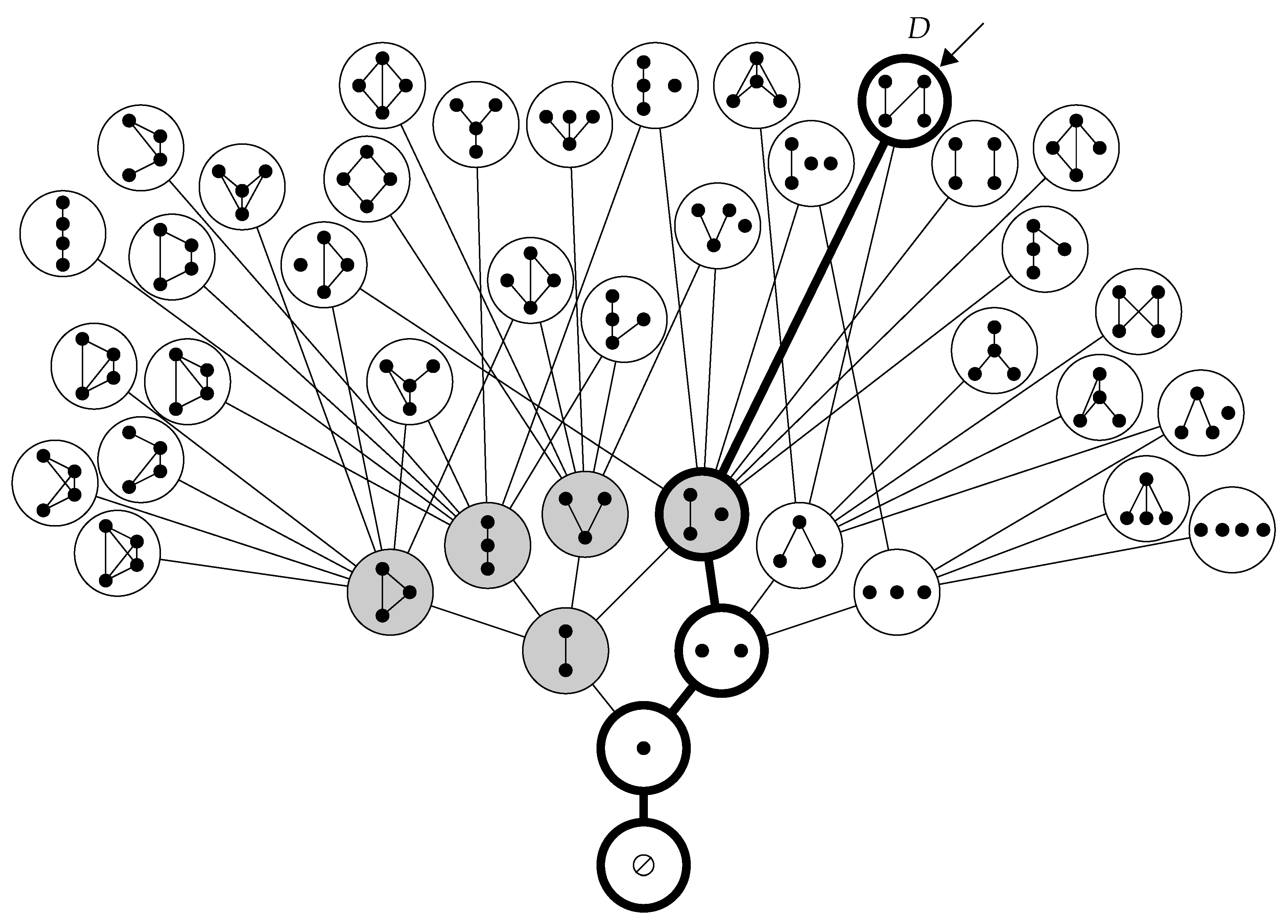
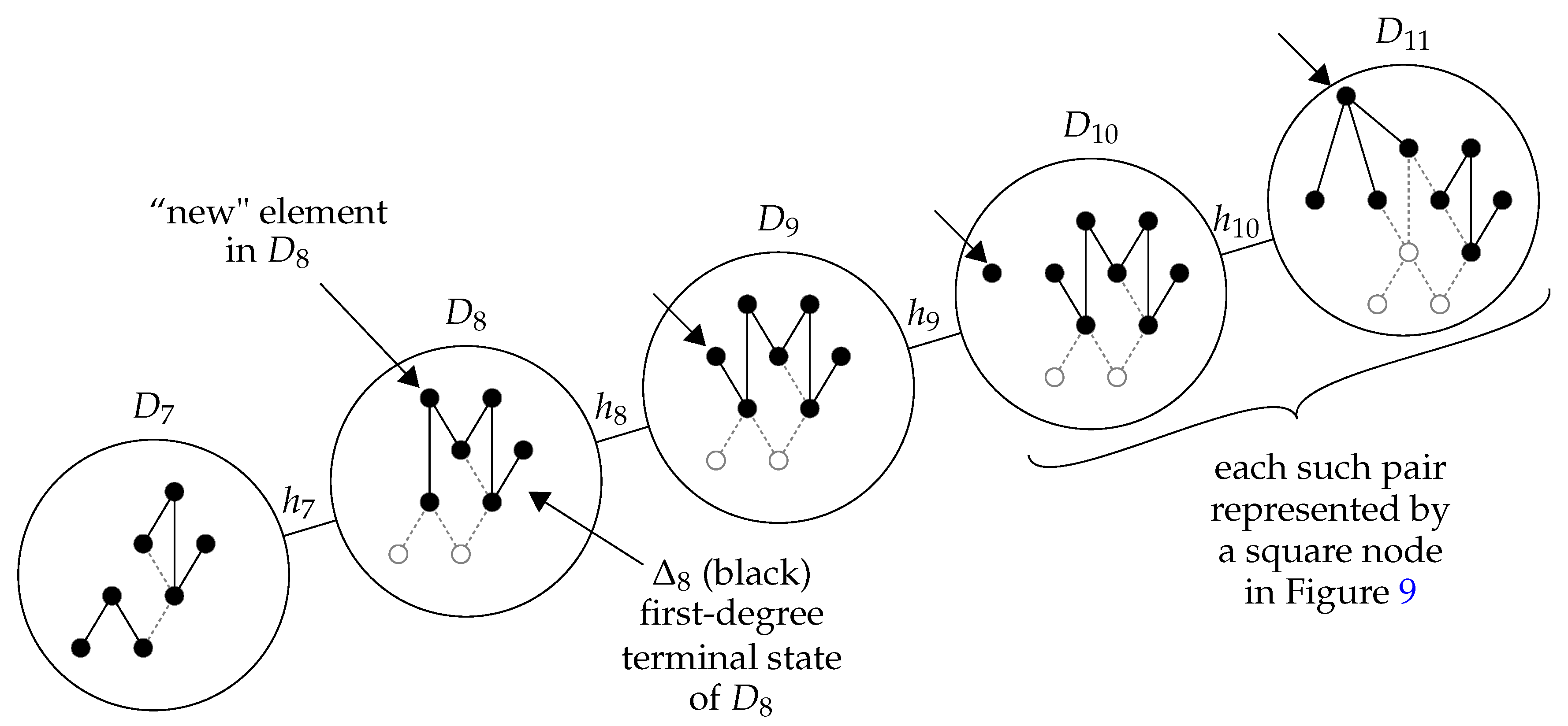
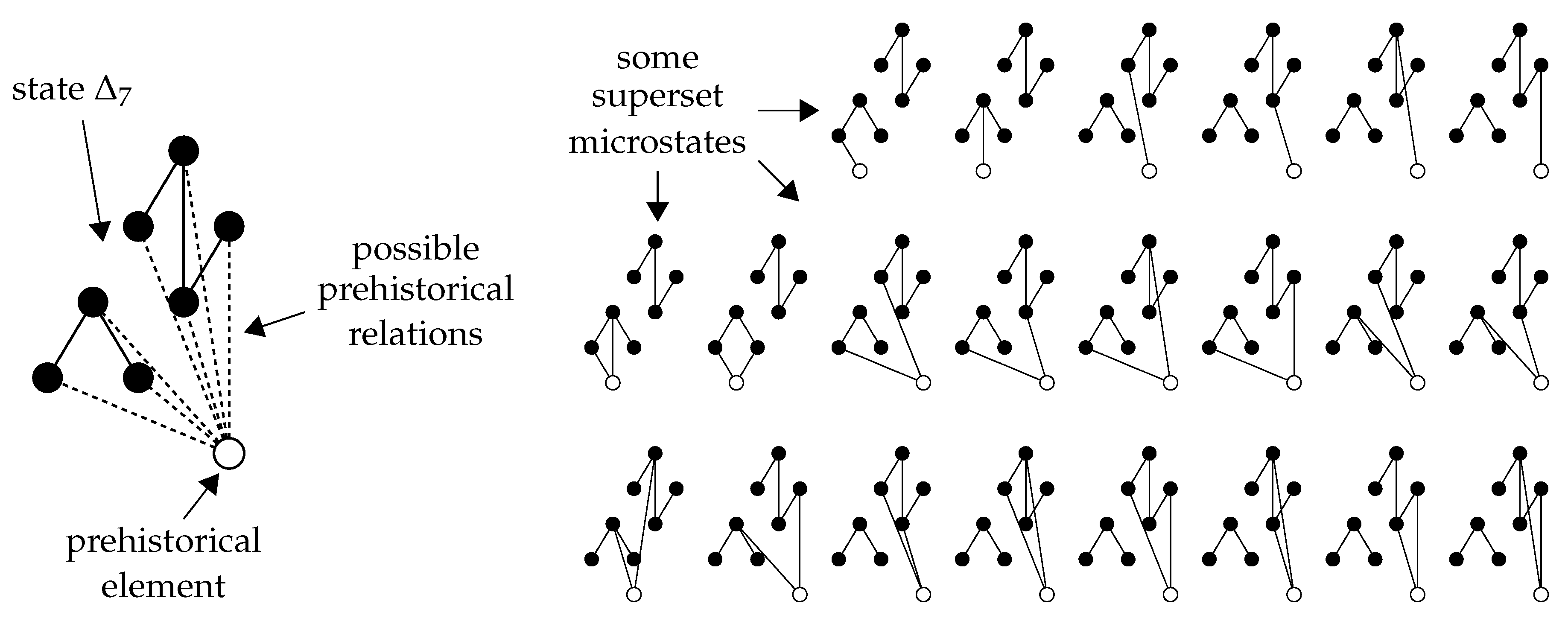
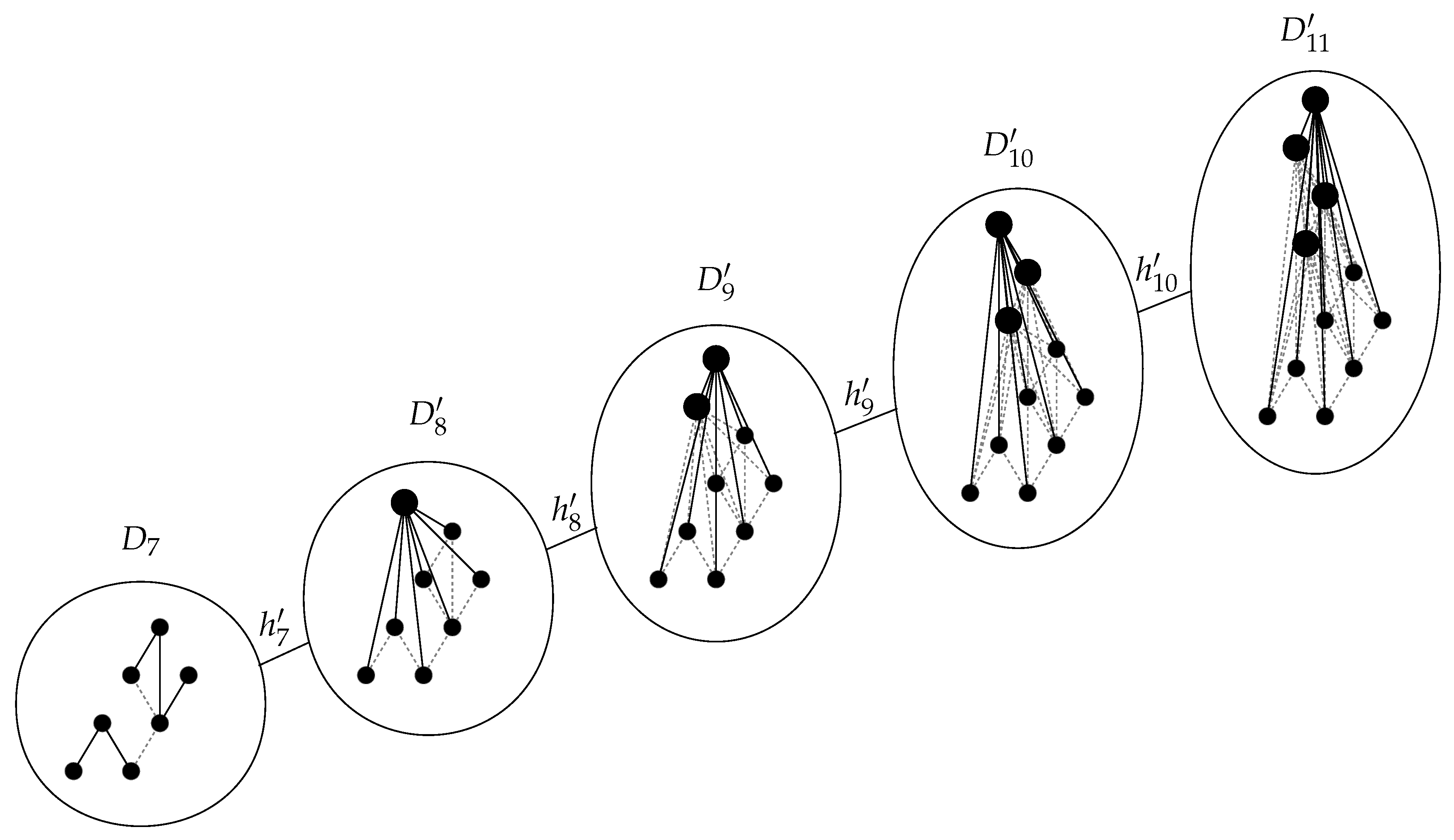
Figure 15 illustrates some of the superset microstates of the first-degree terminal state
appearing in the sequential growth process in
Figure 10. Each of these microstates is constructed by adding a single prehistorical element to
, along with a family of prehistorical relations. The 22 microstates shown in the figure each involve one or two extra relations. Overall, there are 96 such microstates, with between zero and seven extra relations.
For a state
of cardinality
K, the number of superset microstates adding a single element is “roughly”
, if one ignores the contribution of symmetries. This reflects the idea that one may choose any family of elements in
to be in the direct future of the single prehistorical element, since
is the sum of the binomial coefficients
for
. Nontrivial symmetries of
reduce this number; in particular, the number of superset microstates of the first-degree terminal states
to
in
Figure 10 are 96, 64, 72, 144, and 132. Ignoring symmetries need not yield exactly
microstates, due to a curious graph-theoretic phenomenon called
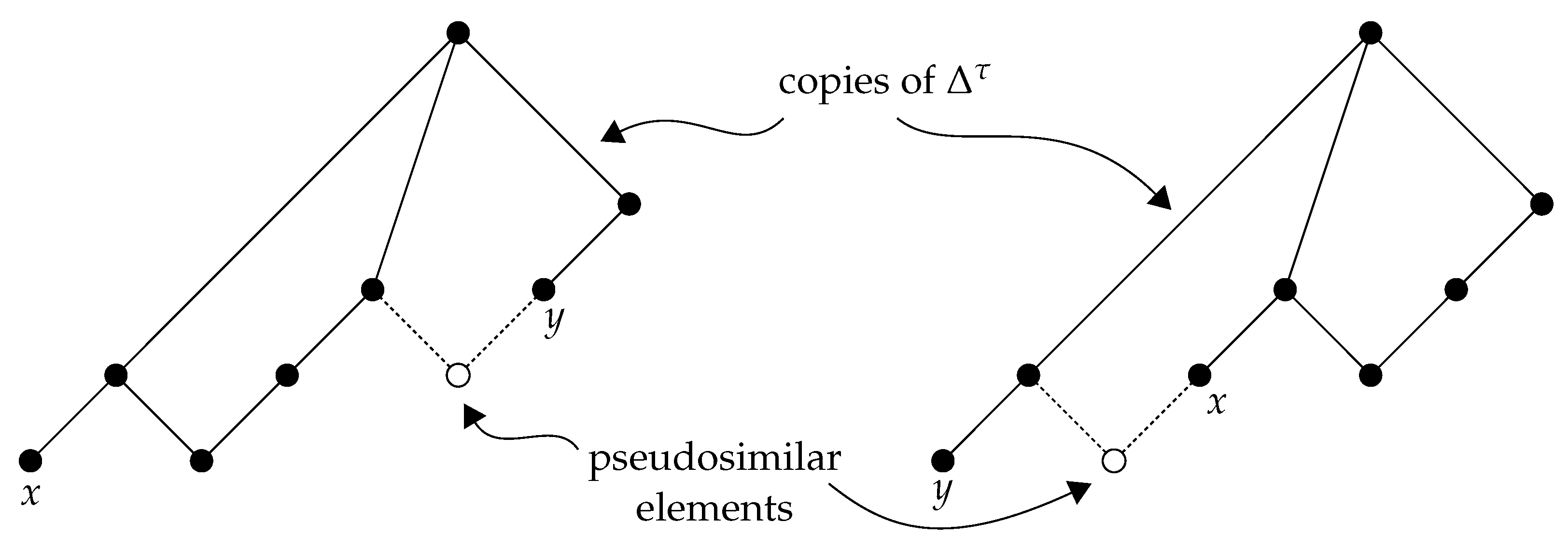
pseudosimilarity, whereby one directed set may be a terminal state of another in multiple distinct ways, even if the two sets differ by only a single element.
Figure 16 illustrates this subtlety via an example provided by Brendan McKay, in which augmenting two copies of a state
by a single prehistorical element in two different ways produces isomorphic supersets. The drawing emphasizes the latter isomorphism; the fact that the black nodes and edges represent two copies of the same state
may be seen by matching up the elements labeled
x and
y.
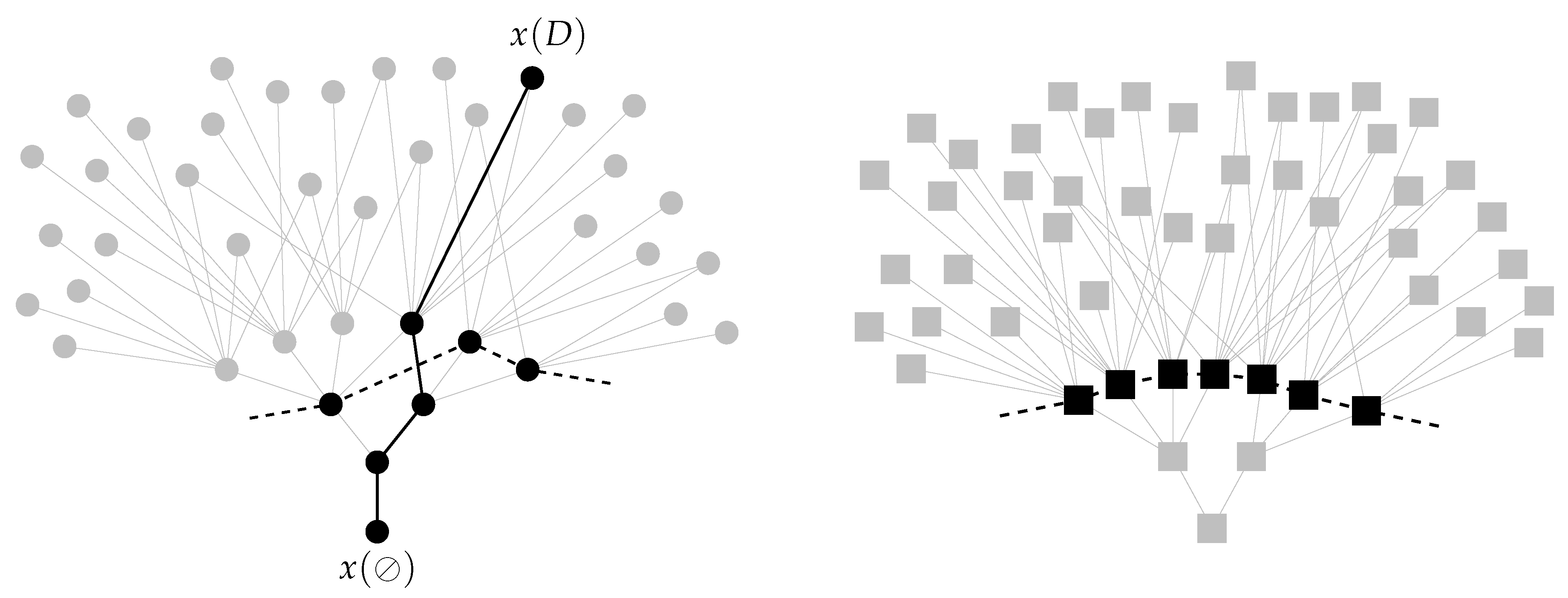
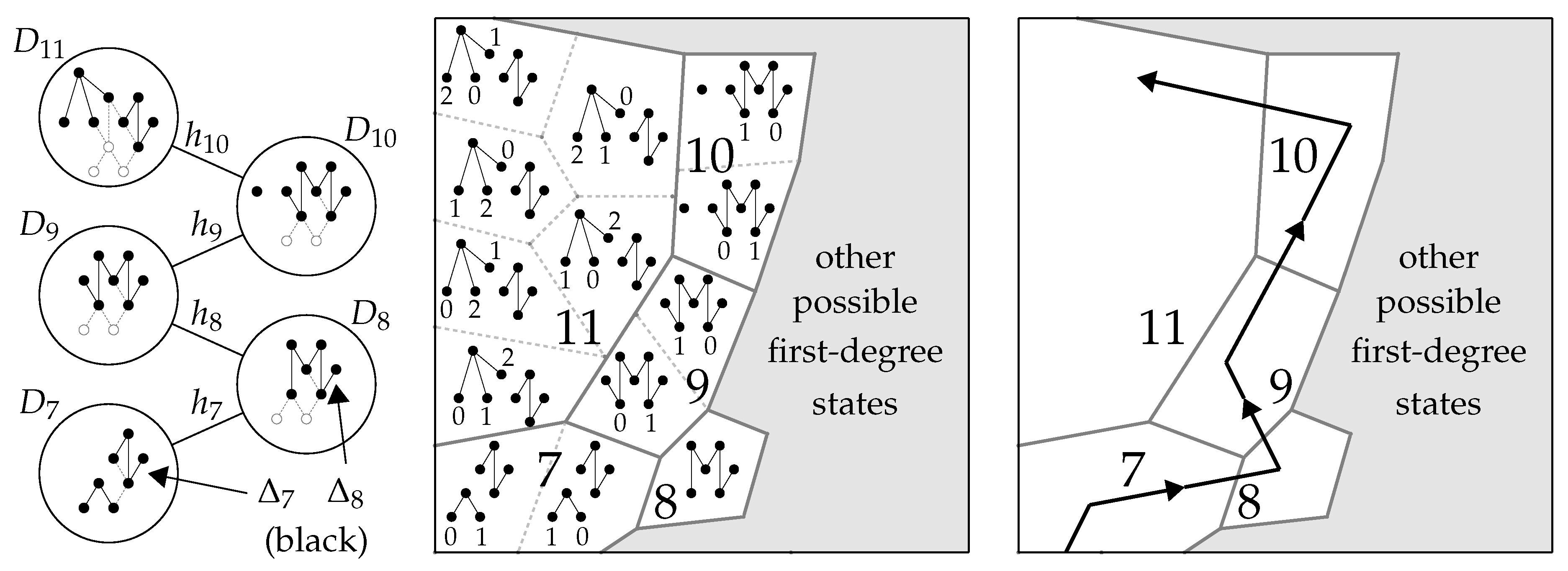
Figure 17 illustrates a small region of
whose macrostates are the first-degree terminal states
to
appearing in the sequential growth process from
Figure 10. The left-hand diagram reproduces this process. In the middle diagram,
to
are represented by large cells labeled 7 to 11, subdivided into smaller cells representing symmetry microstates. Because the histories
to
are rigid,
accurately reflects relative distinguishability properties between terminal states and their histories in this case, since every state symmetry is broken by its ambient history. The figure highlights the fact that symmetry microstates of a given terminal state are isomorphic as partially labeled directed sets, which raises the question of how they are distinct. The answer is that there are multiple ways to break the automorphisms of the original states involved, even though the resulting objects remain
isomorphic.
generally has “too many microstates” for terminal states of nonrigid histories, since it includes symmetry breaking information for symmetries that remain unbroken. This issue may be addressed by restricting the class of permissible labelings. The right-hand diagram represents the sequential growth process abstractly via a “curve” in
. Since
encodes information only up to first order at the level of individual histories, the entire curve is necessary to reconstruct the evolution of
. The corresponding regions of
and
are much too large and cluttered to illustrate here, but the basic structural aspects are similar.
Definitions 14 and 15 identify discrete causal state spaces as sets, but one may recognize additional “geometric” structure on these spaces defined in terms of discrete operations that convert one state to another. It is useful to define such operations for multidirected sets in general.
Definition 16. Let M and be multidirected sets. Elementary operations on such sets are defined as follows:
- 1.
Add or delete an isolated element.
- 2.
Add or delete a relation between two elements.
The absolute distance between M and is the minimal number of elementary operations required to convert M to , if this number is finite. Otherwise, .
Notions of distance between pairs of states facilitate useful analogues of familiar evolutionary ideas. For example, in conventional thermodynamics, one may ask why every system does not immediately transition to the cell in state space representing thermal equilibrium. The answer is that curves in state space are continuous in this context, so a typical system beginning far from thermal equilibrium must pass through a sequence of intervening macrostates before reaching it. Although literal continuity does not apply in the discrete causal context, similar ideas may be invoked whenever one can define notions of distance and neighbors. In particular, even if a given co-relative history is “favored” from a purely entropic perspective, it may be “costly” in the sense that it entails direct passage between widely separated regions of a discrete causal state space. Similarly, “short” paths between a given pair of states might be favored over “long” paths that involve drastic changes in structure. These ideas are revisited in
Section 4.2 in the context of spacetime expansion, and again in
Section 4.3 in the context of discrete causal action principles.
Alternative, relative notions of distance between pairs of directed or multidirected sets may be defined in terms of “ambient” structure from a configuration space. In the case of directed sets, such structure may originate from a kinematic scheme.
Definition 17. Let be a kinematic scheme, and let D be a member of in which every chain is bounded above. Let be the nth-degree terminal state of D, and let Δ be any other element of .
- 1.
The directed distance between and Δ in with respect to D is the minimal length of chains in , where .
- 2.
The undirected distance between and Δ in with respect to D is the minimal length of undirected paths in with initial element and terminal element , where .
The reason why and depend on a choice of D is because and may appear as terminal states of many different histories in . If , then it may be easier to reach a history with nth-degree terminal state from than from . The distinction between a chain and an undirected path is that chains respect the directions of relations in , while undirected paths generally do not. States close together in an undirected sense may be far apart in a directed sense, since undirected paths are more general than chains. Dependence on D implies that and are inherently asymmetric. It is reasonable to expect that and may closely approximate more conventional notions of distance for suitable classes of “large” directed sets, but this topic is not further explored here.
3.4. Multiplicities and Entropies
Four approaches to defining discrete causal microstates via terminal states of transitions were introduced in
Section 3.3. A preliminary step, given in Definition 14, was to define spaces
of
nth-order states, along with larger spaces
and
including states of arbitrary order. The first approach was to treat the states making up these spaces as individual microstates, called resolution microstates, and apply a discrete causal analogue of conventional coarse-graining, called causal atomic resolution, to partition these spaces into cells. The remaining approaches treated such states as macrostates, with finer state spaces of microstates introduced in Definition 15. The second approach was to add detail to terminal states by specifying prehistorical information, leading to the spaces
,
, and
of superset microstates. The third approach was to add detail to terminal states by labeling their elements, leading to the spaces
,
, and
of labeled microstates. The fourth approach was to add detail to terminal states via partial labelings specifying symmetry breaking information, leading to the spaces
,
, and
of symmetry microstates.
Before explaining how discrete causal entropies may be defined via these four approaches, I mention progress in the study of causal set entropy by Sorkin and collaborators [
35,
36]. This work exhibits interesting relationships with analogous continuum-based notions, is supported by numerical simulations involving “low-dimensional” causal sets, and incorporates covariance considerations. However, it is very different in its assumptions and emphasis from the approaches examined in this paper. First, the entropies involved are defined in terms of auxiliary fields on causal sets, and are therefore not completely background independent quantities. Sorkin does consider causal set “vacuum solutions”, whose entropies may be attributed solely to causal structure, but entropies associated with nontrivial interactions typically involve large quantities of extra-causal data. Second, pre-packaged quantum-theoretic machinery such as Hilbert spaces, operator algebras, density matrices, and von Neumann-type entropy are applied to individual causal sets under this approach, rather than emerging naturally from a history configuration space. Third, the permeability problem and other technical obstructions arising in the absence of relation space methods render it difficult to define terminal states or associated entropic data in this setting. The resulting measures of entropy are a priori “higher-dimensional”, and can be associated only indirectly with conventional notions of time-dependent entropy and the second law of thermodynamics. Fourth, many of the cases considered under this approach involve special causal sets of the type mentioned in
Section 2.2, induced by sprinkling elements into relativistic spacetime manifolds. Such causal sets are naturally limited in their potential to reveal structural features beyond the scope of general relativity.
I give only a brief sketch of how one may construct entropy systems via resolution microstates. For simplicity, I describe this construction in terms of an individual
nth-order state space
. The first step is to choose a resolution of each state
in this space. In the simplest case, these resolutions may be chosen to consist of single causal atomic decompositions. A choice of such decompositions defines a coarse-graining of
, which induces an entropy quadruple, while a choice of resolutions involving longer sequences of decompositions, or partially ordered families of decompositions, defines an entropy system. In the general case, one may define a partially ordered family of equivalence relations on
, specified by treating states as equivalent if their resolutions agree beyond a certain level of detail. The associated equivalence classes then define partitions of
, and their cardinalities define multiplicities. The resulting notion of entropy is called
resolution entropy. One may choose to define resolutions in such a way that each decomposition reduces the maximal length of chains in each state by a specified quantity. For example, the decomposition illustrated in the second diagram in
Figure 14 converts a “fine” third-order state to a “rough” first-order state. An analogue of resolution entropy appears in Sorkin’s approach to causal set entropy [
35,
36], but involves a random “decimation” version of coarse-graining that does not incorporate causal structure in the same way that causal atomic resolution does. It also involves “higher-dimensional” entropy, rather than entropy associated with terminal states. However, numerical examples do hint at interesting universal behavior for this type of entropy, and this evidence provides motivation for studying resolution entropy in more detail.
Numerous questions must be answered, however, before one may have confidence in the resolution approach. The most basic is how sensitive resolution entropy is to changes of resolution, since resolutions generally involve arbitrary extraphysical choices regarding the organization of information. Another question, already mentioned in
Section 3.3, is how one may reconcile the increasing “granularity” produced by multi-level resolutions with the basic philosophy of metric recovery, under which discrete causal structure at the fundamental scale should produce effectively smooth structure at sufficiently large scales. A third issue arises from the empirical dynamical irrelevance of details of the distant past. If only very low-order terminal states play a substantial dynamical role in the future evolution of histories, then repeated causal atomic decompositions of dynamically relevant states will produce antichains at relatively fine levels of detail. Antichains possess no internal structure besides cardinality, which seems much too crude to determine meaningful dynamics, especially locally. Therefore, the utility of resolution entropy seems to be limited by the “causal depth” of relevant information. This issue does not necessarily disqualify the resolution approach, however, due to the scales involved. In particular, the difference in magnitude between the Planck scale and presently-measurable scales suggests than information up to order
or
could be relevant without producing noticeable deviations from the empirical obsolescence of high-order information. A resolution involving decompositions similar to the one illustrated in
Figure 14 would require perhaps 30 decompositions to cover 10–15 orders of magnitude, and could therefore contain a large quantity of information. However, such illustrations involving small histories can be misleading; for example, it would not be surprising if each element in a typical physically realistic history were directed related to
or more other elements. Such large numbers of relations would affect the qualitative properties of realistic resolutions.
Superset microstates offer a variety of different ways to define entropy systems via the state spaces , , and . I begin by discussing simple notions of entropy involving individual partitions of these spaces. For simplicity, I focus on the case of finite states. Let be such a state, and consider all superset microstates adding a single prehistorical element to . The number of such microstates is the cardinality of the future relation set in , since the number of different ways in which can be the terminal state of a history with one additional element is the same as the number of ways in which can evolve into a history with one additional element. As a reminder, is the element in the underlying multidirected set of representing , and is the set of relations in beginning at , each of which represent a co-relative history with cobase . The first superset multiplicity of is then defined to be the number of such microstates , and the first superset entropy is defined to be . Following essentially the same reasoning, nth superset multiplicities and entropies may be defined.
Definition 18. The nth superset multiplicity of a finite state Δ is the number of co-relative histories , where the complement of the image of under any transition representing η has cardinality n. The nth superset entropy of Δ is .
An interesting entropy system on is given by filtering superset microstates by both the number of prehistorical elements added to by , and the order of the resulting supersets . has a natural partition whose members are the infinite sets parameterizing all full, originary co-relative histories with cobase and target belonging to . One may partition each set by numbers of elements added to , or by orders of supersets , or by both. A general way to formalize the idea that two superset microstates and of are equivalent up a given level of detail is to specify a common interpolating microstate , characterized by the property that and both factor through . This means that there exist pairs of transitions and , where and both represent , and where the compositions and represent and , respectively. Informally, this means that besides being supersets of , the states and also share common prehistorical elements. One may then define equivalence relations and on , for each , where if and factor through a common interpolating microstate adding m prehistorical elements to , and where if and factor through a common interpolating microstate whose superset has order n. Equivalence relations combine these two requirements. The corresponding partitions are partially ordered lexicographically; i.e., if and only if or and . It is convenient to denote the pair by the single symbol , regarded as an element of . Informally, the partition groups together superset microstates that agree both up to a given number of prehistorical elements and a given order.
Definition 19. Let , and let be the set of partitions of defined by taking superset microstates and of Δ to be equivalent if they factor through a common interpolating microstate of Δ represented by a transition such that and . Let be the corresponding equivalence relation, and for any subset , let be the corresponding quotient set. For any relation under the lexicographic order induced by , and for any subset V belonging to , let be the cardinality of . Let be the family of measures . Then the triple is called the lexicographic superset entropy system.
The measures may take on infinite values; for example, there are infinitely many ways to add a single prehistorical element to . Definition 19 does not specify the number of relations added to by each microstate, or the maximal sizes of antichains in the corresponding supersets, or any of a variety of other basic combinatorial data that may be used to partition in different ways. Using such quantities, one may define alternative entropy systems, involving, for example, “higher-dimensional” lexicographic orders. This particular entropy system merely formalizes some of the simpler properties that may be used to organize families of superset microstates.
Labeled microstates also induce a variety of entropic notions. The most obvious is given by simply counting the number of equivalence classes of labelings of a state . If has cardinality K, then its total number of labelings is . These labelings are partitioned by the action of into equivalence classes of cardinality , so the number of such classes is .
Definition 20. The labeled multiplicity of a state Δ of cardinality K is . The labeled entropy of Δ is .
It is sometimes desirable to decompose the subset of consisting of all equivalence classes of labelings of . This may be accomplished via equivalence classes of partial labelings of , i.e., labelings of special subsets U of . To yield a suitable version of equivalence, U must be a union of orbits under , and the labeling must be by consecutive natural numbers beginning with zero. The set of equivalence classes of such partial labelings is partially ordered by extension of class representatives. A labeling ℓ of U corresponds to a subset of defined by labelings of extending ℓ. Letting U and ℓ vary, one obtains a family of sets that cover , generally in a highly redundant fashion. A partition of induced by partial labelings of is defined to be a partition whose members are open sets in the topology on generated by , i.e., unions of finite intersections of members of . Choosing such a partition for each defines a partition of , and the collection of all such partitions forms a “large” entropy system. Smaller subsystems may be more convenient to work with in practice.
Definition 21. Let Δ be a member of , and let be the subset of consisting of all equivalence classes of labelings of Δ. Let be the set of partitions of induced by partial labelings of Δ, and let be the set of partitions of constructed from the partitions , partially ordered by refinement. For any relation in , and for any subset V belonging to , let be the cardinality of the quotient set of V under the equivalence relation induced by . Let be the family of measures . Then the triple is called the labeled entropy system.
Symmetry microstates share entropic similarities with labeling microstates, since both approaches involve labelings. The principal differences are that symmetry microstates label only elements of a state that are not fixed by its automorphisms, and labelings related by automorphisms are not considered to be equivalent. It is convenient to fix an arbitrary “initial” labeling on the set of elements of not fixed by , i.e., the union of nonsingleton orbits under . A labeling of is then considered permissible if it is generated by applying an element of to this initial labeling. The number of such labelings is just the order of .
Definition 22. The symmetry multiplicity of a finite state Δ is . The symmetry entropy of Δ is .
By Definitions 20 and 22, for a state of cardinality K. Processes exhibiting an increase in therefore exhibit a decrease in for a fixed state cardinality, and vice versa, although “expanding universes” may exhibit simultaneous increases in both types of entropy. As in the case of labeled microstates, it is sometimes desirable to decompose the subset of consisting of all permissible labelings of . This may be accomplished by partially labeling in a suitable manner; in particular, the set U of elements labeled must be a union of nonsingleton orbits under . Such a labeling ℓ defines a subset of consisting of all labelings of extending ℓ. The set of all such labelings for all such U is partially ordered by extension. The collection of sets define a family of partitions of , and hence an entropy system.
Definition 23. Let Δ be a member of , and let be the subset of consisting of all permissible labelings of the set of elements of Δ not fixed by , with respect to an arbitrary initial labeling. Let be the set of partitions of induced by partial labelings of , and let be the set of partitions of constructed from the partitions , partially ordered by refinement. For any relation in , and for any subset V belonging to , let be the cardinality of the quotient set of V under the equivalence relation induced by . Let be the family of measures . Then the triple is called the symmetry entropy system.
It may often suffice on physical grounds to restrict attention to notions of entropy more specific than those associated with the entropy systems of Definitions 19, 21 and 23, although it may be necessary to supersede the simplistic notions of Definitions 18, 20 and 22. For superset microstates,
weighted sums of entropies can be useful to naturally distill finite entropic values from infinite families of microstates. Abstractly, such sums are analogous to Gibbs or Shannon entropies. A practical reason to study such sums is to quantify the degree to which prehistorical data of various orders is dynamically relevant. A simple example of such a weighted sum is
where the denominator
dominates the rapid growth of
as
n increases. For both labeled microstates and symmetry microstates, symmetry considerations are paramount. Interesting generalizations of Definitions 20 and 22 include those involving the study of symmetries that are broken or preserved by specific prehistorical information. This leads to the concept of
extension groups, which measure how many automorphisms of a terminal state extend to automorphisms of a specified superset. One may formalize this idea in terms of pairs of transitions
, where
specifies a terminal state
, and
specifies a superset
of
that breaks some of the symmetries of
. Finiteness assumptions may be added as necessary.
Definition 24. Let τ, and be transitions of directed sets with sources D, and , and common target . Assume that in . Let , and be the terminal states of τ, , and .
- 1.
The state automorphism group of τ is .
- 2.
The relative extension group of is the subgroup of of automorphisms of that extend to automorphisms of .
- 3.
The relative symmetry multiplicity of is .
- 4.
The relative symmetry entropy of is .
The
generational automorphism groups discussed in Section 8.2 of [
14] are special cases of state automorphism groups. The quantities
and
may be derived from the symmetry entropy system, if desired.
is generally not a normal subgroup of
. The superset
may acquire “new” symmetries that do not extend nontrivial symmetries of
, but this is atypical due to rigidity. Since the purpose of studying entropic phase maps is to assign quantum-theoretic phases to co-relative kinematics, it is necessary to adapt the preceding notions to apply to co-relative histories
in a kinematic scheme
. The states of principal interest in this context are terminal states of the cobase
and target
of
h. For generality, it is convenient to work with an unspecified entropy function on a subset of
. Again, finiteness assumptions may be added as necessary.
Definition 25. Let be a co-relative history. Let and be terminal states of and , respectively. Let e be an entropy function on a subset of .
- 1.
The initial entropy of h with respect to is .
- 2.
The terminal entropy of h with respect to is .
- 3.
The relative entropy of h with respect to the pair is .
It is useful to specialize Definition 25 to the case where and are transitions of specific degrees, as specified in Definition 13.
Definition 26. Let be a co-relative history, and let e be an entropy function on a subset of .
- 1.
The nth initial entropy of h is .
- 2.
The nth terminal entropy of h is .
- 3.
The nth relative entropy of h is .