1. Introduction
The book entitled “Do we really understand quantum mechanics?” [
1] was published five years ago. Some fourty years earlier, its author, Laloë, had co-authored a treatise on quantum mechanics, together with Cohen-Tannoudji, later a Nobel laureate, and Diu [
2]. While this recent book illustrates the present strong interest for the foundations of Quantum Theory (QT), already in 1929, Dirac could claim: “
The general theory of quantum mechanics is now almost complete” and “
The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known” [
3]. Since that time, the development of both telecommunications through electromagnetic waves and solid state electronics favoured the appearance first of classical Information Theory, and then of Quantum Information Theory and Processing (QIT, QIP).
This special issue,
Quantum Information and Foundations,in the Quantum Information Section of Entropy, reflects the existence of links between QIP/QIT and the foundations of QT. An instance of such links is given by the approach adopted e.g., in Timpson’s Thesis [
4]. This methodology, in the framework of Philosophy of Science, is difficult because of its rather general character. For the last decade, we have been following another approach. Starting from a problem in the domain of classical information processing, namely Source Separation (SS) with its more difficult so-called Blind version (BSS), introduced around 1985 and now a mature field [
5,
6], we are developing its quantum counterpart, which we proposed to call Blind Quantum Source Separation (BQSS). Each step of this more pedestrian approach may be controlled, presently e.g., through simulations. This approach has been achieved in our 2007 paper introducing BQSS [
7], and in those describing the solutions which we have built since then (see e.g., [
6,
8,
9,
10,
11,
12,
13,
14]), and which led to our recent introduction of Blind Quantum Process Tomography (cf. [
12,
14] and more explanations at the end of this section and in
Part A.2 of the Appendix).
A short presentation of the problem of classical (i.e., non quantum) or conventional BSS, and of its interest, is needed here. In BSS, typically, at first, a set of users (the Writer) presents a set of simultaneous signals (input signals, or sources) at the input of a multi-user communication system (the Mixer). The sources, constrained to possess some general properties (e.g., mutual statistical independence), are combined (mixed, in the SS sense) in the Mixer, often specified through a model, e.g., the linear memoryless one (cf. Chapter 11 from [
15]). Another set of users (the Reader) receives the signals arriving at the Mixer output. The Writer possibly knows the sources, but the Reader does not know them, and cannot access the inputs of the Mixer. That Mixer uses one or several parameter values, unknown to the Reader, who only knows some of its general properties. The Reader’s final task is the restoration of the sources (possibly up to some so-called acceptable indeterminacies) from the signals at the Mixer output, during the inversion phase. An intermediate task is the determination of the unknown parameters of the Mixer, or of its inverse. Before receiving the signals to be separated at the Mixer output, derived from the sources sent by the Writer, the Reader therefore enters an “adaptation phase”, during which he knows that the Writer is sending one (or possibly a limited number of) signal(s) submitted to some definite, and known by the Reader, constraints. The particular signal sent is not known by the Reader (blind separation problem), who knows the class of the input signal(s) and the signal(s) at the Mixer output in the adaptation phase, and, of course, the mixed signals to be separated in the inversion phase.
Conventional BSS is already used to extract some or all source signals in various application fields, e.g., in some audio systems, or when using radio-frequency signals to transmit digital data, or in the biomedical field, in the processing of signals such as electrocardiograms, electroencephalograms or magnetoencephalograms, as explained in
Part A.1 of the Appendix. More information on the applications of conventional BSS may be found in our previous papers [
11,
14], in [
6], and in the papers or books they cite.
BSS is moreover closely linked to a well-known domain of signal processing technology called system identification. More precisely, BSS is linked to Blind Mixture Identification (BMI), as briefly explained in
Part A.1 of the Appendix and developed in [
6], and BSS may be used in the corresponding applications.
Conventional (B)SS has favoured the introduction of concepts and the development of specific methods [
5,
6]. Its extension to the quantum domain seems suitable for at least three reasons. First, the source concept may be extended from a classical to a quantum context. Secondly, as any classical phenomenon, conventional (B)SS may be seen as the limit of a quantum phenomenon. When developing solutions to the BQSS problem, it seems legitimate to try and import concepts and methods from the classical to the quantum SS domain. However, the presence of entanglement in a quantum approach should be clearly identified and the consequences of its existence should not be underestimated. In addition, the concepts of quantum sources and of their statistical independence deserve some discussion, and consequences of the probabilistic aspect of the results of measurements in the quantum domain must be drawn. Furthermore, last but not least, since some of the basic concepts of QT are still open to discussion, when e.g., using measurements, even in an abstract process, the adopted point of view should once be made explicit, in order to minimize confusion. The nature of this special issue gave us the opportunity to clarify concepts and justify properties already used in our previous papers upon BQSS, a task postponed up to now, and which should be of use in the BQSS domain, and maybe in other fields. These two motivations stimulate a third natural one, namely the hope of extending the field of BSS applications toward the quantum world. In the following sections, in order to illustrate our methods and help reading, some aspects or results of our previous papers will be occasionally presented, but the building of any specific BQSS solution is outside their scope. The reader interested in the results from simulations may consult [
8,
11], obtained through BQSS methods with classical processing, and [
14], with quantum processing in the forward path. This recent paper moreover contains a table with a detailed comparison of the key features and performance from the existing methods.
In all of our previous papers, we considered two distinguishable qubits numbered 1 and 2, and we presently keep this situation. When it is meaningful to speak of the state of a quantum system, and specifically if this system is a qubit, this state may be either pure or mixed. In order to avoid any confusion with the meaning of a mixture in the SS context, if it is needed to speak of a (quantum) mixed state in the following, we will systematically speak of a statistical mixture. A typical situation is the following one: at an initial time
, the Writer prepares both qubits, each in a given pure state, described by some ket. This ket carries information, an idea contained in the expression “quantum source”. The initial state
of the qubit pair is then the tensor product of the corresponding kets. The time between
(writing) and
(reading) is supposed to be short enough for the qubit pair to be treated as isolated, a choice already made by Feynman [
16,
17] in the context of the quantum computer, and presently refined at the beginning of
Section 4.1 for qubits physically realized with spins. At any time
t between
and
, the state of the qubit pair may then be described by a ket
. In the Schrödinger picture, this time evolution of the pair is described by a time-dependent unitary operator
. It is assumed that an undesired coupling exists between these qubits. Because of this undesired coupling, as time goes on the state of the pair generally becomes entangled. Coupling is then interpreted as a mixing (in the SS sense), realized by an abstract Mixer depending upon one or several parameter values, unknown to the Reader, who only knows some general properties of that Mixer. It is said that the input of the Mixer receives state
, and that its output provides state
. It should be well appreciated that
inverting in order to get
from
is not that easy, because is unknown (blind QSS). In
Section 2, it is first explained why both state and process quantum tomography are unable to solve this BQSS problem, and secondly why the Schmidt criterion is ill-suited for following the degree of entanglement of
during the adaptation phase. The Peres–Horodecki criterion [
18,
19] is valid for separable statistical mixtures of bipartite systems, and not specifically for unentangled pure states. A better suited unentanglement criterion is therefore established in
Section 2.
In
Section 3, a model situation, for a single spin and then for a pair of spins, in inhomogeneous magnetic fields with random directions, allows us to speak of random and possibly independent variables, in that quantum context. We explain why, although this random quantum state corresponds to a statistical mixture, it is simpler, in the BQSS context, to speak of a random pure state than to introduce a density operator. In
Section 4, we first make brief comments about the description of quantum states (including the existence of statistical mixtures as source states, in a more general context), about the act of measurement and about the physical realization of qubits with electron spins. We then discuss questions related to the probabilities of the possible results obtained in measurements of spin components, in the context of spins 1/2 as qubits. We first present their use when the Reader makes measurements at the Mixer output in order to restore the sources (cf.
Figure 1). These measurements establish a link between the output of the Mixer and the classical world. It is stressed that while the macroscopic support of the results of measurements has a classical behaviour, the probabilities of these results obey quantum laws. We then establish an unentanglement criterion using probabilities, equivalent to the one established in
Section 2 for the probability amplitudes
. It is shown that the
coefficients can be expressed as functions of the probabilities of results in the measurements of well-chosen spin components. In
Section 5, we derive the expression of the above unentanglement criterion for all possible source states, at the output of the so-called separating system, with respect to the parameters of both the cylindrical Heisenberg coupling, an abstract Mixer largely used in our previous papers, and that separating system.
In
Part A.2 of the Appendix, the question of the applications of BQSS is addressed. Partly because the appearance of BQSS is recent, the subject of its applications is presently largely speculative. Two main subdomains should be distinguished. The first one is BQSS in a strict sense. It aims at recovering the source states and is the quantum counterpart of conventional BSS. The second subdomain focuses on an intermediate step possibly found in methods developed for BQSS and aiming at the knowledge of the mixer function or of its inverse. The corresponding classical problem is known as Blind Mixture Identification (BMI), a subfield of System Identification. The non-blind quantum version of System Identification is that already mentioned and well-established field of QIP called Quantum Process Tomography (as opposed to Quantum State Tomography). We recently introduced the quantum version of BMI, which we proposed to call Blind Quantum Process Tomography (BQPT).
2. An Unentanglement Criterion for a Qubit Pair
A superficial look may suggest that it is possible to restore the initial product state through State or Process Tomography (ST, PT). ST aims at determining a quantum state if a lot of copies of that state are available [
20]. However, in BQSS, the Reader is unable to access the input of the Mixer, and ST is therefore obviously presently strictly useless. PT would presently consist of placing (preparing) successive well-defined and known quantum states at the input of the Mixer, thus operating in the non-blind mode (cf. [
15], p. 202) and observing the corresponding signals at its output. However, in the BQSS problem, the Reader is strictly unable to operate that way, as he is unable to ask the Writer to prepare him the quite specific input states asked for by PT. Therefore, quantum tomography is unable to solve the BQSS problem, which needs dedicated methods (for more details, see [
8]).
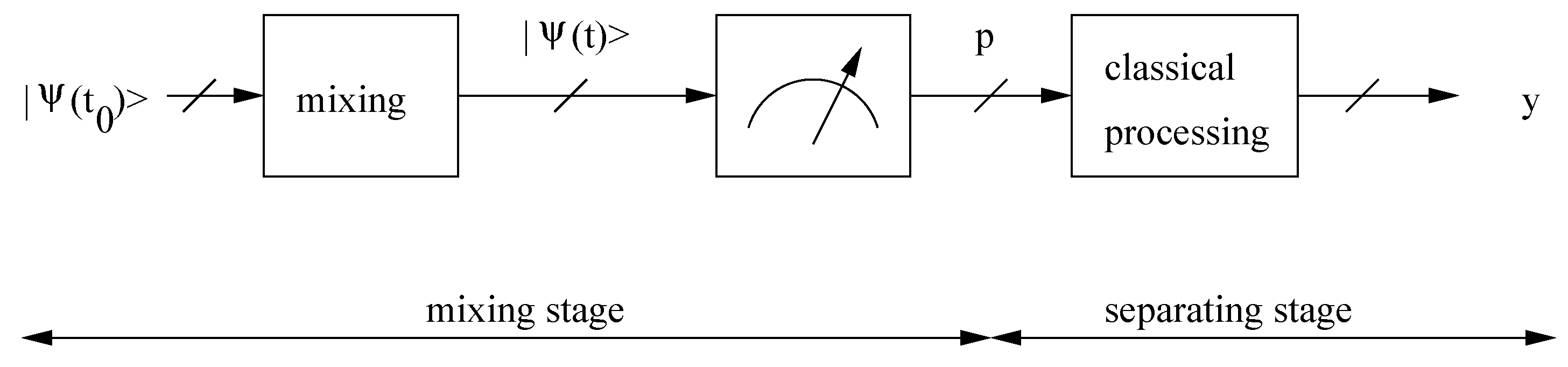
Up to now, in the BQSS problem, we developed two main approaches for both determination of the unknown parameter(s) of the mixing or separating system and source separation. In the first approach [
7,
8,
11], the Reader measures observables, using the signals at the Mixer output (cf.
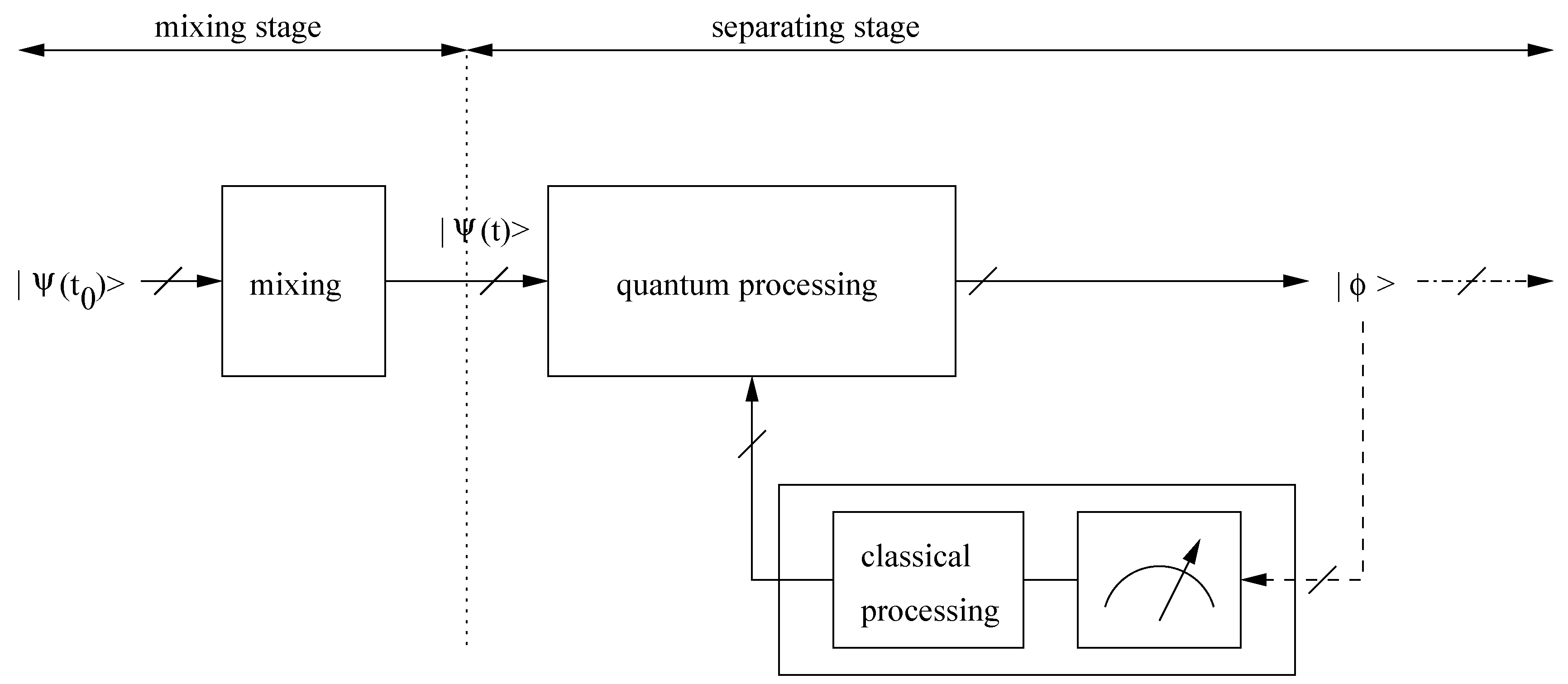
Figure 1). The results, and properties associated with them, e.g., the probabilities of their occurrences, are kept upon a macroscopic device, e.g., the memory of a classical computer, and then used in a separating system. Since this macroscopic device and the separating system have a classical behaviour, we called this processing aimed at restoring the sources “classical-processing BQSS”. In the second, quite different, and more recently introduced approach [
9,
10,
14], the quantum state at the Mixer output is sent to the input of a quantum-processing subsystem (cf.
Figure 2), the inverting block of the separating system. This block is so designed that its output provides a quantum pure state equal to
(possibly up to some acceptable indeterminacies), after the adaptation phase.
From now on, the state spaces of two arbitrary qubits, called qubits 1 and 2, are denoted as
and
, respectively. The possible (pure) states of the pair are the kets in
We assume that the qubits are physically realized with spins 1/2, which, e.g., allows us to speak of the spin component
or
but many results established hereafter keep true without this assumption. We introduce the orthonormal basis
, {
}, where e.g.,
means
and
,
are normed eigenkets of the
component of (reduced) spin
(with
i = 1, 2), for the eigenvalues +1/2 and −1/2, respectively. Any pure pair state, entangled or not, may be expanded in
as
where the complex coefficients
(
j = 1 to 4) respect
. If a pure state or a statistical mixture of a bipartite system
(parts
and
) is described by a density operator
, the corresponding reduced traces
and
have all the mathematical properties of a density operator [
2]. In addition, if
is in a pure state,
and
have the same eigenvalues [
21]. This pure state is unentangled if and only if its Schmidt number
(the number of non-zero eigenvalues of
and
) is equal to 1 [
21]. We are particularly interested in the case when
is the state found at the output of the inverting block. Then, any pure state may be expanded in the standard basis
as in Equation (
1), where the values of the
coefficients are affected by both the coupling between the qubits and, during the adaptation phase, by the adaptation procedure. This adaptation phase typically consists of an iterative numerical algorithm, which aims at optimizing a continuous-valued function, traditionally called the “cost function”. For any given values of the adjustable parameters of the inverting block, the cost function measures a kind of “distance” between
at the output of the inverting block and an unentangled pure state. The Schmidt unentanglement criterion cannot be used in our problem because the considered state remains (at least slightly) entangled throughout the adaptation procedure, and the Schmidt number thus remains higher than one. The Schmidt criterion provides a binary-valued unentanglement detector, with a Schmidt number equal to one or not and, if taking into account all possible integer values of
beyond unentanglement detection, the Schmidt criterion provides a discrete-valued quantity. What we eventually need instead is a quantitative, continuous-valued, measure of that “distance” of the considered state with respect to unentanglement, in order to keep the adjustable parameter values of the inverting block, yielding the state which is the closest to unentanglement. Moreover, even if the Schmidt approach could be modified to this end, it would yield high computational complexity, as it would require one to diagonalize
or
for each of the quite numerous steps of the iterative adaptation algorithm. We avoid these issues as follows. Since the qubit pair is in a pure state, its partial traces
and
satisfy
and the common value for
and
is 1 if and only if the pure state is unentangled (cf. [
21]). One could think of using
as a cost function. However,
depends upon the
, which suggests one to try and establish an unentanglement criterion using the
explicitly. To this end, we consider state
defined through Equation (
1). When it is assumed that
is unentangled, i.e., that it can be written as
then, in Equation (
1),
=
,
=
,
=
,
=
, so
and
are both equal to
:
Conversely, when it is assumed that Equation (
4) is satisfied, if
then
may be written as
which means that
is then unentangled. If Equation (
4) is satisfied and
, then
and
, or
and
, or
=
= 0, and in each case
is unentangled. Therefore, if the qubit pair is in a pure state
written as in Equation (
1), then:
This unentanglement criterion for a qubit pair pure state was used without justification in [
9,
10]. In Equation (
1),
was expanded in the standard basis. It is possible instead to introduce e.g., the normed eigenvectors of
and
or more generally those of
and
the components of the spins along respective arbitrary directions
and
, defined through their Euler angles. For each component, the possible results are again
. The possible results for the pair may be symbolically written as
and
and the corresponding probabilities as
Equation (
1) is replaced by
With the same reasoning within the new basis, (
6) is replaced by
3. Random Quantum Sources and Their Independence
The qubits are again supposed to be physically realized with spins 1/2. Standard Electron Spin and Nuclear Magnetic Resonance (ESR, NMR) use a non-microscopic number of resonant spins, but methods have been proposed for more than twenty years in order to detect a single spin, particularly with Optically Detected Magnetic Resonance (ODMR [
22,
23]) or with Magnetic Resonance Force Microscopy (MRFM [
24]), and more recently at low temperature (0.5 K) with Spin Excitation Spectroscopy [
25], or even with ESR, in extreme conditions [
26]. These approaches are still under development. Here, anticipating upon advances in spintronics, we rather consider a pair of spins, or even a single spin, submitted to a static magnetic field.
When speaking e.g., of a microwave source for satellite television, one speaks of the device emitting the microwave carrier. Similarly, the expression “laser source” generally refers to the device creating the coherent radiation. In conventional SS, “source” is an abbreviation for “source signal”. Furthermore, in Quantum SS with abstract qubits corresponding to physical spins 1/2, the word “source” does not refer to some atomic beam delivering atoms carrying an electron or nuclear magnetic moment, but still means “source signal”, then referring to some information from the quantum states of these qubits.
In conventional SS, an important concept is that of statistical independence of the sources, at the root of the frequent use of Independent Component Analysis (ICA) [
27]. In [
7,
8,
11], we postulated the existence of statistically independent quantum sources when using the classical-processing SS defined at the beginning of
Section 2. Hereafter, we show that statistical independence may exist in that context. Quantum Mechanics (QM) does e.g., consider random
operators, the matrix elements of which are random quantities (see the random lattice operators
in the quantum description of the motions of nuclear moments in liquids, in the study of Spin-Lattice Relaxation (SLR), in [
28]). As a simple model situation, a magnetic moment
associated with a single electron spin 1/2, with
(isotropic
tensor), placed in a Stern–Gerlach device, is now introduced. The static field is
=
, with amplitude
. The system of interest consists of this spin and the magnet. Writing the Zeeman Hamiltonian as
=
indicates that while the spin is a quantum object, the magnetic field is treated classically. The Writer first prepares the spin in the
eigenstate of
(eigenvalue
). The moment is then received by the Reader, supposed to ignore the direction of
, and who chooses some direction attached to the Laboratory as the quantization direction, called
z (unit vector
) and introduces a Laboratory-tied cartesian reference frame
, used to define
and
, the Euler angles of
. Since the field is treated classically,
and
behave as classical variables, while
is an operator. The Reader measures
(eigenstates:
and
), and is interested in the probability
of getting
. An elementary calculation indicates that
with
and therefore
Once the direction of the magnetic field has been chosen, state
is then unambiguously defined. If this direction has a deterministic nature,
r and
are deterministic variables, and
may then be called a deterministic quantum state. If
and
, defining the direction of
chosen by the Writer, obey probabilistic laws, one may consider that the quantum quantities
r and
, which depend upon the classical Random Variables (RV)
and
, do possess the properties of conventional, i.e., classical, RV. It may e.g., happen that they be uncorrelated, or even independent (which happens if
and
are independent). In addition, if
and
depend on time in a random way,
r and
are then random time functions. We are not strictly facing the quantum equivalent of a classical situation here. Rather, the stochastic character of the field direction, with classical nature, is reflected in the random behaviour of the quantum state expressed through Equation (
9). Therefore, rather than a random operator, we meet here a random quantum state. The concept of a random state, if not the expression, was already used e.g., in the early and canonical books [
29,
30]. The probability
, presently a function of the RV
is itself an RV. This results from both the randomness of the field direction and the standard probabilistic interpretation of QM. Probabilities of results of measurements for a qubit pair were treated as RV, without the present justification, in most of our previous papers, including [
7,
8,
11].
If one measures the scalar observable
O when the spin is in the state
=
(where
k is associated with + and −), had the
been deterministic the mean value would have been:
Since the
are random, one must moreover calculate the statistical mean, denoted as
:
where
is the density operator, the matrix elements of which, in the
,
basis, are
=
. Therefore, it is in principle possible to presently introduce a density operator, which is a non-random operator (its matrix elements are not random quantities, but statistical averages). However, this does not present any interest, since in the BQSS problem examined up to now, the Reader knows that e.g., qubit 1 has been prepared in a pure state, but does not know the values of the
coefficients in any basis, and is consequently unable to choose a basis in which
would be diagonal. It is simpler to keep speaking of a random pure state.
As a model situation, we now consider two spins 1/2 numbered 1 and 2, each with conditions similar to the previous ones, with fields along directions with respective unit vectors
and
, and each spin initially prepared in the state
where
and
are the eigenkets of
, the component of
along the quantization direction, for the eigenvalues 1/2 and −1/2, respectively. For the same reason, if the field directions are random,
and
have the properties of conventional RV. If (
) and (
) are mutually statistically independent, the same is then true for the couples of RV (
) and (
). In addition, if e.g.,
and
are independent, the same is true for
and
(cf. Equation (
10)). These properties are of major importance for our quantum-source independent component analysis (QSICA) methods described in [
11]. We may then say that the initial state of each qubit is random, i.e., that in Equation (
13)
and
are RV. When considering the preparation of a pair of qubits each in a pure state, one may assume either a deterministic or a random direction for each magnetic field. This discussion shows that the relevant concept, in the latter case, is that of random quantum states, rather than that of random quantum operators mentioned earlier in this section.
Keeping our assumption of a pair of qubits each prepared in a pure state, we now consider the second approach for the adaptation and inversion phases (cf. the beginning of
Section 2 and
Figure 2), with a quantum state
present at the output of the inverting block. The presence of
and the Reader’s final aim, the recovery of the initial pure state, prompts the Reader: (1) to speak of a deterministic or random pure state, rather than to use a density operator; (2) to consider that the first constraint to be respected in BQSS is then the very existence of an unentangled state at the output of this inverting block. If unentanglement has first been achieved, then and only then is it possible to speak of a deterministic or random state for each part of that product state. While entanglement has no classical counterpart, the following point may be noted here: if a bipartite system is in a pure (deterministic) state
to which a density operator
corresponds,
is unentangled if and only if the partial traces
and
satisfy the equality
[
31]. This unentanglement condition is reminiscent of the relation
·
between
, the joint probability density function of independent classical RV
and
and
and
the respective marginal probability density functions. Presently, operators replace functions, a tensor product replaces the ordinary product, and this reminiscence reflects the existence of a classical analogue to unentangled states. Condition (
4) for unentanglement was established using spins 1/2, but is valid for any pair of two-level systems. This discussion suggests that, in the BQSS problem, when considering a pair of qubits prepared in a pure state, and moreover using the second approach of
Section 2 for adaptation and inversion, instead of trying to directly import ICA methods into the BQSS context, one should focus on disentanglement at the output of the inverting block, which recently led us to introduce a disentanglement-based separation principle [
9,
10].
In the next section, use will be made of the number of real independent parameters necessary to define an arbitrary normed ket
in
written as in Equation (
1), and a ket in
forced to be unentangled. These numbers are specified hereafter. An arbitrary normed ket
in
depends upon the four complex quantities
to
linked through two relations between real numbers (
is equal to
and
and
with
an arbitrary real quantity, should be considered identical). An
arbitrary normedket
in
therefore depends upon
six real independent parameters. If it is forced to be unentangled, it has to satisfy the equality
between complex quantities. An
unentangled normed ket
therefore depends upon
fourreal parameters. This corresponds to the fact that
is then restricted to the form
where the normed kets
and
describing the state of qubits 1 and 2, respectively, each depend upon two real parameters
(cf. Equation (
13)).
5. Disentanglement and Cylindrical-Symmetry Heisenberg Coupling
In
Section 4.2, we considered measurements made at the Mixer output. We now come to the method for BQSS used, e.g., in [
9], with classical processing in the adapting block of the separating system, using the notations of [
9].
, the initial product state of the qubit pair, is given by Equation (
1), with the values of the coefficients
(in the
basis) taken at
and denoted as
. These components form the source vector
Similarly, the state at the Mixer output at time
t, here denoted as
, is given by Equation (
1), with the values of the coefficients
(in the
basis) taken at
t and denoted as
. The coupling-induced transition from state
to
is interpreted as the transformation induced by the Mixer, leading to the appearance of
at its output. In the same basis,
is described by the column vector
given by (
30), with
t replacing
In the matrix formalism, the relation between
and
is written as
where the square fourth-order matrix
M describes the effect of the coupling. In [
8], it was shown that when the coupling may be described by a Heisenberg cylindrical Hamiltonian, then
where
is a square matrix with the following non-zero matrix elements:
and
D is a Diagonal square matrix with its diagonal elements equal to
(
...4), the
being real quantities depending upon
and
, with generally unknown numerical values. The input of the inverting block then receives this state
Its output provides a state
described in the
basis by a column vector
with
where the square matrix
(Unmixing matrix) describes the effect of the inverting block of the separating system. If it is possible to choose
U in the form
, then
will be equal to
However, strictly speaking, operating this way is impossible because
and
D is unknown. In [
9], the inverting block was formally built using a chain of quantum gates globally realizing matrix
U in the form
where
is a diagonal matrix with its four diagonal elements
(
) equal to
is therefore a diagonal matrix with diagonal elements
where
The matrix and the adaptation phase were introduced because it is not possible to modify the values of the D matrix. In the following discussion, it is assumed that the are time-independent and that the adaptation phase has been successful with respect to unentanglement, i.e., that it has been possible to adjust the in such a way that, in the inversion phase, if the Writer has prepared each qubit of the qubit pair in an arbitrary pure state at time , we are then sure that state at the output of the inverting block is unentangled. The column vectors and C are associated with and respectively, and is therefore the column vector
State
is unentangled if and only if Equation (
4) is fulfilled, i.e., if
(
meaning
, for
to 4). We want this relation to be satisfied for any unentangled
. Starting with a
state with
and remembering that
, Equation (
37) may then be written
Equation (
38) is required to be fulfilled for all possible states
with
and for fixed
values (defined once for all during the adaptation phase). The left-hand term does not depend upon the
whereas its right-hand term does depend upon them. Therefore, Equation (
38) is satisfied only if
and then Equation (
38) moreover imposes that
If Equations (
39) and (
40) and relation
are inserted into Equation (
36), it is easy to write
as a product state, which confirms that if Equations (
39) and (
40) are fulfilled, and then
is unentangled indeed.
If one now supposes e.g., a
with
,
and therefore
, then in order for
to be unentangled Equation (
37) has to be fulfilled. Putting
into Equation (
37) leads to Equation (
39), and the
are then not submitted to another constraint. The same behaviour is found if
and
, and this remains true if
When one starts with an
arbitrary initial unentangled state
the following property is a consequence of the results of the previous discussion. If during the adaptation phase it has been possible to rightly fix the
values, one may claim that the corresponding
is unentangled if and only if during that adaptation phase the choice of the
has allowed conditions (
39) and (
40) to be both fulfilled. This, however, does not guarantee that
is identical to
. The latter identification corresponds to source restoration itself, outside the scope of this article.