Hypothesis Tests for Bernoulli Experiments: Ordering the Sample Space by Bayes Factors and Using Adaptive Significance Levels for Decisions
Abstract
1. Introduction
2. Blending Bayesian and Classical Concepts
2.1. Statistical Model
- positive probabilities of the hypotheses, and
- a density on the subset that has the smaller dimension. The choice of this density should be coherent with the original prior density over the global parameter space.
2.2. Significance Index
- Define a prior density over the entire parameter space. This function can be chosen either objectively of subjectively.
- Clearly define the hypotheses to be tested, H and A.
- Obtain the predictive functions under the two alternative hypotheses. In the case for which the parametric subspaces defined by the hypotheses are of different dimensionalities, the definition of a prior density under the subset of smaller dimension, say H, is obtained from the following expression, subject to the condition (on the parameter space as a whole and the hypotheses) that the integral in the denominator can be defined:
- 4.
- Define the loss function, considering mainly the relative importance of the hypotheses and of the two types of error—consider, for example, a governor who is concerned more with the budget than with public health and who will strongly prefer the hypothesis that the apparent wave of meningitis cases in his state do not represent an epidemic.
- 5.
- Use the Bayes factor to order the sample space: establishes the order of each. This ordering can be used independently of the dimensionalities of the spaces .
- 6.
- Using the theorem above, compute the optimal averaged error probabilities and use the value of as the adaptive level of significance, which will depend on the loss function, the probability densities, the prior probability, and especially on the sample size.
- 7.
- Calculate the significance index, the -value, as follows: if is the observed value of a statistic and is the observed tail under the new ordering, the -value is calculated using the expression . Clearly, this may be a single or a multiple integral or sum.
- 8.
- Compare the value with the value of Reject (do not reject) H if . In the case of equality, take either decision without prejudice to optimality.
- 9.
- Finally, if a value of is specified a priori, calculate the sample size needed to make this fixed value as close as possible to optimal according to the generalized Neyman–Pearson Lemma.
3. Illustrative Examples
3.1. Example 1—Comparing Two Proportions
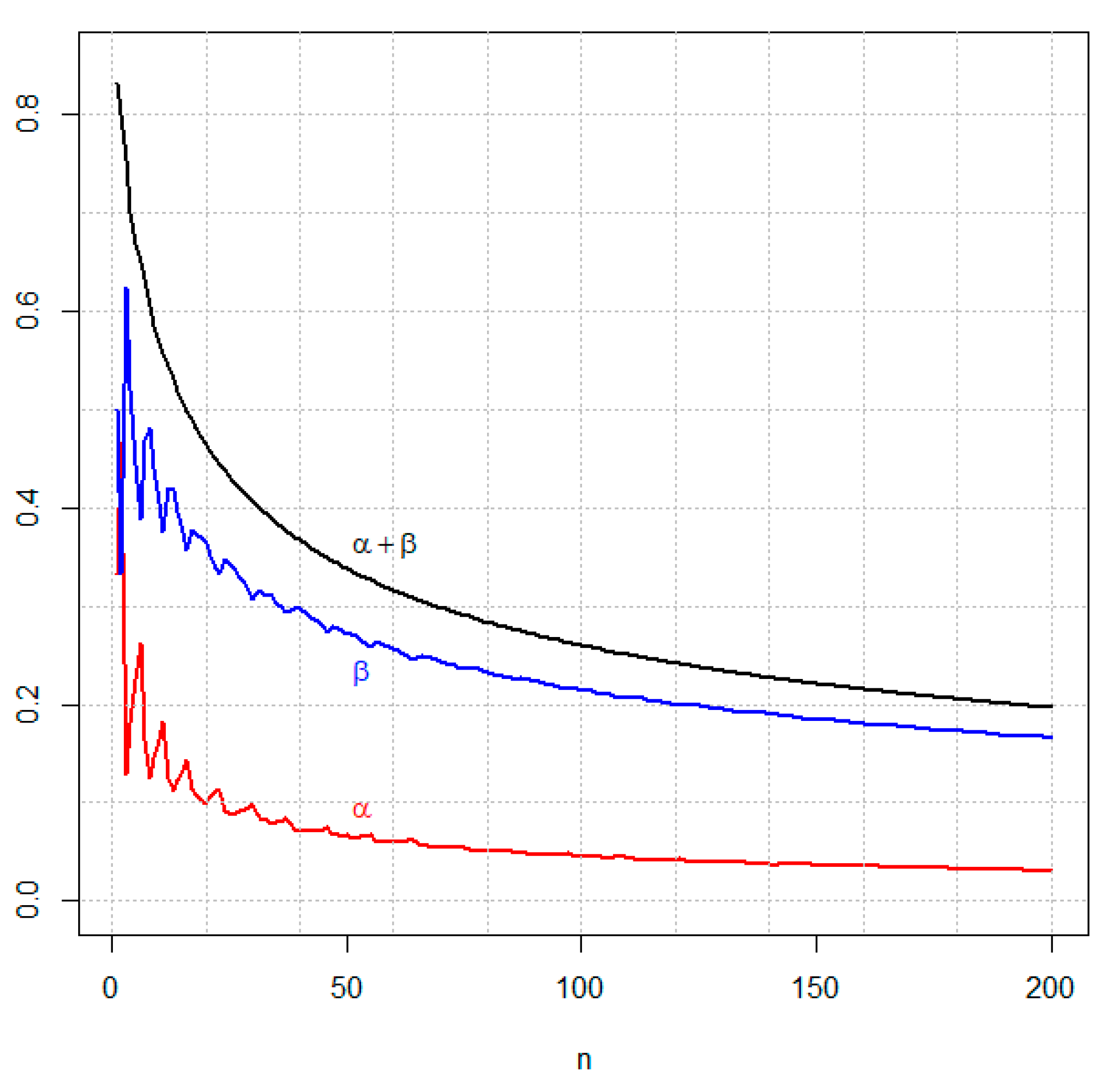
3.2. Example 2—Two Proportions, Varying Sample Sizes
3.3. Example 3—Test for One Proportion and the Likelihood Principle
- for a (positive) binomial,
- for a negative binomial,
3.4. Example 4
4. Final Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Johnson, V.E. Revised standards for statistical evidence. Proc. Natl. Acad. Sci. USA 2013, 110, 19313–191317. [Google Scholar] [CrossRef] [PubMed]
- Gaudart, J.; Huiart, L.; Milligan, P.J.; Thiebaut, R.; Giorgi, R. Reproducibility issues in science, is P value really the only answer? Proc. Natl. Acad. Sci. USA 2014, 111, E1934. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Robert, C.P. Revised evidence for statistical standards. Proc. Natl. Acad. Sci. USA 2014, 111, E1933. [Google Scholar] [CrossRef] [PubMed]
- Pericchi, L.; Pereira, C.A.B.; Pérez, M.E. Adaptive revised evidence for statistical standards. Proc. Natl. Acad. Sci. USA 2014, 111, E1935. [Google Scholar] [CrossRef] [PubMed]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s statement on p-values: Context, process, and purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
- Pericchi, L.R.; Pereira, C.A.B. Adaptive significance levels using optimal decision rules: Balancing by weighting the error probabilities. Braz. J. Probab. Stat. 2016, 30, 70–90. [Google Scholar]
- Benjamin, D.; Berger, J.; Johannesson, M.; Nosek, B.A.; Wagenmakers, E.-J.; Berk, R.; Bollen, K.A.; Brembs, B.; Brown, L.; Camerer, C.; et al. Redefine statistical significance. Nat. Hum. Behav. 2017. [Google Scholar] [CrossRef]
- Nature News. Big Names in Statistics Want to Shake up Much-Maligned P Value. Available online: https://www.nature.com/articles/d41586-017-02190-5?WT.mc_id=TWT_NatureNews&sf101140733=1 (accessed on 28 August 2017).
- Pereira, C.A.B.; Stern, J.M. Evidence and credibility: A full Bayesian test of precise hypotheses. Entropy 1999, 1, 104–115. [Google Scholar]
- Madruga, M.R.; Pereira, C.A.B.; Stern, J.M. Bayesian evidence test for precise hypotheses. J. Stat. Plan. Inference 2002, 117, 185–198. [Google Scholar] [CrossRef]
- Pereira, C.A.B.; Stern, J.M.; Wechsler, S. Can a significance test be genuinely Bayesian? Bayesian Anal. 2008, 3, 79–100. [Google Scholar] [CrossRef]
- Stern, J.M.; Pereira, C.A.B. Bayesian epistemic values: Focus on surprise, measure probability! Log. J. IGPL 2013, 22, 236–254. [Google Scholar] [CrossRef]
- Chakrabarty, D. A New Bayesian Test to Test for the Intractability-Countering Hypothesis. J. Am. Stat. Assoc. 2017, 112, 561–577. [Google Scholar] [CrossRef]
- Diniz, M.A.; Pereira, C.A.B.; Polpo, A.; Stern, J.M.; Wechsler, S. Relationship between Bayesian and frequentist significance indices. Int. J. Uncertain. Quantif. 2012, 2, 161–172. [Google Scholar] [CrossRef]
- Pereira, C.A.B.; Wechsler, S. On the concept of p-value. Braz. J. Probab. Stat. 1993, 7, 159–177. [Google Scholar]
- Pereira, C.A.B. Testing Hypotheses of Different Dimensions: Bayesian View and Classical Interpretation. Professor Thesis, Institute Mathematics & Statistics, USP, Sao Paulo, Brazil, 1985. (In Portuguese). [Google Scholar]
- Irony, T.Z.; Pereira, C.A.B. Bayesian hypothesis test: Using surface integrals to distribute prior information among the hypotheses. Resenhas 1995, 2, 27–46. [Google Scholar]
- Montoya-Delgado, L.E.; Irony, T.Z.; Pereira, C.A.B.; Whittle, M.R. An unconditional exact test for the Hardy-Weinberg equilibrium law: Sample space ordering using the Bayes factor. Genetics 2001, 158, 875–883. [Google Scholar] [PubMed]
- DeGroot, M.H. Probability and Statistics; Addison-Wesley: Boston, MA, USA, 1986. [Google Scholar]
- Dawid, A.P.; Lauritzen, S.L. Compatible Prior Distributions. In Bayesian Methods with Applications to Science Policy and Official Statistics; Monographs of Official Statistics; EUROSTAT: Luxembourg, 2001; pp. 109–118. [Google Scholar]
- Dickey, J.M. The weighted likelihood ratio, linear hypotheses on normal location parameters. Ann. Math. Stat. 1971, 42, 204–223. [Google Scholar] [CrossRef]
- Cox, D.R. The role of significance tests (with discussions). Scand. J. Stat. 1977, 4, 49–70. [Google Scholar]
- Cox, D.R. Principles of Statistical Inference; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Evans, M. Measuring statistical evidence using relative belief. Comput. Struct. Biotechnol. J. 2016, 14, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Lindley, D.V. A Statistical Paradox. Biometrika 1957, 44, 187–192. [Google Scholar] [CrossRef]
- Bartlett, M.S. A comment on D.V. Lindley’s statistical paradox. Biometrika 1957, 44, 533–534. [Google Scholar] [CrossRef]
- Cornfield, J. Sequential trials, sequential analysis and the likelihood principle. Am. Stat. 1966, 20, 18–23. [Google Scholar]
- Neyman, J.; Pearson, E.S. On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Charact. 1933, 231, 289–337. [Google Scholar] [CrossRef]
- García-Donato, G.; Chen, M.-H. Calibrating Bayes factor under prior predictive distributions. Stat. Sin. 2005, 15, 359–380. [Google Scholar]
- Jeffreys, H. The Theory of Probability; The Clarendon Press: Oxford, UK, 1935. [Google Scholar]
- Gu, X.; Hoijtink, H.; Mulder, J. Error probabilities in default Bayesian hypothesis testing. J. Math. Psychol. 2016, 72, 140–143. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. JASA 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Lopes, A.C.; Greenberg, B.D.; Canteras, M.M.; Batistuzzo, M.C.; Hoexter, M.Q.; Gentil, A.F.; Pereira, C.A.B.; Joaquim, M.A.; de Mathis, M.E.; D’Alcante, C.C.; et al. Gamma Ventral Capsulotomy for Obsessive-Compulsive Disorder: A Randomized Clinical Trial. JAMA Psych. 2014, 71, 1066–1076. [Google Scholar] [CrossRef] [PubMed]
- Basu, D. On the elimination of nuisance parameters. JASA 1977, 72, 355–366. [Google Scholar] [CrossRef]
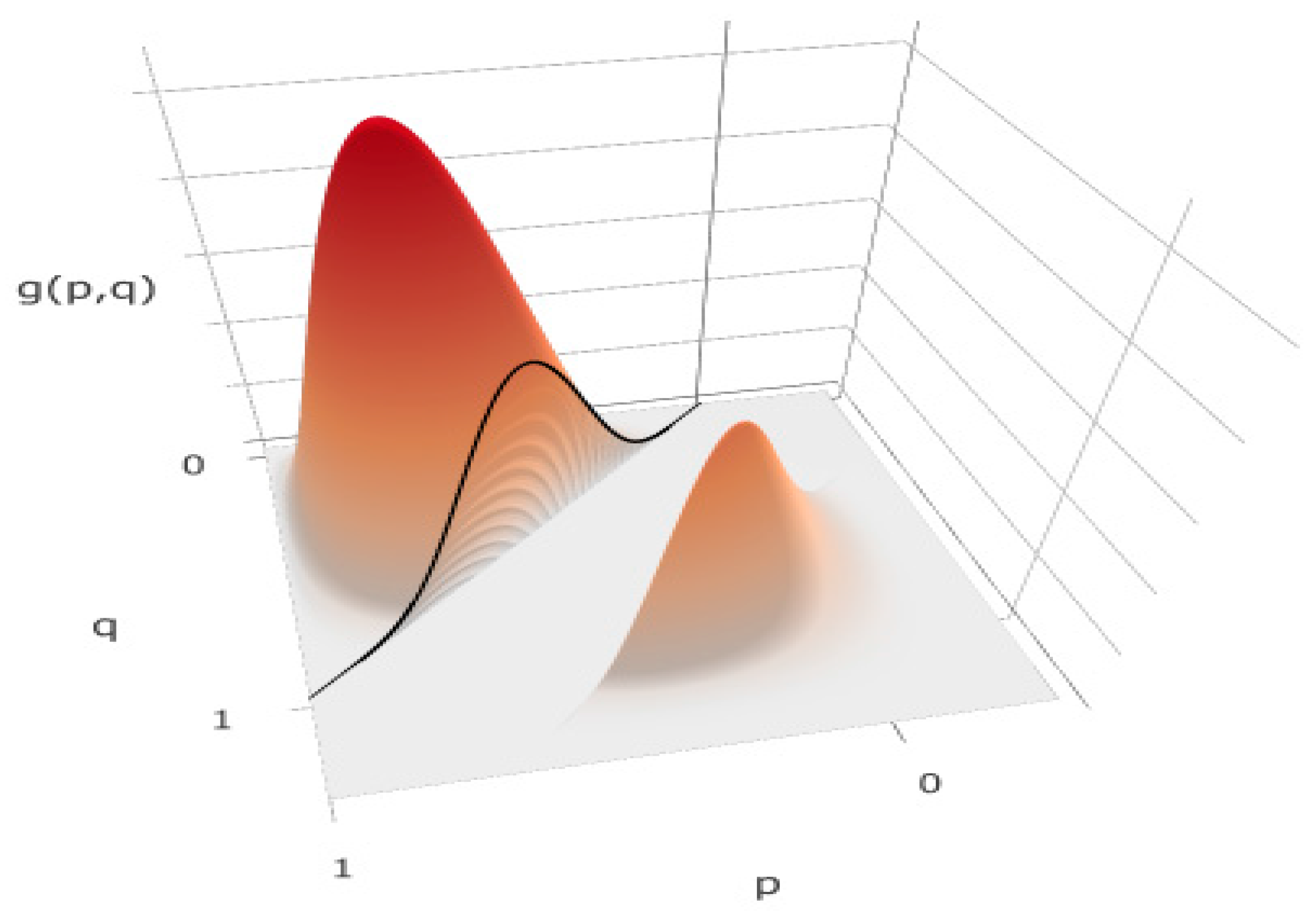


| x | y | Sum | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 0 | 4.765 | 2.382 | 1.112 | 0.476 | 0.183 | 0.061 | 0.017 | 0.003 | 4e-04 | 9 |
| 1 | 2.382 | 2.541 | 1.906 | 1.173 | 0.611 | 0.267 | 0.093 | 0.024 | 0.003 | 9 |
| 2 | 1.112 | 1.906 | 2.052 | 1.710 | 1.166 | 0.653 | 0.290 | 0.093 | 0.017 | 9 |
| 3 | 0.476 | 1.173 | 1.710 | 1.866 | 1.633 | 1.161 | 0.653 | 0.267 | 0.061 | 9 |
| 4 | 0.183 | 0.611 | 1.166 | 1.633 | 1.814 | 1.633 | 1.166 | 0.611 | 0.183 | 9 |
| 5 | 0.061 | 0.267 | 0.653 | 1.161 | 1.633 | 1.866 | 1.710 | 1.173 | 0.476 | 9 |
| 6 | 0.017 | 0.093 | 0.290 | 0.653 | 1.166 | 1.710 | 2.052 | 1.906 | 1.112 | 9 |
| 7 | 0.003 | 0.024 | 0.093 | 0.267 | 0.611 | 1.173 | 1.906 | 2.541 | 2.382 | 9 |
| 8 | 4e-04 | 0.003 | 0.017 | 0.061 | 0.183 | 0.476 | 1.112 | 2.382 | 4.765 | 9 |
| Sum | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 81 |
| 10 | 10 | 0.1639 | 0.4050 | 50 | 50 | 0.0667 | 0.2718 | 80 | 10 | 0.1130 | 0.3648 | 90 | 70 | 0.0529 | 0.2323 |
| 20 | 10 | 0.1318 | 0.3939 | 60 | 10 | 0.1097 | 0.3741 | 80 | 20 | 0.0834 | 0.3122 | 90 | 80 | 0.0493 | 0.2281 |
| 20 | 20 | 0.0995 | 0.3651 | 60 | 20 | 0.0860 | 0.3193 | 80 | 30 | 0.0704 | 0.2847 | 90 | 90 | 0.0468 | 0.2240 |
| 30 | 10 | 0.1159 | 0.3900 | 60 | 30 | 0.0765 | 0.2903 | 80 | 40 | 0.0634 | 0.2671 | 100 | 10 | 0.1111 | 0.3627 |
| 30 | 20 | 0.1045 | 0.3333 | 60 | 40 | 0.0689 | 0.2747 | 80 | 50 | 0.0603 | 0.2530 | 100 | 20 | 0.0818 | 0.3079 |
| 30 | 30 | 0.0997 | 0.3070 | 60 | 50 | 0.0626 | 0.2652 | 80 | 60 | 0.0553 | 0.2455 | 100 | 30 | 0.0684 | 0.2795 |
| 40 | 10 | 0.1250 | 0.3703 | 60 | 60 | 0.0591 | 0.2572 | 80 | 70 | 0.0531 | 0.2380 | 100 | 40 | 0.0617 | 0.2601 |
| 40 | 20 | 0.0868 | 0.3357 | 70 | 10 | 0.1130 | 0.3675 | 80 | 80 | 0.0508 | 0.2327 | 100 | 50 | 0.0559 | 0.2479 |
| 40 | 30 | 0.0850 | 0.3029 | 70 | 20 | 0.0865 | 0.3132 | 90 | 10 | 0.1131 | 0.3626 | 100 | 60 | 0.0538 | 0.2368 |
| 40 | 40 | 0.0706 | 0.2968 | 70 | 30 | 0.0727 | 0.2876 | 90 | 20 | 0.0810 | 0.3114 | 100 | 70 | 0.0512 | 0.2291 |
| 50 | 10 | 0.1126 | 0.3761 | 70 | 40 | 0.0645 | 0.2717 | 90 | 30 | 0.0707 | 0.2804 | 100 | 80 | 0.0483 | 0.2238 |
| 50 | 20 | 0.0883 | 0.3240 | 70 | 50 | 0.0603 | 0.2593 | 90 | 40 | 0.0648 | 0.2608 | 100 | 90 | 0.0467 | 0.2188 |
| 50 | 30 | 0.0767 | 0.2992 | 70 | 60 | 0.0575 | 0.2501 | 90 | 50 | 0.0575 | 0.2506 | 100 | 100 | 0.0449 | 0.2150 |
| 50 | 40 | 0.0718 | 0.2817 | 70 | 70 | 0.0539 | 0.2446 | 90 | 60 | 0.0550 | 0.2401 |
| Hypotheses | Predictive Densities under H 1 |
|---|---|
| H: = 0 | |
| H: 0 | |
| H: ≤0 | |
| H: > 0 | |
| H: 1 ≤ ≤ 2 | |
| H: ( < 1)∪( > 2) | |
| H: (1 ≤ ≤ 2)∪(3 ≤ ≤ 4) | |
| H: ( < 1)∪2 < < 3)∪( > 4) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, C.A.d.B.; Nakano, E.Y.; Fossaluza, V.; Esteves, L.G.; Gannon, M.A.; Polpo, A. Hypothesis Tests for Bernoulli Experiments: Ordering the Sample Space by Bayes Factors and Using Adaptive Significance Levels for Decisions. Entropy 2017, 19, 696. https://doi.org/10.3390/e19120696
Pereira CAdB, Nakano EY, Fossaluza V, Esteves LG, Gannon MA, Polpo A. Hypothesis Tests for Bernoulli Experiments: Ordering the Sample Space by Bayes Factors and Using Adaptive Significance Levels for Decisions. Entropy. 2017; 19(12):696. https://doi.org/10.3390/e19120696
Chicago/Turabian StylePereira, Carlos A. de B., Eduardo Y. Nakano, Victor Fossaluza, Luís Gustavo Esteves, Mark A. Gannon, and Adriano Polpo. 2017. "Hypothesis Tests for Bernoulli Experiments: Ordering the Sample Space by Bayes Factors and Using Adaptive Significance Levels for Decisions" Entropy 19, no. 12: 696. https://doi.org/10.3390/e19120696
APA StylePereira, C. A. d. B., Nakano, E. Y., Fossaluza, V., Esteves, L. G., Gannon, M. A., & Polpo, A. (2017). Hypothesis Tests for Bernoulli Experiments: Ordering the Sample Space by Bayes Factors and Using Adaptive Significance Levels for Decisions. Entropy, 19(12), 696. https://doi.org/10.3390/e19120696







