Combined Forecasting of Rainfall Based on Fuzzy Clustering and Cross Entropy
Abstract
:1. Introduction
2. Improved Fuzzy Clustering Model
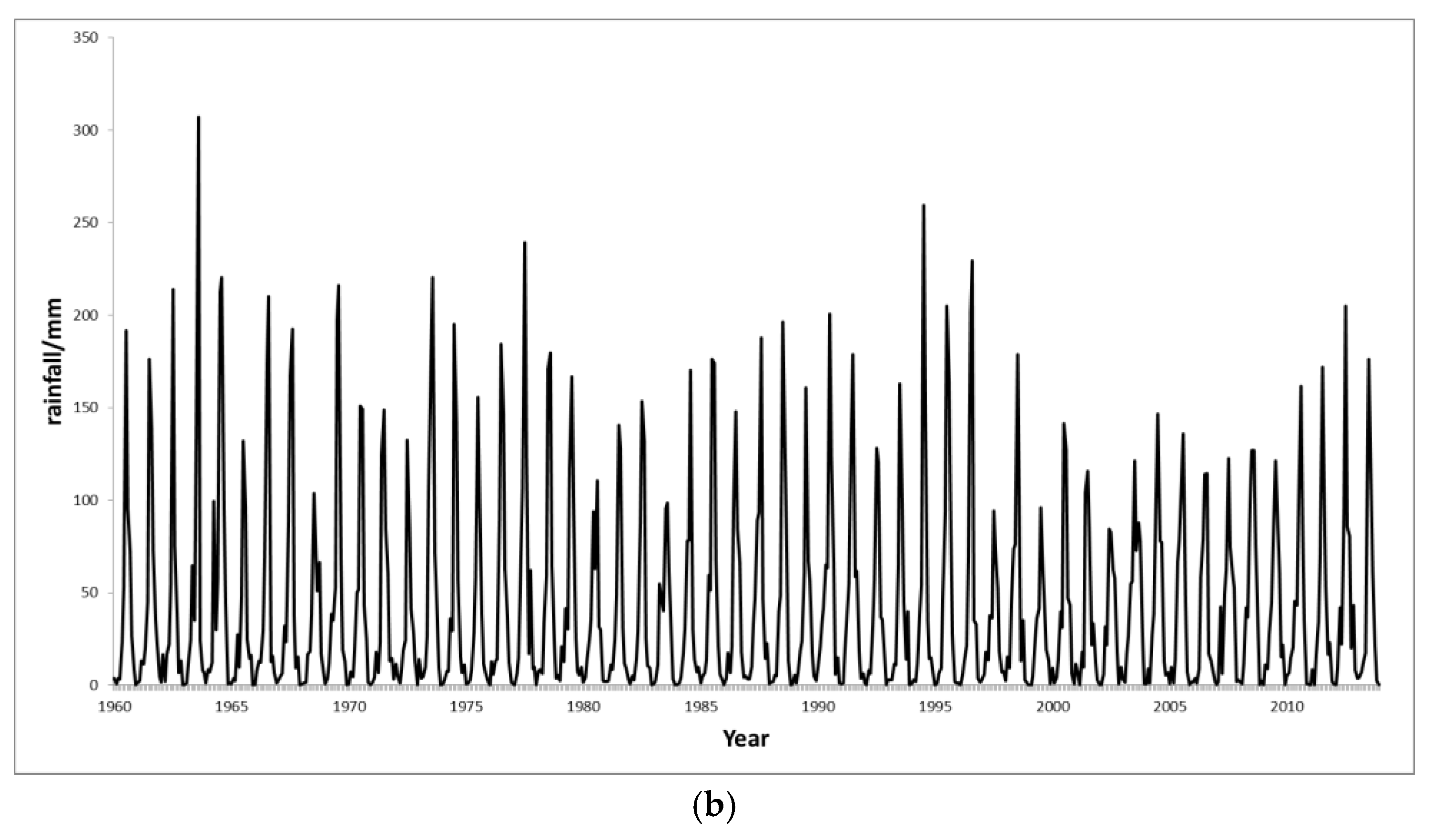
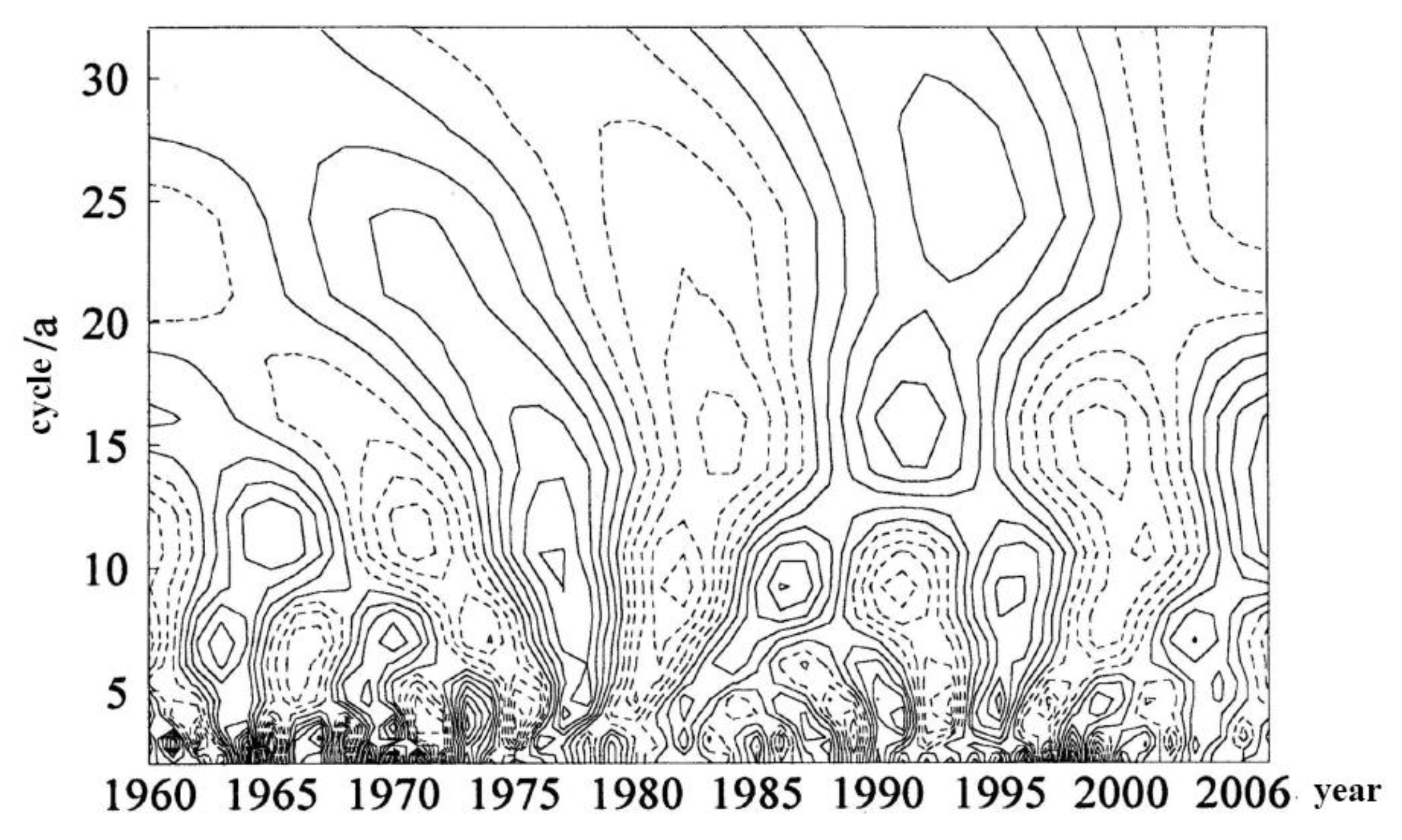
2.1. Research Data
2.2. An Introduction of Ant Colony Algorithm
2.3. Basic Principles of Fuzzy Clustering
2.4. Improvement of Fuzzy Clustering by Ant Colony Algorithm
2.5. Method Validation
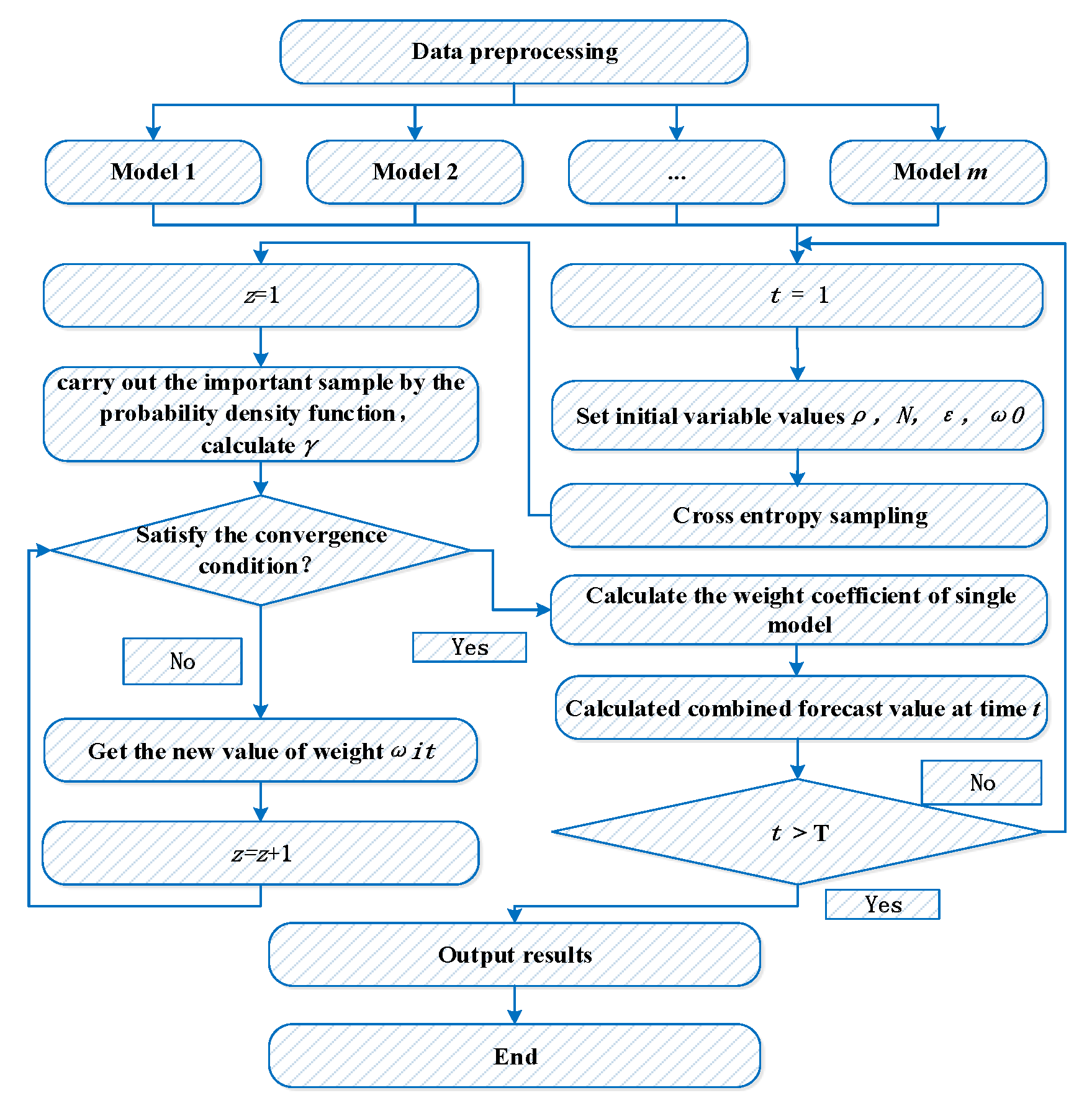
3. Rainfall Forecasting Model Based on CE
3.1. Combined Forecasting Model
3.2. The CE Model
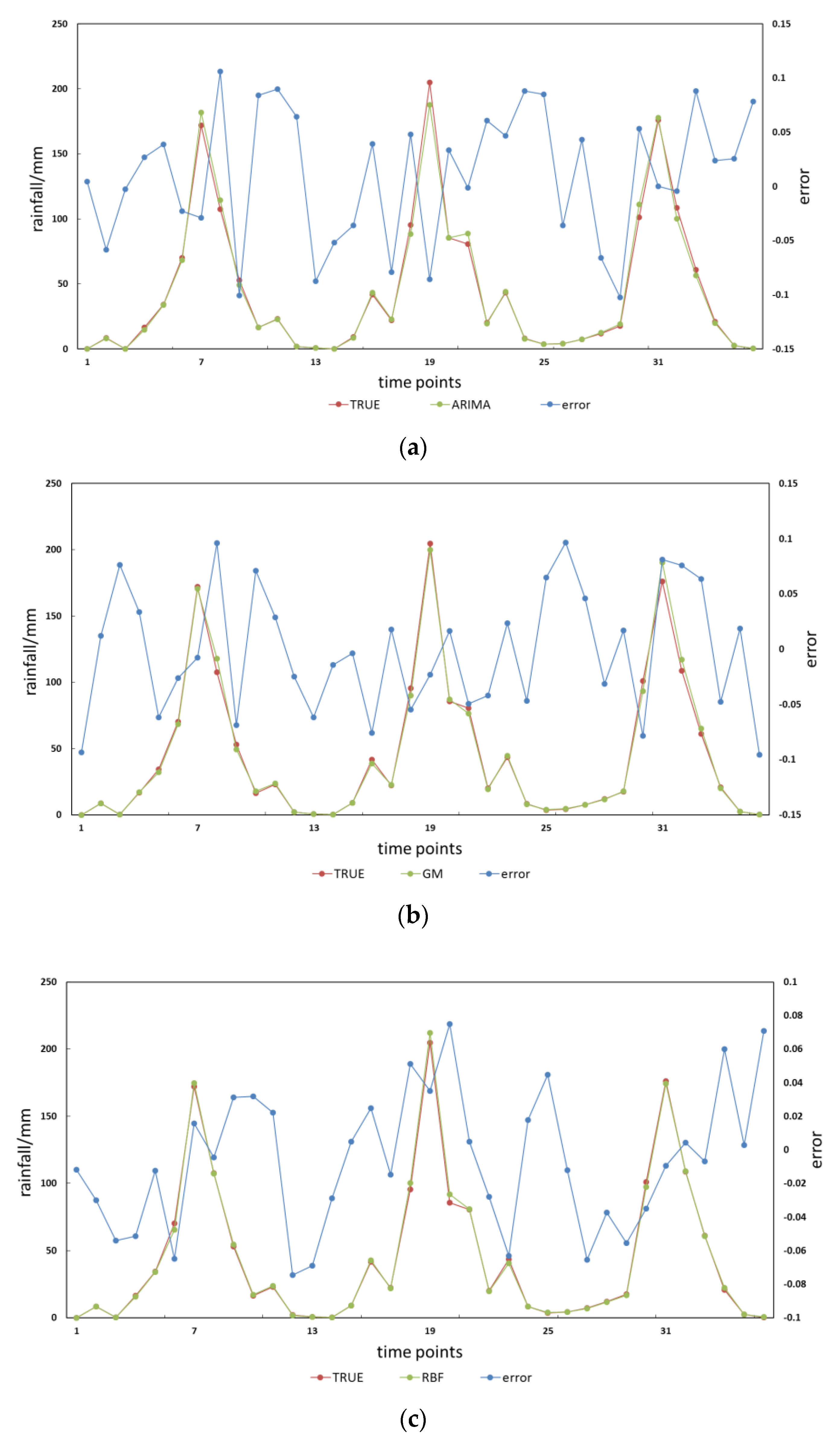
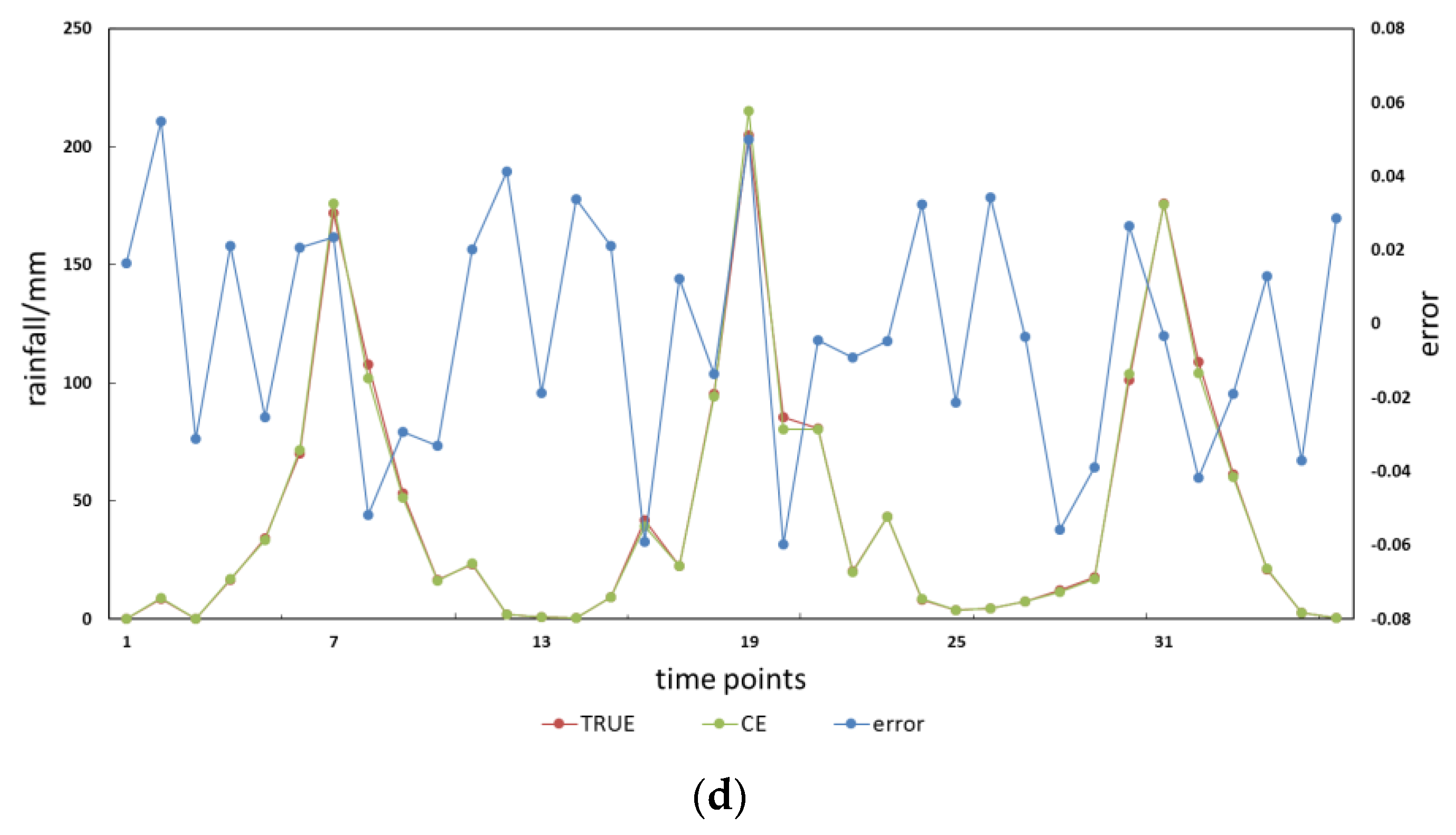
4. Results and Analysis
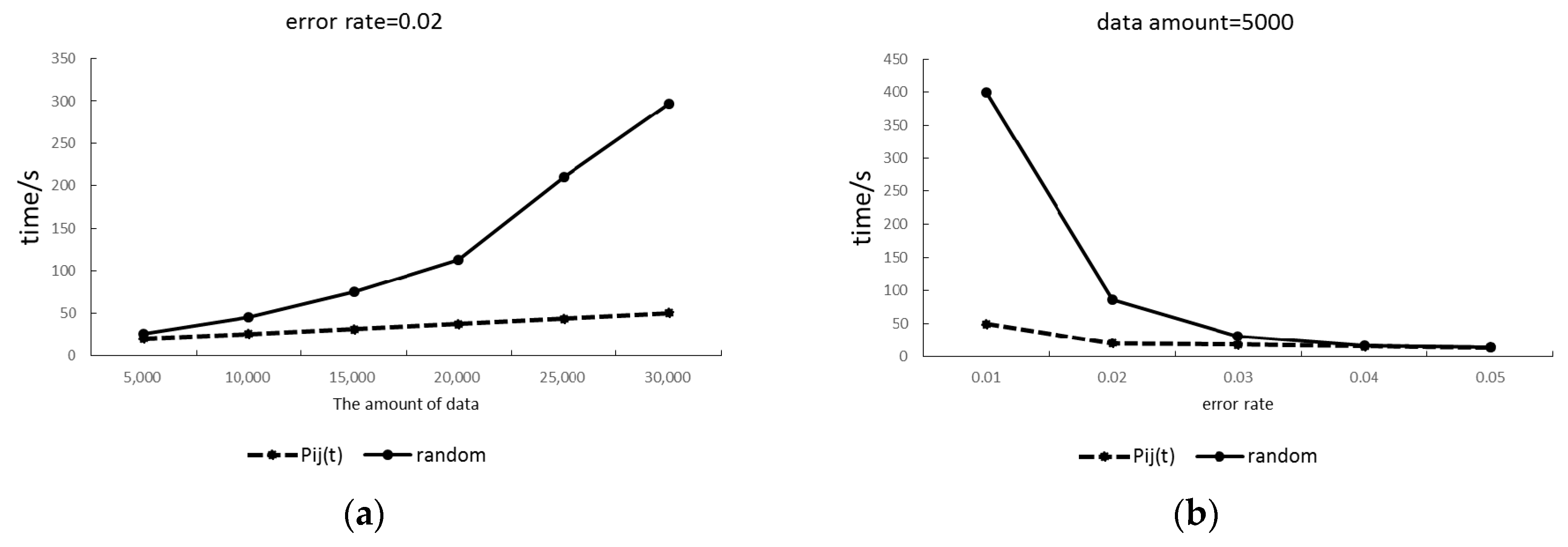
4.1. Predictive Stability Comparison Results
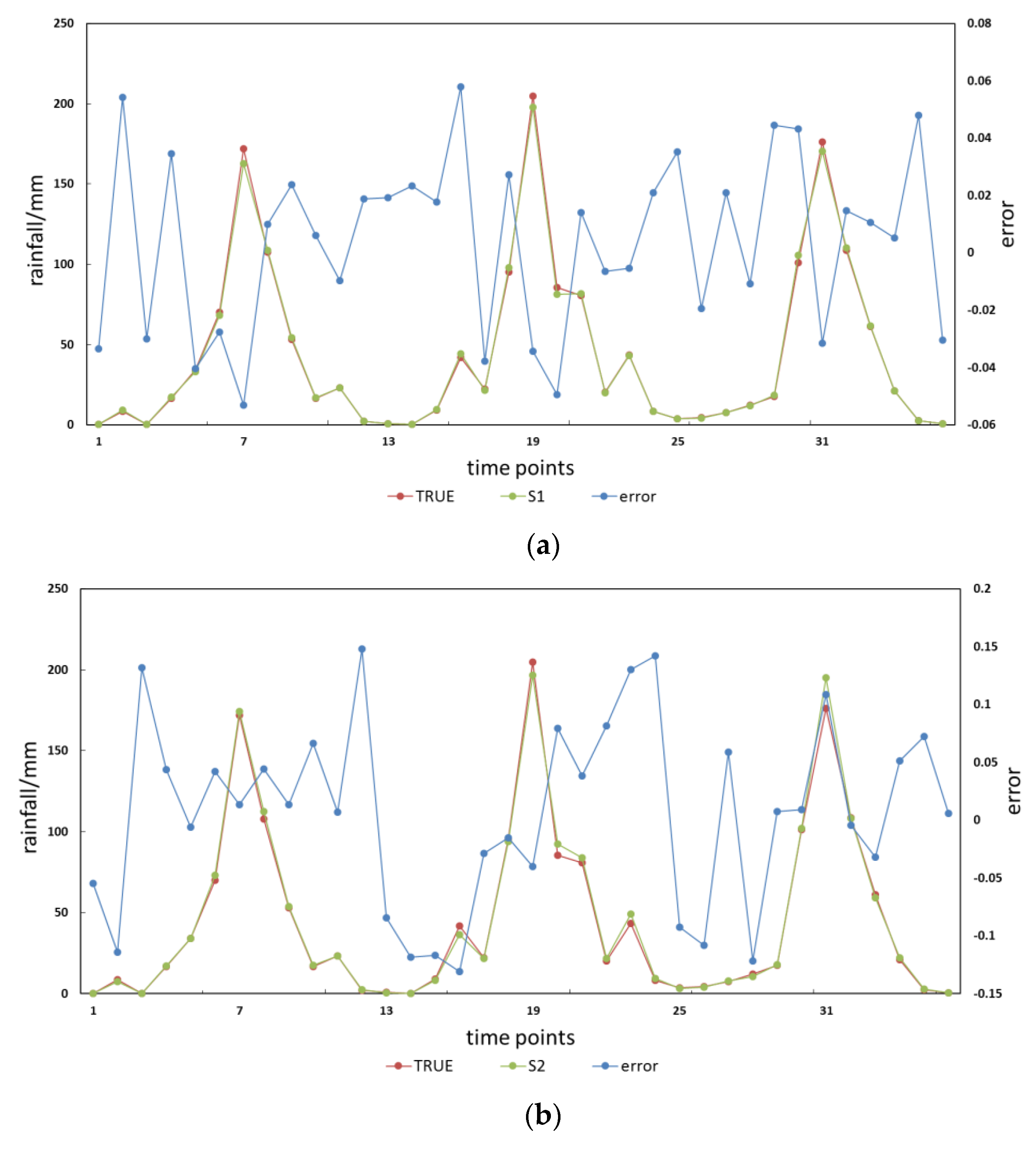
4.2. The Influence of Clustering Method on Prediction Results
- Scenario 1: Traditional c-means clustering method
- Scenario 2: We do not cluster historical data.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Serreze, M.C.; Etringer, A.J. Precipitation characteristics of the Eurasian Arctic drainage system. Int. J. Climatol. 2003, 23, 1267–1291. [Google Scholar] [CrossRef]
- Bustamante, J. Evaluation of April 1999 Rainfall Fore-casts Over South American using the Eta Model Climanalise, Divulgacao Científica. Cachoeira Paulista 1999, 6, 3563–3569. [Google Scholar]
- Black, T. The New NMC Mesoscale ETA Model: Descriptionand Forecast Examples. Whether Forecast. 1994, 9, 265–278. [Google Scholar] [CrossRef]
- Mossad, A.; Alazba, A.A. Drought Forecasting Using Stochastic Models in a Hyper-Arid Climate. Atmosphere 2015, 6, 410–430. [Google Scholar] [CrossRef]
- Bian, H.J.; Lei, H.J.; Wang, Y. Application of Grey Theory to Regional Rainfall Rorecast. Anhui Agri. Sci. 2009, 37, 6059–6060. [Google Scholar]
- Yang, J.L.; Wu, Y.N.; Xie, M.; Li, H.Y. Application of Monte Carlo Method in Rainfall Forecast of Flood Season in Nenjiang Basin. S. N. Water Transf. Water Sci. Technol. 2011, 9, 28–32. [Google Scholar]
- Ramirez, M.C.V.; de Campos Velho, H.F.; Ferreira, N.J. Artificial Neural Network Technique for Rainfall Forecasting Applied to the Sao Paulo Region. J. Hydrol. 2005, 301, 146–162. [Google Scholar] [CrossRef]
- Manzato, A. Sounding-derived indices for neural network based short-term thunderstorm and rainfall forecasts. Atmos. Res. 2007, 83, 349–365. [Google Scholar] [CrossRef]
- Yang, S.; Rui, J.; Feng, H. Application of Support Vector Machine (SVM) Method in Precipitation Classification Forecast. J. Southwest. Agric. Univ. 2006, 28, 252–257. [Google Scholar]
- Cui, L.; Chi, D.; Qu, X. Based on Wavelet De-noising of Stationary Time Series Analysis Method in Rainfall Forecasting. China Rural Water Hydropower 2010, 9, 31–35. [Google Scholar]
- Merlinde, K. The Application of TAPM for Site Specific Wind Energy Forecasting. Atmosphere 2016, 7, 23. [Google Scholar] [CrossRef]
- Lauret, P.; Lorenz, E.; David, M. Solar Forecasting in a Challenging Insular Context. Atmosphere 2016, 7, 18. [Google Scholar] [CrossRef]
- Men, B.; Liu, C.; Xia, J.; Liu, S.; Lin, Z. Application of R/S Analysis Method of Water Runoff Trend in West Route of South-to-North Water Transfer Project. J. Glaciol. Geocryol. 2005, 27, 568–573. [Google Scholar]
- Soro, G.E.; Noufé, D.; Goula Bi, T.A.; Shorohou, B. Trend Analysis for Extreme Rainfall at Sub-Daily and Daily Timescales in Côte d’Ivoire. Climate 2016, 4, 37. [Google Scholar] [CrossRef]
- Chen, C.-S.; Duan, S.; Cai, T. Short-term photovoltaic generation forecasting system based on fuzzy recognition. Trans. China Electrotech. Soc. 2011, 26, 83–88. [Google Scholar]
- Liu, Y.; Fu, X.; Zhang, W. Short-term load forecasting method based on fuzzy pattern recognition and fuzzy cluster theory. Trans. China Electrotech. Soc. 2002, 17, 83–86. [Google Scholar]
- Kolentini, E.; Sideratos, G.; Rikos, V. Developing a Matlab tool while exploiting neural networks for combined prediction of hour’s ahead system load along with irradiation, to estimate the system loadcovered by PV integrated systems. In Proceedings of the IEEE Conferences on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 182–186. [Google Scholar]
- Bates, J.; Granger, C. The combination of forecast. Oper. Res. Q. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, C. Wind Power Generation Forecasting Using Least Squares Support Vector Machine Combined with Ensemble Empirical Mode Decomposition, Principal Component Analysis and a Bat Algorithm. Energies 2016, 9, 261. [Google Scholar] [CrossRef]
- Pedersen, J.W.; Lund, N.S.V.; Borup, M.; Löwe, R.; Poulsen, T.S.; Mikkelsen, P.S.; Grum, M. Evaluation of Maximum a Posteriori Estimation as Data Assimilation Method for Forecasting Infiltration-Inflow Affected Urban Runoff with Radar Rainfall Input. Water 2016, 8, 381. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis, Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Men, B.; Long, R.; Zhang, J. Combined Forecasting of Stream flow Based on Cross Entropy. Entropy 2016, 18, 336. [Google Scholar] [CrossRef]
- Cui, D. Application of Combined Model in Rainfall Forecast. Comput. Simul. 2012, 29, 163–166. [Google Scholar]
- Xiong, L.; O’Connor, K.M.; Kieran, M. Comparison of four updating models for real-time river flow forecasting. Hydrol. Sci. J. 2002, 47, 621–640. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.; Zhou, J.; Vijay, P.; Guo, S.; Zhang, J. Real-time error correction method combined with combination flood forecasting technique for improving the accuracy of flood forecasting. J. Hydrol. 2015, 521, 157–169. [Google Scholar]
- Singh, V.P. Entropy Based Parameter Estimation in Hydrology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Cui, H.; Singh, V.P. Entropy spectral analyses for groundwater forecasting. J. Hydrol. Eng. 2017, 22, 06017002. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Xiong, F. An Entropy-Based Generalized Gamma Distribution for Flood Frequency Analysis. Entropy 2017, 19, 239. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P. Generalized Beta Distribution of the Second Kind for Flood Frequency Analysis. Entropy 2017, 19, 254. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.L.; Zhou, J.; Ye, L. Copula entropy coupled with artificial neural network for rainfall-runoff simulation. Stoch. Environ. Res. Risk Assess. 2014, 28, 1755–1767. [Google Scholar] [CrossRef]
- Li, R.; Liu, H.L.; Lu, Y.; Han, B. A combination method for distribution transformer life prediction based on cross entropy theory. Power Syst. Prot. Control 2014, 42, 97–101. [Google Scholar]
- Chen, N.; Sha, Q.; Tang, Y.; Zhu, L. A Combination Method for Wind Power Predication Based on Cross Entropy Theory. Proc. CSEE 2012, 32, 29–34. [Google Scholar]
- Mehdi, N.; Hossein, N. Image denoising in the wavelet domain using a new adaptive thresholding function. Neurocomputing 2009, 72, 1012–1025. [Google Scholar]
- Asgari, M.S.; Abbasi, A. Comparison of ANFIS and FAHP-FGP methods for supplier selection. Kybernetes 2016, 45, 474–489. [Google Scholar] [CrossRef]
| Month | 12, 1, 2 | 3, 4, 5 | 6, 7, 8 | 9, 10, 11 |
|---|---|---|---|---|
| value | 0.1 | 0.3 | 0.5 | 0.7 |
| ARIMA | GM | RBF | CE | |||||
|---|---|---|---|---|---|---|---|---|
| MRPE | RMSE | MRPE | RMSE | MRPE | RMSE | MRPE | RMSE | |
| 2011 | 12.13% | 5.53% | 11.15% | 4.49% | 10.99% | 4.21% | 10.02% | 3.93% |
| 2012 | 9.44% | 4.99% | 13.15% | 4.97% | 8.65% | 5.01% | 9.45% | 4.32% |
| 2013 | 11.10% | 7.12% | 7.22% | 6.19% | 7.01% | 4.49% | 6.88% | 4.17% |
| Average | 10.89% | 5.88% | 10.51% | 5.22% | 8.88% | 4.57% | 8.78% | 4.14% |
| S1 | S2 | |||
|---|---|---|---|---|
| MRPE | RMSE | MRPE | RMSE | |
| 2011 | 10.04% | 3.89% | 13.01% | 7.12% |
| 2012 | 9.41% | 4.34% | 12.04% | 8.14% |
| 2013 | 6.92% | 4.17% | 10.29% | 7.71% |
| Average | 8.79% | 4.19% | 11.78% | 7.66% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, B.; Long, R.; Li, Y.; Liu, H.; Tian, W.; Wu, Z. Combined Forecasting of Rainfall Based on Fuzzy Clustering and Cross Entropy. Entropy 2017, 19, 694. https://doi.org/10.3390/e19120694
Men B, Long R, Li Y, Liu H, Tian W, Wu Z. Combined Forecasting of Rainfall Based on Fuzzy Clustering and Cross Entropy. Entropy. 2017; 19(12):694. https://doi.org/10.3390/e19120694
Chicago/Turabian StyleMen, Baohui, Rishang Long, Yangsong Li, Huanlong Liu, Wei Tian, and Zhijian Wu. 2017. "Combined Forecasting of Rainfall Based on Fuzzy Clustering and Cross Entropy" Entropy 19, no. 12: 694. https://doi.org/10.3390/e19120694
APA StyleMen, B., Long, R., Li, Y., Liu, H., Tian, W., & Wu, Z. (2017). Combined Forecasting of Rainfall Based on Fuzzy Clustering and Cross Entropy. Entropy, 19(12), 694. https://doi.org/10.3390/e19120694




