Abstract
This study has developed a technique for identifying the presence of muscle fatigue based on the spatial changes of the normalised mutual information (NMI) between multiple high density surface electromyography (HD-sEMG) channels. Muscle fatigue in the tibialis anterior (TA) during isometric contractions at 40% and 80% maximum voluntary contraction levels was investigated in ten healthy participants (Age range: 21 to 35 years; Mean age = 26 years; Male = 4, Female = 6). HD-sEMG was used to record 64 channels of sEMG using a 16 by 4 electrode array placed over the TA. The NMI of each electrode with every other electrode was calculated to form an NMI distribution for each electrode. The total NMI for each electrode (the summation of the electrode’s NMI distribution) highlighted regions of high dependence in the electrode array and was observed to increase as the muscle fatigued. To summarise this increase, a function, M(k), was defined and was found to be significantly affected by fatigue and not by contraction force. The technique discussed in this study has overcome issues regarding electrode placement and was used to investigate how the dependences between sEMG signals within the same muscle change spatially during fatigue.
1. Introduction
Muscle fatigue is caused by multiple factors, and while there is no precise definition [1], it is commonly defined symptomatically as the progressive decline in force during sustained activity [2]. There are a number of neuromuscular parameter changes associated with muscle fatigue, including an increase in lactic acid [2], reduced muscle fibre conduction velocity (MFCV) [3], and an increase in cell hyperpolarization period [4]. There are also changes in the behaviour of the motor units within the fatiguing muscle such as the firing rate, recruitment, and synchronisation of motor units [1,4,5,6,7]. To accurately assess these changes typically requires invasive techniques involving intramuscular electromyography (iEMG) [8,9]. More recently, developments in surface electromyography (sEMG) techniques have led to alternative approaches based upon motor unit decomposition techniques being proposed [10,11].
Using iEMG to investigate changes in motor unit behaviour has shortcomings as it can only record electrical activity from muscle fibres that are in close proximity to the needle and ignores the fibres that are distant. Recent developments in iEMG have led to techniques that could potentially address this issue [12]. However, when investigating muscle fatigue it is more desirable to use sEMG due to its non-invasive nature and its large recording area. There are many studies that have analysed changes in the fundamental spectral and time domain features of the sEMG, such as the median frequency or the root mean square [1,13]. However, these approaches have been found to be unreliable since many other factors can have a significant effect on them [14].
High density surface electromyography (HD-sEMG) is a recent development in the study of neuromuscular activity. It records electrical activity using a dense array of electrodes that cover one or more muscles, hence providing spatial dimensions to the sEMG recording. These recordings can be used to spatially map muscle activity and observe the time-space propagation of motor unit action potentials (MUAP). HD-sEMG has been used to estimate the locations of innervation zones (IZs), muscle fibre length and orientation, MFCV, and motor unit locations [15,16,17] as well as decompose sEMG signals into MUAPs [10,11].
Most studies that have investigated muscle fatigue using HD-sEMG have adopted techniques previously developed with sEMG [18,19,20,21]. However, techniques that rely on measuring the changes in sEMG amplitude or the frequency spectrum, which are aggregate measures, can potentially be misleading [14]. Introducing higher resolution spatial information does not minimise the inherent shortcomings of these techniques. There are some studies that have instead identified alternate features that are more reliable for identifying and studying muscle fatigue. One such feature is the MFCV that relies on HD-sEMG to measure the propagation velocity of action potentials non-invasively [21,22]. However, as discussed by Farina et al. [23], there are many issues surrounding the estimation of MFCV that have not yet been addressed. Similarly, motor unit decomposition could potentially identify changes in motor unit behaviour indicative of muscle fatigue, but there are concerns surrounding how to validate these techniques [24,25,26,27].
One possible alternative is to consider the relationships between the data from an information theoretic point of view and take advantage of the spatial information by studying the shared information in between electrodes using mutual information (MI) [28]. Unlike correlation based measures, MI can be used to measure both linear and nonlinear relationships [29]. MI has recently been used to assess dependences between sEMG signals [30,31,32,33,34]. However, because MI quantifies the amount of shared information between two variables, its value is relative to the total information content of the variables and its maximum value is defined by the variable entropies. Consequently, MI values are not comparable across datasets and therefore not ideally suited to sEMG recordings where there may be considerable inter-experiment variability. An alternative is normalized MI (NMI), which, unlike MI, is bounded and thus comparable across different datasets. NMI has been used in various areas including feature selection [35] and clustering [36] with several different functions of variable entropies proposed as methods for normalising the MI [29,37]. NMI applied to sEMG during fatiguing tasks has been shown to increase with fatigue [30,31,38].
Previous work reported that the NMI between electrodes of a HD-sEMG array increases with muscle fatigue [39]. This work described the NMI between rows of the electrode array running parallel to the muscle fibre direction. Therefore, this work did not take account of the full spatial information provided by the HD-sEMG. Calculating the NMI between all electrode combinations within the array could give a more complete picture of how the dependences vary across the space of the electrode array with the onset of muscle fatigue. Such an approach, unlike many existing approaches, would be less reliant on the amplitude of the signal and would not require careful alignment of the electrodes to the muscle. However, it would also generate a large number of different NMI values to be analysed.
In this paper, we have derived a new measure that incorporates the NMI between all electrode combinations to describe the spatial changes in NMI across the HD-sEMG electrode array during muscle fatigue. The tibialis anterior (TA) during isometric contractions at 40% and 80% maximum voluntary contraction (MVC) levels was investigated to test the hypothesis that the new measure will increase over time for the majority of the electrode array during fatigue. Statistical significance analysis was performed to observe the effect of fatigue and %MVC on the initial and final values of the new measure.
2. Materials and Methods
2.1. Participants
Ten healthy participants (Age range: 21 to 35 years; Mean age = 26 years; Male = 4, Female = 6) volunteered to participate in the experiment. Participants included in the experiment did not have any current muscular injures and no prior muscular disorders. The experimental protocol was approved by RMIT University Human Research Ethics Committee and in accordance with Helsinki Declaration (revised 2004). The experimental protocol was described to the participants and they gave oral and written consent for participation in the experiment.
2.2. Equipment
The HD-sEMG was recorded using a 64 channel monopolar recording system (W-EMG, Bitron, Torino, Italy) configured to use two electrode arrays of 32 electrodes (a 4 by 8 grid of electrodes). The electrodes in the array were exposed metal pads on a Kapton substrate with an inter electrode distance of 5 mm. The arrays were arranged into a 4 by 16 grid (4 columns, 16 rows) of electrodes for easy placement over the TA as shown in Figure 1. Double sided foam tape was used to secure the arrays over the muscle. The tape has holes of 3 mm diameter that line up with the electrodes and were filled with a conductive gel allowing the electrodes to contact the skin. The HD-sEMG device uses a 24 bit Analogue to Digital converter (ADC) to sample the sEMG at 2441 Hz, the signals are amplified by 192.75 V/V and band pass filtered (10–500 Hz).
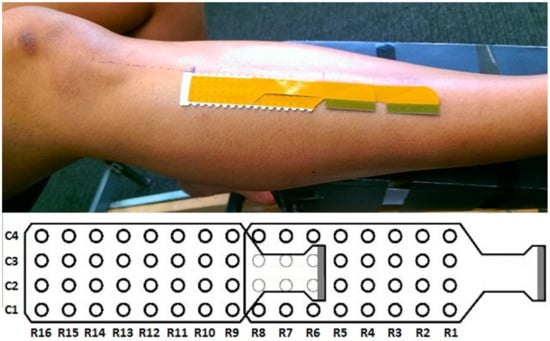
Figure 1.
Electrode arrangement and position.
2.3. Electrode Placement
The electrode array was placed such that the columns of the array ran close to parallel with the muscle fibres direction [40] and the centre of the array passed over the IZ of the TA as shown in Figure 1. The likely location of the IZ for the TA was estimated to be 34% between the tibila tuberosity and intermalleolar line from the tibila tuberosity [41]. The skin was cleaned and exfoliated before placing the electrode array over the TA and the reference electrodes were placed on the ankle.
2.4. Experimental Procedure
The experimental protocol outlined in this section has been reported in our earlier publication [39]. During the experiment, participants were asked to sit in a sturdy chair with their leg extended along a leg rest with their foot secured to a foot plate at the end. This set up was adjusted for each participant so that their hip, knee, and ankle angles were at 90, 140, and 90 degrees (neutral position), respectively. A force sensor was attached between the foot plate and the frame of the leg reset, and the sensor was below the foot and perpendicular to the foot plate.
The first step in the experiment was to determine the MVC of each participant while performing dorsiflexion. In order to achieve this, the participants were asked to perform a dorsiflexion at their maximum force capacity for 5 s. This was repeated three times with a 2 min rest between each contraction. During these trials, the force of the contraction was recorded and the maximum force out of the three trials was noted as the participant’s MVC.
The participants were then asked to perform an isometric dorsiflexion at 40% of their MVC. The real-time output of the force sensor was displayed to the participant, and the display was marked to show the corresponding force required for 40% MVC. The participants matched the mark with their force and maintained the contraction until an endurance limit was met or until they felt pain.
The endurance limit was defined as the time when the measured force output of the participant dropped 5% MVC below the mark and the participant was unable to recover and reach the mark. Similar endurance limit protocols have been used in previous fatigue studies [7,42,43,44]. Having reached their endurance limit, the participant was considered to be fatigued and then rested for a minimum of 30 min and until they reported that they had recovered and had no pain or felt no fatigue in the TA. The experiment was repeated again but for 80% MVC. During these trials, the HD-sEMG output was monitored and recorded.
2.5. Data Analysis
In order to identify the change in the state of the muscle, the NMI between the various physical locations in the electrode array was computed. This section explains the calculation of the NMI and the steps that were followed to analyse the NMI of the EMG.
2.5.1. Computation of NMI
MI can be defined as a function of Shannon entropies and conditional entropies such that
Hence, the mutual information is bounded by [28,45]:
The lower bound of MI takes the value of 0 only when the variables are independent; however, the upper bound is dependent on the information content of the individual variables, which can vary greatly. Thus, it is preferable to normalise the MI to the range of 0 to 1 resulting in a NMI given by
For variables X and Y with measurements and , the entropies can be defined in terms of the probability distributions as
and the MI as
The base of the log, u, determines the units of the information measures. In this study, u was set to 2 making the units bits.
2.5.2. Approximating the Probability Distributions of the Data
Different approaches for estimating the probability distributions used for calculatating the entropy or MI exist in an attempt to overcome problems with possible bias and variance in the estimation [46]. In the present study, we are interested in investigating the changes in NMI due to fatigue. Since we are only considering the relative changes within a single dataset, we have opted to use a straightforward histogram method with uniform partitioning.
For a time series X with N elements, histograms can be constructed using b bins uniformly partitioned across the range of X, with the value of b determined by the rice rule [47] as
The occupancy of the ith bin in the histogram of X is denoted by the function where . The probability distribution of X is then approximated by
where is the approximated probability distribution of X and whose sum is equal to 1.
In order to calculate the mutual information between two time series X and Y, the joint probability distribution of the variables needs to be approximated. In order to achieve this, a 2D plane was created, with each axis assigned to a variable and representing the range of that variable. Both axes were then partitioned into b bins creating bins over the whole plane. The occupancy of each bin was denoted by the function where i refers to the X-axis partitions and j refers to the Y-axis partitions. To allocate data points to the appropriate bins, simultaneously sampled elements of the time series are paired, such that, in total, there were N occupants on the 2D plane. The joint probability distribution of X and Y was then approximated by
where is the approximated joint probability distribution of X and Y and whose sum is equal to 1.
2.5.3. Analysis of NMI of the HD-sEMG
Step 1: Segmentation of the HD-sEMG Data
For each participant, the HD-sEMG data from the electrode array was split into W non-overlapping windows of N samples. Using a fixed value of N ensures that the NMI calculations are performed over the same amount of data but results in the number of windows, W, varying between subjects depending on their individual endurance limits.
A three dimensional matrix of dimensions was generated. Each element of , , is populated with N HD-sEMG samples recorded during window w by the electrode located in row r and column c, where , , and . In this study, , , and W varied between subjects.
Step 2: Computing Normalised Mutual Information
Using the approximated probability distribution outlined in Equation (8), the entropy of each was calculated using Equation (4). From the approximated probability distributions in Equations (8) and (9), the mutual information between pairs of electrodes and were calculated using Equation (6) and then normalised to the range 0 to 1 using Equation (3) to give , where is the normalised mutual information between the electrodes located at positions and during window w. The NMI of and can be considered as a scale of dependence between the elements, where 0 indicates that and are independent and 1 indicates that they are completely dependent.
In all calculations of the entropy and MI, the conventions , , and were used.
Step 3: Measuring Spatial Changes in Normalised Mutual Information
To investigate the spatial changes in NMI across the electrode array, the NMI for every combination of pairs of elements in the row and column dimensions of was computed. This was then repeated for each of the W time windows. This results in NMI values for each electrode, hence making it necessary to consider how best to represent this data to give an understanding of the spatial changes in the NMI across the electrode array. In our previous publication [48], we considered a threshold approach that gave a count of the number of electrodes each electrode could be considered similar to, for any given time window. However, this approach relies on an appropriate selection of the threshold value. As an alternative, to give a more complete overview of the total information across the array, we propose a new approach based on integrating the NMI of each electrode with every other electrode.
A three-dimensional matrix with dimensions was created such that each element, , contains the double summation of the NMI values of the electrode at row i and column j with every other electrode during time window w defined by:
where is the NMI between the elements of corresponding to the electrode at row i column j and the one at row m and column n, for the wth window.
Step 4: Time Normalisation for Inter-Subject Comparison
The proposed matrix provides a measure of the spatial changes in the NMI with time. However, the data from each subject had a different number of windows, making it necessary to normalise the data to a fixed number of segments for comparison between subjects. To achieve this, the number of time windows, W, defined by each subject’s individual endurance limit, was divided into 10 equal segments such that the number of windows in each segment is given by . In the case where W is not a multiple of 10, we define and exclude time windows from the analysis. Since the primary focus of this study is the analysis of muscle fatigue, the time windows excluded were taken from the start of the recording where muscle fatigue is less likely to be present. This resulted in 10 segments with window indices from to where .
Having allocated the windows to be included into each segment, a normalised matrix with dimensions was defined by averaging the NMI from each of the time windows making up the segment. The elements of , , were defined by:
The sum for each time segment of was calculated using the function given by:
The function was then used as an overall summary of the similarities between the electrodes in the high density electrode array. Statistical tests were also performed to determine if fatigue or contraction force had a significant effect on .
2.5.4. Statistical Analysis
A normality test of was performed using the Shapiro–Wilk test. After confirming its normality, an ANOVA statistical significance test was used to determine if contraction force (40% and 80% MVC) or fatigue (Initial () and final ()) had a significant effect on the function.
3. Results
3.1. NMI Result for a Single Electrode
Figure 2 is an example of the NMI for a single electrode with every other electrode using data recorded during 40% and 80% MVC from a representative subject. In this example, we have considered the electrode located in row 9 () and column 3 (); therefore, only the NMI between pair combinations that include this electrode are shown in Figure 2. The NMI for each pair combination is represented by a bar in the plot where the position of the element (or second electrode of the pair) is given by the location in the row and column axis and the NMI axis represents its magnitude. The data has been normalised over time into 10 segments, and the initial (non-fatigued) and final (fatigued) time segments are shown in this plot.
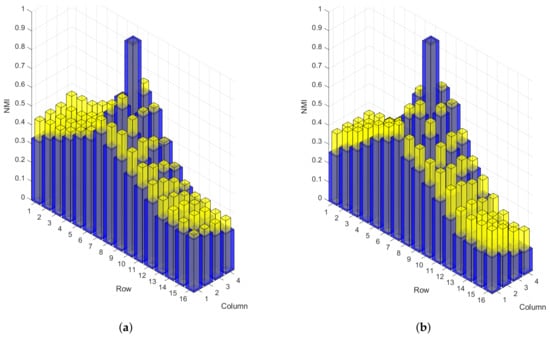
Figure 2.
An example of the Normalised Mutual Information (NMI) between the electrode positioned at row 9 column 3 and every other electrode showing the first (non-fatigued) and last (fatigued) time segments for 40% Maximum Voluntary Contraction (MVC) in plot (a) and 80% MVC in plot (b). Blue bars represent the NMI during the non-fatigued state and yellow bars represent the NMI during the fatigued state.
A peak exists in row 9 column 3 of Figure 2 since the NMI of a signal with itself results in a value of 1. All the other points form a slope around this peak. This indicates that the NMI decreases as the distance in between the pair of electrodes increases. It is also observed that the NMI is comparably larger during the fatigued state for the majority of the array. Since this increase in NMI did not occur in any particular direction relative to row 9 column 3, changes in dependences both parallel and perpendicular to the fibre direction of the muscle were identified. These observations were typical of the results seen as is illustrated by the increase in total NMI discussed in the following section.
Increases in the NMI in both directions of the array can be attributed to a number of different physiological changes that occur during muscle fatigue. Two of the primary changes being motor unit synchronisation and decrease in MFCV. The occurrence of motor unit synchronisation is likely to contribute to the increase in NMI perpendicular to the muscle fibre direction more so than the parallel direction. Electrodes positioned in different columns are more likely recording different combinations of motor units, if these motor units beginning to synchronise the similarity between columns would increase. The decrease in MFCV contributes to the increase in NMI parallel to the fibre direction. The decrease in conduction velocity during muscle fatigue would increase the delay in the propagating MUAP, thereby increasing the dependences between greater numbers of electrodes.
3.2. Comparison of Total NMI for Different MVC Levels
Figure 3 shows the differences in for two MVC levels (40% and 80%) over the duration of the fatiguing contraction from a representative subject. The magnitude maps of shown in Figure 3 are during time segments k = 1, 5, and 10 for one representative subject. The top three plots in Figure 3 show the magnitude of during the 40% MVC contraction and the bottom three are for the 80% MVC contraction. The horizontal axis is the columns of the array and the vertical is the rows in the array. The colour of each point on the plot represents the magnitude of (shown in Equation (10)) or alternatively the total NMI for that electrode during time segment k.
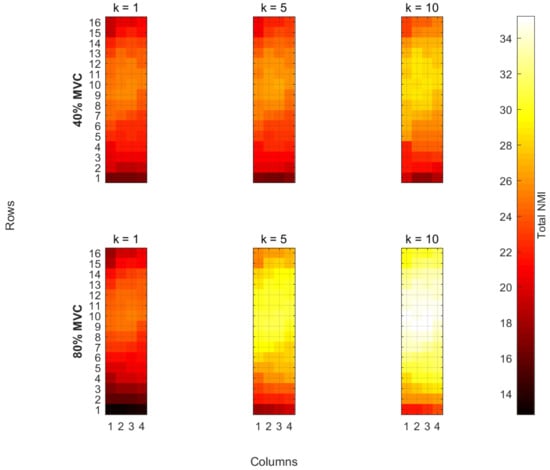
Figure 3.
Eample Magnitude Maps of for one subject.
Visual inspection of Figure 3 shows that there is no significant difference between the start of 40% and 80% MVC trials. It can be seen that the total NMI for each electrode is increasing over the duration of the exercise in most regions of the map during both trials. For this particular subject, the increase in the total NMI is greater in the 80% MVC plots compared with the 40% MVC. However, this was not the case for all subjects, which can be seen from the results of the statistical analysis (Section 3.4) and the similarities in the average plots (Figure 4 and Table 1).
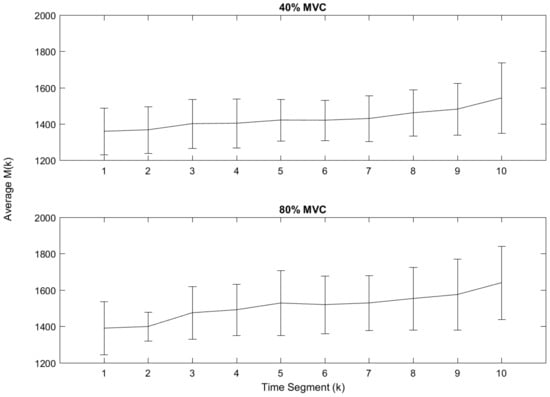
Figure 4.
Average for all participants.

Table 1.
Comparison of average for 40% and 80% Maximum Voluntary Contraction (MVC) for all participants.
The total NMI for each electrode represents a similarity score between itself and the rest of the electrode array where higher scores indicate a greater degree of dependence between electrodes. From Figure 3, it can be seen that, in all of the plots, there is an area of the array which has consistently higher values of . While the exact location of the IZ for each subject was not verified during the study, the electrode array was placed such that it is likely covering an IZ. It can be expected that the regions with higher total NMI scores are likely to be located over the IZ for the muscle. This is because electrodes that are close to the IZ are close to the origin of the action potentials for various motor units and hence should share a dependence with a large number of the other electrodes.
3.3. Comparison of the Average M(k) for Different MVC Levels
The function, which is the sum of during time segment k, is the overall score of dependences between all the electrodes and can also be thought of as a score for overall similarity. Figure 4 shows the average value of the function calculated from each participant for each time segment k. The upper plot in Figure 4 shows the 40% MVC data and the lower shows the 80% MVC data. The vertical axis represents the average value of , the horizontal axis is the time segment, k, and the error bars represent the standard deviation for each point. It can be seen from these plots that the average steadily increases over time for both 80% and 40% MVC, illustrating the progression of muscle fatigue.
Table 1 also gives the initial and final values for the data displayed in Figure 4 with their standard deviations and the range of the average. From this information, it can be seen that the 80% MVC data has slightly larger values and range and, for both the 40% MVC and 80% MVC data, the standard deviation is at its largest when .
3.4. Statistical Analysis
From the ANOVA for , it was found that fatigue has a significant effect (F(1,36) = 16.24, p = 0.00028), while the MVC level did not have a significant effect (F(1,36) = 1.39, p = 0.25). The result also showed that the interaction between MVC and fatigue did not have a significant effect (F(1.36) = 0.38, p = 0.54). This indicates that muscle fatigue had a more significant effect on than the MVC. To further investigate the relationship between and fatigue a linear regression was performed for each subject. The slope of the regression of was positive for nine out of ten participants in both 40% and 80% MVC.
4. Discussion
Previous studies have used measures of dependence to identify muscle fatigue [4,44,49] or have reported changes in the dependence between muscles during fatiguing tasks [30,31,38]. There are many physiological changes that occur in the muscle due to fatigue [1,3,4,5,6,7], many of which will contribute to changes in the dependences between electrodes or muscles. Two well-known examples of changes that occur during muscle fatigue that can influence the similarity of the signals measured at different electrodes are decreases in MFCV and increases in motor unit synchronisation [5,7]. However, when measuring these changes, the orientation of the muscle fibre between electrodes and the location of the IZ relative to the electrodes will impact the measure [7,50]. Therefore, any measures of the dependence between electrodes would also vary depending on the position of the electrode relative to the muscle. This was observed in both our current study and our previous work [39,48]. While the specific underlying physiological causes for the observed changes in dependence between electrodes during fatigue have not been identified in this study, some of the changes associated with fatigue are discussed in terms of how they would affect the dependence.
For this study, HD-sEMG recordings of the TA during muscle fatigue were analysed. Earlier research has shown that, during fatigue of the TA, both synchronisation of motor units [51,52] and decreases in MFCV [40] occur. Therefore, it was anticipated that such symptoms of muscle fatigue would likely occur during our experiment. The results show that, as the participants in our study experienced fatigue in their TA, the NMI of the sEMG recorded from multiple electrodes in the high density array increased. If we consider the known changes in motor unit behaviour during muscle fatigue and the MFCV [1,3,4,5,6,7], we can develop a plausible foundation for why the NMI increases during muscle fatigue.
In the case of a single motor unit, an increase in MFCV will increase the distance between consecutive MUAPs; conversely, a decrease in MFCV will lead to a decrease in the distance. Changes in the distance between MUAPs will result in changes to the spread of the electrodes, parallel to the direction of the muscle fibres, which have high similarity. In the same case, increasing or decreasing the firing rate will also lead to a corresponding increase or decrease in the number of MUAPs within a given fibre length. An increasing number of MUAPs, within the length of the muscle fibres covered by the array, will result in an increase in the similarity of a larger number of electrodes. If multiple motor units are included, then the concepts of motor unit synchronisation and recruitment can be introduced. When motor units synchronise, their firing rates match, while changes in the recruitment of motor units causes an increase or decrease in the overall number of MUAPs within a given area. Changes in synchronisation will lead to changes in dependences, particularly between electrodes perpendicular to the direction of the muscle fibres, whereas, as with the changes in the firing rates, the larger number of MUAPs will lead to a larger number of electrodes with high similarity in the direction parallel to the muscle fibre.
During fatigue, it would be expected that the MFCV is decreasing, motor units are synchronising, and motor unit firing rates and recruitment would vary depending on the force and endurance time. The interaction of these different factors can be captured by the increasing similarity in the sEMG signal recorded from each electrode in the high density array and therefore increase the NMI. However, as the NMI measures all linear and nonlinear dependences between data sets [53], it is not limited to just changes in motor unit behaviour. There may be a number of factors that can affect similarities between different sEMG signals, not all necessarily related to muscle fatigue. It is important to consider these factors when interpreting the NMI.
In the current study, the NMI between every pair combination of electrodes in the electrode array was calculated to investigate how the NMI changes spatially over the muscle during muscle fatigue. Figure 2 provides an example of how the NMI is organised spatially for each electrode, and it clearly illustrates that the larger the distance between electrodes, the smaller their resulting NMI. It also demonstrates that the NMI between a single pair of electrodes is not sufficient to represent or summarise the dependence of each electrode with respect to the region covered by the electrode array. The matrix was developed in response to this issue. It summarises the dependences of each electrode over the entire electrode array by finding the total NMI of each electrode. This matrix also doesn’t necessarily require the electrode array to be oriented with the muscle fibre direction, only that all the electrodes in the array cover the same muscle. The values of the matrix were shown to increase with fatigue as does the function, which was shown to be significantly affected by fatigue.
There is the potential that the magnitude maps produced by the matrix could provide an alternative method for identifying the location of the IZ. Locating the IZ in muscles is not always a simple task for muscles that do not have parallel fibres. Muscles like the biceps are large, have parallel fibres and usually have a well-defined IZ, but if the muscle is small or has a more complex arrangement of muscle fibres, then identifying the IZ can become more difficult. Studies investigating the distribution of IZ in the TA using HD-sEMG [54,55] and chemical analysis [56] have found that the distribution can be scattered and varies between subjects. Visually inspecting HD-sEMG recordings for propagating waveforms is often used to reveal the approximate location of an IZ [41,54,55]. Other techniques have also been developed to automate the process and improve the estimation of the location [57,58,59]. These techniques rely on knowing the fibre orientation of the muscle and typically only consider one spatial dimension. In contrast, the matrix described in this paper can find two-dimensional regions of high dependence irrespective of the fibre orientation of the muscle.
In our previous study [48], a similar methodology to the one used in this paper was developed based on identifying the number of electrodes that were similar to each electrode. An electrode was considered similar to another electrode if the NMI between them was greater than a predefined threshold; such an event was called an interaction. The number of interactions each electrode had during each time window was recorded and analysed during fatiguing contractions. The advantage of the interaction methodology is it directly shows how many electrodes are similar to each electrode. However, there are two inherent problems when using interactions. First, it is not known what threshold value is appropriate for this application. Second, the number of interactions for an electrode does not supply any information about how similar each electrode is to it. The methodology presented in this study addresses the second problem by finding the double summation of the NMI distribution, shown in Figure 2, for each electrode. However, all information about the distribution of the NMI between electrodes is lost.
While this study has not directly investigated the cause of the changes observed, the results support the hypothesis proposed by earlier researchers that there is an increase in dependence between electrodes during muscle fatigue. In future work, motor unit decomposition techniques could be employed to verify and investigate the underlining physiology that contributed to these observed changes in dependence.
5. Conclusions
In this study, HD-sEMG recordings of the TA during a fatiguing contraction were used to analyse the spatial distribution of NMI and identify the presence of muscle fatigue. We developed a technique based on the NMI that minimises the potential for any spatial biases to be introduced. The NMI distribution for each electrode illustrated that the distance between electrodes can affect the NMI, and larger distances resulted in smaller NMI values. The matrix increased in magnitude over the duration of the muscle contraction, which concluded at the participants’ endurance limit due to muscle fatigue. This matrix also highlighted regions of high total NMI values. Further work is required to understand the physiological significance of these regions. The function also increased with muscle fatigue, and this increase was shown to be significantly affected by fatigue and not by contraction force. The technique developed in this study is a unique solution for measuring fatigue whilst also minimizing issues caused by electrode placement.
Acknowledgments
We would like to thank everyone who participated in this study for volunteering their time.
Author Contributions
Adrian Bingham and Sridhar P. Arjunan conceived and designed the experiments; Adrian Bingham also performed the experiments, analysed the data, interpreted the results and wrote the paper; Sridhar P. Arjunan, Beth Jelfs and Dinesh K. Kumar all assisted in interpreting the results and editing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Enoka, R.M. Mechanisms of muscle fatigue: Central factors and task dependency. J. Electromyogr. Kinesiol. 1995, 5, 141–149. [Google Scholar] [CrossRef]
- Al-Mulla, M.R.; Sepulveda, F.; Colley, M. A review of non-invasive techniques to detect and predict localised muscle fatigue. Sensors 2011, 11, 3545–3594. [Google Scholar] [CrossRef] [PubMed]
- Beck, R.B.; O’Malley, M.J.; Stegeman, D.F.; Houtman, C.J.; Connolly, S.; Zwarts, M.J. Tracking motor unit action potentials in the tibialis anterior during fatigue. Muscle Nerve 2005, 32, 506–514. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.K.; Arjunan, S.P.; Naik, G.R. Measuring Increase in Synchronization to Identify Muscle Endurance Limit. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 578–587. [Google Scholar] [CrossRef] [PubMed]
- Carpentier, A.; Duchateau, J.; Hainaut, K. Motor unit behaviour and contractile changes during fatigue in the human first dorsal interosseus. J. Physiol. 2001, 534, 903–912. [Google Scholar] [CrossRef] [PubMed]
- Jensen, B.R.; Pilegaard, M.; Sjøgaard, G. Motor unit recruitment and rate coding in response to fatiguing shoulder abductions and subsequent recovery. Eur. J. Appl. Physiol. 2000, 83, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Holtermann, A.; Grönlund, C.; Karlsson, J.S.; Roeleveld, K. Motor unit synchronization during fatigue: Described with a novel sEMG method based on large motor unit samples. J. Electromyogr. Kinesiol. 2009, 19, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Merletti, R.; Farina, D. Analysis of intramuscular electromyogram signals. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2009, 367, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Semmler, J.G. Motor Unit Synchronization and Neuromuscular Performance. Exerc. Sport Sci. Rev. 2002, 30, 8–14. [Google Scholar] [CrossRef] [PubMed]
- De Luca, C.J.; Chang, S.S.; Roy, S.H.; Kline, J.C.; Nawab, S.H. Decomposition of surface EMG signals from cyclic dynamic contractions. J. Neurophysiol. 2015, 113, 1941–1951. [Google Scholar] [CrossRef] [PubMed]
- Negro, F.; Muceli, S.; Castronovo, A.M.; Holobar, A.; Farina, D. Multi-channel intramuscular and surface EMG decomposition by convolutive blind source separation. J. Neural Eng. 2016, 13, 026027. [Google Scholar] [CrossRef] [PubMed]
- Muceli, S.; Poppendieck, W.; Negro, F.; Yoshida, K.; Hoffmann, K.P.; Butler, J.E.; Gandevia, S.C.; Farina, D. Accurate and representative decoding of the neural drive to muscles in humans with multi-channel intramuscular thin-film electrodes. J. Physiol. 2015, 593, 3789–3804. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Izal, M.; Malanda, A.; Gorostiaga, E.; Izquierdo, M. Electromyographic models to assess muscle fatigue. J. Electromyogr. Kinesiol. 2012, 22, 501–512. [Google Scholar] [CrossRef] [PubMed]
- Öberg, T.; Sandsjö, L.; Kadefors, R. Subjective and objective evaluation of shoulder muscle fatigue. Ergonomics 1994, 37, 1323–1333. [Google Scholar] [CrossRef] [PubMed]
- Roeleveld, K.; Stegeman, D.F. What do we learn from motor unit action potentials in surface electromyography? Muscle Nerve Suppl. 2002, 11, S92–S97. [Google Scholar] [CrossRef] [PubMed]
- Lapatki, B.G.; Oostenveld, R.; Van Dijk, J.P.; Jonas, I.E.; Zwarts, M.J.; Stegeman, D.F. Topographical characteristics of motor units of the lower facial musculature revealed by means of high-density surface EMG. J. Neurophysiol. 2006, 95, 342–354. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Merletti, R. Estimation of average muscle fiber conduction velocity from two-dimensional surface EMG recordings. J. Neurosci. Methods 2004, 134, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Abboud, J.; Nougarou, F.; Lardon, A.; Dugas, C.; Descarreaux, M. Influence of Lumbar Muscle Fatigue on Trunk Adaptations during Sudden External Perturbations. Front. Hum. Neurosci. 2016, 10, 576. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Kouzaki, M.; Moritani, T. Region-specific myoelectric manifestations of fatigue in human rectus femoris muscle. Muscle Nerve 2013, 48, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Gallina, A.; Merletti, R.; Vieira, T.M.M. Are the myoelectric manifestations of fatigue distributed regionally in the human medial gastrocnemius muscle? J. Electromyogr. Kinesiol. 2011, 21, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Troiano, A.; Naddeo, F.; Sosso, E.; Camarota, G.; Merletti, R.; Mesin, L. Assessment of force and fatigue in isometric contractions of the upper trapezius muscle by surface EMG signal and perceived exertion scale. Gait Posture 2008, 28, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Pozzo, M.; Merlo, E.; Bottin, A.; Merletti, R. Assessment of average muscle fiber conduction velocity from surface EMG signals during fatiguing dynamic contractions. IEEE Trans. Biomed. Eng. 2004, 51, 1383–1393. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Merletti, R. Methods for estimating muscle fibre conduction velocity from surface electromyographic signals. Med. Biol. Eng. Comput. 2004, 42, 432–445. [Google Scholar] [CrossRef] [PubMed]
- De Luca, C.J.; Nawab, S.H.; Kline, J.C. Clarification of methods used to validate surface EMG decomposition algorithms as described by Farina et al. (2014). J. Appl. Physiol. 2015, 118, 1084. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Enoka, R.M. Surface EMG Decomposition Requires an Appropriate Validation. J. Neurophysiol. 2011, 105, 981–982. [Google Scholar] [CrossRef] [PubMed]
- Holobar, A.; Minetto, M.A.; Farina, D. Accurate identification of motor unit discharge patterns from high-density surface EMG and validation with a novel signal-based performance metric. J. Neural Eng. 2014, 11, 016008. [Google Scholar] [CrossRef] [PubMed]
- Kline, J.C.; De Luca, C.J. Error reduction in EMG signal decomposition. J. Neurophysiol. 2014, 112, 2718–2728. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2 ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kvalseth, T.O. Entropy and Correlation: Some Comments. IEEE Trans. Syst. Man Cybern. 1987, 17, 517–519. [Google Scholar] [CrossRef]
- Samani, A.; Srinivasan, D.; Mathiassen, S.E.; Madeleine, P. Variability in spatio-temporal pattern of trapezius activity and coordination of hand-arm muscles during a sustained repetitive dynamic task. Exp. Brain Res. 2016, 235, 389–400. [Google Scholar] [CrossRef] [PubMed]
- Kawczynski, A.; Samani, A.; Mroczek, D.; Chmura, P.; Blach, W.; Migasiewicz, J.; Klich, S.; Chmura, J.; Madeleine, P. Functional connectivity between core and shoulder muscles increases during isometric endurance contractions in judo competitors. Eur. J. Appl. Physiol. 2015, 115, 1351–1358. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Liang, J.; Yang, Y.; Wu, Y.; Yan, T.; Song, R. Investigating Aging-Related Changes in the Coordination of Agonist and Antagonist Muscles Using Fuzzy Entropy and Mutual Information. Entropy 2016, 18, 229. [Google Scholar] [CrossRef]
- Ju, Z.; Ouyang, G.; Liu, H. EMG-EMG correlation analysis for human hand movements. In Proceedings of the 2013 IEEE Workshop on Robotic Intelligence in Informationally Structured Space (RiiSS), Singapore, 16–19 April 2013; pp. 38–42. [Google Scholar]
- Mista, C.A.; Salomoni, S.E.; Graven-Nielsen, T. Spatial reorganisation of muscle activity correlates with change in tangential force variability during isometric contractions. J. Electromyogr. Kinesiol. 2014, 24, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Estevez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized Mutual Information Feature Selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Strehl, A.; Ghosh, J. Cluster Ensembles—A Knowledge Reuse Framework for Combining Multiple Partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Vinh, N.X.; Epps, J.; Bailey, J. Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance. J. Mach. Learn. Res. 2010, 11, 2837–2854. [Google Scholar]
- Madeleine, P.; Samani, A.; Binderup, A.T.; Stensdotter, A.K. Changes in the spatio-temporal organization of the trapezius muscle activity in response to eccentric contractions. Scand. J. Med. Sci. Sports 2011, 21, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Bingham, A.; Arjunan, S.P.; Kumar, D.K. Estimating the progression of muscle fatigue based on dependence between motor units using high density surface electromyogram. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 3654–3657. [Google Scholar]
- Farina, D.; Arendt-Nielsen, L.; Merletti, R.; Graven-Nielsen, T. Assessment of single motor unit conduction velocity during sustained contractions of the tibialis anterior muscle with advanced spike triggered averaging. J. Neurosci. Methods 2002, 115, 1–12. [Google Scholar] [CrossRef]
- Barbero, M.; Merletti, R.; Rainoldi, A. Atlas of Muscle Innervation Zones; Springer: Mailand, Italy, 2012; Volume 1, p. 142. [Google Scholar]
- Contessa, P.; Adam, A.; De Luca, C.J. Motor unit control and force fluctuation during fatigue. J. Appl. Physiol. 2009, 107, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Adam, A.; De Luca, C.J. Recruitment Order of Motor Units in Human Vastus Lateralis Muscle Is Maintained During Fatiguing Contractions. J. Neurophysiol. 2003, 90, 2919–2927. [Google Scholar] [CrossRef] [PubMed]
- Arjunan, S.P.; Kumar, D.K.; Naik, G. Computation and Evaluation of Features of Surface Electromyogram to Identify the Force of Muscle Contraction and Muscle Fatigue. BioMed Res. Int. 2014, 2014, 6. [Google Scholar] [CrossRef] [PubMed]
- Ash, R. Information Theory; Interscience Publishers: New York, NY, USA, 1965. [Google Scholar]
- Moddemeijer, R. On estimation of entropy and mutual information of continuous distributions. Signal Process. 1989, 16, 233–248. [Google Scholar] [CrossRef]
- Morris, A.; Langari, R. Measurement and Instrumentation: Theory and Application; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Bingham, A.; Arjunan, S.P.; Kumar, D.K. Measuring the Interactions between Different Locations in a Muscle to Monitor Localized Muscle Fatigue. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 3461–3464. [Google Scholar]
- Naik, G.R.; Kumar, D.K.; Yadav, V.; Wheeler, K.; Arjunan, S. Testing of motor unit synchronization model for localized muscle fatigue. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 360–363. [Google Scholar]
- Roy, S.H.; De Luca, C.J.; Schneider, J. Effects of electrode location on myoelectric conduction velocity and median frequency estimates. J. Appl. Physiol. 1986, 61, 1510–1517. [Google Scholar] [PubMed]
- Hansen, N.L.; Hansen, S.; Christensen, L.; Petersen, N.T.; Nielsen, J.B. Synchronization of Lower Limb Motor Unit Activity During Walking in Human Subjects. J. Neurophysiol. 2001, 86, 1266–1276. [Google Scholar] [PubMed]
- Nielsen, J.; Kagamihara, Y. Synchronization of human leg motor units during co-contraction in man. Exp. Brain Res. 1994, 102, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.; Gore, J.C.; Peterson, B.S. Mutual information analysis of the EEG in patients with Alzheimer’s disease. Clin. Neurophysiol. 2001, 112, 827–835. [Google Scholar] [CrossRef]
- Saitou, K.; Masuda, T.; Michikami, D.; Kojima, R.; Okada, M. Innervation zones of the upper and lower limb muscles estimated by using multichannel surface EMG. J. Hum. Ergol. 2000, 29, 35–52. [Google Scholar]
- Beretta Piccoli, M.; Rainoldi, A.; Heitz, C.; Wüthrich, M.; Boccia, G.; Tomasoni, E.; Spirolazzi, C.; Egloff, M.; Barbero, M. Innervation zone locations in 43 superficial muscles: Toward a standardization of electrode positioning. Muscle Nerve 2014, 49, 413–421. [Google Scholar] [CrossRef] [PubMed]
- Aquilonius, S.M.; Askmark, H.; Gillberg, P.G.; Nandedkar, S.; Olsson, Y.; Stårlberg, E. Topographical localization of motor endplates in cryosections of whole human muscles. Muscle Nerve 1984, 7, 287–293. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.W.; DeFreitas, J.M.; Stock, M.S. Accuracy of three different techniques for automatically estimating innervation zone location. Comput. Methods Programs Biomed. 2012, 105, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Marateb, H.R.; Farahi, M.; Rojas, M.; Mañanas, M.A.; Farina, D. Detection of Multiple Innervation Zones from Multi-Channel Surface EMG Recordings with Low Signal-to-Noise Ratio Using Graph-Cut Segmentation. PLoS ONE 2016, 11, e0167954. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Falces, J. A new method for the localization of the innervation zone based on monopolar surface-detected potentials. J. Electromyogr. Kinesiol. 2017, 35, 47–60. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).