Abstract
The analysis of conformational changes of hydrocarbon molecules is imperative in the prediction of their transport properties in different phases, such as evaporation/condensation coefficients (β) in the gas-liquid interface and evaporation rates of fuel droplets (k) in multiphases. In this letter, we analyze the effects of entropic contributions () to during the evaporation/condensation of chain conformers at the interface with a modified version of the solvation model SMD/ωB97X-D/cc-pVTZ in which the temperature dependency of surface tension and the interfacial flow density of the conformers is taken into account. The evaporation/condensation coefficient (β) and evaporation rate (k) are respectively calculated using the statistical associating fluid theory (SAFT) and a combined quantum-classical reaction rate theory named quantum transition state theory-classical kinetic gas theory (QTST-CKGT). The detailed analyses show the importance of internal entropic states over the interfacial layer induced by meso-confinement phenomena in the very vicinity of fuel droplets surfaces.
1. Introduction
Along with droplets evaporation, understanding interfacial phenomena in multiphasic processes remains one of grand challenges in computational fluid dynamics (CFD). This has led many research groups to investigate the non-isotopic environment in the vicinity of the droplets surfaces. However, the current theoretical and computational efforts may not be adequate for better understanding “fuel” droplets evaporation in engine-like conditions. This is particularly true for long-chain hydrocarbon molecules that involve molecular conformational changes and require new paradigms. Far from being the problem for fluid dynamics, conformational changes or internal dynamics effects in the vapor-liquid interface is important to accurately simulate the transfer of molecular heat and mass during the fuel droplets evaporation/condensation processes. Simple models without considering these effects in liquid and gas phases, and particularly at the interface, fail to reproduce experimental observations such as the temperature dependence of evaporation rates of the hydrocarbons.
Recently, a model was developed by Gun’ko et al. [1] to estimate the evaporation/condensation coefficient (β) and evaporation rate (k) of n-dodecane based on the quantum mechanics solvation model SMD and the Gibbs free energy of evaporation (). SMD is based on the solute electron density, the dielectric constant, and the atomic surface tension [2]. Evaporation/condensation coefficients may be used for modelling multi-scale systems in order to make a connection between atomic-/nano-scale and micro-/macro-scale phenomena (typical scales in fluid dynamics) for the determination of fluids transport properties in multiphase flows such as evaporation rate. This coefficient can explain how the molecular heat and mass transfer take place in the vicinity of the liquid-vapor interface. However, a novel hybrid method of the quantum transition state theory and classical kinetic gas theory (QTST-CKGT) could make this connection in a new way without requiring the evaporation/condensation coefficient [3,4]. In Reference [1], it was assumed that the evaporation of n-dodecane is an enthalpic process with no entropy change in the temperature range of 298.15–648.15 K, as well as no energy barrier over the interfacial layers. However, recently the basis of the entropy-enthalpy competition mechanism [2] and the importance of confinement effects alongside the molecular conformational changes at the interface [3,4] were established during the evaporation/condensation process.
In this letter, we apply density functional theory (DFT) quantum chemical calculations and the SAFT equation of state to understand how the interfacial flows of n-dodecane droplets affect the evaporation/condensation coefficient of n-dodecane thermodynamically. We then present the hybrid method of the QTST-CKGT to distinguish kinetic and thermodynamic effects on the estimate of the evaporation rate.
2. Mass Evaporation Coefficient and Quantum/Statistical Mechanics Methods
The evaporation/condensation coefficient (βg) can be derived from the terms of thermodynamic potentials [1] and SAFT [5,6]. SAFT is a molecular-based equation of state that can be applied to predict the interfacial layer thickness of fluids. It incorporates the effects of chain length, molecular association, and other interactions such as long-range dipolar forces and dispersions. While the interfacial layer effects did not explicitly future in References [1,2], we consider these effects in this study to estimate the evaporation/condensation coefficient to find out whether this thermodynamics-based approach can be suitable for modelling interfacial flows. To set up an equation including interfacial width, δ, a standard state has to be defined for the evaporation/condensation process. With this thickness, the relationship between the free energy of evaporation/condensation () and the coefficient of βg becomes:
Instead of
where and present the average difference values of Gibbs free energy of conformers in the interfacial layer and gas phase, and in the liquid and gas phases, respectively. δ can be estimated as [7]:
where σ is a temperature-independent diameter parameter of the methylene and methyl functional groups in n-dodecane conformers, which is assumed to be equal to 3.93 × 10−10 m; a = 1.16 m and υ = 0.5 are constants; and Tc = 658.2 K is the critical temperature for n-dodecane. The results of DFT calculations are based on multi-structural torsional (MS-T) method and continuum solvation model of SMD [8], in which the conformer temperature Gibbs free energies in the gas () and the interface of droplets () are computed. The temperature dependence of the surface tension can be included using the following formula [9]:
where A and n are constants, namely, A = 80.1946 × 10−3 kcal/(mol × Å2), n = 1.3325, and Tc is the critical temperature of n-dodecane (658.2 K). The temperature dependency of the interfacial density of n-dodecane is also computed with the self-consistent reaction field (SCRF) method, implemented in the Gaussian 09 suite [10]. The interfacial density, ρ(z), can be expressed as a hyperbolic tangent function:
where the superscripts l and g denote liquid and gas phases, respectively, and z0 is the position of the Gibbs dividing surface located at z0 = 0 that is given by:
The saturated densities of liquid and gas at temperatures T = 298.15 K to 648.15 K are taken from the National Institute of Standards and Technology (NIST) [11]. Since the translational motions are suppressed at the surface of the liquid [12,13,14], and as all SMD calculations have also been performed based on the existence of a conformer in the cavity (ideal gas condition), the pressure corrections need to be taken into account using , where p(z0) is the pressure in the center of the interfacial layer and ρ(z0) is the experimental interfacial density of n-dodecane changing from 372.8 kg/m3 at 298.15 K to 117.5 kg/m3 at 648.15 K [10]. Taking all of the aforementioned parameters and correction terms into consideration, this leads to the same results as reported in Reference [1]. One question raised was whether or not adding the interfacial layer using SAFT has an effect on the evaporation/condensation coefficient of n-dodecane. The answer is no, since SAFT, being a thermodynamics-based approach, cannot model properly transient processes such as internal activation dynamics effects [3].
3. Evaporation Rate of Fuel Droplets and Hybrid Kinetics Method
Boltzmann expressed the dynamic behavior of systems at an atomic scale and estimated the number density of molecules at position x and speed v at time t using a distribution function f(x, v, t). We estimated this distribution function in the evaporation process based on the molecular theory of solvation for systems consisting of long-chain molecules, and concluded that “internal molecular dynamic” effects are important in this function rather than intermolecular interactions [3,4]. In order to understand the importance of transient internal activation dynamics during the evaporation process on hydrocarbon molecules, we calculated the evaporation rate, , using a QTST-based expression (T) = which is eventually incorporated as a correction term in the CKGT-based equation (T) = [3]:
where ωi is the magnitude of the transition-state imaginary frequency (see References [3,4] for more detail). While CKGT describes the collision effects among surrounding gases, vapor molecules, clusters, and droplets, assuming those are in the thermodynamic equilibrium states, QTST presents some kinetic quasi-equilibrium phenomena at an atomic level in the vicinity of fuel droplets. This novel hybrid method bridges micro/macro-scale modelling with atomistic-scale modelling to unravel the kinetic effects at the surface of fuel droplets and elucidate the role of equilibrium thermodynamics in the liquid and gas phases and of transient kinetics in the interfacial flows during the evaporation/condensation process (see Figure 1).
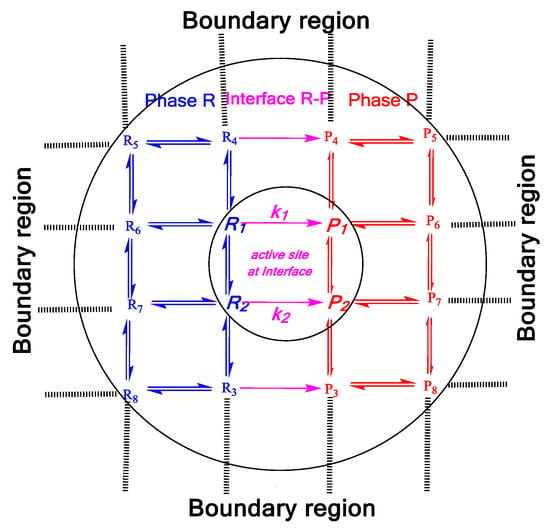
Figure 1.
An overview schematic of the hybrid-kinetic methodology QTST-CKGT.
Traditional kinetic boundary conditions (KBC) were revisited at the interface of fuel droplets, suggesting that the non-equilibrium process in the gas phase (i.e., Stefan flow) does not necessarily imply the shortcomings CKGT in the estimation of the evaporation rates of sprays when interfacial flows are properly tracked using QTST [3]. The developed methodology also solved open problems in the kinetics of fuel droplets evaporation that had existed for well over a century, that is, how the mass and thermal evaporation effects simultaneously affect the evaporation rates in fuel droplets at the atomic level [4]. Indeed, this hybrid quantum-classical reaction rate theory could bring together statistical thermodynamics and chemical kinetics information to track and capture interface dynamics of complex molecules that have multiple conformations in multiphasic flow based on accurate quantum mechanics calculations [3,4].
In summary, this hybrid methodology reproduced the temperature-dependent evaporation rate in n-alkane droplets (see Figure 3 in Reference [3]) and criticized the “traditional” fluid dynamics point of view in which the evaporation/condensation coefficient was required for modelling the dynamics of the evaporation of fluids composed of molecules with multiple conformers in monocomponent [3] and multicomponent fuel droplets [4]. These results were obtained based on the concept that two conformations with different internal activation dynamics and collision behaviors in long-chain hydrocarbon molecules are sufficient to account for experimentally observed kinetic effects. A full description of the evaporation/condensation of fuel droplets must certainly take into account transient internal activation molecular dynamics and collision effects, not only in gas and liquid phases but also in the interfacial flows, which are not the same. Identifying specific conformations and their internal activation dynamics roles in the vicinity of fuel droplet surfaces upon collision suggests meso-confinement effects in this region during the evaporation/condensation process and should be useful in gaining a better understanding of the transient phase transition processes of complex molecules in multiphase flows.
Acknowledgments
The research is funded by the UK Engineering and Physical Sciences Research Council under the project “UK Consortium on Mesoscale Engineering Sciences (UKCOMES)” (Grant No. EP/L00030X/1).
Author Contributions
Rasoul Nasiri conducted the research while Kai Hong Luo was the P.I. of the project. Rasoul Nasiri wrote the first draft of the manuscript and edited all the subsequent versions. Kai Hong Luo reviewed and edited all the versions of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gun’ko, V.M.; Nasiri, R.; Sazhin, S.S. Effects of the surroundings and conformerisation of n-dodecane molecules on evaporation/condensation processes. J. Chem. Phys. 2015, 142, 034502. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, R.; Gun’ko, V.M.; Sazhin, S.S. The effects of internal molecular dynamics on the evaporation/condensation of n-dodecane. Theor. Chem. Acc. 2015, 134, 83. [Google Scholar] [CrossRef]
- Nasiri, R. Revisiting kinetic boundary conditions at the surface of fuel droplet hydrocarbons: An atomistic computational fluid dynamics simulation. Sci. Rep. 2016, 6, 25572. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, R.; Luo, K.H. Specificity switching pathways in thermal and mass evaporation of multicomponent hydrocarbon droplets: A mesoscopic observation. Sci. Rep. 2017, 7, 5001. [Google Scholar] [CrossRef] [PubMed]
- Wertheim, M.S. Fluids of dimerizing hard spheres, and fluid mixtures of hard spheres and dispheres. J. Chem. Phys. 1986, 85, 2929–2936. [Google Scholar] [CrossRef]
- Wertheim, M.S. Thermodynamic perturbation theory of polymerization. J. Chem. Phys. 1987, 87, 7323–7331. [Google Scholar] [CrossRef]
- Maghari, A.; Najafi, M. A novel approach for calculation of liquid—Vapor interfacial thickness. J. Stat. Mech. 2009, P05003. [Google Scholar] [CrossRef]
- Winget, P.; Dolney, D.M.; Giesen, D.J.; Cramer, C.J.; Truhlar, D.G. Minnesota Solvent Descriptor Database; University of Minnesota: Minneapolis, MN, USA, 2010. [Google Scholar]
- Yaws, C.L. Thermophysical Properties of Chemicals and Hydrocarbons; William Andrew Inc.: Norwich, NY, USA, 2008. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- NIST Chemistry WebBook. Saturation Properties for Dodecane—Temperature Increments. Available online: http://webbook.nist.gov/chemistry/ (accessed on 27 April 2016).
- Nasiri, R.; Field, M.J.; Zahedi, M.; Moosavi-Movahedi, A.A. Comparative DFT Study To Determine if α-Oxoaldehydes are Precursors for Pentosidine Formation. J. Phys. Chem. A 2012, 116, 2986–2996. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, R.; Field, M.J.; Zahedi, M.; Moosavi-Movahedi, A.A. Cross-Linking Mechanisms of Arginine and Lysine with α,β-Dicarbonyl Compounds in Aqueous Solution. J. Phys. Chem. A 2011, 115, 13542–13555. [Google Scholar] [CrossRef] [PubMed]
- Nasiri, R.; Zahedi, M.; Jamet, H.; Moosavi-Movahedi, A.A. Theoretical studies on models of lysine-arginine cross-links derived from α-oxoaldehydes: A new mechanism for glucosepane formation. J. Mol. Model. 2011, 18, 1645–1659. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).