Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law
Abstract
:1. Introduction
2. Fractional Operators
3. Cancer Model
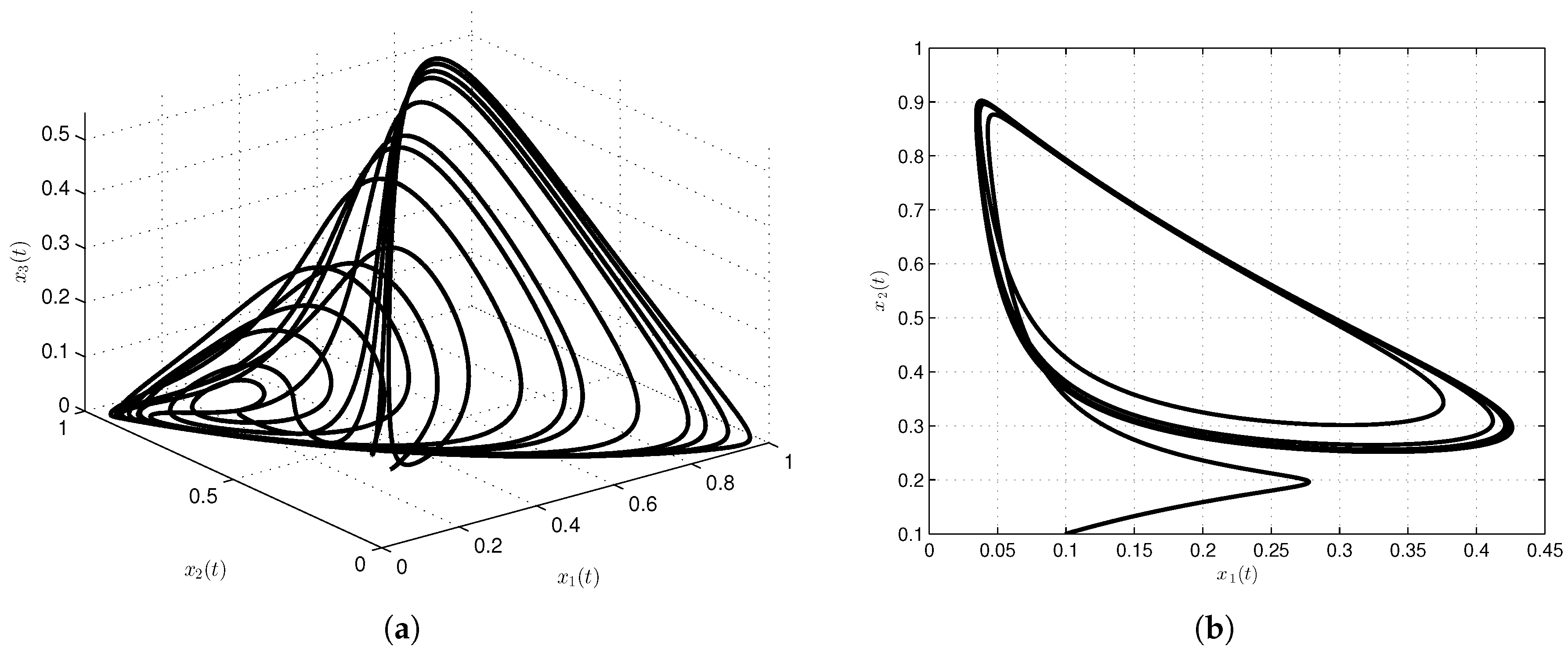
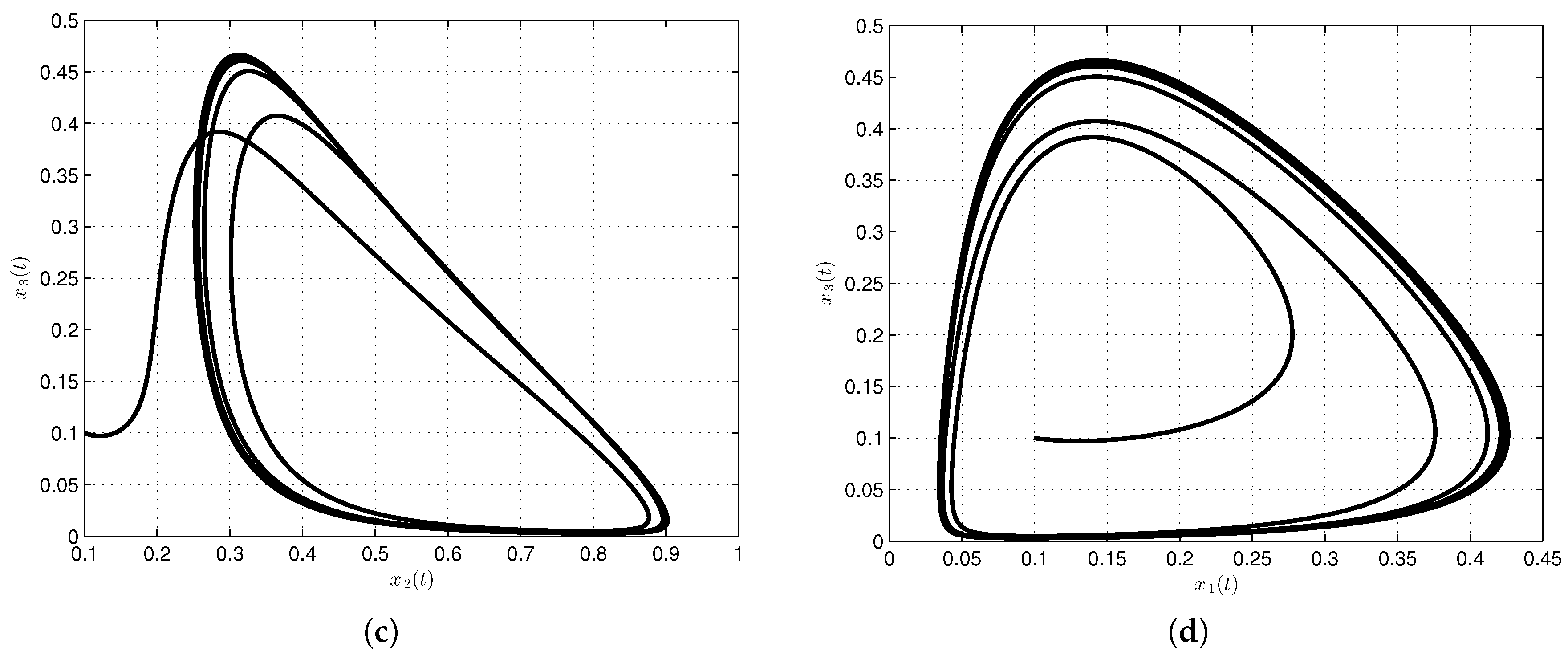
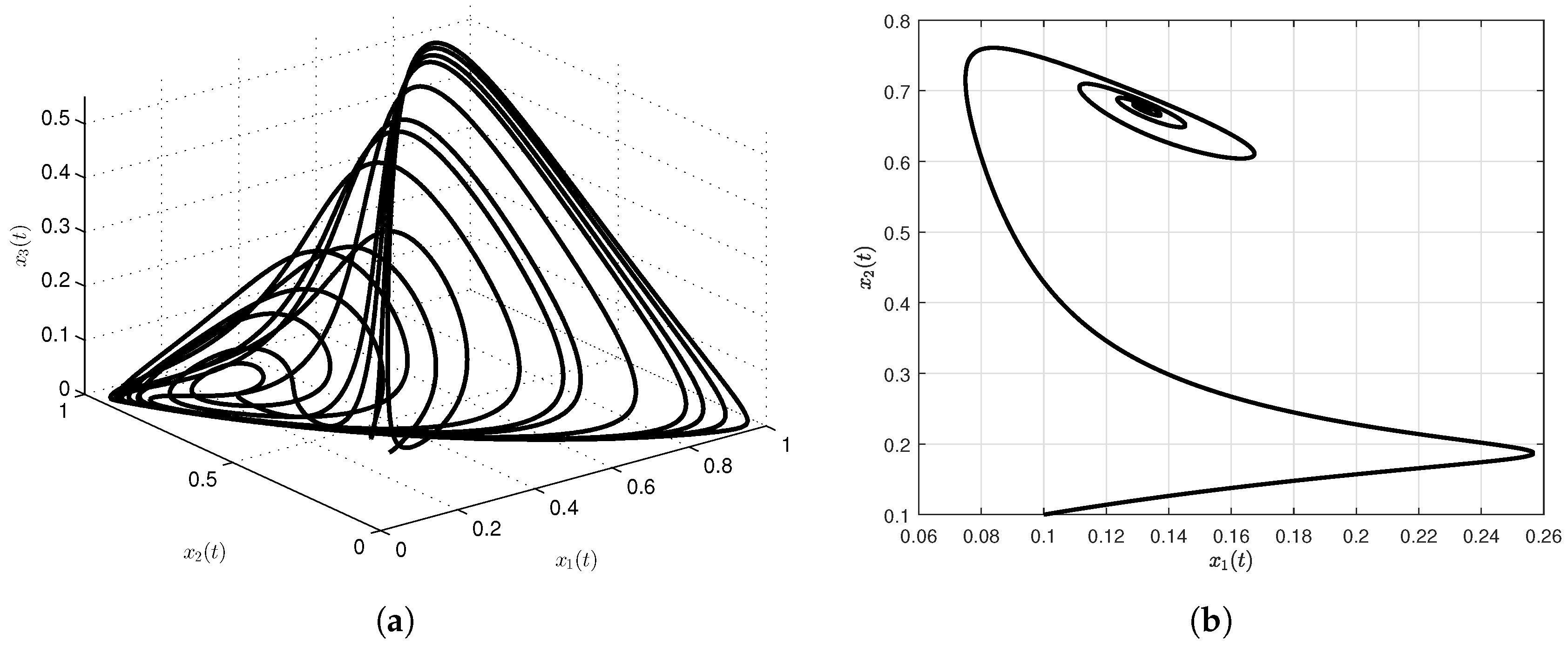
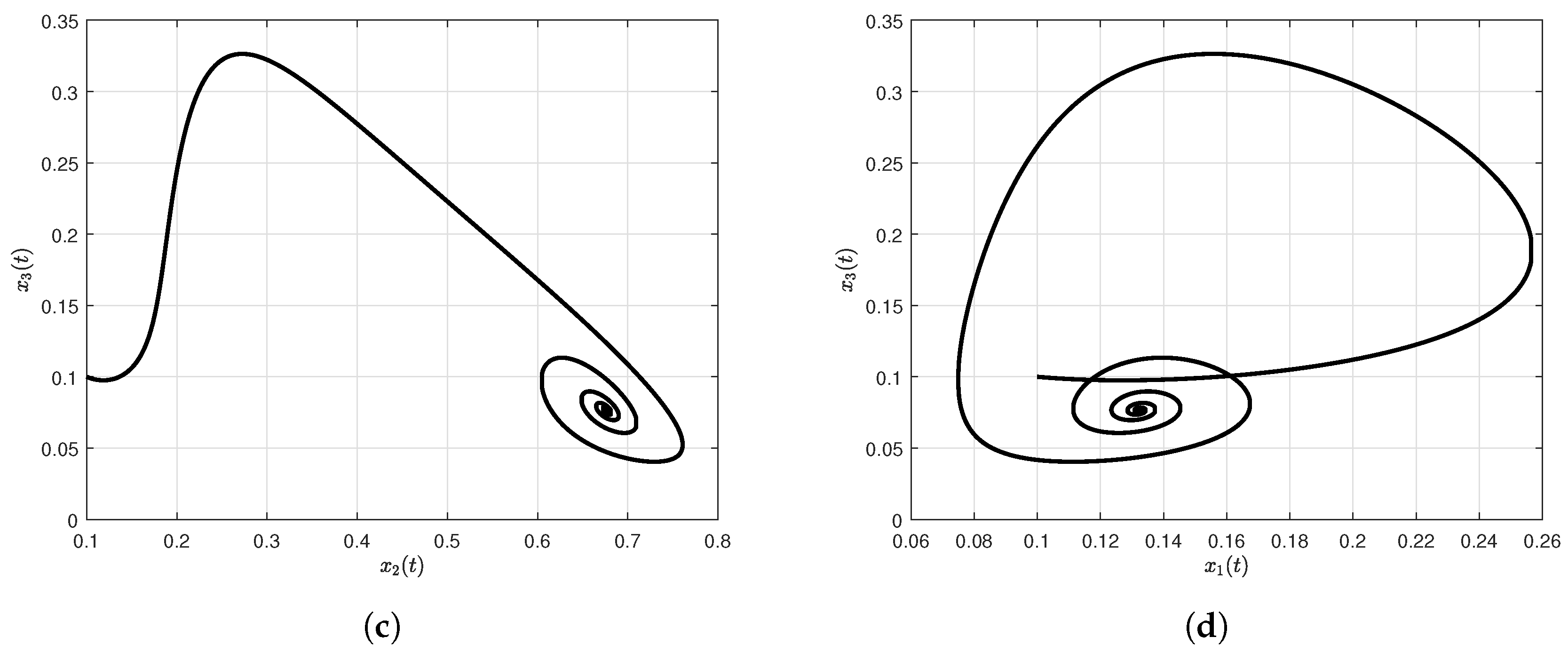
3.1. Cancer Model with Exponential Decay Law
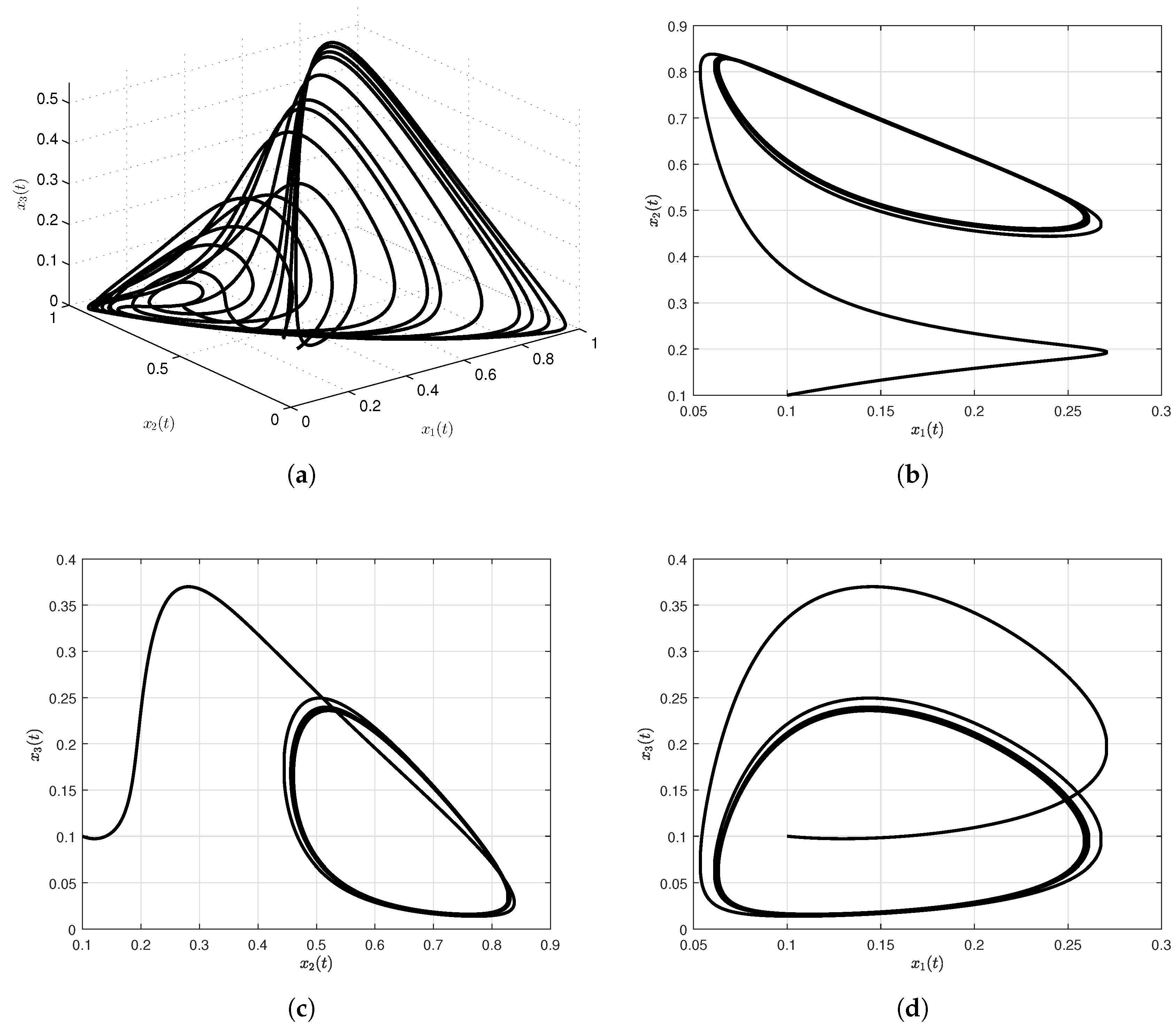
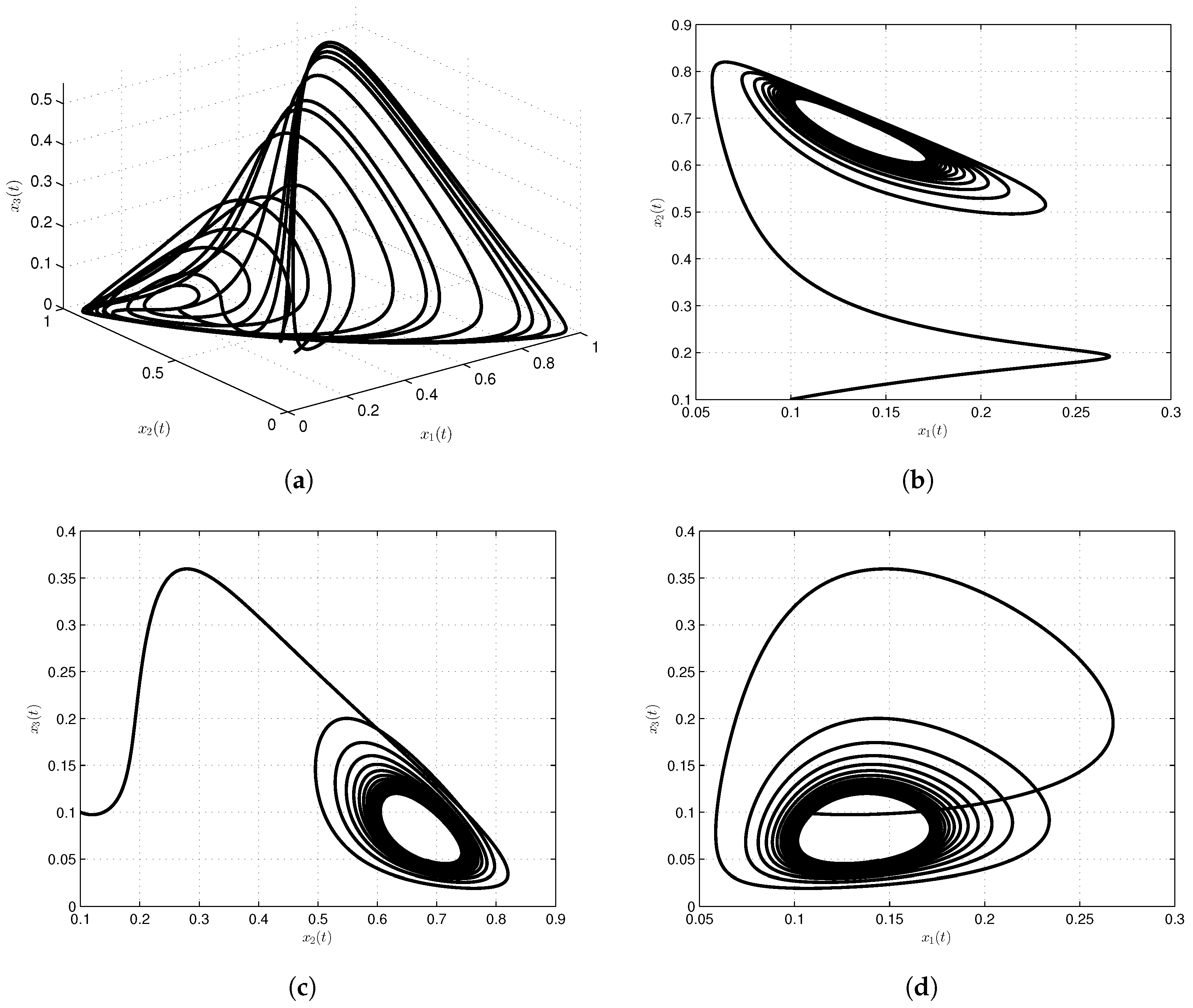
3.2. Cancer Model with Mittag-Leffler Kernel
- The fixed point set of H has at least one element.
- converges to a point .
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic press: New York, NY, USA, 1998; Volume 198. [Google Scholar]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.A.T.; Bates, J.H.T. The role of fractional calculus in modelling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar]
- Nyamoradi, N.; Zhou, Y. Existence of solutions for a Kirchhoff type fractional differential equations via minimal principle and Morse theory. Topol. Methods Nonlinear Anal. 2015, 46, 617–630. [Google Scholar]
- Wang, J.; Feckan, M.; Zhou, Y. Center stable manifold for planar fractional damped equations. Appl. Math. Comput. 2017, 296, 257–269. [Google Scholar]
- Zhou, Y.; Peng, L. On the time-fractional Navier-Stokes equations. Comput. Math. Appl. 2017, 73, 874–891. [Google Scholar]
- Owolabi, K.M.; Atangana, A. Numerical approximation of nonlinear fractional parabolic differential equations with Caputo-Fabrizio derivative in Riemann-Liouville sense. Chaos Solitons Fractals 2017, 99, 171–179. [Google Scholar]
- Caputo, M.; Mainardi, F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. 1971, 91, 134–147. [Google Scholar]
- Zhou, Y.; Peng, L. Weak solutions of the time-fractional Navier-Stokes equations and optimal control. Comput. Math. Appl. 2017, 73, 1016–1027. [Google Scholar]
- Sumelka, W.; Voyiadjis, G.Z. A hyperelastic fractional damage material model with memory. Int. J. Solids Struct. 2017, 124, 151–160. [Google Scholar]
- Drapaca, C.S.; Sivaloganathan, S. A fractional model of continuum mechanics. J. Elast. 2012, 107, 105–123. [Google Scholar]
- Sumelka, W.; Blaszczyk, T.; Liebold, C. Fractional Euler-Bernoulli beams: Theory, numerical study and experimental validation. Eur. J. Mech.-A/Solids 2015, 54, 243–251. [Google Scholar]
- Lazopoulos, K.A. Non-local continuum mechanics and fractional calculus. Mech. Res. Commun. 2006, 33, 753–757. [Google Scholar]
- Kumar, S.; Kumar, A.; Baleanu, D. Two analytical methods for time-fractional nonlinear coupled Boussinesq-Burger’s equations arise in propagation of shallow water waves. Nonlinear Dyn. 2016, 1, 1–17. [Google Scholar]
- Luchko, Y. A New Fractional Calculus Model for the two-dimensional Anomalous Diffusion and its Analysis. Math. Model. Nat. Phenom. 2016, 11, 1–17. [Google Scholar]
- Caputo, M.; Fabricio, M. A New Definition of Fractional Derivative without Singular Kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Lozada, J.; Nieto, J.J. Properties of a New Fractional Derivative without Singular Kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Atangana, A.; Alkahtani, B.S.T. Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar]
- Hristov, J. Transient heat diffusion with a non-singular fading memory: From the Cattaneo constitutive equation with Jeffrey’s kernel to the Caputo-Fabrizio time-fractional derivative. Therm. Sci. 2016, 20, 757–762. [Google Scholar]
- Gao, F.; Yang, X.J. Fractional Maxwell fluid with fractional derivative without singular kernel. Therm. Sci. 2016, 20, 871–877. [Google Scholar]
- Gómez-Aguilar, J.F.; Córdova-Fraga, T.; Escalante-Martínez, J.E.; Calderón-Ramón, C.; Escobar-Jiménez, R.F. Electrical circuits described by a fractional derivative with regular kernel. Rev. Mex. Fis. 2016, 62, 144–154. [Google Scholar]
- Mirza, I.A.; Vieru, D. Fundamental solutions to advection-diffusion equation with time-fractional Caputo-Fabrizio derivative. Comput. Math. Appl. 2017, 1, 1–10. [Google Scholar]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Progr. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Nonlocal and Non-Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 763–769. [Google Scholar]
- Gómez-Aguilar, J.F. Irving-Mullineux oscillator via fractional derivatives with Mittag-Leffler kernel. Chaos Solitons Fractals 2017, 95, 179–186. [Google Scholar]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A. A comparative study of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives to the convective flow of a generalized Casson fluid. Eur. Phys. J. Plus 2017, 132, 54. [Google Scholar]
- Alkahtani, B.S.T. Chua’s circuit model with Atangana-Baleanu derivative with fractional order. Chaos Solitons Fractals 2016, 89, 1–5. [Google Scholar]
- Alqahtani, R.T. Atangana-Baleanu derivative with fractional order applied to the model of groundwater within an unconfined aquifer. J. Nonlinear Sci. Appl. 2016, 9, 3647–3654. [Google Scholar]
- Ahokposi, D.P.; Atangana, A.; Vermeulen, D.P. Modelling groundwater fractal flow with fractional differentiation via Mittag-Leffler law. Eur. Phys. J. Plus 2017, 132, 165. [Google Scholar]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, Á. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar]
- Singh, J.; Kumar, D.; Kılıçman, A. Numerical solutions of nonlinear fractional partial differential equations arising in spatial diffusion of biological populations. In Abstract and Applied Analysis; Hindawi Publishing Corporation: London, UK, 2014. [Google Scholar]
- Singh, J.; Kumar, D.; Al Qurashi, M.; Baleanu, D. A new fractional model for giving up smoking dynamics. Adv. Differ. Equ. 2017, 2017, 88. [Google Scholar]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.M. A fractional order epidemic model for the simulation of outbreaks of influenza A(H1N1). Math. Methods Appl. Sci. 2014, 37, 2218–2226. [Google Scholar]
- Arshad, S.; Baleanu, D.; Bu, W.; Tang, Y. Effects of HIV infection on CD4+ T-cell population based on a fractional-order model. Adv. Differ. Equ. 2017, 2017, 92. [Google Scholar]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar]
- Luo, C.; Wang, X. Chaos in the fractional-order complex Lorenz system and its synchronization. Nonlinear Dyn. 2013, 71, 241–257. [Google Scholar]
- Hu, W.; Ding, D.; Zhang, Y.; Wang, N.; Liang, D. Hopf bifurcation and chaos in a fractional order delayed memristor-based chaotic circuit system. Opt.-Int. J. Light Electron Opt. 2017, 130, 189–200. [Google Scholar]
- Hegazi, A.S.; Ahmed, E.; Matouk, A.E. On chaos control and synchronization of the commensurate fractional order Liu system. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1193–1202. [Google Scholar]
- Rajagopal, K.; Vaidyanathan, S.; Karthikeyan, A.; Duraisamy, P. Dynamic analysis and chaos suppression in a fractional order brushless DC motor. Electr. Eng. 2017, 99, 721–733. [Google Scholar]
- Agarwal, R.P.; El-Sayed, A.M.; Salman, S.M. Fractional-order Chua’s system: Discretization, bifurcation and chaos. Adv. Differ. Equ. 2013, 2013, 320. [Google Scholar]
- N’Doye, I.; Voos, H.; Darouach, M. Chaos in a fractional-order cancer system. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 171–176. [Google Scholar]
- Yasir, M.; Ahmad, S.; Ahmed, F.; Aqeel, M.; Akbar, M.Z. Improved numerical solutions for chaotic-cancer-model. AIP Adv. 2017, 7, 015110. [Google Scholar]
- Arshad, S.; Sohail, A.; Javed, S. Dynamical Study of Fractional Order Tumor Model. Int. J. Comput. Methods 2015, 12, 1550032. [Google Scholar]
- Ahmed, E.; Hashish, A.; Rihan, F.A. On fractional order cancer model. J. Fract. Calc. Appl. Anal. 2012, 3, 1–6. [Google Scholar]
- Itik, K.; Banks, S.P. Chaos in a three-dimensional cancer model. Int. J. Bifurc. Chaos 2010, 20, 71–79. [Google Scholar]
- Alkahtani, B.S.T.; Atangana, A. Chaos on the Vallis model for El Niño with fractional operators. Entropy 2016, 18, 100. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Aguilar, J.F.; López-López, M.G.; Alvarado-Martínez, V.M.; Baleanu, D.; Khan, H. Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law. Entropy 2017, 19, 681. https://doi.org/10.3390/e19120681
Gómez-Aguilar JF, López-López MG, Alvarado-Martínez VM, Baleanu D, Khan H. Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law. Entropy. 2017; 19(12):681. https://doi.org/10.3390/e19120681
Chicago/Turabian StyleGómez-Aguilar, José Francisco, María Guadalupe López-López, Victor Manuel Alvarado-Martínez, Dumitru Baleanu, and Hasib Khan. 2017. "Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law" Entropy 19, no. 12: 681. https://doi.org/10.3390/e19120681
APA StyleGómez-Aguilar, J. F., López-López, M. G., Alvarado-Martínez, V. M., Baleanu, D., & Khan, H. (2017). Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law. Entropy, 19(12), 681. https://doi.org/10.3390/e19120681







