Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO
Abstract
1. Introduction
2. Materials and Methods
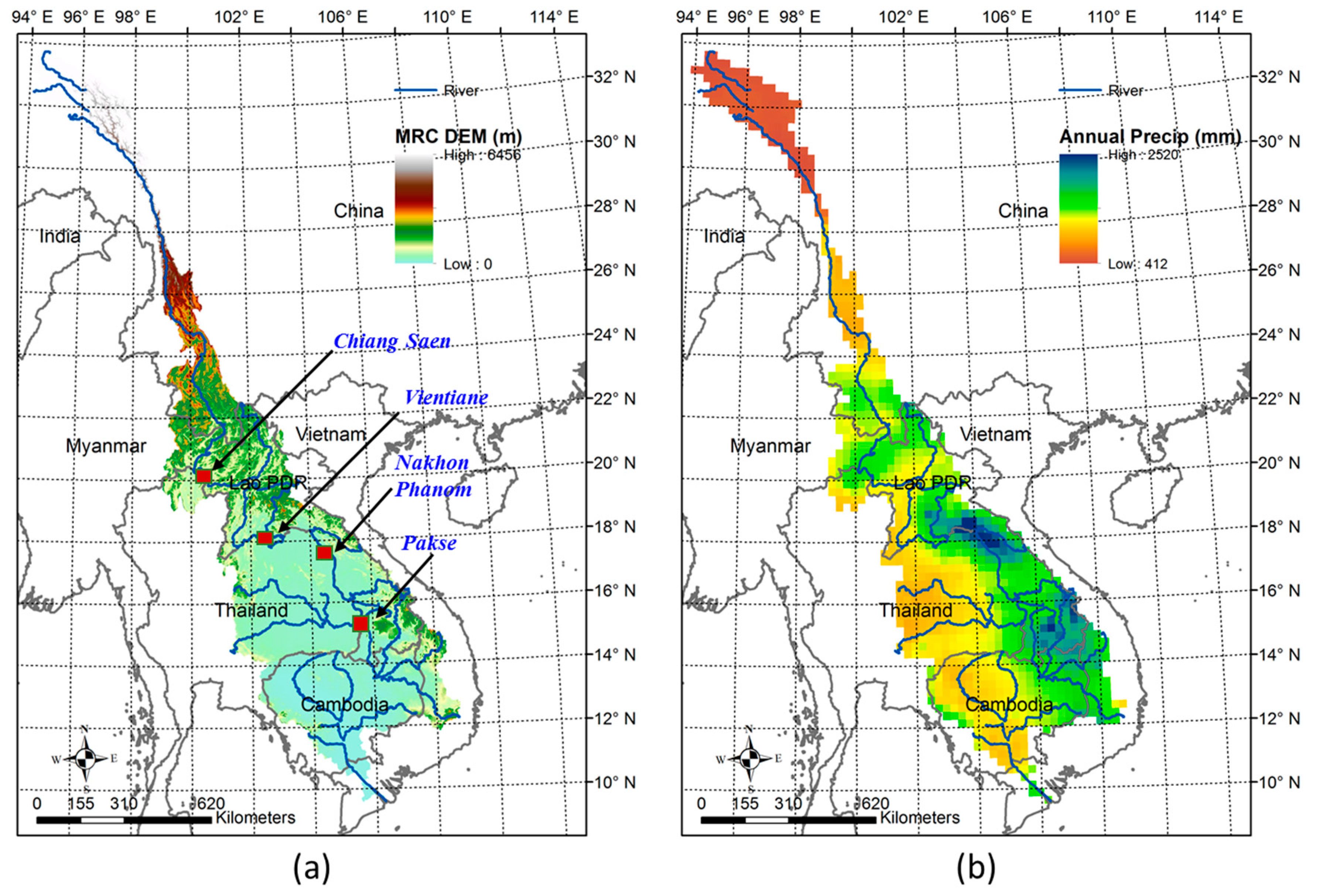
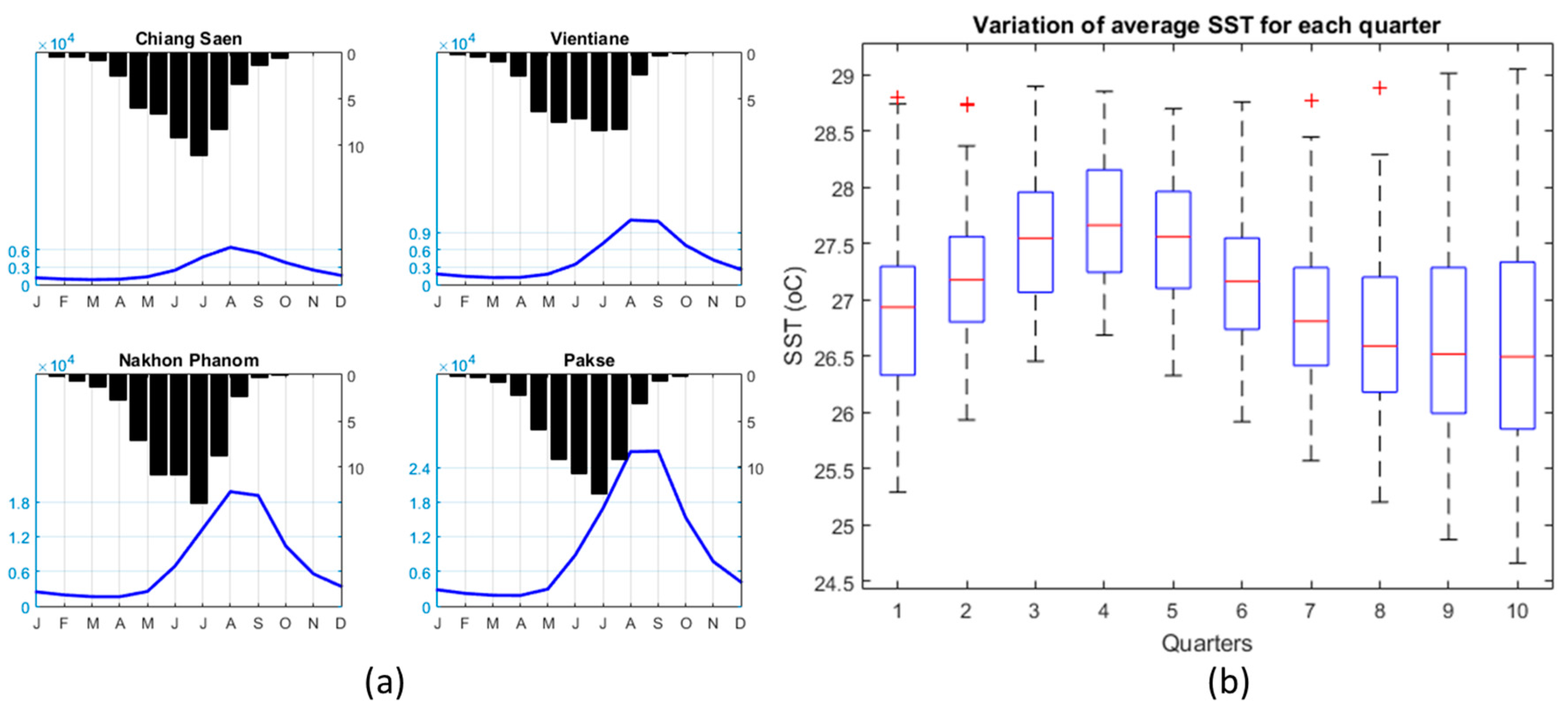
2.1. Hydro-Meteorological Data and ENSO
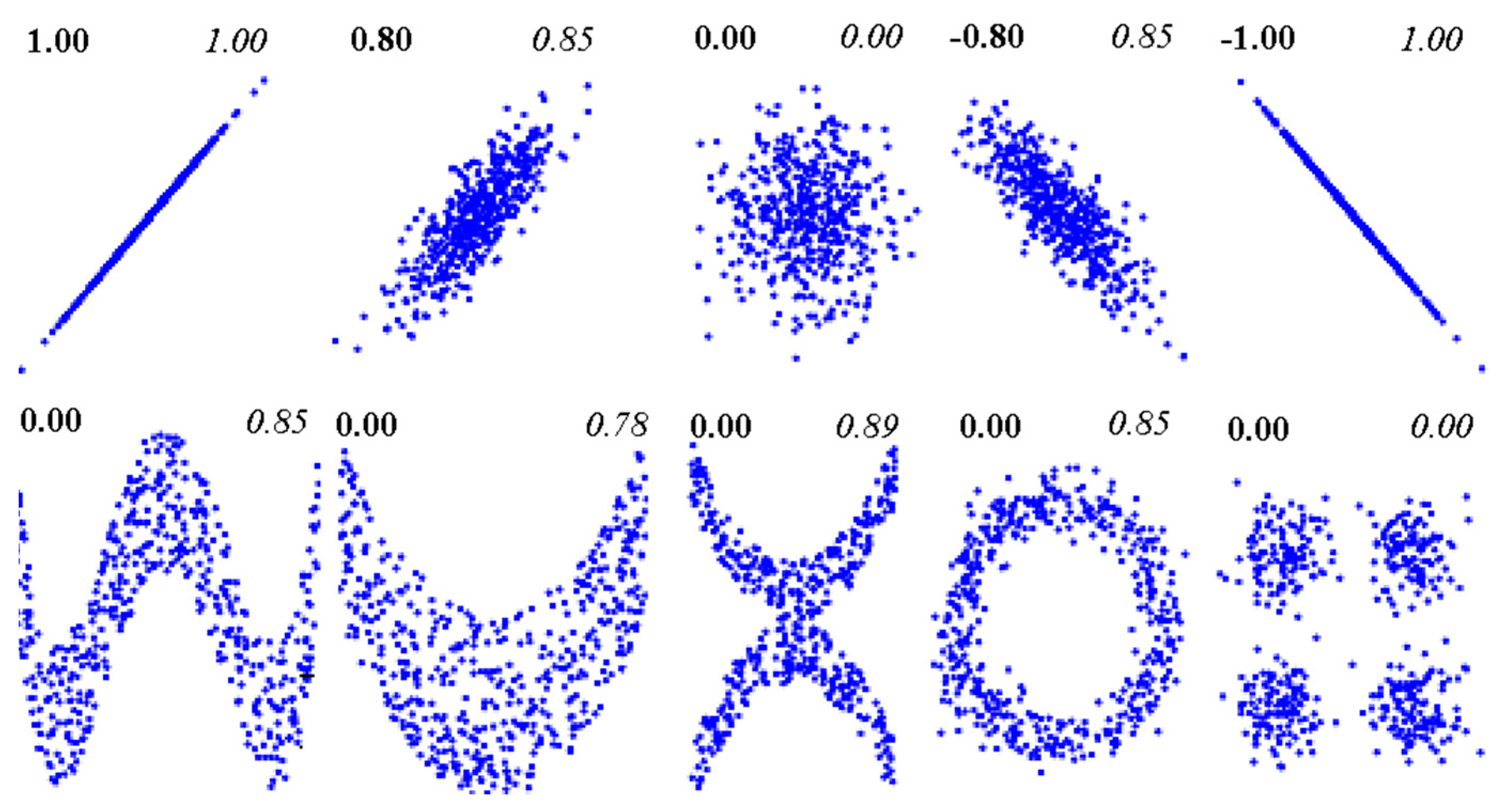
2.2. Mutual Information Estimation
3. Results
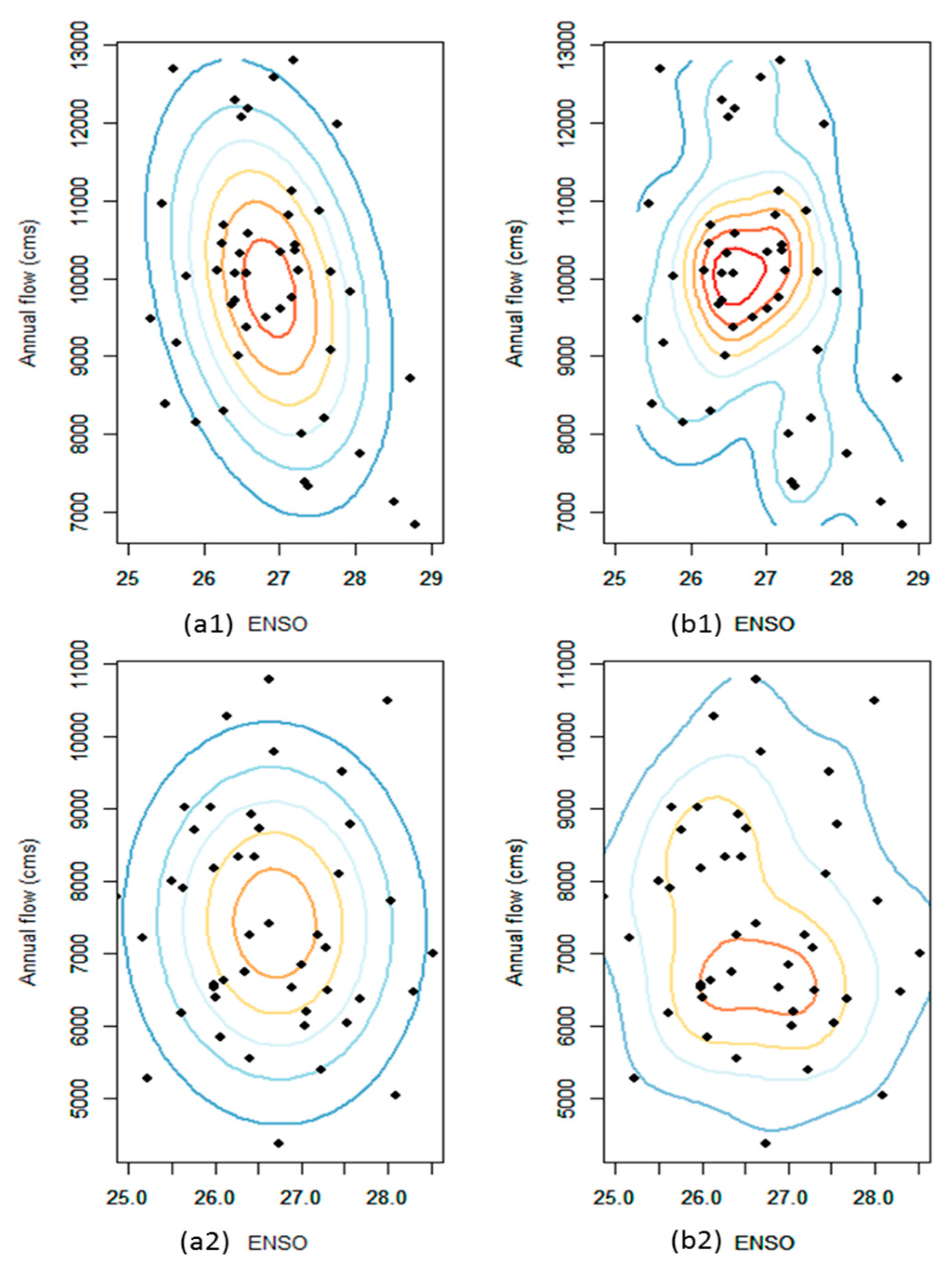
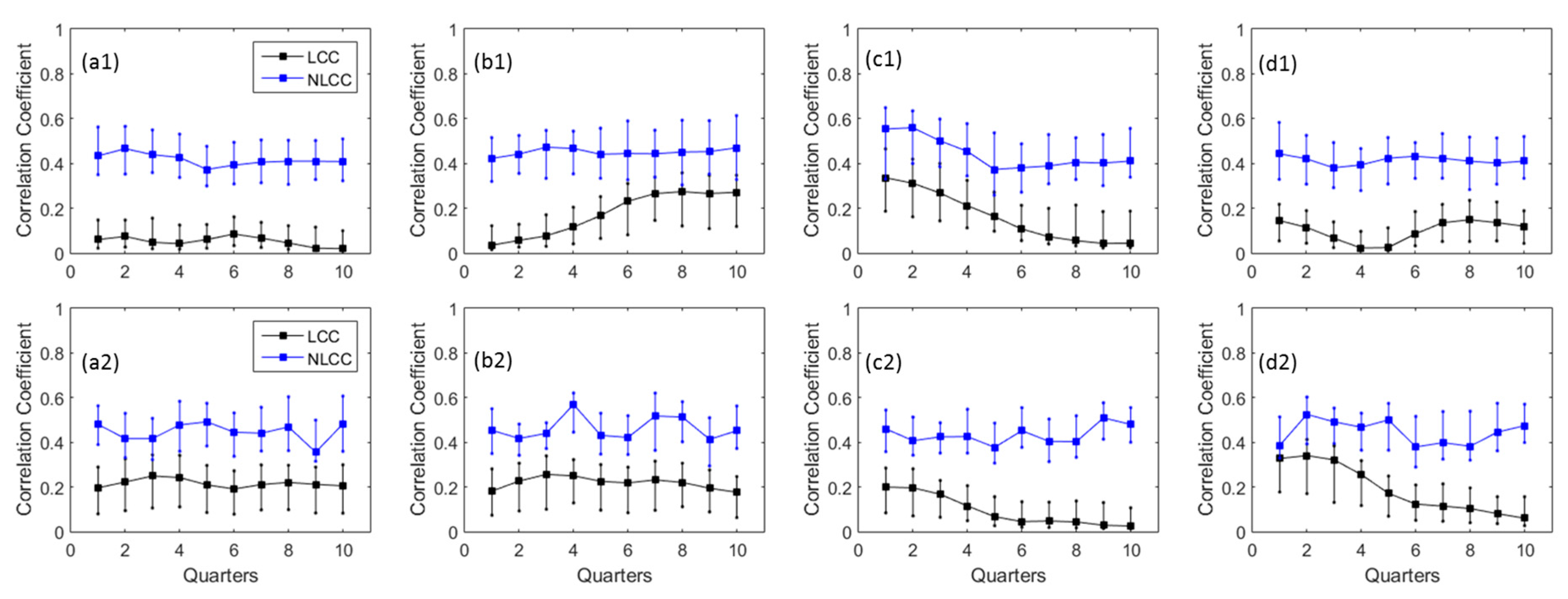
3.1. Linear and Nonlinear Correlation between Annual Precipitation/Streamflow and ENSO Index
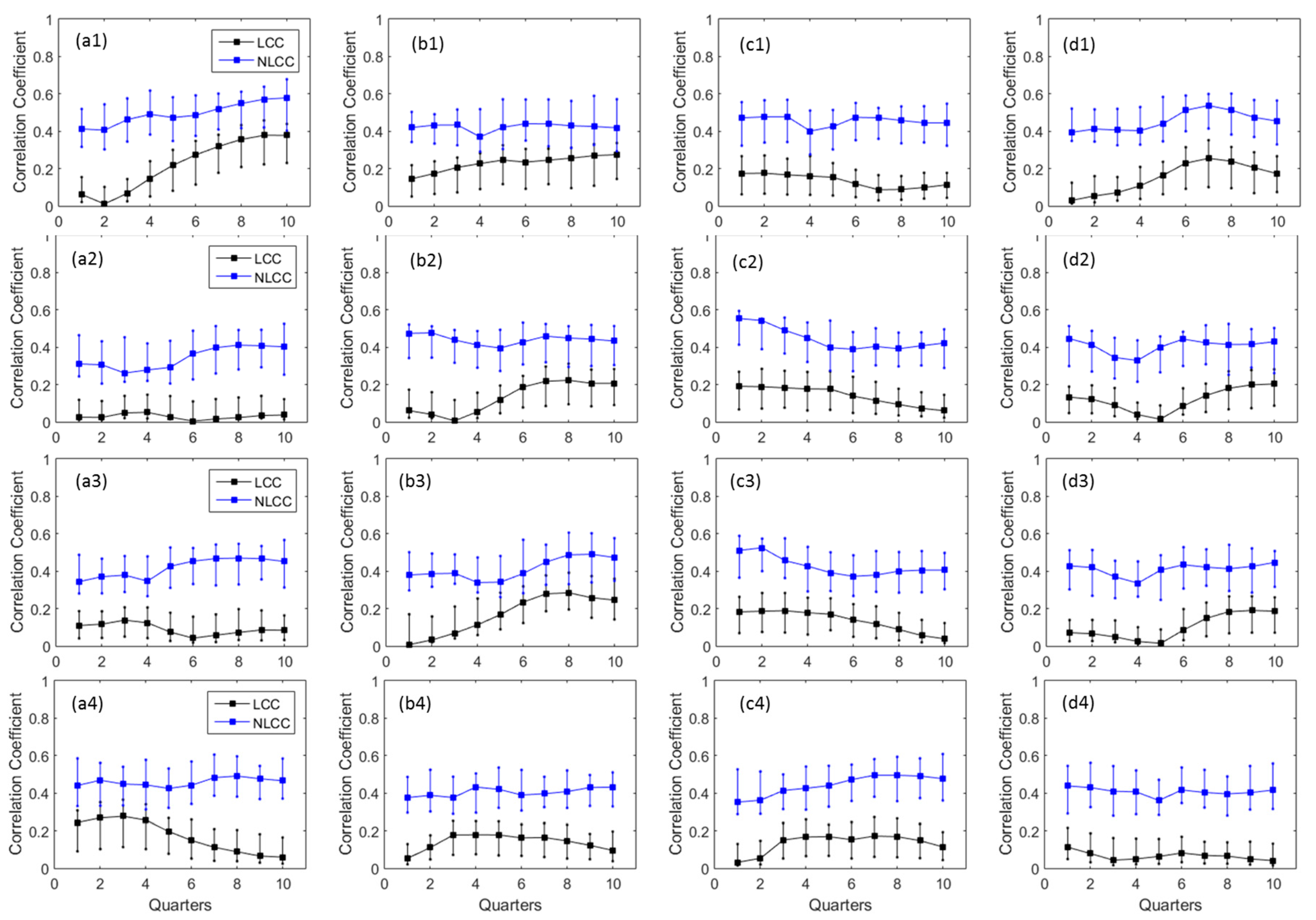
3.2. Linear and Nonlinear Correlation between Precipitation Extreme Indices and ENSO
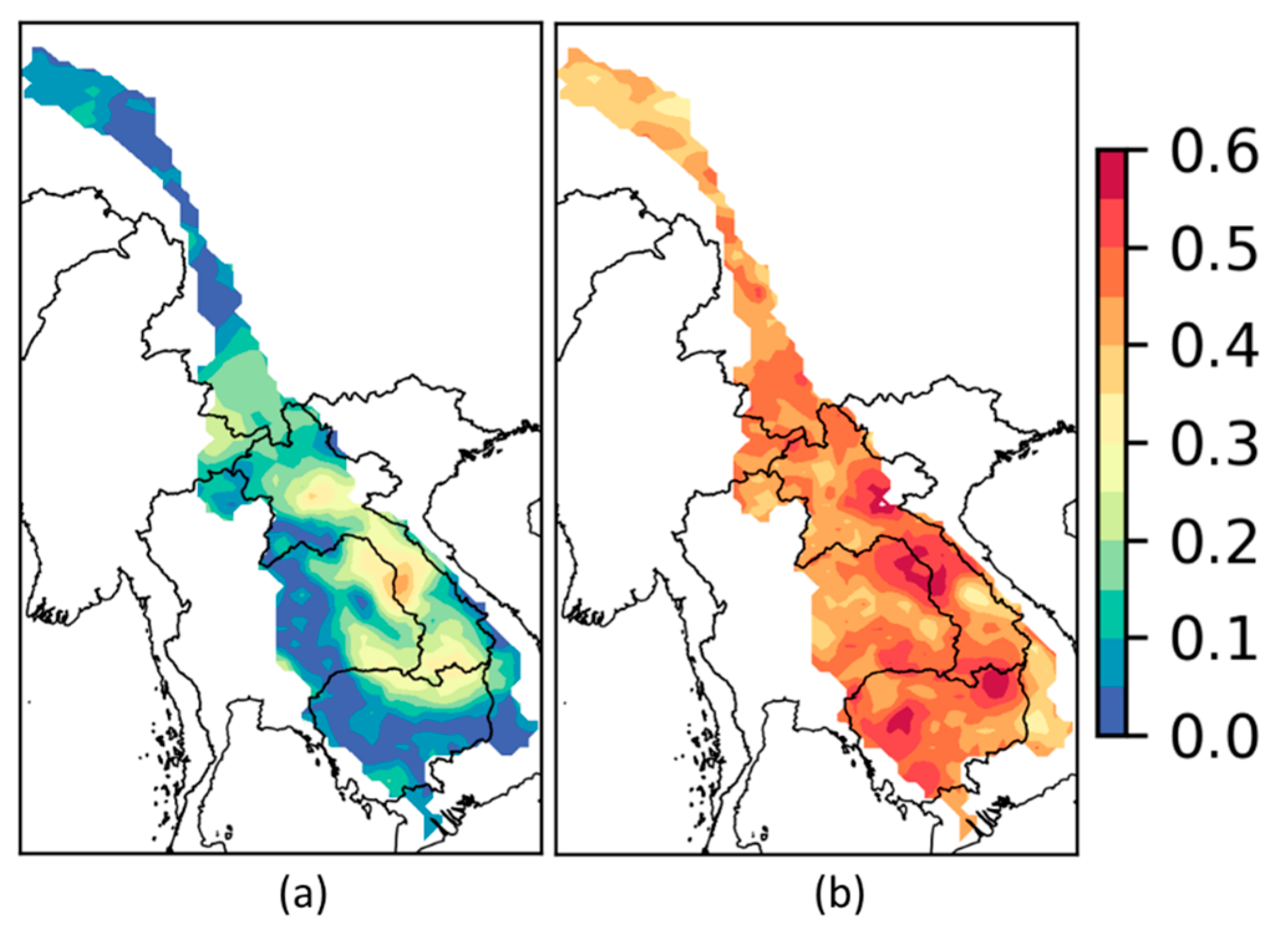
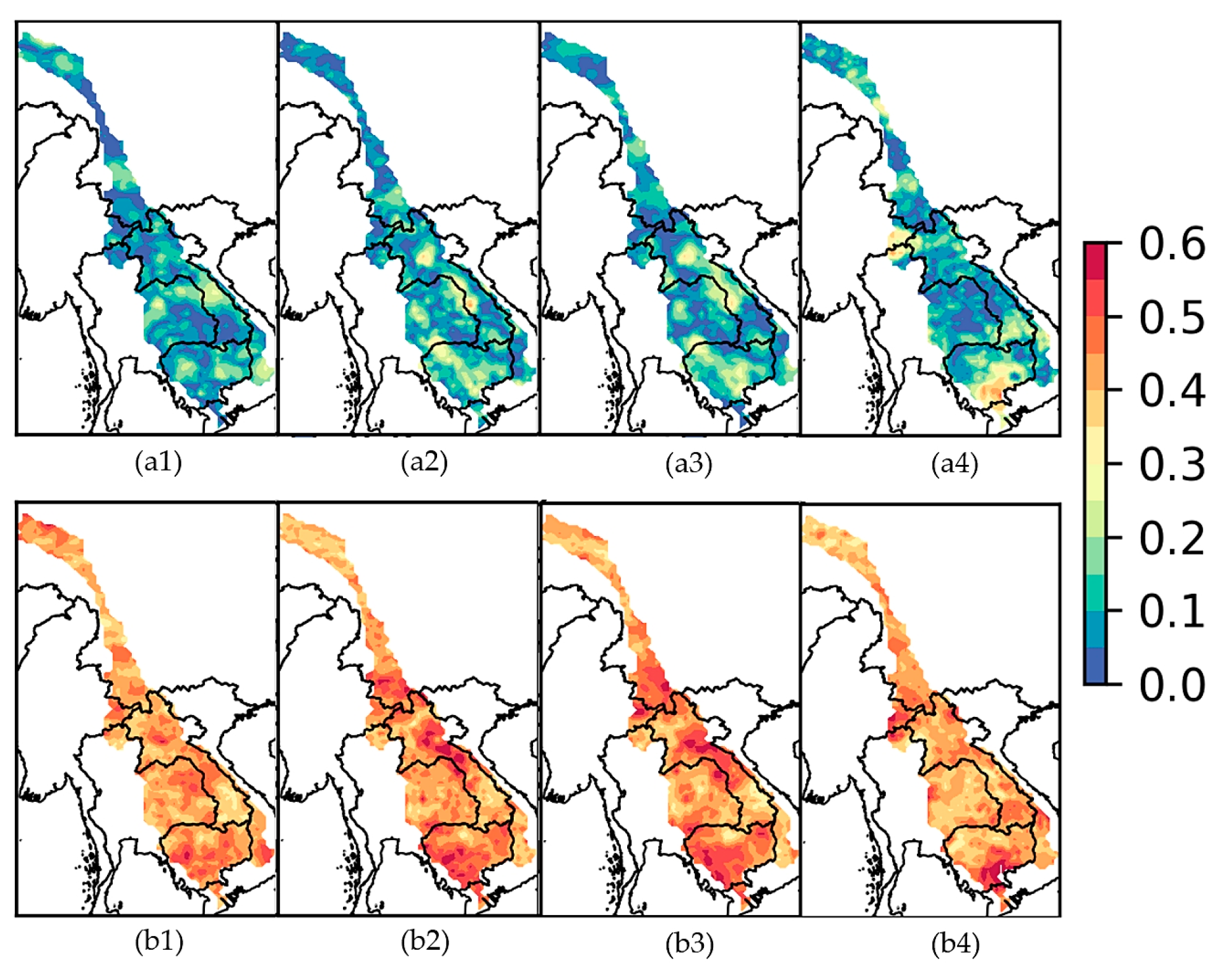
3.3. Spatial Linear and Nonlinear Correlation Maps
4. Discussion
5. Conclusions
- Nonlinear correlation is able to reveal the additional dependence structures between hydro-meteorological data over Mekong River Basin and ENSO indices.
- Both linear and nonlinear correlation exhibits similar varying patterns among different ENSO quarters for most of the stations/indices.
- The results reveal that higher correlation coefficients can be found using the nonlinear correlation coefficients in comparison to the traditional linear correlation analysis.
- Spatial correlation structures for LCCs and NLCCs are also constructed based on extreme precipitation indices and ENSO. The use of spatial maps further complements our analyses based on a single station to other ungagged regions to better inform local stakeholders in building better tools for water resource management.
- Further analyses are required to reveal the non-linear association between other large-scale climate phenomena (SOI, PDO, NAO, etc.) with local meteorological variables. The mutual information between these indices and local meteorological variables can further help policymakers to improve climate-informed adaptation studies.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gu, D.; Philander, S.G.H. Interdecadal climate fluctuations that depend on exchanges between the tropics and extratropics. Science 1997, 275, 805–807. [Google Scholar] [CrossRef] [PubMed]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental US. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Wood, A.W.; Maurer, E.P.; Kumar, A.; Lettenmaier, D.P. Long-range experimental hydrologic forecasting for the eastern United States. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Tootle, G.A.; Piechota, T.C.; Singh, A. Coupled oceanic-atmospheric variability and US streamflow. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Using oceanic-atmospheric oscillations for long lead time streamflow forecasting. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Hallett, T.B.; Coulson, T.; Pilkington, J.G.; Clutton-Brock, T.H.; Pemberton, J.M.; Grenfell, B.T. Why large-scale climate indices seem to predict ecological processes better than local weather. Nature 2004, 430, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Cayan, D.R.; Redmond, K.T.; Riddle, L.G. ENSO and hydrologic extremes in the western United States. J. Clim. 1999, 12, 2881–2893. [Google Scholar] [CrossRef]
- Jones, C. Occurrence of extreme precipitation events in California and relationships with the Madden-Julian oscillation. J. Clim. 2000, 13, 3576–3587. [Google Scholar] [CrossRef]
- DeFlorio, M.J.; Pierce, D.W.; Cayan, D.R.; Miller, A.J. Western U.S. Extreme Precipitation Events and Their Relation to ENSO and PDO in CCSM4. J. Clim. 2013, 26, 4231–4243. [Google Scholar] [CrossRef]
- Barlow, M.; Nigam, S.; Berbery, E.H. ENSO, Pacific Decadal Variability, and U.S. Summertime Precipitation, Drought, and Stream Flow. J. Clim. 2001, 14, 2105–2128. [Google Scholar] [CrossRef]
- Mo, K.C. Drought onset and recovery over the United States. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Özger, M.; Mishra, A.K.; Singh, V.P. Low frequency drought variability associated with climate indices. J. Hydrol. 2009, 364, 152–162. [Google Scholar] [CrossRef]
- Andrews, E.D.; Antweiler, R.C.; Neiman, P.J.; Ralph, F.M. Influence of ENSO on flood frequency along the California coast. J. Clim. 2004, 17, 337–348. [Google Scholar] [CrossRef]
- Ward, P.J.; Jongman, B.; Kummu, M.; Dettinger, M.D.; Weiland, F.C.S.; Winsemius, H.C. Strong influence of El Niño Southern Oscillation on flood risk around the world. Proc. Natl. Acad. Sci. USA 2014, 111, 15659–15664. [Google Scholar] [CrossRef] [PubMed]
- Sivapalan, M. Prediction in ungauged basins: A grand challenge for theoretical hydrology. Hydrol. Process. 2003, 17, 3163–3170. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Samaniego, L.; Bárdossy, A.; Kumar, R. Streamflow prediction in ungauged catchments using copula-based dissimilarity measures. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Chikamoto, Y.; Timmermann, A.; Luo, J.J.; Mochizuki, T.; Kimoto, M.; Watanabe, M.; Ishii, M.; Xie, S.P.; Jin, F.F. Skilful multi-year predictions of tropical trans-basin climate variability. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Hartman, D.; Vejmelka, M.; Novotná, D.; Paluš, M. Non-linear dependence and teleconnections in climate data: Sources, relevance, nonstationarity. Clim. Dyn. 2014, 42, 1873–1886. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Sing, V.P.; Gua, X.; Kong, D.D.; Xiao, M.Z. Impacts of ENSO and ENSO Modoki+A regimes on seasonal precipitation variations and possible underlying causes in the Huai River basin, China. J. Hydrol. 2016, 533, 308–319. [Google Scholar] [CrossRef]
- Wrzesinski, D. Regional differences in the influence of the North Atlantic Oscillation on seasonal river runoff in Poland. Quaest. Geogr. 2011, 30, 127–136. [Google Scholar] [CrossRef]
- Wrzesinski, D. Typology of spatial patterns seasonality in European rivers flow regime. Quaest. Geogr. 2008, 27A, 87–98. [Google Scholar]
- Lanzante, J.R. Resistant, robust and non-parametric techniques for the analysis of climate data: Theory and examples, including applications to historical radiosonde station data. Int. J. Clim. 1996, 16, 1197–1226. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K. Three-parameter-based streamflow elasticity model: Application to MOPEX basins in the USA at annual and seasonal scales. Hydrol. Earth Syst. Sci. 2016, 20, 2545–2556. [Google Scholar] [CrossRef]
- Belle, G.; Hughes, J.P. Nonparametric tests for trend in water quality. Water Resour. Res. 1984, 20, 127–136. [Google Scholar] [CrossRef]
- Li, J.; Tan, S. Nonstationary flood frequency analysis for annual flood peak series, adopting climate indices and check dam index as covariates. Water Resour. Manag. 2015, 29, 5533–5550. [Google Scholar] [CrossRef]
- Zhang, Y.; Cabilio, P.; Nadeem, K. Improved Seasonal Mann–Kendall Tests for Trend Analysis in Water Resources Time Series. In Advances in Time Series Methods and Applications; Li, W.K., Stanford, D.A., Yu, H., Eds.; Springer: New York, NY, USA, 2016; pp. 215–229. ISBN 978-1-4939-6568-7. [Google Scholar]
- Coulibaly, P.; Baldwin, C.K. Nonstationary hydrological time series forecasting using nonlinear dynamic methods. J. Hydrol. 2005, 307, 164–174. [Google Scholar] [CrossRef]
- Khan, S.; Ganguly, A.R.; Bandyopadhyay, S.; Saigal, S.; Erickson, D.J.; Protopopescu, V.; Ostrouchov, G. Nonlinear statistics reveals stronger ties between ENSO and the tropical hydrological cycle. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Fleming, S.W.; Dahlke, H.E. Parabolic northern-hemisphere river flow teleconnections to El Niño-Southern Oscillation and the Arctic Oscillation. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Cannon, A.J. Revisiting the nonlinear relationship between ENSO and winter extreme station precipitation in North America. Int. J. Climatol. 2015, 35, 4001–4014. [Google Scholar] [CrossRef]
- Lin-Ye, J.; Garcia-Leon, M.; Gracia, V.; Ortego, M.I.; Lionello, P.; Sanchez-Arcilla, A. Multivariate statistical modeling of future marine storms. Appl. Ocean Res. 2017, 65, 192–205. [Google Scholar] [CrossRef]
- Kusumastuti, D.I.; Struthers, I.; Sivapalan, M.; Reynolds, D.A. Threshold effects in catchment storm response and the occurrence and magnitude of flood events: Implications for flood frequency. Hydrol. Earth Syst. Sci. 2007, 11, 1515–1528. [Google Scholar] [CrossRef]
- Konapala, G.; Veettil, A.V.; Mishra, A.K. Teleconnection between low flows and large-scale climate indices in Texas River basins. Stoch. Environ. Res. Risk Assess. 2017, 1–14. [Google Scholar] [CrossRef]
- Mishra, A.K.; Özger, M.; Singh, V.P. An entropy based investigation into the variability of precipitation. J. Hydrol. 2009, 370, 139–154. [Google Scholar] [CrossRef]
- Mishra, A.K.; Özger, M.; Singh, V.P. Association between uncertainty in meteorological variables and water resources planning for Texas. J. Hydrol. Eng. 2011, 16, 984–999. [Google Scholar] [CrossRef]
- Mishra, A.K.; Coulibaly, P. Hydrometric network evaluation for Canadian watersheds. J. Hydrol. 2010, 380, 420–437. [Google Scholar] [CrossRef]
- Mishra, A.K.; Coulibaly, P. Variability in Canadian Seasonal Streamflow Information and its Implication for Hydrometric Network Design. J. Hydrol. Eng. 2014, 19. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Entropy theory-based criterion for hydrometric network evaluation and design: Maximum information minimum redundancy. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Analysis of drought severity-area-frequency curves using a general circulation model and scenario uncertainty. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Mishra, A.K.; Özger, M.; Singh, V.P. Trend and persistence of precipitation under climate change scenarios. Hydrol. Proc. 2009, 23, 2345–2357. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Mishra, A.K.; Singh, V.P. Regionalization of drought characteristics using an entropy approach. J. Hydrol. Eng. 2013, 18, 870–887. [Google Scholar] [CrossRef]
- Sharma, A. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 1—A strategy for system predictor identification. J. Hydrol. 2000, 239, 232–239. [Google Scholar] [CrossRef]
- Harrold, T.I.; Sharma, A.; Sheather, S. Selection of a kernel bandwidth for measuring dependence in hydrologic time series using the mutual information criterion. Stoch. Environ. Res. Risk Assess. 2001, 15, 310–324. [Google Scholar] [CrossRef]
- Song, X.; Zhang, J.; Zhan, C.; Xuan, Y.; Ye, M.; Xu, C. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications. J. Hydrol. 2015, 523, 739–757. [Google Scholar] [CrossRef]
- Han, M.; Ren, W.; Liu, X. Joint mutual information-based input variable selection for multivariate time series modeling. Eng. Appl. Artif. Intell. 2015, 37, 250–257. [Google Scholar] [CrossRef]
- Knuth, K.H.; Gotera, A.; Curry, C.T.; Huyser, K.A.; Wheeler, K.R.; Rossow, W.B. Revealing relationships among relevant climate variables with information theory. arXiv, 2013; arXiv:1311.4632. [Google Scholar]
- Khokhlov, V.N.; Glushkov, A.V.; Loboda, N.S. On the nonlinear interaction between global teleconnection patterns. Q. J. R. Meteorol. Soc. 2006, 132, 447–465. [Google Scholar] [CrossRef]
- Hurtado, A.F.; Poveda, G. Linear and global space-time dependence and Taylor hypotheses for rainfall in the tropical Andes. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Naumann, G.; Vargas, W.M. Joint diagnostic of the surface air temperature in southern South America and the Madden–Julian oscillation. Weather Forecast 2010, 25, 1275–1280. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, T. Investigation of hydrological variability in the Korean Peninsula with the ENSO teleconnections. Proc. IAHS 2016, 374. [Google Scholar] [CrossRef]
- Sivakumar, B. Chaos in Hydrology: Bridging Determinism and Stochasticity; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-90-481-2552-4. [Google Scholar] [CrossRef]
- Varis, O.; Kummu, M.; Salmivaara, A. Ten major rivers in monsoon Asia-Pacific: An assessment of vulnerability. Appl. Geogr. 2012, 32, 441–454. [Google Scholar] [CrossRef]
- Wilmott, C.J.; Rowe, C.M.; Philpot, W.D. Small-scale climate maps: A sensitivity analysis of some common assumptions associated with grid-point interpolation and contouring. Am. Cartogr. 1985, 12, 5–16. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, V.S.; Liong, S.Y. SWAT use of gridded observations for simulating runoff—A Vietnam river basin study. Hydrol. Earth Syst. Sci. 2012, 16, 2801–2811. [Google Scholar] [CrossRef]
- Vu, M.T.; Mishra, A.K. Spatial and Temporal Variability of Standardized Precipitation Index over Indochina Peninsula. Cuad. Investig. Geogr. 2016, 42, 221–232. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, S.V.; Liong, S.-Y.; Mishra, A.K. Uncertainties in gridded precipitation observations in characterizing spatio-temporal drought and wetness over Vietnam. Int. J. Climatol. 2017. [Google Scholar] [CrossRef]
- Raghavan, V.S.; Vu, M.T.; Liong, S.Y. Ensemble climate projections of mean and extreme rainfall over Vietnam. Glob. Planet. Chang. 2017, 148, 96–104. [Google Scholar] [CrossRef]
- Raghavan, V.S.; Vu, M.T.; Liong, S.Y. Impact of climate change on future stream flow in the Dakbla river. J. Hydroinform. 2014, 16, 231–244. [Google Scholar] [CrossRef]
- Raghavan, V.S.; Liong, S.Y.; Vu, M.T. Assessment of future stream flow over the Sesan catchment of the Lower Mekong Basin in Vietnam. Hydrol. Proc. 2012, 26, 3661–3668. [Google Scholar] [CrossRef]
- Vu, M.T.; Aribarg, T.; Supratid, S.; Raghavan, V.S.; Liong, S.Y. Statistical downscaling rainfall over Bangkok using Artificial Neural Network. Theor. Appl. Climatol. 2016, 126, 453–467. [Google Scholar] [CrossRef]
- Trenberth, K.E. The Definition of El Niño. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Trenberth, K.E. The Climate Data Guide: Nino SST Indices (Nino 1+2, 3, 3.4, 4; ONI and TNI). Available online: https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni (accessed on 6 January 2018).
- Moon, Y.I.; Rajagopalan, B.; Lall, U. Estimation of mutual information using kernel density estimators. Phys. Rev. E 1995, 52, 2318–2321. [Google Scholar] [CrossRef]
- Granger, C.; Lin, J.L. Using the mutual information coefficient to identify lags in nonlinear models. J. Time Ser. Anal. 1994, 15, 371–384. [Google Scholar] [CrossRef]
- Joe, H. Relative entropy measures of multivariate dependence. J. Am. Stat. Assoc. 1989, 84, 157–164. [Google Scholar] [CrossRef]
- Khan, S.; Bandyopadhyay, S.; Ganguly, A.R.; Saigal, S.; Erickson, D.J., III; Protopopescu, V.; Ostrouchov, G. Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data. Phys. Rev. E 2007, 76. [Google Scholar] [CrossRef] [PubMed]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef] [PubMed]
- Hull, M.M.V. Edgeworth approximation of multivariate differential entropy. Neural Comput. 2005, 17, 1903–1910. [Google Scholar] [CrossRef]
- Cellucci, C.J.; Albano, A.M.; Rapp, P.E. Statistical validation of mutual information calculations: Comparison of alternative numerical algorithms. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall/CRC: London, UK, 1986. [Google Scholar]
- Wand, M.P.; Jones, M.C. Multivariate plug-in bandwidth selection. Comput. Stat. 1994, 9, 97–117. [Google Scholar]
- Ince, R.A.A.; Giordano, B.L.; Kayser, C.; Rousselet, G.A.; Gross, J.; Schyns, P.G. A statistical framework for neuroimaging data analysis based on mutual information estimated via a Gaussian Copula. Hum. Brain Mapp. 2017, 38, 1541–1573. [Google Scholar] [CrossRef] [PubMed]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Xu, Z.X.; Takeuchi, K.; Ishidaira, H. Correlation between El Niño–Southern Oscillation (ENSO) and precipitation in Southeast Asia and the Pacific region. Hydrol. Proc. 2003, 18, 107–123. [Google Scholar] [CrossRef]
- Chen, D.; Cane, M.A.; Kaplan, A.; Zebiak, S.E.; Huang, D. Predictability of El Niño over the past 148 years. Nature 2004, 428, 733–736. [Google Scholar] [CrossRef] [PubMed]
- Ludescher, J.; Gozolchiani, A.; Bogacheva, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Very early warning of next El Niño. Proc. Natl. Acad. Sci. USA 2014, 111, 2064–2066. [Google Scholar] [CrossRef] [PubMed]
- Power, S.; Delage, F.; Chung, C.; Kociuba, G.; Keay, K. Robust twenty-first-century projections of El Niño and related precipitation variability. Nature 2013, 502, 541–545. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Borlace, S.; Lengaigne, M.; Van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L.; et al. Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Chang. 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Zhang, G.; Su, X.; Singh, V.P.; Ayantobo, O.O. Modeling NDVI using Joint Entropy method considering hydro-meteorological driving factors in the middle reaches of Hei river basin. Entropy 2017, 19, 502. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, T.M.; Mishra, A.K.; Konapala, G. Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO. Entropy 2018, 20, 38. https://doi.org/10.3390/e20010038
Vu TM, Mishra AK, Konapala G. Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO. Entropy. 2018; 20(1):38. https://doi.org/10.3390/e20010038
Chicago/Turabian StyleVu, Tue M., Ashok K. Mishra, and Goutam Konapala. 2018. "Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO" Entropy 20, no. 1: 38. https://doi.org/10.3390/e20010038
APA StyleVu, T. M., Mishra, A. K., & Konapala, G. (2018). Information Entropy Suggests Stronger Nonlinear Associations between Hydro-Meteorological Variables and ENSO. Entropy, 20(1), 38. https://doi.org/10.3390/e20010038




