L1-Minimization Algorithm for Bayesian Online Compressed Sensing
Abstract
1. Introduction
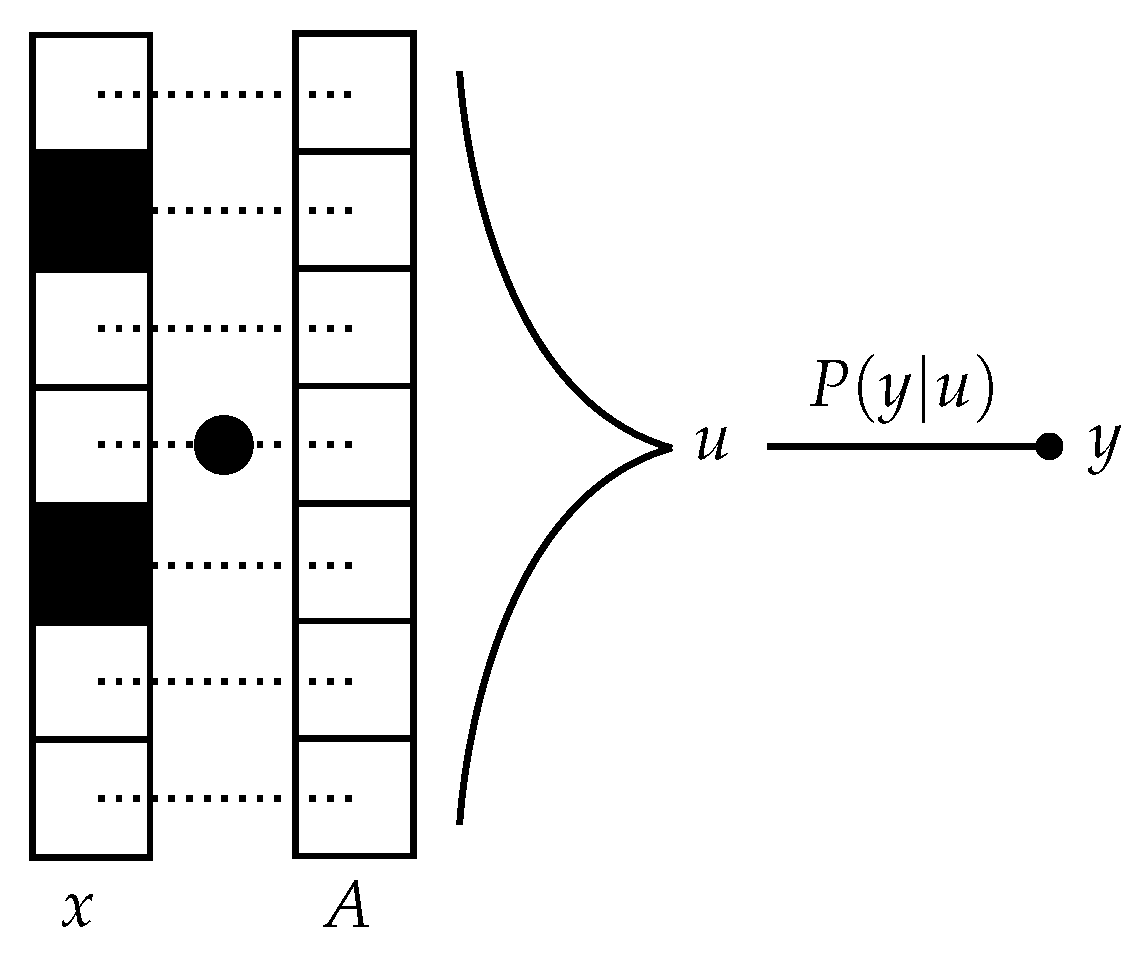
2. Problem Setup
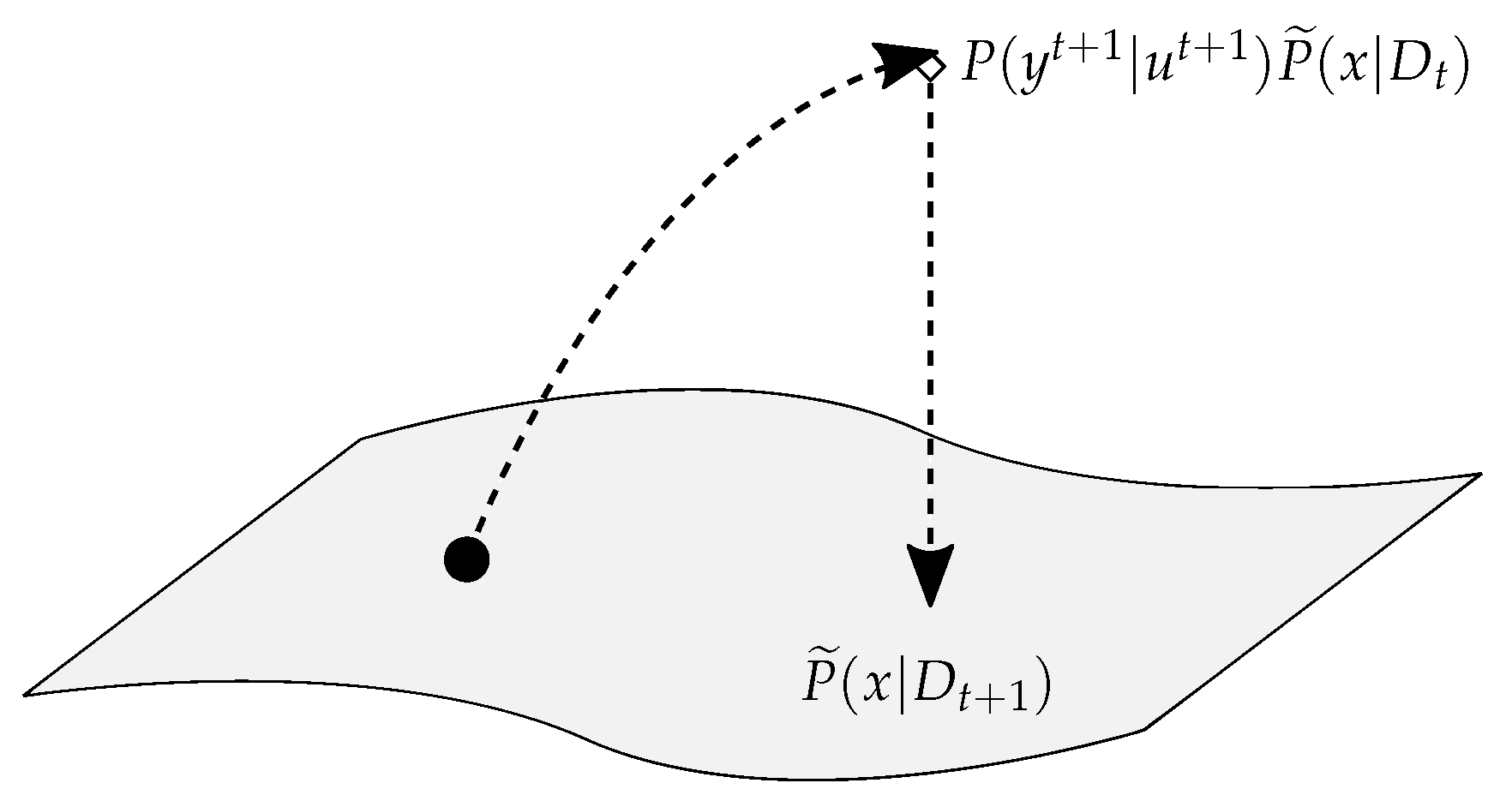
3. Bayesian Online Compressed Sensing
4. Mismatched Priors and L1-Minimization Based Reconstruction
| Algorithm 1 Online -based signal recovery for CS. | |
| 1: Initialize | ▹; |
| 2: while do | |
| 3: Obtain new measurement | |
| 4: Update | ▹ Equations (10) and (11) |
| 5: Find | ▹ Equation (19) |
| 6: Update | |
| 7: Estimate signal means and variances | ▹ Equations (15) and (16) |
| 8: end while | |
| 9: return | |
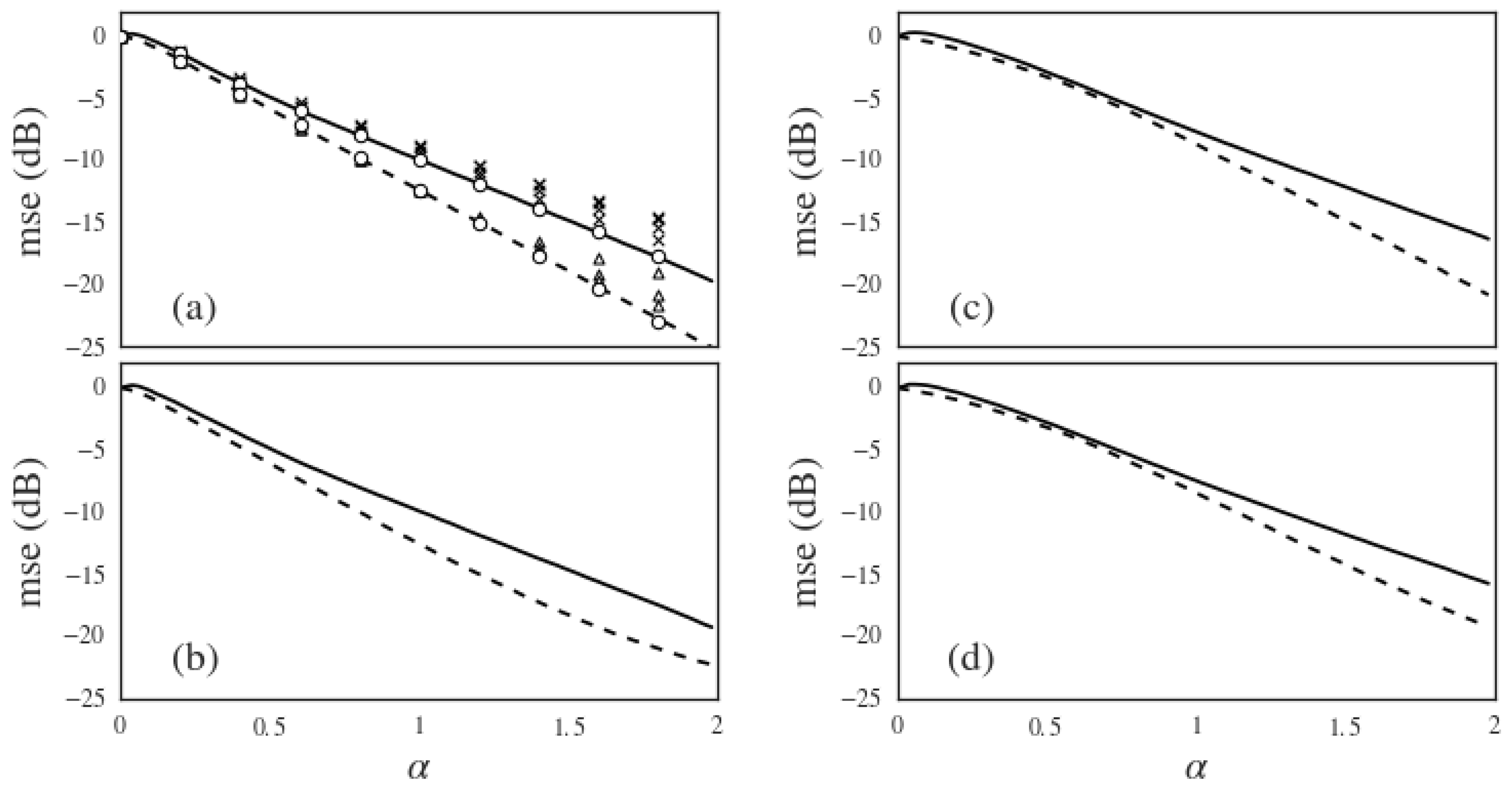
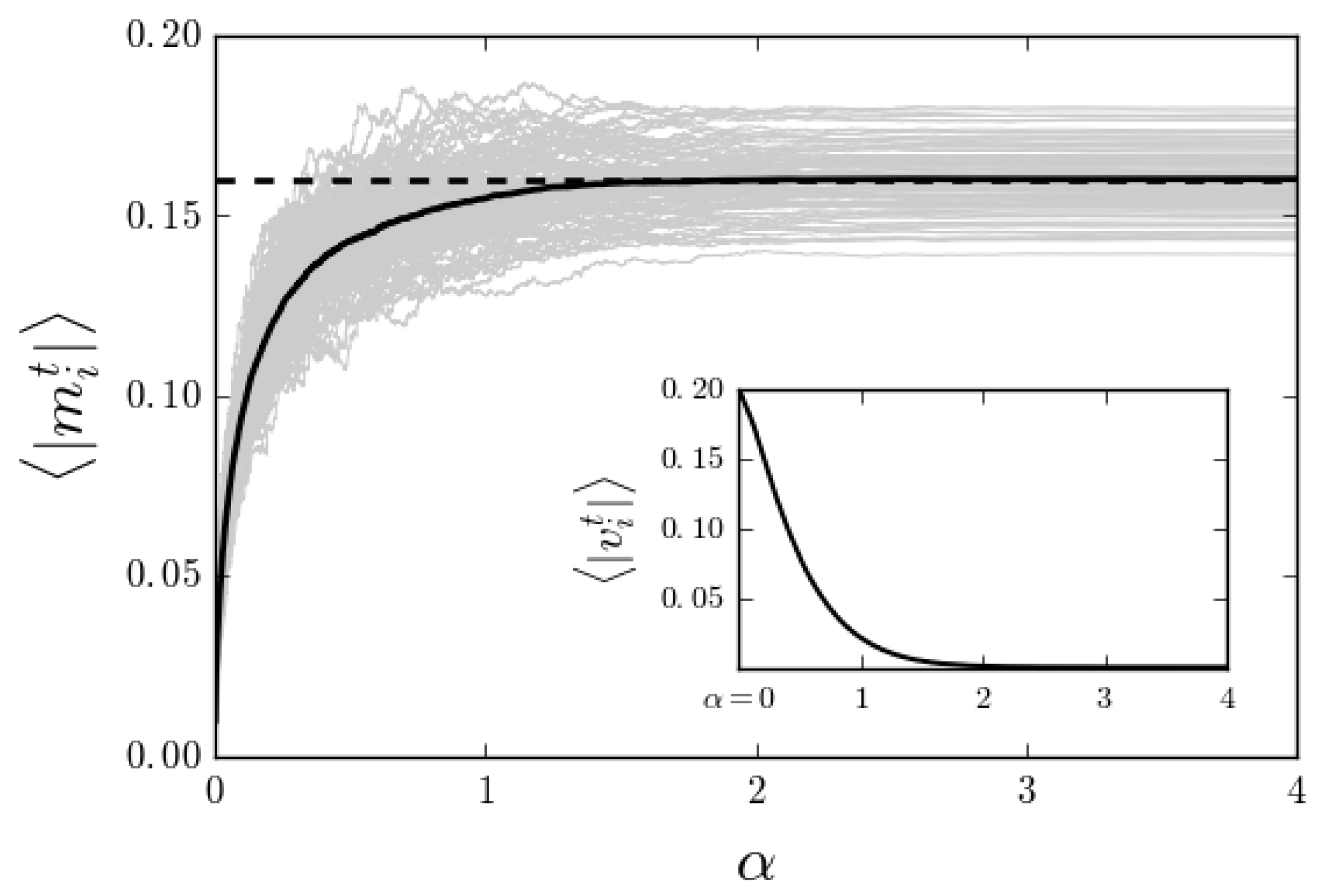
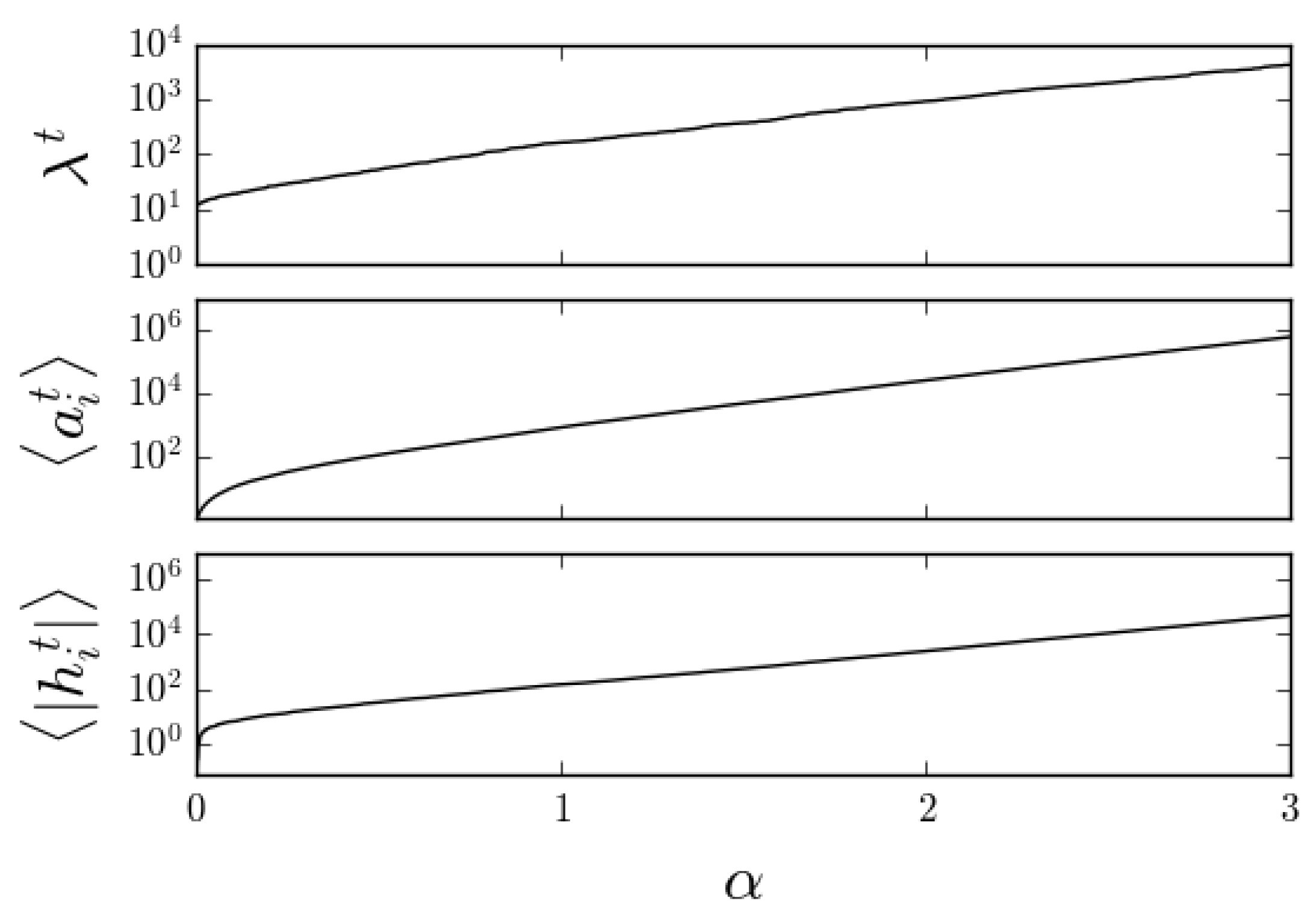
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Strohmer, T. Measure What Should be Measured: Progress and Challenges in Compressive Sensing. IEEE Signal Process. Lett. 2012, 19, 887–893. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Holtz, O. Compressive sensing: A paradigm shift in signal processing. arXiv, 2008; arXiv:0812.3137. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. AIEE 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Shannon, C. Communication in the presence of noise. Proc. Inst. Radio Eng. 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Candès, E.; Tao, T. Near Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Rangan, S. Generalized approximate message passing for estimation with random linear mixing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings (ISIT), St. Petersburg, Russia, 31 July–5 August 2011. [Google Scholar]
- Krzakala, F.; Mezard, M.; Sausset, F.; Zdeborova, L. Statistical-Physics-Based Reconstruction in Compressed Sensing. Phys. Rev. X 2012, 2, 021005. [Google Scholar] [CrossRef]
- Tramel, E.W.; Manoel, A.; Caltagirone, F.; Gabrié, M.; Krzakala, F. Inferring sparsity: Compressed sensing using generalized restricted Boltzmann machines. In Proceedings of the 2016 IEEE Information Theory Workshop (ITW), Cambridge, UK, 11–14 September 2016; pp. 265–269. [Google Scholar]
- Krzakala, F.; Mezard, M.; Sausset, F.; Sun, Y.; Zdeborova, L. Probabilistic reconstruction in compressed sensing: Algorithms, phase diagrams, and threshold achieving matrices. J. Stat. Mech. Theory Exp. 2012, P08009. [Google Scholar] [CrossRef]
- Xu, Y.; Kabashima, Y.; Zdeborova, L. Bayesian signal reconstruction for 1-bit Compressed Sensing. J. Stat. Mech. Theory Exp. 2014. [Google Scholar] [CrossRef]
- Rangan, S.; Fletcher, A.K.; Goyal, V.K. Asymptotic Analysis of MAP Estimation via the Replica Method and Applications to Compressed Sensing. IEEE Trans. Inf. Theory 2012, 58, 1902–1923. [Google Scholar] [CrossRef]
- Opper, M.; Winther, O. Chapter A Bayesian approach to on-line learning. In On-Line Learning in Neural Networks; Cambridge University Press: Cambridge, UK, 1998; pp. 363–378. [Google Scholar]
- De Oliveira, E.A.; Caticha, N. Inference from aging information. IEEE Trans. Neural Netw. 2010, 21, 1015–1020. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Kinouchi, O.; Caticha, N. Statistical mechanics of online learning of drifting concepts: A variational approach. Mach. Learn. 1998, 32, 179–201. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Stengel, R.F. Optimal Control and Estimation; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013; Volume 3. [Google Scholar]
- Broderick, T.; Boyd, N.; Wibisono, A.; Wilson, A.C.; Jordan, M.I. Streaming variational bayes. In Advances in Neural Information Processing Systems; Curran: Red Hook, NY, USA, 2013; pp. 1727–1735. [Google Scholar]
- Manoel, A.; Krzakala, F.; Tramel, E.W.; Zdeborová, L. Streaming Bayesian inference: Theoretical limits and mini-batch approximate message-passing. arXiv, 2017; arXiv:1706.00705. [Google Scholar]
- Rossi, P.V.; Kabashima, Y.; Inoue, J. Bayesian online compressed sensing. Phys. Rev. E 2016, 94, 022137. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodological) 1996, 58, 267–288. [Google Scholar]
- Ganguli, S.; Sompolinsky, H. Statistical Mechanics of Compressed Sensing. Phys. Rev. Lett. 2010, 104, 188701. [Google Scholar] [CrossRef] [PubMed]
- Kabashima, Y.; Wadayama, T.; Tanaka, T. A typical reconstruction limit for compressed sensing based on Lp-norm minimization. J. Stat. Mech. Theory Exp. 2009, 9, L09003. [Google Scholar]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian Compressive Sensing Via Belief Propagation. IEEE Trans. Signal Process. 2010, 58, 269–280. [Google Scholar] [CrossRef]
- Hans, C. Bayesian lasso regression. Biometrika 2009, 96, 835–845. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The bayesian lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Figueiredo, M.A. Adaptive sparseness for supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1150–1159. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, P.V.; Vicente, R. L1-Minimization Algorithm for Bayesian Online Compressed Sensing. Entropy 2017, 19, 667. https://doi.org/10.3390/e19120667
Rossi PV, Vicente R. L1-Minimization Algorithm for Bayesian Online Compressed Sensing. Entropy. 2017; 19(12):667. https://doi.org/10.3390/e19120667
Chicago/Turabian StyleRossi, Paulo V., and Renato Vicente. 2017. "L1-Minimization Algorithm for Bayesian Online Compressed Sensing" Entropy 19, no. 12: 667. https://doi.org/10.3390/e19120667
APA StyleRossi, P. V., & Vicente, R. (2017). L1-Minimization Algorithm for Bayesian Online Compressed Sensing. Entropy, 19(12), 667. https://doi.org/10.3390/e19120667



