Analyzing Information Distribution in Complex Systems
Abstract
:1. Introduction
2. Background
2.1. Partial Information Decomposition
2.1.1. Formulation
2.1.2. Calculating PID Terms
2.1.3. Numerical Estimator
2.2. Ising Model
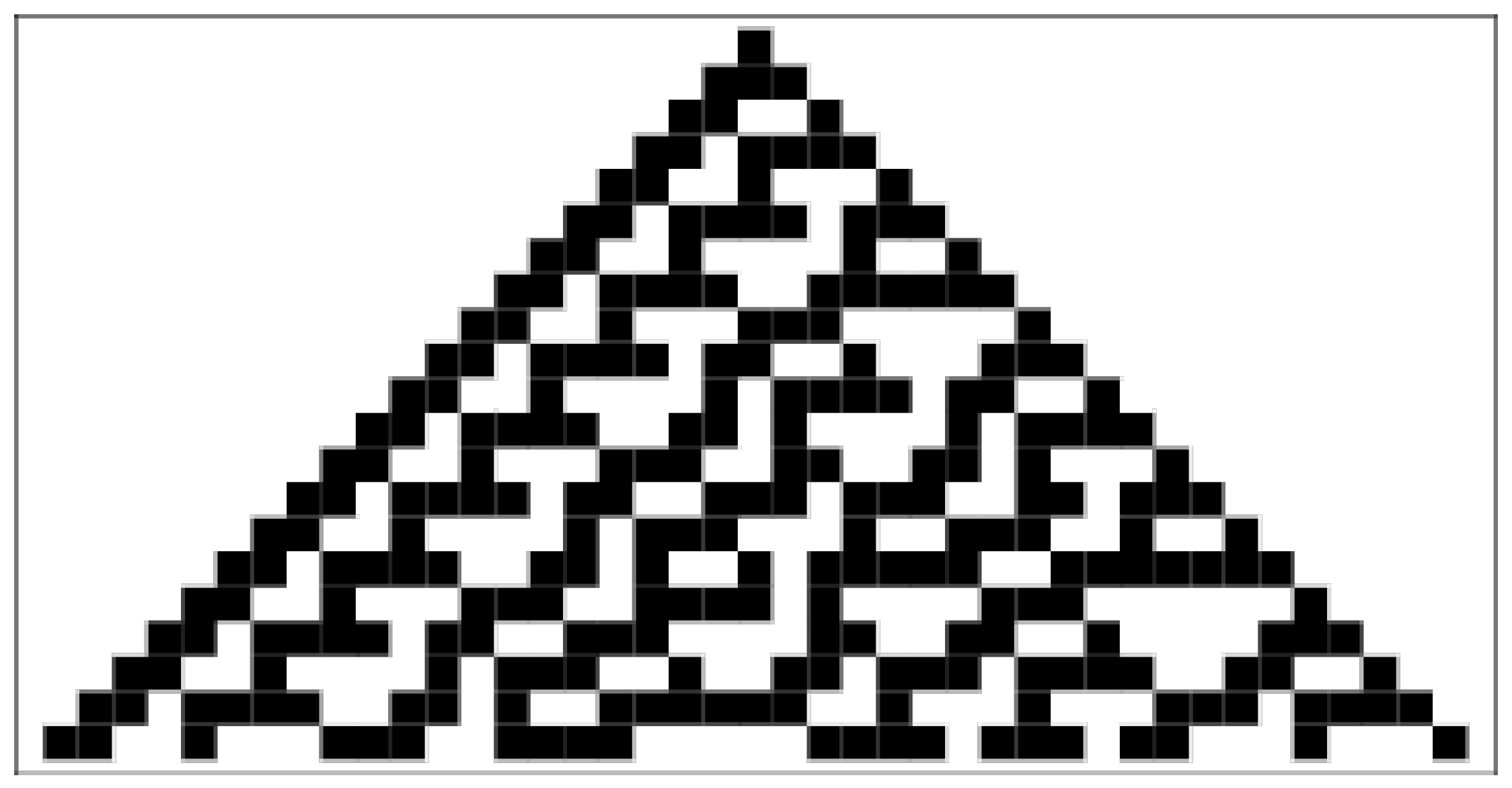
2.3. Elementary Cellular Automata
- Class 1: Cellular automata that converge to a homogeneous state. For example, rule 0, which takes any state into a 0 state, belongs to this class.
- Class 2: Ceullar automata that converge to a repetitive or periodic state. For example, rule 184, which has been used to model traffic, belongs to this class.
- Class 3: Cellular automata that evolve chaotically. For example, rule 30, which Mathematica uses as a random number generator [24], belongs to this class.
- Class 4: Cellular automata in which persistent propagating structures are formed. For example, rule 110, which is capable of universal computation, belongs to this class. It is conjectured that other rules in this class are also universal.
3. Methods
3.1. Methodology for Analyzing the Ising Model
| Algorithm 1: A single Glauber dynamics update, which consists of L spin-flip attempts |
 |
| Algorithm 2: The full Glauber dynamics algorithm |
 |
3.2. Methodology for Analyzing the Elementary Cellular Automata
4. Results
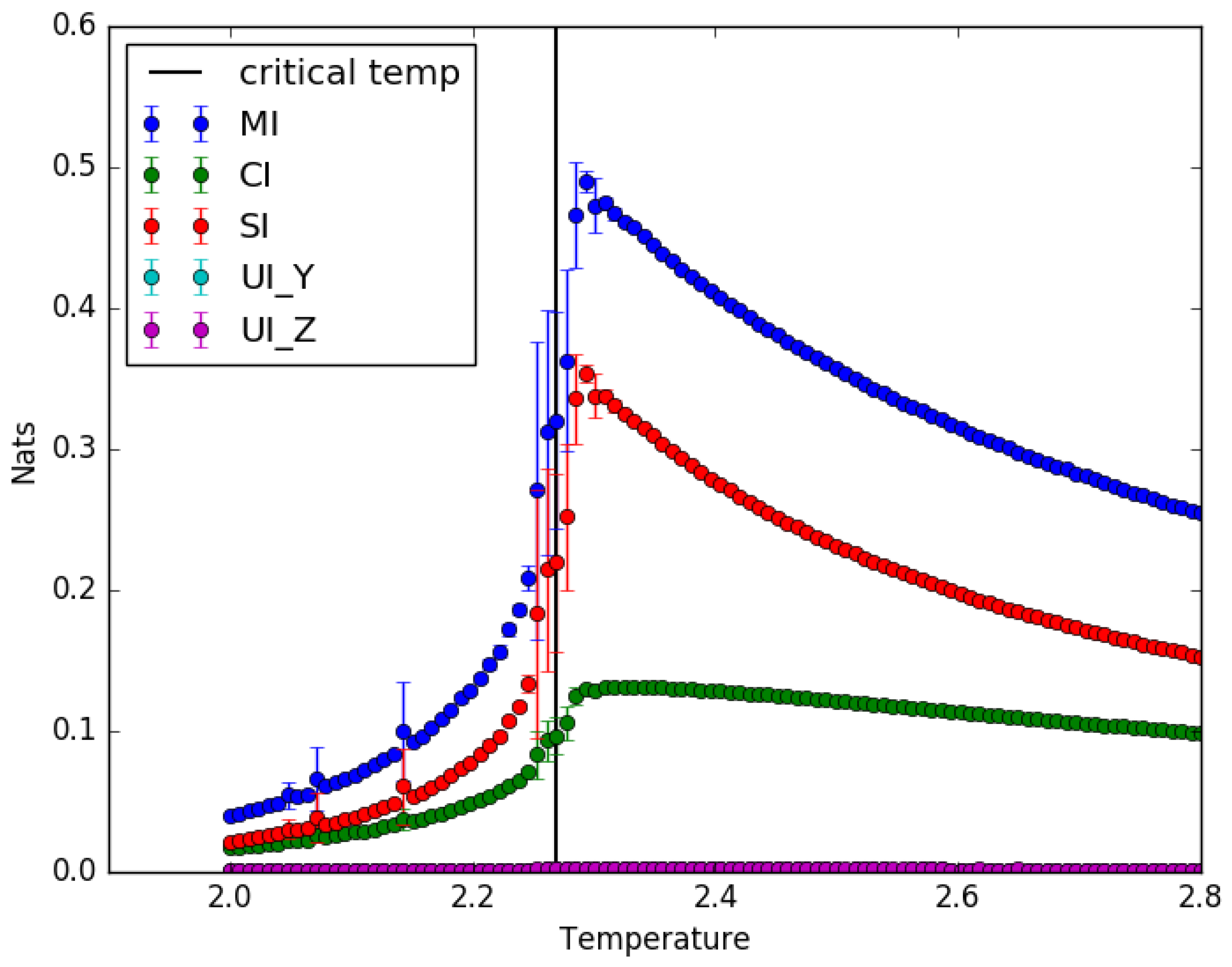
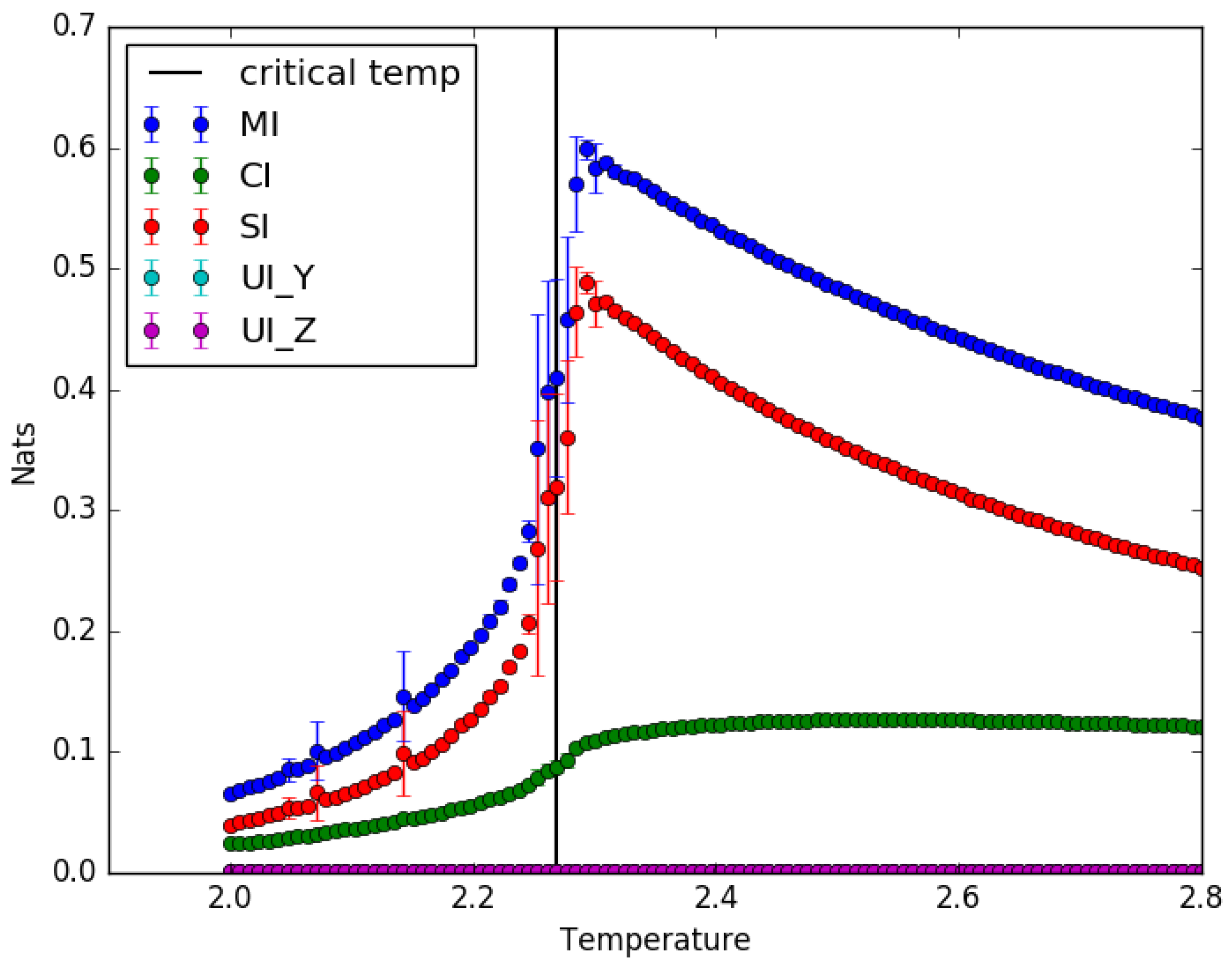
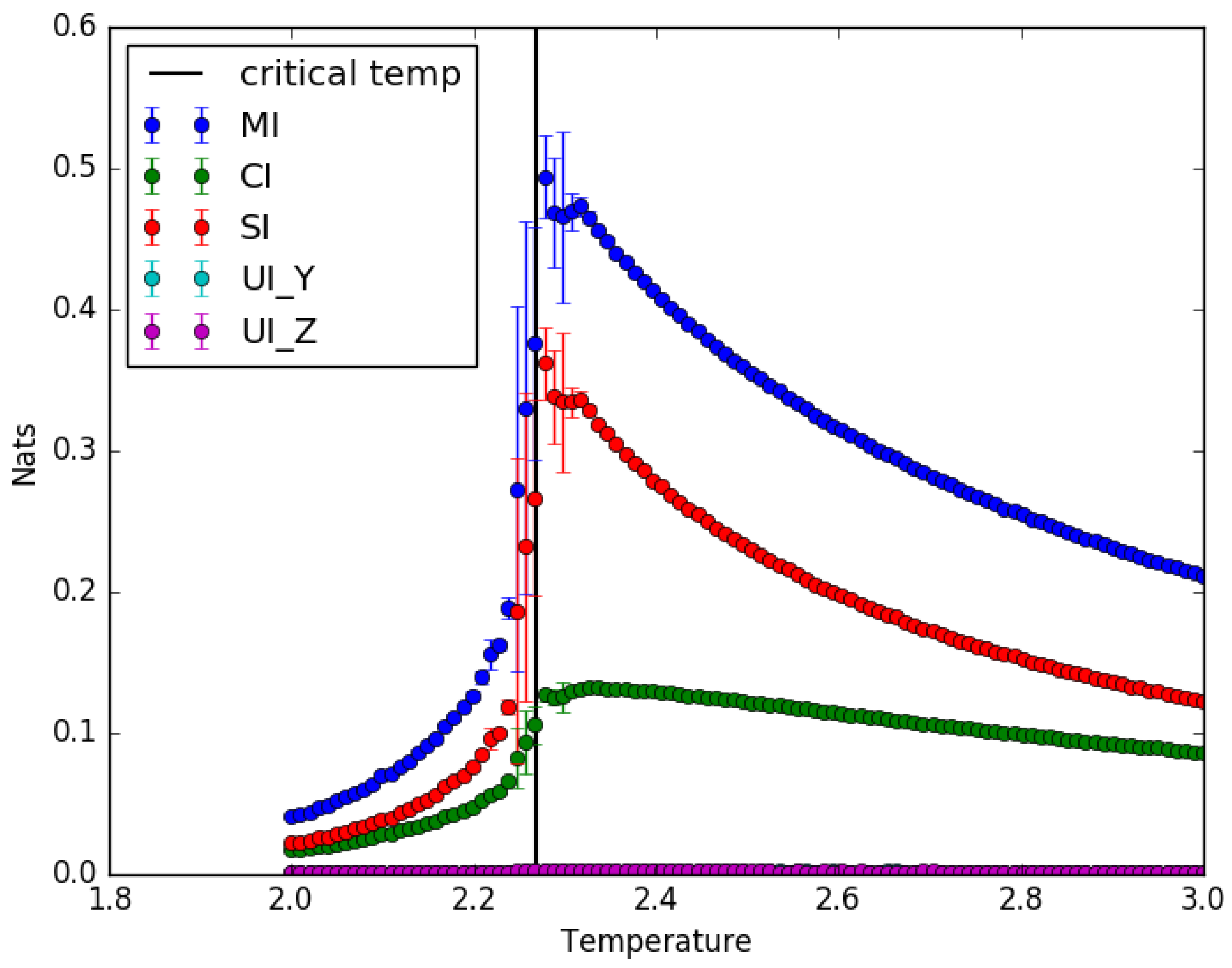
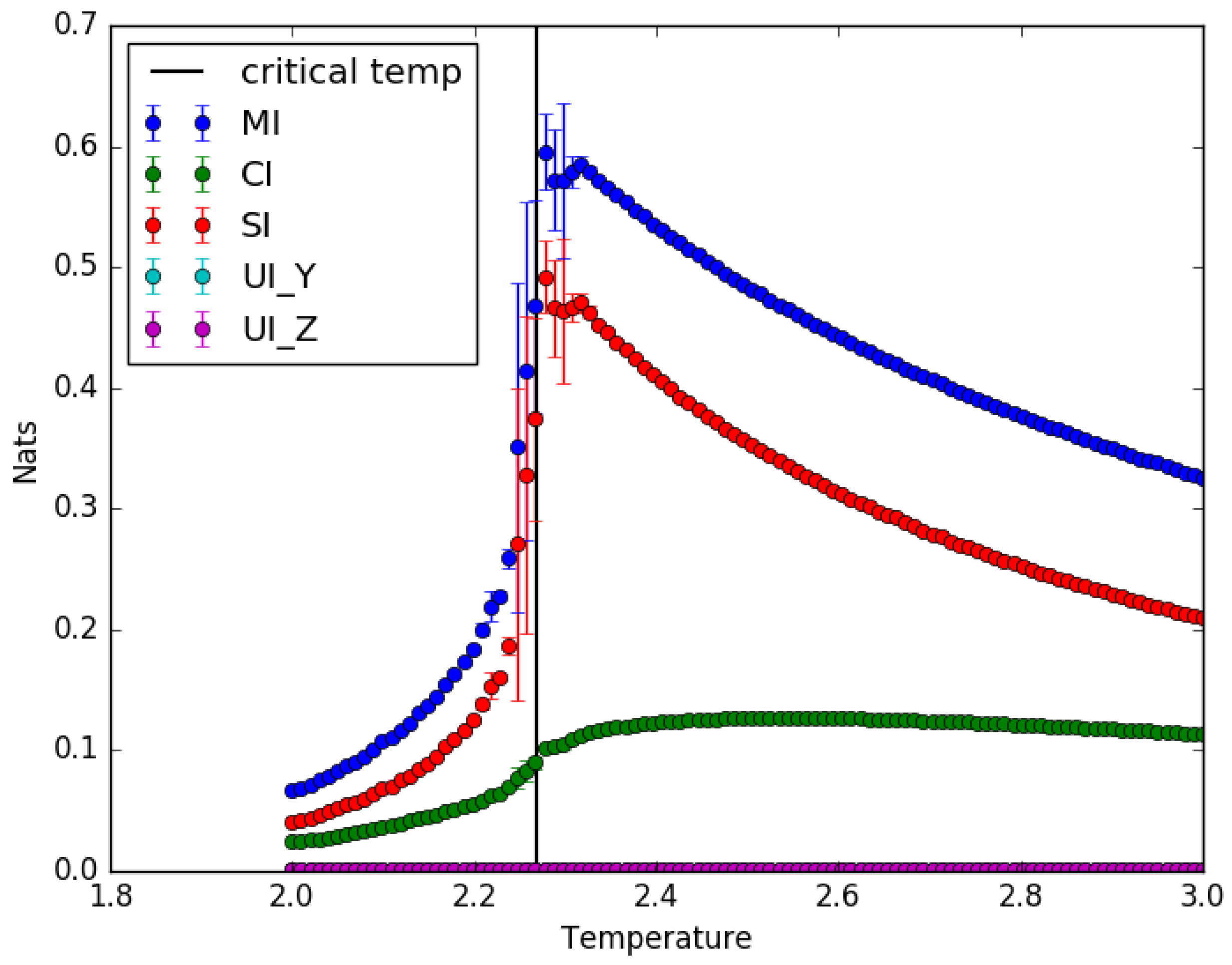
4.1. Ising Model: Partial Information Decomposition as a Function of Temperature
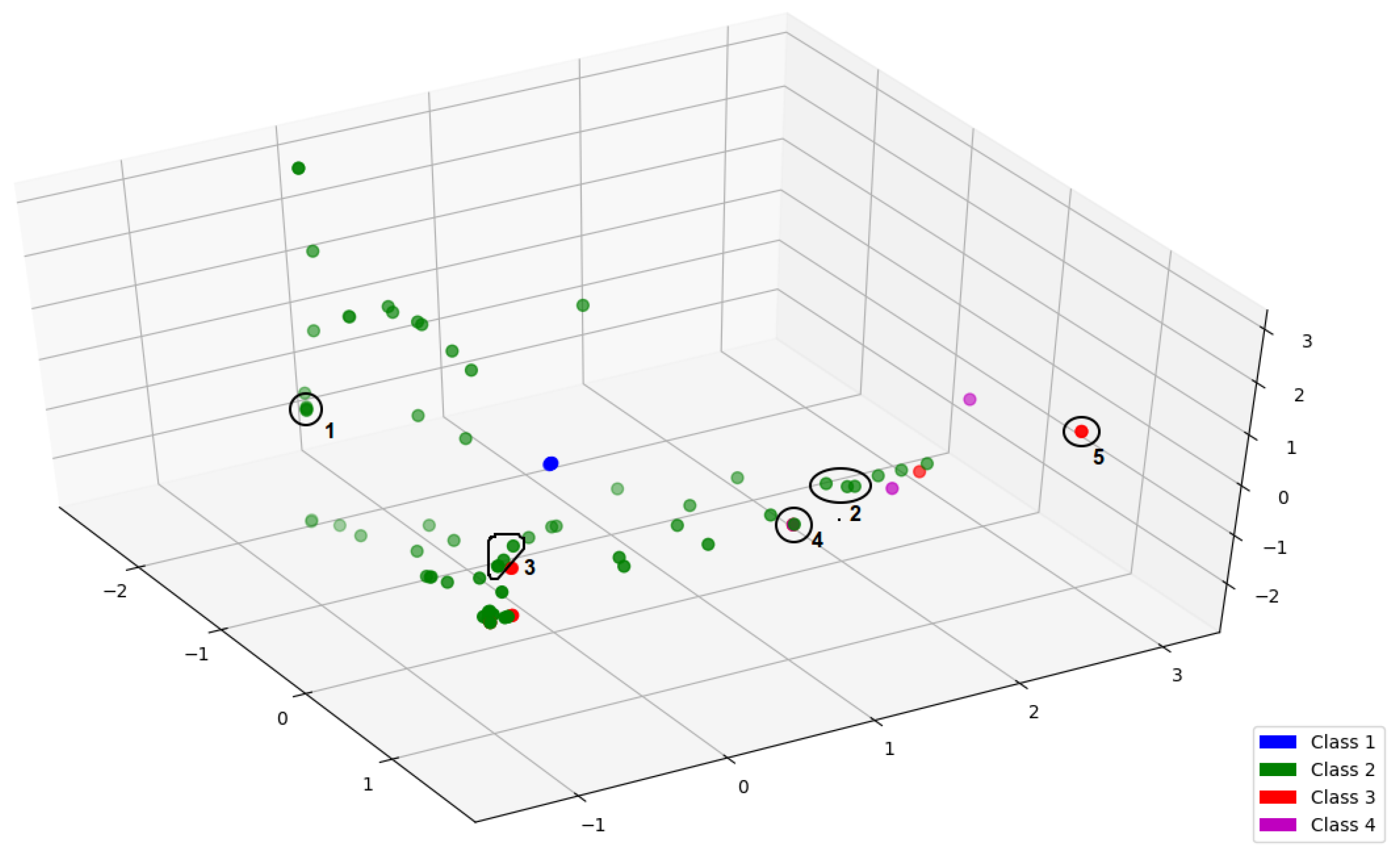
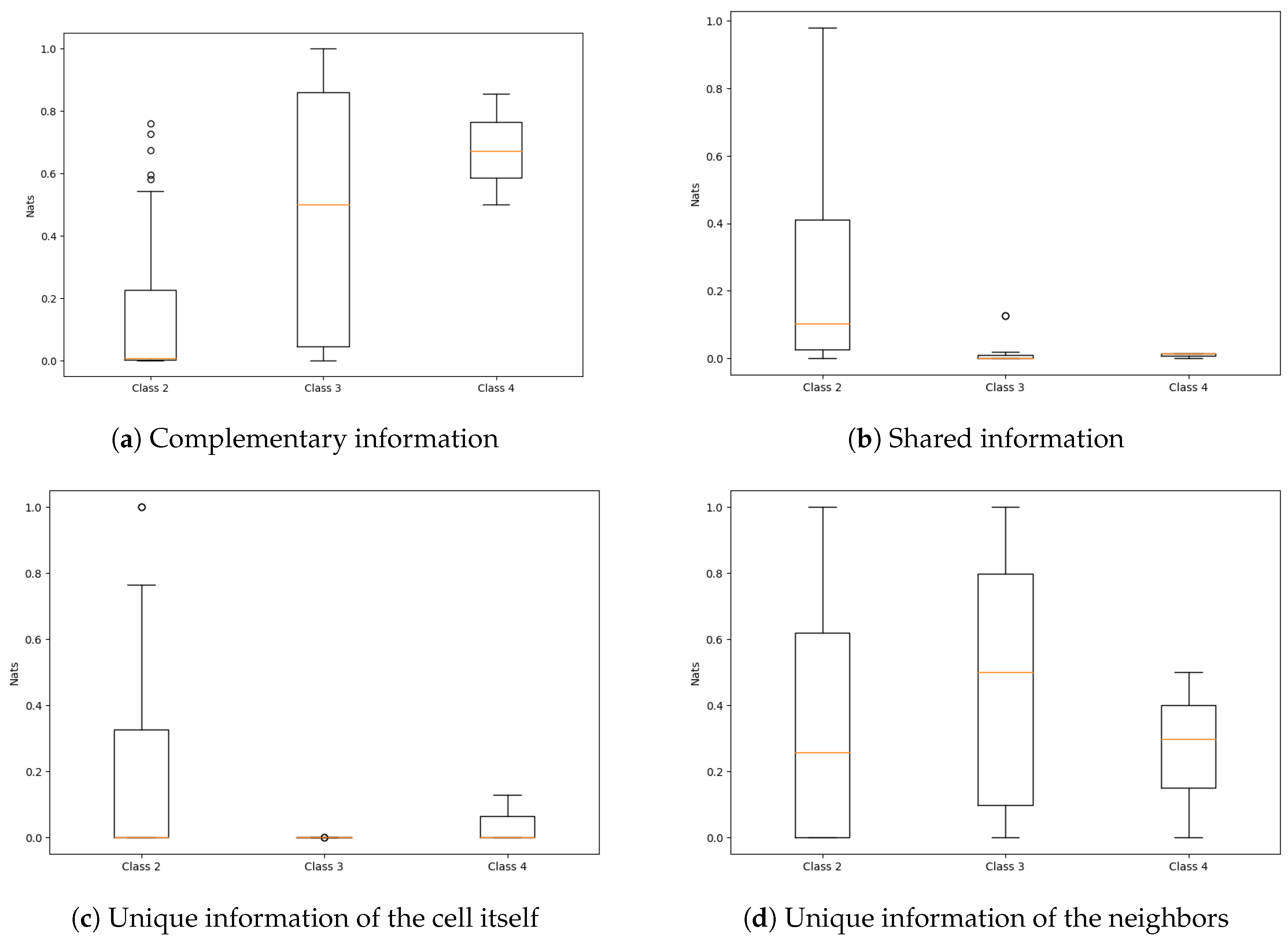
4.2. PID of Elementary Cellular Automata
5. Discussion
5.1. Implications of the Results
5.2. Related Work
5.3. Limitations
5.4. Future Work
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local measures of information storage in complex distributed computation. Inf. Sci. 2012, 208, 39–54. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Vicente, R.; Lindner, M. Transfer Entropy in Neuroscience; Springer: Berlin, Germany, 2014. [Google Scholar]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin, Germany, 2014. [Google Scholar]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Information modification and particle collisions in distributed computation. Chaos 2010, 20, 037109. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Ince, R.A. The Partial Entropy Decomposition: Decomposing Multivariate Entropy and Mutual Information via Pointwise Common Surprisal. arXiv 2017, arXiv:1702.01591. [Google Scholar]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from brains for biologically inspired computing. Front. Robot. AI 2015, 2, 5. [Google Scholar] [CrossRef]
- Wibral, M.; Priesemann, V.; Kay, J.W.; Lizier, J.T.; Phillips, W.A. Partial Information Decomposition as a Unified Approach to the Specification of Neural Goal Functions. arXiv 2015, arXiv:510.00831. [Google Scholar]
- Makkeh, A.; Theis, D.O.; Vicente, R. Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy 2017, 19, 530. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Andersen, M.S.; Dahl, J.; Vandenberghe, L. CVXOPT: A Python Package for Convex Optimization. Available online: http://cvxopt.org/ (accessed on 2 November 2017).
- Niss, M. History of the Lenz-Ising Model 1920-1950: From Ferromagnetic to Cooperative Phenomena. Arch. Hist. Exact Sci. 2005, 59, 267–318. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Wolfram, S. Random Sequence Generation by Cellular Automata. Adv. Appl. Math. 1986, 7, 123–169. [Google Scholar] [CrossRef]
- David, A.; Rosenblueth, C.G. A Model of City Traffic Based on Elementary Cellular Automata. Complex Syst. 2011, 19, 305. [Google Scholar]
- Cook, M. Universality in Elementary Cellular Automata. Complex Syst. 2004, 15, 1–40. [Google Scholar]
- Weisstein, E.W. Elementary Cellular Automaton. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/ElementaryCellularAutomaton.html (accessed on 4 May 2017).
- Wolfram, S. Universality and Complexity in Cellular Automata. Phys. D Nonlinear Phenom. 1984, 10D, 1–35. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media Inc.: Champaign, IL, USA, 2002. [Google Scholar]
- Glauber, R.J. Time-dependent statistics of the Ising model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Barnett, L.; Lizier, J.T.; Harré, M.; Seth, A.K.; Bossomaier, T. Information flow in a kinetic Ising model peaks in the disordered phase. Phys. Rev. Lett. 2013, 111, 177203. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L. A Commentary on Information Flow in a Kinetic Ising Model Peaks in the Disordered Phase. Available online: http://users.sussex.ac.uk/~lionelb/Ising_TE_commentary.html (accessed on 6 April 2017).
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. The information dynamics of phase transitions in random boolean networks. In Proceedings of the Eleventh International Conference on the Simulation and Synthesis of Living Systems (ALife XI), Winchester, UK, 5–8 August 2008; pp. 374–381. [Google Scholar]
- Wicks, R.T.; Chapman, S.C.; Dendy, R.O. Mutual information as a tool for identifying phase transitions in dynamical complex systems with limited data. Phys. Rev. E 2007, 75, 051125. [Google Scholar] [CrossRef] [PubMed]
- Harré, M.; Bossomaier, T. Phase-transition-like behaviour of information measures in financial markets. EPL 2009, 87, 18009. [Google Scholar] [CrossRef]
- Harré, M.S.; Bossomaier, T.; Gillett, A.; Snyder, A. The aggregate complexity of decisions in the game of Go. Eur. Phys. J. B 2011, 80, 555–563. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Harré, M. Information and phase transitions in socio-economic systems. Complex Adapt. Syst. Model. 2013, 1, 9. [Google Scholar] [CrossRef]
- Matsuda, H.; Kudo, K.; Nakamura, R.; Yamakawa, O.; Murata, T. Mutual information of Ising systems. Int. J. Theor. Phys. 1996, 35, 839–845. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 2008, 77, 026110. [Google Scholar] [CrossRef] [PubMed]
- Chliamovitch, G.; Chopard, B.; Dupuis, A. On the Dynamics of Multi-information in Cellular Automata. In Proceedings of the Cellular Automata—11th International Conference on Cellular Automata for Research and Industry (ACRI) 2014, Krakow, Poland, 22–25 September 2014; pp. 87–95. [Google Scholar]
- Courbariaux, M.; Bengio, Y. BinaryNet: Training Deep Neural Networks with Weights and Activations Constrained to +1 or −1. arXiv 2016, arXiv:1602.02830. [Google Scholar]
- Lecun, Y.; Cortes, C.; Burges, C.J. The MNIST Database of Handwritten Digits. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 4 May 2017).
- Sorngard, B. Information Theory for Analyzing Neural Networks. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Tkačik, G.; Mora, T.; Marre, O.; Amodei, D.; Palmer, S.E.; Berry, M.J.; Bialek, W. Thermodynamics and signatures of criticality in a network of neurons. Proc. Natl. Acad. Sci. USA 2015, 112, 11508–11513. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Mitchell, M.; Crutchfield, J.P. A genetic Algorithm discovers particle-based computation in cellular automata. In Parallel Problem Solving from Nature—PPSN III: International Conference on Evolutionary Computation, Proceedings of the Third Conference on Parallel Problem Solving from Nature, Jerusalem, Israel, 9–14 October 1994; Davidor, Y., Schwefel, H.P., Männer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 344–353. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Tax, T.; Mediano, P.A.; Shanahan, M. The Partial Information Decomposition of Generative Neural Network Models. Entropy 2017, 19, 474. [Google Scholar] [CrossRef]



| C | U | R | D | L | Pr |
|---|---|---|---|---|---|
| −1 | −1 | −1 | −1 | −1 | 0.004 |
| −1 | −1 | −1 | −1 | 1 | 0.002 |
| −1 | −1 | −1 | 1 | −1 | 0.003 |
| −1 | −1 | −1 | 1 | 1 | 0.003 |
| .. | .. | .. | .. | .. | .. |
| 1 | 1 | 1 | −1 | 1 | 0.035 |
| 1 | 1 | 1 | 1 | −1 | 0.033 |
| 1 | 1 | 1 | 1 | 1 | 0.776 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sootla, S.; Theis, D.O.; Vicente, R. Analyzing Information Distribution in Complex Systems. Entropy 2017, 19, 636. https://doi.org/10.3390/e19120636
Sootla S, Theis DO, Vicente R. Analyzing Information Distribution in Complex Systems. Entropy. 2017; 19(12):636. https://doi.org/10.3390/e19120636
Chicago/Turabian StyleSootla, Sten, Dirk Oliver Theis, and Raul Vicente. 2017. "Analyzing Information Distribution in Complex Systems" Entropy 19, no. 12: 636. https://doi.org/10.3390/e19120636
APA StyleSootla, S., Theis, D. O., & Vicente, R. (2017). Analyzing Information Distribution in Complex Systems. Entropy, 19(12), 636. https://doi.org/10.3390/e19120636




