Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices
Abstract
:1. Introduction
1.1. Notation
- T, , t,
- denote the target variable, event space, event and complementary event respectively;
- S, , s,
- denote the predictor variable, event space, event and complementary event respectively;
- ,
- represent the set of n predictor variables and events respectively;
- ,
- denote the two-event partition of the event space, i.e., and ;
- ,
- uppercase function names be used for average information-theoretic measures;
- ,
- lowercase function names be used for pointwise information-theoretic measures.
- , , ,
- superscripts distinguish between different different events in a variable;
- , , ,
- subscripts distinguish between different variables;
- ,
- multiple superscripts represent joint variables and joint events.
- sources are sets of predictor variables, i.e., where is the power set without ∅;
- source events are sets of predictor events, i.e., .
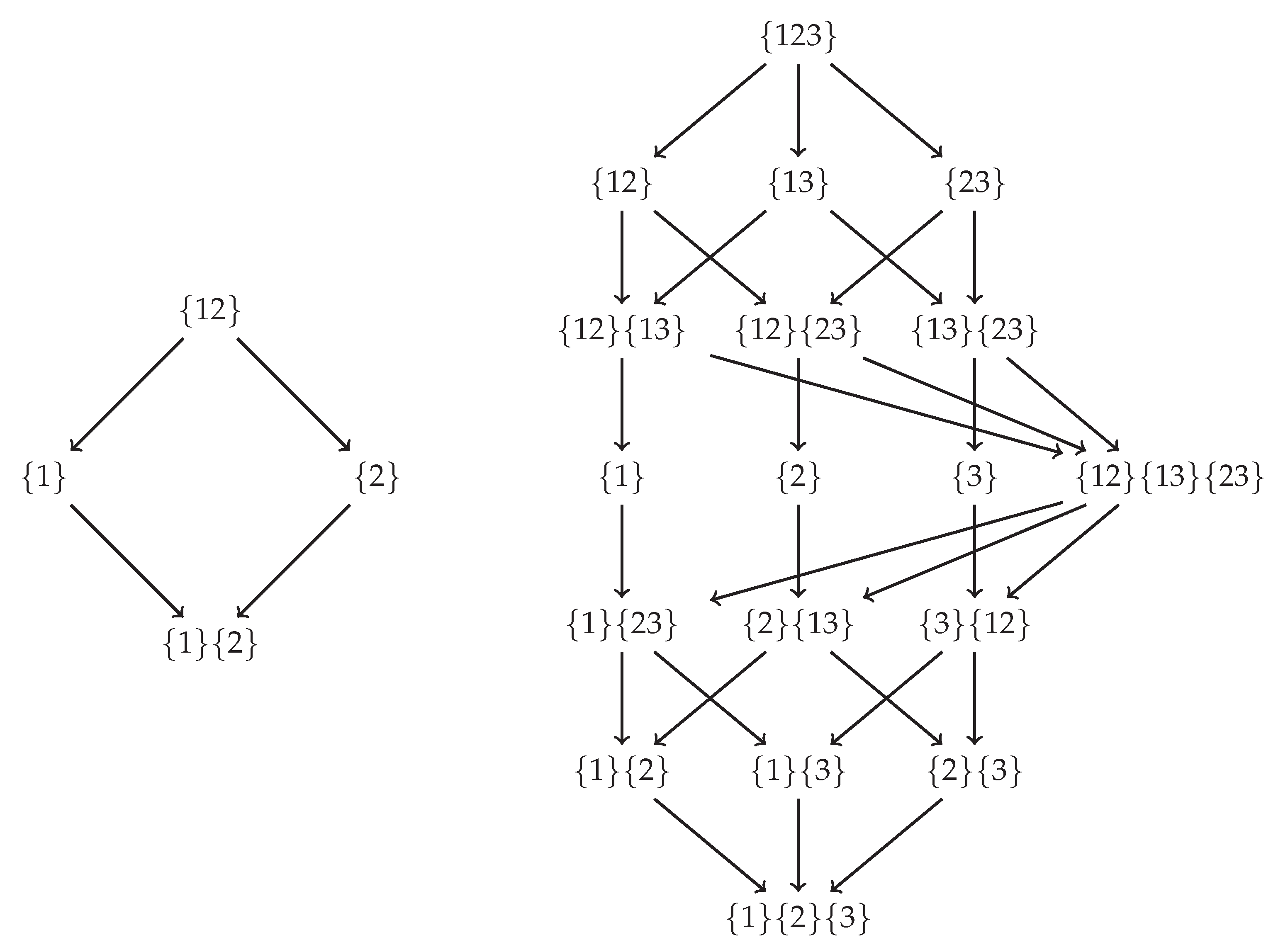
1.2. Partial Information Decomposition
2. Pointwise Information Theory
2.1. Pointwise Information Decomposition
2.2. Pointwise Unique
2.3. Pointwise Partial Information Decomposition
3. Probability Mass Exclusions and the Directed Components of Pointwise Mutual Information
3.1. Two Distinct Types of Probability Mass Exclusions
3.2. The Directed Components of Pointwise Information: Specificity and Ambiguity
- The positive informational component does not depend on t but rather only on s. This can be interpreted as follows: the less likely s is to occur, the more specific it is when it does occur, the greater the total amount of probability mass excluded , and the greater the potential for s to inform about t (or indeed any other target realisation).
- The negative informational component depends on both s and t, and can be interpreted as follows: the less likely s is to coincide with the event t, the more uncertainty in s given t, the greater size of the misinformative probability mass exclusion , and therefore the greater the potential for s to misinform about t.
3.3. Operational Interpretation of Redundant Information
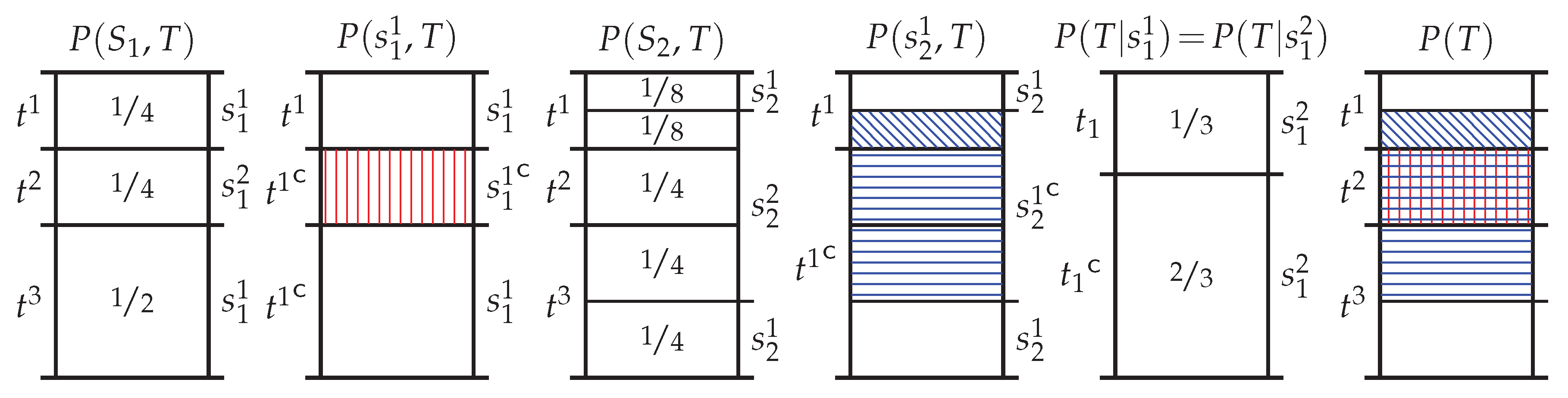
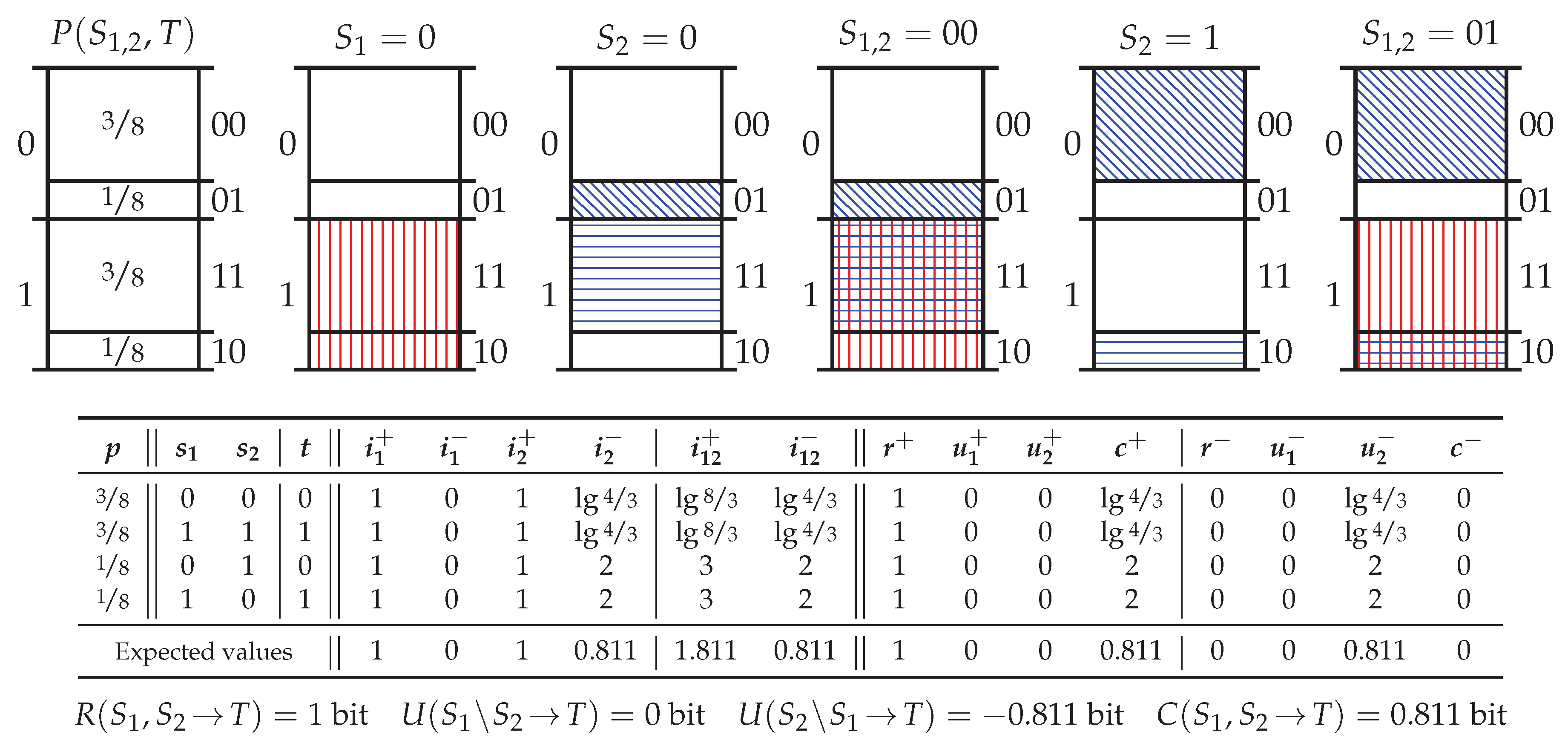
3.4. Motivational Example
4. Pointwise Partial Information Decomposition Using Specificity and Ambiguity
4.1. Bivariate PPID Using the Specificity and Ambiguity
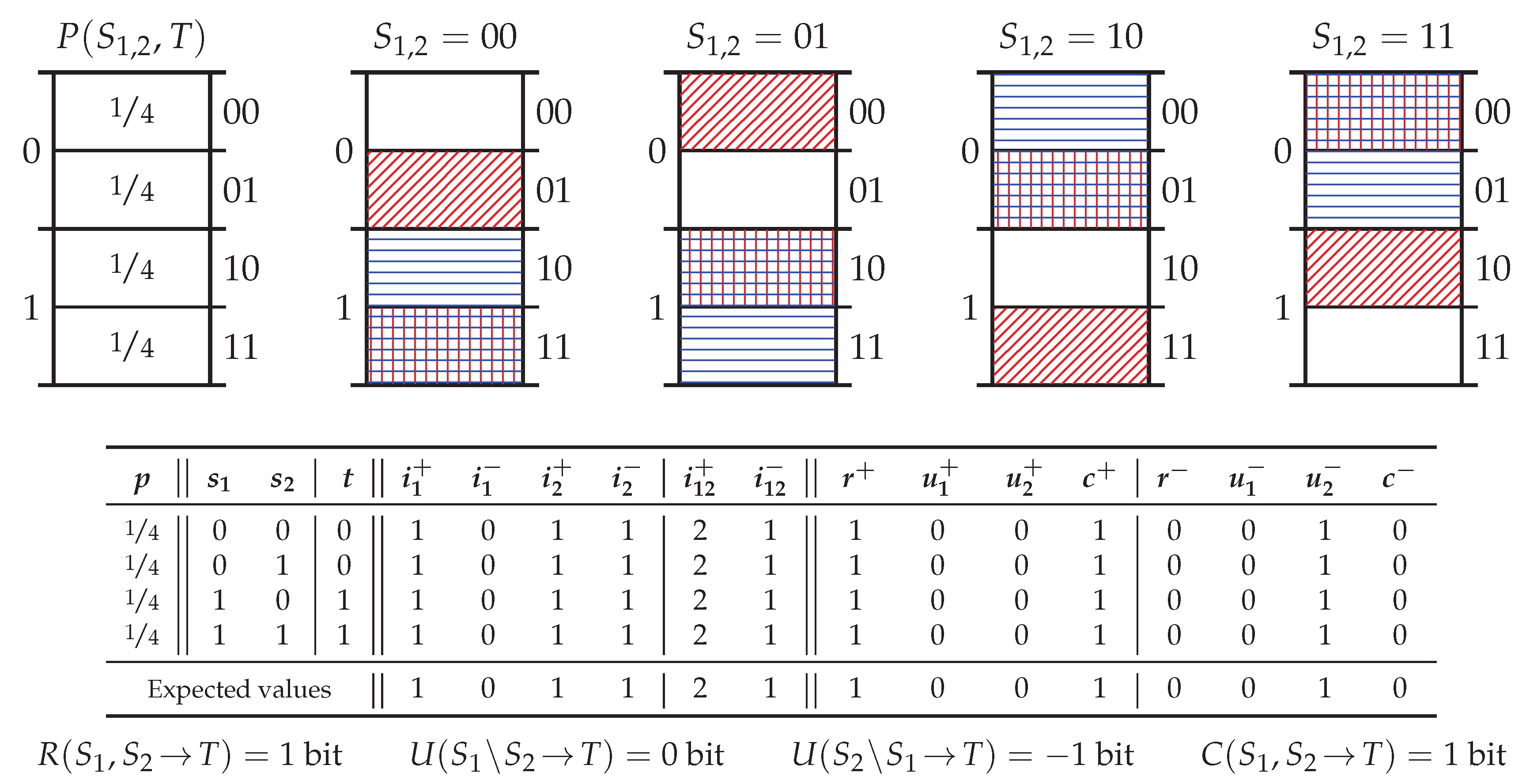
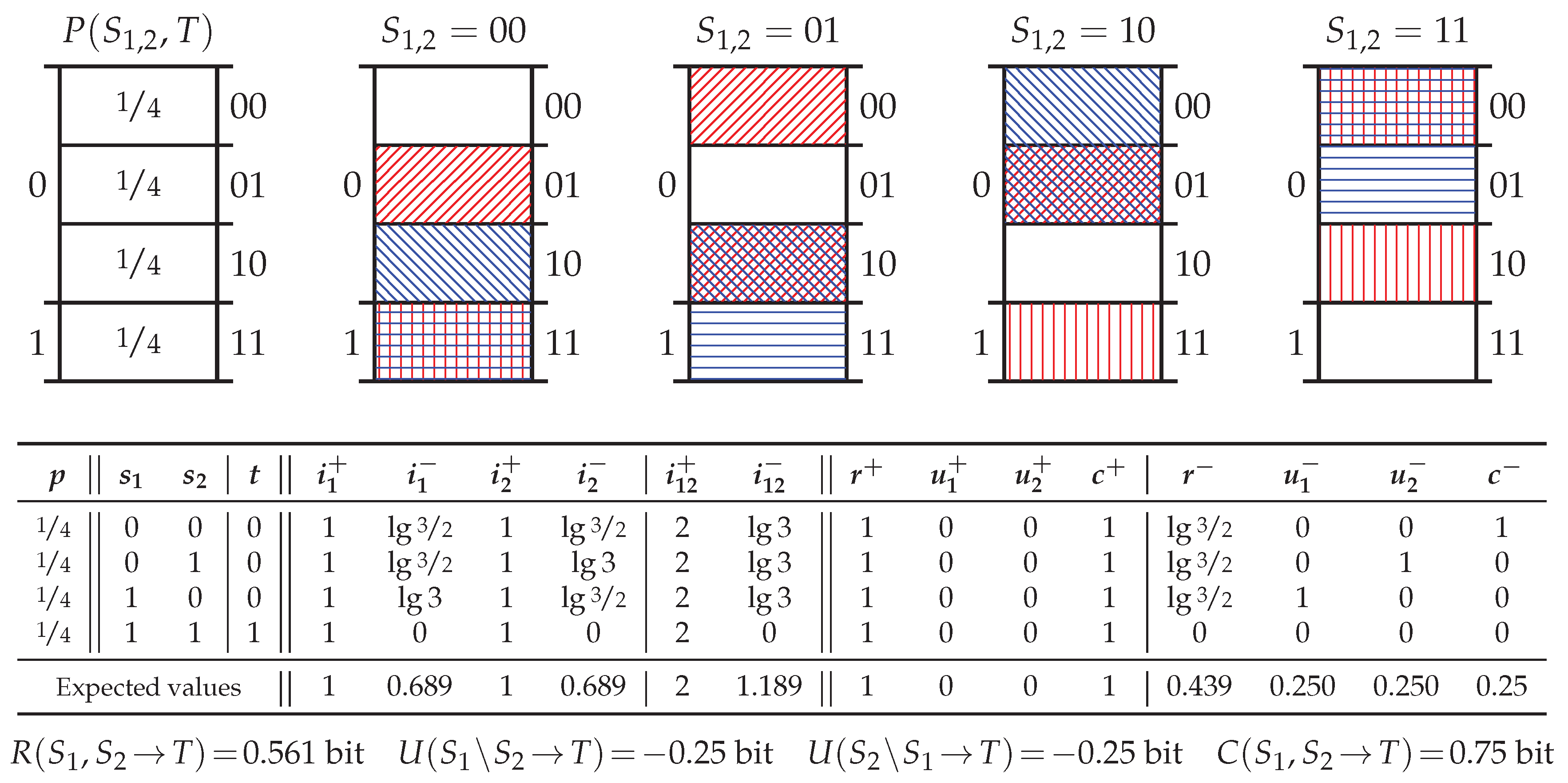
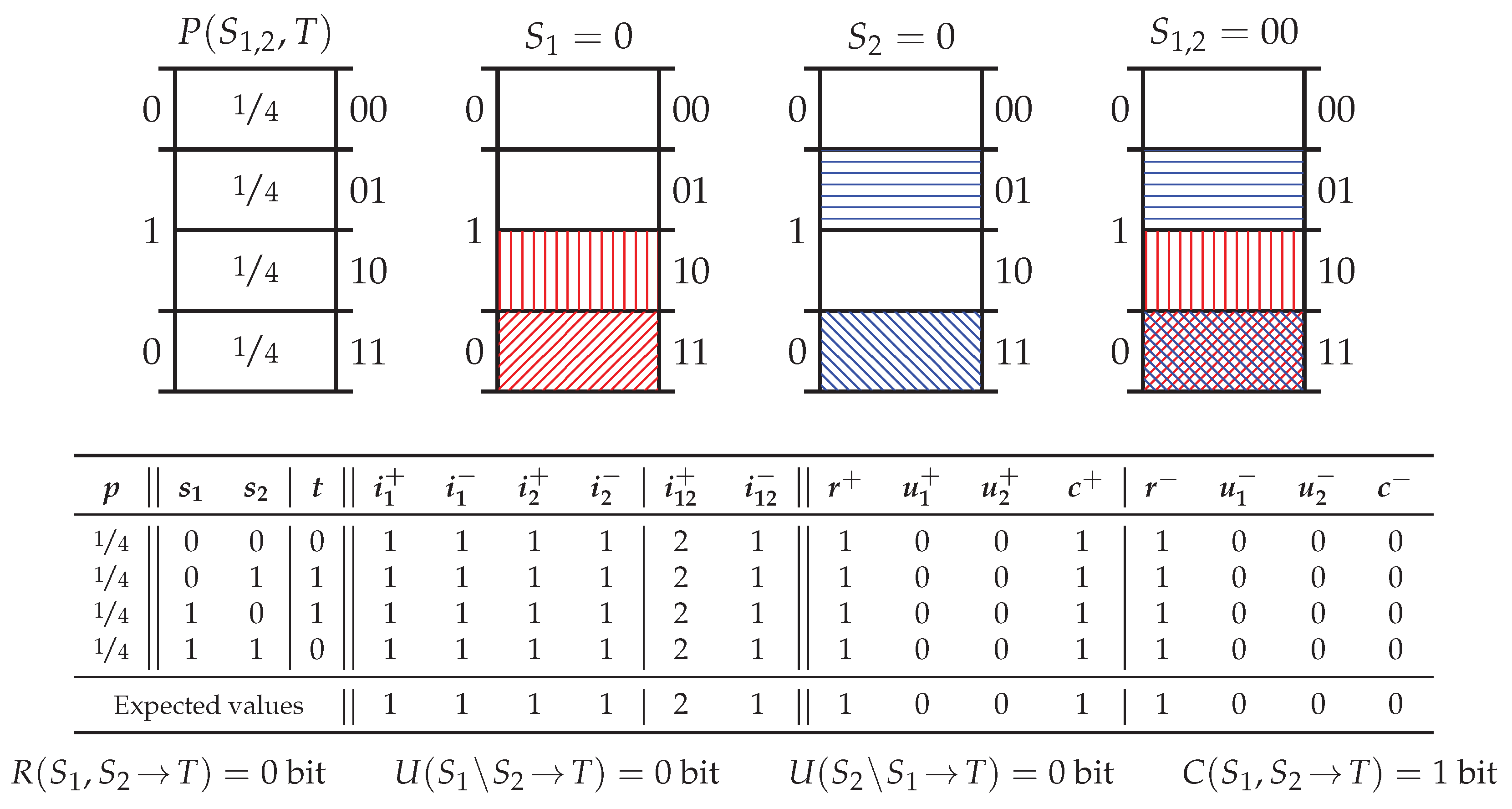
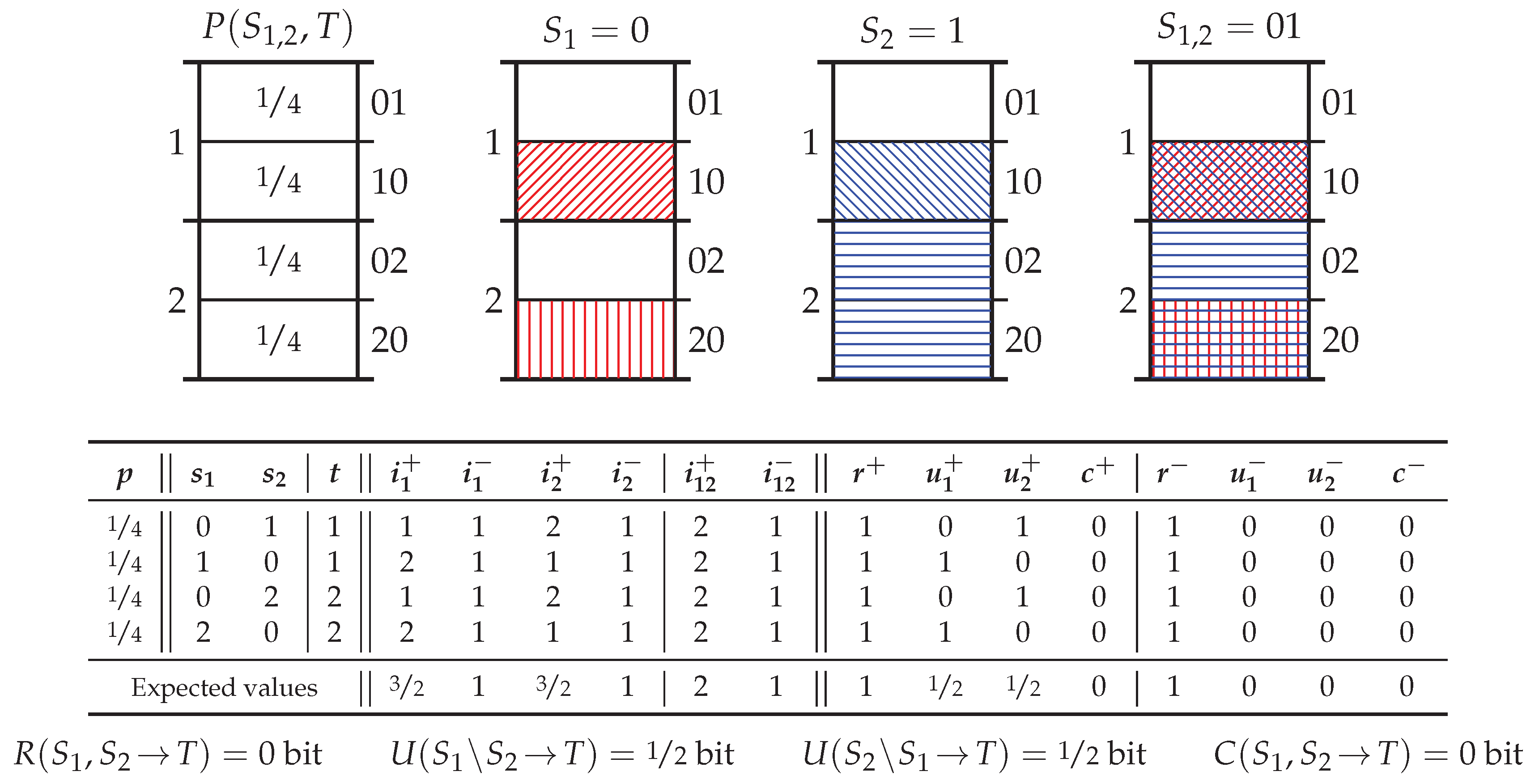
4.2. Redundancy Measures on the Specificity and Ambiguity Lattices
5. Discussion
5.1. Comparison to Existing Measures
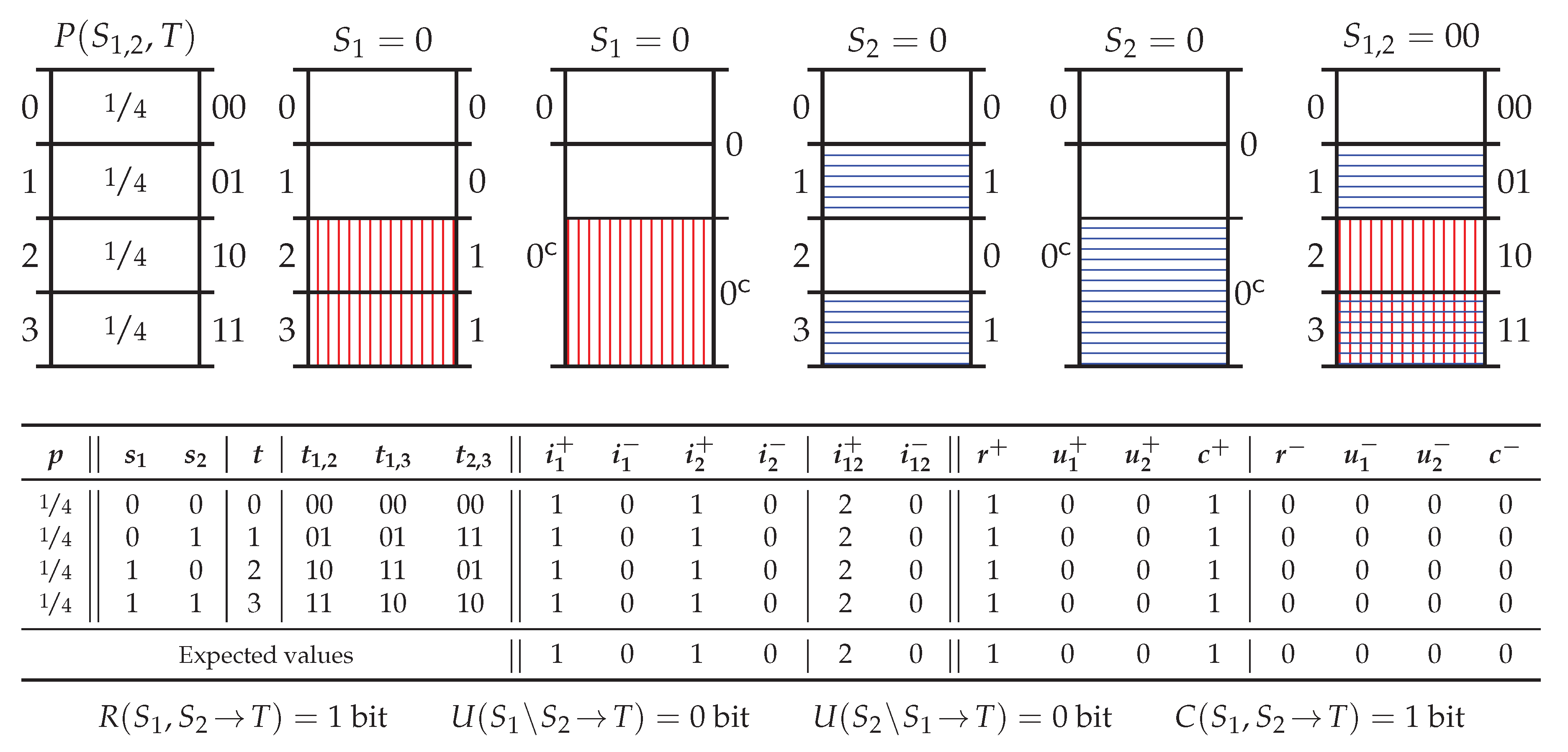
5.2. Probability Distribution Xor
5.3. Probability Distribution PwUnq
5.4. Probability Distribution RdnErr
5.5. Probability Distribution Tbc
5.6. Summary of Key Properties
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Kelly Gambling, Axiom 4, and Tbc
Appendix A.1. Pointwise Side Information and the Kelly Criterion
Appendix A.2. Justification of Axiom 4 and Redundant Information in Tbc
- Horse 0
- is a black horse , ridden by a female jockey , who is wearing a red jersey .
- Horse 1
- is a black horse , ridden by a male jockey , who is wearing a green jersey .
- Horse 2
- is a white horse , ridden by a female jockey , who is wearing a green jersey .
- Horse 3
- is a white horse , ridden by a male jockey , who is wearing a red jersey .
Appendix A.3. Accumulator Betting and the Target Chain Rule
Appendix B. Supporting Proofs and Further Details
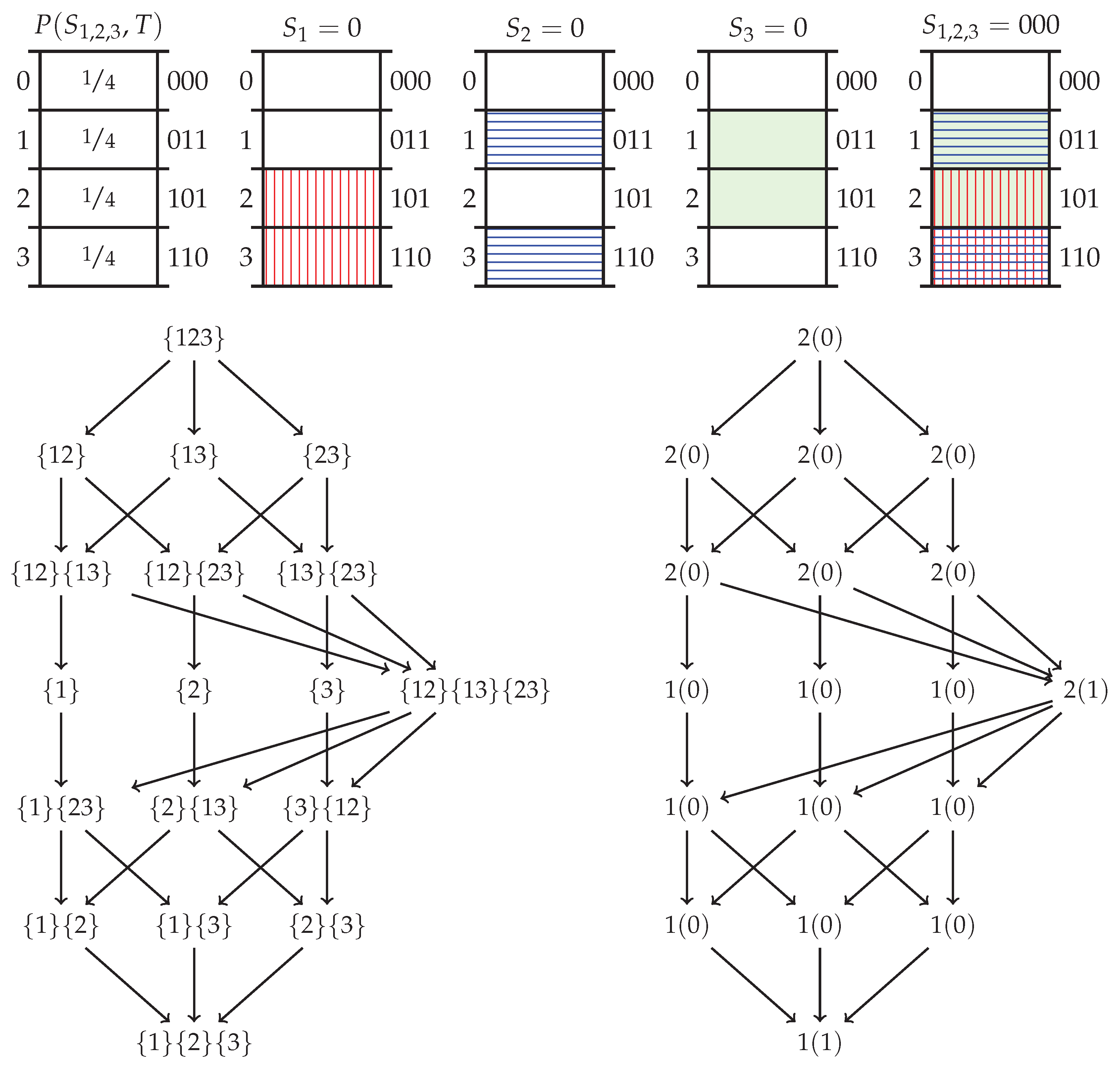
Appendix B.1. Deriving the Specificity and Ambiguity Lattices from Axioms 1–4
Appendix B.2. Redundancy Measures on the Lattices
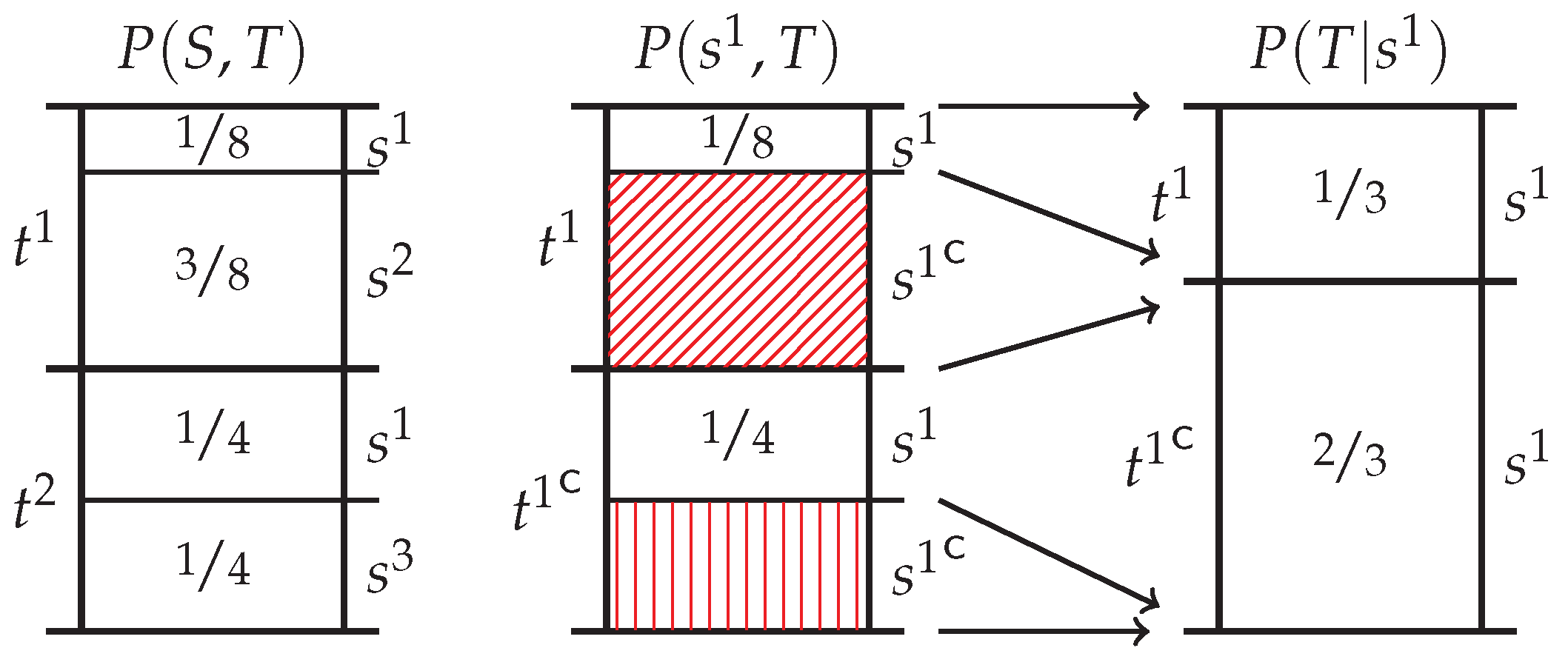
Appendix B.3. Target Chain Rule
Appendix C. Additional Example Probability Distributions
Appendix C.1. Probability Distribution Tbep
Appendix C.2. Probability Distribution Unq
Appendix C.3. Probability Distribution And
References and Note
- Williams, P.L.; Beer, R.D. Information decomposition and synergy. Nonnegative decomposition of multivariate information. arXiv, 2010; arXiv:1004.2515. [Google Scholar]
- Williams, P.L.; Beer, R.D. Indiana University. DecomposingMultivariate Information. Privately communicated, 2010. This unpublished paper is highly similar to [1]. Crucially, however, this paper derives the redundancy lattice from the W&B Axioms 1–3 of Section 1. In contrast, [1] derives the redundancy lattice as a property of the particular measure Imin.
- Olbrich, E.; Bertschinger, N.; Rauh, J. Information decomposition and synergy. Entropy 2015, 17, 3501–3517. [Google Scholar] [CrossRef]
- Lizier, J.T.; Flecker, B.; Williams, P.L. Towards a synergy-based approach to measuring information modification. In Proceedings of the IEEE Symposium on Artificial Life (ALife), Singapore, 16–19 April 2013; pp. 43–51. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared information—New insights and problems in decomposing information in complex systems. In Proceedings of the European Conference on Complex Systems, Brussels, Belgium, 3–7 September 2012; Springer: Cham, The Netherland, 2013; pp. 251–269. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Griffith, V.; Chong, E.K.; James, R.G.; Ellison, C.J.; Crutchfield, J.P. Intersection information based on common randomness. Entropy 2014, 16, 1985–2000. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Fano, R. Transmission of Information; The MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Harder, M. Information driven self-organization of agents and agent collectives. Ph.D. Thesis, University of Hertfordshire, Hertfordshire, UK, 2013. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying Synergistic Mutual Information. In Guided Self-Organization: Inception; Prokopenko, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; Volume 9, pp. 159–190. [Google Scholar]
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering unique information: Towards a multivariate information decomposition. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2232–2236. [Google Scholar]
- Perrone, P.; Ay, N. Hierarchical Quantification of Synergy in Channels. Front. Robot. AI 2016, 2, 35. [Google Scholar] [CrossRef]
- Griffith, V.; Ho, T. Quantifying redundant information in predicting a target random variable. Entropy 2015, 17, 4644–4653. [Google Scholar] [CrossRef]
- Rosas, F.; Ntranos, V.; Ellison, C.J.; Pollin, S.; Verhelst, M. Understanding interdependency through complex information sharing. Entropy 2016, 18, 38. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Ince, R. Measuring Multivariate Redundant Information with Pointwise Common Change in Surprisal. Entropy 2017, 19, 318. [Google Scholar] [CrossRef]
- Ince, R.A. The Partial Entropy Decomposition: Decomposing multivariate entropy and mutual information via pointwise common surprisal. arXiv, 2017; arXiv:1702.01591. [Google Scholar]
- Chicharro, D.; Panzeri, S. Synergy and Redundancy in Dual Decompositions of Mutual Information Gain and Information Loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef]
- Rauh, J.; Banerjee, P.K.; Olbrich, E.; Jost, J.; Bertschinger, N. On Extractable Shared Information. Entropy 2017, 19, 328. [Google Scholar] [CrossRef]
- Rauh, J.; Banerjee, P.K.; Olbrich, E.; Jost, J.; Bertschinger, N.; Wolpert, D. Coarse-Graining and the Blackwell Order. Entropy 2017, 19, 527. [Google Scholar] [CrossRef]
- Rauh, J. Secret sharing and shared information. Entropy 2017, 19, 601. [Google Scholar] [CrossRef]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale information decomposition: Exact computation for multivariate Gaussian processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- Pica, G.; Piasini, E.; Chicharro, D.; Panzeri, S. Invariant components of synergy, redundancy, and unique information among three variables. Entropy 2017, 19, 451. [Google Scholar] [CrossRef]
- James, R.G.; Crutchfield, J.P. Multivariate dependence beyond shannon information. Entropy 2017, 19, 531. [Google Scholar] [CrossRef]
- Makkeh, A.; Theis, D.O.; Vicente, R. Bivariate Partial Information Decomposition: The Optimization Perspective. Entropy 2017, 19, 530. [Google Scholar] [CrossRef]
- Kay, J.W.; Ince, R.A.; Dering, B.; Phillips, W.A. Partial and Entropic Information Decompositions of a Neuronal Modulatory Interaction. Entropy 2017, 19, 560. [Google Scholar] [CrossRef]
- Angelini, L.; de Tommaso, M.; Marinazzo, D.; Nitti, L.; Pellicoro, M.; Stramaglia, S. Redundant variables and Granger causality. Phys. Rev. E 2010, 81, 037201. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Angelini, L.; Wu, G.; Cortes, J.M.; Faes, L.; Marinazzo, D. Synergetic and redundant information flow detected by unnormalized Granger causality: Application to resting state fMRI. IEEE Trans. Biomed. Eng. 2016, 63, 2518–2524. [Google Scholar] [CrossRef] [PubMed]
- Ghazi-Zahedi, K.; Langer, C.; Ay, N. Morphological computation: Synergy of body and brain. Entropy 2017, 19, 456. [Google Scholar] [CrossRef]
- Maity, A.K.; Chaudhury, P.; Banik, S.K. Information theoretical study of cross-talk mediated signal transduction in MAPK pathways. Entropy 2017, 19, 469. [Google Scholar] [CrossRef]
- Tax, T.; Mediano, P.A.; Shanahan, M. The partial information decomposition of generative neural network models. Entropy 2017, 19, 474. [Google Scholar] [CrossRef]
- Wibral, M.; Finn, C.; Wollstadt, P.; Lizier, J.T.; Priesemann, V. Quantifying Information Modification in Developing Neural Networks via Partial Information Decomposition. Entropy 2017, 19, 494. [Google Scholar] [CrossRef]
- Woodward, P.M. Probability and Information Theory: With Applications to Radar; Pergamon Press: Oxford, UK, 1953. [Google Scholar]
- Woodward, P.M.; Davies, I.L. Information theory and inverse probability in telecommunication. Proc. IEE-Part III Radio Commun. Eng. 1952, 99, 37–44. [Google Scholar] [CrossRef]
- Gray, R.M. Probability, Random Processes, and Ergodic Properties; Springer: New York, NY, USA, 1988. [Google Scholar]
- Martin, N.F.; England, J.W. Mathematical Theory of Entropy; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Finn, C.; Lizier, J.T. Probability Mass Exclusions and the Directed Components of Pointwise Mutual Information. arXiv, 2018; arXiv:1801.09223. [Google Scholar]
- Kelly, J.L. A new interpretation of information rate. Bell Labs Tech. J. 1956, 35, 917–926. [Google Scholar] [CrossRef]
- Ash, R. Information Theory; Interscience tracts in pure and applied mathematics; Interscience Publishers: Geneva, Switzerland, 1965. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1998. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1988. [Google Scholar]
- Rota, G.C. On the foundations of combinatorial theory I. Theory of Möbius functions. Probab. Theory Relat. Field 1964, 2, 340–368. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics. In Cambridge Studies in Advanced Mathematics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; Volume 1. [Google Scholar]
- Davey, B.A.; Priestley, H.A. Introduction to Lattices and Order, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ross, S.M. A First Course in Probability, 8th ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
| p | t | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 2 | 2 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |
| 2 | 0 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | |
| Expected values | 1 | 0 | 0 | |||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finn, C.; Lizier, J.T. Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices. Entropy 2018, 20, 297. https://doi.org/10.3390/e20040297
Finn C, Lizier JT. Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices. Entropy. 2018; 20(4):297. https://doi.org/10.3390/e20040297
Chicago/Turabian StyleFinn, Conor, and Joseph T. Lizier. 2018. "Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices" Entropy 20, no. 4: 297. https://doi.org/10.3390/e20040297
APA StyleFinn, C., & Lizier, J. T. (2018). Pointwise Partial Information Decomposition Using the Specificity and Ambiguity Lattices. Entropy, 20(4), 297. https://doi.org/10.3390/e20040297






