Parametric PET Image Reconstruction via Regional Spatial Bases and Pharmacokinetic Time Activity Model
Abstract
1. Introduction
- Noise model:A Poisson distribution model is employed. The distance between the given measured sinogram and the projection of the reconstructed PET image is measured by using the KL divergence.
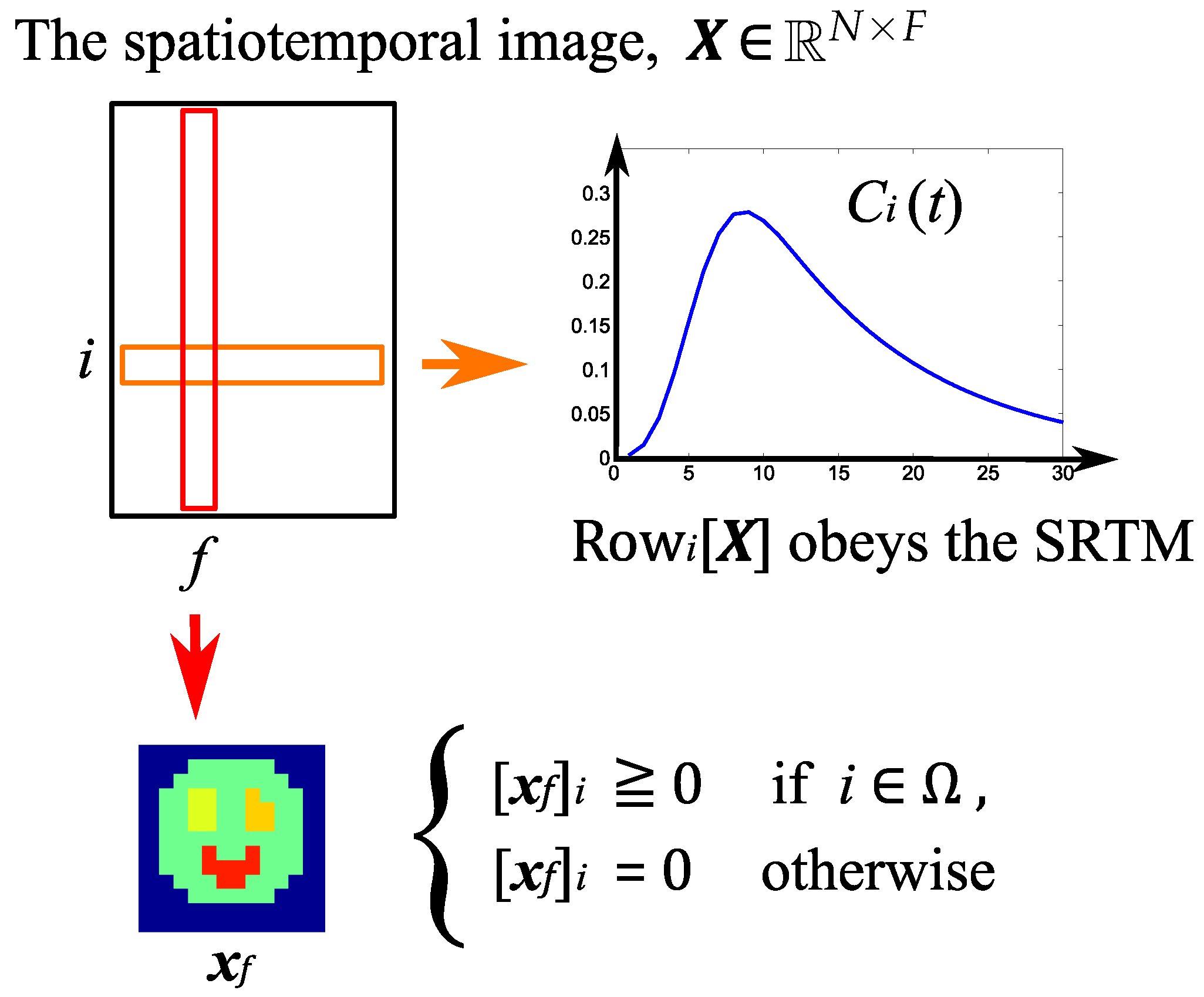
- Spatial model:The nonnegativity of voxel values is assumed. In addition, it is assumed that the foreground/background regions and the reference region in an image are known in advance. The voxel values in the background are set to zero.
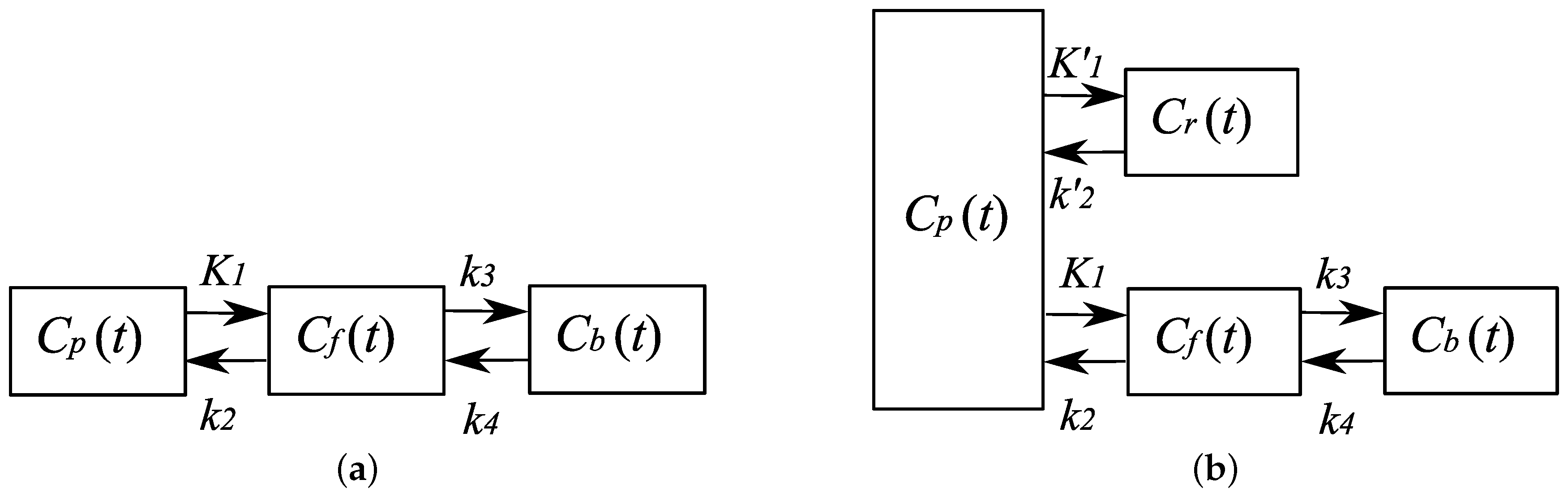
- Temporal model:A compartment model is employed. It is assumed that, given the ligand, one can identify the number of compartments appropriate for the representation of the kinetics. In this paper, we assume a three-compartment model, which is appropriate for a variety of ligands, such as a []carfentanil and a []fludeoxyglucose [23,24].
- A compartment model-based constraint is explicitly introduced in order to constrain the tTACs to the solution space in which the relationships between the tTACs are consistent with the compartment model, while retaining the KL-divergence of data fidelity as a convex function.
- A constraint of a target region in an image is introduced to restrict the pixel values of the background to be zero.
- The dependency of the solutions on the initial values is discussed and is experimentally shown.
2. Basic Materials
2.1. PET Image Reconstruction
2.2. Compartment Model
3. Proposed Method
3.1. Notation
3.2. Description of Proposed Method
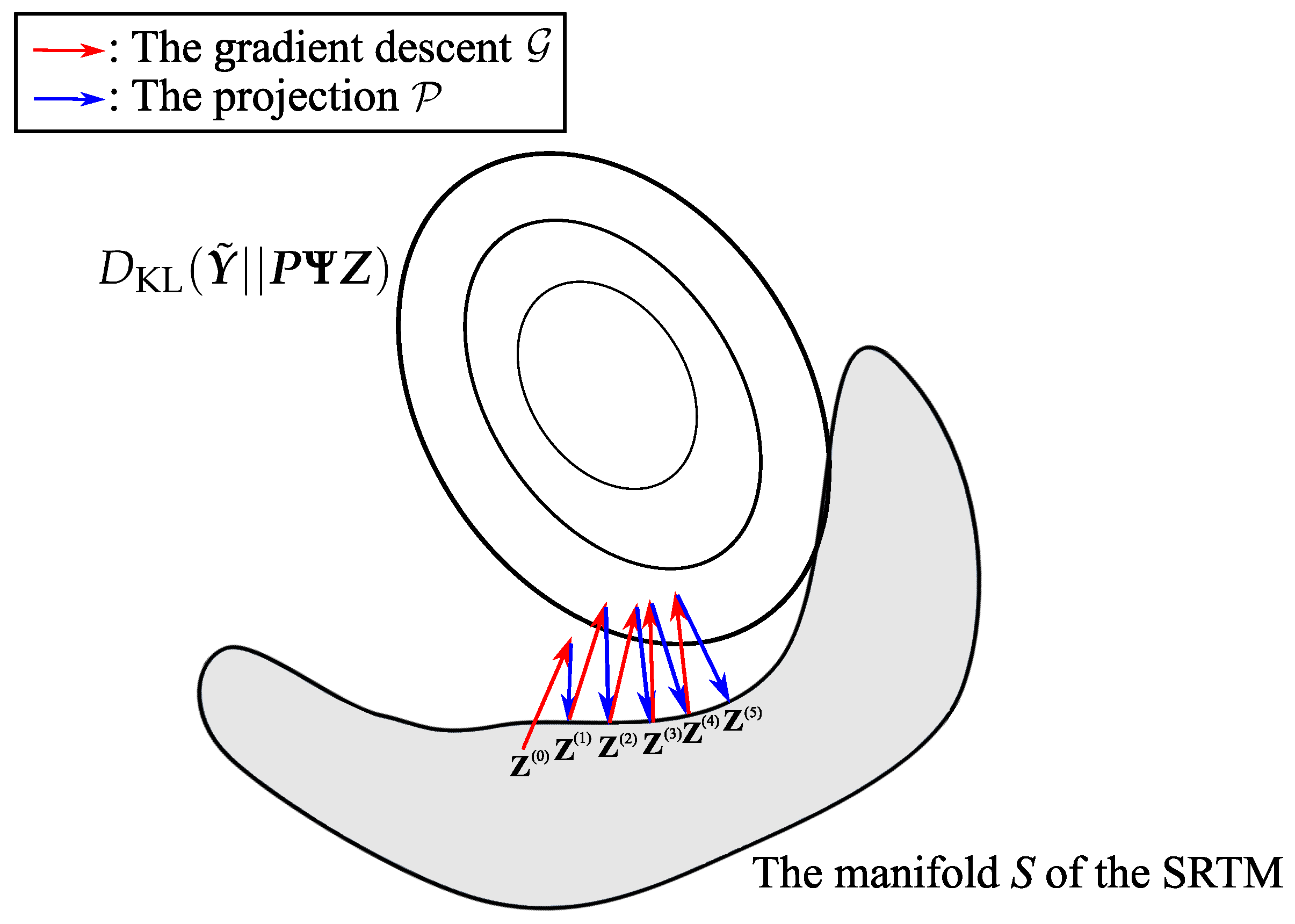
3.2.1. The Gradient Step,
3.2.2. The Projection Step,
| Algorithm 1 Description of proposed method. |
4. Experimental Results
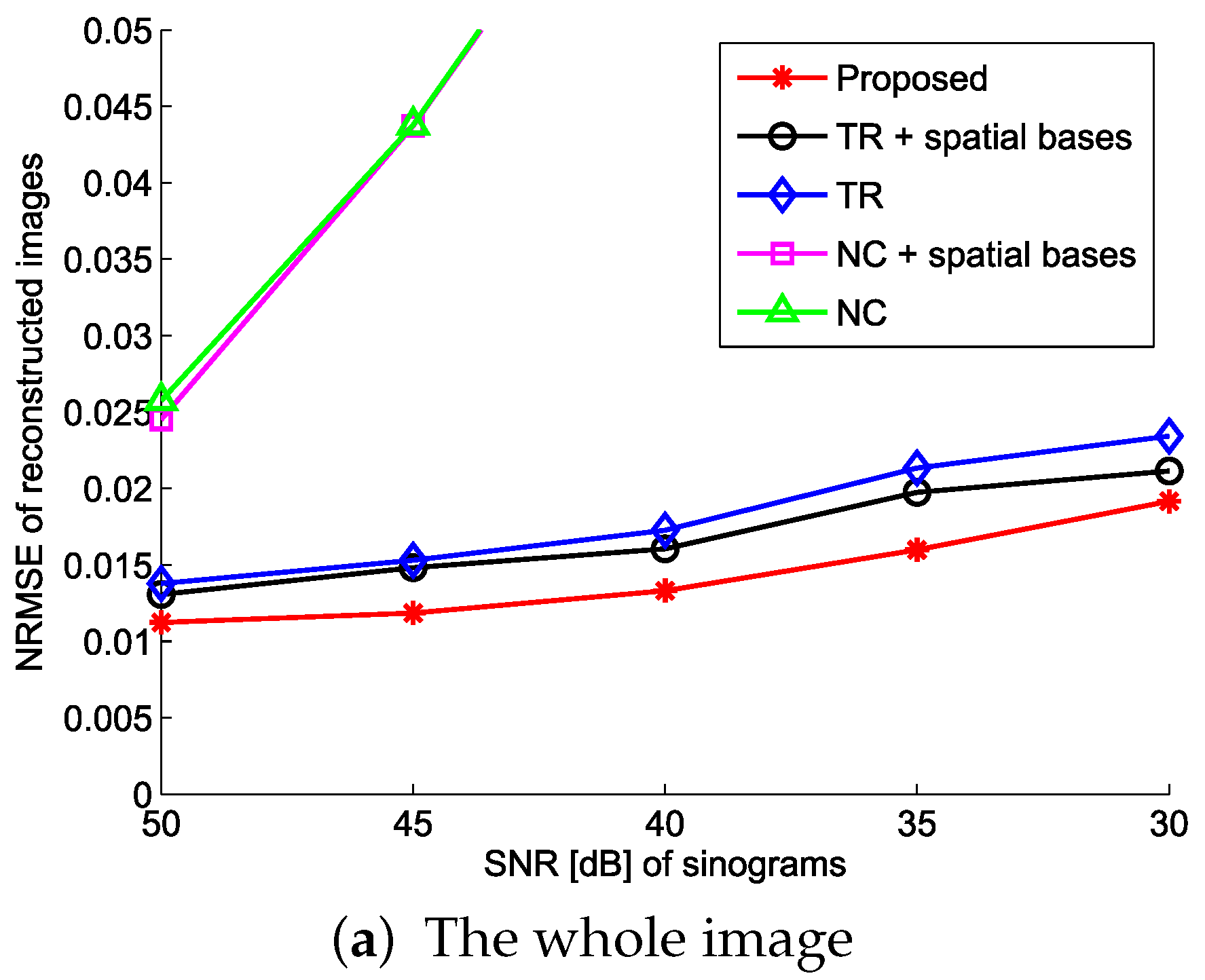
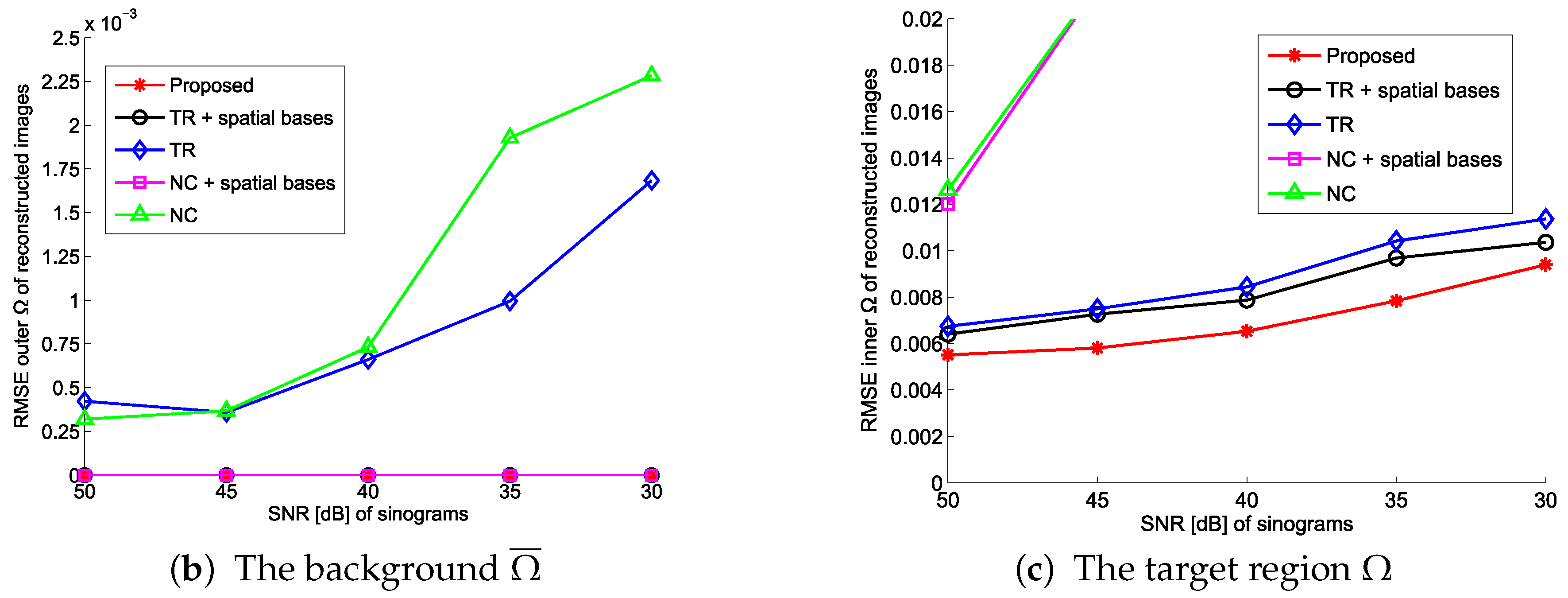
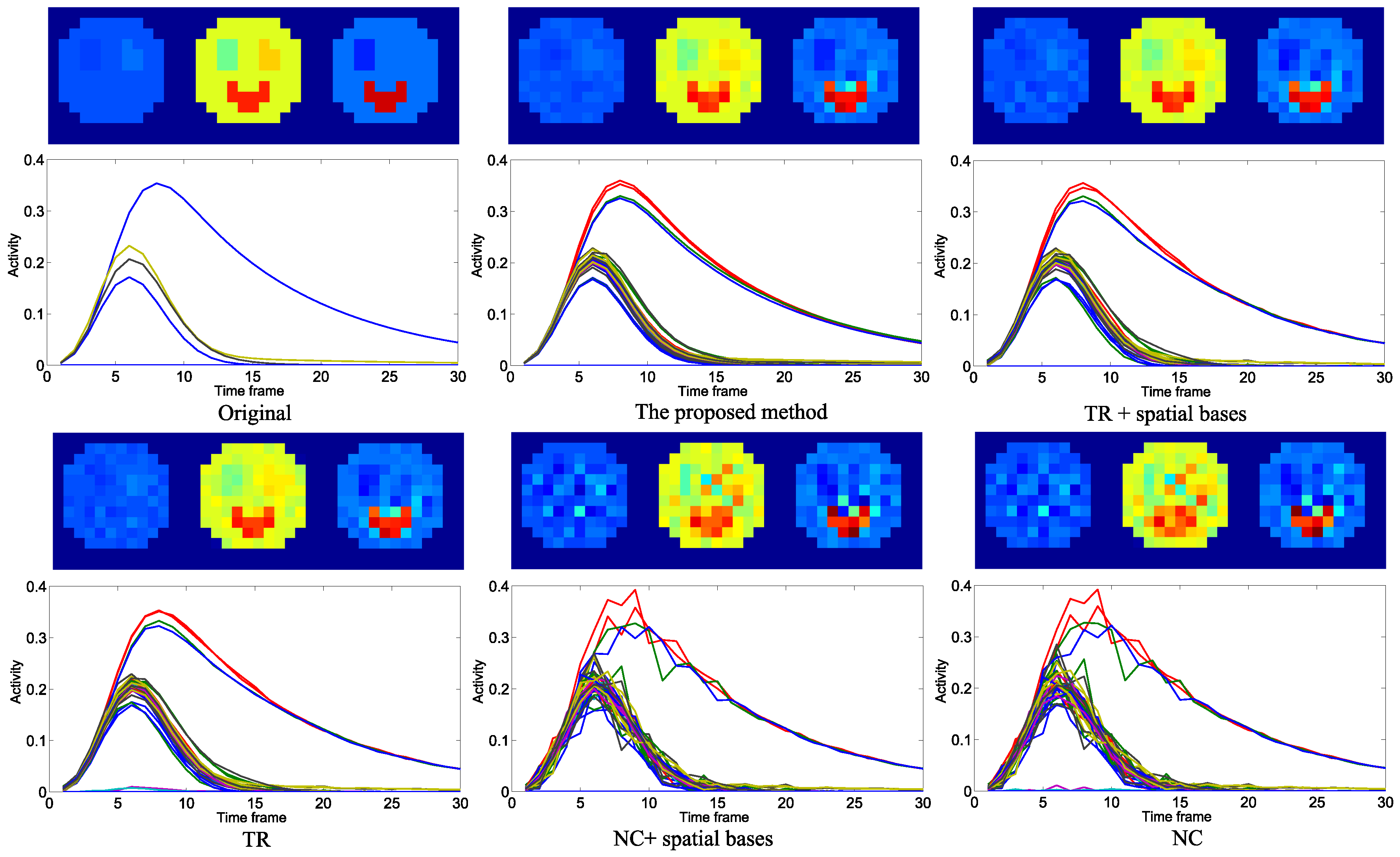
4.1. Evaluation with Simulated Data
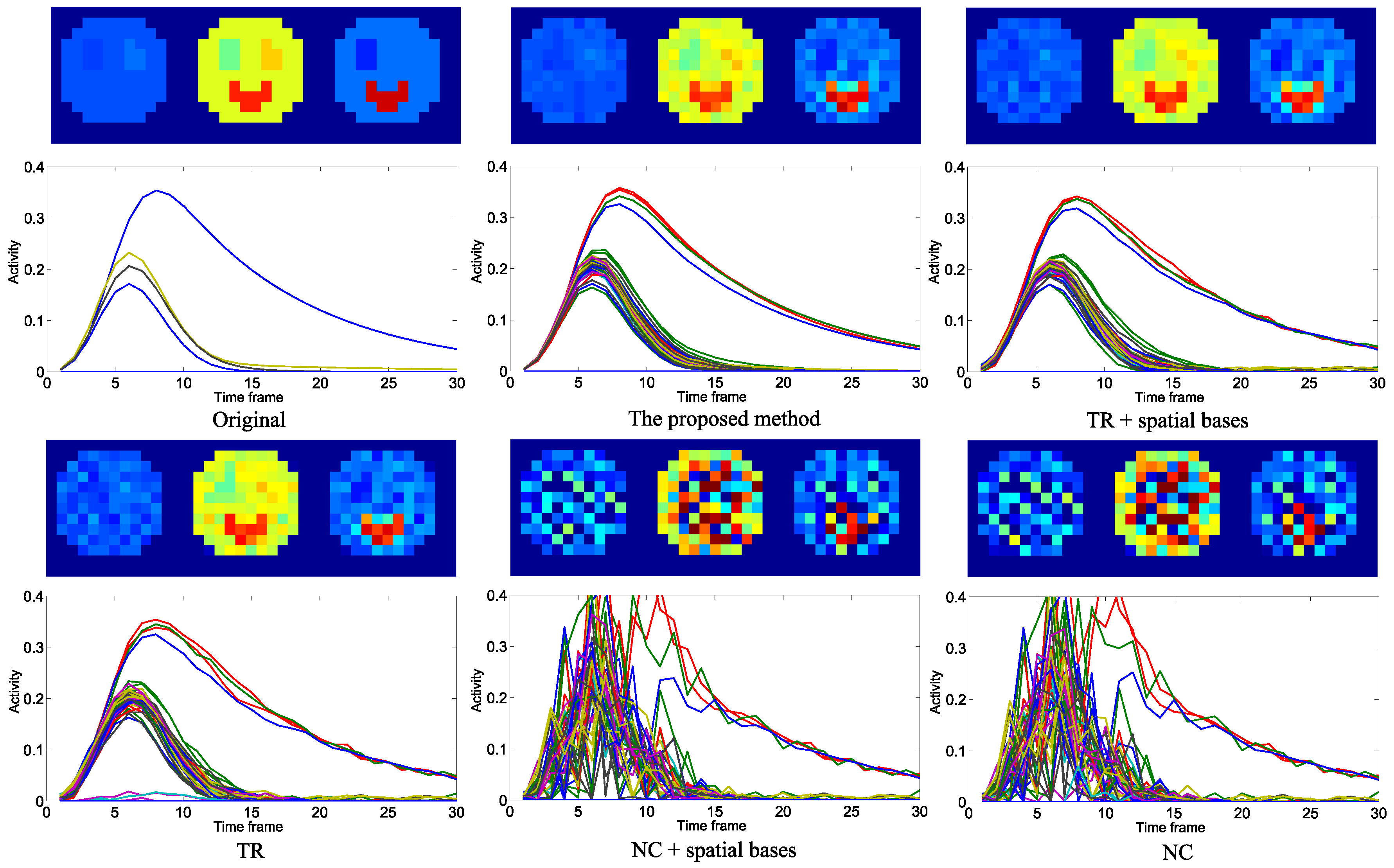
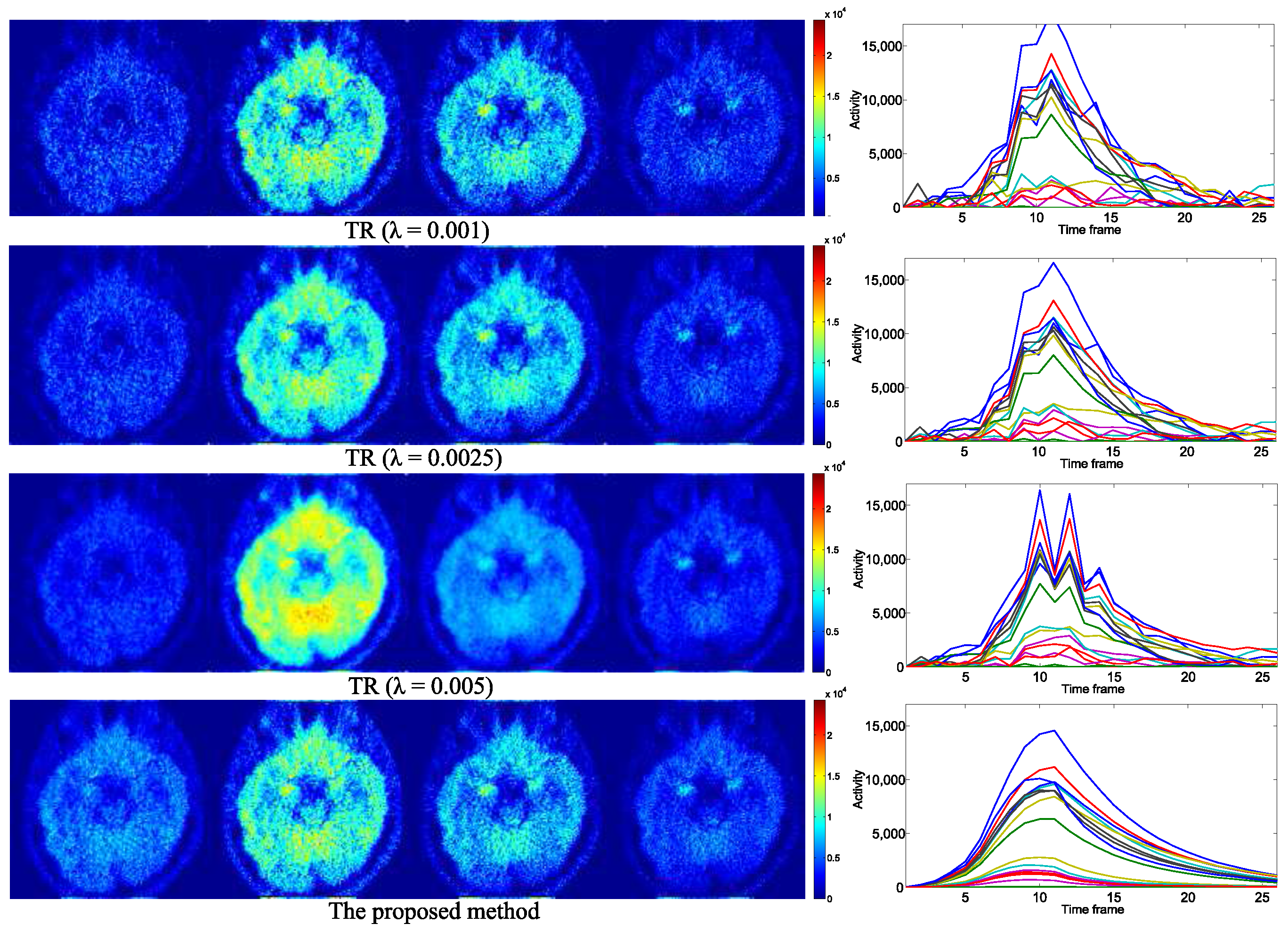
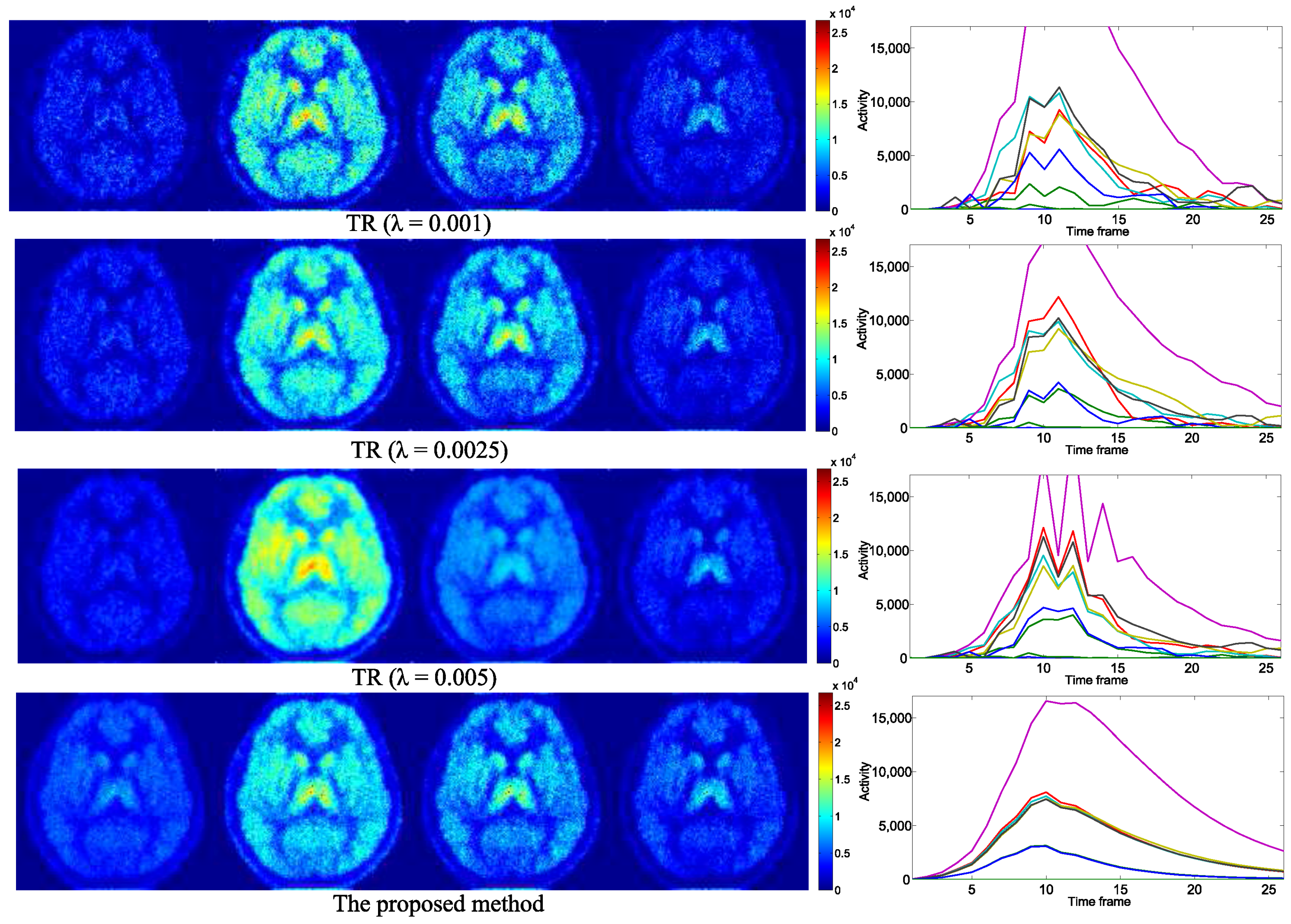
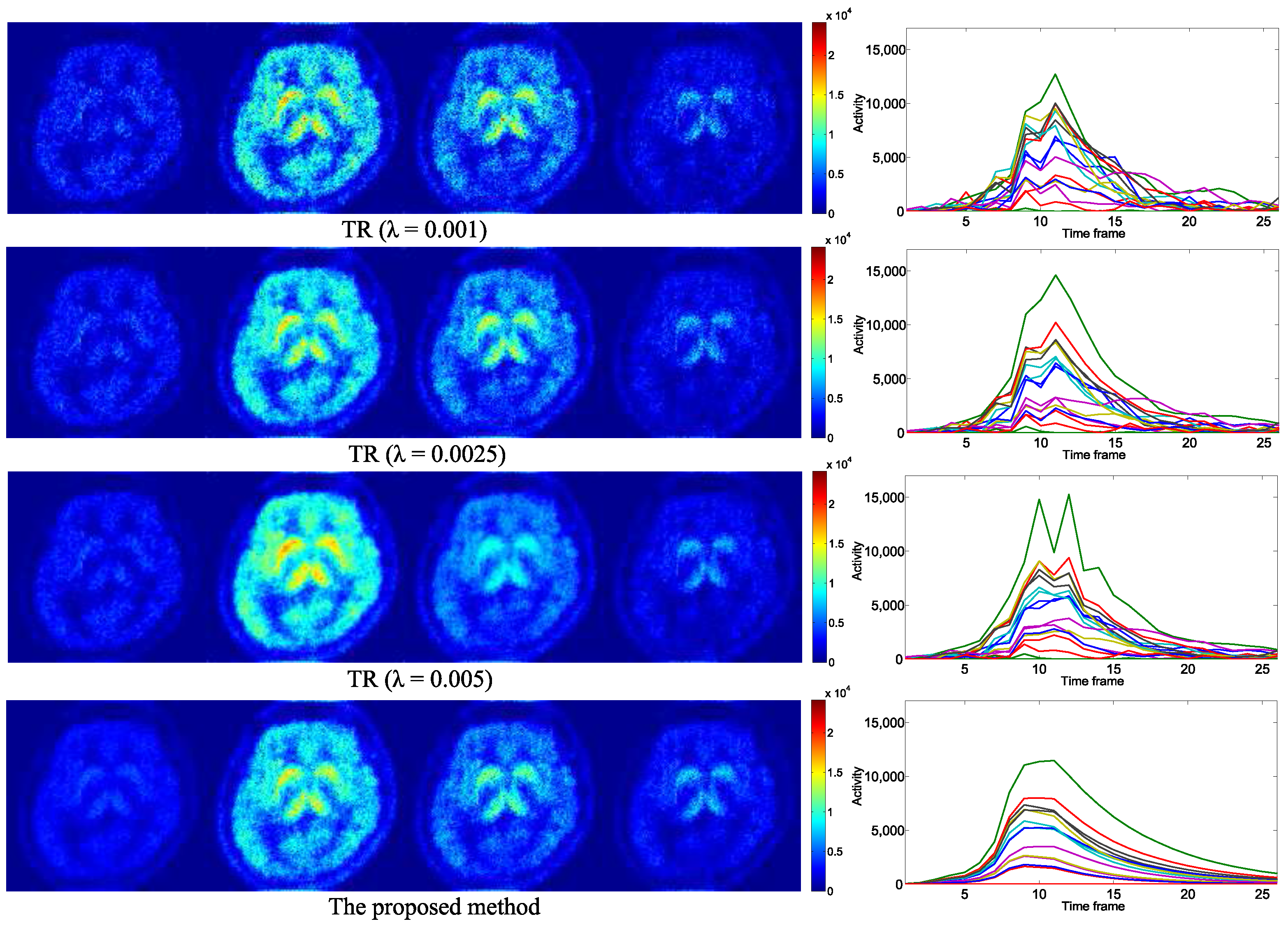
4.2. Practical PET Images Reconstruction from Clinical Sinograms
5. Discussion
5.1. Optimization Strategy
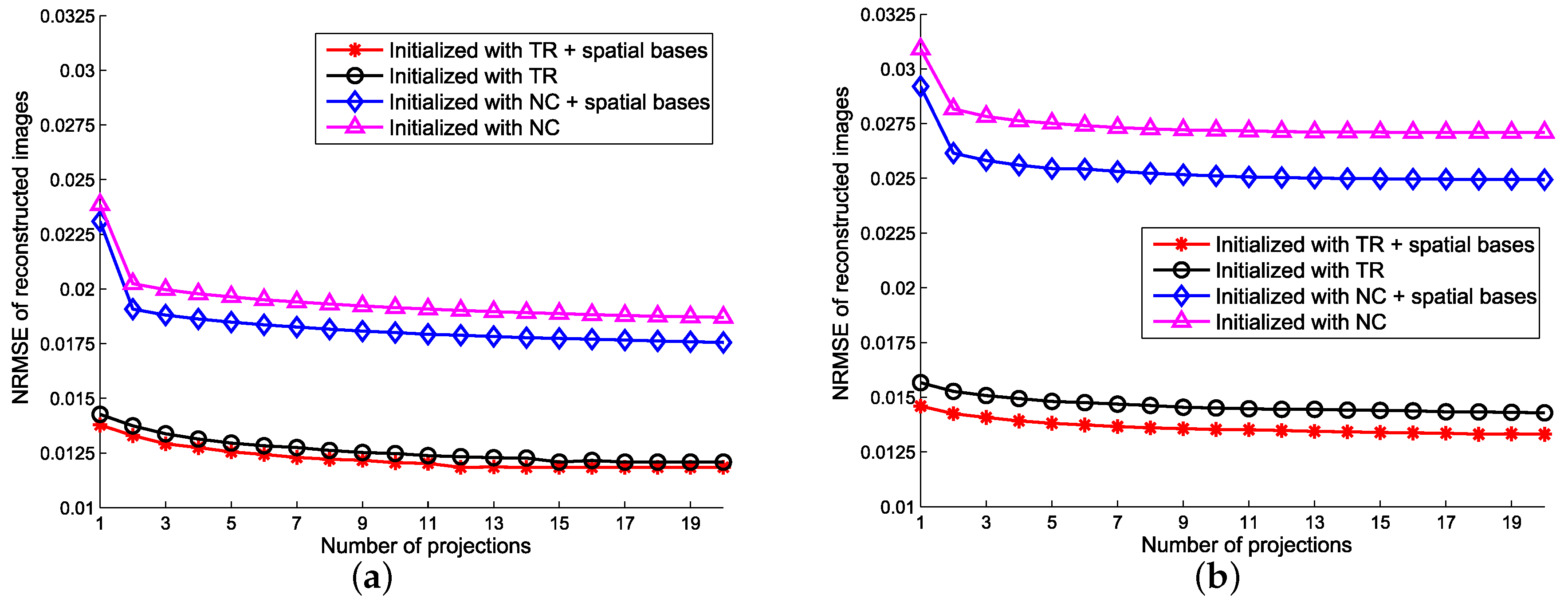
5.2. Sensitivity to Initialization
5.3. Related Works
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Watabe, H.; Ikoma, Y.; Kimura, Y.; Naganawa, M.; Shidahara, M. PET kinetic analysis—Compartmental model. Ann. Nucl. Med. 2006, 20, 583–588. [Google Scholar] [CrossRef] [PubMed]
- Hudson, H.M.; Larkin, R.S. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans. Med. Imaging 1994, 13, 601–609. [Google Scholar] [CrossRef] [PubMed]
- Fessler, J.A.; Rogers, W.L. Spatial resolution properties of penalized-likelihood image reconstruction: Space-invariant tomographs. IEEE Trans. Image Process. 1996, 5, 1346–1358. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Leahy, R.M.; Cherry, S.R.; Chatziioannou, A.; Farquhar, T.H. High-resolution 3D Bayesian image reconstruction using the microPET small-animal scanner. Phys. Med. Biol. 1998, 43, 1001–1013. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Qi, J. Generalized algorithms for direct reconstruction of parametric images from dynamic PET data. IEEE Trans. Med. Imaging 2009, 28, 1717–1726. [Google Scholar] [CrossRef] [PubMed]
- Ross, S.Q. Clear WhitePaper; GE Healthcare: Little Chalfont, UK, 2014; pp. 1–9. [Google Scholar]
- Mumcuoglu, E.U.; Leahy, R.; Cherry, S.R.; Zhou, Z. Fast gradient-based methods for Bayesian reconstruction of transmission and emission PET images. IEEE Trans. Med. Imaging 1994, 13, 687–701. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Lee, D.D.; Choi, S.; Park, K.S.; Lee, D.S. Non-negative matrix factorization of dynamic images in nuclear medicine. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, San Diego, CA, USA, 4–10 November 2001; Volume 4, pp. 2027–2030. [Google Scholar]
- Lee, J.S.; Lee, D.D.; Choi, S.; Lee, D.S. Application of nonnegative matrix factorization to dynamic positron emission tomography. In Proceedings of the 3rd International Conference on Independent Component Analysis and Blind Signal Separation, San Diego, CA, USA, 9–13 December 2001; pp. 629–632. [Google Scholar]
- Pustelnik, N.; Chaux, C.; Pesquet, J.C.; Comtat, C. Parallel algorithm and hybrid regularization for dynamic PET reconstruction. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Knoxville, TN, USA, 30 October–6 November 2010; pp. 2423–2427. [Google Scholar]
- Ahn, S.; Kim, S.M.; Son, J.; Lee, D.S.; Sung Lee, J. Gap compensation during PET image reconstruction by constrained, total variation minimization. Med. Phys. 2012, 39, 589–602. [Google Scholar] [CrossRef] [PubMed]
- Burger, M.; Müller, J.; Papoutsellis, E.; Schönlieb, C.B. Total variation regularization in measurement and image space for PET reconstruction. Inverse Probl. 2014, 30, 105003. [Google Scholar] [CrossRef]
- Li, T.; Thorndyke, B.; Schreibmann, E.; Yang, Y.; Xing, L. Model-based image reconstruction for four-dimensional PET. Med. Phys. 2006, 33, 1288–1298. [Google Scholar] [CrossRef] [PubMed]
- Kamasak, M.E.; Bouman, C.A.; Morris, E.D.; Sauer, K. Direct reconstruction of kinetic parameter images from dynamic PET data. IEEE Trans. Med. Imaging 2005, 24, 636–650. [Google Scholar] [CrossRef] [PubMed]
- Matthews, J.C.; Angelis, G.I.; Kotasidis, F.A.; Markiewicz, P.J.; Reader, A.J. Direct reconstruction of parametric images using any spatiotemporal 4D image based model and maximum likelihood expectation maximisation. In Proceedings of the Nuclear Science Symposium Conference Record, Knoxville, TN, USA, 30 October–6 November 2010; pp. 2435–2441. [Google Scholar]
- Reader, A.J.; Zaidi, H. Advances in PET image reconstruction. PET Clin. 2007, 2, 173–190. [Google Scholar] [CrossRef] [PubMed]
- Vardi, Y.; Shepp, L.; Kaufman, L. A statistical model for positron emission tomography. J. Am. Stat. Assoc. 1985, 80, 8–20. [Google Scholar] [CrossRef]
- Carson, R.E.; Yan, Y.; Daube-Witherspoon, M.E.; Freedman, N.; Bacharach, S.L.; Herscovitch, P. An approximation formula for the variance of PET region-of-interest values. IEEE Trans. Med. Imaging 1993, 12, 240–250. [Google Scholar] [CrossRef] [PubMed]
- Barrett, H.H.; Wilson, D.W.; Tsui, B.M. Noise properties of the EM algorithm. I. Theory. Phys. Med. Biol. 1994, 39, 833. [Google Scholar] [CrossRef] [PubMed]
- Fessler, J.A. Penalized weighted least-squares image reconstruction for positron emission tomography. IEEE Trans. Med. Imaging 1994, 13, 290–300. [Google Scholar] [CrossRef] [PubMed]
- Gerchberg, R. Super-resolution through error energy reduction. J. Mod. Opt. 1974, 21, 709–720. [Google Scholar] [CrossRef]
- Wernick, M.N.; Infusino, E.J.; Milosevic, M. Fast spatio-temporal image reconstruction for dynamic PET. IEEE Trans. Med. Imaging 1999, 18, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Gunn, R.N.; Lammertsma, A.A.; Hume, S.P.; Cunningham, V.J. Parametric imaging of ligand-receptor binding in PET using a simplified reference region model. Neuroimage 1997, 6, 279–287. [Google Scholar] [CrossRef] [PubMed]
- Turkheimer, F.E.; Edison, P.; Pavese, N.; Roncaroli, F.; Anderson, A.N.; Hammers, A.; Gerhard, A.; Hinz, R.; Tai, Y.F.; Brooks, D.J. Reference and target region modeling of [11C]-(R)-PK11195 brain studies. J. Nucl. Med. 2007, 48, 158–167. [Google Scholar] [PubMed]
- Logan, J.; Fowler, J.S.; Volkow, N.D.; Wolf, A.P.; Dewey, S.L.; Schlyer, D.J.; MacGregor, R.R.; Hitzemann, R.; Bendriem, B.; Gatley, S.J.; et al. Graphical analysis of reversible radioligand binding from time—Activity measurements applied to [N-11C-methyl]-(-)-cocaine PET studies in human subjects. J. Cereb. Blood Flow Metab. 1990, 10, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Lammertsma, A.A.; Hume, S.P. Simplified reference tissue model for PET receptor studies. Neuroimage 1996, 4, 153–158. [Google Scholar] [CrossRef] [PubMed]
- Logan, J. Graphical analysis of PET data applied to reversible and irreversible tracers. Nucl. Med. Biol. 2000, 27, 661–670. [Google Scholar] [CrossRef]
- Yaqub, M.; Van Berckel, B.N.; Schuitemaker, A.; Hinz, R.; Turkheimer, F.E.; Tomasi, G.; Lammertsma, A.A.; Boellaard, R. Optimization of supervised cluster analysis for extracting reference tissue input curves in (R)-[11C] PK11195 brain PET studies. J. Cereb. Blood Flow Metab. 2012, 32, 1600–1608. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Carson, R.E. Noise reduction in the simplified reference tissue model for neuroreceptor functional imaging. J. Cereb. Blood Flow Metab. 2002, 22, 1440–1452. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems 13 (NIPS 2000); Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Reader, A.J.; Matthews, J.C.; Sureau, F.C.; Comtat, C.; Trebossen, R.; Buvat, I. Iterative kinetic parameter estimation within fully 4D PET image reconstruction. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, San Diego, CA, USA, 29 October–1 November 2006; Volume 3, pp. 1752–1756. [Google Scholar]
- Shepp, L.A.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Logan, J.; Fowler, J.S.; Volkow, N.D.; Wang, G.J.; Ding, Y.S.; Alexoff, D.L. Distribution volume ratios without blood sampling from graphical analysis of PET data. J. Cereb. Blood Flow Metab. 1996, 16, 834–840. [Google Scholar] [CrossRef] [PubMed]
- Gravel, P.; Reader, A.J. Direct 4D PET MLEM reconstruction of parametric images using the simplified reference tissue model with the basis function method for [11C] raclopride. Phys. Med. Biol. 2015, 60, 4533–4549. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Qi, J. Direct estimation of kinetic parametric images for dynamic PET. Theranostics 2013, 3, 802–815. [Google Scholar] [CrossRef] [PubMed]
- Tsoumpas, C.; Turkheimer, F.E.; Thielemans, K. A survey of approaches for direct parametric image reconstruction in emission tomography. Med. Phys. 2008, 35, 3963–3971. [Google Scholar] [CrossRef] [PubMed]

| Notations of Methods | Problems to Be Optimized |
|---|---|
| NC | |
| NC + spatial bases | |
| TR | |
| TR + spatial bases | |
| Proposed |
| Data | Methods | ROI #1 | ROI #2 | ROI #3 | ROI #4 | ROI #5 | ROI #6 | ROI #7 |
|---|---|---|---|---|---|---|---|---|
| PET Data | TR () | 0.507 | 0.663 | 0.515 | 0.645 | 0.660 | 0.486 | 0.647 |
| Proposed | 0.174 | 0.302 | 0.219 | 0.236 | 0.214 | 0.240 | 0.304 | |
| PET Data | TR () | 0.859 | 1.01 | 0.864 | 0.795 | 1.166 | 0.745 | 0.752 |
| Proposed | 0.136 | 0.245 | 0.164 | 0.124 | 0.134 | 0.165 | 0.153 | |
| PET Data | TR () | 0.710 | 0.812 | 0.640 | 0.616 | 0.618 | 0.616 | 0.772 |
| Proposed | 0.240 | 0.295 | 0.251 | 0.199 | 0.240 | 0.221 | 0.351 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawamura, N.; Yokota, T.; Hontani, H.; Sakata, M.; Kimura, Y. Parametric PET Image Reconstruction via Regional Spatial Bases and Pharmacokinetic Time Activity Model. Entropy 2017, 19, 629. https://doi.org/10.3390/e19110629
Kawamura N, Yokota T, Hontani H, Sakata M, Kimura Y. Parametric PET Image Reconstruction via Regional Spatial Bases and Pharmacokinetic Time Activity Model. Entropy. 2017; 19(11):629. https://doi.org/10.3390/e19110629
Chicago/Turabian StyleKawamura, Naoki, Tatsuya Yokota, Hidekata Hontani, Muneyuki Sakata, and Yuichi Kimura. 2017. "Parametric PET Image Reconstruction via Regional Spatial Bases and Pharmacokinetic Time Activity Model" Entropy 19, no. 11: 629. https://doi.org/10.3390/e19110629
APA StyleKawamura, N., Yokota, T., Hontani, H., Sakata, M., & Kimura, Y. (2017). Parametric PET Image Reconstruction via Regional Spatial Bases and Pharmacokinetic Time Activity Model. Entropy, 19(11), 629. https://doi.org/10.3390/e19110629





