Dynamic and Thermodynamic Properties of a CA Engine with Non-Instantaneous Adiabats
Abstract
:1. Introduction
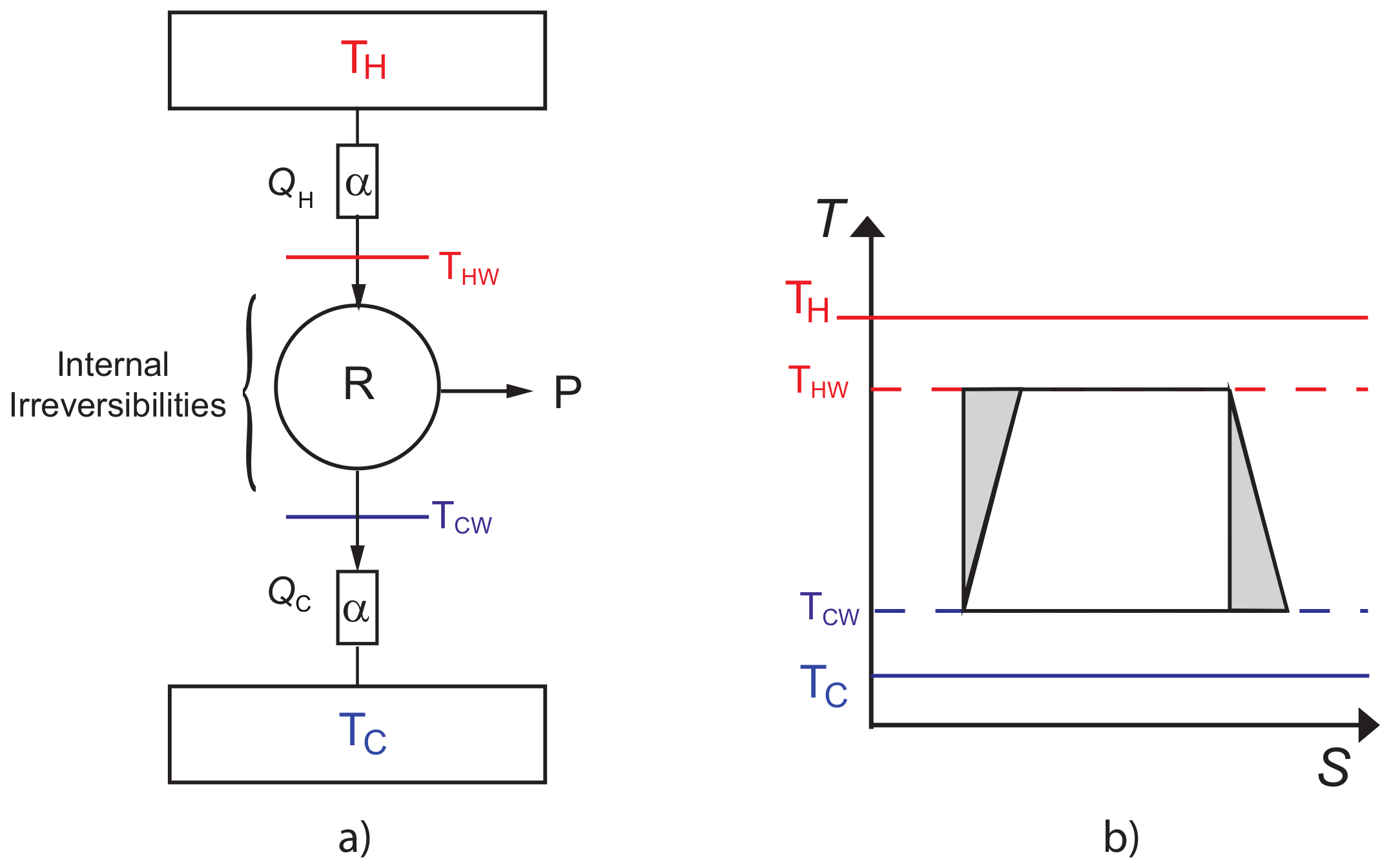
2. Thermal Properties of CA Engine with Internal Irreversibilities
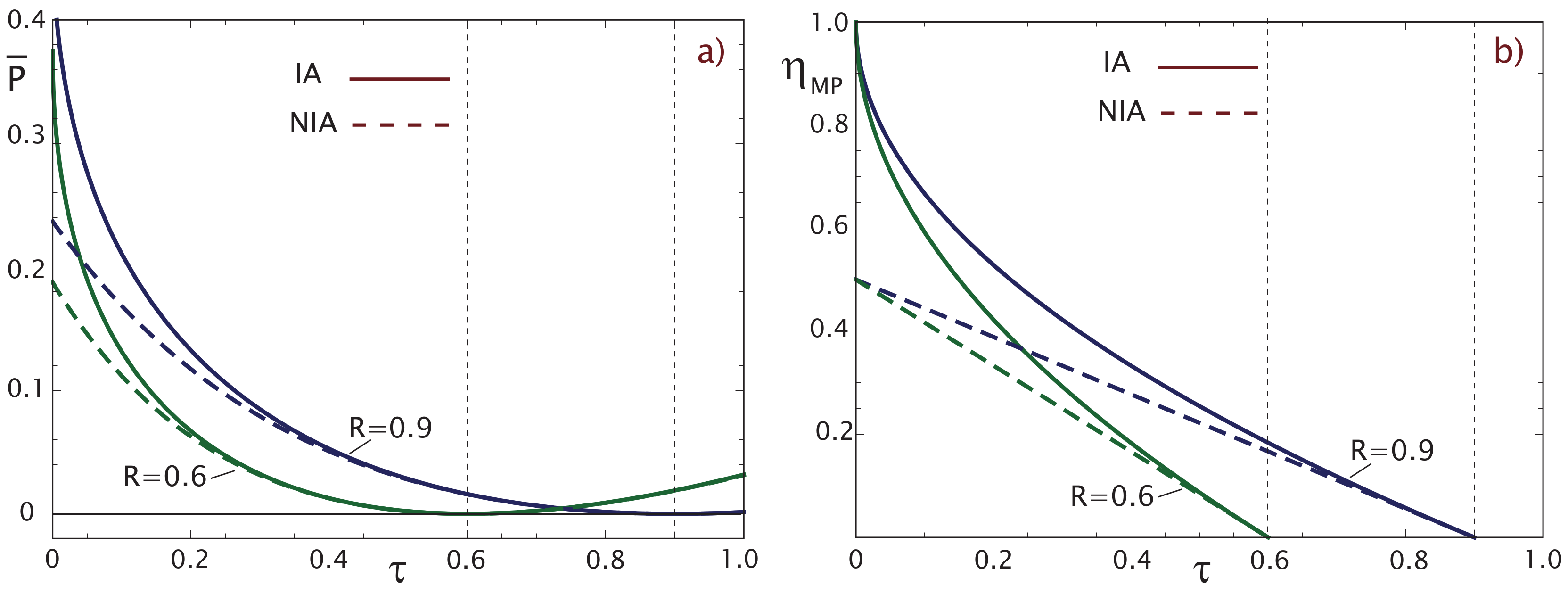
2.1. Maximum Power Output (MP)
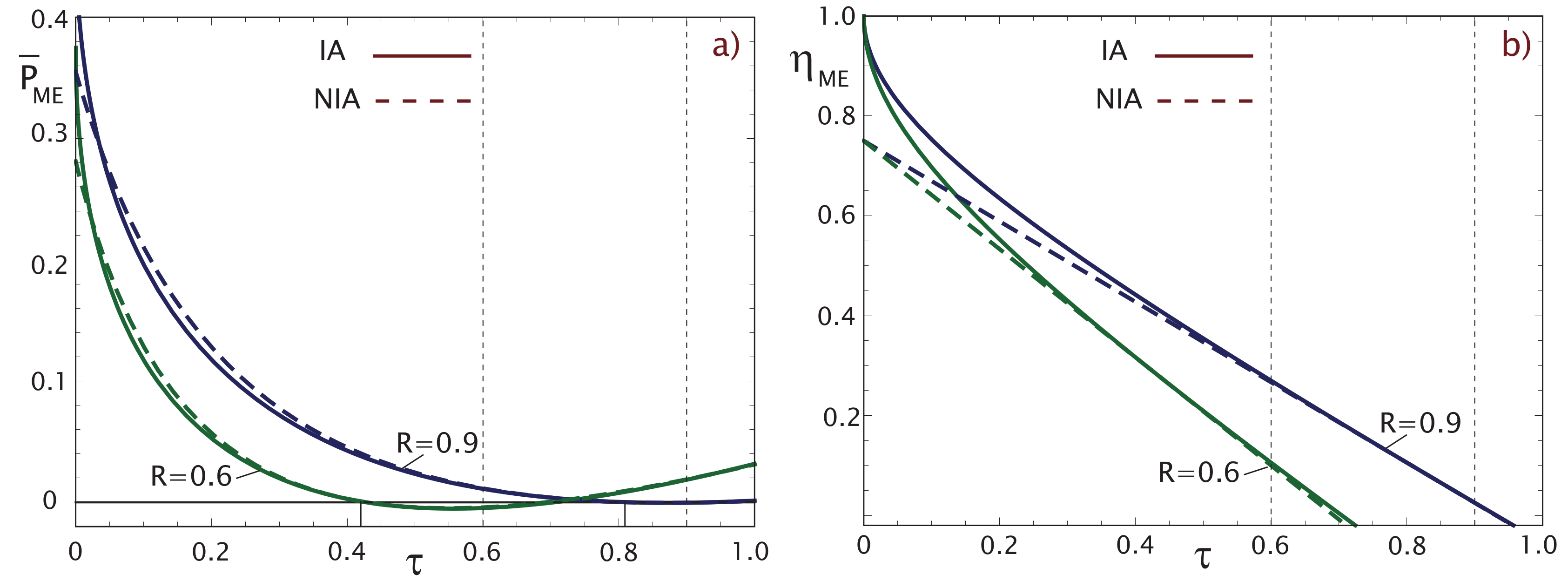
2.2. Maximum Ecological Criterion (ME)
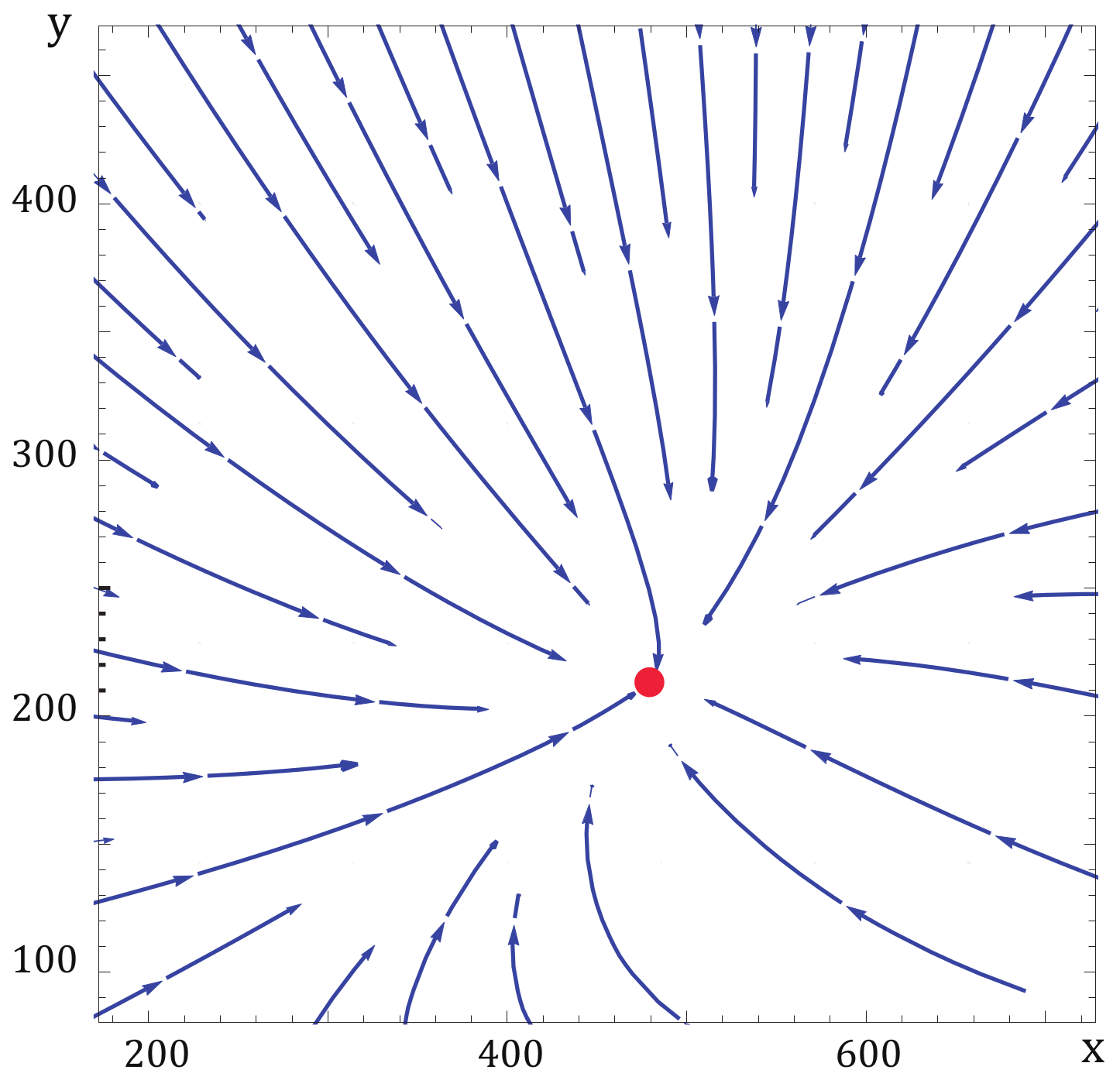
3. Steady-State Properties and Stability Analysis of the CA Engine
Dynamic Equations and Local Stability Analysis
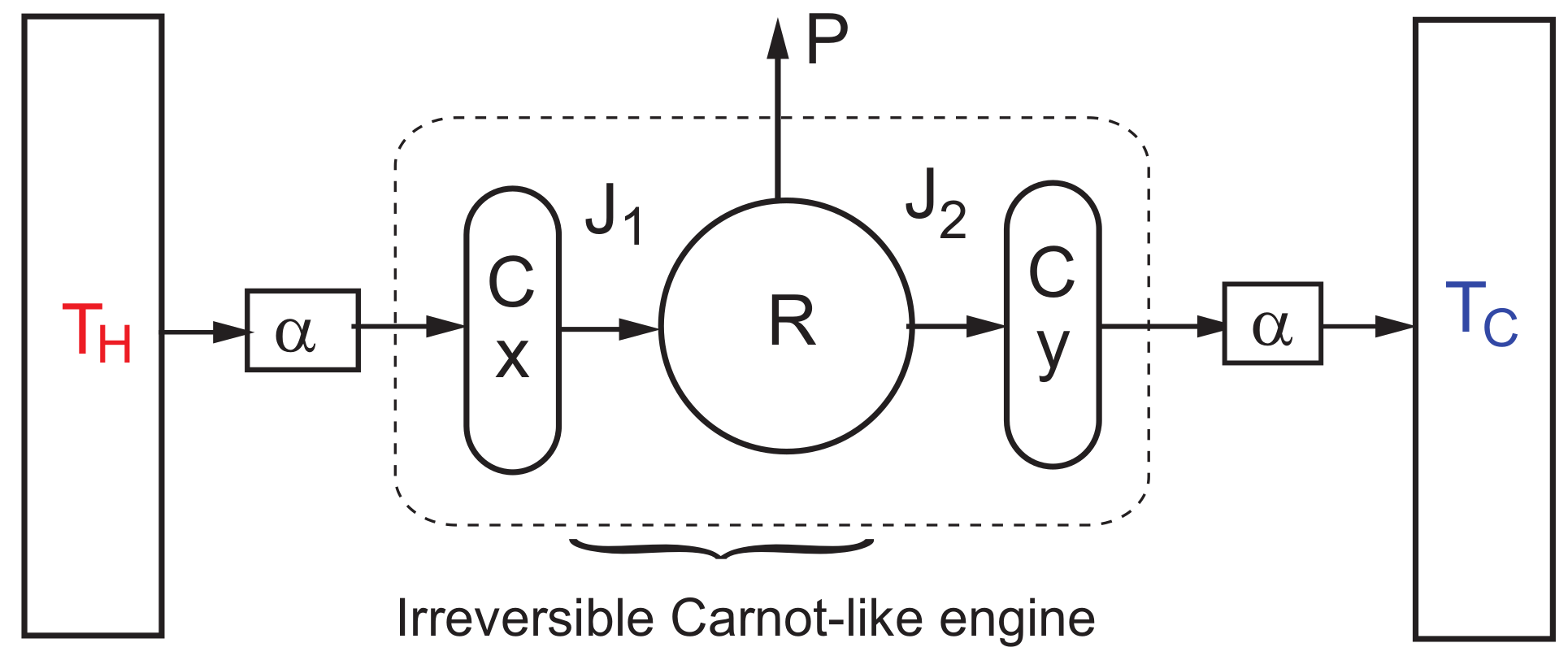
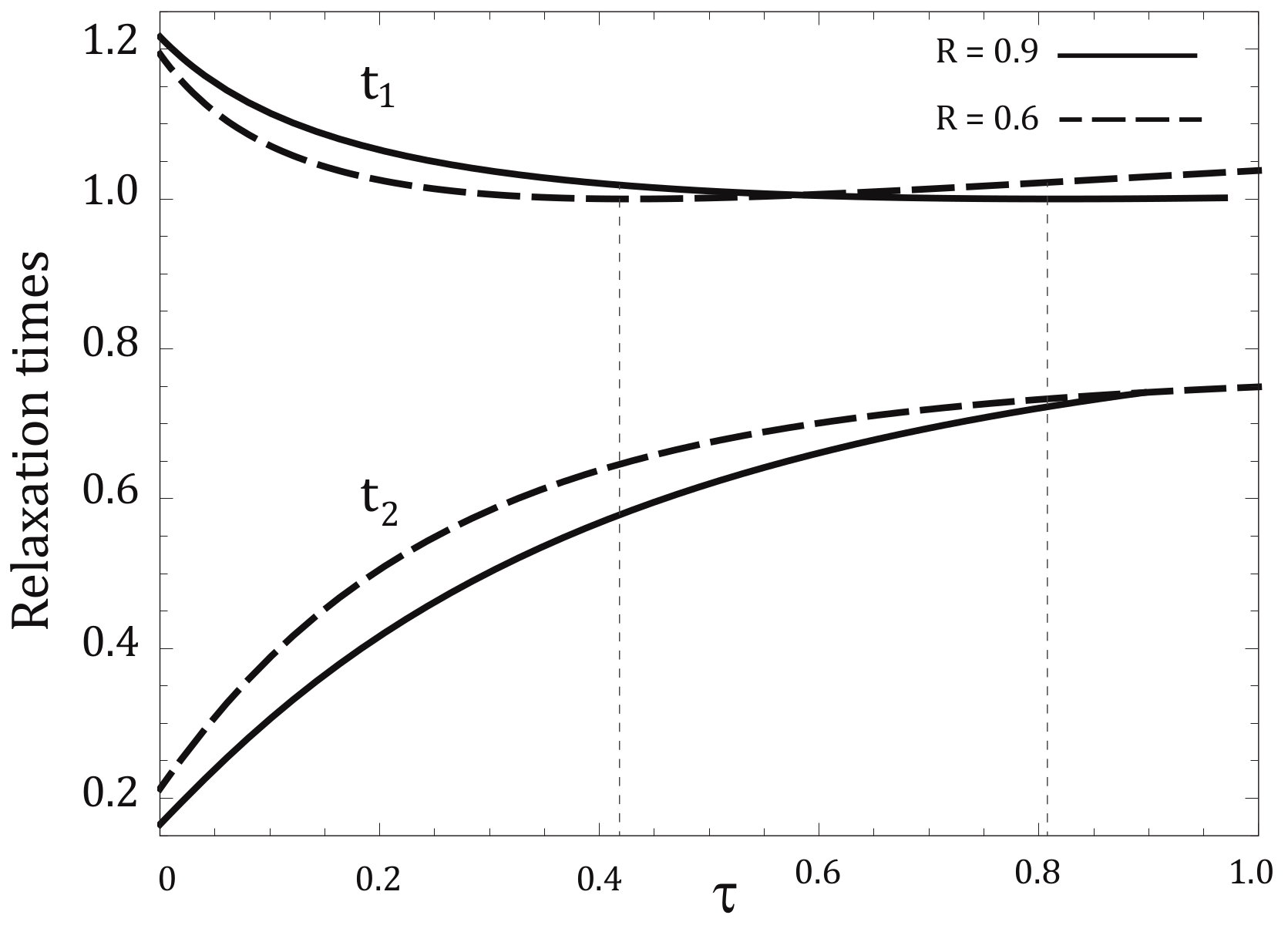
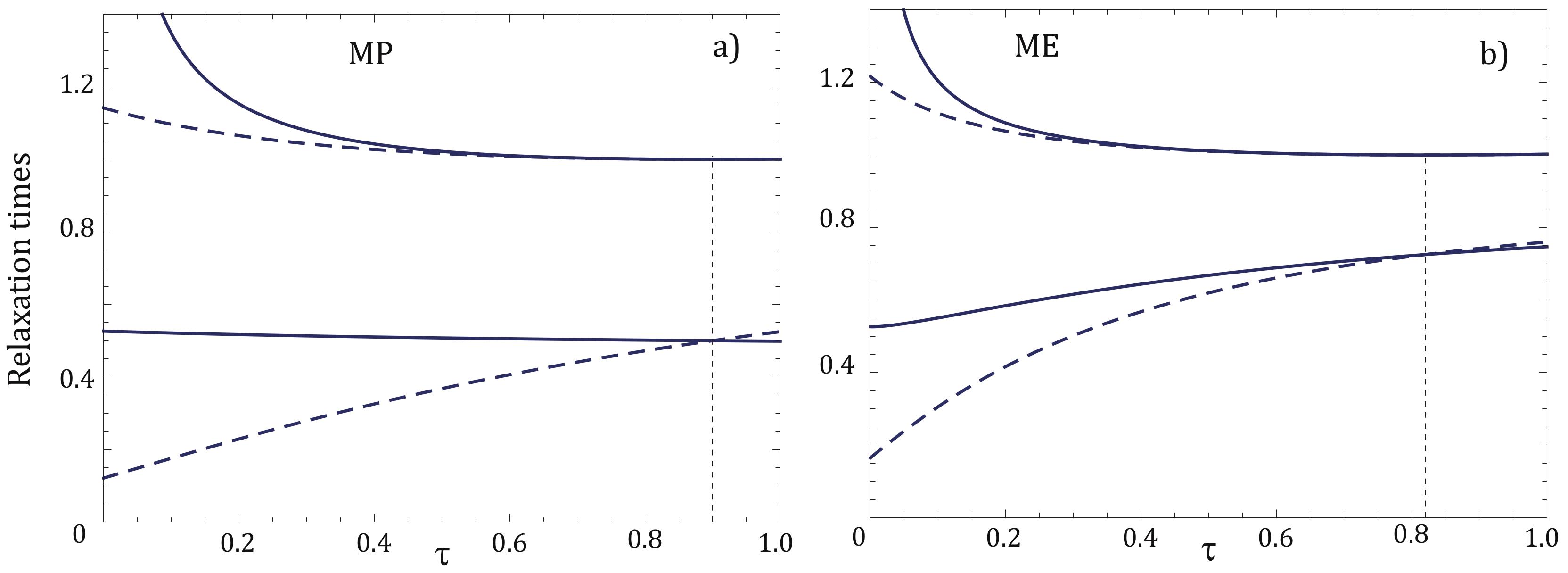
4. Relaxation Times for NI and NIA Adiabats: A Comparative Analysis
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot Engine at Maximum Power Output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Novikov, I.I. The efficiency of atomic power stations (a review). J. Nucl. Energy 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Chambadal, P. Les Centrales Nuclaires; Armand Colin: Paris, France, 1957. (In French) [Google Scholar]
- Rubin, M.H. Optimal configuration of a class of irreversible heat engines. I. Phys. Rev. A 1979, 19, 1272–1276. [Google Scholar] [CrossRef]
- Berry, R.S.; Kazakov, V.A.; Sieniutycz, S.; Szwast, Z.; Tsirlin, A.M. Thermodynamics Optimization of Finite-Time Processes; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- Chen, L.; Sun, F. Advances in Finite Time Thermodynamics: Analysis and Optimization; Nova Science Publisher: New York, NY, USA, 2004. [Google Scholar]
- Ozkaynak, S.; Gokun, S.; Yavuz, H. Finite-time thermodynamic analysis of a radiative heat engine with internal irreversibility. J. Phys. D Appl. Phys. 1994, 27, 1139–1143. [Google Scholar] [CrossRef]
- Chen, J. The maximum power output and maximum efficiency of an irreversible Carnot heat engine. J. Phys. D Appl. Phys. 1994, 27, 1144–1149. [Google Scholar]
- Feidt, M.; Costea, M.; Petrescu, S.; Stanciu, C. Nonlinear Thermodynamic Analysis and Optimization of a Carnot Engine Cycle. Entropy 2016, 18, 243. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Agrawal, D.C.; Gordon, J.M.; Huleihil, M. Endoreversible engines with finite-time adiabats. Indian J. Eng. Mater. Sci. 1994, 1, 195–198. [Google Scholar]
- Gutkowicz-Krusin, D.; Procaccia, I.; Ross, J. On the efficiency of rate processes. Power and efficiency of heat engines. J. Chem. Phys. 1978, 69, 3898–3906. [Google Scholar] [CrossRef]
- Ladino-Luna, D.; de la Selva, S.T. The ecological efficiency of a thermal finite time engine. Rev. Mex. Fís. 2000, 46, 52–56. [Google Scholar]
- Ladino-Luna, D. Van der Waals gas as working substance in a Curzon and Ahlborn-Novikov engine. Entropy 2005, 7, 108–121. [Google Scholar] [CrossRef]
- Martínez, I.A.; Roldán, E.; Dinis, L.; Petrov, D.; Rica, R.A. Adiabatic Processes Realized with a Trapped Brownian Particle. Phys. Rev. Lett. 2015, 114, 120601. [Google Scholar] [CrossRef] [PubMed]
- Martínez, I.A.; Roldán, E.; Dinis, L.; Rica, R.A. Colloidal heat engines: A review. Soft Matter 2017, 13, 22–36. [Google Scholar] [CrossRef] [PubMed]
- Blickle, V.; Bechinger, C. Realization of a micrometre-sized stochastic heat engine. Nat. Phys. 2012, 8, 143–146. [Google Scholar] [CrossRef]
- Santillán, M.; Maya, G.; Angulo-Brown, F. Local stability analysis of an endoreversible Curzon-Ahborn-Novikov engine working in a maximum-power-like regime. J. Phys. D Appl. Phys. 2001, 34, 2068–2072. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Reyes-Ramírez, I.; Sánchez, N. The effect of heat transfer laws and thermal conductances on the local stability of an endoreversible heat engine. J. Phys. D Appl. Phys. 2005, 38, 1282–1291. [Google Scholar] [CrossRef]
- Chimal-Eguía, J.C.; Barranco-Jiménez, M.A.; Angulo-Brown, F. Stability Analysis of an Endoreversible Heat Engine with Stefan-Boltzmann Heat Transfer Law Working in Maximum-Power-Like Regime. Open Syst. Inf. Dyn. 2006, 13, 43–53. [Google Scholar] [CrossRef]
- Nie, W.; He, J.; Deng, X. Local stability analysis of an irreversible Carnot heat engine. Int. J. Therm. Sci. 2008, 47, 633–640. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, D.; Kang, Y. Local stability characteristics of a non-endoreversible heat engine working in the optimum region. Appl. Therm. Eng. 2009, 29, 358–363. [Google Scholar] [CrossRef]
- Sanchez-Salas, N.; Chimal-Eguia, J.C.; Guzman-Aguilar, F. On the Dynamic Robustness of a Non-Endoreversible Engine Working in Different Operation Regimes. Entropy 2011, 13, 422–436. [Google Scholar] [CrossRef]
- Chen, L.; Yan, Z. The effect of heat-transfer law on performance of a two-heat-source endoreversible cycle. J. Chem. Phys. 1989, 90, 3740–3743. [Google Scholar] [CrossRef]
- Páez-Hernández, R.; Angulo-Brown, F.; Santillán, M. Dynamic Robustness and Thermodynamic Optimization in a Non-Endoreversible Curzon-Ahlborn Engine. J. Non-Equilib. Thermodyn. 2006, 31, 173–188. [Google Scholar]
- Ladino-Luna, D. Linear approximation of efficiency for a non-endoreversible cycle. J. Energy Inst. 2011, 84, 61–65. [Google Scholar] [CrossRef]
- Páez-Hernández, R.; Ladino-Luna, D.; Portillo-Díaz, P. Dynamic properties in an endoreversible Curzon-Ahlborn engine using a van der Waals gas as working substance. Phys. A Stat. Mech. Appl. 2011, 390, 3275–3282. [Google Scholar] [CrossRef]
- Páez-Hernández, R.; Ladino-Luna, D.; Portillo-Díaz, P.; Barranco-Jiménez, M. Local Stability Analysis of a Curzon-Ahlborn Engine without Ideal Gas Working at the Maximum Ecological Regime. J. Energy Power Eng. 2013, 7, 928–936. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2001. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paéz-Hernández, R.T.; Sánchez-Salas, N.; Chimal-Eguía, J.C.; Ladino-Luna, D. Dynamic and Thermodynamic Properties of a CA Engine with Non-Instantaneous Adiabats. Entropy 2017, 19, 632. https://doi.org/10.3390/e19110632
Paéz-Hernández RT, Sánchez-Salas N, Chimal-Eguía JC, Ladino-Luna D. Dynamic and Thermodynamic Properties of a CA Engine with Non-Instantaneous Adiabats. Entropy. 2017; 19(11):632. https://doi.org/10.3390/e19110632
Chicago/Turabian StylePaéz-Hernández, Ricardo T., Norma Sánchez-Salas, Juan C. Chimal-Eguía, and Delfino Ladino-Luna. 2017. "Dynamic and Thermodynamic Properties of a CA Engine with Non-Instantaneous Adiabats" Entropy 19, no. 11: 632. https://doi.org/10.3390/e19110632
APA StylePaéz-Hernández, R. T., Sánchez-Salas, N., Chimal-Eguía, J. C., & Ladino-Luna, D. (2017). Dynamic and Thermodynamic Properties of a CA Engine with Non-Instantaneous Adiabats. Entropy, 19(11), 632. https://doi.org/10.3390/e19110632



