Random Walk Null Models for Time Series Data
Abstract
:1. Introduction
1.1. Notation and Terminology
1.2. Permutation Entropy and KL Divergence
1.3. Contributions
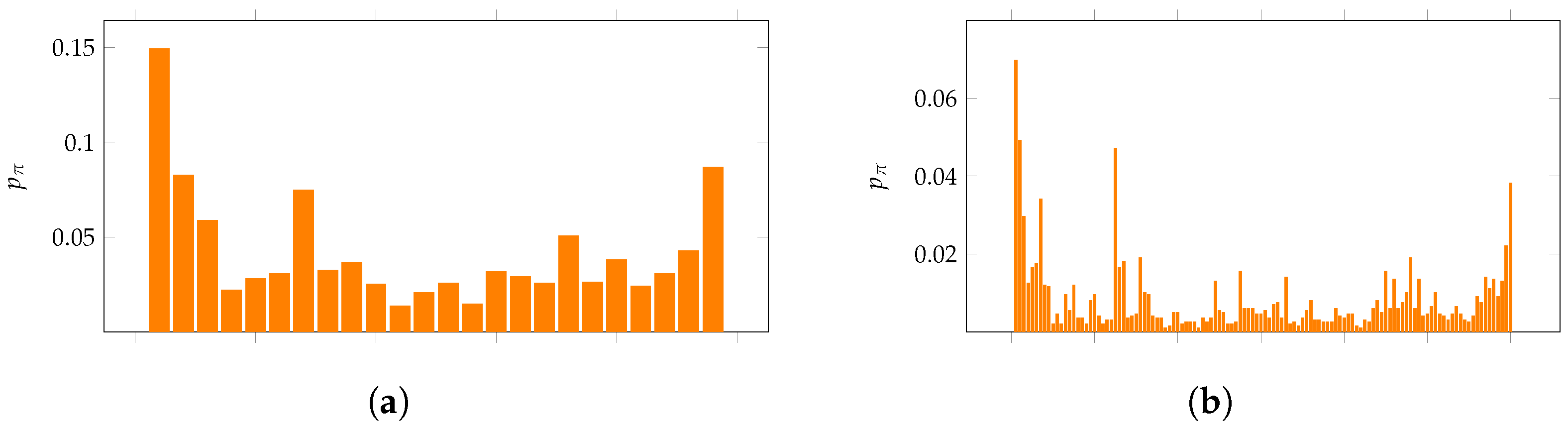
2. Distributions of Patterns in Random Walks
2.1. Equality in Any Random Walk
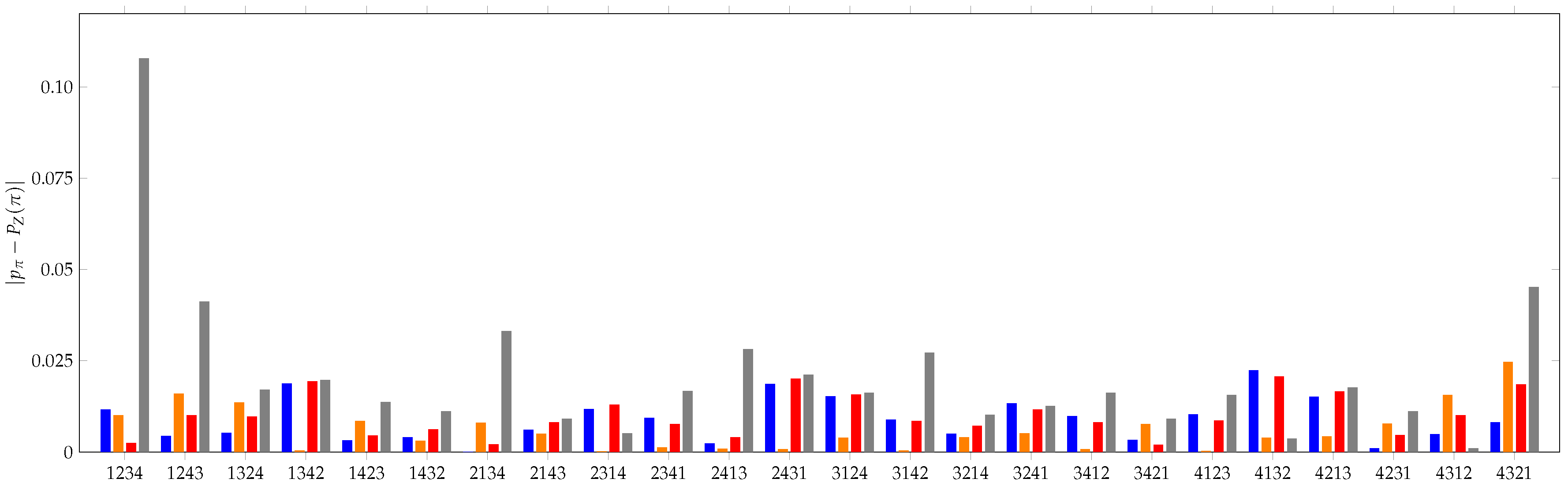
3. KL Divergence Method
3.1. Simple Validation Measure
4. Motivating Examples
5. Data Descriptions
- RAND: A sequence of 2000 uniform random numbers drawn between zero and one;
- NORM RW: A simulated random walk whose steps are drawn at random from the standard normal distribution, ;
- N-DRIFT RW: A simulated random walk whose steps are drawn at random from the normal distribution with ; this is the normal curve fitted to the returns in the S&P 500 data below.
- UNIF RW: A simulated random walk whose steps are drawn uniformly at random from the uniform distribution on the interval ;
- SP500: The daily closing values of the S&P 500 from 24 January 2009–31 December 2016. Data provided by Morningstar and accessed through [31];
- MEX: Average daily temperatures in Mexico City from 20 June 2011–31 December 2016. Data provided by the World Meteorological Organization through [31];
- NYC: Average daily temperatures in New York City from 20 June 2011–31 December 2016; data provided by the National Oceanic and Atmospheric Administration through [31];
- HEART: Instantaneous heart rate measurements taken at s intervals collected at the Massachusetts Institute of Technology [32].
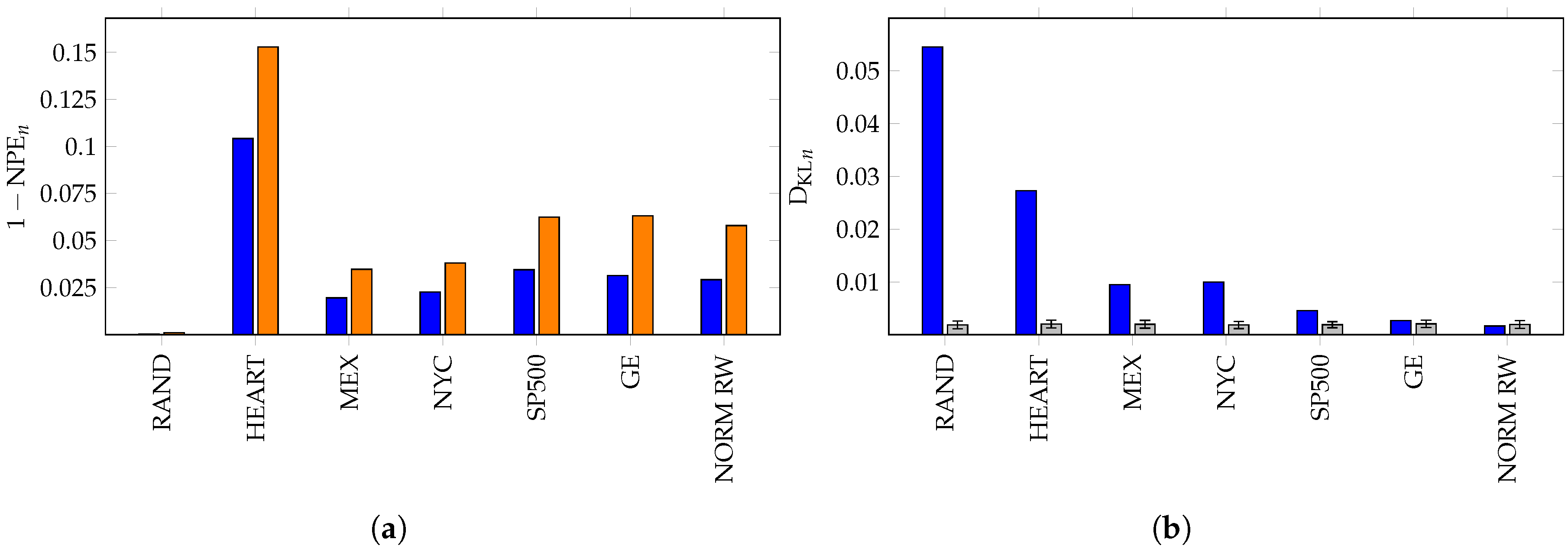
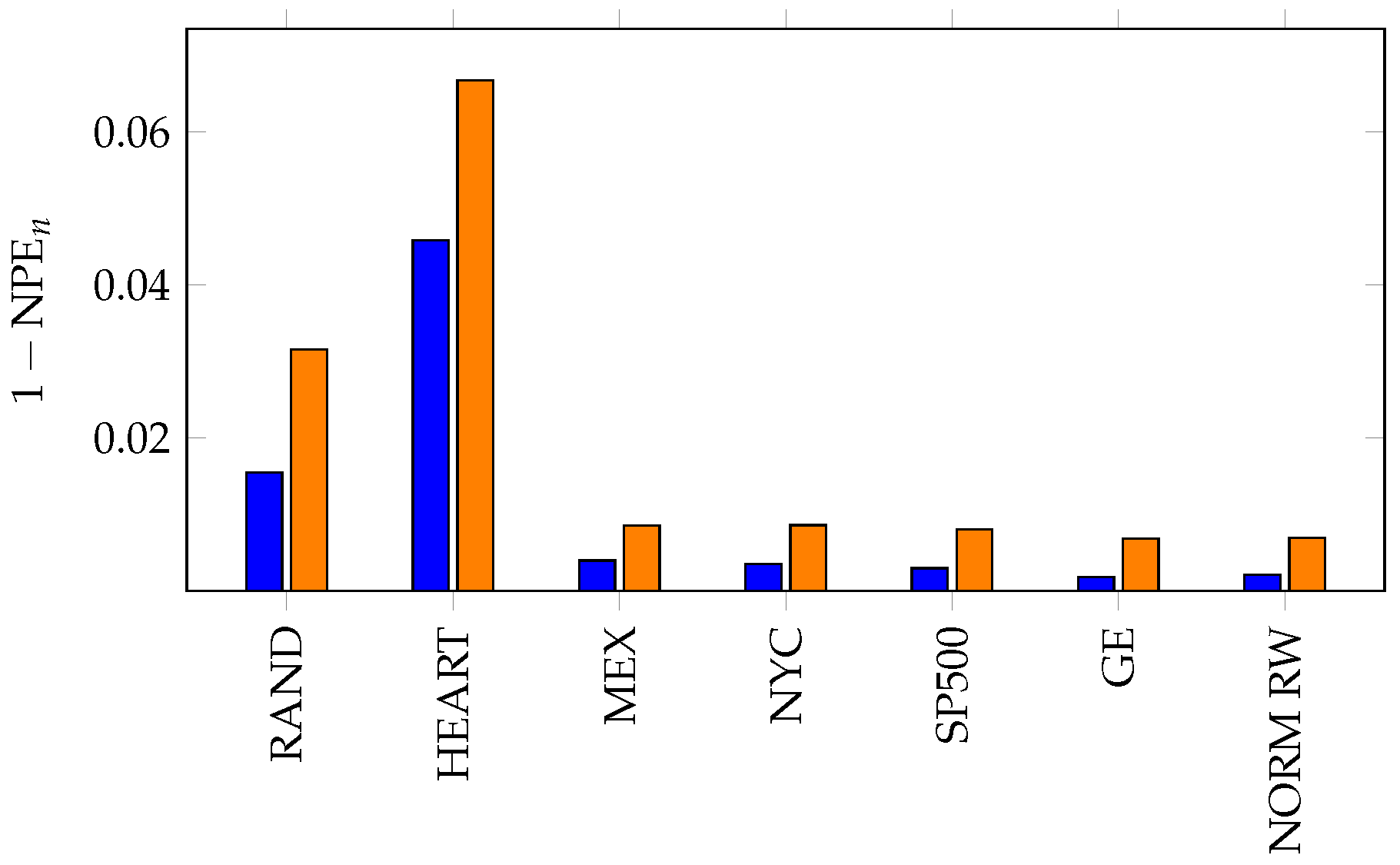
6. Applications of KL Divergence Method
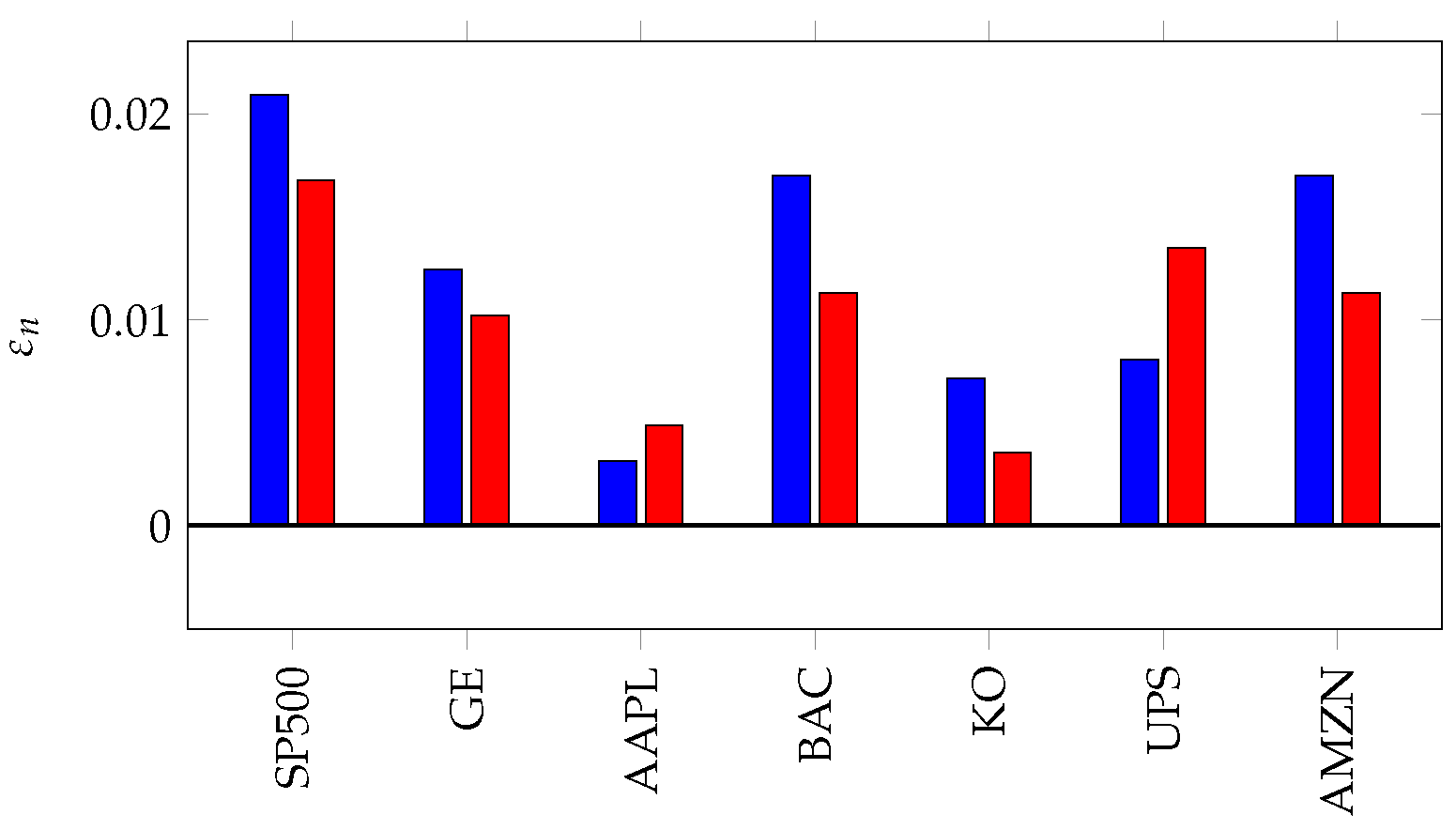
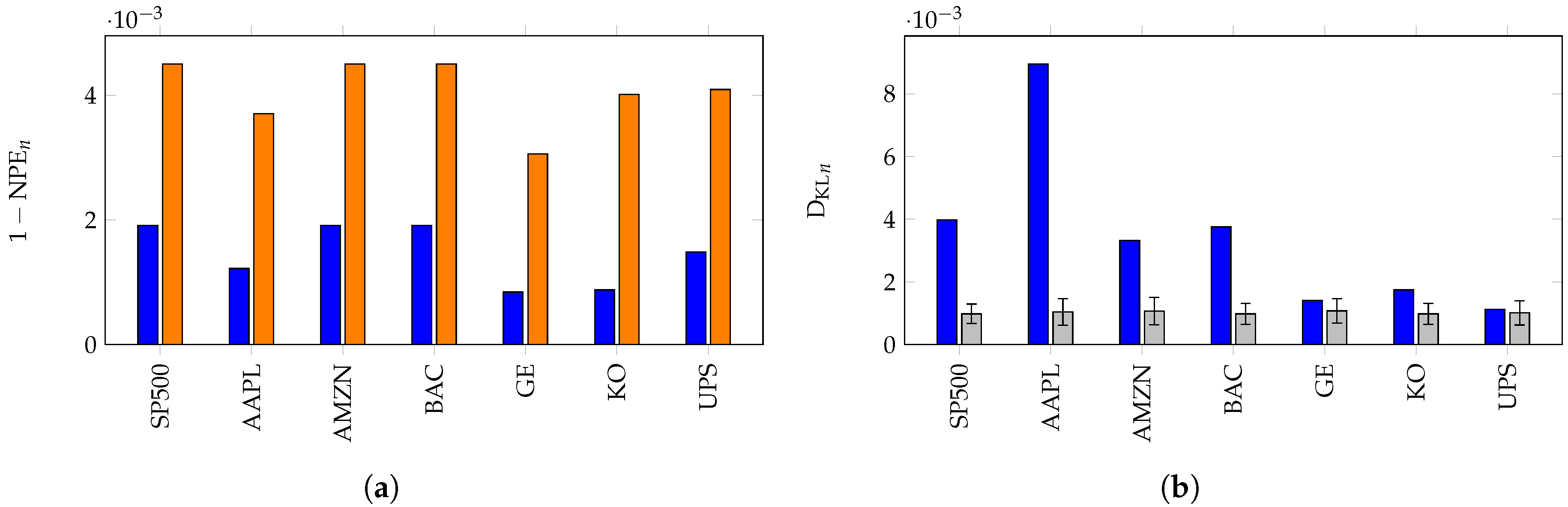
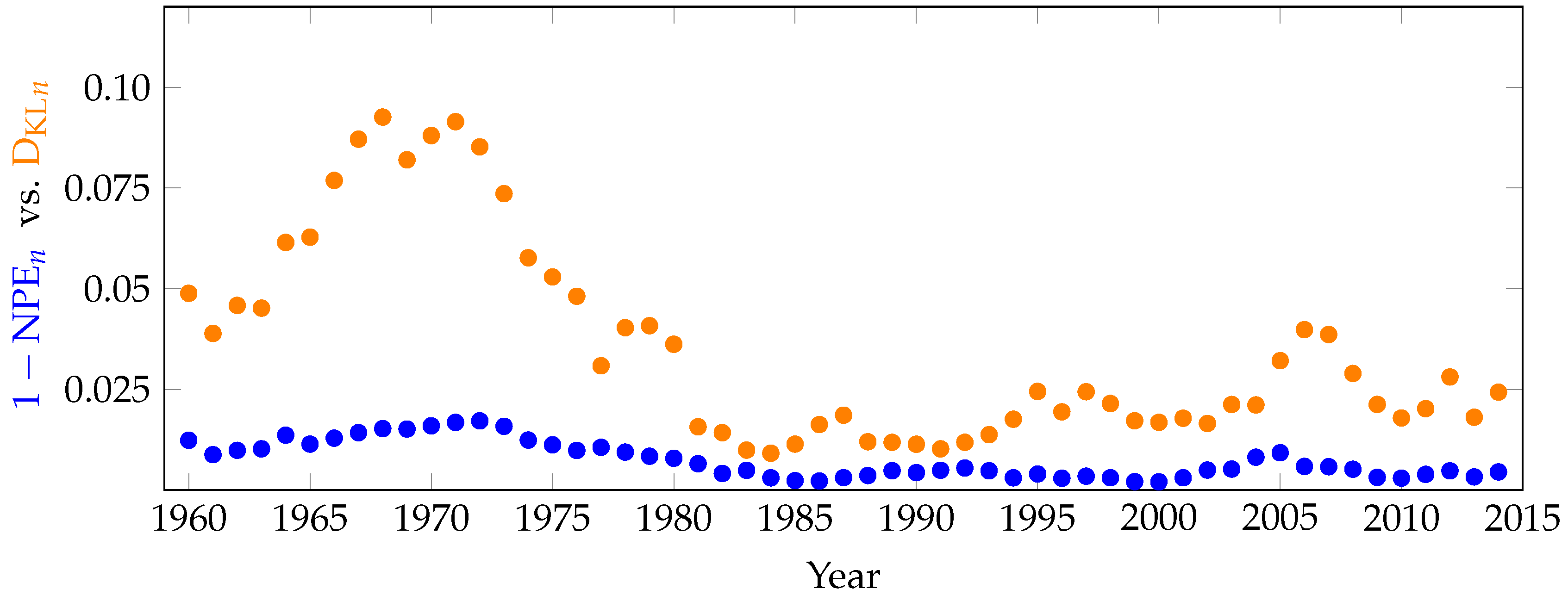
7. Inefficiency in Financial Markets
8. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| KL | Kullback–Liebler |
| PE | Permutation Entropy |
| NPE | Normalized Permutation Entropy |
Appendix A. Null Model Distributions
| Pattern | Normal: | Uniform: | Uniform: |
|---|---|---|---|
| {123} | |||
| {132, 213} | |||
| {231, 312} | |||
| {321} | |||
| {1234} | 0.1250 | ||
| {1243, 2134} | 0.0625 | 1/16 | |
| {1324} | 0.0417 | 1/24 | |
| {1342, 3124} | 0.0208 | 1/24 | |
| {1423, 2314} | 0.0355 | 1/48 | |
| {1432, 2143, 3214} | 0.0270 | 1/48 | |
| {2341, 3412, 4123} | 0.0270 | 1/48 | |
| {2413} | 0.0146 | 1/48 | |
| {2431, 4213} | 0.0208 | 1/24 | |
| {3142} | 0.0146 | 1/48 | |
| {3241, 4132} | 0.0355 | 1/48 | |
| {3421, 4312} | 0.0625 | 1/16 | |
| {4231} | 0.0417 | 1/24 | |
| {4321} | 0.1250 | 1/8 |
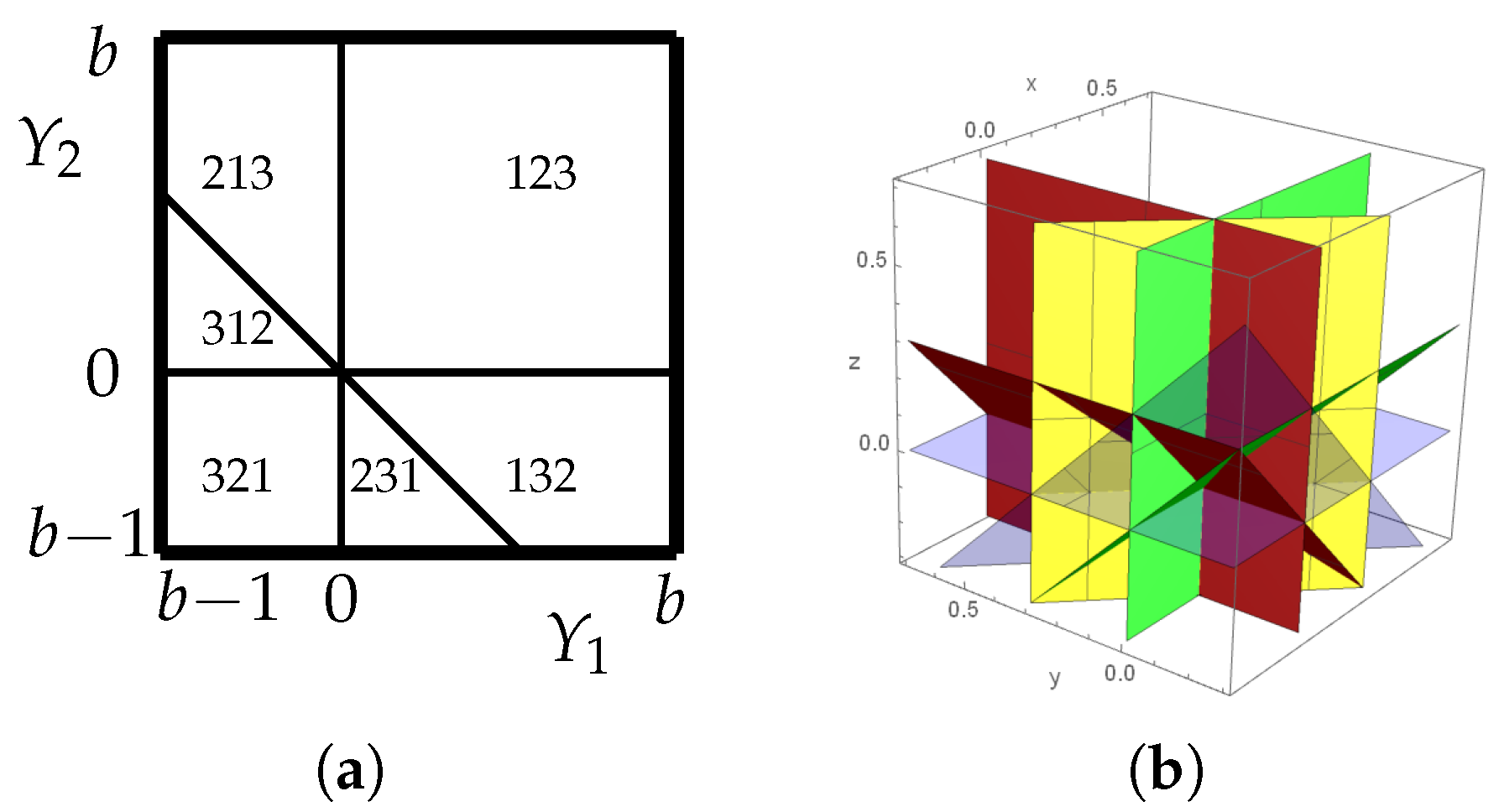
Appendix B. Permutation Equivalence Classes
Appendix C. Data Plots
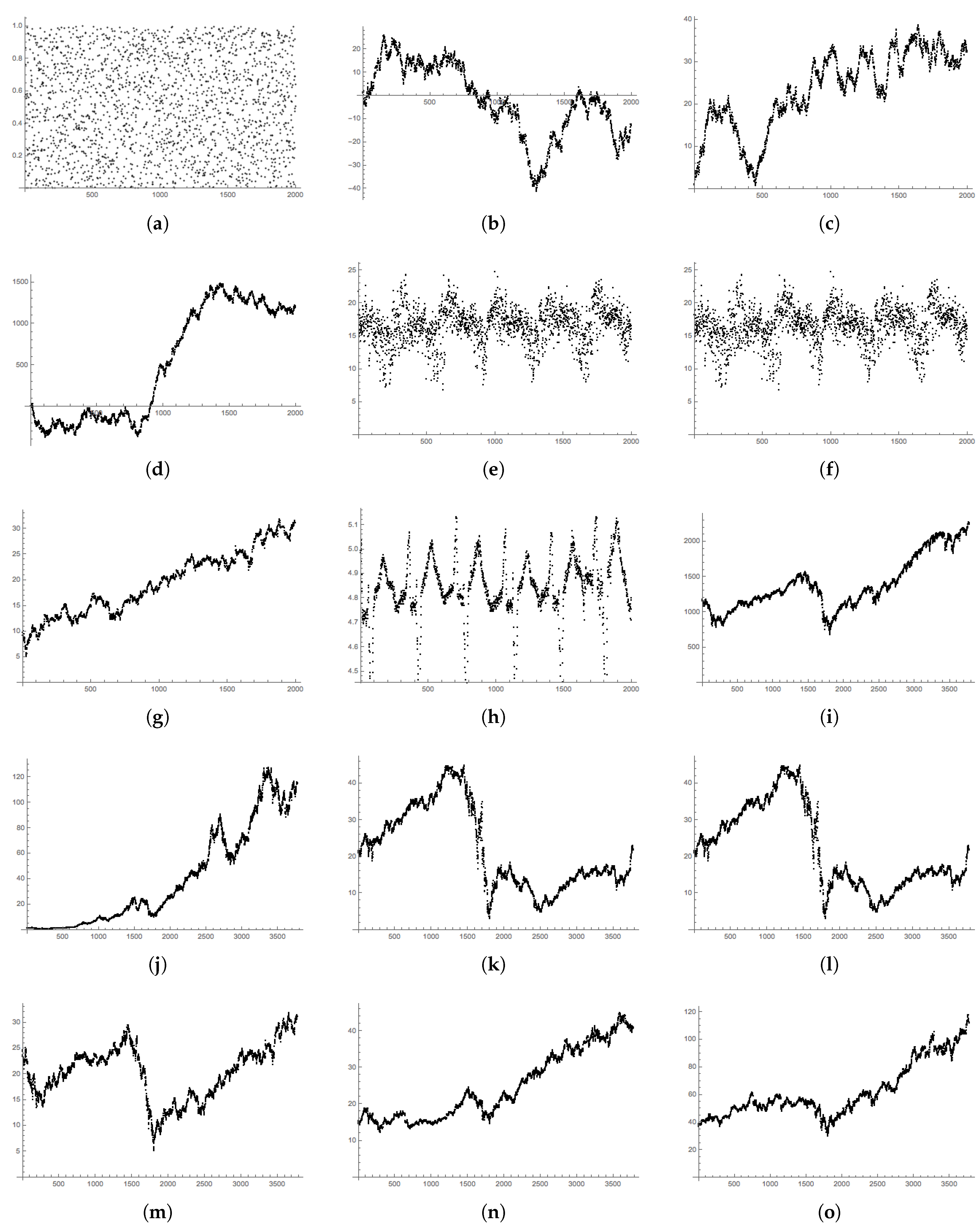
References
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A.F. Combinatorial detection of determinism in noisy time series. Europhys. Lett. 2008, 83, 60005. [Google Scholar] [CrossRef]
- Bandt, C. Autocorrelation type functions for big and dirty data series. arXiv, 2014; arXiv:1411.3904. [Google Scholar]
- Bariviera, A.F.; Zunino, L.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. Revisiting the European sovereign bonds with a permutation-information-theory approach. Eur. Phys. J. B 2013, 86, 509. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Lim, J.R. Rapid Evaluation of Permutation Entropy for Financial Volatility Analysis—A NovelHash Function using Feature-Bias Divergence. Available online: https://www.doc.ic.ac.uk/teaching/distinguished-projects/2014/j.lim.pdf (accessed on 15 Novermber 2017).
- Ortiz-Cruz, A.; Rodriguez, E.; Ibarra-Valdez, C.; Alvarez-Ramirez, J. Efficiency of crude oil markets: Evidences from informational entropy analysis. Energy Policy 2012, 41, 365–373. [Google Scholar] [CrossRef]
- Zunino, L.; Bariviera, A.F.; Guercio, M.B.; Martinez, L.B.; Rosso, O.A. On the efficiency of sovereign bond markets. Phys. A Stat. Mech. Appl. 2012, 391, 4342–4349. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Phys. A Stat. Mech. Appl. 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Liang, Z.; Voss, L.J.; Sleigh, J.W. Multiscale permutation entropy analysis of EEG recordings during sevoflurane anesthesia. J. Neural Eng. 2010, 7, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ouyang, G.; Richards, D.A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Res. 2007, 77, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Yao, W.; Wu, M.; Shi, Z.; Wang, J.; Ning, X. Multiscale permutation entropy analysis of electrocardiogram. Phys. A Stat. Mech. Appl. 2017, 471, 492–498. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Olofsen, E.; Sleigh, J.W.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Weck, P.J.; Schaffner, D.A.; Brown, M.R.; Wicks, R.T. Permutation entropy and statistical complexity analysis of turbulence in laboratory plasmas and the solar wind. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91, 023101. [Google Scholar] [CrossRef] [PubMed]
- Zunino, L.; Pérez, D.G.; Martín, M.T.; Garavaglia, M.; Plastino, A.; Rosso, O.A. Permutation entropy of fractional Brownian motion and fractional Gaussian noise. Phys. Lett. A 2008, 372, 4768–4774. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation Entropy: New Ideas and Challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Fama, E.F. The Behavior of Stock-Market Prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Fama, E.F. Random Walks in Stock Market Prices. Financ. Anal. J. 1995, 51, 75–80. [Google Scholar] [CrossRef]
- Bandt, C.; Shiha, F. Order Patterns in Time Series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Sinn, M.; Keller, K. Estimation of ordinal pattern probabilities in Gaussian processes with stationary increments. Comput. Stat. Data Anal. 2011, 55, 1781–1790. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Dang, C.; Richards, D.A.; Li, X. Ordinal pattern based similarity analysis for EEG recordings. Clin. Neurophysiol. 2010, 121, 694–703. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C. Permutation Entropy and Order Patterns in Long Time Series. In Time Series Analysis and Forecasting; Springer: Berlin, Germany, 2016; pp. 61–73. [Google Scholar]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Martinez, M.; Elizalde, S. The frequency of pattern occurrence in random walks. In Proceedings of the 27th International Conference on Formal Power Series and Algebraic Combinatorics (FPSAC 2015), Discrete Mathematics & Theoretical Computer Science, DMTCS Proceedings, Daejeon, Korea, 6–10 July 2105. [Google Scholar]
- Kenyon, R.; Kral, D.; Radin, C.; Winkler, P. Permutations with fixed pattern densities. arXiv, 2015; arXiv:1506.02340. [Google Scholar]
- Elizalde, S.; Moore, K. Patterns of Negative Shifts and Beta-Shifts. arXiv, 2015; arXiv:1512.04479. [Google Scholar]
- Martinez, M.A. Equivalences on Patterns in Random Walks. Ph.D. Thesis, Dartmouth College, Hanover, NH, USA, 2015. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 11.2. Available online: http://support.wolfram.com/kb/472 (accessed on 15 Novermber 2017).
- Goldberger, A.L.; Rigney, D.R. Nonlinear Dynamics at the Bedside. In Institute for Nonlinear Science; Theory of Heart; Springer: New York, NY, USA, 1991; pp. 583–605. [Google Scholar]
- Jegadeesh, N.; Titman, S. Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency. J. Financ. 1993, 48, 65–91. [Google Scholar] [CrossRef]
- Jegadeesh, N.; Titman, S. Profitability of Momentum Strategies: An Evaluation of Alternative Explanations. Natl. Bur. Econ. Res. 1999. [Google Scholar] [CrossRef]
| Data | Forbidden Patterns | Permutation Entropy | ||||
|---|---|---|---|---|---|---|
| RAND | 0 | 0 | 48 | 0.999 | 0.992 | 0.970 |
| NORM RW | 0 | 0 | 190 | 0.942 | 0.916 | 0.875 |
| N-DRIFT RW | 0 | 0 | 207 | 0.932 | 0.900 | 0.857 |
| UNIF RW | 0 | 0 | 216 | 0.930 | 0.899 | 0.855 |
| MEX | 0 | 0 | 129 | 0.965 | 0.952 | 0.926 |
| NYC | 0 | 0 | 115 | 0.962 | 0.950 | 0.924 |
| SP500 | 0 | 0 | 199 | 0.938 | 0.907 | 0.863 |
| GE | 0 | 2 | 210 | 0.937 | 0.906 | 0.863 |
| HEART | 0 | 8 | 344 | 0.847 | 0.813 | 0.777 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
DeFord, D.; Moore, K. Random Walk Null Models for Time Series Data. Entropy 2017, 19, 615. https://doi.org/10.3390/e19110615
DeFord D, Moore K. Random Walk Null Models for Time Series Data. Entropy. 2017; 19(11):615. https://doi.org/10.3390/e19110615
Chicago/Turabian StyleDeFord, Daryl, and Katherine Moore. 2017. "Random Walk Null Models for Time Series Data" Entropy 19, no. 11: 615. https://doi.org/10.3390/e19110615
APA StyleDeFord, D., & Moore, K. (2017). Random Walk Null Models for Time Series Data. Entropy, 19(11), 615. https://doi.org/10.3390/e19110615




