Complexity-Entropy Maps as a Tool for the Characterization of the Clinical Electrophysiological Evolution of Patients under Pharmacological Treatment with Psychotropic Drugs
Abstract
:1. Introduction
2. Method
2.1. Signal Analysis
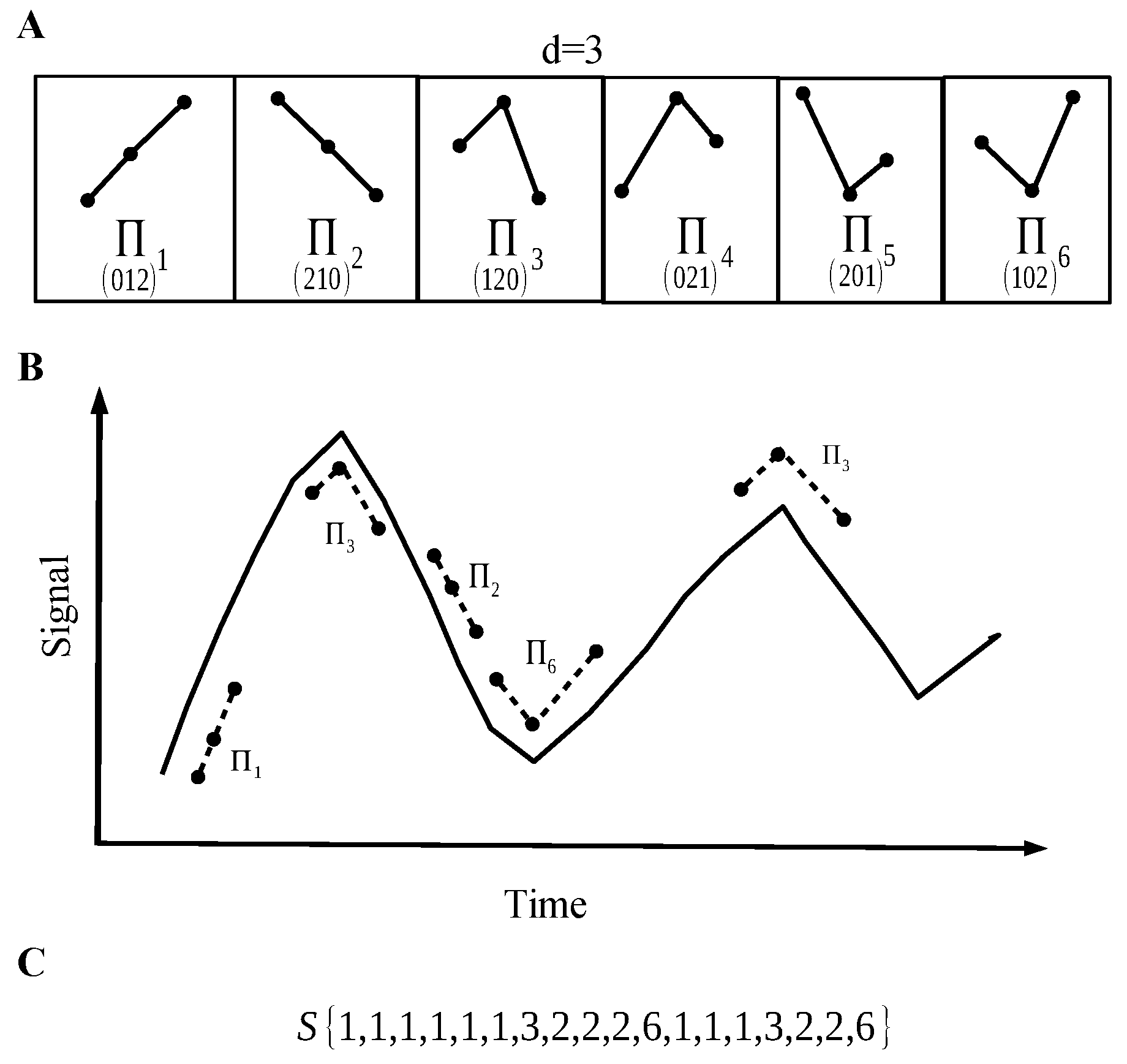
2.1.1. Data Quantification
2.1.2. Permutation Entropy
2.1.3. Lempel–Ziv Complexity
- Reproduction: it consists of extending a sequence to a sequence via recursive copy–paste operations, which leads to , i.e., where the first letter is in , that is to say , the second one is the following one in the extended sequence of size , i.e., , etc.: is a subsequence of . In a sense, all of the “information” of the extended sequence is in .
- Production: the extended sequence is now such that can be reproduced by , but the last symbol of the extension can either follow the recursive copy–paste operation (thus is a reproduction) or can be “new”. Note that a reproduction is a production, not the other way round. Let us denote a production by .
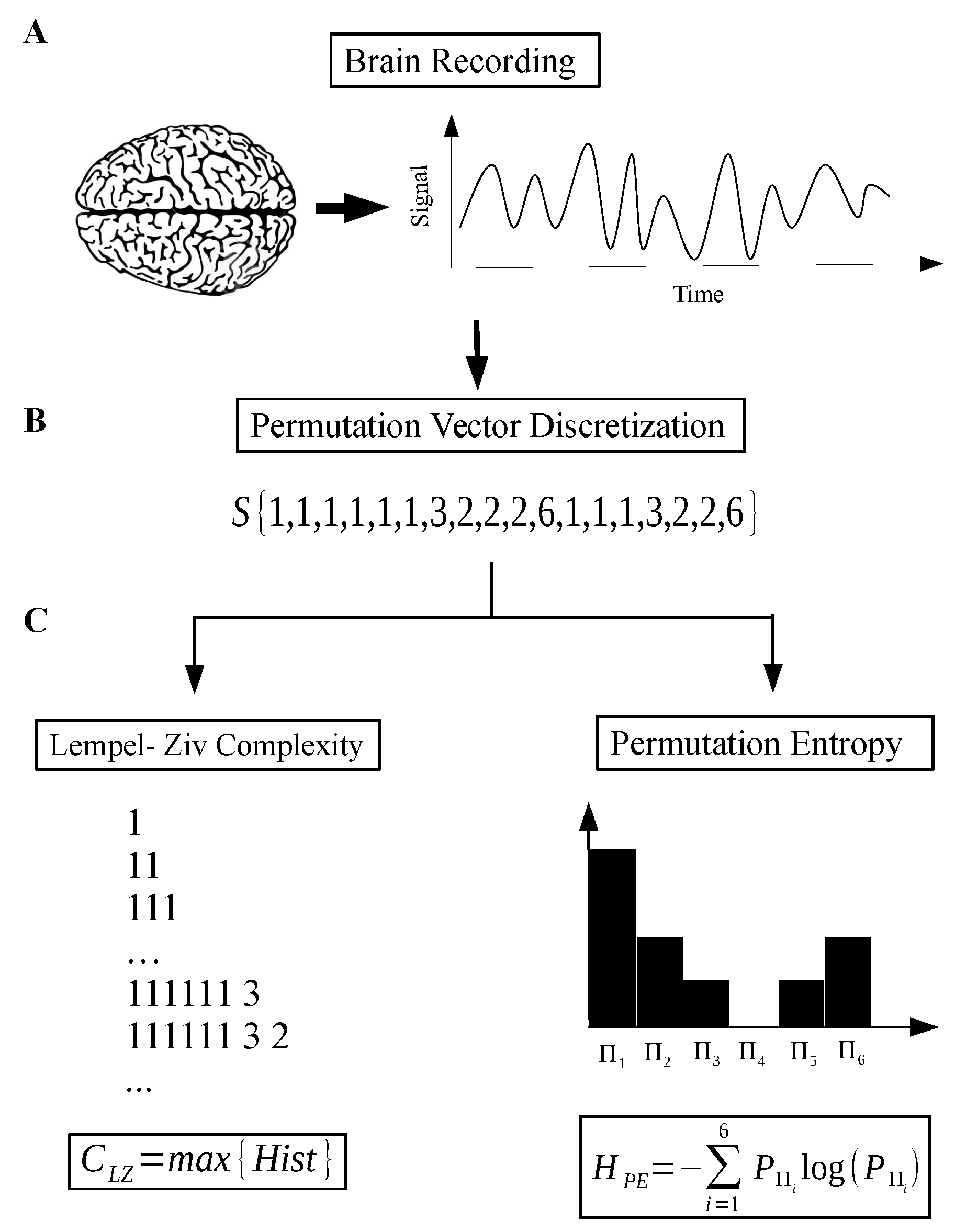
2.1.4. Complexity vs. Entropy Map
- Step 1: Record and reprocess the signal—using band pass filter and notch filter at 60 Hz (Figure 2A).
- Step 2: Discretize the raw signal using a permutation vector approach (Figure 2B).
- Step 3: Calculate the Lempel–Ziv complexity for the sequence taken from step 2 (Figure 2C).
- Step 4: Take the sequence from step 2 and, using a histogram, estimate the probability distribution (PD) of permutation vectors. Then, calculate the Shannon entropy related with this PD.
- Step 5: Finally, with the two measures, we have the coordinates of the map corresponding to the recorded signal.
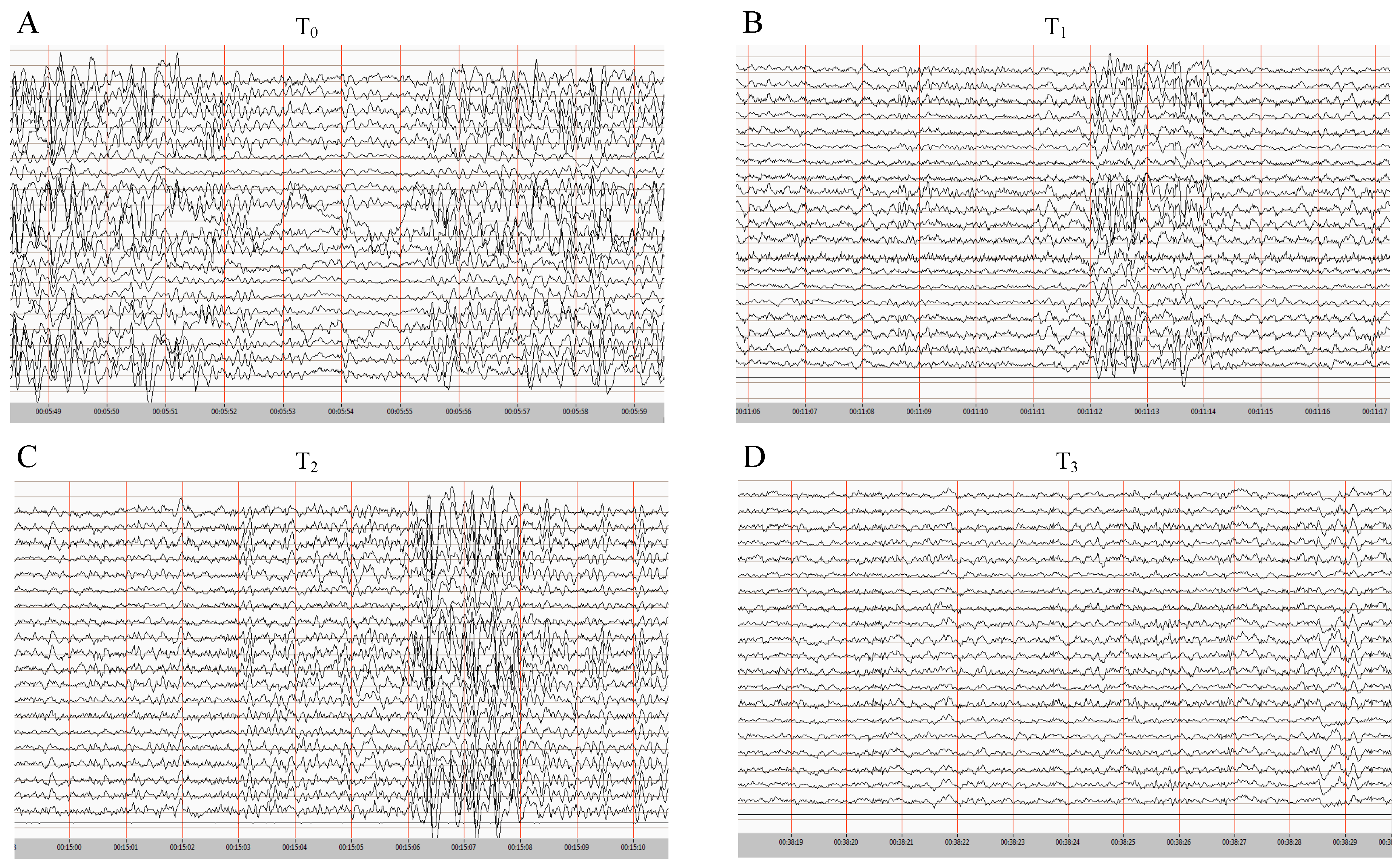
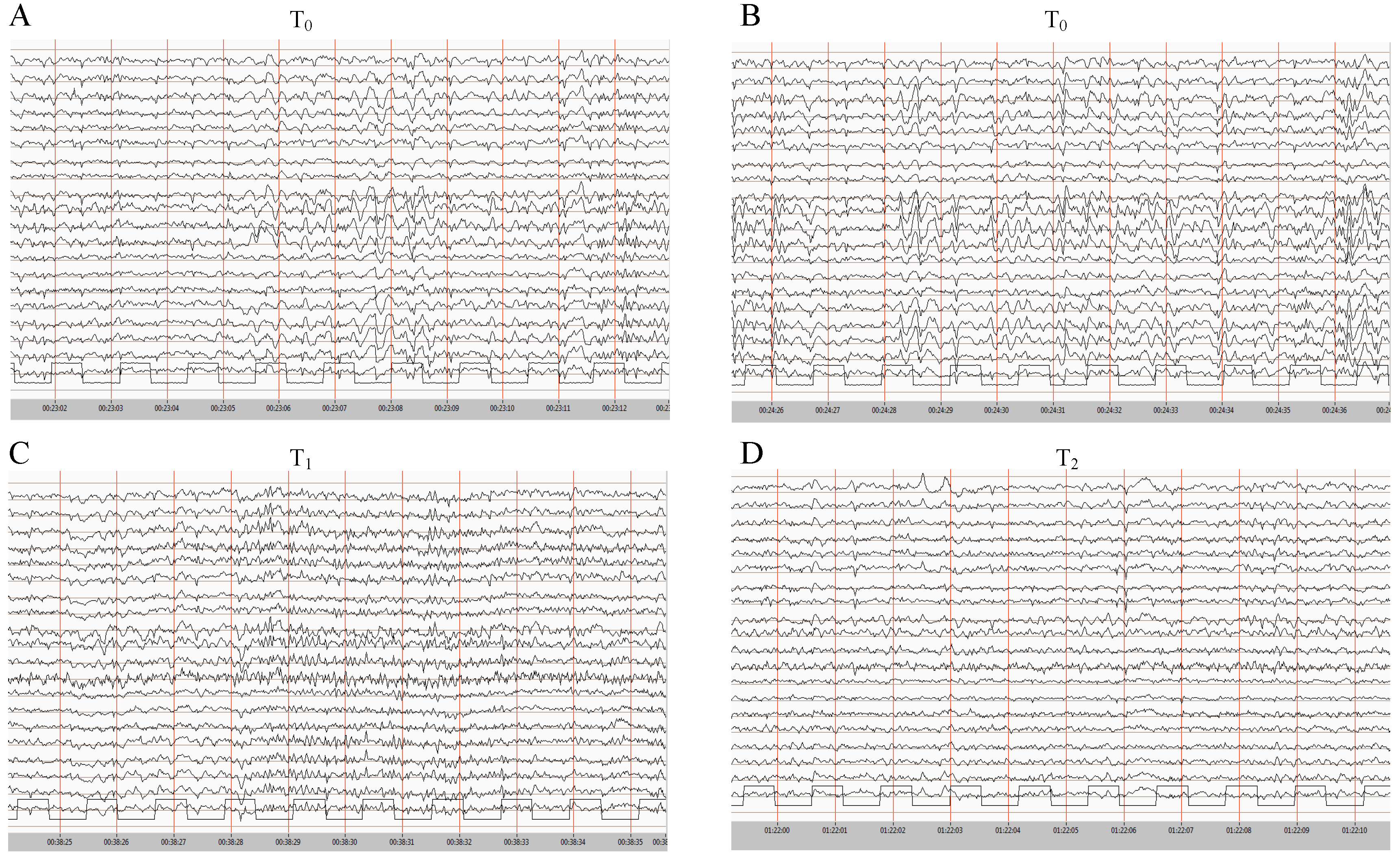
2.2. Patient Recording
Technical Procedures and Clinical Description
2.3. Clinical Description of the Cases
2.3.1. Case I
2.3.2. Case II
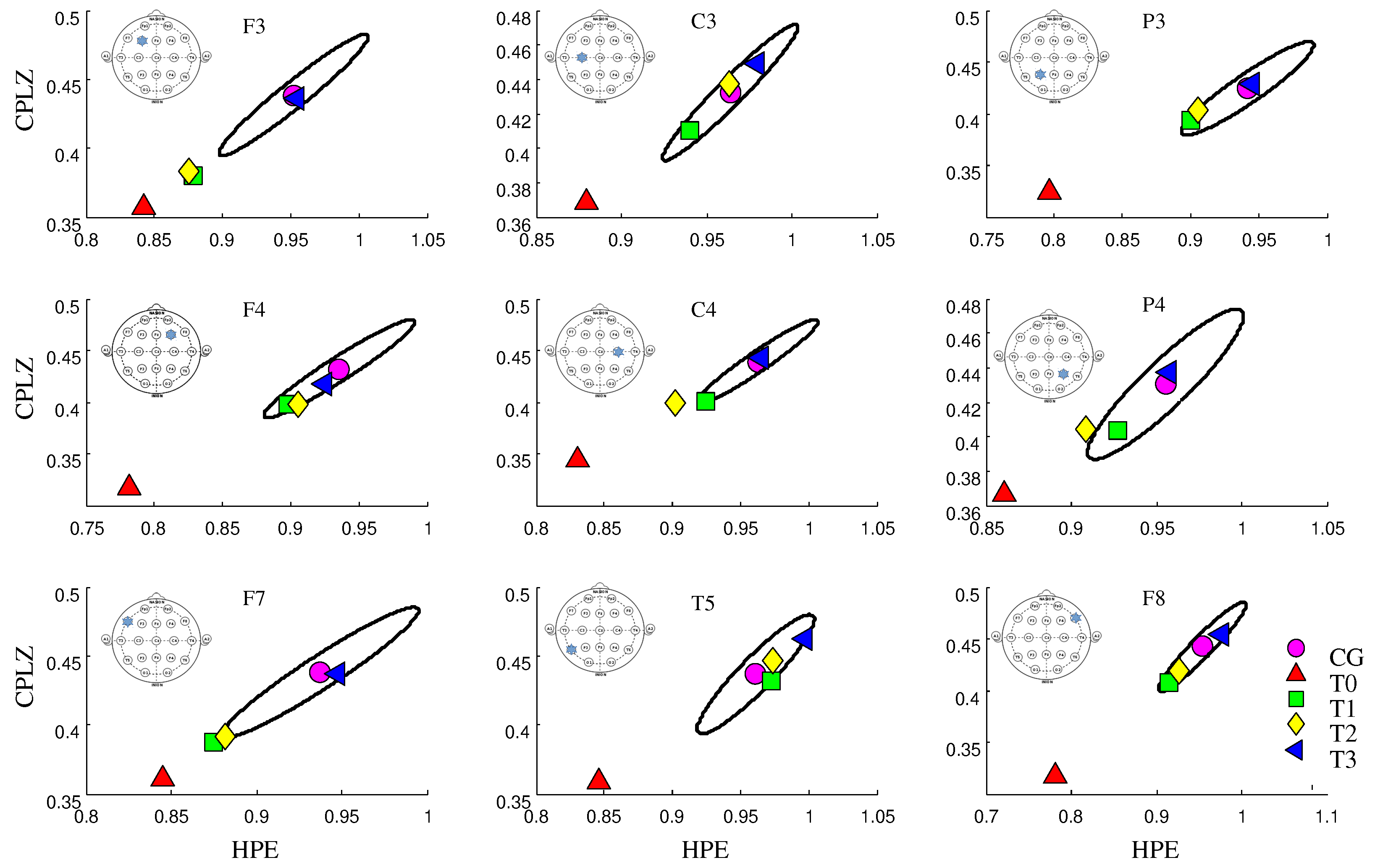
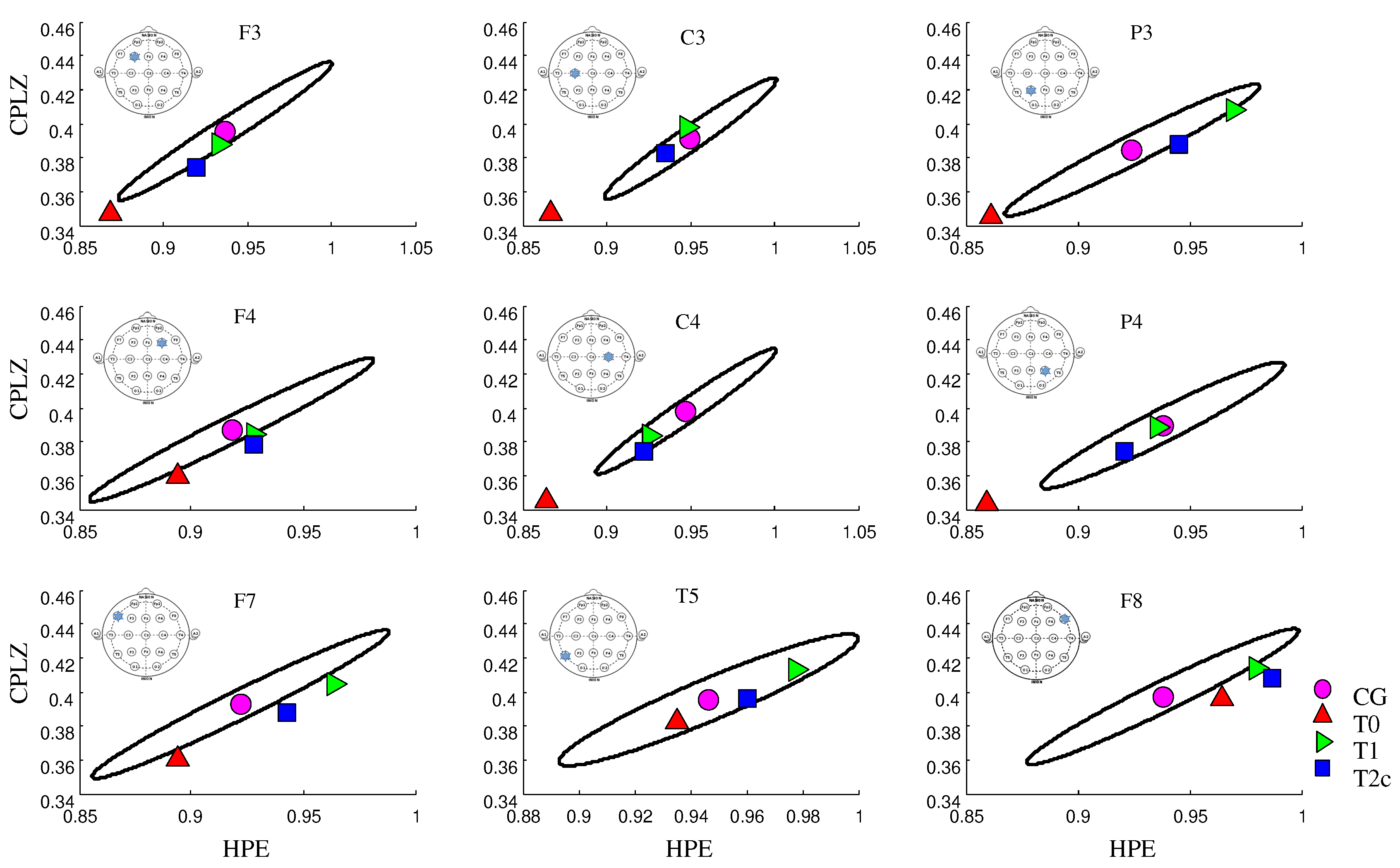
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Janáčková, S.; Boyd, S.; Yozawitz, E.; Tsuchida, T.; Lamblin, M.D.; Gueden, S.; Pressler, R. Electroencephalographic characteristics of epileptic seizures in preterm neonates. Clin. Neurophysiol. 2016, 127, 2721–2727. [Google Scholar] [CrossRef] [PubMed]
- Purdon, P.L.; Pierce, E.T.; Mukamel, E.A.; Prerau, M.J.; Walsh, J.L.; Wong, K.F.K.; Salazar-Gomez, A.F.; Harrell, P.G.; Sampson, A.L.; Cimenser, A.; et al. Electroencephalogram signatures of loss and recovery of consciousness from propofol. Proc. Natl. Acad. Sci. USA 2013, 110, E1142–E1151. [Google Scholar] [CrossRef] [PubMed]
- Olofsen, E.; Sleigh, J.; Dahan, A. Permutation entropy of the electroencephalogram: A measure of anaesthetic drug effect. Br. J. Anaesth. 2008, 101, 810–821. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zozor, S.; Mateos, D.; Lamberti, P.W. Mixing Bandt-Pompe and Lempel-Ziv approaches: Another way to analyze the complexity of continuous-states sequences. Eur. Phys. J. B 2014, 87, 107. [Google Scholar] [CrossRef]
- Jung, T.P.; Makeig, S.; Stensmo, M.; Sejnowski, T.J. Estimating alertness from the EEG power spectrum. IEEE Trans. Biomed. Eng. 1997, 44, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Adeli, H.; Zhou, Z.; Dadmehr, N. Analysis of EEG records in an epileptic patient using wavelet transform. J. Neurosci. Methods 2003, 123, 69–87. [Google Scholar] [CrossRef]
- Rosso, O.; Larrondo, H.; Martin, M.; Plastino, A.; Fuentes, M. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Rosso, O.A.; Craig, H.; Moscato, P. Shakespeare and other English Renaissance authors as characterized by Information Theory complexity quantifiers. Physica A 2009, 388, 916–926. [Google Scholar] [CrossRef]
- Montani, F.; Rosso, O.A. Entropy-Complexity Characterization of Brain Development in Chickens. Entropy 2014, 16, 4677–4692. [Google Scholar] [CrossRef]
- Mateos, D.M.; Zozor, S.; Olivarez, F. On the Analysis of Signals in a Permutation Lempel–Ziv Complexity-Permutation Shannon Entropy Plane. arXiv 2017, arXiv:1707.05164. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Thakor, N.V.; Zhu, Y.S.; Pan, K.Y. Ventricular Tachycardia and Fibrillation Detection by a Sequantial Hypothesis Testing Algorithm. IEEE Trans. Biomed. Eng. 1990, 37, 837–843. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.S.; Zhu, Y.S.; Thakor, N.V.; Wang, Z.Z. Detecting ventricular tachycardia and fibrillation by complexity measure. IEEE Trans. Biomed. Eng. 1999, 46, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, N.; Gangadhar, B.N. Estimating Regularity in Epileptic Seizure Time-Series Data—A Complexity-Measure Approach. IEEE Eng. Med. Biol. Mag. 1998, 17, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Hansel, G. Estimation of the entropy by the Lempel-Ziv method. In Lecture Notes in Computer Science (Electronic Dictionaries and Automata in Computational Linguistics); Springer: Berlin/Heidelberg, Germany, 1987; Volume 377, pp. 51–65. Available online: https://link.springer.com/chapter/10.1007/3-540-51465-1_4 (accessed on 13 October 2017).
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos 1996, 6, 414. [Google Scholar] [CrossRef] [PubMed]
- Amigo, J.; Kennel, M.B. Variance estimators for the Lempel-Ziv entropy rate estimator. Chaos 2006, 16. [Google Scholar] [CrossRef] [PubMed]
- Mateos, D.; Erra, R.G.; Wennberg, R.; Velazquez, J. Measures of Entropy and Complexity in Altered States of Consciousness. arXiv 2017, arXiv:1701.07061. [Google Scholar]
- Deuschl, G.; Eisen, A.; International Federation of Clinical Neurophysiology; International Federation of Societies for Electroencephalography and Clinical Neurophysiology. Recommendations for the Practice of Clinical Neurophysiology: Guidelines of the International Federation of Clinical Neurophysiology. 1999. Available online: http://www.clinph-journal.com/content/guidelinesIFCN (accessed on 13 October 2017).
- Popov, A.; Avilov, O.; Kanaykin, O. Permutation entropy of EEG signals for different sampling rate and time lag combinations. In Proceedings of the Signal Processing Symposium (SPS), Serock, Poland, 5–7 June 2013; pp. 1–4. [Google Scholar]
- De Micco, L.; Fernández, J.G.; Larrondo, H.A.; Plastino, A.; Rosso, O.A. Sampling period, statistical complexity, and chaotic attractors. Physica A 2012, 391, 2564–2575. [Google Scholar] [CrossRef]
- Mammone, N.; Duun-Henriksen, J.; Kjaer, T.W.; Morabito, F.C. Differentiating interictal and ictal states in childhood absence epilepsy through permutation Rényi entropy. Entropy 2015, 17, 4627–4643. [Google Scholar] [CrossRef]
- Taylor, I.; Marini, C.; Johnson, M.R.; Turner, S.; Berkovic, S.F.; Scheffer, I.E. Juvenile myoclonic epilepsy and idiopathic photosensitive occipital lobe epilepsy: Is there overlap? Brain 2004, 127, 1878–1886. [Google Scholar] [CrossRef] [PubMed]
- Kryger, M.; Roth, T.; Dement, W. Principles and Practice of Sleep Medicine; Elsevier: Amsterdam, The Netherlands, 2017; pp. 1592–1601. [Google Scholar]
- Goldman, L.; Bennett, J.C. Tratado De Medicina Interna; Macgraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Bandt, C. A New Kind of Permutation Entropy Used to Classify Sleep Stages from Invisible EEG Microstructure. Entropy 2017, 19, 197. [Google Scholar] [CrossRef]
| Subject | Time Record (MIN) | Segment Time Analyzed (MIN) | Gender | Age |
|---|---|---|---|---|
| 1 | 60 | 44 | M | 24 |
| 2 | 60 | 49 | M | 20 |
| 3 | 60 | 44 | M | 31 |
| 4 | 60 | 44 | M | 48 |
| 5 | 60 | 44 | M | 25 |
| 6 | 60 | 48 | M | 38 |
| 7 | 30 | 30 | F | 27 |
| 8 | 30 | 30 | F | 28 |
| 9 | 30 | 30 | M | 19 |
| 10 | 60 | 30 | F | 32 |
| 11 | 30 | 30 | F | 44 |
| 12 | 30 | 25 | F | 40 |
| 13 | 30 | 25 | F | 38 |
| 14 | 60 | 48 | M | 48 |
| 15 | 60 | 39 | M | 34 |
| 16 | 60 | 50 | M | 50 |
| 17 | 60 | 40 | M | 23 |
| 18 | 30 | 30 | M | 23 |
| 19 | 60 | 41 | M | 31 |
| 20 | 60 | 45 | F | 27 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaz, J.M.; Mateos, D.M.; Boyallian, C. Complexity-Entropy Maps as a Tool for the Characterization of the Clinical Electrophysiological Evolution of Patients under Pharmacological Treatment with Psychotropic Drugs. Entropy 2017, 19, 540. https://doi.org/10.3390/e19100540
Diaz JM, Mateos DM, Boyallian C. Complexity-Entropy Maps as a Tool for the Characterization of the Clinical Electrophysiological Evolution of Patients under Pharmacological Treatment with Psychotropic Drugs. Entropy. 2017; 19(10):540. https://doi.org/10.3390/e19100540
Chicago/Turabian StyleDiaz, Juan M., Diego M. Mateos, and Carina Boyallian. 2017. "Complexity-Entropy Maps as a Tool for the Characterization of the Clinical Electrophysiological Evolution of Patients under Pharmacological Treatment with Psychotropic Drugs" Entropy 19, no. 10: 540. https://doi.org/10.3390/e19100540
APA StyleDiaz, J. M., Mateos, D. M., & Boyallian, C. (2017). Complexity-Entropy Maps as a Tool for the Characterization of the Clinical Electrophysiological Evolution of Patients under Pharmacological Treatment with Psychotropic Drugs. Entropy, 19(10), 540. https://doi.org/10.3390/e19100540




