Abstract
In recent years, the interpretation of our observations of animal behaviour, in particular that of cetaceans, has captured a substantial amount of attention in the scientific community. The traditional view that supports a special intellectual status for this mammalian order has fallen under significant scrutiny, in large part due to problems of how to define and test the cognitive performance of animals. This paper presents evidence supporting complex cognition in cetaceans obtained using the recently developed intelligence and embodiment hypothesis. This hypothesis is based on evolutionary neuroscience and postulates the existence of a common information-processing principle associated with nervous systems that evolved naturally and serves as the foundation from which intelligence can emerge. This theoretical framework explaining animal intelligence in neural computational terms is supported using a new mathematical model. Two pathways leading to higher levels of intelligence in animals are identified, each reflecting a trade-off either in energetic requirements or the number of neurons used. A description of the evolutionary pathway that led to increased cognitive capacities in cetacean brains is detailed and evidence supporting complex cognition in cetaceans is presented. This paper also provides an interpretation of the adaptive function of cetacean neuronal traits.
1. Introduction
Cetaceans (whales, dolphins, and porpoises) are marine mammals that resulted from the re-adaptation to the aquatic environment by terrestrial species. This evolutionary process of re-adaptation was accompanied by extreme anatomical and physiological changes in the brain that resulted in the most successful mammalian colonization of the aquatic environment. Cetaceans possess not only extremely large and convoluted brains that set them apart from most other mammals but also many other neurological features, such as a high glia-to-neuron ratio, reduction of the olfactory system, or a cytoarchitectural organization of the cerebral cortex that does not resemble that of terrestrial mammals [1,2,3,4] Among the toothed whales (Odontocetes), one family, the Delphinidae or dolphins, evolved not only a relatively large size of the cortex but also a new and highly sophisticated sonar system for underwater orientation and navigation. For example, the encephalization quotient (a relative brain size measure) of the bottlenose dolphin (Tursiop truncatus) is greater compared to all non-human primates.In the Physeteridae (another toothed whale family), which comprises the sperm whale (Physeter macrocephalus), adult males can attain a brain mass of up to 9200 g [5]. Surprisingly, the absolute brain size of the biggest member of the family Delphinidae, that is, the killer whale (Orcinus orca), is more similar to that of the sperm whale than has previously been recognized [6], which leads to both of them being classed as the animals having the largest brains in absolute terms. Undoubtedly, cetacean’s brains harbor many mysteries, including why they evolved a cortex that is less highly laminated and in general much thinner than the neocortex of primates, the ability to sleep with one cerebral hemisphere at a time [7,8], or simply which evolutionary strategies were used to cope with the network scaling costs of an increased brain size. The current understanding of how brain anatomy and physiology relate to animal behavior is still so incomplete that in spite of the fact that several hypotheses have been proposed for most of the neuronal traits [7,9,10,11,12], it is difficult to comprehend what their adaptive function might have been [13]. Thus, the interpretation of the evolutionary and functional significance of such specializations has long been a challenge to neurobiologists. For example, the development of this high encephalization level of dolphins and other toothed whales has been correlated with social competition [14], water temperature during the Eocene-Oligocene transition period [2], enhanced auditory processing [15,16], and audiomotor navigation [17].
Perhaps the largest challenge is to determine how these various specializations of the cetacean brain relate to intelligence. The large size of the cetacean brain and their reported behaviors have been popularly accepted as being indicative of high levels of intelligence. However, from the scientific community’s viewpoint, the interpretation of behavioral observations in cetaceans and especially whether there is real support (or not) for a special intellectual status for this mammalian order has generated a substantial amount of controversy [2,18,19,20,21,22,23].
Historically, humans have tended to undervalue the cognitive capacities of animals (e.g., their exceptional sensory skills), over-evaluating at the same time our problem-solving ability, our capacity to modify our environment, and our ability to communicate with one another. For example, the notion that only humans can remember specific episodes of their life or the image of man as the only toolmaker were destroyed by the findings that some crows and chimpanzees also use and manufacture tools, and more recently, other species such as elephants or cetaceans have been found to do so [24,25]. Thus, ideas about what marks the boundary between human and nonhuman intelligence have undergone repeated revision. Certainly, the accurate assessment of animal intelligence requires evaluating cognitive functioning against simpler accounts and, at the same time, requires determining the conditions that maximally elicit the animal’s cognitive capacity [26], for example, most reptiles, perform much better in learning tasks if they are given warmth, rather than food, as a reward. Similarly, chimpanzees are better at learning human sign language than spoken language partly because they naturally use their hands to gesture and also because their vocal tract does not allow them to produce well-formed speech sounds [13]. These goals are especially important in the case of cetaceans not only because of the clearly perceptible logistical difficulties of studying them but also because there is a compelling need to relate these supposed differences in animal intelligence to brain properties and to understand them in neural-computational terms [27].
In this paper, attention is placed on presenting an analysis of the cognitive capacities of cetaceans from the perspective of the intelligence and embodiment hypothesis [28]. In doing so, the goal is to reveal further insights that are of relevance to the current debate on cetacean intelligence. The hypothesis postulates the existence of a common information-processing principle that is being exploited in naturally evolved nervous systems, and that this serves as the founding pillar of intelligence. A mathematical model that is suited for making quantitative predictions about the cognitive capacities of species for comparative purposes is also provided. As the order Cetacea is a very diverse group [29], and due to the aforementioned reasons, little is currently known about the intelligence of most cetaceans [30]; hence, it is important to emphasize that the focus of the present study is primarily on large-brained cetacean species and/or those species with brains of comparable size to terrestrial species on which there are sufficient neurophysiological statistics and also documented behavioural evidence of their overall cognitive sophistication. Furthermore, the principal conclusions derived from this study must be interpreted according to the premises of the scientific method, that is, as predictions resulting from the extension of the mathematical model and a hypothesis that must subsequently be verified or refuted by future studies.
2. Materials and Methods
2.1. Hypothesis Background
The intelligence and embodiment hypothesis [28] subscribes to the idea of cognition as an evolutionary adaptational redeployment of movement control [31]. This term is used to express, from an evolutionary perspective the idea that the extensive neuronal machinery developed to control animal movement was expanded to control new brain structures instead of muscles (Figure 1). Specifically, discrete bodies of neuronal tissue specifically evolved to exploit the pre-existing neuronal muscle-control mechanism but instead of conferring motility, these new brain structures would carry out a type of information processing that is currently denoted as cognition. This information-processing principle common to the nervous systems that evolved in nature is postulated to be the basis for the emergence of intelligence. Furthermore, the hypothesis associates this information-processing principle to the cortex and its homologues (i.e., functionally similar cerebral structures in other species), in other words, the neurobiological structures that emerged as a result of the aforementioned evolutionary adaptational redeployment of movement control. Particularly, in the insect’s brain the mushroom body (a sensory associative brain center) is the homologue structure of the cerebral cortex in mammals [32]. The amphibian dorsal pallium is the most likely homologue of the mammalian cortex and is a bi-laminar structure. Similarly, in bird and reptile brains, the dorsal ventricular ridge is a cerebral structure with gross differences in morphology (i.e., forming nuclei instead of layers) compared to the mammalian cortex but fullfilling similar functions [13,33,34].
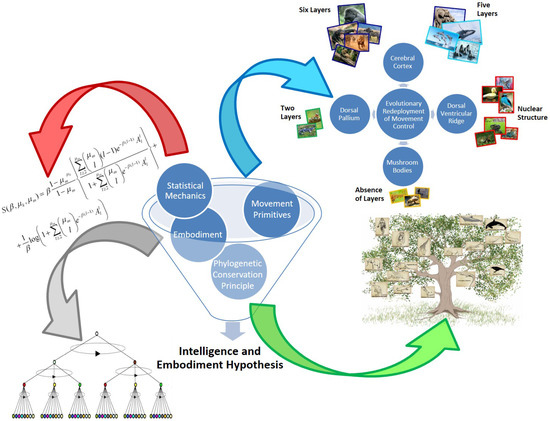
Figure 1.
Graphical synthesis of the essential components of the Intelligence and embodiment hypothesis [28]. This hypothesis postulates the existence of a common information-processing principle being exploited by the nervous systems that evolved from nature as the basis for the emergence of intelligence. The hypothesis subscribes to the idea of cognition as an evolutionary adaptational redeployment of movement control [31]. Specifically, discrete bodies of neuronal tissue specifically evolved to exploit the pre-existing neuronal muscle-control mechanism but instead of conferring motility, these new brain structures would carry out a type of information processing that is currently denoted as cognition. This information-processing principle common to the nervous systems that evolved in nature is postulated to be the basis for the emergence of intelligence. Furthermore, the hypothesis associates this information-processing principle to the cerebral cortex and its homologues (i.e., functionally similar cerebral structures in other species). A cognitive architecture is defined to capture the aforementioned principles, and also the structural (e.g., physiologic) and functional (e.g., dynamic) characteristics of these cerebral structures with a certain level of abstraction. The cognitive architecture consists of a hierarchical symbol-based architecture of varying size and complexity, where the symbols act as the embodiment of brain representations. These hierarchical symbol-based structures are used to model the fact that progressive functional abstraction over network depth is a fundamental feature of brains [35,36,37]. Brain representations are assumed to be physically encoded by neuron assemblies [38]. The interactions between symbols in the cognitive architecture are grounded in the concept of movement primitives. This qualifier is used to emphasize the fact that is inherited from primitive animals as a result of the phylogenetic conservation principle. This computational mechanism models the evolutionary adaptational redeployment of movement control. Furthermore, these movement primitives are postulated as the underlying substrate that is common to any cognitive function. The hypothesis is accompanied with a mathematical model grounded in statistical mechanics that is used to analyze the information-processing capacities of the described architecture. In summary, the hypothesis provides some answers to the efficiency of the brain’s computations and to the quantitative discontinuities in the cognitive capacities across species, simultaneously explaining the similarities in the intelligence levels that are observed.
From a computational point of view the hypothesis describes this information-processing principle in terms of combinatorial operations that are carried out over brain representations. This computational mechanism is denoted as movement primitives to emphasize the fact that is inherited from primitive animals as a result of the phylogenetic conservation principle. These movement primitives are postulated as the underlying substrate that is common to any cognitive function. They are proposed to put forward for consideration the idea of an information-processing mechanism that is designed to combine sensorimotor representations into rule-conforming higher-order brain representations. Such high-order or more complex representations are postulated to be the basis for context-independent representations in a hierarchically organized information-processing system.
A cognitive architecture is defined to capture the aforementioned principles, and also some aspects of the structural (e.g., physiologic) and functional (e.g., dynamic) characteristics of these cerebral structures with a certain level of abstraction. The cognitive architecture consists of a hierarchical symbol-based architecture of varying size and complexity to account for certain neurobiological differences between species, where the symbols act as the embodiment of brain representations. These hierarchical symbol-based structures are used to account for certain neurobiological differences between species, and especially to model the fact that progressive functional abstraction over network depth is a fundamental feature of brains [35]. Specifically, in spite of the fact that recurrent connectivity is a fundamental feature of brain’s structural networks, cortical functional networks display a global hierarchical organization. In other words, information representation in the brain demonstrates a hierarchical structure [35,36,37]. Brain representations are assumed to be physically encoded by neuron assemblies (i.e., as states of attractor networks). In other words, a piece of information is represented as the simultaneous activity of a group of neurons [38]. It is important to note that nervous systems are physical devices that are configured in such a way that their states represent the external world, the body and, in some instances, parts of the nervous system itself, but the whole concept is that their physical state transitions execute computations [39]. Furthermore, the interactions between symbols in the cognitive architecture are grounded in the concept of movement primitives. Specifically, they are modeled in terms of permutations operations between symbols.
Moreover, the hypothesis is accompanied with a mathematical model that is used to analyze the information-processing capacities of the described architecture with the overall goal of checking whether an animal’s intelligence can be explained as an emergent phenomenon that results from the interaction of a large number of brain representations (i.e., neuron assemblies) grounded on the hypothesized principles. In other words, how neurobiological differences in the cerebral structures that appeared as a result of the evolutionary redeployment of movement control might explain differences in the cognitive capacities across species. The main innovative contribution of the mathematical model is the analysis of a cognitive architecture in terms of its free energy and entropy using a statistical mechanics formulation. In summary, although the hypothesis is not intended to fully explain cognition, it provides some answers with regards to the efficiency of the brain’s computations and to the quantitative discontinuities in the cognitive capacities across species, simultaneously explaining the similarities in the intelligence levels that are observed.
2.2. Statistical Mechanics
The aim of this discipline of theoretical Physics [40,41] is to bridge the gap between the microscopic and macroscopic worlds [42]. Its first step consists in stating hypotheses about the microscopic behavior of the constituents (e.g., atoms, molecules, particles, or neuron assemblies in the present study) of a macroscopic system. The objective is then the prediction of macroscopic properties, which can be measured in experiments. Furthermore, the quantities which are of interest in statistical mechanics are the averaged values of the observables. The macroscopic system under study in this case is the brain, specifically the cerebral cortex and its homologues, and the macroscopic property under study is intelligence. Exactly, intelligence is interpreted as an emergent phenomenon that results from the microscopic interactions of millions of neurons (i.e., neuron assemblies) grounded in the concept of movement primitives. Furthermore, neurons are considered information-processing elements that receive, process, store, and communicate information to other neurons being this fact independent of its morphology. Entropy is used as an approximative measure of intelligence. This concept was originally developed by physicists in the context of equilibrium thermodynamics and later introduced into information theory. There are two distinct but related interpretations of entropy the first based on information content (Information Theory) and the second based on degree of disorder (Thermodynamics), here the former is used. Intuitively, as higher is the information-content of the cerebral structures modeled as higher will be the degree of intelligence that can be associated to them. The free energy is used as an approximate measure of energetic requirements (i.e., metabolic costs) incurred by cognitive operations in the aforementioned structures due to its relationship with the work theorem in Physics.
2.3. The Principal Actor of Energy Consumption in the Brain
Previous studies focused on the metabolic budget of the brain had overestimated the energy cost of action potentials in mammalian neurons. Action potentials within mammalian neurons are more energetically efficient than previously assumed. A recent work [43] updates those previous estimations of energy use associated with neural computation in the cerebral cortex and cerebellum demonstrating that the principal actor of energy consumption in the brain is synaptic transmission. Therefore, neural connectivity can be assumed as the principal factor considered in the energetic requirements of the cerebral cortex and its homologues given that the higher the number of synapses contained in those cerebral structures the higher the associated metabolic costs will be. Furthermore, a higher number of synapses (in absolute terms) may be the result of a higher number of synapses per neuron, a larger number of neurons, or a combination of those two facts.
2.4. Neurophysiologic Indicators of Neural Connectivity
The qualifier connectivity between brain representations used by the model must be interpreted as mainly involving both the neurophysiologic concept of local and non-local connectivity. Local connectivity is related to the connectivity between neighbouring neurons encoding and processing similar representations and is provided by axon collaterals of neurons. Non-local connectivity, consists of the main axon and its ramifications (axonal branches) to more remote neurons, and involves representations created from associative links between distant groups of neurons encoding different pieces of information (e.g., information coming from different sensory modalities). However, it is important to note that the total number of synapses that are present in the cerebral cortex and its homologues constitutes the primarily physiological indicator of neural connectivity. A higher number of synapses (in absolute terms) in these structures may be the result of a higher number of synapses per neuron, a larger number of neurons, or a combination of both. The cortex of mammals ranges from millions to billions of neurons, whereas the number of synapses per neuron ranges from hundreds to thousands [44,45,46,47,48]. Thus, it can be reasonably assumed that the strongest contribution in the resulting product is predominantly due to the total amount of neurons.
Moreover, it is important to emphasize that the ability to perform associations constitutes an important resource for intelligent behavior. Accordingly, higher levels of connectivity are also expected to correlate with increased ratios of cortical white matter over gray matter because, as stated before, most of the white matter fibers are used to create associative links between different cortical regions [49]. The gyrification index is a quantitative calculation of the degree of folding of the cerebral cortex. This parameter is strongly linked to the properties of the white matter (e.g., strongly connected cortical regions tend to face one another within gyri [12,50]). More highly folded cortices are those that have more neurons connected through the white matter [51]. Thus, gyrification index can also be considered as an indicator of neural connectivity. Finally, higher ratios of glial cells to neurons are also expected to correlate with higher levels of neural connectivity. The ratio of glial cells to neurons does not increase with the brain size, but instead increases with decreasing neuronal density [12]. Taking into consideration that neuronal density correlates with the inverse of neuronal size [52] (measured in terms of the soma size, dendritic and axonal arborizations volume), it can be deduced that glia–neuron ratio correlates with the size of the dendritic arborizations and length of axons since the size of individual cell bodies changes relatively little (compared to the changes in the volume of arborizations) as brain size goes up [13]. Further arguments under this view come from past studies that suggested that the interspecific variation in the neocortical glia–neuron ratio correlated with the size of the dendritic tree and the length of the axons because the increased scale of these structures would require a larger number of astrocytes (i.e., one of the major glial cells) to regulate the glucose uptake and more oligodendrocytes (i.e., another type of glial cell) to actively synthesize the myelin for long-range projecting axons fibers [53].
2.5. An Extension of the Mathematical Model of the Hypothesis
The cognitive architecture [28] models with a certain level of abstraction the patterns of functional connectivity that are observed between regions of the cerebral cortex and its homologues. It is important to emphasize that the constraints imposed by the structural connectivity in the functional interactions cause that the topological parameters are generally conserved between structural and functional networks [54]. These patterns of functional connectivity are characterized by displaying a certain degree of randomness. This peculiarity is modelled by the randomness associated to the symbolic structures, i.e., the connectivity between symbols and the number of information processing levels are random variables. Thus, the size and complexity of the cerebral structures that are modelled is abstractly represented in terms of the number of symbols and their connectivity through the hierarchical symbolic structures defined by the cognitive architecture.
Taking into consideration that a larger number of neurons correlates with a larger number of brain representations (i.e., more neurons provide more resources to store more information), and also that a higher connectivity between brain representations correlates, from the physiological point of view, with a higher number of synapses, and thus with a higher neural connectivity, it can be deduced that the number of symbols provides a reasonable estimate of the descriptive power of a symbolic structure and therefore of the underlying cognitive power of the cerebral structures that are modelled. It is important to emphasize again that symbols act as embodiments of brain representations, and brain representations correspond to the simultaneously activity of a group of neurons (i.e., the states of attractor networks).
In the following, the focus is put on the calculation of a mathematical expression for the number of symbols implemented by the symbolic structures (in terms of its structural parameters) under the assumption that the content of higher-order symbols (i.e., symbols close to the root node of the symbolic structures) is built from lower-order symbols (i.e., symbols belonging to lower information-processing levels). It is important to note that the content of higher-order brain representations (i.e., semantic representations) includes sensorimotor representations [55,56,57]. In other words, sensory and motor information is activated whenever a higher-order brain representation (e.g., a semantic representation) is accessed since the content of higher-order representations includes perception and action information representations (i.e., lower-order representations).
Without a loss of generality let us suppose a tree-like structure (see Figure 2). The structure is composed of k levels where the branching factor associated to each level is indicated by the variable where . The circular arrows represent the combinatorial operations that model how brain representations (i.e., symbols in the cognitive architecture) are combined according to the hypothesis. More specifically, the circular arrows represent permutations operations carried out over the nodes of the structure. Furthermore, each of the circular arrows is affecting the corresponding set of nodes involved in the combinatorial operations. The goal here is to calculate as a function of the parameters k (levels of the structure) and the branching factors where , the number of possible symbol configurations that can be attained by a structure of this kind as a result of the combinatorial operations described before. To this end, the calculation is done iteratively expressing at each iteration step the calculation recursively in terms of the calculation carried out in the previous step. More specifically, the calculation starts with a structure containing just the root node, and thereby only one possible configuration (iteration ), afterwards a structure with the root node plus nodes (i.e., a structure with just one level and with a branching factor equal to ) leading to a number of configurations equal to (iteration ), and so forth:
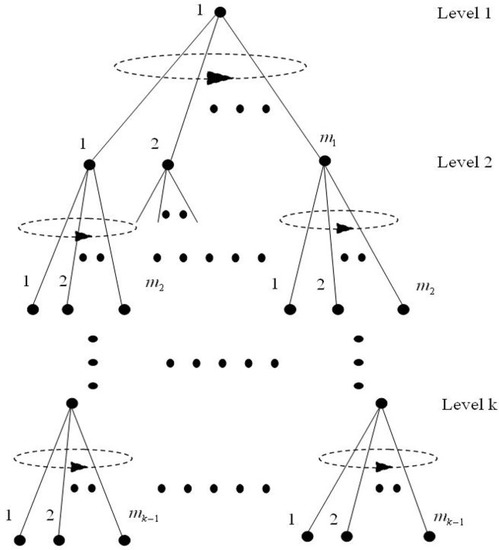
Figure 2.
General example of the Cayley-like structures used by the cognitive architecture of the intelligence and embodiment hypothesis [28]. It is important to remember that the branching factor associated to each level is fixed for all the nodes belonging to that level and represented by the variables where , for instance, the branching factor of level 1 is represented by the variable , the branching factor associated to the second level of the structure by and so forth. The circular arrows are used to represent the combinatorial operations described in the model.
Thus, for a generic structure of depth equal to k and branching factors the number of possible configurations reads:
The variables correspond to the branching factor associated to level i (see Figure 2), where . As can be deduced, the function that expresses the number of possible configurations in terms of the structural parameters k (depth of the structures) and (branching factors). The randomness associated to the branching factors and the depth of the structures is encapsulated in two random variables m and k respectively. Thus, and the function expressing the number of configurations becomes a random function that reads:
The random function provides the number of configurations that can be supported by any instance of the cognitive architecture, which is expressed in terms of the Euler gamma function . To extract the typical behavior of the system, i.e., the average number of symbols implemented by the cognitive architecture, the expectation of this random function, i.e., quenched averages in statistical mechanics terminology, must be calculated:
In expression (4) the operator is used to express the expectation of the random function. The function is representing the joint probability distribution of the random variables k (information-processing levels) and m (connectivity between brain representations). It is assumed that the random variables m and k are independent. Furthermore, limit Gaussian probability distributions are assumed for and respectively. Specifically, Dirac delta functions are used simulating the concentration of the probability mass around the mean of the Gaussian distribution. These assumptions permit to capture the essence of the processes being modeled allowing at the same time a considerable simplification of the calculation:
Thus, the expectation of the random function finally reads:
In order to justify this approximation, it is important to note that the random variable k modelled the depth of the structures (i.e., the number of information processing levels) that correlate to the number of physical laminae (i.e., layers, and/or nuclei) associated to the cerebral structures postulated by the hypothesis. This value is practically constant for each species. For example, in terrestrial mammals, the cerebral cortex is typically a six-layered structure, although in certain regions it is difficult to appreciate the characteristics of this layered pattern, or it is poorly developed [48,58,59]. Moreover, the typical laminar organisation of the mammalian cortex (or the dorsal pallium in amphibians) is not as obvious in bird or reptile DVR since it is mainly a nuclear structure (i.e., large clusters of very densely packed neurons), although these nuclear clusters of neurons are homologous to lamina-specific populations of the mammalian cerebral cortex [33,34,36,60]. Furthermore, the characteristic laminar organisation that is seen in the cerebral cortex of mammals is also observed in the DVR’s principal sensory zones [13,61]. Pigeons, for instance, have at least six distinct visual areas within their DVR, whereas turtles and lizards only possess between one and three [62,63,64]. In other words, the avian DVR contains more subdivisions than the DVR of reptiles. Many of these DVR subdivisions (i.e., clusters) are arranged like the layers of an onion, or geological strata, and connected by relatively short axons that course at right angles to those laminae [13]. According to the hypothesis [28], the number of clusters of densely packed neurons (or nuclei) correlates to the depth of the information-processing hierarchy.
Similarly, to justify the use of a limit Gaussian probability distribution with respect to the random variable m (i.e., connectivity between brain representations) studies concerning the functional networks of the brain carried out in humans as well as in other mammalian species [54] revealed the following conclusions:
- These studies demonstrated that the pattern of functional connectivity between cortical areas was consistent with a small-world network architecture. This is of particular interest since this architecture is mainly characterized by being modular and hierarchical. Furthermore, these studies also revealed that as a result of the constraints imposed by the structural connectivity in the functional interactions, the topological parameters are generally conserved between structural and functional networks.
- The patterns of functional connectivity between cortical regions undergo spontaneous fluctuations and are highly responsive to perturbations (i.e., sensory input or cognitive tasks) on a timescale of hundreds of milliseconds. However, these rapid reconfigurations do not affect the stability of global topological characteristics. In other words, on longer timescales of seconds to minutes (i.e., in equilibrium from a statistical mechanics point of view), correlations between spontaneous fluctuations in brain activity form functional networks that are particularly robust.
Physical Interpretation of Equation
The principal characteristic of the function is that it is a monotonically increasing function. Thus, for any two arbitrary points in the averaged variable (i.e., average number of information-processing levels), for example and such as , the expression holds for all values of (i.e., the average connectivity between brain representations). Similarly, choosing two arbitrary points in the averaged variable , for example, and such as , then for all values of . In turn, combining the joint graph of entropy and free energy of Figure 3 with the properties of the function the following statements can be inferred:
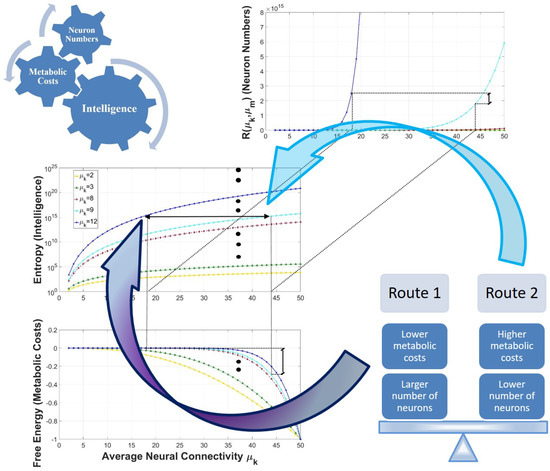
Figure 3.
Graphical illustration of the study’s results. The top-left figure shows that higher levels of intelligence require more neurons in the cerebral cortex and its homologues, but also lead to unavoidable growth of the energetic requirements. The figure on the right shows two routes to attain higher levels of intelligence, each of them reflecting a trade-off between energetic requirements and the number of neurons used. Animal intelligence is explained by increased neural connectivity, a deeper information-processing hierarchy, or a combination of these in the cerebral structures postulated by the hypothesis as responsible of intelligence.
- If the average connectivity between symbols is fixed to any given value, for example, then increasing the average number of information processing levels from to not only increases the average number of symbols encoded, i.e., , but also the associated entropy values . It is important to remember that if the connectivity is fixed, then the differences in the information-content in the structures varies exponentially when different numbers of information-processing levels are considered [28].
- Similarly, if the average number of information processing levels is fixed to , then if the average connectivity is increased, for example, from to , then the average number of symbols encoded and the associated entropy values also increases, i.e., and . However, in this case the values of the free energy (in absolute value) are also higher (i.e., ).
- Higher entropy values are always linked to structures encoding a higher number of symbols independently of the parameterization of and . For example, if then . Similarly, if then .
- For all , if the average connectivity is fixed to any particular value, for example, , there always exists a value for the average connectivity , such as the values that are reached by the entropy function in these points, i.e., and respectively, that is identical (or very close because the entropy is an integer function), i.e., , then the following inequalities hold: and . In other words, the average number of representations is higher for the point in the space of parameters with the highest number of information-processing levels, i.e., ) in this case, but at the same time the values of the free energy are lower compared to the point in the space of parameters with a lower number of information-processing levels but a higher average connectivity, i.e., ).
To interpret these mathematical properties, it is important to emphasize that a concrete parameterization of the average connectivity and the average number of information processing levels mapped to the graphs of entropy and free energy of Figure 3 quantitatively represents the average information content and associated metabolic costs, respectively, that are incurred by the cognitive operations that take place in the cerebral cortex or in its homologues.
The first statement suggests that for similar values of the average neural connectivity, those cerebral structures possessing a deeper information-processing hierarchy have the potential to encode a higher number of brain representations (e.g., for any value of such as, ). Similarly, with respect to the second statement, considering cerebral structures with an identical number of information-processing levels, encoding a higher number of brain representations is also possible for those structures possessing a higher neural connectivity but at the cost of supporting increased metabolic costs. In both cases, encoding a higher number of brain representations is not possible without increasing the number of neurons recruited to encode such representations, which requires cerebral structures with a larger number of neurons and thereby with an implicit increase on the associated metabolic costs. The third statement suggests that higher levels of intelligence are associated to those cerebral structures encoding a higher number of brain representations. In other words, the number of neurons in the cerebral structures defined by the hypothesis correlates with the expected levels of intelligence (e.g., a larger range and versatility of behaviours and cognitive abilities). This result seems to corroborate the general assumption in neuroscience that associates brains possessing a larger number of neurons with better cognitive functioning and/or behavioural flexibility of some kind (i.e., higher levels of intelligence).
However, this preliminary conclusion must be analyzed with a greater detail in light of the fact that is strongly linked to the implications derived from the interpretation of the fourth statement. More specifically, the last statement suggests the existence of two pathways to reach similar levels of intelligence, the first possibility (implicitly evidenced in the first statement) requires a larger number of neurons because it involves cerebral structures with a higher number of information-processing levels but at relatively lower metabolic costs when compared to the second possibility (remember that but ). In contrast, the second possibility (evidenced in the second statement), needs an increased average neural connectivity in the cerebral structures that are studied but requires a fewer number of neurons when compared to the first possibility (remember that but , where and ), although at the cost of a substantial increase in the associated metabolic costs when compared to the first possibility.
Of particular interest is the fact that the number of neurons needed implicitly increase when considering higher values of the average neural connectivity, cerebral structures with a deeper information-processing hierarchy or a combination of those two facts. This is due to the procedure that is used to encode brain representations according to the hypothesis (based on the concept of movement primitives). For example, when increasing the connectivity between representations at any generic level of the hierarchy, the number of possibilities (i.e., the number of combinations) to generate higher-order representations at the upper levels of the hierarchy automatically increase and thus, the number of neurons required for their codification. In turn, this explanation also arises for the other possibility offered by the model, because to the extent the depth of the hierarchy increases (i.e., the successive stages of information processing), the amount of higher-order representations also increases and therefore the number of neurons needed to encode such representations.
In summary, the theoretical evidence presented before put forward not only the importance of the absolute number of neurons in the cerebral structures postulated by the hypothesis as a proxy for intelligence but especially the primary role of neural connectivity with regards to intelligence and cognitive capacities in general.
3. Results
3.1. An Equation Relating Intelligence, Energetic Requirements, and Neuron Numbers
The most important aspects of the intelligence and embodiment hypothesis (see Section 2.1) are synthesized in a space of cognitive architecture complexity that is defined by the average number of information-processing levels () and the average connectivity between symbols (), where symbols act as embodiments of brain representations. Brain representations are assumed to be physically the states of attractor networks. In other words, a piece of information is represented as the simultaneous activity of a group of neurons. The average number of information processing levels is hypothesized to be a function of the density of neurons and the number of physical laminae (i.e., layers, and/or nuclei) that are present in the cerebral structures postulated by the hypothesis as mainly responsible of intelligence in macroscopic moving animals. The main innovative contribution of the mathematical model of the hypothesis is the analysis of the cognitive architecture in terms of its free energy and entropy, macroscopic magnitudes that are derived using a statistical mechanics formulation. The expectation of the entropy is used as an approximated measure to the concept of intelligence, whereas the expectation of the free energy is used to analyze the computational properties that emerge at a macroscopic scale as a result of the defined interactions between brain representations, providing, at the same time, a quantitative measure of the metabolic costs incurred by cognitive operations in the cerebral structures studied. Both functions are expressed in terms of the parameters of the model, i.e., the variables , and .
Equation (7) (see also Section 2.5) provides an estimation of the average number of brain representations that are used by the cognitive operations that take place in the cerebral cortex and its homologues. This equation is obtained under the assumption that sensory and motor systems are directly modulated by higher-order processing [55,56,57]. In other words, sensory and motor information is activated whenever a higher-order brain representation (e.g., a semantic representation) is accessed since the content of higher-order representations includes perception and action information representations (i.e., lower-order representations).
Taking into consideration the fact that brain representations are assumed to be physically encoded by neuron assemblies (i.e., as states of attractor networks), Equation (7) provides a quantitative estimation on the number of neurons used. Thus, using a concrete parameterization of the averaged variables , and the equation allows to associate any value of the entropy (i.e., intelligence) and free energy (i.e., metabolic costs) functions with the expected number of brain representations (i.e., neuron numbers) needed to reach those points (see Figure 3 and also the supporting information in the suplement). In other words, it permits quantitatively to relate intelligence, brain energetic requirements, and neuron numbers.
3.2. The Limiting Factors of Intelligence: Neuron Numbers and Energetic Requirements
Higher levels of intelligence are explained as a result of an increased connectivity between brain representations, a deeper information processing hierarchy, or a combination of those two facts. In any of those cases, increasing the intelligence levels is always accompanied by an increase in the number of brain representations but also in the associated metabolic costs (i.e., higher levels of intelligence always require higher energetic requirements). Thus, higher levels of intelligence cannot be achieved without implicitly increasing the absolute number of neurons in the cerebral cortex and its homologues. Correspondingly, higher levels of intelligence are not possible without the existence of higher metabolic costs in the cerebral cortex and its homologues (Figure 3). This result provides a theoretical justification to the general assumption in neuroscience that associates brains possessing a larger number of neurons with better cognitive functioning and/or behavioral flexibility. In addition, it supports the belief that brain size cannot be increased indefinitely due to metabolic considerations. For example, from an evolutionary neuroscience perspective several studies have correlated increases in relative brain size with changes in diet, size of other organs, or neural rate of energy consumption to make those large brains possible [9,13,65].
This result appears also to corroborate previously formulated hypotheses from studies of social intelligence [66]. Particularly, they had hypothesized that within a given taxonomic group, larger animals always have larger brains and that these additional neurons may well provide more computing power. This argument follows even if one accepts the argument that larger bodies require more neurons to control them, since the number of neurons not dedicated to muscular control or sensory processing is almost certainly larger in larger brains and these extra neurons may permit more complex computations [13]. As a matter of fact, the largest species of ants, bees, and wasps tend to have the most complex social instincts; rats (Rattus norvegicus) tend to perform better than mice (Mus musculus) in learning tasks, i.e., 15 million cortical neurons against 4 million cortical neurons; ravens (Corvus corax) learn better than small corvids like jackdaws (Corvus monedula), i.e., 1204 million of pallium neurons against 492 millions; and large parrots seem smarter than parakeets, e.g., 850 million of pallium neurons in the grey parrot (Psittacula erithacus) against 575 millions pallium neurons in the alexandrine parakeet (Psittacula eupatria) [13,67].
It is important to remark that the adult vertebrate brain is divisible into telencephalon, diencephalon, mesencepahlon, and rhombencephalon, where the telencephalon and diencephalon are collectively referred as the forebrain. The qualifier pallium is used in anatomy to denote the most dorsal part of the telencephalon which in birds includes the DVR as well as other cerebral structures (e.g., the hyperpallium or wulst). Similarly, in mammals the pallium includes the cerebral cortex, and other cerebral structures like the claustrum or the hippocampal formation just to mention a few [13].
3.3. Two Routes for the Attainment of Higher Levels of Intelligence
The interpretation of the mathematical model (see Section 2.5) implies the existence of two pathways to reach similar levels of intelligence, each of them showing the existence of a trade-off between the energetic requirements and the number of neurons used (Figure 3). Specifically, the first pathway (Route 1) of considering cerebral structures with a deeper information-processing hierarchy achieves higher levels of intelligence at relatively lower metabolic costs but at the price of requiring a larger number of neurons when compared to the second possibility. In contrast, the second pathway (Route 2) characterized by the existence of cerebral structures with higher levels of neural connectivity requires fewer neurons compared to the former but at the cost of a substantial increase in the associated metabolic costs. From a physiologic point of view both routes are linked to an increase in encephalization since they implicitly require an increase in neuron numbers and/or neural connectivity, thus leading to an overall increase in the volume of gray matter (i.e., the neuronal cell bodies, their dendrites and the local ramification of axons plus glial cells and blood vessels) and/or an increase in the volume of white matter (i.e., mostly the bundles of axons that run a long distance).
The existence of a trade-off between energetic requirements and the number of neurons used in given pathways, seen as an increase in cognitive capacities following the natural evolution of brains, might help to explain the evolutionary changes in both brain region size and structure occurring across vertebrate species. Clearly, brain region size and structure can differ in a variety of ways, and different types of changes have different consequences for brain function [13]. Furthermore, changes in brain region size and/or structure are implicitly linked to changes in overall brain size. In particular, it is plausible to hypothesize that the observed differences (or non-uniformity) in the cytoarchitecture of the mammalian cerebral cortex—demonstrating modifications linked to the evolution of this cerebral structure (e.g., changes in size and/or structure)—are driven by the interplay between these two pathways. For example, the area considered unique to the primate brain, albeit controversial, is the prefrontal cortex which lies rostral to the premotor cortex.
Non-primate mammals do have a prefrontal cortex, but it consists of only two major regions rather than the three found in primates [13]. The two prefrontal regions shared with primates are firstly, the orbital prefrontal region and second, the anterior cingulate cortex. The third prefrontal region that is unique to primates is the lateral (or granular) prefrontal cortex. This region consists of an additional granular layer connected to part of the prefrontal cortex [13]. This add-on suggests an increase in the number of information-processing levels of the brain according to the theoretical model (i.e., the first route) with the resulting entropy increase. What is more, the small-celled granular layer that characterises the lateral prefrontal cortex in primates is missing in most other mammals [13]. This fact is of particular interest because there is ample behavioural evidence documenting overall cognitive sophistication in primates.
In addition, the prefrontal cortex is an area of upmost importance for human evolution because it mediates complex behaviours such as planning, working memory, memory for serial order and temporal information, aspects of language, and social information processing [68], thus making it the principal actor behind human intelligence. The human prefrontal cortex is approximately twice as large as predicted on the basis of the size of the rest of the brain. It averages approximately 12.7% of total brain volume, compared with an average of 10.3% for the great apes (i.e., chimpanzees, gorillas, and orangutans) [69]. Similarly, the volume of the non-prefrontal cerebral in humans is, on average, 3.7 times larger than that of chimpanzees (Pan paniscus and Pan troglodytes) but the prefrontal regions are, on average, 4.9 times larger [69]. Furthermore, humans appear to have substantially more convoluted cortex (i.e., higher values of the gyrification index) in the prefrontal regions [68,70].
Surprisingly, when compared against other primates, the volume of prefrontal white matter is disproportionately larger in humans [69]. More specifically, when comparing humans against chimpanzees, prefrontal gray matter volumes were, on average, 4.8 times larger in humans, whereas nonprefrontal gray volumes were 4.2 times larger. By contrast, prefrontal white matter volumes were, an average, of 5.0 times larger in humans, whereas nonprefrontal white volumes averaged only 3.3 times larger [68]. In other words, the differences in humans appeared to demonstrate a bias toward the growth of white matter rather than gray matter. These data appear to suggest an increase in average connectivity (e.g., higher white matter versus gray matter ratios, and higher cortical folding in this area) accompanied with a moderate increase in neuron numbers in the human prefrontal cortex with respect to other cortical regions, but most notably, substantially higher numbers when compared to the great apes. Thus, it is plausible to hypothesize that the evolution of the prefrontal areas in the hominid lineage is the result of the interplay between the routes derived from the theoretical model, in particular, to the pathway evidencing a strong influence of neural connectivity on cognitive capacities.
In summary, although the level of hierarchy for birds, amphibians and mammals is agreed upon in neuroscience [13], the exact number of information-processing levels that can be associated with a particular brain is still unclear. Bearing this fact in mind, the existence of these pathways has also helped to clarify the difficulties encountered in trying to explain the complex cognitive behaviours documented across different vertebrates species that have substantially different physiological characteristics in their brains (e.g., animals with high intelligence but relatively small brains like corvid birds, see Figure 4). Thus, differences in intelligence are predominantly explained in terms of the absolute number of neurons, and the average number of synapses per neuron that are present in the cerebral cortex and its homologues.
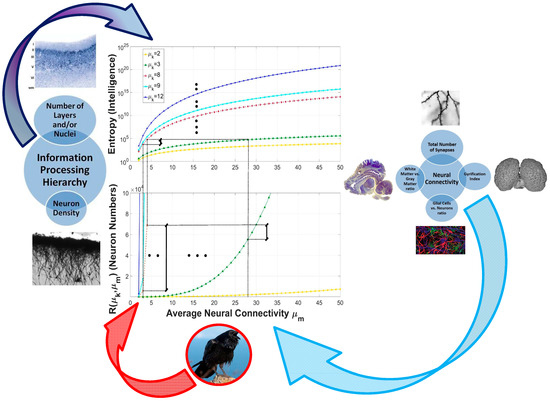
Figure 4.
The pictures on the left and right side of the figure show how the mathematical model and the physiological parameters of the brain correspond (reprinted with kind permission of Springer [71], Wiley [4], and the Nature Publishing Group [72]). Regarding the picture of the raven at the bottom, the high intelligence in animals with small brains, such as corvid birds, is explained in terms of the first route which regards how nature evolved brains to increase their cognitive capacities: A deeper information-processing hierarchy combined, in this case, with an extremely reduced average connectivity to mitigate the cost of requiring larger number of neurons. From a neurophysiologic point of view this results from higher packing of neurons, which also results in a reduced overall connectivity (shorter interneuronal distances). The dorsal ventricular ridge, especially that of corvids, owls, and parrots (all exceptionally intelligent birds), is particularly more developed in birds when compared to reptiles. This indicates a higher number of neurons compared to other birds and reptiles. Indeed, it has been recently shown that large-brained parrots and corvids have forebrain neuron numbers equal or greater than primates with much larger brains as a result of the extremely high packing densities of their brains [67].
3.4. The Primary Role of Connectivity in Intelligence
Intelligence is not only a result of a higher number of neurons in the cerebral cortex and its homologues but is also the result of the interplay between the absolute number of neurons in these structures and their connectivity (i.e., local and non-local connectivity). A brain that in absolute terms has a lower number of neurons in the cerebral structures studied might have the potential to exhibit similar or higher levels of intelligence with respect to a brain that has a higher number of neurons if the former possesses a higher average neural connectivity and is able to sustain the higher associated metabolic costs (see Figure 3).
For example, two recent studies of the cellular composition of both the brain of the African elephant and those of great apes have shown that the African elephant (Loxodonta africana) contains 257,000 million neurons, whereas the brain of the gorila (Gorilla gorilla) and the orangutan (Pongo pygmaeus) contain respectively 29,300 and 28,500 million neurons [73,74]. In contrast, the elephant cerebral cortex, which has twice the mass of the human cerebral cortex, holds only 5600 million neurons, about one-third of the number of neurons found in the human cerebral cortex. Furthermore, the cortex of the gorilla and the orangutan hold respectively 9100 and 8900 million neurons, whereas for the cortex of chimpanzees (Pan troglodytes), the authors provide an estimation of 9000 million neurons, values that surpass the number of neurons found in the cortex of the elephant.
Moreover, with regards to neural connectivity, the average number of dendritic spines per neuron can be used as an approximate measure of the average number of synapses per neuron (e.g., each spine can have one, two, three, or even zero synapses). Using a Golgi quantification technique, Jacobs et al. [71] reported an average number of 2693 basilar dendritic spines per neuron for pyramidal neurons in layer III of the frontal cortex of elephants, whereas they reported a value of 2018 spines for the occipital cortex. Surprisingly, these values are almost one order of magnitude higher than those found in the cerebral cortex of chimpanzees when using an identical quantification technique. Specifically, an average of 401 spines per neuron (basilar dendritic spines) were reported for the typical layer III pyramidal neuron in the frontal cortex of chimpanzees, and 169 spines for the occipital cortex [44,75]. Furthermore, the remaining neural connectivity indicators (i.e., cortical gyrification index, white matter versus gray matter ratio, and cortical glia–neuron ratio), including the energetic requirements of the brain, are higher in elephants compared to those found in great apes (see Table 1). Differences in intelligence between the great apes and elephants have not yet been sufficiently tested, however, these data are of particular interest given the lower number of neurons found in the cerebral cortex of elephants when compared to great apes, especially as both species are cognitively sophisticated and possess an extensive cognitive repertoire [24,76]. Perhaps, the most surprising cognitive ability in elephants, which appear to be somewhat unique among non-human species, is their reaction to disabled and deceased conspecifics: they exhibit behaviours that are characteristic of the theory of mind phenomena (i.e., the ability to understand another individual’s mental state and take it into account with regards to one’s own behaviour). In summary, these data appear to corroborate the existence of increased cortical connectivity in the elephant brain compared to great apes, therefore, increasing the likelihood of the formulated prediction.

Table 1.
The above image highlights the current available statistics for the cerebral cortex of cognitive sophisticated terrestrial mammal species as well as several species of cetaceans (see [2,3,12,13,17,29,30,48,53,67,70,77,78,79,80,81,82,83,84,85]). The table on top of the figure provides estimations of different physiological parameter for the brains of great apes, humans, and African elephants. The table on the bottom provides identical estimations for the brain of several cetacean species. The lack of neurophysiological data for cetacean species reflects the logistical difficulties that are associated with the study of cetaceans (e.g., obtaining materials that are in sufficiently good condition for histological analysis is known to be purely opportunistic).
Finally, to complement the aforementioned connectivity data, a quantitative Golgi study performed in humans (Homo sapiens) to study the dendritic and spine variation of the cerebral cortex reported an average number of 1377 basilar dendritic spines per neuron [46] for area 10 (frontal cortex). In other words, a value very close to that reported for humans in the study of Bianchi et al. [44] (i.e., approximately 1340 basilar dendritic spines), but lower than those found for the elephant. In particular, the study of Jacobs et al. [71] reported that in the elephant frontal cortex, basilar dendrites exhibited a 63.6% higher number of spines per neuron than in humans, whereas in the elephant occipital cortex, basilar dendrites exhibited a 52.3% higher number of spines per neuron than in humans. Similarly, as in the case of the chimpanzee, the rest of the neural connectivity indicators, including the energetic requirements of the brain, are higher in elephants compared to humans. However, it is important to note two facts: the cerebral cortex of the elephant lacks granular layer IV (i.e., a lower number of information-processing levels compared to humans and great apes) [71]; and the human cerebral cortex contains approximately three times the number of neurons of the elephant’s cortex (see Table 1). Both these facts clearly mark the differences in intelligence that have been observed.
4. Discussion
From a behavioral perspective, there have been extensive studies of cognitive capabilities of captive bottlenose dolphins (Tursiops truncatus) demonstrating their sophisticated cognitive abilities [21,22,86,87]. These various studies illustrate impressive learning capacities and behavioral flexibility in dolphins. For example, (just to mention a few) dolphins can reliably understand indicatives cues provided by a human informant such as pointing an object, or gazing the particular sample object with a turn of the head. Dolphins can understand spontaneously the use of pointing gestures substituted for symbolic gestures in language-like tasks. Additionally, dolphins can spontaneously produce pointing (using rostrum and body alignment) to communicate desired objects to a human observer, and appear to understand that the human observer must be present and attending to the pointing dolphin for communication to be effective. Dolphins have demonstrated rapid and spontaneous vocal imitation, vocal learning, and the ability to develop learned associations between temporally paired elements in the absence of explicit training. Furthermore, field studies of social complexity in bottlenose dolphins in the wild in Shark Bay (Australia) revealed a society of great size with complex social relationships including nested alliances, affiliative behaviors, and individual foraging specializations and tool use [14,25].
Moreover, recent field studies have evidenced complex cognitive abilities in large-brained delphinids-like killer whales (Orcinus orca): a special type of cooperative hunting in which the animals work together to create waves to displace penguins and seals on ice floes [88], evidence for vocal learning [89], and observational evidence for imitation and teaching, such as intentional stranding on beaches to catch pinnipeds [90]. These field studies have evidenced not only that cultural transmission is important for killer whales but also that the complex and stable vocal and behavioral cultures of sympatric groups appear to have no parallel outside humans and represent an independent evolution of cultural faculties [91].
Data on mysticete (baleen whales) behavior are much more limited than for odontocetes (toothed whales). The available information suggests that social communication and structure are often complex in mysticetes [92], and include long-term social bonds, long-range communication, cooperative hunting, cultural traditions, and fission-fusion like social behavior [91]. These behaviors are observed in some large-brained odontocetes like the Sperm whale (Physeter macrocephalus) and primates, and are considered cognitively demanding [92]. For instance, the discovery of complex learned songs, i.e., structured sequences of vocalizations that cycle with a period of 5–25 min and clever fish corralling strategy techniques, including the use of bubble clouds to encircle prey, the production of loud feeding calls and the waving of their large pectoral flippers as a feeding tactic [93] certainly suggest that humpback whales (Megaptera novaeangliae) are quite intelligent [13,91]. Furthermore, to date, the social calling repertoire of humpback whales has received considerably less attention than either the song or foraging calls. Social calls are defined as phonations that do not possess the rhythmic or continuous patterning of song [94]. A recent study on the vocal repertoire and social calling behavior of the Southeast Alaska humpback whale has evidenced a more varied and diverse repertoire of social vocalizations than has previously been documented, identifying variability in the vocal behavior as a function of the social-spatial context [95].
The support for cognitive sophistication in humpback whales, and its tremendous behavioral flexibility come also from recent reports of whale watchers who observed, on several occasions, groups of humpbacks whales attempting to help a member of another species. Examples include a group of humpback whales intervening when a pod of killer whales was in the process of trying to separate a grey whale’s calf from its mother or humpback whales rescuing a seal from killer whales in the Antarctic. These observations have been corroborated by a recent study [96] that investigated humpback whales interfering with attacking killer whales. The authors concluded that these behaviors, even if unintentional, might be the focus of future research into possible genetic or cultural drivers of interspecific altruism. To date, altruism among cetaceans has been attributed almost exclusively to smaller odontocetes [96]. For example, some odontocetes species are famously known for coming to the aid of threatened or injured conspecifics, as well as other species, including humans [91], although these behaviors have also been reported for killer whales and sperm whales [97].
Having said this, it is important to emphasize that the interpretation of the cognitive capacities of cetaceans has been a subject of active discussion over the past decade. For example, cetacean’s modest use of tools when compared to those of primates. The fact that a greater proportion of cetacean’s cerebral cortex when compared to great apes and other mammals of similar brain sizes is occupied by white matter rather than by gray matter (where neuronal computation occurs), and particularly an unfavourable combination of high interneuronal distance plus low axonal conduction velocity has lead to the scientific judgement that cetacean’s brains have less computational power [2,98,99]. Further it has lead to the belief that there is not a single behavioral achievement that has not also been shown in several other species [18,20]. This has increased the reluctance of one part of the scientific community to believe that cetaceans’ large brain is related to intelligence or any special intellectual capacities. This controversy has increased even further as a result of a recent study that showed that large and highly convoluted brains, such as the elephant brain, are not necessarily composed of an enormously large number of cortical neurons [74].
However, concerning the assumption that cetacean’s brains have less computational power, the study by Dicke and Roth [99] identifies the principal factors determining general information processing capacity in the brain, and thus intelligence among mammals, as a combination of the number of cortical neurons, the number of cortical synapses, and processing speed. Addressing these in turn, firstly, it is important to note that processing speed provides a necessary but not sufficient condition for intelligence [100,101]. For instance, Sheppard and Vernon [102] compiled results from 172 studies on processing speed and intelligence in humans that involved more than 53,500 participants. They concluded that although the understanding of differences in mental speed may be essential to an improved understanding of intelligence, these differences do not provide a full account of differences in intelligence. Secondly, with regards to the total number of cortical neurons, the present study showed that intelligence is not only a result of a higher number of neurons in the cerebral cortex and its homologues but that it is also the result of the interplay between the absolute number of neurons in these structures and their connectivity (see Section 3.4). Surprisingly, Mortensen et al. [30], using modern unbiased stereological methods [103], recently found that the number of neurons in the cerebral cortex of long-finned pilot whales (Globicephala melas)—a delphinid with an average brain mass of 3500 g—was 37,200 million. This is a figure that is beyond the number of cortical neurons reported for the human brain [104,105].
Furthermore, Dicke and Roth [99] initially explored whether the number of synapses (i.e., neural connectivity) in the cerebral cortex is potentially of importance to the cortical information processing capacity, however this factor is finally rejected on two assumptions: that it is compensated for by a decrease in NPD and that the number of cortical synapses per neuron is approximately constant throughout mammals. Nevertheless, recent studies on the morphology, regional dendritic and spine variation in the cerebral cortex of several mammal species have revealed substantial differences in the average number of dendritic spines per cortical neuron. This is found not only between species, but is also true when different areas of the cerebral cortex are sampled [44,45,46,71]. Once again, it is important to bear in mind that dendritic spines can be used as a proxy for the number of synapses. Thus, one cannot assume that the increase in the number of synapses in large-brained animals is compensated for by a decrease in NPD, as has been suggested for the cetacean’s brain. This is especially relevant when considering the major role played by the total number of synapses (i.e., a major indicator of neural connectivity) as an important neurobiological structure that determines intelligence, according to the results presented earlier (see Section 3). The importance of neural connectivity as a major neurobiological structure governing intelligence may be further elicited by the comparison of extreme cases, such as a comparison between the brain of one of the greatest intellectual giants of recorded history, Albert Einstein, and control groups. The study of Witelson et al. [106] found that brain length, height, the size of the corpus callosum, and measurements of the frontal and temporal lobes did not differ between Einstein and the control subjects. Furthermore, the limited data on Einstein’s brain do not point to a difference in the number of neurons throughout the depth of the cortex in the frontal or temporal lobes. In contrast, in the parietal lobes, Witelson et al. [106] found quantitative differences such as an increased expansion of the inferior parietal region, suggesting a difference in the ratio of glial cells relative to neurons in the left parietal cortex. In other words, according to the results presented herein, they were observing increased neural connectivity in the region when compared to control subjects. This region is a secondary association area that provides cross-modal associations among visual, somatosensory, and auditory stimuli. For example, visuospatial cognition, mathematical thought, and imagery of movement are strongly dependent on this region. Admitting to the fact that the ability to perform associations constitutes an important resource for intelligent behaviour, higher neural connectivity (i.e., a higher connectivity between brain representations) in a deeper associative area may be of particular importance for abstract thinking, and thus for intelligence.
The number of computations within a given timeframe that can be supported by neural tissue is dependent on, amongst other things, absolute brain size, the number and size of the neurons, and the number of connections among neurons. The energy available for neural processing, which is affected by the specific metabolic rate, is also an important variable in determining computational power [107]. For example, two brains with similar neurophysiologic characteristics, i.e., a similar number of neurons and neural connectivity, may exhibit substantial differences in the number of computations they are able to perform per unit of time as a result of differences in the metabolic turnover of their brains. This fact is particularly interesting, especially when taking into consideration that bottlenose dolphins (and other cetaceans) have a higher basal metabolic rate than terrestrial mammals of the same size and they consume oxygen at a rate that is greater than that documented for both humans and elephants [65,108,109].
According to Dicke and Roth [99], processing speed depends on interneuronal distance, axonal conduction velocity, and synaptic transmission speed. Interneuronal distance is determined by neuron packing density (NPD hereafter), and in large-brained animals such as cetaceans and elephants there exists an unfavourable combination of high interneuronal distance plus low axonal conduction velocity, which strongly impairs their neuronal information processing capacity. However, it is important to note that rapid hard-wired connections are present in the brains of cetaceans. For instance, De Graaf [110] reported the existence of large diameter myelinated axons in the nervous system of toothed whales. These large axons are reported in the auditory system, visual system, and even in the nervus terminalis. Such rapid connections might explain, for example, why the evoked potentials in the dolphin’s central nervous system have shorter latencies (i.e., faster conduction times) compared to similarly sized human brains [111]. In experiments involving a cognitive processing paradigm and phonatory response times (i.e, the time from information reception, processing, and voluntary acoustic response), dolphins were faster than in humans in the majority of instances. Surprisingly, dolphins were able to select individual responses in the aforementioned paradigm in as little as 20 ms (i.e., faster than in humans) [112].
Further arguments falling under this umbrella can be found in the work of Wang et al. [113] who showed that from shrews to whales, the composition of white matter shifts from compact, slow-conducting, and energetically expensive unmyelinated axons to large, fast-conducting, and energetically inexpensive myelinated axons. The fastest axons have conduction times of 1–5 ms across the cerebral cortex and below 1 ms from the eye to the brain. More specifically, Wang et al. [113] analyzed specimens from 14 species (including the great apes) whose brain volumes span nearly five orders of magnitude, starting right down with the shrew (Cryptotis parvus; brain weight 120 mg) and all the way up to the Humpback whale (Megaptera novaeangliae; brain weight 7.5 kg). These authors found very large axons in all cetaceans brains (Phocoena phocoena, the harbour porpoise; Stenella coeruleoalba, the striped dolphin; Tursiop truncatus, the bottlenose dolphin; and Megaptera novaeangliae, the humpback whale) as well as in the remainder of the species analyzed. In larger brains, they found a clear tendency for axons to be wider in diameter and greater myelination. It is important to note that in addition to myelination, axon diameter also affects conduction times in vertebrates axons, and both factors (increased myelination and diameter) increase axonal volume. Furthermore, the existence of subpopulations of exceptionally wide axons with submillisecond conduction times appears to be a recurring theme in large brains. Similarly, large myelinated axons also constituted a small fraction of the total number present in white matter, suggesting they compose highly specialised highways of neural activity.
With respect to synaptic transmission speed, this parameter is assumed to be constant among mammals, occurring at synapses requiring the release of neurotransmitters from a presynaptic neuron and their detection by a postsynaptic nerve cell. Glutamate is the main excitatory neurotransmitter in the mammalian brain. After it is released, glutamate is promptly removed from the synapse by uptake into an adjacent astrocyte (the other major cell type in the brain). There, glutamate is converted to glutamine before being returned to the neuron and recycled [114]. The energy needed to process glutamate is provided by glycolysis (i.e., a molecule of glucose is degraded in a series of enzyme-catalyzed reactions to yield two molecules of pyruvate), using glucose obtained from blood and, during sudden increases in activity, from a glycogen store (i.e., a polymer storage form of glucose) in astrocytes through glycogenolysis (i.e., catabolic pathway to convert glycogen to glucose). Of particular importance is the fact that there are large difference in both the rates of glucose consumption as well as the total amount of glucose consumption when these processes (i.e., glycolysis and glycogenolysis) follow aerobic or anaerobic pathways. Under anaerobic conditions, consumption rates are considerably higher than under aerobic conditions [115].
The baseline metabolic rate of large-brained mammals is very high. The energy needed is supplied by glucose oxidation and the brain vasculature is precisely organized to meet the accompanying ongoing oxygen demands. However, changes in activity associated with activation (e.g., echolocation in odontocetes), despite only requiring a small and brief increment in energy expenditure, occur in the span of milliseconds. The brain vasculature simply cannot respond quickly enough to meet these energy requirements in a timely fashion, thus causing it to resort to glycolysis, or even to glycogenolysis in extreme cases [114]. This is of particular importance when the speed of information processing in the brain is of the essence, i.e., when the brain has to process information from the highly sophisticated echolocation system of odontocetes (echolocating animals emit trains of clicks to detect a target); not forgetting that the speed of sound in water is approximately four times faster than air.
Although glycolysis and glycogenolysis yield less energy overall, they produce this energy faster than glucose oxidation. It is now generally accepted that the metabolic needs of active neural tissue are met, at least partially, by anaerobic glucose metabolism occurring in the astrocytes. Astrocytes can oxidise fatty acids in another energy-yielding pathway that frequently occurs in the mitochondrion. The four-step process called oxidation leads to acetyl-CoA, a molecule that is also an intermediate product used for energy production through the citric acid cycle during glucose oxidation. Importantly, astrocytes are more resilient to hypoxia (low oxygen conditions) compared to neurons [115,116,117,118,119].
Cetaceans possess a number of adaptations that aid diving, including increased myoglobin levels (i.e., an oxygen-storing and iron-carrying protein found in the muscles of all mammals); increased blood volume; and a higher concentration of hemoglobin than in terrestrial mammals [120]. However, dive limits are also dictated by rates of oxygen consumption, which is of particular relevance when discussing a very oxygen-sensitive organ like the brain. In other words, in addition to the primary source of neural energy substrate, which is the direct entry of glucose into neurons, there is evidence that a second source of energy is provided by the entry of glucose into astrocytes. Thus, it is plausible to hypothesize that a faster synaptic transmission speed is possible in the cerebral cortex of cetaceans compared to terrestrial mammals as their metabolism may have evolved to rely more on anaerobic glucose metabolism, especially during periods of increased energy requirements and/or under oxygen deprived conditions (i.e., diving conditions) [121]. For example, the dolphin lineage showed positive for the inheritance of genes involved in the metabolism of glucose and lipids, as well as faster rates of evolution in genes expressed in the mitochondria, both of which indicate an evolution in energy metabolism [65]. Further arguments supporting this perspective come from the work of Williams et al. [122] who studied the physiology of the bottlenose dolphin during exercise (i.e., animals either pushing against a load cell or swimming next to a boat). Surprisingly, the authors found that the dolphins’ behaviour, dynamic metabolic scope and level of maximal oxygen consumption fell short of those reported for elite terrestrial athletes such as the horse and the dog (i.e., animals with smaller brains in absolute terms). This suggests that a swimming dolphin may rely on metabolic pathways or oxygen reserves (e.g., large oxygen reserves in the lungs, blood or muscle) that were not identified by conventional evaluation methods. In other words, the study documented evidence of the possibility that marine mammals might rely on anaerobic metabolism, at least during high work loads. Moreover, the work of Ridgway et al. [121] using functional imaging to study the metabolism of the brain of the bottlenose dolphin concluded that there may be more advantages to the unihemispheric physiology observed in the dolphin brain than just its ability to have slow brain waves in one hemisphere while maintaining the ability to swim and remain alert in the other. Specifically, the ability to partially `shut down’ or at least reduce oxygen and glucose consumption in a major portion of the dolphin’s large and active brain—evidence of the use of alternative metabolic pathways [117,118,119,123]—may be an advantage to a dolphin making repetitive, prolonged feeding dives [121].
Finally, with respect to the behavioural data, it is important to note that the intelligence of most cetaceans is currently unknown despite the large body of older or more recent studies that have shown the complex cognitive abilities of cetaceans. Currently, available data has led to much debate and controversy within the scientific community, but as yet no clear consensus has been reached. One of many possible factors causing this may be the logistical difficulties that are associated with the study of cetaceans; these difficulties often give rise to incomplete information that lacks important details for analytical purposes. Another factor, if not the major factor, is the intrinsic difficulty of defining and testing the cognitive performance of animals, and thus reaching a consensus on how to interpret the gathered data. Indeed, the development of truly rigorous comparative tests through which the intelligence of members of distantly related taxa, such as corvid birds, primates and cetaceans can be tested whilst ensuring they are under same conditions [98] still remains a challenge to comparative psychologists. Hence, the discussion presented hereafter must be interpreted according to the premises of the scientific method, namely, as predictions of the hypothesis that should subsequently be verified or refuted by future studies, once more data becomes available.
4.1. Implications for Cetacean Cognition
The first important implication of this study was to show that a brain which in absolute terms has a lower number of neurons in the cerebral structures considered might have the potential to exhibit similar or higher levels of intelligence with respect to a brain that has a higher number of neurons. This is always possible if the former possesses a higher average neural connectivity and is able to sustain the higher associated metabolic costs. The second important implication was to show that higher levels of intelligence are not possible without implicitly increasing the number of neurons in the cerebral cortex and its homologues. The increase in neuron numbers is always accompanied by unavoidable growth of the associated energetic requirements, but imposing, at the same time, a limit due to metabolic considerations. Thus, animals possessing a large number of neurons in the cerebral structures postulated by the hypothesis have the potential for displaying higher levels of intelligence (i.e., a larger range and versatility of behaviors and cognitive abilities).
However, the most important result of the present study is to show from the perspective of the hypothesis [28] the existence of two routes to augment intelligence each of them evidencing the specific manifestation of a trade-off between metabolic necessities and the unavoidable requirement on neuron numbers. For the first route, the attainment of higher levels of intelligence evidenced the existence of cerebral structures (i.e., the cortex and its homologues) with a deeper information-processing hierarchy that required a higher growth on neuron numbers compared to the second route, but at relatively lower metabolic costs. In contrast, the second route evoked by the existence of cerebral structures with higher levels of neural connectivity, the attainement of higher levels of intelligence was possible with a more moderate growth on neuron numbers compared with the first route but at the cost of a substantial (or faster) increase in the associated metabolic costs.
The order Cetacea comprises highly diversified species distributed into two suborders: the Mysticeti (baleen whales) and the Odontoceti (toothed whales). The suborder Odontoceti contains 72 species of toothed whales, dolphins, and porpoises, distributed into four families. In general, cetaceans possess large brains when compared to terrestrial mammals, both in absolute and relative terms. Their brains also have much lower neuronal density, but at the same time, higher ratios of glial cells to neurons, and greater proportion of cortical white matter versus gray matter [2,17,65]. Furthermore, one of the most fascinating characteristics of their brains is the high degree of cortical gyrification and the resulting neocortical surface area. Therefore, in spite of the fact that recent studies have revealed great diversity amongst the brains found across this order (e.g., differences in brain parts, as well as body and brain measurements) [6,29], based on available data it is plausible to argue that, generally speaking, their brains appear to have followed the second pathway (Route 2), presented by the mathematical model being used to support the hypothesis exploring how brains evolved naturally and the causes of increased cognitive capacities. More specifically, if the assumption being made is that the depth of the information-processing hierarchy in the cerebral cortex of cetaceans is lower when compared to most of the intelligent terrestrial mammals species, then those defending complex cognition in cetaceans would need to demonstrate the existence of a higher neural connectivity (and thus higher metabolic costs), but, at the same time, a comparable (or higher) number of neurons in their cortices when compared to terrestrial mammal species for which there is enough documented evidence (besides humans) for their overall cognitive superiority, for example the great apes.
Having said this, in contrasting the data provided in Table 1, it is possible to deduce that all the neurophysiologic indicators of neural connectivity are higher for the cetacean species that were selected when compared to primates. For example, the highest gyrification index in primates is on par with humans with a value of 2.57, whereas the average value in cetaceans is 5.43 (i.e., the most gyrencephalic mammals). In primates, the highest ratios of white matter to cortical gray matter, and glial cells to neurons, also correspond to humans. When comparing the glia–neuron ratio in the cerebral cortex of the bottlenose dolphin with that of humans (two brains of similar size), a ratio of 2–3.1/1 against 1.68–1.78/1 is obtained. Similarly, the ratio between cortical white matter and gray matter in the bottlenose dolphin is approximately 0.76, whilst this ratio is 0.71 in humans [2,70]. Moreover, when comparing the glia–neuron ratio in the cerebral cortex of the harbour porpoise with that of the gorilla (both brains of similar size), a ratio of 2.34/1 against 1.21/1 is obtained, respectively. Similarly, the ratio between cortical white matter and gray matter in the harbour porpoise is approximately 0.66, while this ratio is approximately 0.62 in gorillas. Finally, comparing the available neurophysiologic indicators of neural connectivity for the killer whale with those of the African Elephant (the only terrestrial mammal with a comparable absolute brain size) it can be deduced that indicators such as the gyrification index and the cortical surface area are higher in the killer whale. In particular, their cortex is extremely convoluted and thin which results in an expansion of the surface area by approximately 13,629 cm. This means that this animal has a cerebral cortex with the highest gyrification index reported thus far (i.e., ).
Increased neural connectivity is implicitly linked to the existence of a higher number of synapses but also a larger number of neurons (second route). Thus, higher metabolic costs are expected in cetaceans’ brains compared to primates and terrestrial mammals possessing brains of a similar size. The energetic requirements of the brain of the bottlenose dolphin and humans can be calculated using a past study which relates the basal body (or resting) metabolic rate (RMR hereafter) to brain metabolism in vertebrates [82]. The measured resting metabolic rate for captive bottlenose dolphins (Tursiops truncatus) is within the range of 8000–9000 kcal/day [77], whereas the RMR for an adult human (Homo sapiens) is approximately 1400 kcal/day [83]. For the bottlenose dolphin, 4.77 % of the RMR is dedicated to its brain’s metabolism, which produces a value within the range of 429–477 kcal/day. Similarly, for humans, the energetic requirements of the brain account for 20% of the RMR, leading to 280 kcal/day for the human brain. Hence, according to these data, the energetic requirements of the brain of the bottlenose dolphin are higher when compared to those of the human brain (considered the most intelligent organism in the animal kingdom by far, and the only primate with a comparable brain size). Furthermore, the energetic requirements of the brain of the killer whale (see Table 1) are also higher compared to those of the elephant—within the range 1800–2200 kcal/day compared to 1200 kcal/day for the elephant brain.
However, it is important to note that for reliable comparisons the energetic requirements calculated above must refer to the cerebral cortex and not to the entire brain (e.g., 97.5% of the neurons of the elephant are located in the cerebellum [74]). The energetic requirements of the cerebral cortex can be estimated whenever the absolute number of neurons, the total number of cortical neurons, and the ratio of brain to basal body metabolism (e.g, 13.14 % of the RMR for the chimpanzee brain) are available for a given species. The total number of neurons in the elephant brains is 257,000 millions [74], whereas in human and chimpanzee brains these numbers stand at approximately 86,000, and 27,900 million neurons respectively [73,104]. For these species, the aforementioned neuron numbers (see also Table 1) were obtained using an identical quantification technique, that is, the isotropic fractionator [124], which produces (in combination with the data on the brain to body basal metabolic ratio of the study of Mink et al. [82]) an energetic requirement of approximately 53 kcal/day for the cerebral cortex of the human brain, 26 kcal/day for the cerebral cortex of the elephant, and 22 kcal/day for the cerebral cortex of the chimpanzee (Pan troglodytes). These data, although approximative, appear to corroborate the prediction that higher levels of intelligence are not possible without higher energetic requirements in the cerebral cortex and its homologues (see Section 3.2). Specifically, the higher levels of intelligence observed in humans compared to chimpanzees and elephants are evidenced by the higher metabolic requirements of the cerebral cortex. Furthermore, the similarity of the values obtained for the energetic requirements of the cortices of chimpanzees and elephants appear to suggest the existence of comparable levels of intelligence, in spite of the substantial differences in cortical neuron numbers.
The total number of synapses in the cerebral cortex are correlated to the brain’s metabolic costs, however, the principal contribution to the resulting energetic requirements of the brain was due to the total number of neurons (see Section 2.4). Thus, it is reasonable to expect a large number of neurons in the cerebral cortex of the bottlenose dolphin and the killer whale, perhaps comparable to the neuronal numbers found for great apes, and/or a higher average number of synapses per neuron compared to great apes. Unfortunately, the neocortical neuron number (or the absolute neuronal numbers) of the bottlenose dolphin is unknown. Similarly, data on neuronal numbers and/or the dendritic system in the cerebral cortex of killer whales are not currently available. However, a Mysticeti such as the minke whale (Balaenoptera acutorostrata) has a higher number of cortical neurons compared to great apes [3] (see also Table 1). Moreover, using a Golgi quantitative methodology, the average number of dendritic spines (both basilar and apical dendrites) in the visual and motor cortices of the minke whale was found to be approximately 2436 and 2814 respectively for a typical pyramidal neuron [45]. It is important to remember that dendritic spine counts are used as an approximate measure (or proxy) to the number of synapses per neuron.
Average values of 169 and 166 spines were found in the visual and motor cortices of the chimpanzee using an identical quantitative technique, although these values are not directly comparable because of the fact that only basilar dendrites are reported in the quantification study of the primates [44]. To roughly calculate the number of spines per neuron (basilar and apical dendritic spines) in the chimpanzee brain, one needs to multiply these numbers by the dendritic trees count that is reported by the authors (see Table 2 in [44]). This produces an average number of 723 and 745 spines in the visual and motor cortices respectively. These values, although approximative, are more than three times lower compared to those found for the minke whale in the same areas, thus providing at least a preliminary comparison among these two species.
Furthermore, using stereology quantification techniques [125,126], it was shown that odontocetes such as the long-finned pilot whale (Globicephala melas), or the harbour porpoise (Phocoena phocoena) have an unexpectedly high number of cortical neurons [30,127]. Figures for harbour porpoises approach the lowest cortical neuron number found in humans [104,105], and long-finned pilot whales possessing the highest number of cortical neurons of any species studied so far, including humans [30]. Of particular interest is the study by Kazu et al. [128] which predicted that the large cerebral cortex of cetaceans will have fewer neurons than the human cerebral cortex. For the bottlenose dolphin, they predicted numbers close to 1750 million cortical neurons. These predictions for other delphinid such as the pilot whale (Globicephala macrorhynchus) and phocoenidae the harbour porpoise (477 g of brain mass) translated into values of 3010 and 1127 million cortical neurons respectively. Furthermore, recent studies have hypothesized that the larger absolute number of neurons in the human cerebral cortex (but not in the whole brain) is correlated with the superior cognitive abilities of humans compared to elephants and other large-brained mammals [12,23,129]. For example, Herculano-Houzel [129] suggested that even the cerebral cortex of the largest whales might be composed of only a fraction of the average 16,300 million neurons found in the human cerebral cortex. In fact, both Kazu et al. [128], and Herculano-Houzel [129] do not agree with the aforementioned results concerning the neuronal numbers found in the cerebral cortex of the harbour porpoise and the minke whale, [3,127] suggesting that the neuron numbers obtained might be over-estimations of the real values due to undersampling problems associated with the stereology quantification technique.
Having said this, it is important to highlight that modern unbiased stereology techniques make use of efficient sampling techniques [103,126], therefore even when accounting for the existence of errors, it is unlikely that variance errors that are of the magnitude needed to explain the discrepancies obtained between the predictions of Kazu et al. [128] and the neuronal numbers found by Wallöe et al. [127], and Mortensen et al. [30] would have been made; this is especially so for the study by Mortensen et al. [30] which used a meaningful sample of specimens (i.e., ). Furthermore, according to the results of the theoretical model, these data do not falsify, but rather refine the aforementioned hypotheses concerning the levels of intelligence that would be expected for a species based on the cortical neuron numbers [12,23,129], as a larger absolute number of neurons in the cerebral cortex is a necessary but not a sufficient condition for exhibiting higher levels of intelligence. For example, as previously evidenced in the differences found in cortical neuronal numbers between the chimpanzee and the elephant, in spite of a similarity in the energetic requirements of their cortices.
In summary, it has been possible to demonstrate the following for the cetacean species listed in Table 1: all the indicators of neural connectivity are higher compared to great apes; cortical neuronal numbers are comparable with those of great apes; the energetic requirements of the brain are also higher compared to the brains of similarly sized cognitively sophisticated terrestrial mammal species such as the great apes and the elephant. In accepting the strong influence of neural connectivity on cognitive capacities—e.g., doubling the average connectivity between brain representations may lead to a substantial increase of the entropy values of one order of magnitude or higher depending on the average number of information-processing levels contemplated—and reviewing the behavioural data presented earlier, it is plausible to conclude that the brains of cetaceans primarily reflect the second pathway (Route 2). Thus, within the debate on the complexity of cetacean cognition, the author defends the position that there is evidence of complex cognition as the second pathway is an evolutionary adaption that has lent itself to increased cognitive capacities. Furthermore, data from future studies may confirm the existence of an unexpectedly large number of neurons in the cerebral cortex of the bottlenose dolphin (Tursiops truncatus), and particularly, in other large-brained cetaceans such as killer whales (Orcinus orca), humpback whales (Megaptera novaeangliae), or sperm whales (Physeter macrocephalus), which would confirm predictions made using the theoretical and mathematical models, which together point to the possibility of the existence of levels of intelligence in these mammals that go beyond what has previously been hypothesized.
However, it is also important to emphasize that the conclusions obtained may vary to the extent that new data becomes available from studies using novel quantification techniques, especially those related to brain energetics, since current data are currently very scarce and relatively out-dated. However, the theoretical results used to reach such conclusions shall not vary.
4.2. Brain Evolution: The Loss of Layer IV in the Cerebral Cortex
One of the most intriguing neuronal traits of cetaceans is the lack (or underdevelopment) of layer IV in their cerebral cortex. The laminar organization of the cetacean cerebral cortex has been considered a heterotypical formation resulting from a reduction in the number of cortical layers. Currently, it is generally accepted that the common ancestor of all cetaceans possessed layer IV granule cells [2,48]. The loss of the granule cells in layer IV in cetaceans has been regarded a rare derived trait in which layer II has undergone a secondary transformation specific to the cetaceans. This secondary transformation has been correlated with the shift of the orphaned terminations of the specific thalamic afferents (originally terminating in layer IV) back to layers I and II, thus allowing more neurons in layer II to persist [48].
One of the principal theoretical results inferred from Equation (7) was to show the existence of two routes for the attainment of higher levels of intelligence. Particularly, an increase in intelligence was possible with a more economical but inevitable increase on the total neuron numbers if the depth of the information-processing hierarchy was reduced, although at the cost of increasing the average neural connectivity (i.e., increased local and non-local connectivity), and thus leading to a substantial (or faster) increase in the associated metabolic costs. Therefore, the loss of layer IV in the cerebral cortex of cetaceans may be interpreted as an evolutionary modification representing a solution to the need of increasing cognitive abilities in a brain previously adapted to the aquatic environment. In other words, the heterotypical agranularity of the cetacean cerebral cortex (i.e., the lack or underdevelopment of layer IV) is hypothesized to be the result of the causal linkage between two ecological pressures, firstly the readaptation to the aquatic environment, especially to the progressive adquisition of endurance underwater without breathing, and later to the cooling of water temperatures during the Eocene-Oligocene transition period [2] both leading to an overall increase of the glial cells, secondly the response to selective pressures for increasing cognitive skills principally driven by social demands [14] that were responsible of the encephalization spurts observed in this lineage (see Section 4.3 for further details).
It is important to note that from a physiological point of view, a fewer number of cortical layers permits that the radially coursing dendrites and axons of neurons have more room to pass between the neocortical cell bodies. In other words, more space becomes available in the neuropil if the number of neurons and especially the average cortical connectivity need to be increased, something impractical for the six layered pattern of the ancestral cetacean neocortex, when a greater proportion of the neuropil was already occupied by glial processes, and especially by the faster increase on the cortical neuron numbers required, as suggested by Equation (7). Furthermore, it can be argued that the unavoidable increase in neuron numbers, needed to augment their cognitive capacities, was absorbed mainly by its cortical densely populated layer II, and also by layer I since is far more cellular and thick than in most terrestrial species [1].
Moreover, evolutionary modifications have always been made within the context of the organization and architecture already in place and computational solutions invented by nature may be well neither optimal nor predictable from generally accepted human assumptions [39]. According to the model the cost incurred by this evolutionary modification resulted in a substantial increase of the associated brain metabolic costs, however, the energetic costs of maintaining an enlarged brain were possible, probably, because of their dietary quality (i.e., the energetic and nutrient density of their diet) accompanied by an increase in basal metabolic rate and/or efficiency of metabolism to accomodate expanded energy demands. For instance, the dolphin lineage showed faster rates of evolution in genes expressed in the mitochondria, the source of aerobic metabolism suggesting the increased need to provide additional energy to such a large organ. Furthermore, of all terrestrial and aquatic animals tested, only primates and cetaceans have red blood cells that are extraordinarily permeable to glucose (large brains require readily available blood glucose in order to function) [65,130].
Terrestrial Mammals Lacking Internal Granular Layer IV in the Cerebral Cortex
From a cytoachitecture point of view the cerebral cortex of terrestrial mammals, such as elephants, or hippopotamids, also lack granular layer IV. This fact is of particular interest because the closest phylogenetic relatives to elephants are sirenians [1] whose order includes two extant families Dugondidae (dugongs) and Trichechidae (manatees), and both species possess a fully developed cortex (i.e., the six characteristic layers of the cerebral cortex are present). However, it has recently been shown that elephants had an aquatic ancestor [131].
One of the adaptations seen in diving marine mammals is the presence of higher concentrations of myoglobin in muscles when compared to terrestrial mammals. What is more, those that dive regularly, e.g., sperm whales, have the highest concentrations. Indeed, sperm whales are better than any other animal at staying underwater for long periods without having to take air (e.g., they can stay underwater for approximately 73 min at a time [120]). Diving mammals have higher concentrations of this protein, but according to Mirceta et al. [131] they also exhibit an adaptation: the surface of this oxygen-binding protein possesses a net surface charge causing it to repel itself more strongly, thus enabling deep diving animals to pack their myoglobin into even higher concentrations (proteins tend to stick together at high concentrations impairing their function). Furthermore, it appears that myoglobin with the aforementioned molecular signature is a clear sign of a diving lifestyle. Increased myoglobin net surface charge was observed in lineages of expert divers like cetaceans and pinnipeds, to name a few). However, it did not occur in a common ancestor of whales or their closest living relatives, the semiaquatic hippopotamuses, which implies a low degree of aquatic specialization in their last common ancestor. Surprisingly, they found that terrestrial mammals like elephants and hyraxes descend from ancestors with the aforementioned adaptation of myoglobin (i.e., the protein has a net surface charge), suggesting that they have aquatic ancestors. Thus, the lack or underdevelopment of layer IV in the cerebral cortex of the elephant together with their resulting cognitive capacities (remember that elephants have a complex social structure and sophisticated cognitive abilities) is also explained in terms of the second pathway and how the selective advantages and natural evolution led to an increase in cognitive capacities. Specifically, as the result of selective pressures for increasing cognitive abilities driven by the social demands of a brain ancestrally adapted to the aquatic environment. It is important to note that the cerebral cortex of the elephant also possess a high glia-to-neuron ratio (see Table 1).
A similar conclusion cannot be drawn to explain the agranularity of the cerebral cortex of hippopotamids, firstly because there is not enough physiological data about its cerebral cortex at this time (e.g., glial-to-neuron ratio, neuron numbers and white matter to gray matter ratio), but primarily because of the fact that there is a large ghost lineage (i.e, missing fossils inferred from the phylogeny throughout significant periods of history) between the family Hippopotamidae and the base of the order Cetacea [132]. Thus, as a consequence of the uncertainity surrounding the exact closest fossil relatives for hippopotamids, it is not clear whether their most recent common ancestor was terrestrial, aquatic or semi-aquatic.
4.3. Brain Evolution: Large Brains, Thinner Cortices, and an Extreme Gyrencephaly
The large brain of cetaceans, and the combination of extreme cortical surface area together with a narrow cortical width put forward a unique underlying cerebral cortex organization scheme that has been the focal point of longstanding and unresolved controversy about the computational capacities (and resulting intelligence) of the cetacean brain [2]. It has been recently shown that the most encephalized mammals were odontocetes, not primates as traditionally believed. Specifically, the rate of increase in encephalization along the terminal Homo lineage is exceeded by three primate and four cetacean branches, with the terminal Tursiops truncatus branch (i.e., bottlenose dolphins) having the highest rate [92].
These data are of particular interest, firstly, because from an evolutionary perspective, whenever evolution increased absolute brain size, it has apparently done so mainly by increasing neuron number, not neuron size [13]. Secondly, because the focus on explanatory theories about brain evolution, the discussion has currently shifted to theories proposing social benefits of enhanced intelligence [133,134]. In other words, the spurts in brain enlargement in cetacean and hominid lineages are principally explained in response to the especially challenging demands of a complex social life of constant competition and cooperation with others in the social group [14,133,134].
Thus, the large size of the cetacean brain, and especially the intriguing cortical organization scheme based on an extreme gyrencephaly are explained in terms of the second route derived from the theoretical model which regards how nature evolved brains to increase their cognitive capacities. From a physiologic point of view both routes leads to an increase in encephalization because of the need of increased neuron numbers. Particularly, the second route is implicitly linked to an overall increase in the volume of white matter as a result of the postulated increase in the average connectivity that happened as the result of the two selective pressures mentioned before. Therefore, the evolutionary process favoured the extreme gyrification that is observed in the cetacean brain since highly folded cortices are those that have more neurons connected through the white matter [51] (i.e., a higher non-local connectivity), which leads to a thinner cortex because it offers less mechanical resistance to folding, but at the same time leading to the remarkable large brains that are currently observed in this order.
5. Conclusions
Many researchers have attempted to specify what marks the intellectual divide between species, especially between human and nonhuman intelligence. Clearly, the role of human intelligence in the domination of other species appears to be obvious, and perhaps this fact is one of the reasons that could explain why the notion of an evolutionary scale with humans at the top is still popularly held. However, researchers have tended to under-evaluate the cognitive capacities of other animals, for example, because of the difficulty in providing animals with task instructions, which one can quite easily do with humans [135]; our bias is to present animals with tasks that are convenient to the human sensory, response, and motivational systems. In the case of cetaceans, there are also obvious logistical difficulties associated with their study. From a broader perspective, an extensive amount of positive research findings in the field of animal intelligence have suggested that many of the special capacities that have been attributed to humans might be more quantitative than qualitative [26,28]. Thus, ideas about what marks the boundary between human and nonhuman intelligence have undergone repeated revision and will continue to do so in the near future (Figure 5). Most notably, the cognitive capacities and intelligence of cetaceans have most likely been one of the research subjects that have been highly debated in recent years. The present study is expected to provide plausible evidence not only to respect the position of defending the potential of cetaceans for complex cognition but also to stimulate more focused studies that could support or refute the concepts that are presented throughout this paper, possibly narrowing the existing boundary between human and nonhuman intelligence.
Figure 5.
Graphical illustration of the study’s implications. The exact number of information-processing levels that can be associated with a particular brain is still unclear. Furthermore, the cortical neuron numbers in most of the large-brained cetacean species is not currently known. Recent studies have hypothesized that the larger absolute number of neurons in the human cerebral cortex (but not in the whole brain) is correlated with the superior cognitive abilities of humans compared to elephants and other large-brained mammals [12,23,129]. Furthermore, it has been suggested that the cerebral cortex of the largest whales might be composed of only a fraction of the average 16,300 million neurons found in the human cerebral cortex. Surprisingly, it has also been shown by another study that long-finned pilot whales (Globicephala melas) possess the highest number of cortical cells of any specie studied so far, including humans [30]. A larger absolute number of neurons in the cerebral cortex is a necessary but not a sufficient condition for exhibiting superior cognitive abilities or higher levels of intelligence. However, if future studies confirm the existence of unexpected large number of neurons in the cerebral cortex of the bottlenose dolphin (Tursiops truncatus), and particularly, in other large-brained cetaceans such as killer whales (Orcinus orca), humpback whales (Megaptera novaeangliae), or sperm whales (Physeter macrocephalus), the predictions made by the model would suggest the possibility of the existence of levels of intelligence in these animals that might go beyond what has previously been assumed.
Supplementary Materials
Supporting data information are available online at www.mdpi.com/1099-4300/19/10/543/s1.
Acknowledgments
The author would like to thank the University of Massachussets, Amherts (UMASS) to give time for the writing part of this paper during a postdoctoral research position at the College of Information and Computer Sciences (CICS) concerning a personal and previous research not covered by the funds of CICS, and especially to Kerry Shaw (the director of External Relations and Communications at CICS) for her valued help in the proof reading of some important parts of the manuscript. The author furthermore thanks Angel Acebes Vindel for his help on questions concerning the anatomy and physiology of the vertebrate’s brain, Nina Eriksen for providing important information on stereology techniques, Patrick Hof for the pictures of the brain of the Humpback whale, Ciro Romero Manrique de Lara for the illustration of the Phylogenetic tree, and Constatine Alexander for the picture of the Humpback whale breaching off the coast of Juneau (Alaska).
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RMR | Resting Metabolic Rate |
| DVR | Dorsal Ventricular Ridge |
| NPD | Neuron Packing Density |
References
- Butti, C.; Raghanti, M.A.; Sherwood, C.C.; Hof, P.R. The neocortex of cetaceans: Cytoarchitecture and comparison with other aquatic and terrestrial species. Ann. N. Y. Acad. Sci. 2011, 1225, 7–58. [Google Scholar] [CrossRef] [PubMed]
- Manger, P.R. An examination of cetacean brain structure with a novel hypothesis correlating thermogenesis to the evolution of a big brain. Biol. Rev. 2006, 81, 293–338. [Google Scholar] [CrossRef] [PubMed]
- Eriksen, N.; Pakkenberg, B. Total neocortical cell number in the Mysticete brain. Anat. Rec. 2007, 290, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Hof, P.R.; Van Der Gucht, E. Structure of the cerebral cortex of the Humpback whale, Megaptera Novaeangliae (Cetacean, Mysticety, Balaenopteridae). Anat. Rec. A 2007, 290, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Kojima, T. On the brain of the sperm whale (Physeter catodon L.). Sci. Rep. Whales Res. Inst. Tokyo 1951, 6, 49–72. [Google Scholar]
- Ridgway, S.H.; Hanson, A.C. Sperm Whales and Killer Whales with the Largest Brain of All Toothed Whales Show Extreme Differences in Cerebellum. Brain Behav. Evol. 2014, 83, 266–274. [Google Scholar] [CrossRef] [PubMed]
- Lyamin, O.I.; Manger, P.R.; Ridgway, S.H.; Mukhameov, L.M.; Siegel, J.M. Cetacean sleep: An unusual form of mammalian sleep. Neurosci. Biobehav. Rev. 2008, 32, 1451–1484. [Google Scholar] [CrossRef] [PubMed]
- Ridgway, S.H. The central nervous system of the bottlenose dolphin. In The Bottlenose Dolphin; Leatherwood, S., Reeves, R.R., Eds.; Academic Press: New York, NY, USA, 1990; pp. 69–97. [Google Scholar]
- Isler, K.; van Schaik, P. Metabolic costs of brain size evolution. Biol. Lett. 2006, 2, 557–560. [Google Scholar] [CrossRef]
- Mota, B.; Herculano-Houzel, S. How the cortex gets its folds and inside-out connectivity-driven model for the scaling of mammalian cortical folding. Front. Neuroanat. 2012. [Google Scholar] [CrossRef] [PubMed]
- Prothero, J.W.; Sundsten, J.W. Folding of the cerebral cortex in mammals. Brain Behav. Evol. 1984, 24, 152–167. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S. Not All Brains Are Made the Same: New Views on Brain Scaling in Evolution. Brain Behav. Evol. 2011, 78, 22–36. [Google Scholar] [CrossRef] [PubMed]
- Striedter, G.F. Principles of Brain Evolution; Sinauer Associates: Sunderland, MA, USA, 2005. [Google Scholar]
- Connor, R.C. Dolphin social intelligence: Complex alliance relationships in bottlenose dolphins and a consideration of selective environments for extreme brain size evolution in mammals. Philos. Trans. R. Soc. B 2007, 362, 587–602. [Google Scholar]
- Oelschläger, H.H.A.; Kemp, B. Ontogenesis of the sperm whale brain. J. Comp. Neurol. 1998, 399, 210–228. [Google Scholar] [CrossRef]
- Ridgway, S.H.; Au, W.W.L. Hearing and echolocation: Dolphin. In Elsevier’s Encyclopedia of Neuroscience, 2nd ed.; Adelman, G., Smith, B.H., Eds.; Elsevier: New York, NY, USA, 1999; pp. 858–862. [Google Scholar]
- Oelschläger, H.H.A.; Oelschläger, J. Brain. In Encyclopedia of Marine Mammals; Wursig, B., Thewissen, J.G.M., Eds.; Academic Press: San Diego, CA, USA, 2008; pp. 134–149. [Google Scholar]
- Güntürkun, O. Is dolphin cognition special? Brain Behav. Evol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Huggenberger, S. The size and complexity of dolphin brains a paradox? J. Mar. Biol. Assoc. UK 2008, 88, 1103–1108. [Google Scholar] [CrossRef]
- Manger, P.R. Questioning the interpretation of behavioral observations of cetaceans: Is there really support for a special intellectual status for this mammalian order? Neuroscience 2013, 250, 664–696. [Google Scholar] [CrossRef] [PubMed]
- Marino, L. Dolphin cognition. Curr. Biol. 2004, 14, R910–R911. [Google Scholar] [CrossRef] [PubMed]
- Marino, L.; Butti, C.; Connor, R.C.; Fordyce, R.E.; Herman, L.M.; Hof, P.R.; Lefevre, L.; Lusseau, D.; McCowan, B.; Nimchincky, E.A.; et al. A claim in search of evidence: Reply to Manger’s thermogenesis hypothesis of cetacean brain structure. Biol. Rev. Camb. Philos. 2008, 83, 417–440. [Google Scholar] [CrossRef] [PubMed]
- Patzke, N.; Spocter, M.A.; Karlsson, K.A.; Bertelsen, M.F.; Haagensen, M.; Chawana, R.; Streicher, S.; Kaswera, C.; Gilissen, E.; Alagaili, A.N.; et al. In contrast to many other mammals, cetaceans have relatively small hippocampi that appear to lack adult neurogenesis. Brain Struct. Funct. 2013, 220, 361–383. [Google Scholar] [CrossRef] [PubMed]
- Hart, B.L.; Hart, L.A.; Pinter-Wollman, N. Large brains and cognition: Where do elephants fit in? Neurosci. Biobehav. R. 2008, 32, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Mann, J.; Patterson, E.M. Tool use by aquatic animals. Philos. Trans. R. Soc. B 2013, 368. [Google Scholar] [CrossRef] [PubMed]
- Zentall, T.R. Animal intelligence. In The Cambridge Handbook of Intelligence; Sternberg, R.J., Kaufman, S.B., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 309–327. [Google Scholar]
- Chittka, L.; Rossiter, S.J.; Skorupski, P.; Fernando, C. What is comparable in comparative cognition? Philos. Trans. R. Soc. B 2012, 367, 2677–2685. [Google Scholar] [CrossRef] [PubMed]
- Chinea, A.; Korutcheva, E. Intelligence and embodiment: A statistical mechanics approach. Neural Netw. 2013, 40, 52–72. [Google Scholar] [CrossRef] [PubMed]
- Ridgway, S.H.; Carln, P.C.; Van Alstyne, K.R.; Hanson, A.C.; Tarpley, R.J. Comparison of Dolphins’ Body and Brain Measurements with Four other Groups of Cetaceans Reveals Great Diversity. Brain Behav. Evol. 2016, 88, 235–257. [Google Scholar] [CrossRef] [PubMed]
- Mortensen, H.S.; Pakkenberg, B.; Dam, M.; Dietz, R.; Sonne, C.; Mikkelsen, B.; Eriksen, N. Quantitative relationships in delphinid neocortex. Front. Neuroanat. 2014, 8, 132. [Google Scholar] [CrossRef] [PubMed]
- Hecht-Nielsen, R. Confabulation Theory: The Mechanism of Thought; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Tomer, R.; Denes, A.S.; Tessmar-Raible, K.; Arendt, D. Profiling by image registration reveals common origin of annelid mushroom bodies and vertebrate pallium. Cell 2010, 142, 800–809. [Google Scholar] [CrossRef] [PubMed]
- Dugas-Ford, J.; Rowell, J.J.; Ragsdale, C.W. Cell-type homologies and the origins of the neocortex. Proc. Natl. Acad. Sci. USA 2012, 109, 16974–16979. [Google Scholar] [CrossRef] [PubMed]
- Karten, H.J. Vertebrate brains and evolutionary connectomics: On the origins of the mammalian ‘neocortex’. Philos. Trans. R. Soc. B 2015, 370, 60. [Google Scholar] [CrossRef] [PubMed]
- Taylor, P.; Hobbs, J.N.; Burroni, J.; Siegelmann, H. The global landscape of cognition:hierarchical aggregation as an organizational principle of human cortical networks and functions. Sci. Rep. 2015, 5, 18112. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, A.; Woolley, S.M.N. Coding principles in the avian brain. Proc. Natl. Acad. Sci. USA 2015, 112, 3517–3522. [Google Scholar] [CrossRef] [PubMed]
- Felleman, D.J.; Van Essen, D.C. Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1991, 1. [Google Scholar] [CrossRef]
- Salazar, R.F.; Dotson, N.M.; Bressler, S.L.; Gray, C.M. Content Specific Fronto-Parietal Synchronization during Visual Working Memory. Science 2012, 338, 1097–1100. [Google Scholar] [CrossRef] [PubMed]
- Churchland, P.; Sejnowski, T. The Computational Brain; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Reichl, L.E. A Modern Course in Statistical Physics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Hermann, C. Statistical Physics (Including Applications to Condensed Matter); Springer: New York, NY, USA, 2005. [Google Scholar]
- Howarth, C.; Gleeson, P.; Attwell, D. Updated energy budgets for neural computation in the neocortex and cerebellum. J. Cerebr. Blood Flow Metab. 2012, 32, 1222–1232. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, S.; Stimpson, C.D.; Bauernfeind, A.L.; Schapiro, S.J.; Baze, W.B.; McArthur, M.J.; Bronson, E.; Hopkins, W.D.; Semendeferi, K.; Jacobs, B.; et al. Dendritic morphology of pyramidal neurons in the chimpanzee neocortex: Regional specializations and comparison to humans. Cereb. Cortex 2013, 23, 2429–2436. [Google Scholar]
- Butti, C.; Janeway, C.M.; Townshend, C.; Wicinski, B.A.; Reidenberg, J.S.; Ridgway, S.H.; Sherwood, C.C.; Hof, P.R.; Jacobs, B. The neocortex of cetartiodactyls: I. A comparative Golgi analysis of neuronal morphology in the bottlenose dolphin (Tursiops truncatus), the minke whale (Balaenoptera acutorostrata), and the humpback whale (Megaptera novaeangliae). Brain Struct. Funct. 2015, 220, 3339–3368. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, B.; Schall, M.; Prather, M.; Kapler, E.; Driscoll, L.; Baca, S.; Jacobs, J.; Ford, K.; Wainwright, M.; Treml, M. Regional dendritic and spine variation in human cerebral cortex: A quantitative golgi study. Cereb. Cortex 2001, 11, 558–571. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, B.; Harland, T.; Kennedy, D.; Schall, M.; Wicinski, B.; Butti, C.; Hof, P.R.; Sherwood, C.C.; Manger, P.R. The neocortex of cetartiodactyls. II. Neuronal morphology of the visual and motor cortices in the giraffe (Giraffa camelopardalis). Brain Struct. Funct. 2015, 220, 2851–2872. [Google Scholar] [CrossRef] [PubMed]
- Nieuwenhuys, R.; Ten Donkelaar, H.J.; Nicholson, C. The Central Nervous System of Vertebrates; Springer: Berlin, Germany, 1998; Volume 3. [Google Scholar]
- Van Essen, D.C. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 1997, 385, 313–318. [Google Scholar] [CrossRef] [PubMed]
- Harrison, K.H.; Hof, P.; Wang, S.S.H. Scaling laws in the mammalian neocortex: Does form provides clues to function? J. Neurocytol. 2002, 31, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Ventura-Antunes, L.; Mota, B.; Herculano-Houzel, S. Different scaling of white matter volume, cortical connectivity, and gyrification across rodent and primate brains. Front. Neuroanat. 2013, 7. [Google Scholar] [CrossRef]
- Herculano-Houzel, S.; Manger, P.R.; Kaas, J.H. Brain scaling in mammalian evolution as a consequence of concerted and mosaic changes in number of neurons and average neuronal size. Front. Neuroanat. 2014, 8, 77. [Google Scholar] [CrossRef] [PubMed]
- Goodman, M.; Sterner, K.N.; Islam, M.; Uddin, M.; Sherwood, C.C.; Hof, P.R.; Hou, Z.C.; Lipovich, L.; Jia, H.; Grossman, L.I.; et al. Phylogenetic analyses reveal convergent patterns of adaptive evolution in elephants and human ancestries. Proc. Natl. Acad. Sci. USA 2009, 106, 20824–20829. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Bedny, M.; Caramazza, A. Perception, action, and word meanings in the human brain: The case from action verbs. Ann. N. Y. Acad. Sci. 2011, 1224, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Pullvermüller, F.; Huss, M.; Kheriff, F.; Moscoso del Prado Martin, F.; Hauk, O. Motor cortex maps articulatory features of speech sounds. Proc. Natl. Acad. Sci. USA 2006, 103, 7865–7870. [Google Scholar] [CrossRef] [PubMed]
- Pullvermüller, F. Semantic embodiment, disembodiment or misembodiment? In search of meaning in modules and neuron circuits. Brain Lang. 2013, 127, 86–103. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S.; Collins, C.E.; Wong, P.; Kaas, J.H. The basic nonuniformity of the cerebral cortex. Proc. Natl. Acad. Sci. USA 2010, 105, 12593–12598. [Google Scholar] [CrossRef] [PubMed]
- Nieuwenhuys, R.; Voogd, J.; Van Huijzen, C. The Human Central Nervous System; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wang, Y.; Brzozowska-Prechtl, A.; Karten, H.J. Laminar and columnar auditory cortex in avian brain. Proc. Natl. Acad. Sci. USA 2010, 107, 12676–12681. [Google Scholar] [CrossRef] [PubMed]
- Ahumada-Galleguillos, P.; Fernandez, M.; Marin, G.J.; Letelier, J.C.; Mpodozis, J. Anatomical Organization of the Visual Dorsal Ventricular Ridge in the Chick (Gallus gallus): Layers and Columns in the Avian Pallium. J. Comp. Neurol. 2015, 406, 329–345. [Google Scholar] [CrossRef] [PubMed]
- Husband, S.A.; Shimizu, T. Efferent projections of the ectostriatum in the pigeon Columba livia. J. Comp. Neurol. 1999, 406, 329–345. [Google Scholar] [CrossRef]
- Ulinsky, P. Dorsal Ventricular Ridge: A Treatise on Forebrain Organization in Reptiles and Birds; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Manger, P.R.; Slutsky, D.A.; Molnar, Z. Visual subdivisions of the dorsal ventricular ridge of the iguana (Iguana iguana) as determined by electrophysiologic mapping. J. Comp. Neurol. 2002, 453, 226–246. [Google Scholar] [CrossRef] [PubMed]
- McGowen, M.R.; Grossman, L.I.; Wildman, D.E. Dolphin genome provides evidence for adaptive evolution of nervous system genes and molecular rate slowdown. Philos. Trans. R. Soc. B 2012, 279, 3643–3651. [Google Scholar] [CrossRef] [PubMed]
- Byrne, R.W.; Whiten, A. Machiavellian Intelligence: Social Expertise and the Evolution of the Intellect in Monkeys, Apes and Humans; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Olkowicz, S.; Kocourek, M.; Lucan, R.K.; Portes, M.; Fitch, W.T.; Herculano-Houzel, S.; Nemec, P. Birds have primate-like numbers of neurons in the forebrain. Proc. Natl. Acad. Sci. USA 2016, 113, 7255–7260. [Google Scholar] [CrossRef] [PubMed]
- Schoenemann, P.T.; Sheehan, M.J.; Glotzer, D.L. Prefrontal white matter volume is disproportionately larger in humans than in other primates. Nat. Rev. Neurosci. 2005, 8, 242–252. [Google Scholar] [CrossRef] [PubMed]
- Schoenemann, P.T. Evolution of the size and functional areas of the human brain. Annu. Rev. Anthropol. 2006, 35, 379–406. [Google Scholar] [CrossRef]
- Rilling, J.K.; Insel, T.R. The primate neocortex in comparative perspective using magnetic resonance imaging. J. Hum. Evol. 1999, 37, 191–223. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, B.; Lubs, J.; Hannan, M.; Anderson, K.; Butti, C.; Sherwood, C.C.; Hof, P.R.; Manger, P.R. Neuronal morphology in the African elephant (Loxodonta africana) neocortex. Brain Struct. Funct. 2011, 215, 273–298. [Google Scholar] [CrossRef] [PubMed]
- Douglas-Fields, R. Map the other brain. Nature 2013, 501, 25–26. [Google Scholar] [CrossRef]
- Herculano-Houzel, S.; Kaas, J.H. Gorilla and orangutan brains conform to the primate cellular scaling rules: implications for human evolution. Brain Behav. Evol. 2011, 77, 33–44. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S.; Avelino-de-Souza, K.; Neves, K.; Porfírio, J.; Messeder, D.; Mattos Feijó, L.; Maldonado, J.; Manger, P. The elephant brain in numbers. Front. Neuroanat. 2014, 8. [Google Scholar] [CrossRef]
- Bianchi, S.; Stimpson, C.D.; Duka, T.; Larsen, M.D.; Janssen, W.G.M.; Collins, Z.; Bauernfeind, A.L.; Schapiro, S.J.; Baze, W.B.; McArthur, M.J.; et al. Synaptogenesis and development of pyramidal neuron dendritic morphology in the chimpanzee neocortex resembles humans. Proc. Natl. Acad. Sci. USA 2013, 110, 10395–10401. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, M.; Call, J. The Gestural Communication of Apes and Monkeys; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2007. [Google Scholar]
- Costa, D.P.; Williams, T.M. Marine Mammals Energetics. In The Biology of Marine Mammals; Reynold, J., Twiss, J., Eds.; The Smithsonian Institution Press: Washington, DC, USA, 2000; pp. 176–211. [Google Scholar]
- Hakeem, A.Y.; Hof, P.R.; Sherwood, C.C.; Switzer, R.C.; Rasmussen, L.R.L.; Allman, J.M. Brain of the African elephant (Loxodonta africana): Neuroanatomy from magnetic resonance images. Anat. Rec. 2005, 287, 1117–1127. [Google Scholar] [CrossRef] [PubMed]
- Hof, P.R.; Chanis, R.; Marino, L. Cortical Complexity in Cetacean Brains. Anat. Rec. 2005, 287, 1142–1152. [Google Scholar] [CrossRef] [PubMed]
- McKay, G.M. Behavior and Ecology of the Asiatic Elephant in Southeastern Ceylon; Smithsonian Institution, Government Printing Office: Washington, DC, USA, 1973.
- Manger, P.R.; Prowse, M.; Haagensen, M.; Hemingway, J. A quantitative analysis of neocortical gyrencephaly in African elephants (Loxodonta Africana) and six species of cetaceans: comparisons to other mammals. J. Comp. Neurol. 2012, 520, 2430–2439. [Google Scholar] [CrossRef] [PubMed]
- Mink, J.W.; Blumenschine, R.J.; Adams, D.B. Ratio of central nervous system to body metabolism in vertebrates: Its constancy and functional basis. Am. J. Physiol. 1981, 241, 203–212. [Google Scholar]
- Leonard, W.R.; Snodgrass, J.J.; Robertson, M.L. Effects of brain evolution on human nutrition and metabolism. Annu. Rev. Nutr. 2007, 27, 311–327. [Google Scholar] [CrossRef] [PubMed]
- Lockyer, C. All creatures great and smaller: A study in cetacean life history energetics. J. Mar. Biol. Assoc. UK 2007, 87, 1035–1045. [Google Scholar] [CrossRef]
- Sherwood, C.C.; Stimpson, C.D.; Raghanti, M.A.; Wildman, D.E.; Uddin, M.; Grossman, L.I.; Goodman, M.; Redmond, J.C.; Bonar, C.J.; Erwin, J.M. Evolution of increased glia-neuron ratios in the human frontal cortex. Proc. Natl. Acad. Sci. USA 2006, 103, 13606–13611. [Google Scholar] [CrossRef] [PubMed]
- Herman, L.M. Body and self in dolphins. Conscious. Cogn. 2012, 21, 526–545. [Google Scholar] [CrossRef] [PubMed]
- Xitco, J.M.; Gory, J.D.; Kuczaj, S.A. Spontaneous pointing by bottlenose dolphins (Tursiops truncatus). Anim. Cogn. 2001, 4, 115–123. [Google Scholar] [CrossRef]
- Visser, I.N.; Smith, T.G.; Bullock, I.D.; Green, G.D.; Carlsson, O.G.L.; Imberti, S. Antartica peninsula killer whales (Orcinus orca) hunt seals and penguin on floating ice. Mar. Mamm. Sci. 2008, 24, 225–234. [Google Scholar] [CrossRef]
- Foote, A.D.; Griffin, R.M.; Howitt, D.; Larsson, L.; Miller, P.J.O.; Hoelzel, A.R. Killer whales are capable of vocal learning. Biol. Lett. 2006, 2, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Baird, R.W. The killer whale: Foraging specializations and group hunting. In Cetacean Societies: Field Studies of Dolphins and Whales; Mann, J., Conno, R.C., Tyack, P.L., Whitehead, H., Eds.; University of Chicago Press: Chicago, IL, USA, 2000. [Google Scholar]
- Whitehead, H.; Rendell, L. The Cultural Lives of Whales and Dolphins; University of Chicago Press: Chicago, IL, USA, 2015. [Google Scholar]
- Montgomery, S.H.; Geisler, J.H.; McGowen, M.R.; Fox, C.; Marino, L.; Gatesy, J. The Evolutionary History of Cetacean Brain and Body Size. Evolution 2013, 67, 3339–3353. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, F.S.; Szabo, A.S.; Pack, A.; Nahmens, J. The social structure of bubble net feeding whales in SE Alaska. In Proceedings of the 20th Biennal Conference on the Biology of Marine Mammals, Dunedin, New Zealand, 9 December 2013. [Google Scholar]
- Stimpert, A.K.; Au, W.W.; Parks, S.E.; Hurst, T.; Wiley, D.N. Common humpback whale (Megaptera novaeangliae) sound types for passive acoustic monitoring. J. Acoust. Soc. Am. 2011, 129, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Fournet, M.; Szabo, A. Vocal repertoire of southeast Alaska humpback whales (Megaptera novaeangliae). J. Acoust. Soc. Am. 2013, 134, 3988. [Google Scholar] [CrossRef]
- Pitman, R.L.; Deecke, V.B.; Gabriele, C.M.; Srinivasan, M.; Black, N.; Denkinger, J.; Durban, J.W.; Mathews, E.A.; Matkin, D.R.; Neilson, J.L.; et al. Humpback whales interfering when mammal-eating killer whales attack other species: Mobbing behavior and interspecific altruism? Mar. Mamm. Sci. 2016. [Google Scholar] [CrossRef]
- Whitehead, H. Sperm Whales: Social Evolution in the Ocean; University of Chicago Press: Chicago, IL, USA, 2003. [Google Scholar]
- Roth, G.; Dicke, U. Evolution of the brain and intelligence. Trends Cogn. Sci. 2005, 9, 250–257. [Google Scholar] [CrossRef] [PubMed]
- Dicke, U.; Roth, G. Neuronal Factors Determining High Intelligence. Philos. Trans. R. Soc. Lond. B 2016, 371. [Google Scholar] [CrossRef] [PubMed]
- Nettelbeck, T. Basic processes of intelligence. In The Cambridge Handbook of Intelligence; Sternberg, R.J., Kaufman, S.B., Eds.; Cambridge University Press: Cambridge, UK, 2011; pp. 371–388. [Google Scholar]
- Nettelbeck, T.; Wilson, C. A cross-sequential analysis of developmental differences in speed of visual information processing. J. Exp. Child Psychol. 1985, 40. [Google Scholar] [CrossRef]
- Sheppard, L.D.; Vernon, P.A. Intelligence and speed of information-processing: A review of 50 years of research. Personal. Individ. Differ. 2008, 44, 535–551. [Google Scholar] [CrossRef]
- Howard, C.V.; Reid, M.G. Unbiased Stereology: Three-Dimensional Measurement in Microscopy; BIOS: Oxford, UK, 1998; ISBN 1-85996-071-5. [Google Scholar]
- Azevedo, F.A.C.; Carvalho, L.R.B.; Grinberg, L.T.; Farfel, J.M.; Ferretti, R.E.L.; Leite, R.E.P.; Filho, W.J.; Lent, R.; Herculano-Houzel, S. Equal Numbers of Neuronal and Nonneuronal Cells Make the Human Brain an Isometrically Scaled-up Primate Brain. J. Comp. Neurol. 2009, 513, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Pakkenberg, B.; Gundersen, H.J. Neocortical neuron number in humans: Effect of sex and age. J. Comp. Neurol. 1997, 384, 312–320. [Google Scholar] [CrossRef]
- Witelson, S.F.; Kigar, D.L.; Harvey, T. The exceptional brain of Albert Einstein. Lancet 1999, 353, 2149–2153. [Google Scholar] [CrossRef]
- Chittka, L.; Niven, J. Are bigger brains better? Curr. Biol. 2009, 19, R995–R1008. [Google Scholar] [CrossRef] [PubMed]
- Irving, L.; Scholander, P.F.; Grinnell, S.W. The respiration of the porpoise, Tursiops truncatus. J. Cell. Comp. Physiol. 1941, 17, 145–168. [Google Scholar] [CrossRef]
- Hampton, I.F.G.; Whittow, G.C.; Szekercezes, J.; Rutherford, S. Heat transfer and body temperature in the Atlantic bottlenosed dolphin, Tursiops truncatus. Int. J. Biometeorol. 1971, 15, 247–253. [Google Scholar] [CrossRef] [PubMed]
- De Graaf, A.S. Anatomical Aspects of the Cetacean Brain Stem; Von Gorcum: Assen, The Netherlands, 1967; pp. 1–169. [Google Scholar]
- Ridgway, S.H.; Bullock, T.H.; Carder, T.A.; Seeley, R.L.; Woods, D.; Galanbos, R. Auditory brainstem response in dolphins. Proc. Natl. Acad. Sci. USA 1981, 78, 1943–1947. [Google Scholar] [CrossRef]
- Ridgway, S.H. Neural time and movement time in choice of whistle or pulse burst responses to different auditory stimuli by dolphins. J. Acoust. Soc. Am. 2011, 129, 1073–1080. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.S.H.; Shultz, J.R.; Burish, M.J.; Harrison, K.H.; Hof, P.R.; Towns, L.C.; Wagers, M.W.; Wyatt, K.D. Functional trade-offs in white matter axonal scaling. J. Neurosci. 2008, 28, 4047–4056. [Google Scholar] [CrossRef] [PubMed]
- Gusnard, D.A.; Raichle, M.E. Searching for a Baseline: Functional Imaging and the Resting Human Bran. Nat. Rev. Neurosci. 2001, 2, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.L.; Cox, M.M. Lehninger Principles of Biochemistry, 6th ed.; Macmillan Learning Publishers: London, UK, 2012. [Google Scholar]
- Belanger, M.; Allaman, I.; Magistretti, P. Brain Energy Metabolism: Focus on Astrocyte-Neuron Metabolism Cooperation. Cell 2011, 14. [Google Scholar] [CrossRef] [PubMed]
- Pellerin, L.; Magistretti, P.J. Food for Thought: Challenging the Dogmas. J. Cereb. Blood Flow Metab. 2003, 23, 1282–1286. [Google Scholar] [CrossRef] [PubMed]
- Pellerin, L.; Magistretti, P.J. Neuroenergetics: Calling up astrocytes to satisfy hungry neurons. Neuroscientist 2004, 10, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Pellerin, L.; Bouzier-Store, A.K.; Aubert, A.; Serres, S.; Merle, M.; Costalat, R.; Magistretti, P.J. Activity-dependent regulation of energy metabolism by astrocytes: An update. Glia 2007, 55, 1251–1262. [Google Scholar]
- Marino, L.; Sol, D.; Toren, K.; Lefebvre, L. Does Diving Limit rain Size in Cetaceans? Mar. Mamm. Sci. 2006, 22, 413–425. [Google Scholar] [CrossRef]
- Ridgway, S.H.; Houser, D.; Finneran, J.J.; Carder, D.A.; Keogh, M.; Van Bonn, W.; Smith, C.R.; Scadeng, M.; Mattrey, R.; Hoh, C. Functional Imaging of Dolphin Brain Metabolism and Blood Flow. J. Exp. Biol. 2014, 209, 2902–2910. [Google Scholar] [CrossRef] [PubMed]
- Williams, T.M.; Friedl, W.A.; Haun, J.E. The physiology of bottlenose dolphins (Tursiops truncatus): Heart rate, metabolic rate and plasma kactate concentrations during exercise. J. Exp. Biol. 1993, 179, 31–46. [Google Scholar] [PubMed]
- Wyss, M.T.; Jolivet, R.; Buck, A.; Magistretti, P.J.; Weber, B. In Vivo Evidence for Lactate as a Neuronal Energy Source. J. Neurosci. 2011, 31, 7477–7485. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S.; Lent, R. Isotropic fractionator: A simple, rapid method for the quantification of total cell and neuron numbers in the brain. J. Neurosci. 2005, 25, 2518–2521. [Google Scholar] [CrossRef] [PubMed]
- Gundersen, H.J.; Jensen, E.B. The Efficiency of systematic sampling in stereology and its prediction. J. Microsc. 1987, 147, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Gundersen, H.J.; Jensen, E.B.; Kiêu, K.; Nielsen, J. The Efficiency of systematic sampling in stereology reconsidered. J. Microsc. 1999, 193, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Wallöe, S.; Eriksen, N.; Dabelsteen, T.; Pakkenberg, B. A Neurological comparative study of the harp seal (Pagophylus groenlandicus) and harbour porpoise (Phocoena phocoena). Anat. Rec. 2010, 293, 2129–2135. [Google Scholar] [CrossRef] [PubMed]
- Kazu, R.S.; Maldonado, J.; Mota, B.; Manger, P.R.; Herculano-Houzel, S. Cellular scaling rules for the brain of Artiodactyla include a highly folded cortex with few neurons. Front. Neuroanat. 2014, 8, 128. [Google Scholar] [CrossRef] [PubMed]
- Herculano-Houzel, S. The Human Advantage: A New Understanding of How Our Brain Became Remarkable; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Venn-Watson, S.; Carlin, K.; Ridgway, S. Dolphins as animal models for type 2 diabetes: Sustained, post-prandial hyperglycemia and hyperinsulinemia. Gen. Comp. Endocrinol. 2011, 170, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Mirceta, S.; Signore, A.V.; Burns, J.M.; Cossins, A.R.; Campbell, K.L.; Berenbrink, M. Evolution of Mammalian Diving Capacity Traced by Myoglobin Net Surface Charge. Science 2013, 340, 1234192. [Google Scholar] [CrossRef] [PubMed]
- Marino, L.; Connor, R.C.; Fordyce, E.R.; Herman, L.M.; Hof, P.R.; Lefebvre, L.; Lusseau, D.; McCowan, B.; Nimchinsky, E.A.; Pack, A.A.; et al. Cetaceans Have Complex Brains for Complex Cognition? PLoS Biol. 2007, 22, 413–425. [Google Scholar]
- Herrmann, E.; Call, J.; Hernandez-LLoreda, M.V.; Hare, B.; Tomasello, M. Humans Have Evolved Specialized Skills of Social Cognition: The Cultural Intelligence Hypothesis. Science 2007, 317, 1360–1366. [Google Scholar] [CrossRef] [PubMed]
- van Schaik, C.P.; Burkart, J.M. Social Learning and evolution: The cultural intelligence hypothesis. Philos. Trans. R. Soc. Lond. Biol. Sci. 2011, 366, 1008–1026. [Google Scholar] [CrossRef] [PubMed]
- Zentall, T.R. Animal memory: The role of instructions. Learn. Motiv. 1997, 28, 248–267. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).