Abstract
One of the central questions of humankind is: which chemical and physical conditions are necessary to make life possible? In this “origin-of-life” context, formamide plays an important role, because it has been demonstrated that prebiotic molecules can be synthesized from concentrated formamide solutions. Recently, it could be shown, using finite-element calculations combining thermophoresis and convection processes in hydrothermal pores, that sufficiently high formamide concentrations could be accumulated to form prebiotic molecules (Niether et al. (2016)). Depending on the initial formamide concentration, the aspect ratio of the pores, and the ambient temperature, formamide concentrations up to 85 wt % could be reached. The stationary calculations show an effective accumulation, only if the aspect ratio is above a certain threshold, and the corresponding transient studies display a sudden increase of the accumulation after a certain time. Neither of the observations were explained. In this work, we derive a simple heuristic model, which explains both phenomena. The physical idea of the approach is a comparison of the time to reach the top of the pore with the time to cross from the convective upstream towards the convective downstream. If the time to reach the top of the pore is shorter than the crossing time, the formamide molecules are flushed out of the pore. If the time is long enough, the formamide molecules can reach the downstream and accumulate at the bottom of the pore. Analysing the optimal aspect ratio as function of concentration, we find that, at a weight fraction of , a minimal pore height is required for effective accumulation. At the same concentration, the transient calculations show a maximum of the accumulation rate.
1. Introduction
One of the main issues about the origin of life is the question how organic material could have accumulated in the primordial ocean to reach high enough concentrations so that reactions towards larger, more complex molecules outweigh hydrolysis. For the formation of ribonucleic acid (RNA) from nucleotides, an active transport mechanism in a temperature gradient has been suggested to reach high concentrations of these prebiotic molecules [1]. The investigated accumulation process results from a combination of convection and thermophoresis inside a pore with an asymmetrical temperature profile. A probable setting for such systems in great number are porous minerals which are heated by hydrothermal vents from one side and cooled by the ocean from the other.
In our earlier paper [2], we posed the question whether the reaction from simple, anorganically formed molecules, such as hydrogen cyanide and formamide (FA), into the building blocks of RNA could be promoted by the same accumulation mechanism. Formamide has been discussed as an educt for the formation of prebiotic molecules for almost 50 years [3,4,5,6,7,8]. Saladino et al. synthesized all nucleobases from concentrated aqueous FA solutions [5]. In our previous work, we measured the thermophoretic properties of FA in water as a function of temperature and concentration and used these data to conduct finite element calculations. We investigated how the distribution of FA in water develops as function of time in hydrothermal pores, which underlie a temperature gradient. In pores with sufficiently large aspect ratios, we found a very high FA concentration in the order of 85 wt %, which can be reached even with very small initial concentrations, as low as wt %, if the time for accumulation is long enough. In a previous study, restricted to the dilute regime, Baaske et al. [1] found an exponential rise of the accumulation as function of the aspect ratio of the pore. In their study, they used the approximation . Using the full expression, we identified three regimes of the accumulation fold: a weak exponential growth at low aspect ratios, a sharp rise in the intermediate range, and finally, a saturation of the accumulation fold at large aspect ratios. Independent of the initial concentration, these three regimes could always be identified, if it was possible to reach the high aspect ratios. Due to numerical instabilities this was not always the case, if the diffusion was too fast or the Soret coefficient too low. The focus of this work is to expand on our previous paper by additional time-dependent simulations and a heuristic model that explains the strong dependence of the accumulation on pore geometry as well as its progression with time.
Thermophoresis, also known as thermodiffusion or Ludwig-Soret effect, is the mass diffusion of particles or molecules induced by a temperature gradient [9]. Several theoretical approaches exist to describe thermodiffusion of polymer solutions, colloidal suspensions, and other liquid mixtures [10,11,12,13]. A good overview on the physics of the effect is given by the recent reviews by Würger [11] and by Köhler and Morozov [13], highlighting theoretical and experimental aspects of the phenomena for colloids and non-polar liquid mixtures, respectively. Further, simulations have been performed to investigate attractive and repulsive interactions between charged and uncharged colloidal particles [14,15] or to study the influence of chain length and stiffness of polymers [16]. For aqueous low molecular weight mixtures, specific interactions and the addition of salt have been investigated [17,18]. The influence of interfacial effects on the thermophoresis have been studied systematically using microemulsions [19], but it turned out that it was not possible to describe the experimental results by using existing theories [19,20]. The best agreement between experiment and theoretical concepts are found for charged spherical and rod-like colloids [21,22,23], but when interfacial effects like the coverage by surfactants play a role, existing theoretical concepts fail [24]. For polar liquid mixtures, such as aqueous FA solutions, there is so far no microscopic theory to describe thermophoresis. In a binary fluid mixture the mass flux in a temperature gradient can be expressed as
with contributions from the thermodiffusion along the temperature gradient and from the Fickian diffusion along the resulting concentration gradient . For a stationary temperature gradient, the Fickian diffusions balances after some time the thermodiffusion and a steady state is reached. This defines the Soret coefficient , which is also a measure for the resulting concentration gradient, if a certain temperature gradient is applied. Generally, the magnitude of the Soret coefficient becomes larger, if the diffusion slows down. This implies that for slow diffusing molecules or particles smaller gradients are required to obtain the same concentration difference. Aqueous systems are of special interest due to their relevance in biotechnology. While charge contributions to the thermophoresis of solute molecules are well understood, the influence of contributions by the hydration layer are still unclear. It is known that the breaking of hydrogen bonds due to the surrounding solvent increases the Soret coefficient of the solute molecules. To induce a breakage of hydrogen bonds, one can add an ingredient with a strong affinity to water [25] or the bonds can be disrupted by increasing the temperature [26]. This leads to a temperature dependence of that is alike for a great number of biological and synthetic molecules in water [27]. Iacopini and Piazza [28] descibed the dependence with the empirical equation
where , and are fitting parameters. Recently, it became clear that the number of hydrogen-bond sites in the solute molecule is an important parameter when describing the temperature dependence of and the thermodiffusion coefficient . It turns out that, for solutes belonging to a homologous series, there is a linear dependence of to the difference of donor and acceptor sites [29]. Although the reason for this linearity is not yet clear, it can be safely assumed that hydrogen bonding is relevant to the FA/water system as well.
2. Accumulation in Hydrothermal Pores
Figure 1 shows the investigated system, a 2D pore with width and height . The aspect ratio is . It has been shown that finite element calculations of 3D systems give qualitatively the same results as calculations of 2D systems [1]. The reservoir with an initial concentration is implemented by holding the concentration at the upper wall constant at . Finite element calculations with different initial concentrations were performed. The naturally occurring concentration of FA in the primordial ocean at a pH between 6–8 and an average temperature of 10 °C is estimated to be only of the order wt %. In shallow lakes, where the large surface leads to faster vaporization of water and a more effective diffusion of FA from the atmosphere into the lake, higher concentrations (about wt %) are estimated [4]. The left and the right walls are set to different temperatures (with a temperature difference of 30 K), which results in thermodiffusion of FA (grey arrows in Figure 1) and convection (white arrows). We solved the coupled Navier-Stokes-, diffusion-, and heat-transfer equations, using commercial finite element software (COMSOL), and determined the accumulation of FA. For the FA/water system, the whole concentration range from 0 (pure water) to 1 (pure formamide) is accessible, because they are miscible in any ratio. We measured the temperature and concentration dependence of and (thermal- and mass diffusion coefficient) and used the results as well as literature data of specific mass density, viscosity, heat capacity, and heat conductivity of FA/water mixtures as input for the numerical calculations [2].
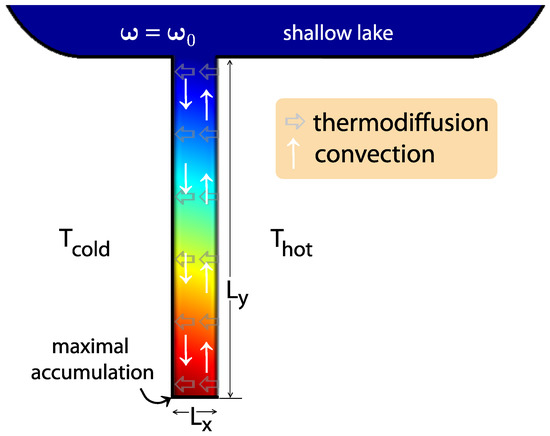
Figure 1.
Contour plot of the concentration profile in a pore with aspect ratio 10 connected to a reservoir in the stationary state. The vertical and horizontal arrows mark the convective and thermodiffusive flow, respectively.
The combination of convection and thermodiffusion inside the pore results in accumulation of FA in the cold bottom corner of the pore. From an initially constant concentration within the whole pore, a concentration profile arises as illustrated by the contour plot in Figure 1. We see the highest concentrations within the dark red region at the cold bottom corner; here, a possible formation of nucleobases from FA would take place. The concentration in this corner defines the accumulation-fold that is of interest in the following work. We analysed the dependence of FA accumulation on initial FA concentration, ambient temperature, and aspect ratio of the pore.
3. Experimental Results
We used a transient grating technique to measure the Soret coefficient of FA in water [2]. Figure 2 displays as a function of the weight fraction in the temperature range between 10 °C and 70 °C. Note that is positive in the entire invesigated temperature and concentration range indicating that FA is thermophobic and accumulates in cold regions. In order to describe the concentration dependence, we use an empirical equation,
with the fitting parameters a, K and . A least square fit according to Equation (3), often denoted as Hill equation [30,31], is depicted as dashed lines in Figure 2. With increasing temperature, the concentration dependent slope decreases, so that we observe an intersection around a weight fraction of 0.2. This is typical and has also been found for other associated mixtures [32]. Peculiar is the fact that of FA increases with concentration, which can support a self-enhanced accumulation process.
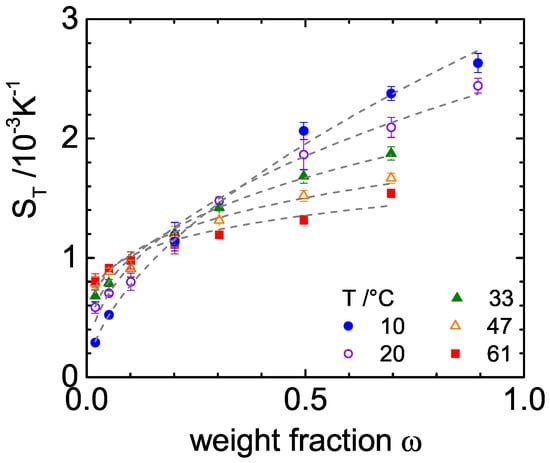
Figure 2.
Soret coefficient as function of the formamide weight fraction, ω, for various temperatures. The solid lines correspond to a fit according to Equation (3).
We studied for three different mean temperatures = 25, 45 and 75 °C the accumulation-fold in a hydrothermal pore as function of the aspect ratio height over width. At each ambient temperature, the width of the pore was fixed to its optimal value, which decreased with increasing ambient mean temperature from 180 to 100 m [2]. Note that an optimum is only found for very low concentrations, while at high concentrations the accumulation-fold remains on the same level for low aspect ratios. At high aspect ratios, we observe always a decrease, because in this case the convection process becomes very fast and prevents an accumulation inside the pore. In Figure 3a the accumulation-fold is displayed as a function of the aspect ratio r. We varied the initial concentration between –. For all studies, we observe for the accumulation-fold as function of the aspect ratio r an initial weak exponential growth, followed by a steep rise at a specific aspect ratio (an expression for is derived in the heuristic model (see Equation (7))) and finally the accumulation-fold passes on to a plateau. In this regime, the accumulation-fold is approaching a value of , so that we have almost pure FA in the lower left corner of the hydrothermal pore. It turns out that the saturation plateau is reached at lower aspect ratios for larger temperatures. At lower ambient temperatures, an accumulation in longer pores is favoured. In conclusion, we can say that the steep increase of the accumulation fold strongly depends on the magnitude of the Soret coefficient at low FA concentrations.
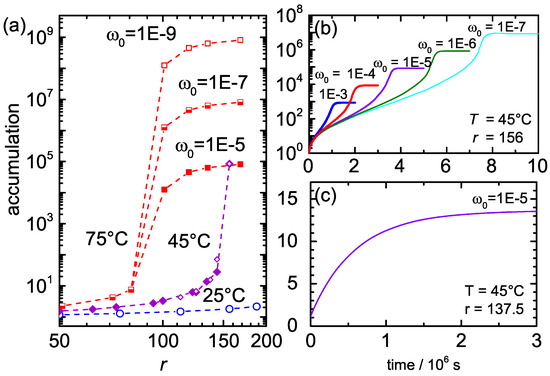
Figure 3.
(a) Accumulation-fold of formamide as function of the aspect ratio r for various initial weight fractions, , and temperatures as indicated. The accumulation-fold of formamide at 25, 45 and 75 °C has been determined at an optimal width of 180, 160 and 100 m, respectively [2]. All curves show an initial exponential growth and then a steep increase, which levels off when the accumulation becomes so strong that it is close to the pure component; (b) Time-dependent study of the accumulation as function of time at 45 °C for various initial concentrations at a high aspect ratio of ; (c) Time dependence of the accumulation fold for a low aspect ratio of .
The time dependence of the accumulation-fold is shown in Figure 3b. We fixed the ambient temperature and pore aspect ratio to = 45 °C and , respectively. For the highest studied initial concentration , the saturation plateau is reached after 11 days, while for the lowest concentration of the saturation time is reached after 90 days. For the more likley low initial concentrations between and , the accumlations takes several months, which seems plausible. As in the case of Figure 3a, we observe at high aspect ratios () that the accumulation-fold as function of time increases steeply before it saturates. A similar behaviour can be observed for all initial concentrations. In contrast, Figure 3c shows that, for a lower aspect ratio of (), we do not observe a steep rise of the accumulation fold as function of time. This signifies that there is no influx of FA molecules into the pore, but only a slight increase of concentration in the cold bottom corner due to relocation of the FA already present inside the pore.
In Figure 4a the accumulation rate is plotted against time (derivative of the accumulation displayed in Figure 3b). For all concentrations, there is a clear maximum before the accumulation rate drops. Figure 4b shows the maximum concentration in the pore at the time of maximum accumulation rates. Independently of initial concentration (x-axis), the accumulation slows down once the concentration reaches 50 wt %. Figure 4c shows a contour plot of the flow speed and illustrates the three types of mass transport occurring inside the pore: convection, Fickian diffusion, and thermodiffusion.
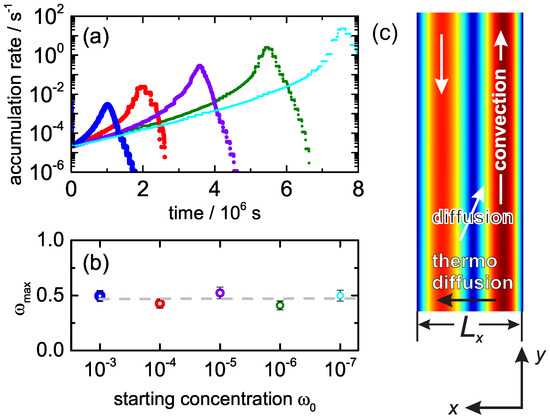
Figure 4.
(a) Accumulation rate as function of time for the same five different initial concentrations as in Figure 3b; (b) Concentration at the maximum accumulation rate as function of the initial concentration, ; (c) Illustration of the three processes, diffusion, thermal diffusion, and convection, in the hydrothermal pore with the width . The colour scale illustrates flow speed.
4. Discussion
In order to answer the question, why a certain height to width ratio, , is required to achieve high accumulation-folds of the order of 85 wt %, we looked at the time derivative of the accumulation fold. The determined accumulation rate versus time is shown in Figure 4a. For all simulation studies, we find a maximum of the accumulation rate at a certain time. We find for all initial concentrations that the time at which the accumulation speed shows a maximum corresponds to the same accumulated concentration of approximately 50 wt % (see Figure 4b).
To get an estimate for the height at which the accumulation becomes effective, we suggest the following Gedankenexperiment. The time to reach the top of the pore, which scales with its height, needs to be long enough so that the molecule can cross the middle of the pore in x-direction to reach the down stream on the cold side. This leads to a depletion of FA in the upper region of the pore. Once the concentration there is lower than , a diffusion of FA from the reservoir into the pore occurs. Then, an efficient accumulation in the pore becomes possible. If the pore is too short, the molecule will be flushed out into the shallow lake reservoir.
Figure 4 illustrates the different processes occurring in a 2D-hydrothermal pore. Due to convection, there is an upstream on the hot side and a down stream on the cold side in y-direction. The thermodiffusion is across the pore in x-direction and it gets stronger, if the temperature difference or the thermal diffusion coefficient become larger. The diffusion has a component in both directions. In an heuristic approach, the velocity in x and y-direction might be estimated by,
with the convection velocity and the temperature difference between cold and warm side. In this simplified approach, we assume a linear change of the concentrations between top and bottom and between cold and warm side with and , respectively. Note that in a full description of the problem the concentration w depends on x or y. For a symmetrical velocity profile, we assume that the accumulation becomes effective, when the particles, which are located on average in the middle of the upstream are moving at least a distance of to reach the downstream before they reach the end of the column, . Therefore, the time to leave the hydrothermal pore needs to be larger than the time to cross a quarter of the pore width,
so follows the inequality for the height ratio
Using the expressions for the velocities (Equation (4)) and assuming that the concentration difference in x direction is small compared to the concentration difference in y-direction, we then find
Solving Equation (7) for and differentiating with respect to the concentration w, we find a maximum at . This result is in agreement with our transient simulations. It indicates the strongest accumulation around a concentration of 50 wt % (see Figure 4a,b). Further, Equation (7) shows that the height ratio has to increase, if the temperature difference or the thermal diffusion coefficient decreases. Additionally, an increasing diffusion coefficient requires a longer column, because due to the faster diffusion the molecules can leave the pore to the reservoir before reaching the down stream. This simple heuristic model gives an intuitive understanding, why the numerical simulations show for some height ratios a steep increase in the accumulation rate.
5. Conclusions
On the early earth, the estimated formamide concentrations were fairly low of the order of – wt % [3,4,5,6,7,8,33]. The highest concentrations were probably reached in lakes with depths of up to 10 m. In these regions, the formamide concentration increased because of preferential vaporization of water, with a roughly two times lower boiling point compared to formamide [4]. Recently, numerical finite-element calculations for initial FA concentrations between – wt % have been performed [2], which showed that FA could be concentrated at the bottom of hydrothermal pores in about 1–3 months. The possible FA concentrations were around wt %. As an input for the numerical calculations, we used experimentally determined thermal and mass diffusion coefficients, measured over a wide concentration and temperature range, as well as literature data of thermophysical properties of the FA/water mixture. Note that in the entire experimental range, the Soret coefficient of FA is positive and it is increasing with concentration, leading to a self-enhanced accumulation. The heights and widths of the simulated pores were in the range of 5–35 mm and 100–200 m, respectively, resulting in aspect ratios between 50–200. The open question of the previous work was, why the aspect ratio had to be above a certain threshold to reach an effective accumulation of FA in the pores. At these aspect ratios, the transient calculations also showed a steep increase of the accumulation at a certain time, which was not observed at the lower aspect ratios.
Compared to the previous study [2] we examined more closely how the accumulation process works and how it is influenced by the pore geometry. Using an heuristic model we could show that the accumulation becomes effective if the aspect ratio is so large that FA molecules diffuse into the convective down stream on the cold side of the pore before the convective upstream flushes FA into the reservoir outside of the pore. Analysing the optimal aspect ratio as function of concentration, we find a minimal aspect ratio at a weight fraction of . The result agrees with the analysis of our transient simulations, which show a maximal accumulation at .
The here proposed times for accumulation of formamide in hydrothermal pores should only be considered as an order of magnitude. The accumulation times will be influenced by many other unknown factors such as pore dimensions, porosity and temperature fluctuations. Beside shallow lakes, also mineral surfaces are proposed for the “origin-of-life” conundrum. They can work as catalyst in the synthesis of small biological molecules [5] and initiate polymerization [34,35]. Adsorption leads to enrichment on the surface and it has been shown that adsorption slows down the degradation of RNA [36]. Mechanisms proposed in this context might also be applicable for other chemical reactions discussed. In principle, the thermophoretic accumulation is combinable with the concept of surface adsorption since the hydrothermal pores would offer a large mineral surface area that might promote reactions or retain relatively high concentrations of material when the temperature gradient that drives the accumulation decays. For future work, it would be interesting to realize this scenario experimentally.
6. Materials and Methods
In the following two subsection the experimental and simulation details are given.
6.1. Sample Preparation and IR-TDFRS Measurements
We used formamide with a purity of better than % (Sigma-Aldrich, Steinheim am Albuch, Germany) and water from a Millipore filtration system. Part of the prepared solutions were stored as stock solutions in a fridge. To ensure the stability of the mixtures, we validated the refractive index before each measurement. We did not observe significant changes over the maximum storage time of 8 weeks.
For the Infra-Red Thermal Diffusion Forced Rayleigh Scattering (IR-TDFRS) measurements, the solutions had to be free of dust. By filtering the solutions with a membrane filter with a diameter of 0.22 m directly into the Hellma quartz cells, we avoided contamination of the solutions with dust particles in the air. The optical path length was only 0.2 mm to minimize convection effects. Additionally, we performed measurements at different laser intensities to ensure that the measurements were not influenced by convection. Further details about the set-up can be found elsewhere [37] and details about the measurements of the refractive index contrast factors with temperature and concentration can be found in the supporting information of Reference [2].
6.2. Finite Element Calculations
Using the commercially available finite element software (COMSOL Multiphysiscs 5.1) we solved a combination of thermodiffusion-, heat transfer-, and Navier-Stokes-equations to calculate the spatial- and time distribution of FA in a hydrothermal pore. We compared our model with Baaske et al. [1] calculating the accumulation of diluted nucleotide solutions. In the diluted regime we obtained the same results, but at higher concentrations deviations were observed. It turned out that the model by Baaske et al. was limited to very diluted solutions, because they used the approximation in the thermophoretic flux equation. In our model, we used the full expression and all calculations were done in 2D.
The temperature difference across the rectangular pore was kept to 30 K for all simulations. The temperatures at the cold side of the pore was fixed to and at the warm side to . At top and bottom of the pore, we assumed thermal isolation so that the temperatures were given by the solution of the heat equation. For all walls, non-slip boundary conditions were used. Further, the normal flux at the bottom and at the side walls was fixed to zero. To simulate the connection to the reservoir we fixed the concentration at the top of the pore to . This approach is in accordance with the simulations by Baaske et al. [1]. Due to this assumptions, it is possible to suck FA molecules into the pore. Note that a fixed concentration at the top is in agreement with the non-slip boundary conditions we use for the Navier-Stokes equations, because it is possible to connect the top of the pore by using for instance a porous membrane with a reservoir with concentration . Due to the use of a suitable membrane the flow velocity can approach zero by simultaneously allowing a material exchange with the reservoir. The thermo- and mass diffusion coefficient had been determined by IR-TDFRS [2], while the other thermophysical properties have been taken from literature [38,39,40,41,42,43,44]. We accounted for the temperature and concentration dependence of all properties and the temperature and concentration dependent equations can be found in the supporting information of Reference [2].
We carefully checked the stability of the stationary and transient calculations for different mesh sizes. It turned out the numerical calculations were stable, when the mesh size was in the order of 3 m between junctions. As was shown in previous studies [1], there is an optimal width of the pore for maximum accumulation, independent from height. We ran calculation at a fixed height to find the optimal width and observed that it varies with temperature. Then, we ran height and time dependent calculations with the respective optimal widths at three different mean temperatures, °C, 45 °C and 75 °C. Different initial weight fractions of formamide in the range from to were used, taking into account estimations of concentrations during the early history of the earth [4].
Acknowledgments
We thank Jan Dhont for the continuous support of our work and we acknowledge Dzmitry Afanansenkau for his help setting up the COMSOL model. We thank Dieter Braun, Fernando Bresme, Wim Briels, and Marisol Ripoll for fruitful discussions. Part of the experimental data presented was obtained with financial support from the European Commission under the Seventh Framework Program by means of the grant agreement for the Integrated Infrastructure Initiative No. 262348 European Soft Matter Infrastructure (ESMI) which is gratefully acknowledged.
Author Contributions
Doreen Niether and Simone Wiegand conceived and designed the experiments; Doreen Niether performed the experiments; Doreen Niether and Simone Wiegand analyzed the data; Doreen Niether and Simone Wiegand wrote the paper. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IR-TDFRS | infrared thermal diffusion forced Rayleigh scattering |
| FA | formamide |
| RNA | ribonucleic acid |
| DNA | deoxyribonucleic acid |
References
- Baaske, P.; Weinert, F.M.; Duhr, S.; Lemke, K.H.; Russell, M.J.; Braun, D. Extreme Accumulation of Nucleotides in Simulated Hydrothermal Pore Systems. Proc. Natl. Acad. Sci. USA 2007, 104, 9346–9351. [Google Scholar] [CrossRef] [PubMed]
- Niether, D.; Afanasenkau, D.; Dhont, J.K.G.; Wiegand, S. Accumulation of Formamide in Hydrothermal Pores to Form Prebiotic Nucleobases. Proc. Natl. Acad. Sci. USA 2016, 113, 4272–4277. [Google Scholar] [CrossRef] [PubMed]
- Harada, K. Formation of Amino-Acids by Thermal Decomposition of Formamide—Oligomerization of Hydrogen Cyanide. Nature 1967, 214, 479–480. [Google Scholar] [CrossRef]
- Miyakawa, S.; Cleaves, H.J.; Miller, S.L. The Cold Origin of Life: A. Implications Based on the Hydrolytic Stabilities of Hydrogen Cyanide and Formamide. Orig. Life Evol. Biosph. 2002, 32, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Crestini, C.; Pino, S.; Costanzo, G.; di Mauro, E. Formamide and the Origin of Life. Phys. Life Rev. 2012, 9, 84–104. [Google Scholar] [CrossRef] [PubMed]
- Mulkidjanian, A.Y.; Bychkov, A.Y.; Dibrova, D.V.; Galperin, M.Y.; Koonin, E.V. Origin of First Cells at Terrestrial, Anoxic Geothermal Fields. Proc. Natl. Acad. Sci. USA 2012, 109, E821–E830. [Google Scholar] [CrossRef] [PubMed]
- Ferus, M.; Nesvorny, D.; Sponer, J.; Kubelik, P.; Michalcikova, R.; Shestivska, V.; Sponer, J.E.; Civis, S. High-Energy Chemistry of Formamide: A Unified Mechanism of Nucleobase Formation. Proc. Natl. Acad. Sci. USA 2015, 112, 657–662. [Google Scholar] [CrossRef] [PubMed]
- Pino, S.; Sponer, J.E.; Costanzo, G.; Saladino, R.; di Mauro, E. From Formamide to RNA, the Path Is Tenuous but Continuous. Life 2015, 5, 372–384. [Google Scholar] [CrossRef] [PubMed]
- De Groot, S.; Mazur, P. Non-Equilibrium Thermodynamics; Dover: New York, NY, USA, 1984. [Google Scholar]
- Morozov, K.I.; Köhler, W. Thermophoresis of Polymers: Nondraining vs. Draining Coil. Langmuir 2014, 30, 6571–6576. [Google Scholar] [CrossRef] [PubMed]
- Würger, A. Thermal Non-Equilibrium Transport in Colloids. Rep. Prog. Phys. 2010, 73, 126601. [Google Scholar] [CrossRef]
- Dhont, J.K.G.; Briels, W.J. Single-Particle Thermal Diffusion of Charged Colloids: Double-Layer Theory in a Temperature Gradient. Eur. Phys. J. E 2008, 25, 61–76. [Google Scholar] [CrossRef] [PubMed]
- Köhler, W.; Morozov, K.I. The Soret Effect in Liquid Mixtures—A Review. J. Non-Equilb. Thermodyn. 2016, 41, 151–197. [Google Scholar] [CrossRef]
- Yang, M.C.; Ripoll, M. Driving Forces and Polymer Hydrodynamics in the Soret Effect. J. Phys. Condens. Matter 2012, 24, 195101. [Google Scholar] [CrossRef] [PubMed]
- Galliero, G.; Volz, S. Thermodiffusion in Model Nanofluids by Molecular Dynamics Simulations. J. Chem. Phys. 2008, 128, 064505. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Müller-Plathe, F. The Soret Effect in Dilute Polymer Solutions: Influence of Chain Length, Chain Stiffness, and Solvent Quality. J. Chem. Phys. 2006, 125, 124903. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, B.; Nieto-Draghi, C.; Avalos, J.B. The Role of Molecular Interactions in the Change of Sign of the Soret Coefficient. Europhys. Lett. 2004, 67, 976–982. [Google Scholar] [CrossRef]
- Römer, F.; Wang, Z.; Wiegand, S.; Bresme, F. Alkali Halide Solutions under Thermal Gradients: Soret Coefficients and Heat Transfer Mechanisms. J. Phys. Chem. B 2013, 117, 8209–8222. [Google Scholar] [CrossRef] [PubMed]
- Naumann, P.; Datta, S.; Sottmann, T.; Arlt, B.; Frielinghaus, H.; Wiegand, S. Isothermal Behavior of the Soret Effect in Nonionic Microemulsions: Size Variation by Using Different n-Alkanes. J . Phys. Chem. B 2014, 118, 3451–3460. [Google Scholar] [CrossRef] [PubMed]
- Parola, A.; Piazza, R. A Microscopic Approach to Thermophoresis in Colloidal Suspensions. J. Phys. Condens. Matter 2005, 17, S3639–S3643. [Google Scholar] [CrossRef]
- Ning, H.; Dhont, J.K.G.; Wiegand, S. Thermal-Diffusive Behavior of a Dilute Solution of Charged Colloids. Langmuir 2008, 24, 2426–2432. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Kriegs, H.; Buitenhuis, J.; Dhont, J.K.G.; Wiegand, S. Thermophoresis of Charged Colloidal Rods. Soft Matter 2013, 9, 8697–8704. [Google Scholar] [CrossRef]
- Sehnem, A.L.; Neto, A.M.F.; Aquino, R.; Campos, A.F.C.; Tourinho, F.A.; Depeyrot, J. Temperature Dependence of the Soret Coefficient of Ionic Colloids. Phys. Rev. E 2015, 92, 042311. [Google Scholar] [CrossRef] [PubMed]
- Syshchyk, O.; Afanasenkau, D.; Wang, Z.; Kriegs, H.; Buitenhuis, J.; Wiegand, S. Influence of Temperature and Charge Effects on Thermophoresis of Polystyrene Beads. Eur. Phys. J. E 2016, 39. [Google Scholar] [CrossRef] [PubMed]
- Sugaya, R.; Wolf, B.A.; Kita, R. Thermal Diffusion of Dextran in Aqueous Solutions in the Absence and the Presence of Urea. Biomacromolecules 2006, 7, 435–440. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Kriegs, H.; Wiegand, S. Thermal Diffusion of Nucleotides. J. Phys. Chem. B 2012, 116, 7463–7469. [Google Scholar] [CrossRef] [PubMed]
- Kishikawa, Y.; Wiegand, S.; Kita, R. Temperature Dependence of Soret Coefficient in Aqueous and Nonaqueous Solutions of Pullulan. Biomacromolecules 2010, 11, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Iacopini, S.; Rusconi, R.; Piazza, R. The “Macromolecular Tourist”: Universal Temperature Dependence of Thermal Diffusion in Aqueous Colloidal Suspensions. Eur. Phys. J. E 2006, 19, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Maeda, K.; Shinyashiki, N.; Yagihara, S.; Wiegand, S.; Kita, R. Ludwig-Soret Effect of Aqueous Solutions of Ethylene Glycol Oligomers, Crown Ethers, and Glycerol: Temperature, Molecular Weight, and Hydrogen Bond Effect. J. Chem. Phys. 2015, 143, 124504. [Google Scholar] [CrossRef] [PubMed]
- Hill, A. The Possible Effects of the Aggregation of the Molecules of Haemoglobin on Its Dissociation Curves. J. Physiol. 1910, 40, 4–7. [Google Scholar]
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill Equation: A Review of Its Capabilities in Pharmacological Modelling. Fundam. Clin. Pharmacol. 2008, 22, 633–648. [Google Scholar] [CrossRef] [PubMed]
- Polyakov, P.; Wiegand, S. Systematic Study of the Thermal Diffusion in Associated Mixtures. J. Chem. Phys. 2008, 128, 034505. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, R.A.; Ferris, J.P.; Orgel, L.E. Studies in Prebiotic Synthesis: 2. Synthesis of Purine Precursors and Amino Acids from Aqueous Hydrogen Cyanide. J. Mol. Biol. 1967, 30, 223–253. [Google Scholar] [PubMed]
- Orgel, L.E. Polymerization on the Rocks: Theoretical Introduction. Orig. Life Evol. Biosph. 1998, 28, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.P.; Hill, A.R.; Liu, R.H.; Orgel, L.E. Synthesis of Long Prebiotic Oligomers on Mineral Surfaces. Nature 1996, 381, 59–61. [Google Scholar] [CrossRef] [PubMed]
- Franchi, M.; Gallori, E. A Surface-Mediated Origin of the RNA World: Biogenic Activities of Clay-Adsorbed RNA Molecules. Gene 2005, 346, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, S.; Ning, H.; Kriegs, H. Thermal Diffusion Forced Rayleigh Scattering Setup Optimized for Aqueous Mixtures. J. Phys. Chem. B 2007, 111, 14169–14174. [Google Scholar] [CrossRef] [PubMed]
- Egan, E.P.; Luff, B.B. Heat of Solution Heat Capacity and Density of Aqueous Formamide Solutions at 25 °C. J. Chem. Eng. Data 1966, 11, 194–196. [Google Scholar] [CrossRef]
- Akhtar, S.; Faruk, A.N.M.O.; Saleh, M.A. Viscosity of aqueous solutions of formamide, N-methylformamide and N,N-dimethylformamide. Phys. Chem. Liq. 2001, 39, 383–399. [Google Scholar] [CrossRef]
- Wohlfarth, C. Viscosity of the mixture (1) water; (2) formamide. In Supplement to IV/18; Lechner, M.D., Ed.; Landolt-Börnstein—Group IV Physical Chemistry; Springer: Berlin/Heidelberg, Germany, 2009; pp. 709–711. [Google Scholar]
- Tobitani, A.; Tanaka, T. Predicting Thermal-Conductivity of Binary-Liquid Mixtures on Basis of Coordination-Number. Can. J. Chem. Eng. 1987, 65, 321–328. [Google Scholar] [CrossRef]
- Checoni, R.F.; Volpe, P.L.O. Measurements of the Molar Heat Capacities and Excess Molar Heat Capacities for Water plus Organic Solvents Mixtures at 288.15 K to 303.15 K and Atmospheric Pressure. J. Solut. Chem. 2010, 39, 259–276. [Google Scholar] [CrossRef]
- Ganiev, Y.A.; Rastorguev, Y.L. Thermal Conductivity of Organic Liquids. J. Eng. Phys. 1968, 15, 519–525. [Google Scholar]
- Young, H.D. University Physics; Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).