Kinetic Theory of a Confined Quasi-Two-Dimensional Gas of Hard Spheres
Abstract
:1. Introduction
2. A Collisional Model for the Effective Two-Dimensional Dynamics
3. Hydrodynamic Equations
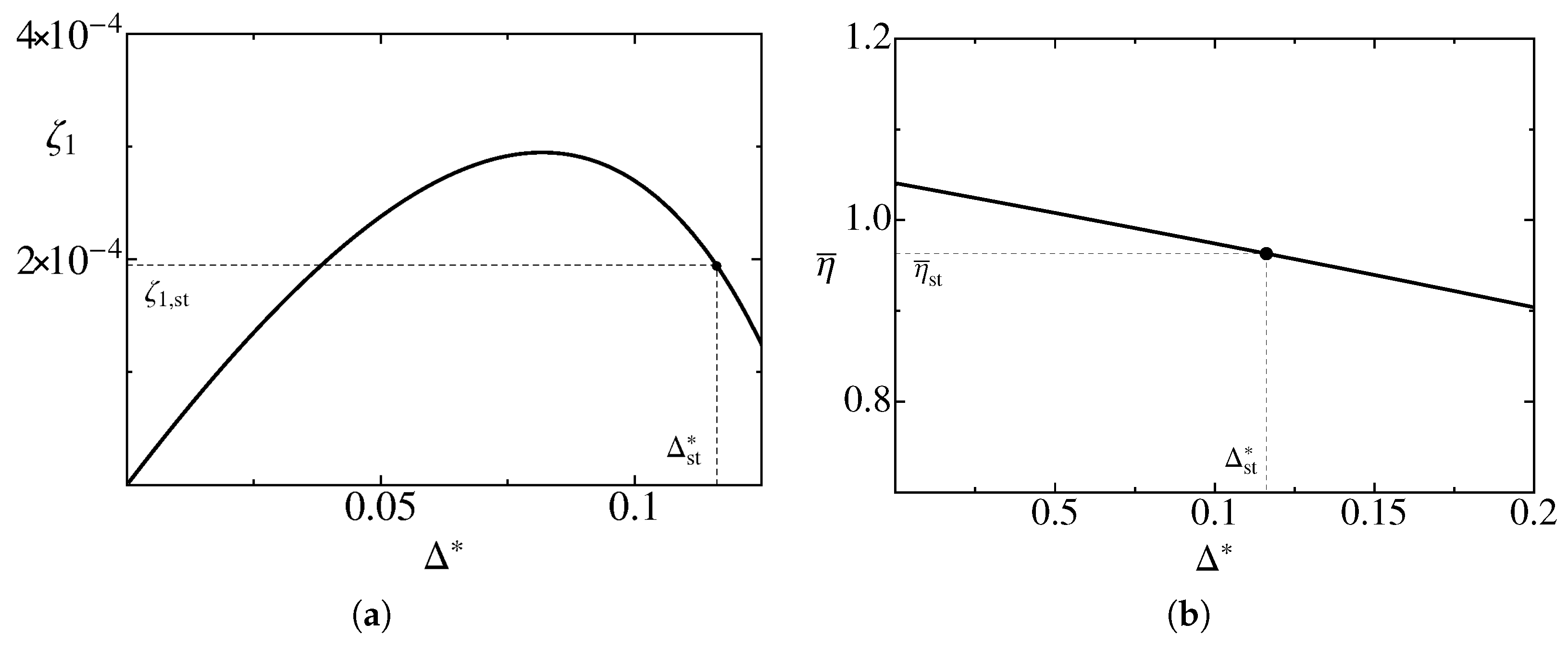
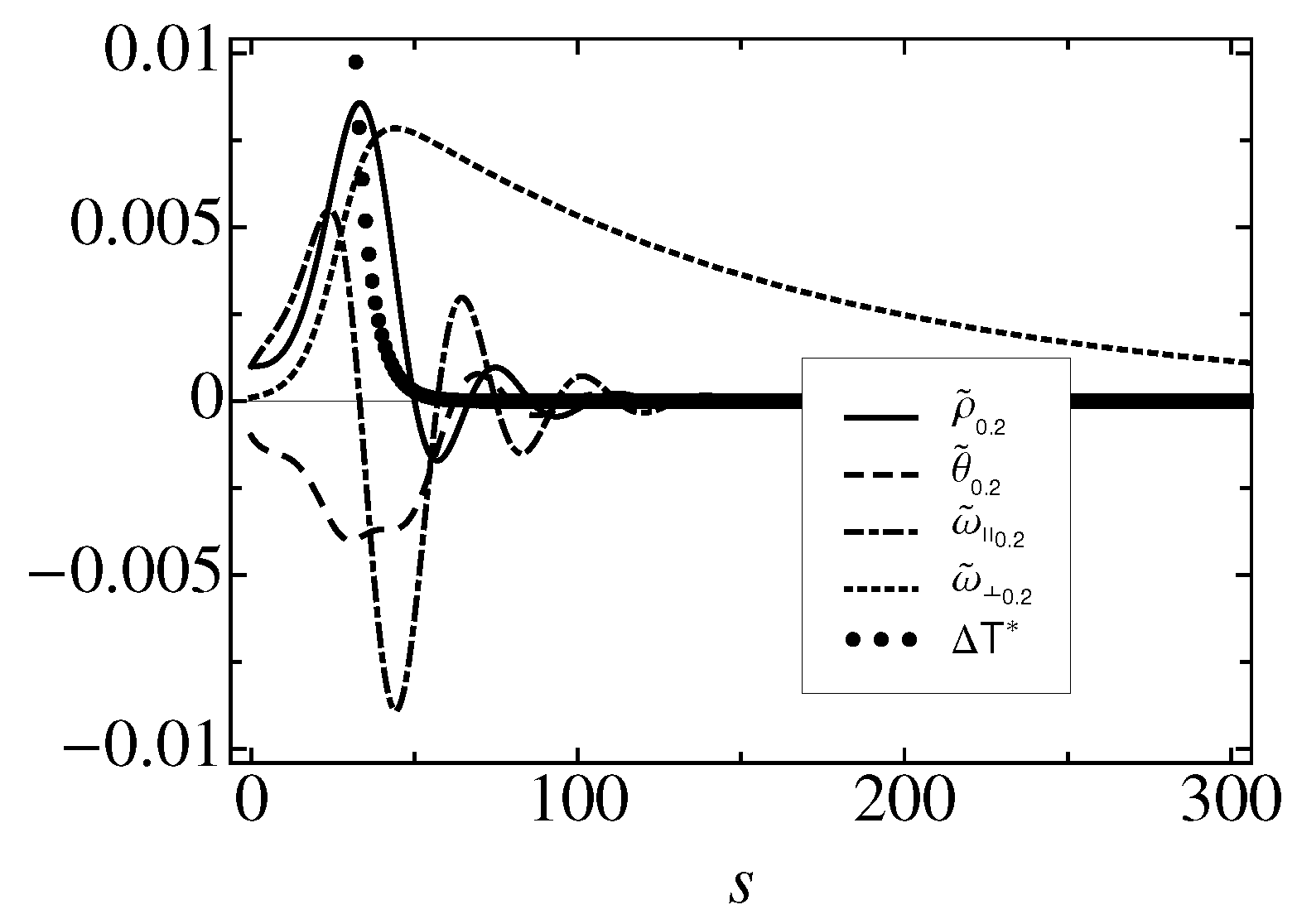
4. Stability Analysis
5. Back to the Origins: Boltzmann–Enskog Kinetic Equation
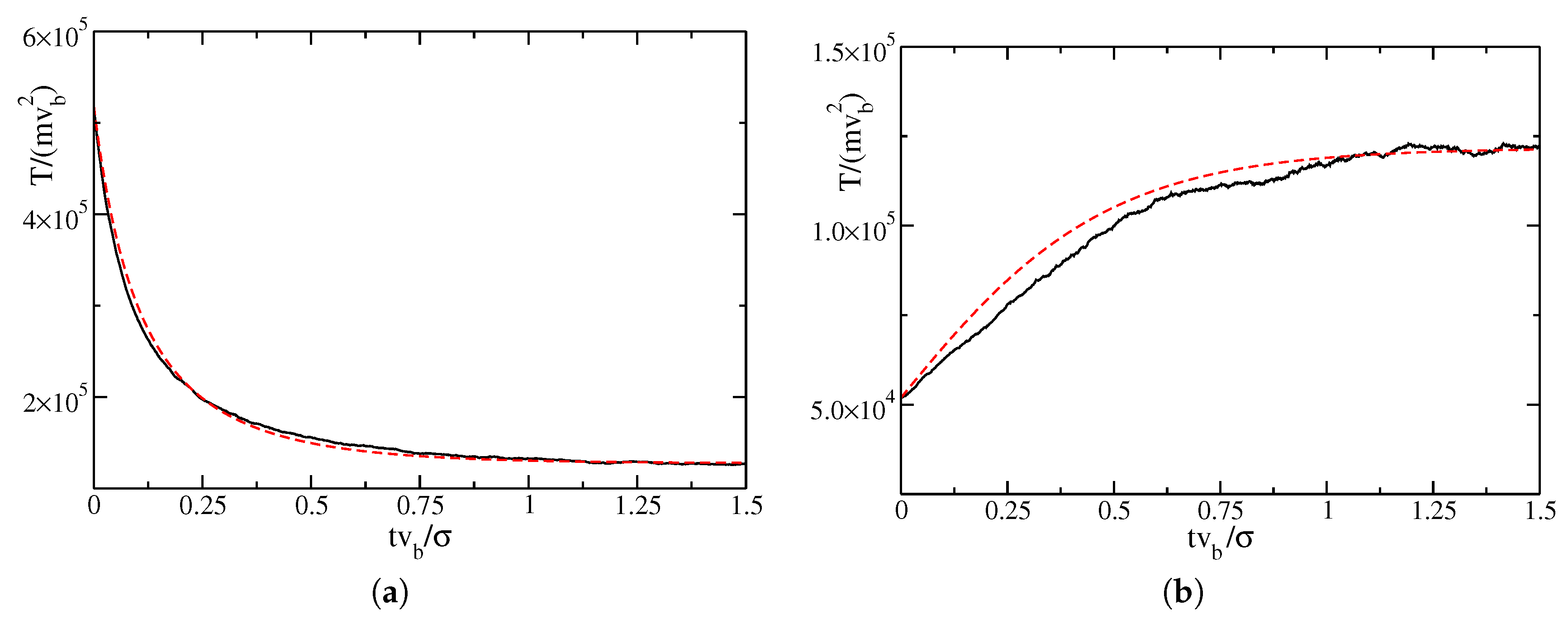
6. Homogeneous Approximation: The Evolution of the Temperature
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Melby, P.; Reyes, V.F.; Prevost, A.; Robertson, R.; Kumar, P.; Egolf, D.A.; Urbach, J.S. The dynamics of thin vibrated granular layers. J. Phys. Condens. Matter 2005, 17, S2689–S2704. [Google Scholar] [CrossRef]
- Reis, P.M.; Ingale, R.A.; Shattuck, M.D. Crystallization of a Quasi-two-dimensional Granular Fluid. Phys. Rev. Lett. 2006, 96, 258001. [Google Scholar] [CrossRef] [PubMed]
- Rivas, N.; Ponce, S.; Gallet, B.; Risso, D.; Soto, R.; Cordero, P.; Mújica, N. Sudden Chain Energy Transfer Events in Vibrated Granular Media. Phys. Rev. Lett. 2011, 106, 088001. [Google Scholar] [CrossRef] [PubMed]
- Castillo, G.; Mújica, N.; Soto, R. Fluctuations and Criticality of a Granular Solid-Liquid-Like Phase Transition. Phys. Rev. Lett. 2012, 109, 095701. [Google Scholar] [CrossRef] [PubMed]
- Olafsen, J.S.; Urbach, J.S. Clustering, Order, and Collapse in a Driven Granular Monolayer. Phys. Rev. Lett. 1998, 81, 4369–4372. [Google Scholar] [CrossRef]
- Olafsen, J.S.; Urbach, J.S. Two-Dimensional Melting Far from Equilibrium in a Granular Monolayer. Phys. Rev. Lett. 2005, 95, 098002. [Google Scholar] [CrossRef] [PubMed]
- Khain, E.; Aranson, I.S. Hydrodynamics of a vibrated granular monolayer. Phys. Rev. E 2011, 84, 031308. [Google Scholar] [CrossRef] [PubMed]
- Willians, D.R.M.; MacKintoch, F.C. Driven granular media in one dimension: Correlations and equation of state. Phys. Rev. E 1996, 54, R9–R12. [Google Scholar] [CrossRef]
- Van Noije, T.P.C.; Ernst, M.H. Velocity distributions in homogeneous granular fluids: The free and the heated case. Granul. Matter 1998, 1, 57–64. [Google Scholar] [CrossRef]
- Puglisi, A.; Loreto, V.; Marini Bettolo Marconi, U.; Vulpiani, A. Kinetic approach to granular gases. Phys. Rev. E 1999, 59, 5582–5595. [Google Scholar] [CrossRef]
- Brito, R.; Risso, D.; Soto, R. Hydrodynamic modes in a confined granular fluid. Phys. Rev. E 2013, 87, 022209. [Google Scholar] [CrossRef] [PubMed]
- Soto, R.; Risso, D.; Brito, R. Shear viscosity of a model for confined granular media. Phys. Rev. E 2014, 90, 062204. [Google Scholar] [CrossRef] [PubMed]
- Goldhirsch, I. Rapid Granular Flows. Annu. Rev. Fluid Mech. 2003, 35, 267–293. [Google Scholar] [CrossRef]
- Brey, J.J.; García de Soria, M.I.; Maynar, P.; Buzón, V. Homogeneous steady state of a confined granular gas. Phys. Rev. E 2013, 88, 062205. [Google Scholar] [CrossRef] [PubMed]
- Haff, P.K. Grain flow as a fluid-mechanical phenomenon. J. Fluid Mech. 1983, 134, 401–430. [Google Scholar] [CrossRef]
- Brey, J.J.; Buzón, V.; García de Soria, M.I.; Maynar, P. Stability analysis of the homogeneous hydrodynamics of a model for a confined granular gas. Phys. Rev. E 2016, 93, 062907. [Google Scholar] [CrossRef] [PubMed]
- Brey, J.J.; García de Soria, M.I.; Maynar, P.; Buzón, V. Memory effects in the relaxation of a confined granular gas. Phys. Rev. E 2014, 90, 032207. [Google Scholar] [CrossRef] [PubMed]
- Brey, J.J.; Dufty, J.W.; Kim, C.S.; Santos, A. Hydrodynamics for granular flow at low density. Phys. Rev. E 1998, 58, 4638–4653. [Google Scholar] [CrossRef]
- Brey, J.J.; Buzón, V.; García de Soria, M.I.; Maynar, P. Hydrodynamics for a model of a confined quasi-two-dimensional granular gas. Phys. Rev. E 2015, 91, 052201. [Google Scholar] [CrossRef] [PubMed]
- Brey, J.J.; Maynar, P.; García de Soria, M.I.; Buzón, V. Homogeneous hydrodynamics of a collisional model of confined granular gases. Phys. Rev. E 2014, 89, 052209. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Lowën, H. Phase diagram of hard spheres confined between two parallel plates. Phys. Rev. E 1997, 55, 7228–7241. [Google Scholar] [CrossRef]
- Résibois, P.; de Leener, M. Classical Kinetic Theory of Fluids; John Wiley and Sons: New York, NY, USA, 1977. [Google Scholar]
- Brey, J.J.; Maynar, P.; García de Soria, M.I. Kinetic equation and non-equilibrium entropy for a quasi-two-dimensional gas. Phys. Rev. E 2016, 94, 040103. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, J.R.; van Beijeren, H. The Kinetic Theory of Gases. In Statistical Mechanics, Part B; Berne, B.J., Ed.; Plenum Press: New York, NY, USA, 1977; pp. 65–178. [Google Scholar]
- Dufty, J.W.; Brey, J.J. Green-Kubo expressions for a granular gas. J. Stat. Phys. 2002, 109, 433–448. [Google Scholar] [CrossRef]
- Brey, J.J.; Ruiz-Montero, M.J. Simulation study of the Green-Kubo relations for dilute granular gases. Phys. Rev. E 2004, 70, 051301. [Google Scholar] [CrossRef] [PubMed]

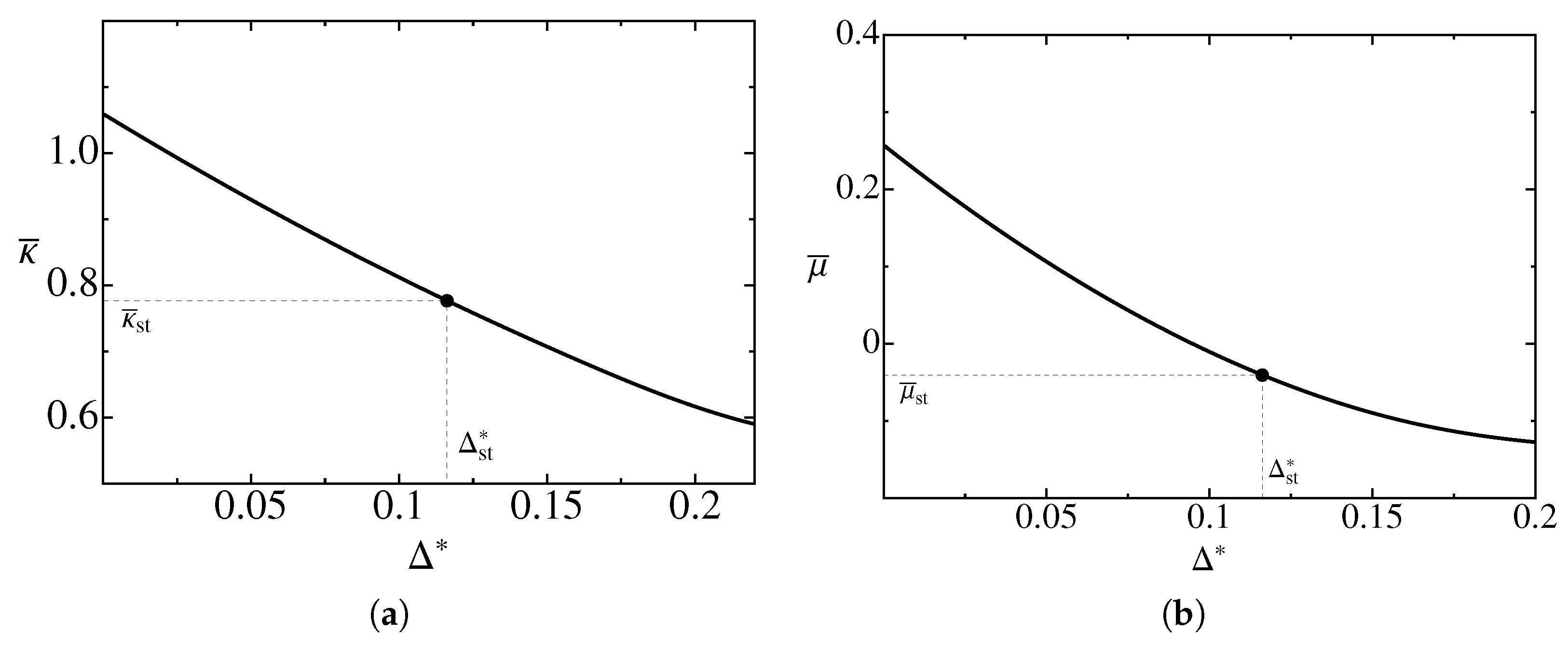
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brey, J.J.; Buzón, V.; García de Soria, M.I.; Maynar, P. Kinetic Theory of a Confined Quasi-Two-Dimensional Gas of Hard Spheres. Entropy 2017, 19, 68. https://doi.org/10.3390/e19020068
Brey JJ, Buzón V, García de Soria MI, Maynar P. Kinetic Theory of a Confined Quasi-Two-Dimensional Gas of Hard Spheres. Entropy. 2017; 19(2):68. https://doi.org/10.3390/e19020068
Chicago/Turabian StyleBrey, J. Javier, Vicente Buzón, Maria Isabel García de Soria, and Pablo Maynar. 2017. "Kinetic Theory of a Confined Quasi-Two-Dimensional Gas of Hard Spheres" Entropy 19, no. 2: 68. https://doi.org/10.3390/e19020068
APA StyleBrey, J. J., Buzón, V., García de Soria, M. I., & Maynar, P. (2017). Kinetic Theory of a Confined Quasi-Two-Dimensional Gas of Hard Spheres. Entropy, 19(2), 68. https://doi.org/10.3390/e19020068




