Implementing Demons and Ratchets
Abstract
:1. Introduction
- They are supported by test results;
- We believe they are conceptually clean and easily explained; and
- They may have commercial application.
- Epicatalysis: Tests demonstrate that opposing catalysts can create a temperature differential needed for a heat engine heat.
- LEDs: Emission measurements show that unbiased light emitting diodes (LED’s) emit a small amount of light.
- Doped semiconductor structure: A sandwich-like structure of semiconductors presents a persistent, harvestable voltage. We call this an ambient thermal electric converter (ATEC).
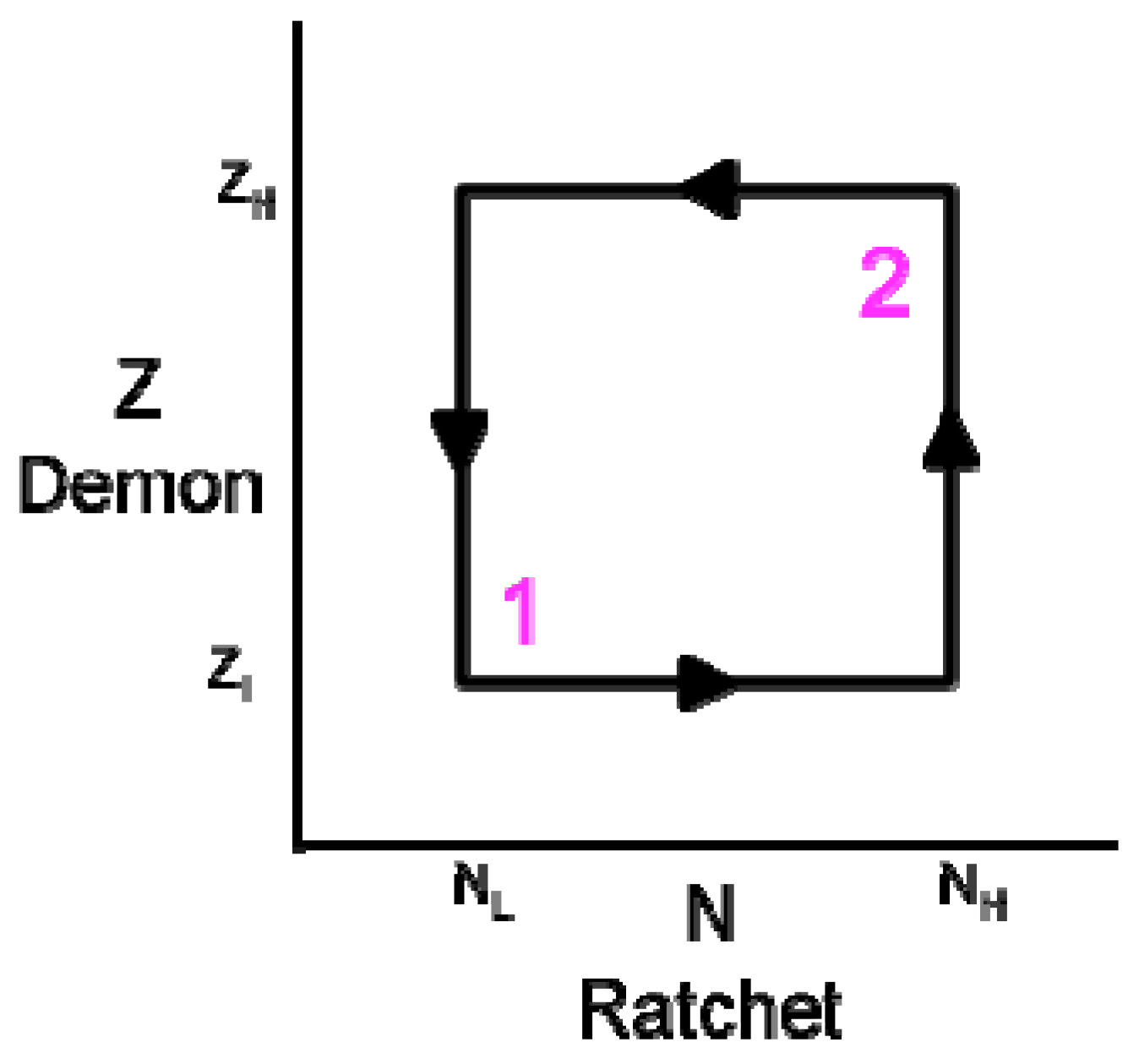
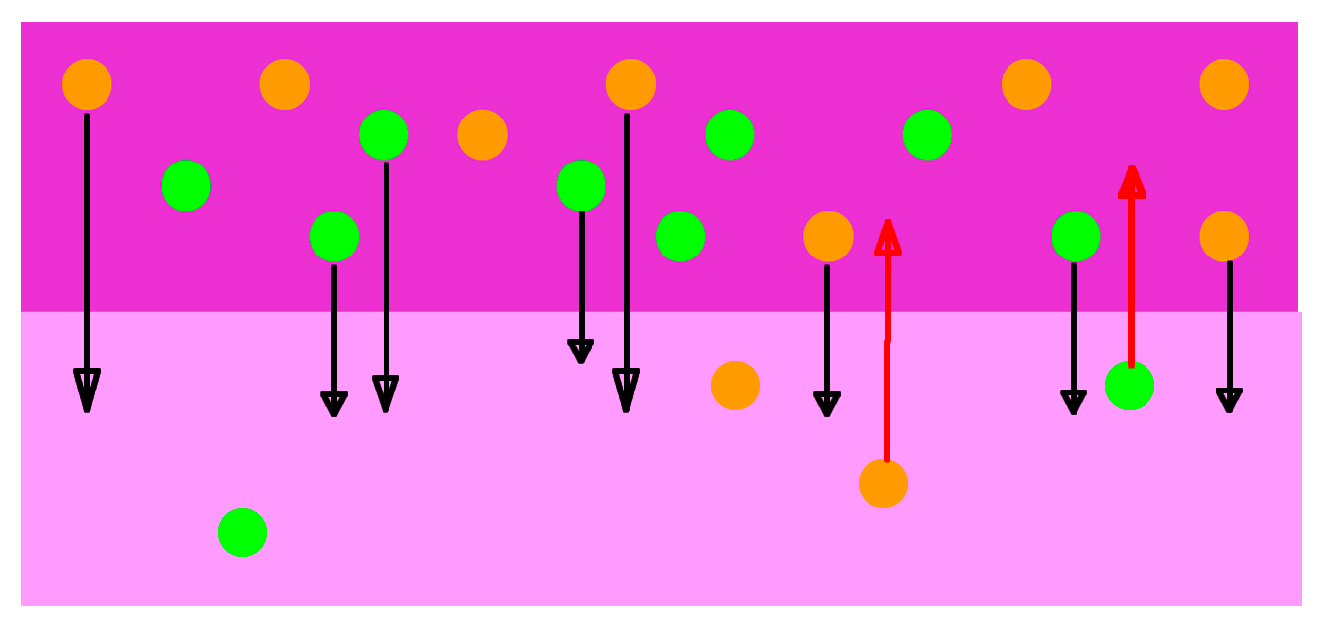
- The bottom line represents the creation of particles at Location 1.
- Some particles move across the potential to Location 2, driven by thermal energy through diffusion. This creation process fills the role of Maxwell’s demon.
- Some of those particles are then destroyed.
- Remaining particles return to Location 1.
2. Materials and Methods
2.1. LEDs
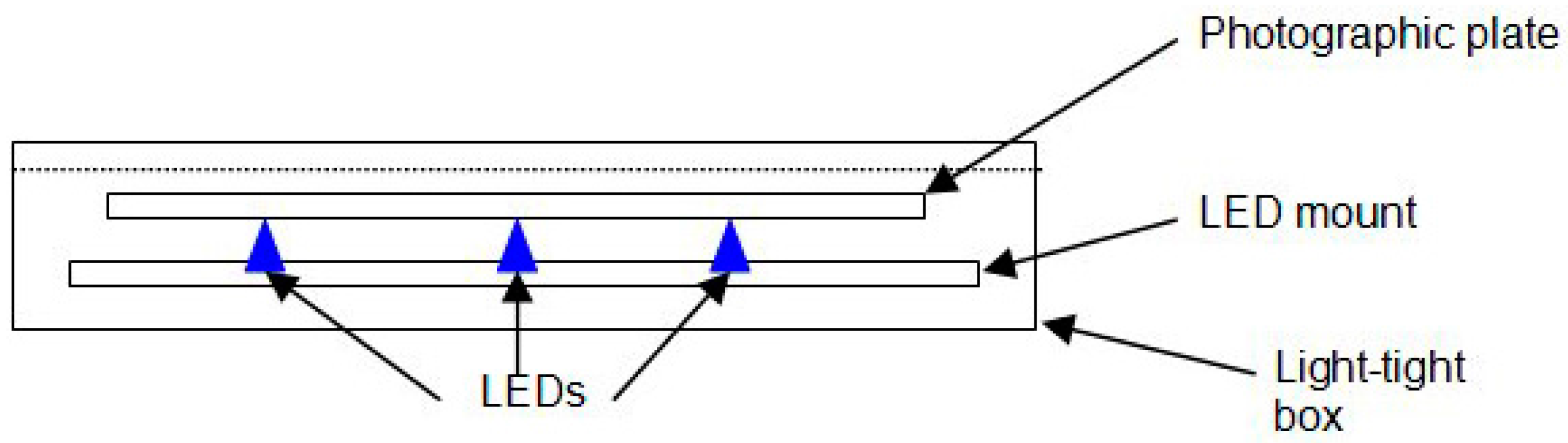
2.1.1. Direct Film Exposure
2.1.2. Digital Imaging of Heated, Unbiased LED
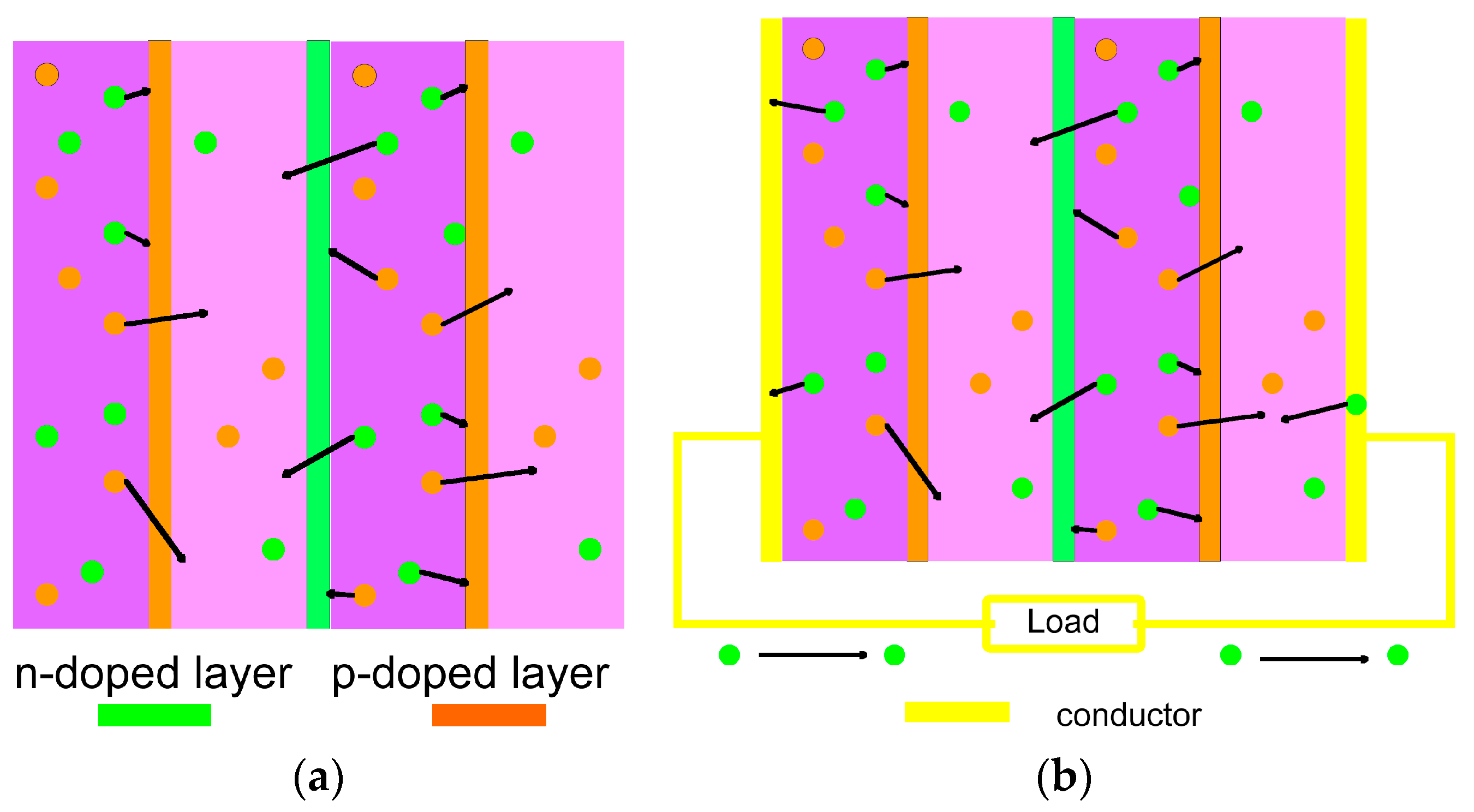
2.2. Doped Semiconductor Structures (ATEC)
2.2.1. The ATEC Structure
- It is 10 ½ cycles of AlGaAs with either 33% or 50% Al, 5.5 µm thick
- It is on a base of n-GaAs, 0.5 mm thick and 75 mm (3”) in diameter
- It has a gold conductor final layer. The surface features you see are reflections of the room.
2.2.2. Simulation Tools
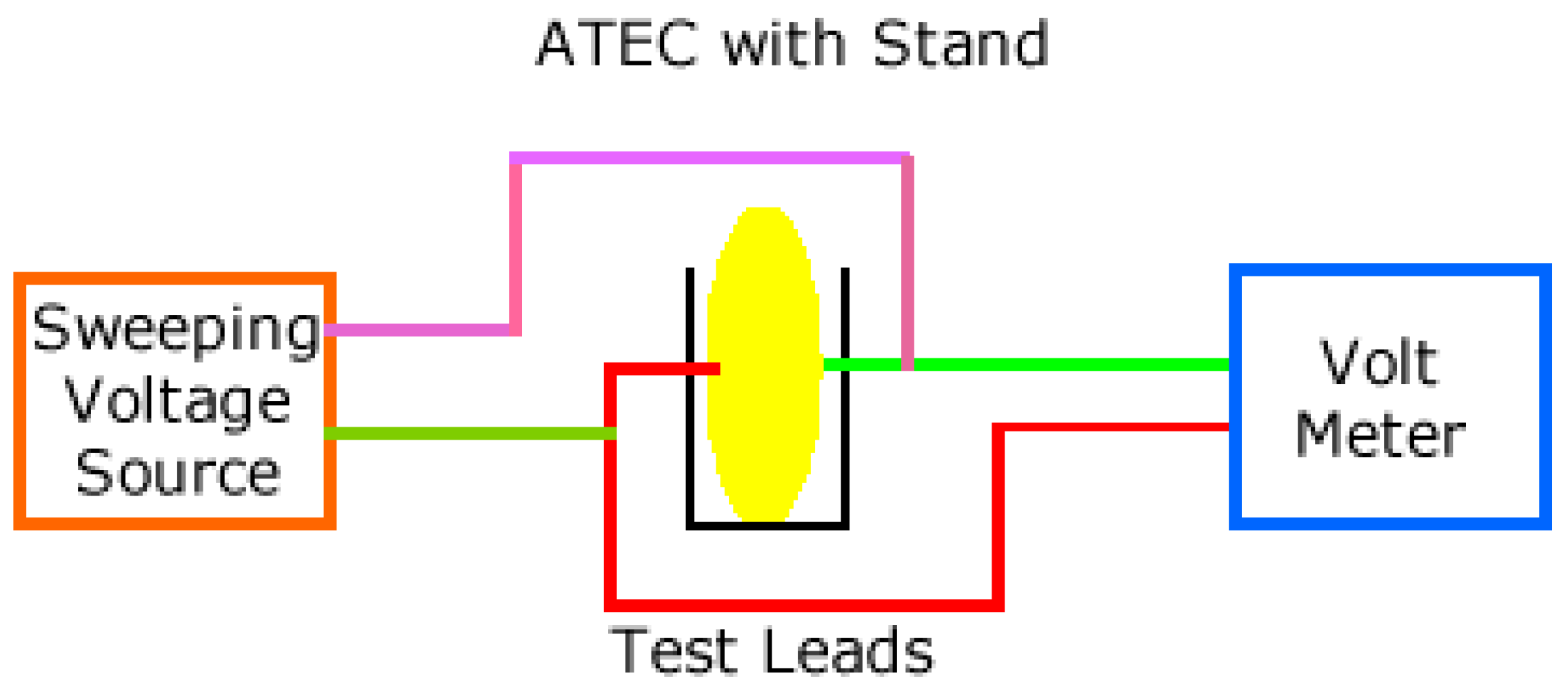
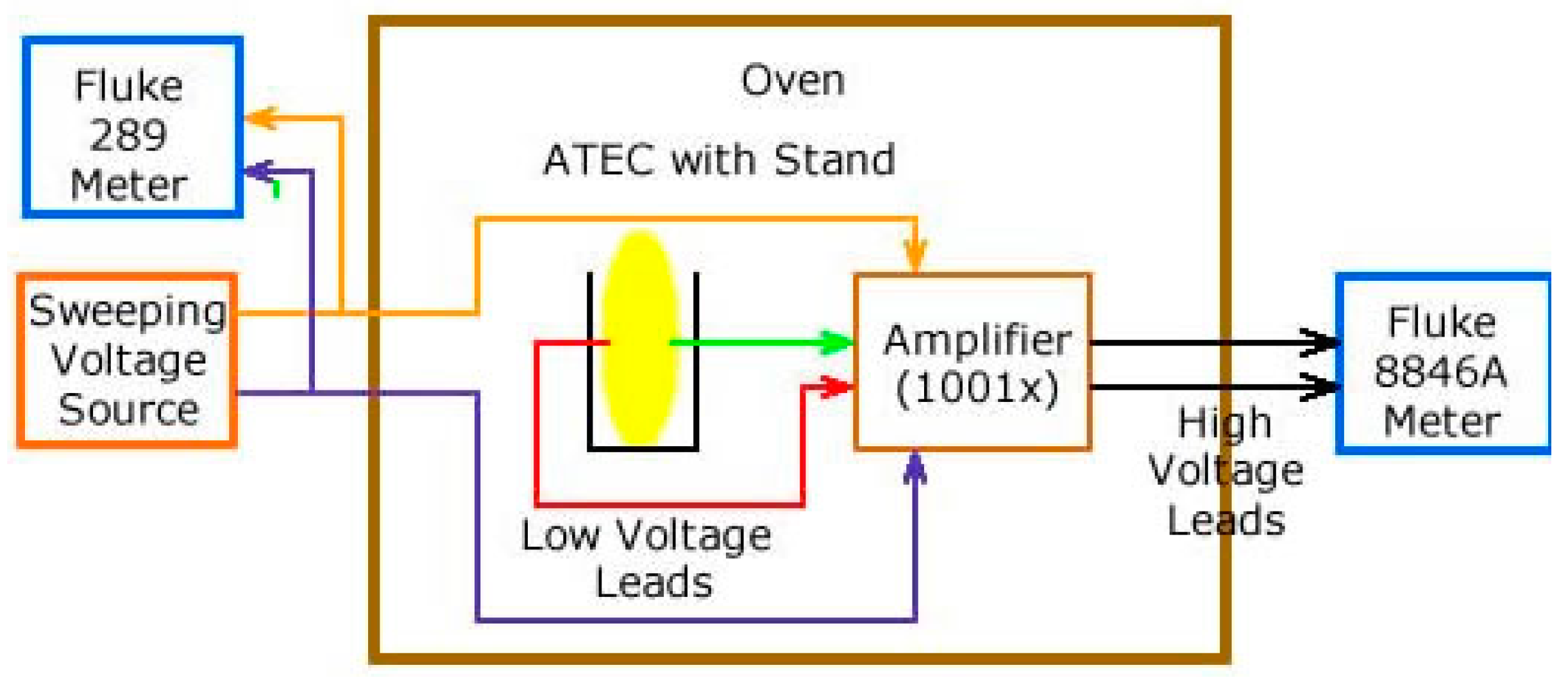
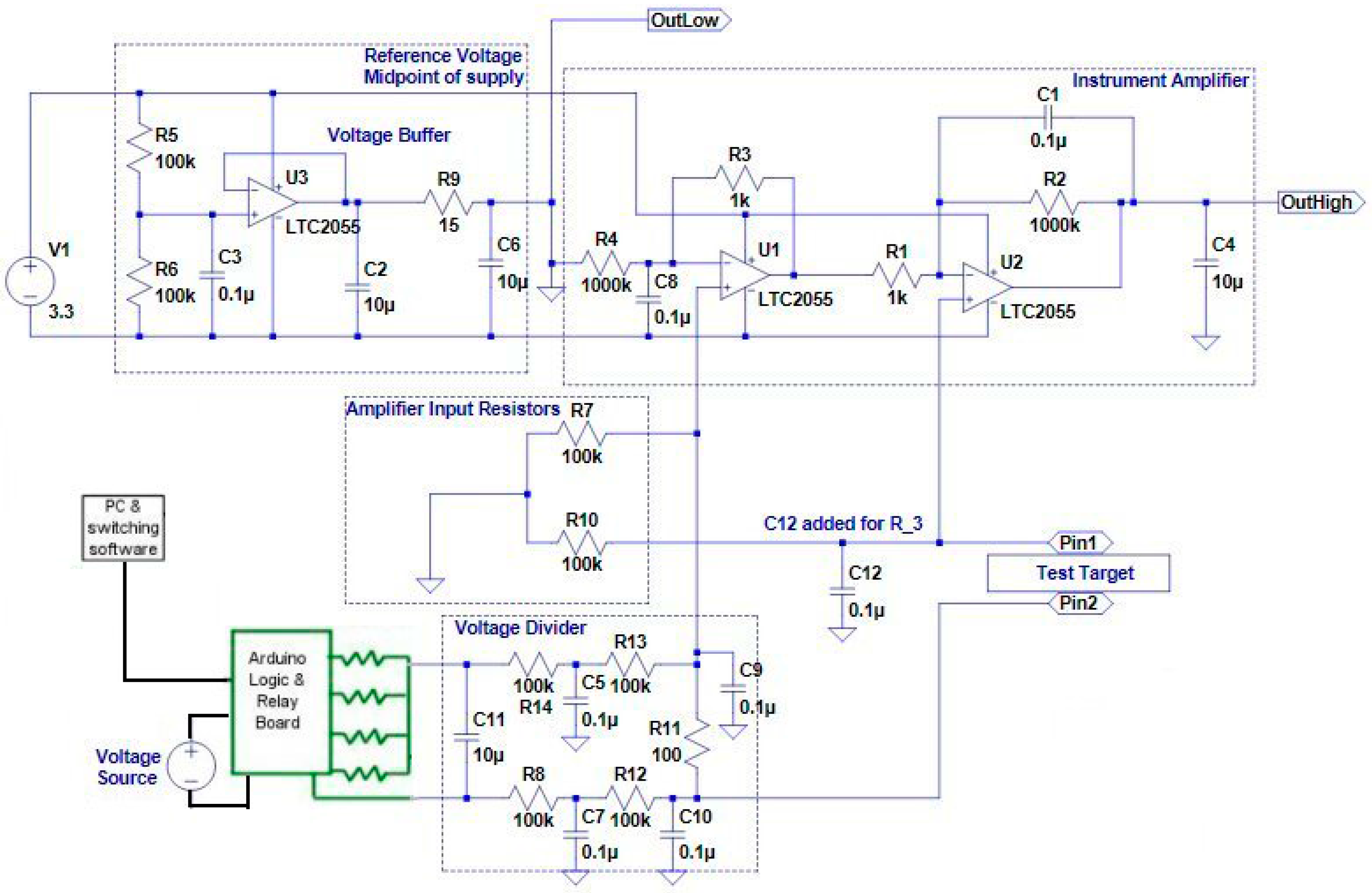
2.2.3. Laboratory Test Tools
- Costs: since our prototype ATEC material set was constrained by costs, we could look for only microvolt outputs, which are hard to measure without high-end equipment (also cost-constrained)
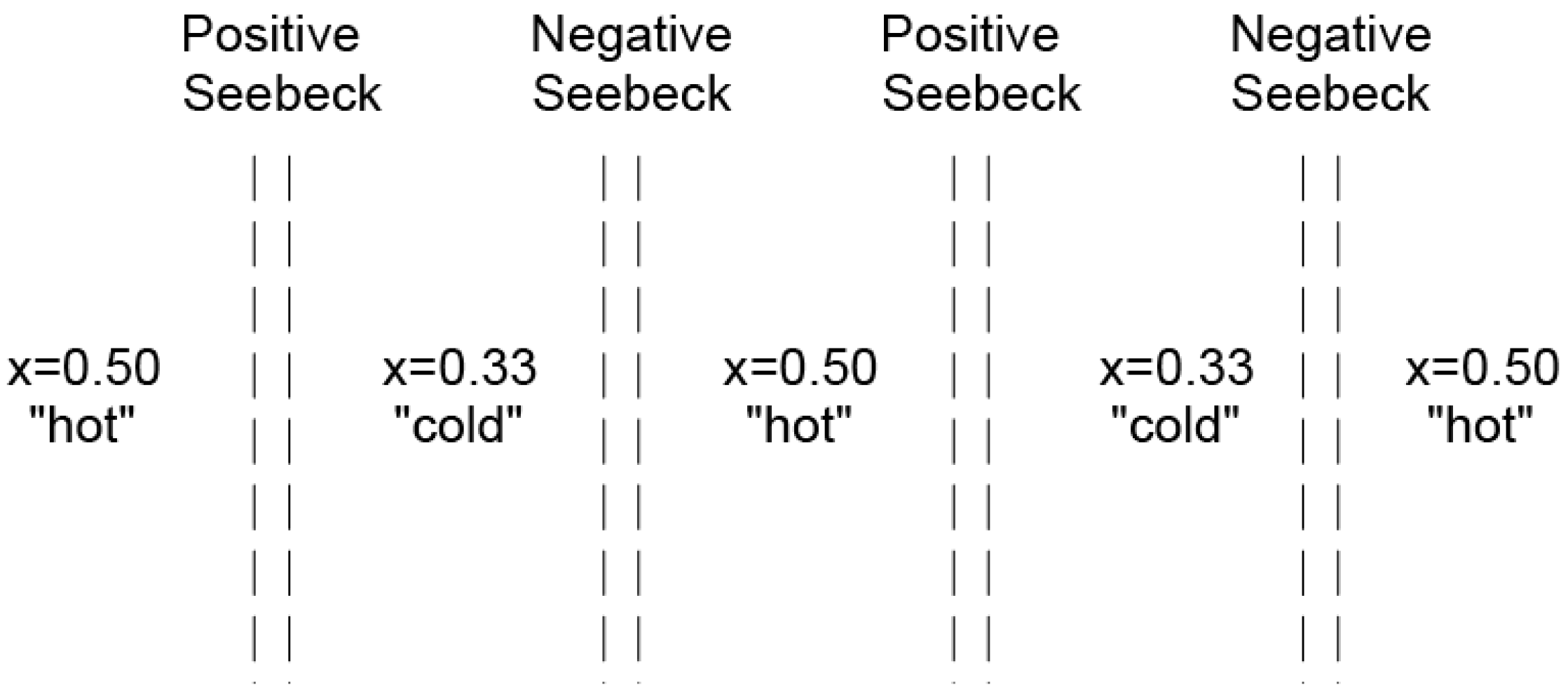
- Seebeck effect
- Voltage across the ATEC from electrical noise induced through wiring and the ATEC and then rectified by the ATEC, which is inherently a diode
- Meter bias
- Apply a known sweep voltage to the ATEC and a known resistor in series
- Amplify the voltage across the known resistor to bring it from the microvolt to millivolt range
- Put the test target, measurement circuitry and wiring (as much as possible) into the oven (environmental chamber)
- Design all low voltage signals such that they are in a small region at a uniform temperature, with short wires; longer runs were amplified (or not yet divided) by 1000 or 4000, respectively.
- ATEC on a stand, with wiring, inside an environmental chamber.
- ATEC on a custom ceramic stand, with contact wires.
- Relay control board and Arduino processor for sweep control logic.
3. Results
- Unbiased LEDs emitting light
- Harvestable voltage across a doped semiconductor structure (ATEC)
3.1. LEDs
3.1.1. Direct Film Exposure
3.1.2. Digital Imaging of Heated, Unbiased LED
3.2. Doped Semiconductor Structure
3.2.1. Simulation
3.2.2. Laboratory Tests
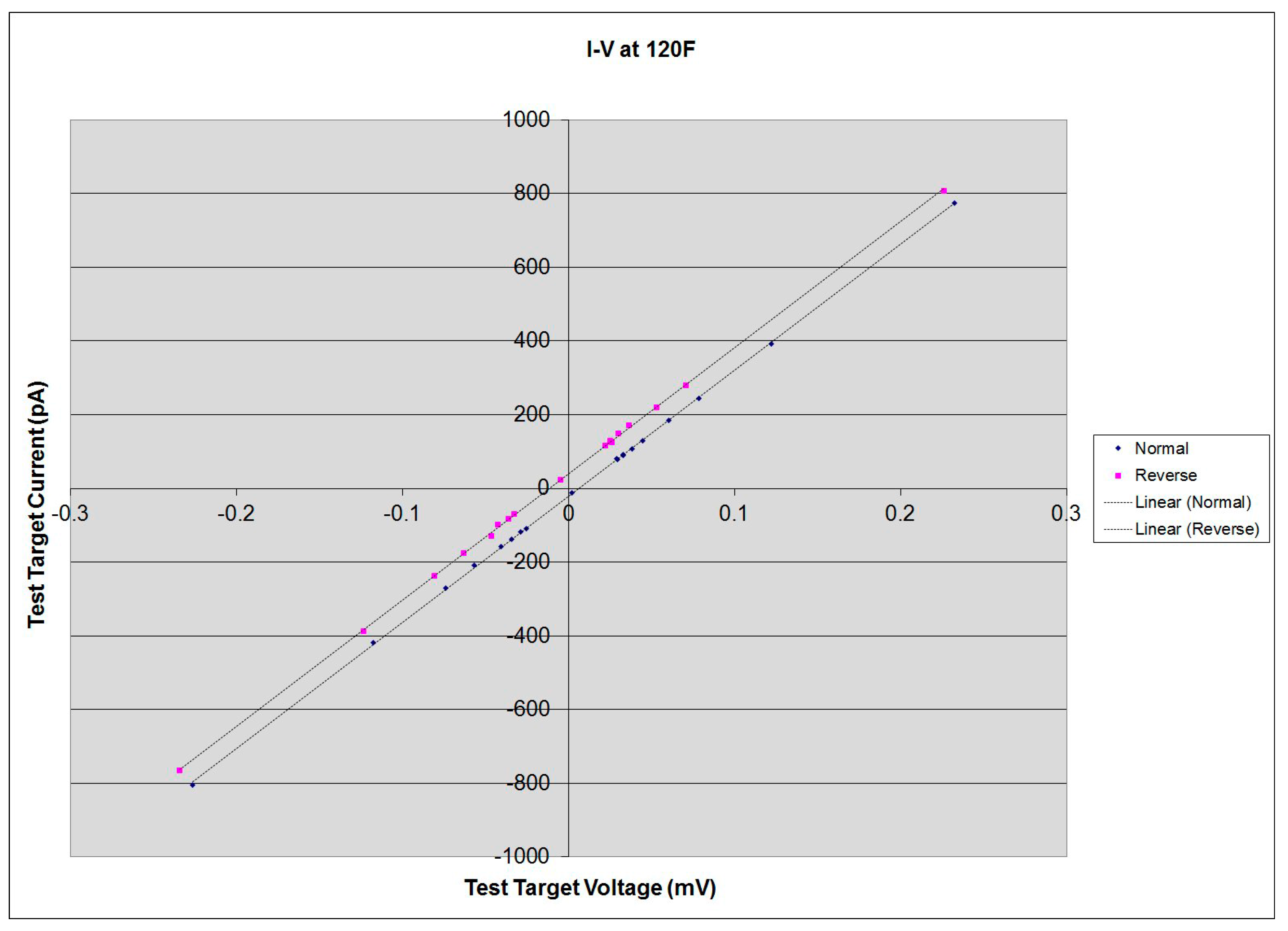
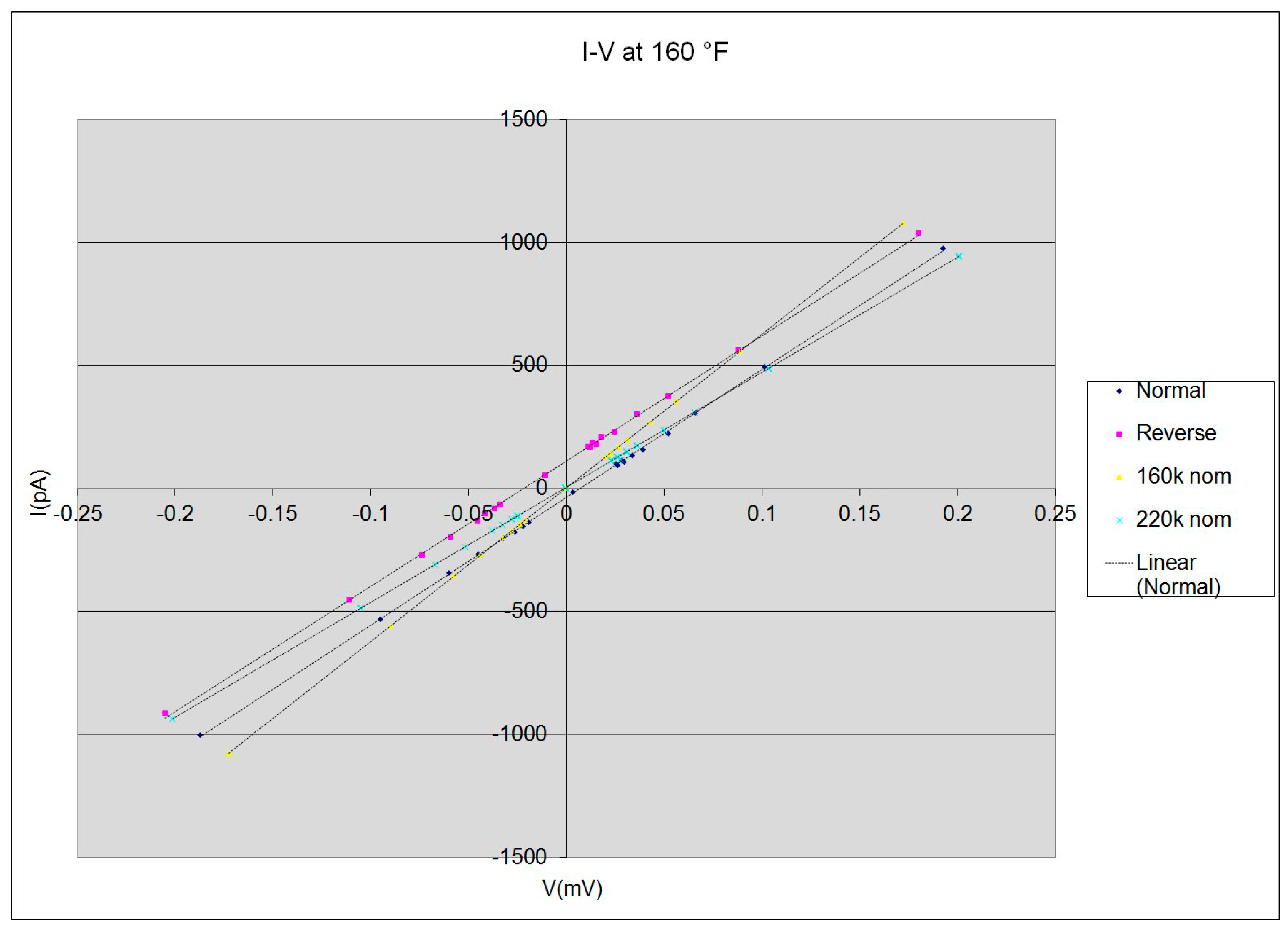
- Parallel lines across the sweep of bias, one for each orientation of the ATEC. The blue dots are from the “normal” ATEC orientation, and the red dots are for “reverse.”
- Linear offset of voltage across the target.
- The ATEC normal and reverse run results are again separated and again do not pass through zero current at zero voltage;
- The resistor plots both pass through zero (at this scale) and have different slopes, as expected.
4. Discussion
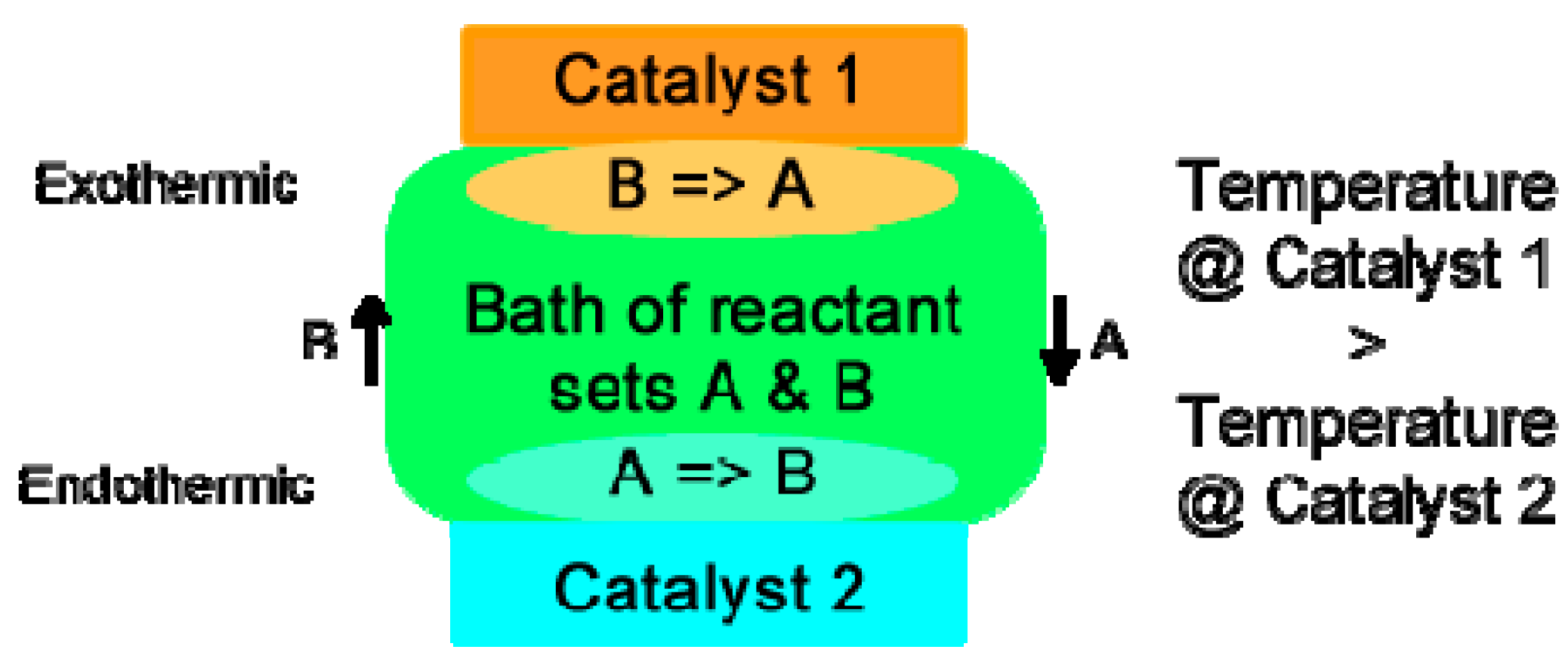
4.1. Epicatalysis
- Catalyst 1 one will create Reactant Set A in favor of Reactant Set B, and Catalyst 2 will create Reactant Set B in favor of Reactant Set A.
- By diffusion, the bath will tend to equalize the reactants in the reverse direction, B diffusing toward Catalyst 1 and A toward Catalyst 2.
- One of the reactions (A => B or B => A) will generate more net heat (be exothermic) than the other, so the catalyst surface will warm, and the other will absorb more net heat (be endothermic).
4.2. LED Emissions at Zero Bias
4.2.1. Direct Film Exposure
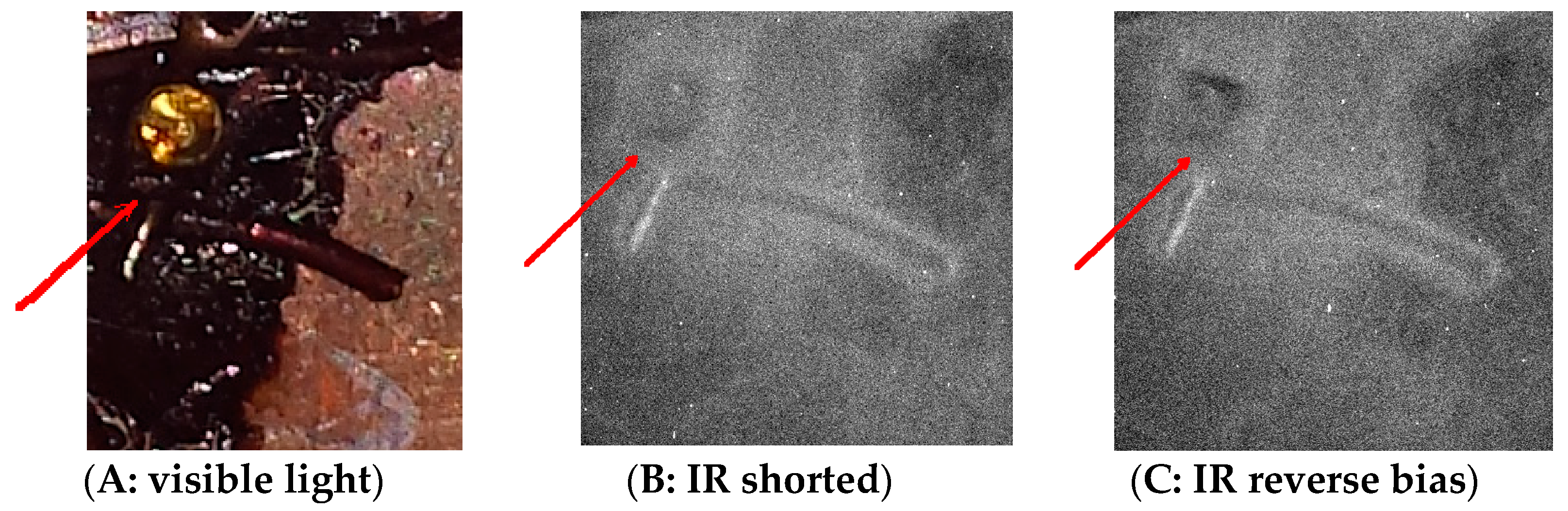
- Photographic film is actually tricky stuff. It is sort of a chemical bath. It reacts to photons, but the chemical images therefrom degrade over time, smearing and fading. It may be that the long exposure time used actually led to reduced image capture.
- Some of the frames had large crescent images, which did not seem to correspond to LEDs. These may have resulted from bending the film during mounting or dismounting, so we discounted those images.
- The “light-tight box” may not have been so. We discount this because of the box assembly and because the shape and location of images are inconsistent with how light might have leaked in.
- The film may have interacted chemically with the LED lens. We discount that because such an interaction should have occurred with many of the LEDs, which seems not to be reflected in the images.
- The LED tails might be acting as antenna to electrical noise, providing an oscillating pump across the LEDs. Although the tails are small and twisted together, we cannot discount this possibility. Were we to rerun this experiment, we would want to put the box in a Faraday cage (perhaps a wrap of metal foil or mesh); or we could perhaps measure the antenna effect of similarly-sized wires across a diode.
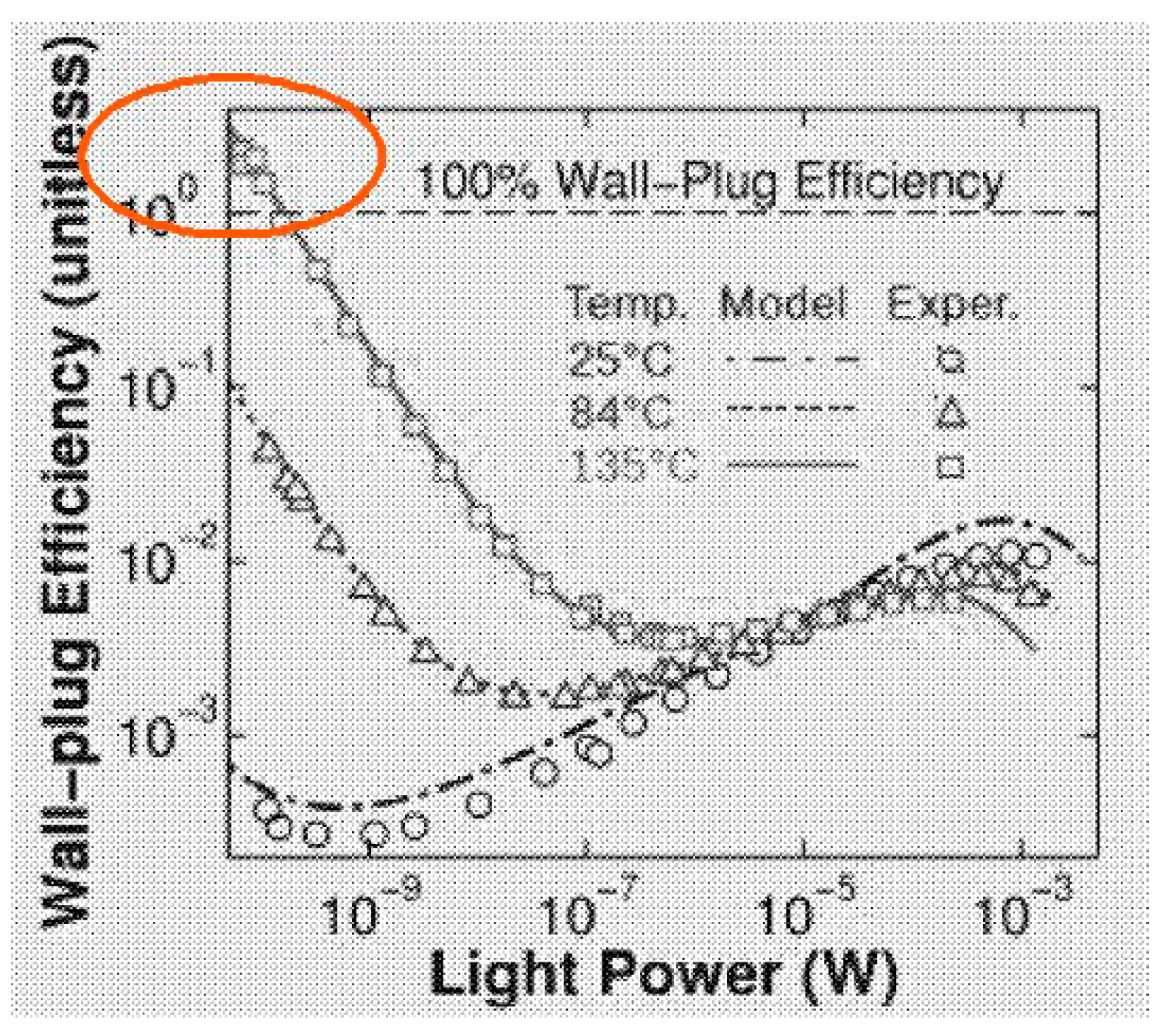
4.2.2. Over-Unity LED Output
4.2.3. Digital Imaging of Heated, Unbiased LED
- Choose an LED with a wavelength where its output is strongest at a high temperature (therefore, some red).
- Balance that wavelength against the quantum efficiency of the camera, so that drop-off would not be too severe.
- Filter the output of the LED (blackbody and possible recombination emission) to the camera at a wavelength matching the LED.
- Observe the image captured for open and closed connection to the LED leads and with reverse bias on the leads. Sufficient reverse bias will surely block electron leaps across the LED junction. If there are photons being generated at no bias, the image with reverse bias should be different from the other two.
- The temperatures of test runs with and without reverse bias could differ. We discount this because considerable care was taken to control temperature, and settling time was allowed. This might be improved further with automated control of the heater.
- The exposure time could vary between test runs. We discount this because exposure times were software controlled.
- The setup does not completely control the location of its image in the field. While true, the LED shape is pretty clearly identifiable, so this appears not to be a problem.
- Noise could be creating the apparent differences in images. We discount this because noise tends to be uniformly distributed across the field, whereas the area of the LED image is clearly consistently locatable.
- Post-processing the images with any of several techniques
- Using a yet-more-sensitive camera, perhaps a liquid nitrogen-cooled camera, such as Princeton Instrument’s Pylon® CCD BRX (Trenton, NJ, USA).
4.2.4. Rationale for Light Emissions from Unbiased LEDs
4.3. Doped Semiconductor Structure (ATEC)
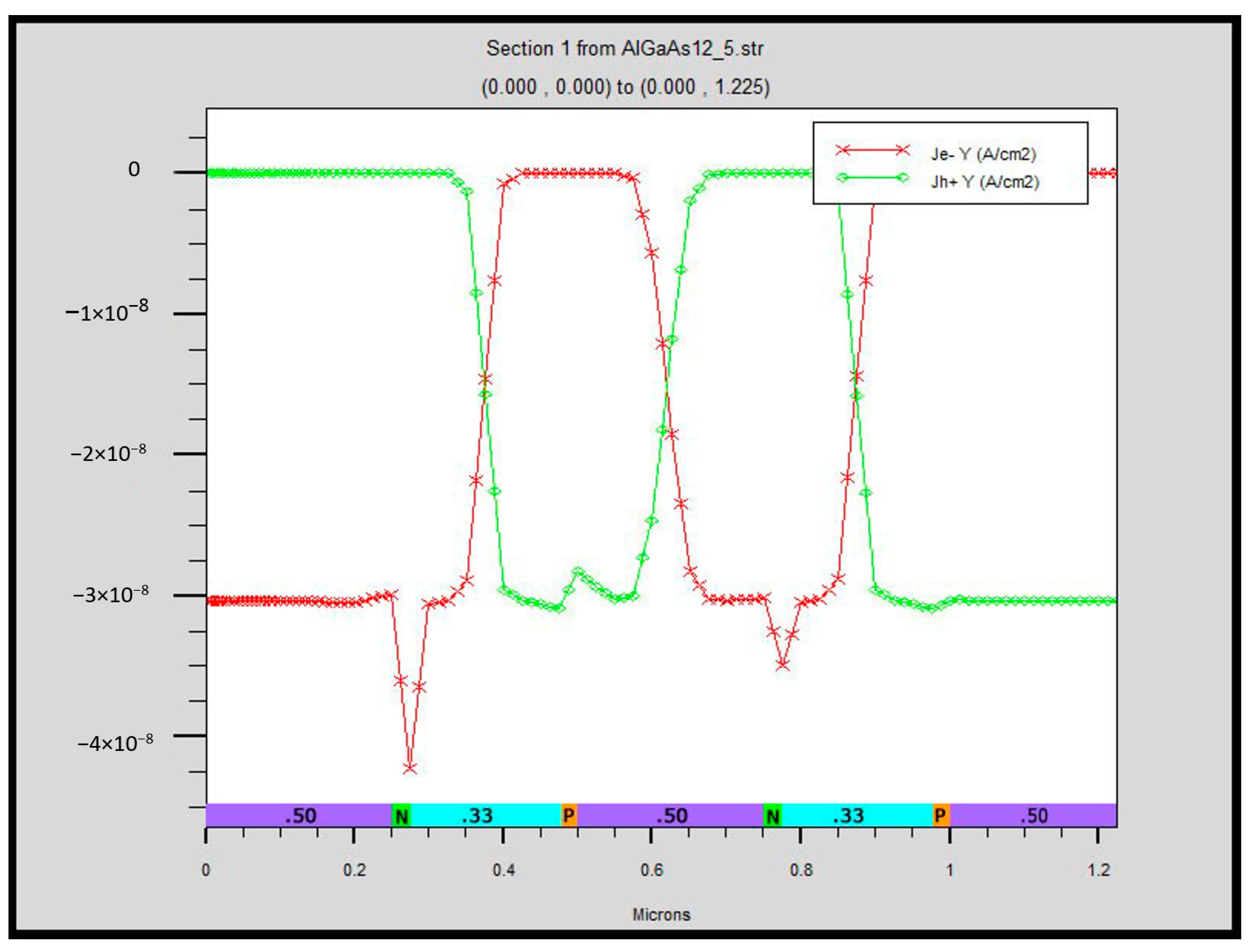
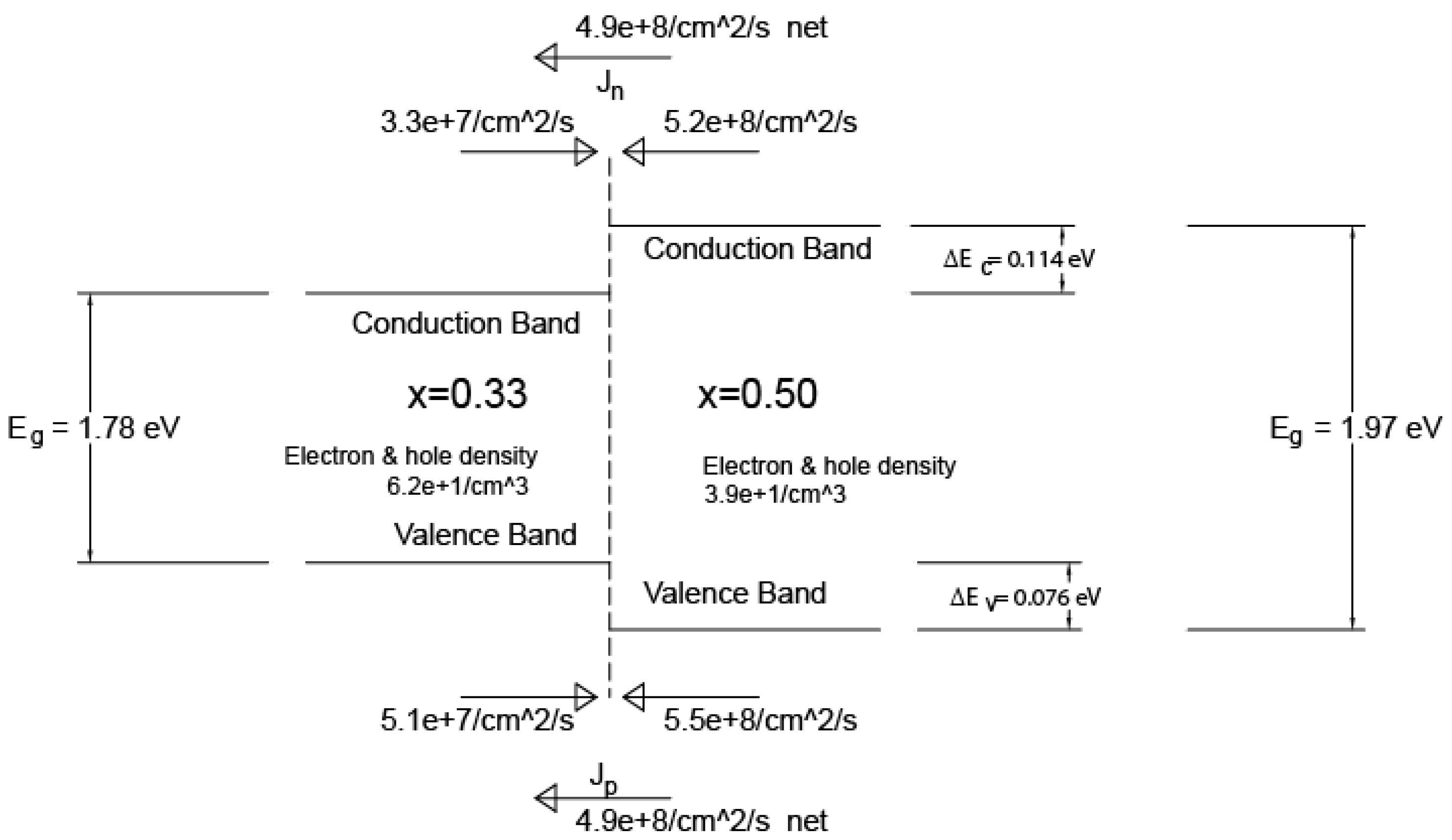
- Generation in a semiconductor material at a given temperature is a function of the bandgap.
- The recombination rate in a semiconductor material is a function of carrier density and band structure.
- Generation and recombination produce an intrinsic (equilibrium) carrier density, which is a function of the bandgap and band structure.
- Some materials have band structures that support higher carrier densities than others, independent of the bandgap.
- Carriers move by diffusion from higher density to lower density regions (given no electrical force on them), including across a heterojunction.
- If two materials with different band structures are joined at a heterojunction, the transport across the junction will typically be out of equilibrium with the internal generation/recombination equilibrium of each material.
- Each material will move to balance at its intrinsic density (for a given temperature) through a change in rate of recombination.
- While there is a flow of carriers, there is no net flow of charge.
- There must be a flow of heat in the opposite direction of carriers, since generation is endothermic and recombination is exothermic. Because this creates a temperature differential, it is in itself an exception to the second law. The temperature difference measurement was cited by George Levy [12], which references offsets encountered by Iwanaga et al. [13].
- This is a generally useless and sometimes annoying feature of heterojunctions (so far).
5. Conclusions
- Epicatalysis created a harvestable temperature difference. That, alone, is enough to prove we must move past laws.
- The light emitted by unbiased LEDs, as captured by the experiments, could in theory be harvested. While not as dramatic as epicatalysis, it also proves the point.
- Consistent voltage measurements from a doped semiconductor structure also demand looking forward.
5.1. Interpretation
- For AlGaAs, the largest bandgap that we used in the ATEC construction is 1.79 eV.
- The test results for our AlGaAs prototypes are, we think, significant. However, they do not scream “useful”. We remind you that we used AlGaAs because many shops could fabricate it.
5.2. Areas for Research and for Engineering
- Replicating experiments in epicatalysis, LEDs and ATECs;
- Using better material sets for ATECs and lower temperature epicatalysis;
- Developing application-specific packages at least for ATECs (largely an engineering process);
- Looking for other instances of particle creation and destruction, coupled with opportunities for the diffusion of particles (demons and ratchets), for other useful exceptions to the second law.
Supplemental Materials
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Nikulov, A.V.; Sheehan, D.P. Special Issue on Quantum Limits to the Second Law of Thermodynamics. Entropy 2004, 6, 1–10. [Google Scholar] [CrossRef]
- Sheehan, D.P. Second law of thermodynamics: Status and challenges. In Proceedings of the AIP Conference, San Diego, CA, USA, 14–15 June 2011.
- ThermaWatts, LLC. Available online: http://www.ThermaWatts.com (accessed on 11 January 2017).
- Sheehan, D.P. Nonequilibrium heterogenous catalysis in long term mean-free-path regime. Phys. Rev. E 2013, 88, 032125. [Google Scholar] [CrossRef] [PubMed]
- Sheehan, D.P.; Garamella, J.T.; Mallin, D.J.; Sheehan, W.F. Steady-state non-equilibrium temperature gradients in hydrogen gas-metal systems: Challenging the second law of thermodynamics. Phys. Scr. 2012, 2012, 014030. [Google Scholar] [CrossRef]
- Sheehan, D.P.; Mallin, D.J.; Garamella, J.T.; Sheehan, W.F. Experimental Test of a Thermodynamic Paradox. Found. Phys. 2014, 44, 235–247. [Google Scholar] [CrossRef]
- Miller, D. Apparatus and Procedures for Detecting Temperature Differentials with Epicatalytic Materials. Entropy 2017. submitted. [Google Scholar]
- Santhanam, P.; Gray, D.J.; Ram, R.J. Thermoelectrically pumped light emitting diodes operating above unity efficiency. Phys. Rev. Lett. 2012, 108, 097403. [Google Scholar] [CrossRef] [PubMed]
- Gray, D. Thermal Pumping of Light Emitting Diodes. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2011. [Google Scholar]
- Santhanam, P.; Dodd, J.G.; Ram, R.J. Thermo-Electrically Pumped Light-Emitting Diodes. U.S. Patent US 20140159582, 12 June 2014. [Google Scholar]
- Yang, K.Y.; East, J.R.; Haddad, G.I. Numerical Modeling of Abrupt Heterojunctions Using a Thermionic-Field Emission Boundary Condition. Solid State Electron. 1993, 36, 321–330. [Google Scholar] [CrossRef]
- Levy, G.S. Thermoelectric Effects under Adiabatic Conditions. Entropy 2013, 15, 4700–4715. [Google Scholar] [CrossRef]
- Iwanaga, S.; Toberer, E.S.; LaLonde, A.; Snyder, G.J. A High Temperature Apparatus for Measurement of Seebeck Coefficient. Rev. Sci. Instrum. 2011, 82, 063905. [Google Scholar] [CrossRef] [PubMed]





| Al Fractions | Units | Notes and References | |||
|---|---|---|---|---|---|
| 0.33 | 0.5 | - | - | ||
| ni | 3.82 × 103 | 1.52× 103 | /cm3 | Carrier density at 310 K, per ATLAS | |
| Eg | 1.78 | 1.97 | 0.19 | eV | Per ATLAS |
| ∆Ec | - | 0.6 | 0.114 | eV | 60/40 rule for AlGaAs |
| ∆Ev | - | 0.4 | 0.076 | eV | 60/40 rule for AlGaAs |
| kBT | - | - | 0.0267138 | eV | kB from ATLAS |
| ∆Ec/kBT | - | - | 4.27 | - | - |
| ∆Ev/kBT | - | - | 2.84 | - | - |
| exp(∆Ec/kBT) | - | - | 1.40 × 10−2 | - | - |
| exp(∆Ev/kBT) | - | - | 5.81 × 10−2 | - | - |
| vn | 3.86 × 107 | 1.34 × 108 | - | cm/s | Yang [11] Equations (5) and (9) |
| vp | 1.42 × 107 | 1.40 × 108 | - | cm/s | Yang [11] Equations (12) and (13) |
| Densities | - | - | - | - | - |
| n | 6.18 × 10 | 3.90 × 10 | - | /cm3 | - |
| p | 6.18× 10 | 3.90 × 10 | - | /cm3 | - |
| Currents | - | - | Net | - | - |
| Jn | −3.34 × 107 | 5.22 × 108 | 4.89 × 108 | /cm2/s | Net of 0.33 => 0.50 minus 0.50 => 0.33 for electrons |
| Jp | 5.10 × 107 | −5.46 × 108 | −4.95 × 108 | /cm2/s | Net of 0.33 => 0.50 minus 0.50 => 0.33 for holes |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orem, P.M.; Orem, F.M. Implementing Demons and Ratchets. Entropy 2017, 19, 34. https://doi.org/10.3390/e19010034
Orem PM, Orem FM. Implementing Demons and Ratchets. Entropy. 2017; 19(1):34. https://doi.org/10.3390/e19010034
Chicago/Turabian StyleOrem, Peter M., and Frank M. Orem. 2017. "Implementing Demons and Ratchets" Entropy 19, no. 1: 34. https://doi.org/10.3390/e19010034
APA StyleOrem, P. M., & Orem, F. M. (2017). Implementing Demons and Ratchets. Entropy, 19(1), 34. https://doi.org/10.3390/e19010034





