Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. EEG Recordings
2.3. Methods
2.3.1. Multiscale Entropy Based on Mean and Variance
- (I)
- Assume we have a signal with length C. Each element of the coarse-grained time series for MSEµ and recently proposed MSEσ2 are respectively calculated as:where λ, , and N denote the scale factor, the coarse-grained signal, and its length, respectively [17,25]. In fact, the coarse-grained time series of MSEµ and MSEσ2 are respectively the mean and variance values of consecutive sample points [17,25]. Note that the coarse-graining process based on the mean and variance start from scale factor 1 and 2, respectively [17,25].
- (II)
- At each scale factor, the SampEn of the coarse-grained signal is calculated in the next step. For the sake of conciseness, here, we use yi for both the coarse-grained signals and . At each time t of y, a vector for t = 1, 2, …, N−(m−1), including the m-th subsequent values is constructed, where m, named embedding dimension, stands for how many samples are contained in each vector. Next, the distance between such vectors as the maximum difference of their corresponding scalar components, are calculated. A match happens when the distance is smaller than a predefined tolerance r. The probability Bm(r) shows the total number of m-dimensional matched vectors [15]. Similarly, Bm+1(r) is defined for embedded dimension of m + 1. Finally, the SampEn is defined as follows [15]:where m and r for SampEn were, respectively, chosen as 2, and 0.15 multiplied by the SD of the original time series following recommendations in [15].
2.3.2. Multivariate Multiscale Entropy Based on Mean and Variance
- (I)
- Assume we have a p-channel (multivariate) time series , q = 1, …, p, where C is the length of each channel’s signal. Each element of the coarse-grained time series is calculated as follows:where λ is the time scale factor [17,22,37]. As an extension of MSEσ2 [25] to multi-channel signals, we propose to use variance, instead of mean value, in the coarse-graining process as follows:
- (II)
- Second, for the defined scale factor λ, the mvSE of the coarse-grained signal is calculated [24,37,38]. To calculate the mvSE, multivariate embedded vectors are initially generated [24]. In [39], the Takens embedding theorem for multivariate concept is described. Using the p-channel signal where N is the length of each coarse-grained time series , the multivariate embedded reconstruction is defined as:where and are the embedding and the time lag vectors, respectively.
- Form multivariate embedded vectors where and .
- Calculate the distance between any two composite delay vectors and as the maximum norm.
- For a given and a threshold r, count the number of instances Pi where . Next, calculate the frequency of occurrence as and define a global quantity .
- Extend the dimensionality of the multivariate delay vector in (6) from m to (m + 1) (keep the dimension of the other variables unchanged).
- Repeat steps 1–4 and find . Next, calculate which denotes the average over all n of . Finally, find which stands for the average over all i of in an (m + 1)-dimensional space.
- Finally, mvSE is defined as:where mk, τk, and r for all of the approaches were, respectively, chosen as 2, 1, and 0.15 multiplied by the SD of the original time series according to [15,24]. Note that the number of sample points is at least 10m, or preferably at least 30m, to robustly estimate SampEn and mvSE, according to [24,40,41].
2.4. Experimental Procedures
3. Results
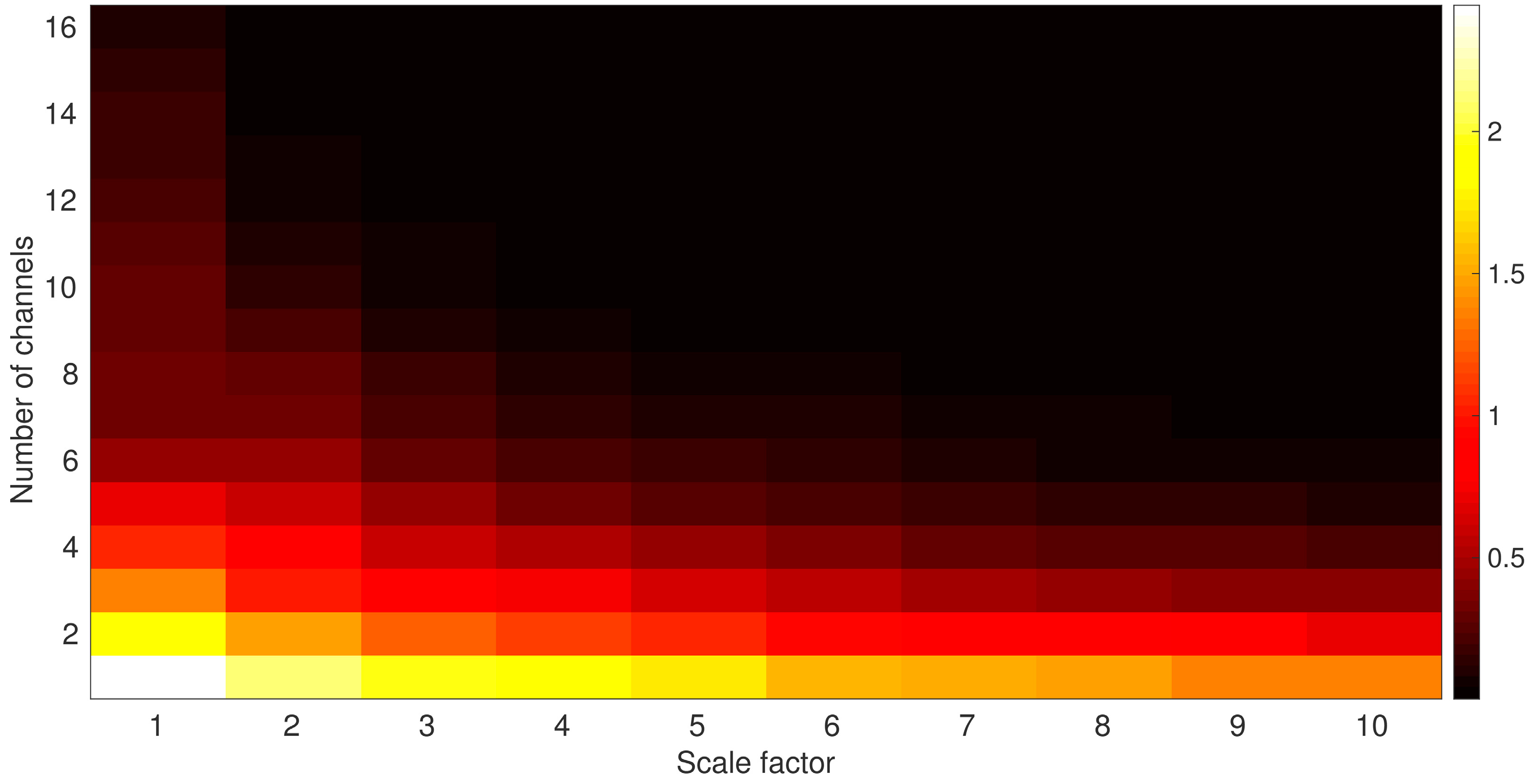
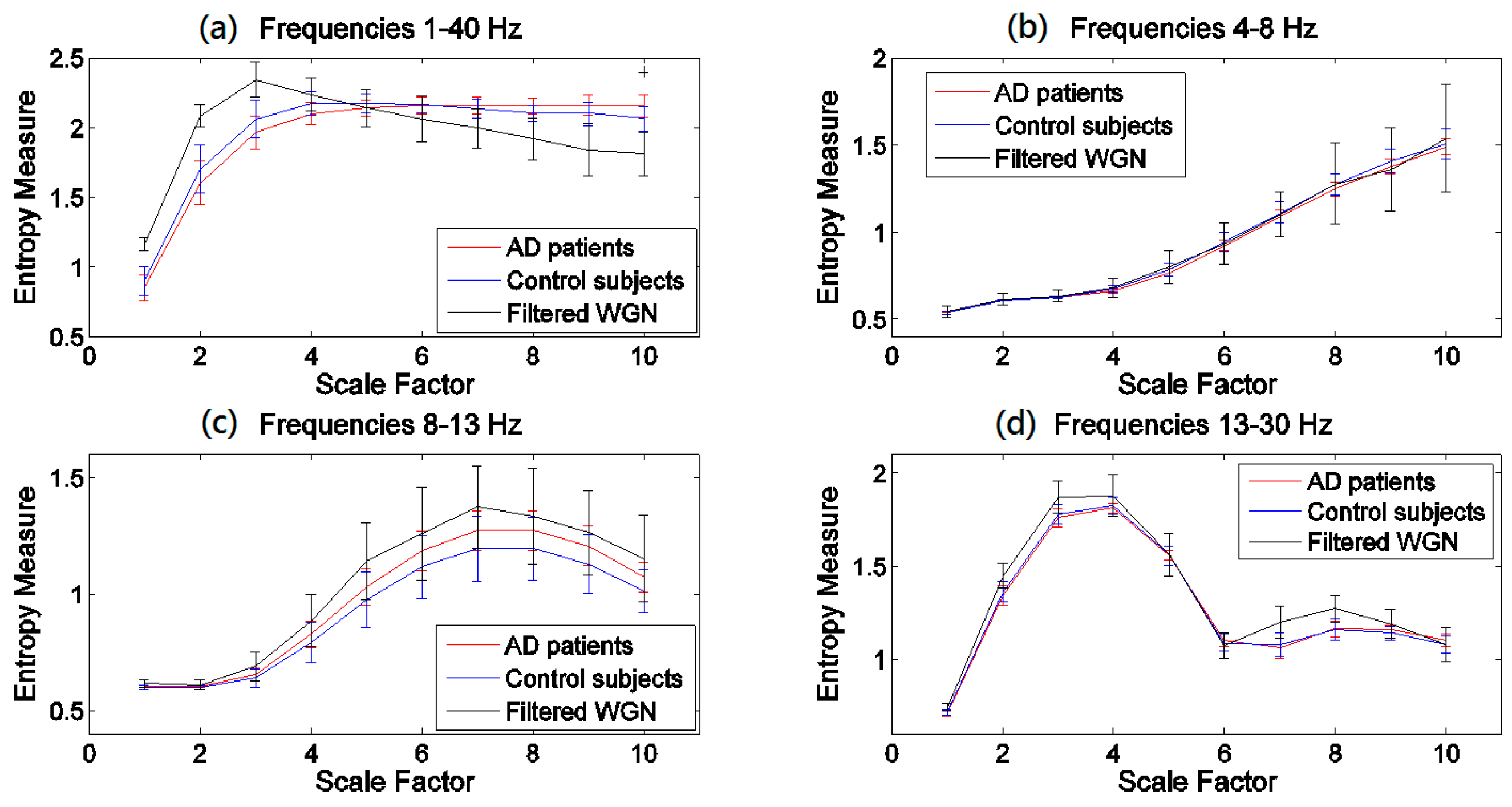
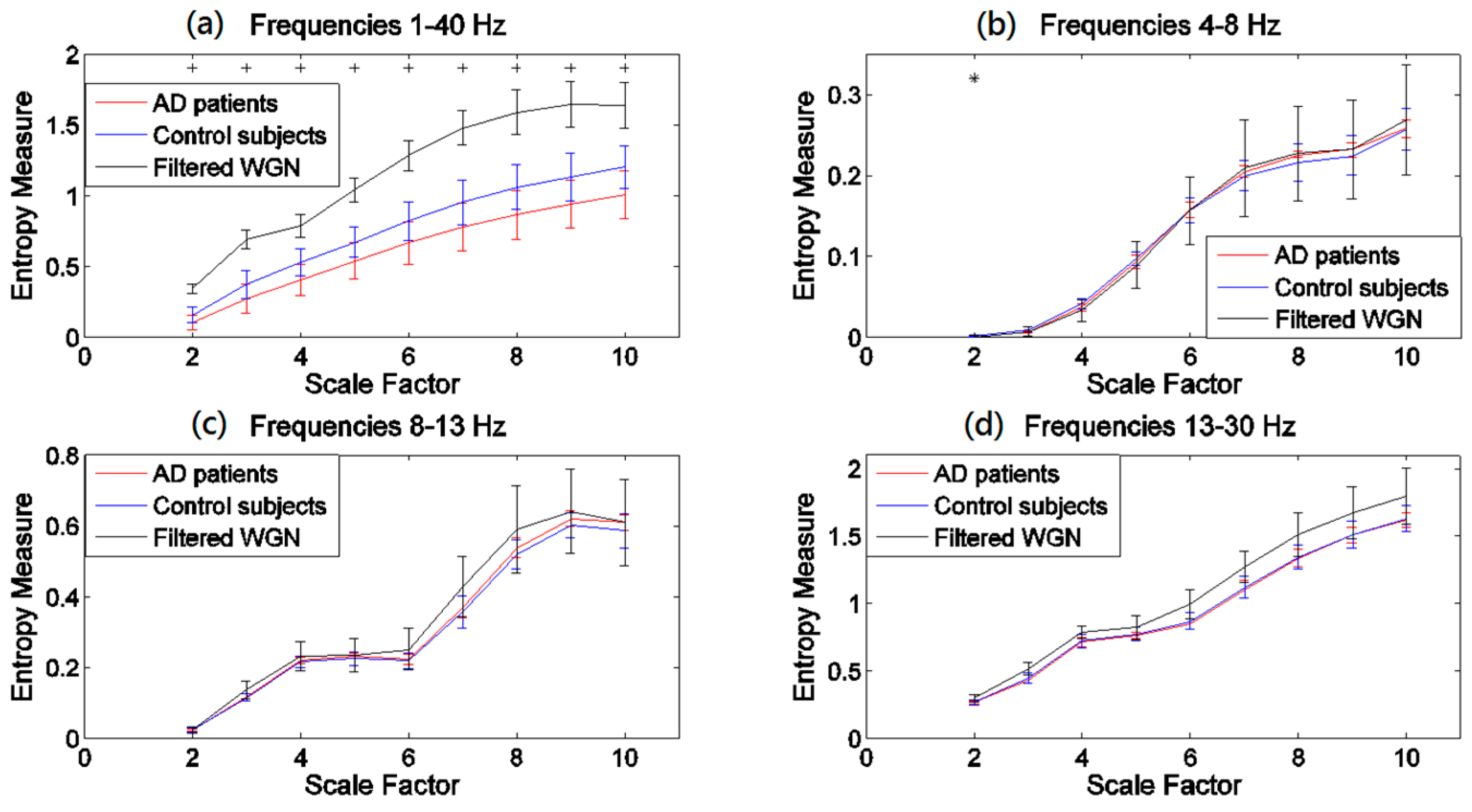
3.1. Global Evaluation of Multivariate and Univariate Multiscale Entropies
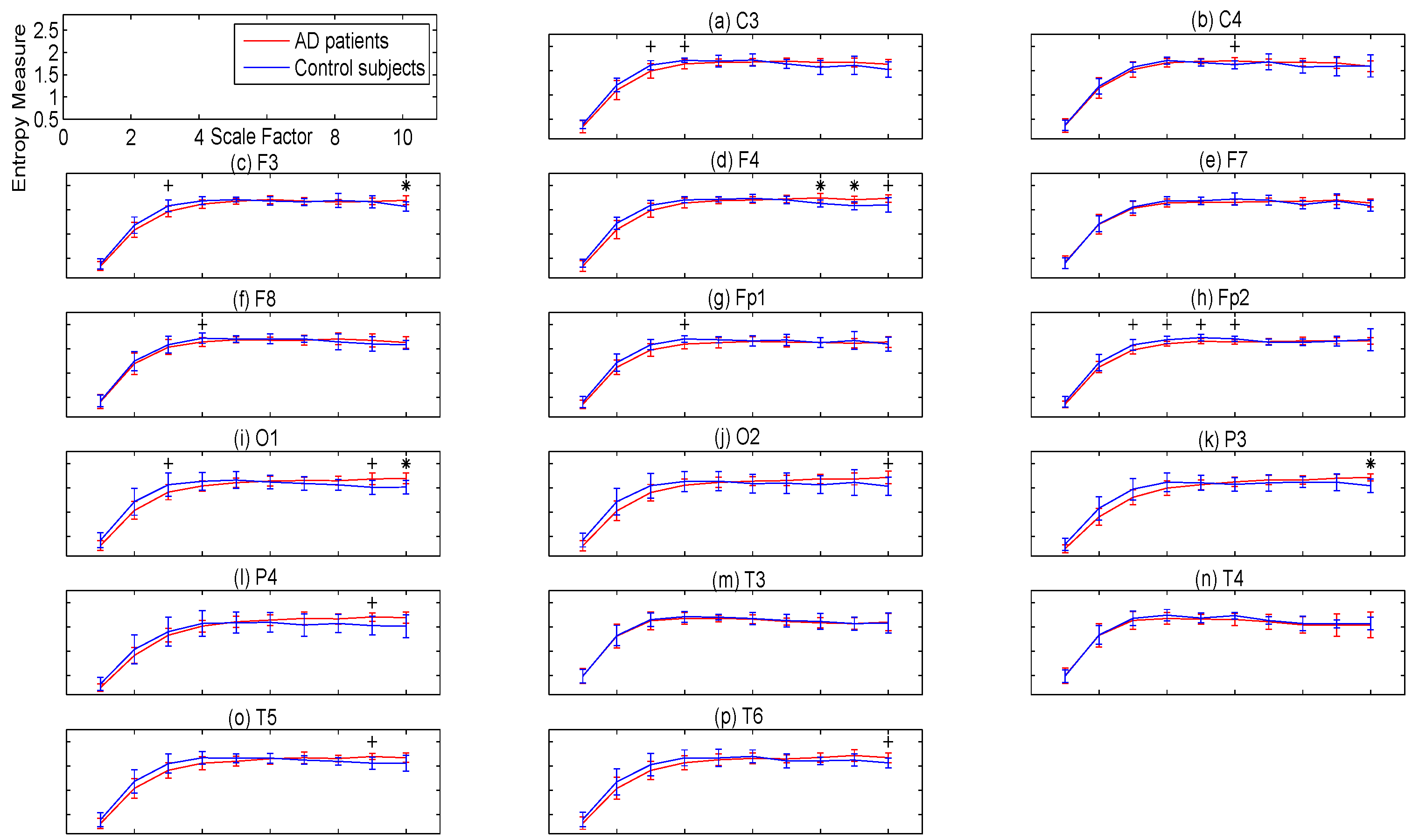
3.2. Regional Evaluation with Univariate Metrics
3.3. Features (Slopes) from Univariate and Multivariate Multiscale Profiles
4. Discussion and Conclusions
4.1. Global Evaluation of Multivariate and Univariate Multiscale Entropies
4.2. Regional Evaluation with Univariate Metrics
4.3. Features (Slopes) from Univariate and Multivariate Multiscale Profiles
4.4. Limitations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Bhat, S.; Acharya, U.R.; Dadmehr, N.; Adeli, H. Clinical neurophysiological and automated EEG-based diagnosis of the Alzheimer’s disease. Eur. Neurol. 2015, 74, 202–210. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Vialatte, F.; Cichocki, A. Diagnosis of Alzheimer’s disease from eeg signals: Where are we standing? Curr. Alzheimer Res. 2010, 7, 487–505. [Google Scholar] [CrossRef] [PubMed]
- Alzheimer’s Association. 2016 Alzheimer’s disease facts and figures. Alzheimers Dement. 2016, 12, 459–509. [Google Scholar]
- Sanei, S. Adaptive Processing of Brain Signals; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Stam, C. Use of magnetoencephalography (MEG) to study functional brain networks in neurodegenerative disorders. J. Neurol. Sci. 2010, 289, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Escudero, J.; Fernández, A.; Poza, J.; Gómez, C. Spectral and nonlinear analyses of MEG background activity in patients with Alzheimer’s disease. IEEE Trans. Biomed. Eng. 2008, 55, 1658–1665. [Google Scholar] [CrossRef] [PubMed]
- Van der Hiele, K.; Vein, A.; Reijntjes, R.; Westendorp, R.; Bollen, E.; Van Buchem, M.; Van Dijk, J.; Middelkoop, H. EEG correlates in the spectrum of cognitive decline. Clin. Neurophysiol. 2007, 118, 1931–1939. [Google Scholar] [CrossRef] [PubMed]
- Czigler, B.; Csikós, D.; Hidasi, Z.; Gaál, Z.A.; Csibri, É.; Kiss, É.; Salacz, P.; Molnár, M. Quantitative EEG in early Alzheimer’s disease patients—Power spectrum and complexity features. Int. J. Psychophysiol. 2008, 68, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Moretti, D.; Fracassi, C.; Pievani, M.; Geroldi, C.; Binetti, G.; Zanetti, O.; Sosta, K.; Rossini, P.; Frisoni, G. Increase of theta/gamma ratio is associated with memory impairment. Clin. Neurophysiol. 2009, 120, 295–303. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Escudero, J.; Abásolo, D.; Hornero, R.; Espino, P.; López, M. Analysis of electroencephalograms in Alzheimer’s disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J. EEG dynamics in patients with Alzheimer’s disease. Clin. Neurophysiol. 2004, 115, 1490–1505. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; La Foresta, F.; Morabito, G.; Palamara, I.; Morabito, F.C. Entropic measures of EEG complexity in Alzheimer’s disease through a multivariate multiscale approach. IEEE Sens. J. 2013, 13, 3284–3292. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion entropy: A measure for time series analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Sanei, S.; Chambers, J. EEG Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Ahmed, M.; Rehman, N.; Looney, D.; Rutkowski, T.; Mandic, D. Dynamical complexity of human responses: A multivariate data-adaptive framework. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 433–445. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.E.V.; Cabella, B.C.T.; da Costa Neves, U.P.; Junior, L.O.M. Multiscale entropy-based methods for heart rate variability complexity analysis. Phys. A Stat. Mech. Its Appl. 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Fogedby, H. On the phase space approach to complexity. J. Stat. Phys. 1992, 69, 411–425. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. Multivariate refined composite multiscale entropy analysis. Phys. Lett. A 2016, 380, 1426–1431. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.D.; Goldberger, A.L. Generalized multiscale entropy analysis: Application to quantifying the complex volatility of human heartbeat time series. Entropy 2015, 17, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.; Montez, T.; Jones, B.; Rombouts, S.; Van Der Made, Y.; Pijnenburg, Y.; Scheltens, P. Disturbed fluctuations of resting state EEG synchronization in Alzheimer’s disease. Clin. Neurophysiol. 2005, 116, 708–715. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, T.; Takahashi, T.; Cho, R.Y.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Assessment of EEG dynamical complexity in alzheimer’s disease using multiscale entropy. Clin. Neurophysiol. 2010, 121, 1438–1446. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Takahashi, T.; Cho, R.Y.; Mizuno, T.; Kikuchi, M.; Murata, T.; Takahashi, K.; Wada, Y. Antipsychotics reverse abnormal EEG complexity in drug-naive schizophrenia: A multiscale entropy analysis. Neuroimage 2010, 51, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Dang, C.; Li, X. Multiscale entropy analysis of EEG recordings in epileptic rats. Biomed. Eng. Appl. Basis Commun. 2009, 21, 169–176. [Google Scholar] [CrossRef]
- Chung, C.-C.; Kang, J.-H.; Yuan, R.-Y.; Wu, D.; Chen, C.-C.; Chi, N.-F.; Chen, P.-C.; Hu, C.-J. Multiscale entropy analysis of electroencephalography during sleep in patients with parkinson disease. Clin. EEG Neurosci. 2013. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Smith, K.; Fernandez, A.; Escudero, J. Evaluation of resting-state magnetoencephalogram complexity in Alzheimer’s disease with multivariate multiscale permutation and sample entropies. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 5–29 August 2015; pp. 7422–7425.
- McKhann, G.; Drachman, D.; Folstein, M.; Katzman, R.; Price, D.; Stadlan, E.M. Clinical diagnosis of Alzheimer’s disease: Report of the nincds-adrda work group* under the auspices of department of health and human services task force on Alzheimer’s disease. Neurology 1984, 34, 939. [Google Scholar] [CrossRef] [PubMed]
- Folstein, M.F.; Folstein, S.E.; McHugh, P.R. “Mini-mental state”: A practical method for grading the cognitive state of patients for the clinician. J. Psychiatr. Res. 1975, 12, 189–198. [Google Scholar] [CrossRef]
- Abásolo, D.; Escudero, J.; Hornero, R.; Gómez, C.; Espino, P. Approximate entropy and auto mutual information analysis of the electroencephalogram in alzheimer’s disease patients. Med. Biol. Eng. Comput. 2008, 46, 1019–1028. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Espino, P.; Alvarez, D.; Poza, J. Entropy analysis of the EEG background activity in Alzheimer’s disease patients. Physiol. Meas. 2006, 27, 241. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. Multivariate generalized multiscale entropy analysis. Entropy 2016, 18, 411. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Phys. D Nonlinear Phenom. 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Pincus, S.M.; Goldberger, A.L. Physiological time-series analysis: What does regularity quantify? Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1643–H1656. [Google Scholar]
- Azami, H.; Escudero, J. Refined composite multivariate generalized multiscale fuzzy entropy: A tool for complexity analysis of multichannel signals. Phys. A Stat. Mech. Its Appl. 2017, 465, 261–276. [Google Scholar] [CrossRef]
- Valencia, J.F.; Porta, A.; Vallverdú, M.; Claria, F.; Baranowski, R.; Orlowska-Baranowska, E.; Caminal, P. Refined multiscale entropy: Application to 24-h holter recordings of heart period variability in healthy and aortic stenosis subjects. IEEE Trans. Biomed. Eng. 2009, 56, 2202–2213. [Google Scholar] [CrossRef] [PubMed]
- Morabito, F.C.; Labate, D.; Bramanti, A.; La Foresta, F.; Morabito, G.; Palamara, I.; Szu, H.H. Enhanced compressibility of EEG signal in Alzheimer’s disease patients. IEEE Sens. J. 2013, 13, 3255–3262. [Google Scholar] [CrossRef]
- Yang, A.C.; Wang, S.-J.; Lai, K.-L.; Tsai, C.-F.; Yang, C.-H.; Hwang, J.-P.; Lo, M.-T.; Huang, N.E.; Peng, C.-K.; Fuh, J.-L. Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer’s disease. Prog. Neuro Psychopharmacol. Biol. Psychiatry 2013, 47, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Hornero, R.; Abásolo, D.; Escudero, J.; Gómez, C. Nonlinear analysis of electroencephalogram and magnetoencephalogram recordings in patients with Alzheimer’s disease. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 317–336. [Google Scholar] [CrossRef] [PubMed]
- Courtiol, J.; Perdikis, D.; Petkoski, S.; Müller, V.; Huys, R.; Sleimen-Malkoun, R.; Jirsa, V.K. The multiscale entropy: Guidelines for use and interpretation in brain signal analysis. J. Neurosci. Methods 2016, 273, 175–190. [Google Scholar] [CrossRef] [PubMed]
- Rish, I. An empirical study of the naive bayes classifier. In IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence; IBM: New York, NY, USA, 2001; pp. 41–46. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The weka data mining software: An update. ACM SIGKDD Explor. Newslett. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Jelles, B.; Van Birgelen, J.; Slaets, J.; Hekster, R.; Jonkman, E.; Stam, C. Decrease of non-linear structure in the EEG of alzheimer patients compared to healthy controls. Clin. Neurophysiol. 1999, 110, 1159–1167. [Google Scholar] [CrossRef]
- Kyriazis, M. Practical applications of chaos theory to the modulation of human ageing: Nature prefers chaos to regularity. Biogerontology 2003, 4, 75–90. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Gómez, C.; García, M.; López, M. Analysis of EEG background activity in Alzheimer’s disease patients with lempel–ziv complexity and central tendency measure. Med. Eng. Phys. 2006, 28, 315–322. [Google Scholar] [CrossRef] [PubMed]



| MSEµ | mvMSEµ | MSEσ2 | mvMSEσ2 |
|---|---|---|---|
| 4.77 s | 21.78 s | 2.4 s | 8.05 s |
| Method | AD Patients | Controls | p-Value | Classification Ratio |
|---|---|---|---|---|
| MSEµ | 0.4107 ± 0.0226 | 0.4185 ± 0.0238 | 0.3933 | 63.64% |
| MSEµ + | 0.0022 ± 0.0195 | −0.0216 ± 0.0240 | 0.0215 | 72.73% |
| MSEσ2 + | 0.1130 ± 0.0154 | 0.1301 ± 0.0137 | 0.0151 | 72.73% |
| mvMSEµ | 0.0074 ± 0.0088 | 0.0077 ± 0.0092 | 0.5114 | 31.82% |
| mvMSEµ * | −0.0048 ± 0.0037 | −0.0099 ± 0.0033 | 0.0071 | 72.73% |
| mvMSEσ2 + | 0.0030 ± 0.0009 | 0.0041 ± 0.0012 | 0.0302 | 63.64% |
| Electrode | AD Patients | Controls | p-Value |
|---|---|---|---|
| C3 | −0.006 ± 0.0302 | −0.0360 ± 0.0356 | 0.0762 |
| C4 | −0.018 ± 0.0264 | −0.0160 ± 0.0472 | 0.8955 |
| F3 | −0.001 ± 0.0171 | −0.0209 ± 0.0238 | 0.0878 |
| F4 * | 0.0076 ± 0.0244 | −0.0318 ± 0.0220 | 0.0031 |
| F7 | 0.0018 ± 0.0219 | −0.0206 ± 0.0317 | 0.1150 |
| F8 + | −0.007 ± 0.0285 | −0.0279 ± 0.0149 | 0.0418 |
| Fp1 | −0.001 ± 0.0174 | −0.0136 ± 0.0443 | 0.1007 |
| Fp2 | 0.0029 ± 0.0115 | −0.0099 ± 0.0378 | 0.0660 |
| O1 * | 0.0162 ± 0.0285 | −0.0306 ± 0.0256 | 0.0031 |
| O2 + | 0.0194 ± 0.0277 | −0.0136 ± 0.0415 | 0.0418 |
| P3 + | 0.0276 ± 0.0238 | −0.0040 ± 0.0453 | 0.0488 |
| P4 | 0.0177 ± 0.0303 | −0.0151 ± 0.0399 | 0.0660 |
| T3 | −0.019 ± 0.0379 | −0.0267 ± 0.0390 | 0.8438 |
| T4 | −0.029 ± 0.0496 | −0.0324 ± 0.0297 | 0.7427 |
| T5 + | 0.0139 ± 0.0278 | −0.0246 ± 0.0312 | 0.0126 |
| T6 | 0.0120 ± 0.0361 | −0.0213 ± 0.0494 | 0.0660 |
| Electrode | AD Patients | Controls | p-Value |
|---|---|---|---|
| C3 + | 0.1163 ± 0.0178 | 0.1296 ± 0.0119 | 0.0488 |
| C4 | 0.1213 ± 0.0186 | 0.1289 ± 0.0135 | 0.2643 |
| F3 | 0.1127 ± 0.0127 | 0.1257 ± 0.0173 | 0.0660 |
| F4 + | 0.1139 ± 0.0164 | 0.1278 ± 0.0123 | 0.0418 |
| F7 | 0.1161 ± 0.0133 | 0.1273 ± 0.0204 | 0.1891 |
| F8 | 0.1165 ± 0.0183 | 0.1326 ± 0.0154 | 0.0569 |
| Fp1 | 0.1079 ± 0.0212 | 0.1253 ± 0.0182 | 0.1486 |
| Fp2 | 0.1085 ± 0.0148 | 0.1226 ± 0.0214 | 0.1310 |
| O1 + | 0.1080 ± 0.0186 | 0.1342 ± 0.0208 | 0.0126 |
| O2 * | 0.1078 ± 0.0195 | 0.1358 ± 0.0219 | 0.0071 |
| P3 + | 0.1023 ± 0.0193 | 0.1231 ± 0.0183 | 0.0356 |
| P4 + | 0.1038 ± 0.0180 | 0.1255 ± 0.0201 | 0.0215 |
| T3 | 0.1267 ± 0.0218 | 0.1406 ± 0.0201 | 0.1486 |
| T4 | 0.1301 ± 0.0314 | 0.1389 ± 0.0210 | 0.4307 |
| T5 + | 0.1069 ± 0.0203 | 0.1307 ± 0.0215 | 0.0418 |
| T6 + | 0.1091 ± 0.0216 | 0.1327 ± 0.0187 | 0.0256 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azami, H.; Abásolo, D.; Simons, S.; Escudero, J. Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease. Entropy 2017, 19, 31. https://doi.org/10.3390/e19010031
Azami H, Abásolo D, Simons S, Escudero J. Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease. Entropy. 2017; 19(1):31. https://doi.org/10.3390/e19010031
Chicago/Turabian StyleAzami, Hamed, Daniel Abásolo, Samantha Simons, and Javier Escudero. 2017. "Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease" Entropy 19, no. 1: 31. https://doi.org/10.3390/e19010031
APA StyleAzami, H., Abásolo, D., Simons, S., & Escudero, J. (2017). Univariate and Multivariate Generalized Multiscale Entropy to Characterise EEG Signals in Alzheimer’s Disease. Entropy, 19(1), 31. https://doi.org/10.3390/e19010031








