Information Decomposition in Multivariate Systems: Definitions, Implementation and Application to Cardiovascular Networks

Abstract

The continuously growing framework of information dynamics encompasses a set of tools, rooted in information theory and statistical physics, which allow to quantify different aspects of the statistical structure of multivariate processes reflecting the temporal dynamics of complex networks. Building on the most recent developments in this field, this work designs a complete approach to dissect the information carried by the target of a network of multiple interacting systems into the new information produced by the system, the information stored in the system, and the information transferred to it from the other systems; information storage and transfer are then further decomposed into amounts eliciting the specific contribution of assigned source systems to the target dynamics, and amounts reflecting information modification through the balance between redundant and synergetic interaction between systems. These decompositions are formulated quantifying information either as the variance or as the entropy of the investigated processes, and their exact computation for the case of linear Gaussian processes is presented. The theoretical properties of the resulting measures are first investigated in simulations of vector autoregressive processes. Then, the measures are applied to assess information dynamics in cardiovascular networks from the variability series of heart period, systolic arterial pressure and respiratory activity measured in healthy subjects during supine rest, orthostatic stress, and mental stress. Our results document the importance of combining the assessment of information storage, transfer and modification to investigate common and complementary aspects of network dynamics; suggest the higher specificity to alterations in the network properties of the measures derived from the decompositions; and indicate that measures of information transfer and information modification are better assessed, respectively, through entropy-based and variance-based implementations of the framework.

1. Introduction

The framework of information dynamics is rapidly emerging, at the forefront between the theoretical fields of information theory and statistical physics and applicative fields such as neuroscience and physiology, as a versatile and unifying set of tools that allow to dissect the general concept of “information processing” in a network of interacting dynamical systems into basic elements of computation reflecting different aspects of the functional organization of the network [1,2,3]. Within this framework, several tools that include the concept of temporal precedence within the computation of standard information-theoretic measures have been proposed to provide a quantitative description of how collective behaviors in multivariate systems arise from the interaction between the individual system components. These tools formalize different information-theoretic concepts applied to a “target” system in the observed dynamical network: the predictive information about the system describes the amount of information shared between its present state and the past history of the whole observed network [4,5]; the information storage indicates the information shared between the present and past states of the target [6,7]; the information transfer defines the information that a group of systems designed as “sources” provide about the present state of the target [8,9]; and the information modification reflects the redundant or synergetic interaction between multiple sources sending information to the target [3,10]. Operational definitions of these concepts have been proposed in recent years, which allow to quantify predictive information through measures of prediction entropy or full-predictability [11,12], information storage through the self-entropy or self-predictability [11,13], information transfer through transfer entropy or Granger causality [14], and information modification through entropy and prediction measures of net redundancy/synergy [11,15] or separate measures derived from partial information decomposition [16,17]. All these measures have been successfully applied in diverse fields of science ranging from cybernetics to econometrics, climatology, neuroscience and others [6,7,18,19,20,21,22,23,24,25,26,27,28]. In particular, recent studies have implemented these measures in cardiovascular physiology to study the short-term dynamics of the cardiac, vascular and respiratory systems in terms of information storage, transfer and modification [12,13,29].

In spite of its growing appeal and widespread utilization, the field of information dynamics is still under development, and several aspects need to be better explored to fully exploit its potential, favor the complete understanding of its tools, and settle some issues about its optimal implementation. An important but not fully explored aspect is that the measures of information dynamics are often used in isolation, thus limiting their interpretational capability. Indeed, recent studies have pointed out the intertwined nature of the measures of information dynamics, and the need to combine their evaluation to avoid misinterpretations about the underlying network properties [4,12,30]. Moreover, the specificity of measures of information storage and transfer is often limited by the fact that their definition incorporates multiple aspects of the dynamical structure of network processes; the high flexibility of information-theoretic measures allows to overcome this limitation by expanding these measures into meaningful quantities [13,29]. Finally, from the point of view of their implementation, the outcome of analyses based on information dynamics can be strongly affected by the functional used to define and estimate information measures. Model-free approaches for the computation of these measures are more general but more difficult to implement, and often provide comparable results than simpler and less demanding model-based techniques [31,32]; even within the class of model-based approaches, prediction methods and entropy methods—though often used interchangeably to assess network dynamics—may lead to strongly different interpretations [16,30].

The aim of the present study is to integrate together several different concepts previously proposed in the framework of information dynamics into a unifying approach that provides quantitative definitions of these concepts based on different implementations. Specifically, we propose three nested information decomposition strategies that allow: (i) to dissect the information contained in the target of a network of interacting systems into amounts reflecting the new information produced by the system at each moment in time, the information stored in the system and the information transferred to it from the other connected systems; (ii) to dissect the information storage into the internal information ascribed exclusively to the target dynamics and three interaction storage terms accounting for the modification of the information shared between the target and two groups of source systems; and (iii) to dissect the information transfer into amounts of information transferred individually from each source when the other is assigned (conditional information transfer) and a term accounting for the modification of the information transferred due to cooperation between the sources (interaction information transfer). With this approach, we define several measures of information dynamics, stating their properties and reciprocal relations, and formulate these measures using two different functionals, based respectively on measuring information either as the variance or as the entropy of the stochastic processes representative of the system dynamics. We also provide a data-efficient approach for the computation of these measures, which yields their exact values in the case of stationary Gaussian systems. Then, we study the theoretical properties and investigate the reciprocal behavior of all measures in simulated multivariate processes reflecting the dynamics of networks of Gaussian systems. Finally, we perform the first exhaustive application of the complete framework in the context of the assessment of the short-term dynamics of the cardiac, vascular and respiratory systems explored in healthy subjects in a resting state and during conditions capable of altering the cardiovascular, cardiopulmonary and vasculo-pulmonary dynamics, i.e., orthostatic stress and mental stress [33]. Both the theoretical formulation of the framework and its utilization on simulated and physiological dynamics are focused on evidencing the usefulness of decompositions that evidence peculiar aspects of the dynamics, and illustrate the differences between variance- and entropy-based implementations of the proposed measures.

2. Information Decomposition in Multivariate Processes

2.1. Information Measures for Random Variables

In this introductory section we first formulate two possible operational definitions, respectively based on measures of variance and measures of entropy, for the information content of a random variable and for its conditional information when a second variable is assigned; moreover we show how these two formalizations relate analytically under the case of multivariate Gaussian variables. Then, we recall the basic information-theoretic concepts that build on the previously provided operational definitions and will be used in the subsequent formulation of the framework for information decomposition, i.e., the information shared between two variables, the interaction information between three variables, as well as the conditioned versions of these concepts.

2.1.1. Variance-Based and Entropy-Based Measures of Information

Let us consider a scalar (one-dimensional) continuous random variable X with probability density function f_X(x), x∈D_X, where D_X is the domain of X. As we are interested in the variability of their outcomes, all random variables considered in this study are supposed to have zero mean: $\mathrm{E}[X]=0$. The information content of X can be intuitively related to the uncertainty of X, or equivalently, the unpredictability of its outcomes x∈D_X: if X takes on many different values inside D_X, its outcomes are uncertain and the information content is assumed to be high; if, on the contrary, only a small number of values are taken by X with high probability, the outcomes are more predictable and the information content is low. This concept can be formulated with reference to the degree of variability of the variable, thus quantifying information in terms of variance:

$$H_V(X)=\mathrm{E}[X^2]={\displaystyle \underset{D_X}{\int }{x}^2{f}_X(x)dx},$$

(1)

or with reference to the probability of guessing the outcomes of the variable, thus quantifying information in terms of entropy:

$$H_E(X)=\mathrm{E}[-\text{log} f_X]=-{\displaystyle \underset{D_X}{\int }{f}_X(x)\text{log} f_X(x)dx},$$

(2)

where log is the natural logarithm and thus entropy is measured in “nats”. In the following the quantities defined in Equations (1) and (2) will be used to indicate the information H(X) of a random variable, and will be particularized to the variance-based definition H_V(X) of Equation (1) or to the entropy-based definition H_E(X) of Equation (2) when necessary.

Now we move to define how the information carried by the scalar variable X relates with that carried by a second k-dimensional vector variable Z = [Z₁∙∙∙Z_k]^T with probability density $f_Z(\mathit{z})$. To this end, we introduce the concept of conditional information, i.e., the information remaining in X when Z is assigned, denoted as H(X|Z). This concept is linked to the resolution of uncertainty about X, or equivalently, the decrement of unpredictability of its outcomes x∈D_X, brought by the knowledge of the outcomes z∈D_Z of the variable Z: if the values of X are perfectly predicted by the knowledge of Z, no uncertainty is left about X when Z is known and thus H(X|Z) = 0; if, on the contrary, knowing Z does not alter the uncertainty about the outcomes of X, the residual uncertainty will be maximum, H(X|Z) = H(X). To formulate this concept we may reason again in terms of variance, considering the prediction of X on Z and the corresponding prediction error variable $U=X-\mathrm{E}[X|\mathit{Z}]$, and defining the conditional variance of X given Z as:

$$H_V(X|\mathit{Z})=\mathrm{E}[U^2],$$

(3)

or in terms of entropy, considering the joint probability density $f_{X,\mathit{Z}}(x,\mathit{z})$ and the conditional probability of X given Z, $f_{X|\mathit{Z}}(x|\mathit{z})=f_{X,\mathit{Z}}(x,\mathit{z})/f_{\mathit{Z}}(\mathit{z})$, and defining the conditional entropy of X given Z as:

$$H_E(X|\mathit{Z})=\mathrm{E}[-\text{log} f_{X|\mathit{Z}}].$$

(4)

2.1.2. Variance-Based and Entropy-Based Measures of Information for Gaussian Variables

The two formulations introduced above to quantify the concepts of information and conditional information exploit functionals which are intuitively related with each other (i.e., variance vs. entropy, and prediction error variance vs. conditional entropy). Here we show that the connection between the two approaches can be formalized analytically in the case of variables with joint Gaussian distribution. In such a case, the variance and the entropy of the scalar variable X are related by the well-known expression [34]:

$$H_E(X)=\frac{1}{2}\text{log}\left(2\pi e H_V(X)\right),$$

(5)

while the conditional entropy and the conditional variance of X given Z are related by the expression [35]:

$$H_E(X|\mathit{Z})=\frac{1}{2}\text{log}\left(2\mathsf{\pi }e H_V(X|\mathit{Z})\right).$$

(6)

Moreover, if X and Z have a joint Gaussian distribution their interactions are fully described by a linear relation of the form $X=\mathit{A}\mathit{Z}+U$, where A is a k-dimensional row vector of coefficients such that $\mathrm{E}[X|\mathit{Z}]=\mathit{A}\mathit{Z}$ [36]. This leads to computing the variance of the prediction error as $\mathrm{E}[U^2]=\mathrm{E}[X^2]-\mathit{A}\Sigma (\mathit{Z}){\mathit{A}}^{\mathrm{T}}$, where $\Sigma (\mathit{Z})=\mathrm{E}[\mathit{Z}{\mathit{Z}}^{\mathrm{T}}]$ is the covariance of Z; additionally, the uncorrelation between the regressor Z and the error U, $\Sigma (\mathit{Z};U)=0$, leads to express the coefficients as $\mathit{A}=\Sigma (X;\mathit{Z})\Sigma {(\mathit{Z})}^{-\mathrm{T}}$, which yields:

$$H_V(X|\mathit{Z})=H_V(X)-\Sigma (X;\mathit{Z})\Sigma {(\mathit{Z})}^{-1}\Sigma {(X;\mathit{Z})}^{\mathrm{T}}.$$

(7)

This enables computation of all the information measures defined in Equations (1)–(4) for joint Gaussian variables X and Z starting from the variance of X, $H_V(X)$, the covariance of Z, $\Sigma (\mathit{Z})$, and their cross covariance, $\Sigma (X;\mathit{Z})$.

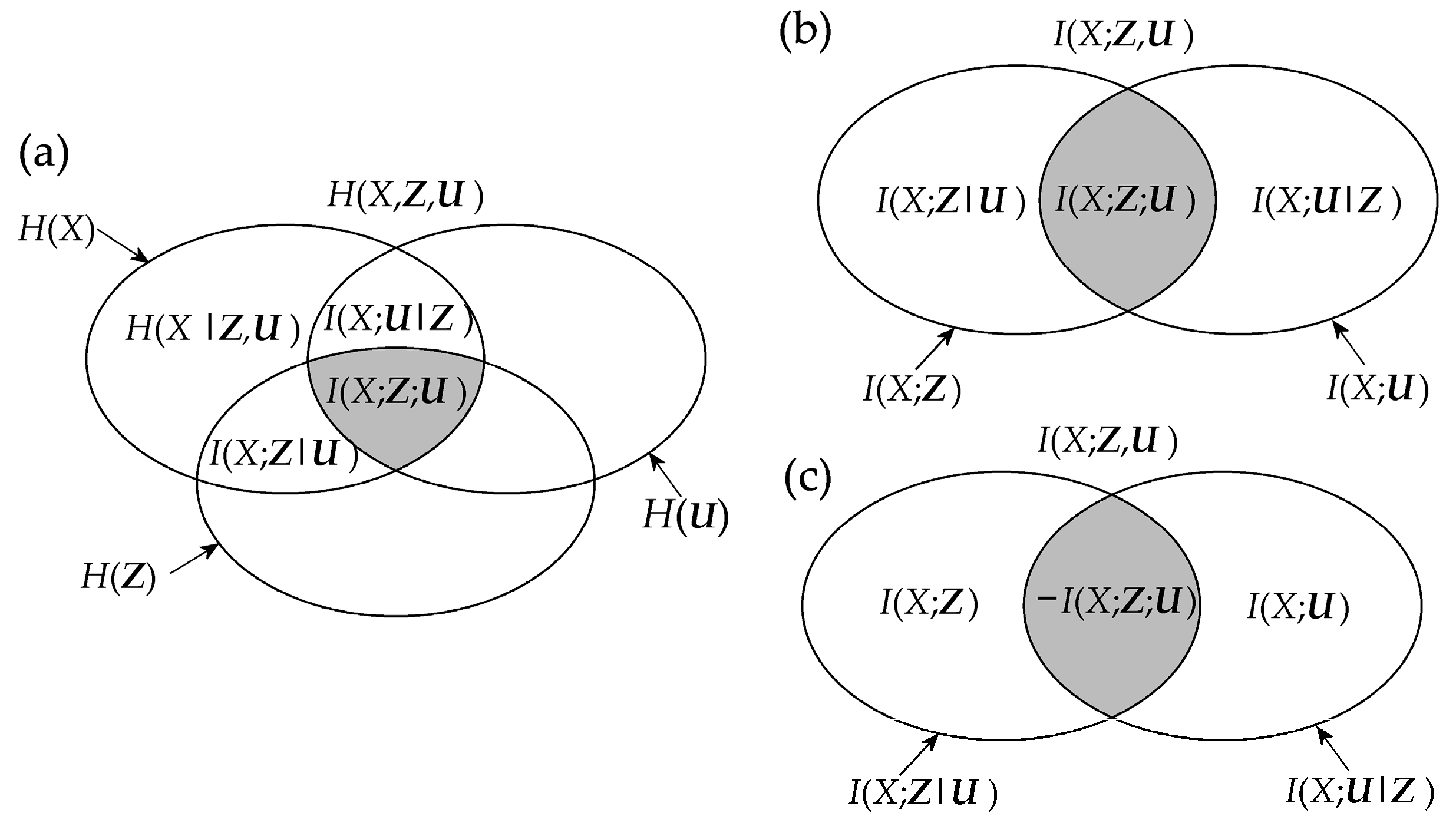
2.1.3. Measures Derived from Information and Conditional Information

The concepts of information and conditional information defined in the Section 2.1.1 form the basis for the formulation of other important information-theoretic measures. The most popular is the well-known mutual information, which quantifies the information shared between two variables X and Z as:

$$I(X;\mathit{Z})=H(X)-H(X|\mathit{Z}),$$

(8)

intended as the average reduction in uncertainty about the outcomes of X obtained when the outcomes of Z are known. Moreover, the conditional mutual information between X and Z given a third variable U, I(X;Z|U), quantifies the information shared between X and Z which is not shared with U, intended as the reduction in uncertainty about the outcomes of X provided by the knowledge of the outcomes of Z that is not explained by the outcomes of U:

$$I(X;\mathit{Z}|\mathit{U})=H(X|\mathit{U})-H(X|\mathit{Z},\mathit{U})=I(X;\mathit{Z},\mathit{U})-I(X;\mathit{U}).$$

(9)

Another interesting information-theoretic quantity is the interaction information, which is a measure of the amount of information that a target variable X shares with two source variables Z and U when they are taken individually but not when they are taken together:

$$I(X;\mathit{Z};\mathit{U})=I(X;\mathit{Z})+I(X;\mathit{U})-I(X;\mathit{Z},\mathit{U}).$$

(10)

Alternatively, the interaction information can be intended as the negative of the amount of information bound up in the set of variables {X,Z,U} beyond that which is present in the individual subsets {X,Z} and {X,U}. Contrary to all other information measures which are never negative, the interaction information defined in Equation (10) can take on both positive and negative values, with positive values indicating redundancy (i.e., I(X;Z,U) < I(X;Z) + I(X;U)) and negative values indicating synergy (i.e., I(X;Z,U) > I(X;Z) + I(X;U)) between the two sources Z and U that share information with the target X. Note that all the measures defined in this Section can be computed as sums of information and conditional information terms. As such, the generic notations I(∙;∙), I(∙;∙|∙), and I(∙;∙;∙) used to indicate mutual information, conditional mutual information and interaction information will be particularized to I_V(∙;∙), I_V(∙;∙|∙), I_V(∙;∙;∙), or to I_E(∙;∙), I_E(∙;∙|∙), I_E(∙;∙;∙), to clarify when their computation is based on variance measures or entropy measures, respectively. Note that, contrary to the entropy-based measure I_E(∙;∙), the variance-based measure I_V(∙;∙) is not symmetric and thus fails to satisfy a basic property of “mutual information” measures. However, this disadvantage is not crucial for the formulations proposed in study which, being based on exploiting the flow of time that sets asymmetric relations between the analyzed variables, do not exploit the symmetry property of mutual information (see Section 2.2).

Mnemonic Venn diagrams of the information measures recalled above, showing how these measures quantify the amounts of information contained in a set of variables and shared between variables, are shown in Figure 1. The several rules that relate the different measures with each other can be inferred from the figure; for instance, the chain rule for information decomposes the information contained in the target variable X as H(X) = I(X;Z,U) + H(X|Z,U), the chain rule for mutual information decomposes the information shared between the target X and the two sources Z and U as I(X;Z,U) = I(X;Z) + I(X;U|Z) = I(X;U) + I(X;Z|U), and the interaction information between X, Z and U results as I(X;Z;U) = I(X;Z) − I(X;Z|U) = I(X;U) − I(X;U|Z).

2.2. Information Measures for Networks of Dynamic Processes

This Section describes the use of the information measures defined in Section 2.1, applied by taking as arguments proper combinations of the present and past states of the stochastic processes representative of a network of interacting dynamical systems, to formulate a framework quantifying the concepts of information production, information storage, information transfer and information modification.

Let us consider a network formed by a set of M possibly interacting dynamic systems, and assume that the course of visitation of the system states is suitably described as a multivariate stationary stochastic process S. We consider the problem of dissecting the information carried by an assigned “target” process Y, into contributions resulting either from its own dynamics and from the dynamics of the other processes X = S\Y, that are considered as “sources”. We further suppose that two separate (groups of) sources, identified by the two disjoint sets V = {V₁,...,V_P} and W = {W₁,...,W_Q} (Q + P = M − 1), have effects on the dynamics of the target, such that the whole observed process is S = {X,Y} = {V,W,Y}. Moreover, setting a temporal reference frame in which n represents the present time, we denote as $Y_n$ the random variable describing the present of Y, and as $Y_n^{-}=[Y_{n-1},Y_{n-2},\dots ]$ the infinite-dimensional variable describing the past of Y. The same notation applies for each source component V_i∈V and W_j∈W, and extends to ${\mathit{X}}_n^{-}=[{\mathit{X}}_{n-1},{\mathit{X}}_{n-2},\dots ]$ and ${\mathit{S}}_n^{-}=[{\mathit{X}}_n^{-},Y_n^{-}]$ to denote the past of the source process X and of the full network process S. This simple operation of separating the present from the past allows to consider the flow of time and to study the causal interactions within and between processes by looking at the statistical dependencies among these variables [1]. An exemplary diagram of the process interactions is depicted in Figure 2a.

Note that, while the elements of the information decompositions defined in the following will be denoted through the generic notations H(∙) and I(∙;∙) for information and mutual information, they can be operationally formulated either in terms of variance (i.e., using H_V and I_V) or in terms of entropy (i.e., using H_E and I_E).

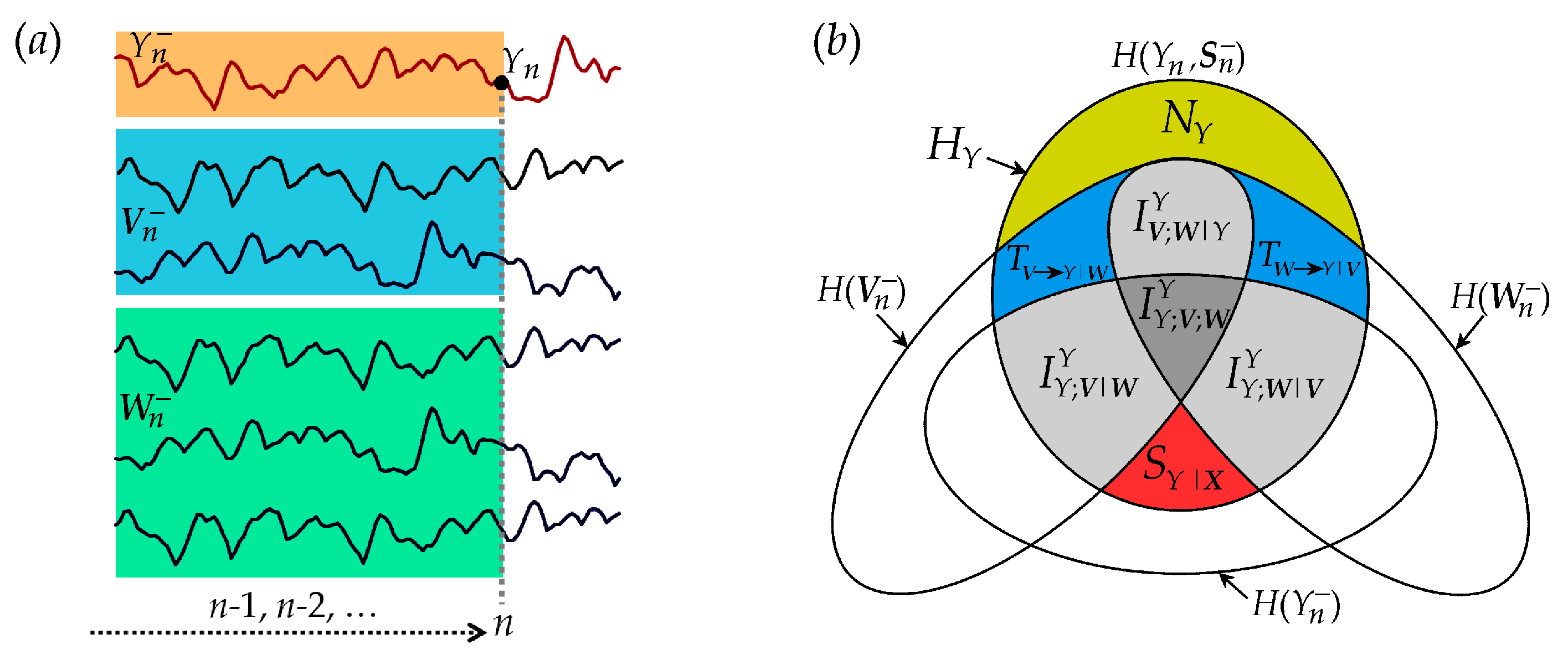
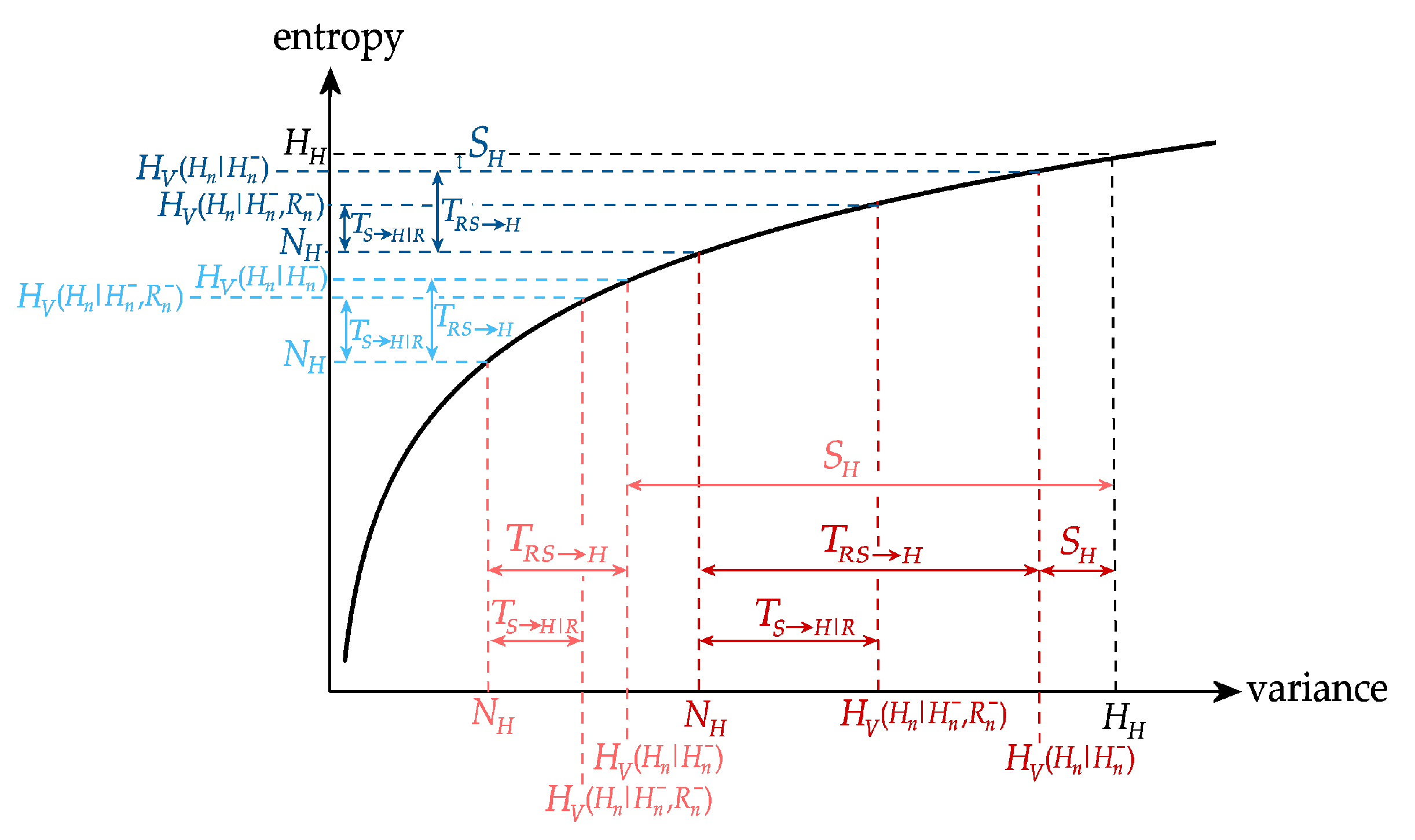
2.2.1. New Information and Predictive Information

First, we define the information content of the target process Y as the information of the variable obtained sampling the process at the present time n:

$$H_Y=H(Y_n),$$

(11)

where, under the assumption of stationarity, dependence on the time index n is omitted in the formulation of the information H_Y. Then, exploiting the chain rule for information [34], we decompose the target information as:

$$H_Y=P_Y+N_Y=I(Y_n;{\mathit{S}}_n^{-})+H(Y_n|{\mathit{S}}_n^{-}),$$

(12)

where $P_Y=I(Y_n;{\mathit{S}}_n^{-})$ is the predictive information of the target Y, measured as the mutual information between the present $Y_n$ and the past of the whole network process ${\mathit{S}}_n^{-}$, and $N_Y=H(Y_n|{\mathit{S}}_n^{-})$ is the newly generated information that appears in the target process Y after the transition from the past states to the present state, measured as the conditional information of c given ${\mathit{S}}_n^{-}$.

The decomposition in Equation (12) evidences how the information carried by the target of a network of interacting processes can be dissected into an amount that can be predicted from the past states of the network, which is thus related to the concept of information stored in the network and ready to be used at the target node, and an amount that is not predictable from the history of any other observed process, which is thus related to the concept of new information produced by the target.

2.2.2. Predictive Information Decomposition (PID)

The predictive information quantifies how much of the uncertainty about the current state of the target process is reduced by the knowledge of the past states visited by the whole network. To understand the contribution of the different parts of the multivariate process to this reduction in uncertainty, the predictive information can be decomposed into amounts related to the concepts of information storage and information transfer. Specifically, we expand the predictive information of the target process Y as:

$$P_Y=S_Y+T_{X\to Y}=I(Y_n;Y_n^{-})+I(Y_n;{\mathit{X}}_n^{-}|Y_n^{-}),$$

(13)

where $S_Y=I(Y_n;Y_n^{-})$ is the information stored in Y, quantified as the mutual information between the present $Y_n$ and the past $Y_n^{-}$, and $T_{X\to Y}=I(Y_n;{\mathit{X}}_n^{-}|Y_n^{-})$ is the joint information transferred from all sources in X to the target Y, quantified as the amount of information contained in the past of the sources ${\mathit{X}}_n^{-}$ that can be used to predict the present of the target $Y_n$ above and beyond the information contained in the past of the target $Y_n^{-}$.

Thus, the decomposition resulting from Equation (13) is useful to dissect the whole information that is contained in the past history of the observed network and is available to predict the future states of the target into a part that is specifically stored in the target itself, and another part that is exclusively transferred to the target from the sources.

2.2.3. Information Storage Decomposition (ISD)

The information storage can be further expanded into another level of decomposition that evidences how the past of the various processes interact with each other in determining the information stored in the target. In particular, the information stored in Y is expanded as:

$$S_Y=S_{Y|X}+I_{Y;X}^Y=I(Y_n;Y_n^{-}|{\mathit{X}}_n^{-})+I(Y_n;Y_n^{-};{\mathit{X}}_n^{-}),$$

(14)

where $S_{Y|X}=I(Y_n;Y_n^{-}|{\mathit{X}}_n^{-})$ is the internal information of the target process, quantified as the amount of information contained in the past of the target $Y_n^{-}$ that can be used to predict the present $Y_n$ above and beyond the information contained in the past of the sources ${\mathit{X}}_n^{-}$, and $I_{Y;X}^Y=I(Y_n;Y_n^{-};{\mathit{X}}_n^{-})$ is the interaction information storage of the target Y in the context of the network process {X,Y}, quantified as the interaction information of the present of the target $Y_n$, its past $Y_n^{-}$, and the past of the sources ${\mathit{X}}_n^{-}$.

In turn, considering that X = {V,W}, the interaction information storage can be expanded as:

$$I_{Y;\mathit{X}}^Y=I_{Y;\mathit{V}}^Y+I_{Y;\mathit{W}}^Y-I_{Y;\mathit{V};\mathit{W}}^Y=I_{Y;\mathit{V}|\mathit{W}}^Y+I_{Y;\mathit{W}|\mathit{V}}^Y+I_{Y;\mathit{V};\mathit{W}}^Y,$$

(15)

where $I_{Y;\mathit{V}}^Y=I(Y_n;Y_n^{-};{\mathit{V}}_n^{-})$ and $I_{Y;\mathit{W}}^Y=I(Y_n;Y_n^{-};{\mathit{W}}_n^{-})$ quantify the interaction information storage of the target Y in the context of the bivariate processes {V,Y} and {W,Y}, $I_{Y;\mathit{V}|\mathit{W}}^Y=I(Y_n;Y_n^{-};{\mathit{V}}_n^{-}|{\mathit{W}}_n^{-})$ and $I_{Y;\mathit{W}|\mathit{V}}^Y=I(Y_n;Y_n^{-};{\mathit{W}}_n^{-}|{\mathit{V}}_n^{-})$ quantify the conditional interaction information storage of Y in the context of the whole network processes {V,W,Y}, and $I_{Y;\mathit{V};\mathit{W}}^Y=I(Y_n;Y_n^{-};{\mathit{V}}_n^{-};{\mathit{W}}_n^{-})$ is the multivariate interaction information of the target Y in the context of the network itemized evidencing the two sources V and W. This last term quantifies the interaction information between the present of the target $Y_n$, its past $Y_n^{-}$, the past of one source ${\mathit{V}}_n^{-}$, and the past of the other source ${\mathit{W}}_n^{-}$.

Thus, the expansion of the information storage puts in evidence basic atoms of information about the target, which quantify respectively the interaction information of the present and the past of the target with one of the two sources taken individually, and the interaction information of the present of the target and the past of all processes. This last term expresses the information contained in the union of the four variables $(Y_n,Y_n^{-},{\mathit{W}}_n^{-},{\mathit{V}}_n^{-})$, but not in any subset of these four variables.

2.2.4. Information Transfer Decomposition (ITD)

The information transferred from the two sources V and W to the target Y can be further expanded to evidence how the past of the sources interact with each other in determining the information transferred to the target. To do this, we decompose the joint information transfer from X = (V,W) to Y as:

$$T_{\mathit{X}\to Y}=T_{\mathit{V}\to Y}+T_{\mathit{W}\to Y}-I_{\mathit{V};\mathit{W}|Y}^Y=T_{\mathit{V}\to Y|\mathit{W}}+T_{\mathit{W}\to Y|\mathit{V}}+I_{\mathit{V};\mathit{W}|Y}^Y,$$

(16)

where $T_{\mathit{V}\to Y}=I(Y_n;{\mathit{V}}_n^{-}|Y_n^{-})$ and $T_{\mathit{W}\to Y}=I(Y_n;{\mathit{W}}_n^{-}|Y_n^{-})$ quantify the information transfer from each individual source to the target in the context of the bivariate processes {V,Y} and {W,Y}, $T_{\mathit{V}\to Y|\mathit{W}}=I(Y_n;{\mathit{V}}_n^{-}|Y_n^{-},{\mathit{W}}_n^{-})$ and $T_{\mathit{W}\to Y|\mathit{V}}=I(Y_n;{\mathit{W}}_n^{-}|Y_n^{-},{\mathit{V}}_n^{-})$ quantify the conditional information transfer from one source to the target conditioned to the other source in the context of the whole network process {V,W,Y}, and $I_{\mathit{V};\mathit{W}|Y}^Y=I(Y_n;{\mathit{V}}_n^{-};{\mathit{W}}_n^{-}|Y_n^{-})=I(Y_n;{\mathit{V}}_n^{-}|Y_n^{-})-I(Y_n;{\mathit{V}}_n^{-}|Y_n^{-};{\mathit{W}}_n^{-})$ is the interaction information transfer between V and W to Y in the context of the network process {V,W,Y}, quantified as the interaction information of the present of the target $Y_n$ and the past of the two sources ${\mathit{V}}_n^{-}$ and ${\mathit{W}}_n^{-}$, conditioned to the past of the target $Y_n^{-}$.

Thus, the decomposition of the information transfer allows to dissect the overall information transferred jointly from the two group of sources to the target into sub-elements quantifying the information transferred individually from each source, and an interaction term that reflects how the two sources cooperate with each other while they transfer information to the target.

2.2.5. Summary of Information Decomposition

The proposed decomposition of predictive information, information storage and information transfer are depicted graphically by the Venn diagram of Figure 2. The diagram evidences how the information contained in the target process Y at any time step (all non-white areas) splits in a part that can be explained from the past of the whole network (predictive information) and in a part which is not explained by the past (new information). The predictable part is the sum of a portion explained only by the target (information storage) and a portion explained by the sources (information transfer). In turn, the information storage is in part due exclusively to the target dynamics (internal information, $S_{Y|\mathit{X}}$) and in part to the interaction of the dynamics of the target and the two sources (interaction information storage, $I_{Y;\mathit{V};\mathit{W}}^Y$, which is the sum of the interaction storage of the source and each target plus the multivariate interaction information). Similarly, the information transfer can be ascribed to an individual source when the other is assigned (conditional information transfer, $T_{\mathit{V}\to Y|\mathit{W}},T_{\mathit{W}\to Y|\mathit{V}}$) or to the interaction between the two sources (interaction information transfer, $I_{\mathit{V};\mathit{W}|Y}^Y$).

Note that all interaction terms (depicted using gray shades in Figure 2) can take either positive values, reflecting redundant cooperation between the past states of the processes involved in the measures while they are used to predict the present of the target, or negative values, reflecting synergetic cooperation; since the interaction terms reflect how the interaction between source variables may lead to the elimination of information in the case of redundancy or to the creation of new information in the case of synergy, they quantify the concept of information modification. This concept and those of information storage and information transfer constitute the basic elements to dissect the more general notion of information processing in networks of interacting dynamic processes.

2.3. Computation for Multivariate Gaussian Processes

In this section we provide a derivation of the exact values of any of the information measures entering in the decompositions defined above under the assumption that the observed dynamical network S = {X,Y} = {V,W,Y} is composed by Gaussian processes [12]. Specifically, we assume that the overall vector process S has a joint Gaussian distribution, which means that any vector variable extracted sampling the constituent processes at present and past times takes values from a multivariate Gaussian distribution. In such a case, the information of the present state of the target process, H(Yn), and the conditional information of the present of the target given any vector Z formed by past variables of the network processes, H(Yn|Z), can be computed using Equations (5) and (6) where the conditional variance is given by Equation (7). Then, any of the measures of information storage, transfer and modification appearing in Equations (12)–(16) can be obtained from the information H(Yn) and the conditional information H(Yn|Z)—where Z can be any combination of $Y_n^{-},{\mathit{V}}_n^{-}$ and ${\mathit{W}}_n^{-}$.

Therefore, the computation of information measures for jointly Gaussian processes amounts to evaluating the relevant covariance and cross-covariance matrices between the present and past variables of the various processes. In general, these matrices contain as scalar elements the covariance between two time-lagged variables taken from the processes V, W, and Y, which in turn appear as elements of the M × M autocovariance of the whole observed M-dimensional process S, defined at each lag k ≥ 0 as ${\mathbf{\Gamma }}_k=\mathrm{E}[{\mathit{S}}_n{\mathit{S}}_{n-k}]$. Now we show how this autocovariance matrix can be computed from the parameters of the vector autoregressive (VAR) formulation of the process S:

$${\mathit{S}}_n={\displaystyle \sum _{k=1}^m{\mathbf{A}}_k{\mathit{S}}_{n-k}+}{\mathit{U}}_n,$$

(17)

where m is the order of the VAR process, ${\mathbf{A}}_k$ are M × M coefficient matrices and Un is a zero mean Gaussian white noise process with diagonal covariance matrix Λ. The autocovariance of the process (17) is related to the VAR parameters via the well-known Yule–Walker equations:

$${\mathbf{\Gamma }}_k={\displaystyle \sum _{l=1}^m{\mathbf{A}}_l{\mathbf{\Gamma }}_{k-l}+}{\delta }_{k0}\mathbf{\Lambda },$$

(18)

where δ_k0 is the Kronecher product. In order to solve Equation (18) for Γ_k, with k = 0, 1, ..., m − 1, we first express Equation (17) in a compact form as ${\mathit{\phi }}_n=\mathbf{A}{\mathit{\phi }}_{n-1}+{\mathit{E}}_n$, where:

$${\mathit{\phi }}_n={[{\mathit{S}}_n^{\mathrm{T}}{\mathit{S}}_{n-1}^{\mathrm{T}}\cdots {\mathit{S}}_{n-m+1}^{\mathrm{T}}]}^{\mathrm{T}} , \mathbf{A}=\left[\begin{array}{cccc}{\mathbf{A}}_1& \cdots & {\mathbf{A}}_{m-1}& {\mathbf{A}}_m\\ {\mathbf{I}}_M& \cdots & {\mathbf{0}}_M& {\mathbf{0}}_M\\ ⋮& \ddots & ⋮& ⋮\\ {\mathbf{0}}_M& \cdots & {\mathbf{I}}_M& {\mathbf{0}}_M\end{array}\right] , {\mathit{{\rm E}}}_n={[{\mathit{U}}_n^{\mathrm{T}}{\mathbf{0}}_{1\times M(m-1)}]}^{\mathrm{T}}.$$

(19)

Then, the covariance matrix of ${\mathit{\phi }}_n$, which has the form:

$$\mathbf{\Psi }=\mathrm{E}[{\mathit{\phi }}_n{\mathit{\phi }}_n^{\mathrm{T}}]=\left[\begin{array}{cccc}{\mathbf{\Gamma }}_0& {\mathbf{\Gamma }}_1& \cdots & {\mathbf{\Gamma }}_{m-1}\\ {\mathbf{\Gamma }}_1^{\mathrm{T}}& {\mathbf{\Gamma }}_0& \cdots & {\mathbf{\Gamma }}_{m-2}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathbf{\Gamma }}_{m-1}^{\mathrm{T}}& {\mathbf{\Gamma }}_{m-2}^{\mathrm{T}}& \cdots & {\mathbf{\Gamma }}_0\end{array}\right],$$

(20)

can be expressed as $\mathbf{\Psi }=\mathbf{A}\mathbf{\Psi } {\mathbf{A}}^{\mathrm{T}}+\mathbf{\Xi }$, where $\mathbf{\Xi }={\rm E}[{\mathit{E}}_n{\mathit{E}}_n^{\mathrm{T}}]$ is the covariance of En. This last equation is a discrete-time Lyapunov equation, which can be solved for $\mathbf{\Psi }$ yielding the autocovariance matrices Γ₀, ..., Γ_m−1. Finally, the autocovariance can be calculated recursively for any lag k ≥ m by repeatedly applying Equation (18). This shows how the autocovariance sequence can be computed up to arbitrarily high lags starting from the parameters of the VAR representation of the observed Gaussian process.

3. Simulation Study

In this Section we show the computation of the terms appearing in the information decompositions defined in Section 2 using simulated networks of interacting stochastic processes. In order to make the interpretation free of issues related to practical estimation of the measures, we simulate stationary Gaussian VAR processes and exploit the procedure described in Section 2.3 to quantify all information measures in their variance-based and entropy-based formulations from the exact values of the VAR parameters.

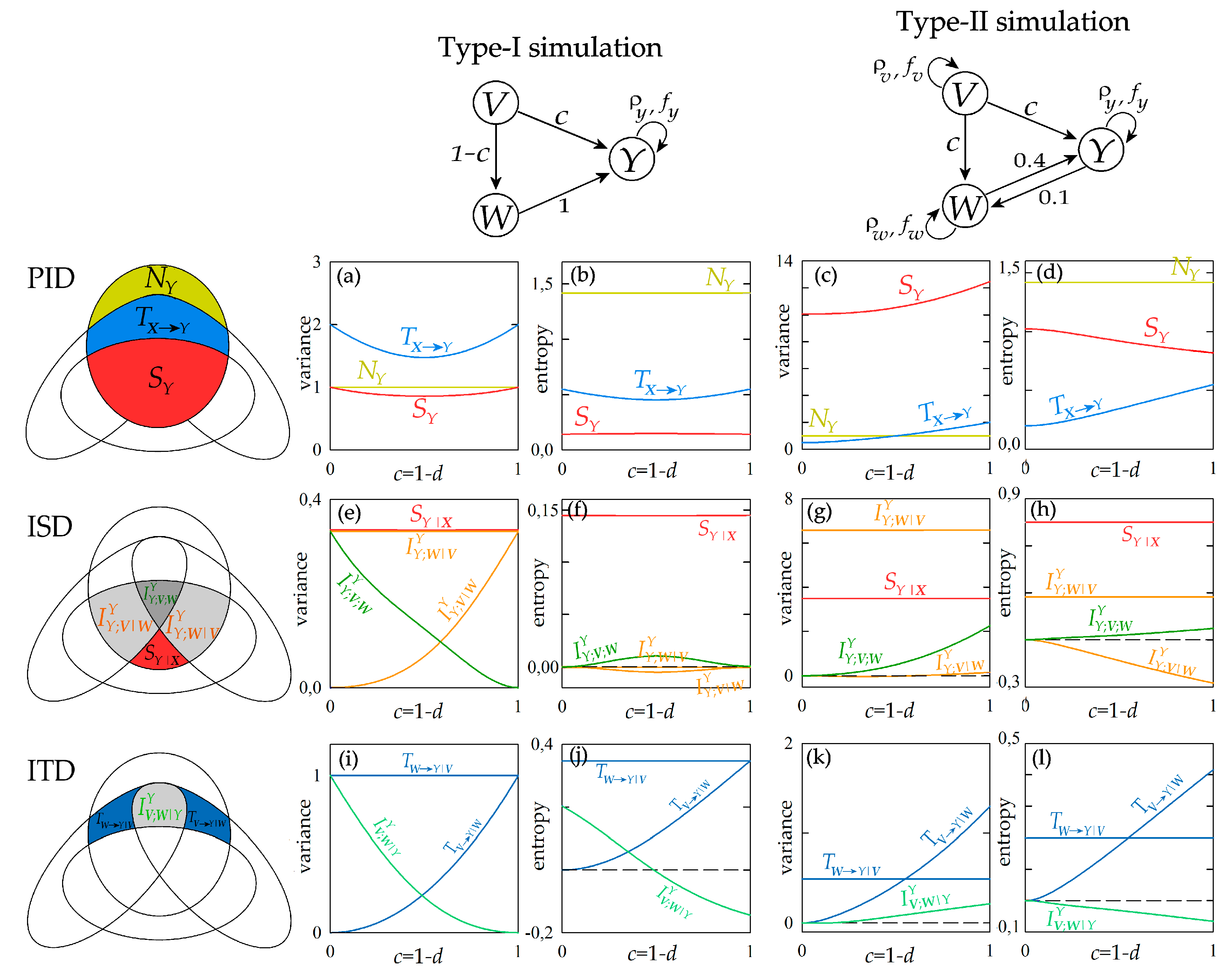
3.1. Simulated VAR Processes

Simulations are based on the general trivariate VAR process S = {X,Y} = {V,W,Y} with temporal dynamical structure defined by the equations:

$$\begin{array}{l}{V}_n=2{\rho }_v\cdot \text{cos} 2\pi f_v\cdot V_{n-1}-{\rho }_v^2\cdot V_{n-2}+U_{v,n}\\ W_n=2{\rho }_w\cdot \text{cos} 2\pi f_w\cdot W_{n-1}-{\rho }_w^2\cdot V_{n-2}+a\cdot Y_{n-2}+d\cdot V_{n-1}+U_{w,n}\\ Y_n=2{\rho }_y\cdot \text{cos} 2\pi f_y\cdot Y_{n-1}-{\rho }_w^2\cdot Y_{n-2}+b\cdot W_{n-1}+c\cdot V_{n-1}+U_{y,n}\end{array}$$

(21)

where ${\mathit{U}}_n=[U_{v,n},U_{w,n},U_{y,n}]$ is a vector of zero mean white Gaussian noises of unit variance and uncorrelated with each other (Λ = I). The parameter design in Equation (21) is chosen to allow autonomous oscillations in the three processes, obtained placing complex-conjugate poles with amplitude ${\rho }_v,{\rho }_w,{\rho }_y$ and frequency $f_v,f_w,f_y$ in the complex plane representation of the transfer function of the vector process, as well as causal interactions between the processes at fixed time lag of 1 or 2 samples and with strength modulated by the parameters a, b, c, d [37]. Here we consider two parameter configurations describing respectively basic dynamics and more realistic dynamics resembling rhythms and interactions typical of cardiovascular and cardiorespiratory signals.

The type-I simulation is obtained setting ${\rho }_v={\rho }_w=0,a=0,{\rho }_y=\sqrt{0.5},f_y=0.25,b=1$ in Equation (21), and letting the parameters c and d free to vary between 0 and 1 while keeping the relation d = 1 − c. With this setting, depicted in Figure 3a, the processes V and W have no internal dynamics, while the process Y exhibits negative autocorrelations with lag 2 and strength 0.5; moreover causal interactions are set from W to Y with fixed strength, and from V to Y and to W with strength inversely modulated by the parameter c.

In type-II simulation we set the parameters to reproduce oscillations and interactions commonly observed in cardiovascular and cardiorespiratory variability (Figure 3b) [37,38]. Specifically, the autoregressive parameters of the three processes are set to mimic the self-sustained dynamics typical of respiratory activity (process V, ${\rho }_v=0.9,f_v=0.25$) and the slower oscillatory activity commonly observed in the so-called low-frequency (LF) band in the variability of systolic arterial pressure (process W, ${\rho }_w=0.8,f_v=0.1$) and heart rate (process W, ${\rho }_y=0.8,f_y=0.1$). The remaining parameters identify causal interactions between processes, which are set from V to W and from V to Y (both modulated by the parameter c = d) to simulate the well-known respiration-related fluctuations of arterial pressure and heart rate, and along the two directions of the closed loop between W and Y ($a=0.1,b=0.4$) to simulate bidirectional cardiovascular interactions. The tuning of all these parameters was performed to mimic the oscillatory spectral properties commonly encountered in short-term cardiovascular and cardiorespiratory variability; an example is seen in Figure 3c, showing that the theoretical power spectral densities of the three processes closely resemble the typical profiles of real respiration, arterial pressure and heart rate variability series [39].

3.2. Information Decomposition

Figure 4 reports the results of information decomposition applied to the VAR process of Equation (21) considering Y as the target process and V and W as the source processes. Setting the process structures of the two types of simulations depicted on the top, we computed the decompositions of the predictive information (PID), information storage (ISD) and information transfer (ITD) described graphically on the left. The measures appearing in these decompositions are plotted as a function of the coupling parameter varying in the range (0, 1). In order to favor the comparison, all measures are computed both using variance and using entropy to quantify conditional and mutual information. Note that we performed also an estimation of all measures starting from short realizations (300 points) of Equation (21), finding high consistency between estimated and theoretical values (results are in the Supplementary Material, Figure S1).

Considering the PID measures reported in Figure 4a–d, first we note that the new information produced by the target process, $N_Y$, is constant in all cases and measures the variance or the entropy of the innovations $U_v$. The information storage $S_Y$ displays different behaviour with the coupling parameter depending on the simulation setting and on the functional used for its computation: in type-I simulation, the variance-based measure varies non-monotonically with c and the entropy-based measure is stable at varying c (Figure 4a,b); in type-II simulation, increasing c determines an increase of the variance-based measure and a decrease of the entropy-based measure (Figure 4c,d). The information storage is sensitive to variations in both the internal dynamics of the target process and the causal interactions from source to target [7]; in our simulations where auto-dependencies within the processes are not altered, the variations of the information stored in the target process reflect the coupling effects exerted from the two sources to the target. The information transferred jointly from the two sources to the target, $T_{\mathit{X}\to Y}$, is related in a more straightforward way to the causal interactions: in the type-I simulation, the opposite changes imposed in the strength of the direct effects (V→Y, increasing with c) and the indirect effects (V→W→Y, decreasing with c) from source to target results in the non-monotonic behaviour of $T_{\mathit{X}\to Y}$ (Figure 4a,b); in the type II simulation, the concordant changes of direct and indirect effects from V to Y determine a monotonic increase of $T_{\mathit{X}\to Y}$ with the parameter c (Figure 4c,d).

The behaviour observed for the information storage at varying the parameter c can be better interpreted by looking at the terms of the ISD reported in Figure 4e–h. First, we find that the internal information S_r|x is not affected by c, documenting the insensitivity to causal interactions of this measure that is designed to reflect exclusively variations in the internal dynamics of the target process [12]. We note that also the interaction information storage between the target Y and the source W conditioned to the other source V, $I_{Y;W|V}^Y$, is constant in all simulated conditions, reflecting the fact that the direct interaction between Y and W is not affected by c. Therefore, the ISD allows to evidence that in our simulations variations in the information storage are related to how the target Y interacts with a specific source (in this case, V); such an interaction is documented by the trends of the interaction information measure $I_{Y;V|W}^Y$ and $I_{Y;V;W}^Y$. In type-I simulation, the increasing coupling between V and Y determines a monotonic increase of the interaction storage $I_{Y;V|W}^Y$ and a monotonic decrease of the multivariate interaction $I_{Y;V;W}^Y$ (Figure 4e); in particular, $I_{Y;V|W}^Y$ is zero and $I_{Y;V;W}^Y$ is maximum when c = 0, and the opposite occurs when c = 1, reflecting respectively the conditions of absence of direct coupling V→Y and presence of exclusive direct coupling V→Y. In type-II simulation, the concordant variations set for the couplings V→Y and V→W lead to a similar but smoothed response of the interaction storage ($I_{Y;V|W}^Y$ slightly increases with c) and to an opposite response of the multivariate interaction information ($I_{Y;V;W}^Y$ increases with c) (Figure 4g). These trends of the interaction measures $I_{Y;V|W}^Y$ and $I_{Y;V;W}^Y$ are apparent when information is measured in terms of variance, but become of difficult interpretation when information is measured as entropy: in such a case, the variations with c of $I_{Y;V|W}^Y$ and $I_{Y;V;W}^Y$ are non-monotonic (Figure 4f) or even opposite to those observed before (Figure 4h).

The expansion of the joint information transferred from the two sources V and W to the target Y into the terms of the ITD is reported in Figure 4i–l. Again, this decomposition allows to understand how the modifications of the information transfer with the simulation parameter result from the balance among the constituent terms of $T_{\mathit{X}\to Y}$. In particular, we note that the information transferred from W to Y after conditioning on V, $T_{W\to Y|V}$, does not change with c, documenting the invariance of the direct coupling W→Y in all simulation settings. The information transferred from V to W after conditioning on W, $T_{V\to Y|W}$, increases monotonically with c, reflecting the higher strength of the direct causal interactions V→Y. Note that both these findings are documented clearly using either variance or entropy to measure the information transfer. On the contrary, different indications are provided about the interaction information transfer $I_{V;W|Y}^Y$ when this measure is computed through variance or entropy computations. In the type-I simulation, the variance-based measure of $I_{V;W|Y}^Y$ decreases from 1 to 0 at increasing c from 0 to 1 (Figure 4i), reflecting the fact that the target of the direct effects originating in V shifts progressively from W to Y; a similar trend is observed for the entropy-based measure of $I_{V;W|Y}^Y$ with the difference that the measure assumes negative values indicating synergy for high values of c (Figure 4j). In the type-II simulation, inducing a variation from 0 to 1 in the parameter c determines an increase from 0 to positive values of $I_{V;W|Y}^Y$—denoting redundant source interaction—when variance measures are used (Figure 4k), but determines a decrease from 0 to negative values of $I_{V;W|Y}^Y$—denoting synergetic source interaction—when entropy measures are used (Figure 4k).

3.3. Interpretation of Interaction Information

The analysis of information decomposition discussed above reveals that the information measures may lead to different interpretations depending on whether they are based on the computation of variance or on the computation of entropy. In particular we find, also in agreement with a recent theoretical study [16], that the interaction measures can greatly differ when computed using the two approaches. To understand these differences, we analyze how variance and entropy measures relate to each other considering two examples of computation of the interaction information transfer. We recall that this measure can be expressed as $I_{V;W|Y}^Y=T_{V\to Y}-T_{V\to Y|W}$, where the information transfer is given by the conditional information terms $T_{V\to Y}=H(Y_n|Y_n^{-})-H(Y_n|Y_n^{-},V_n^{-})$ and $T_{V\to Y|W}=H(Y_n|Y_n^{-},W_n^{-})-H(Y_n|Y_n^{-},W_n^{-},V_n^{-})$. Then, exploiting the relation between conditional variance and conditional entropy of Equation (6) we show in Figure 5 that, as a consequence of the concave property of the logarithmic function, subtracting $T_{V\to Y|W}$ from $T_{V\to Y}$ can lead to very different values of $I_{V;W|Y}^Y$ when the information transfer is based on variance (i.e., $H_V$ is computed: horizontal axis of Figure 5a,c) or is based on entropy (i.e., $H_E$ is computed: vertical axis of Figure 5a,c).

First, we analyze the case c = 1 in type-I simulation, which corresponds to uncorrelation between the two sources V and W, and yields $I_{V;W|Y}^Y=0$ using variance and $I_{V;W|Y}^Y<0$ using entropy (Figure 4i,j). In Figure 5a this corresponds to $T_{V\to Y}=T_{V\to Y|W}$ using variance measures (see also Figure 5b, where the past of V and W are disjoint), denoting no source interaction, and to $T_{V\to Y}<T_{V\to Y|W}$ using variance measures (see also Figure 5c, where considering the past of W adds information), denoting synergy between the two sources. Thus, in the case of uncorrelated sources there is no interaction transfer if information is quantified by variance, reflecting an intuitive behaviour, while there is negative interaction transfer if information is quantified by entropy, reflecting a counter-intuitive synergetic source interaction. The indication of net synergy provided by entropy based-measures in the absence of correlation between sources was first pointed out in [16].

Then, we consider the case c = 1 in type-II simulation, which yields $I_{V;W|Y}^Y>0$ using variance and $I_{V;W|Y}^Y<0$ using entropy (Figure 4k,l). As seen in Figure 5d, in this case we have $T_{V\to Y}>T_{V\to Y|W}$ using variance measures (see also Figure 5e, where considering the past of W removes information), denoting redundancy between the two sources, and to $T_{V\to Y}<T_{V\to Y|W}$ using variance measures (see also Figure 5d, where considering the past of W adds information), denoting synergy between the two sources. Thus, there can be situations in which the interaction between two sources sending information to the target is seen as redundant or synergetic depending on the functional adopted to quantify information.

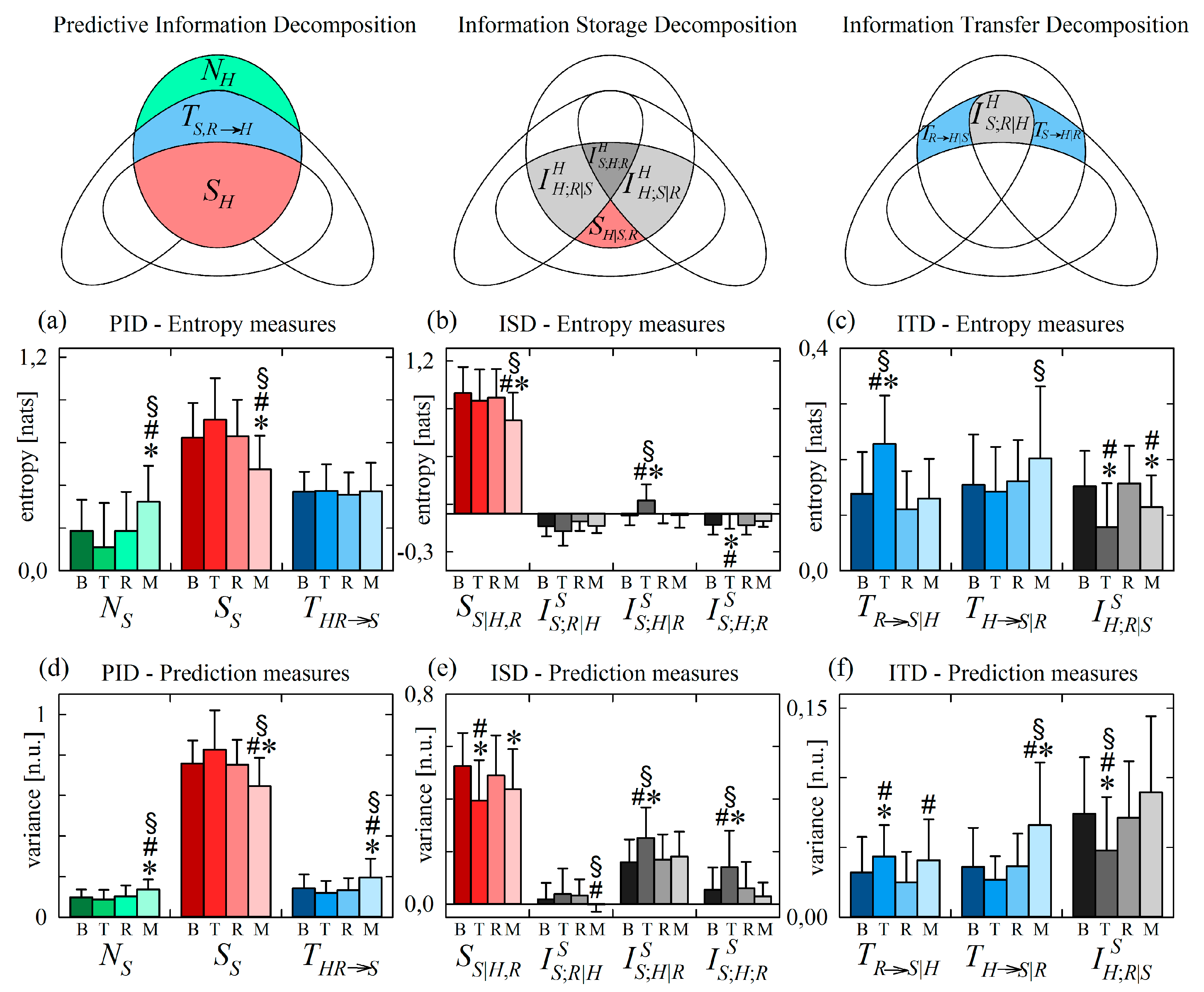
4. Application to Physiological Networks

This Section is relevant to the practical computation of the proposed information-theoretic measures on the processes that compose the human physiological network underlying the short-term control of the cardiovascular system. The considered processes are the heart period, the systolic arterial pressure, and the breathing activity, describing respectively the dynamics of the cardiac, vascular and respiratory systems. Realizations of these processes were measured noninvasively in a group of healthy subjects in a resting state and in conditions capable of altering the cardiovascular dynamics and their interactions, i.e., orthostatic stress and mental stress [33,40,41]. Then, the decomposition of predictive information, information storage and information transfer were performed computing the measures defined in Section 2.2, estimated using the linear VAR approach described in Section 2.3 and considering the cardiac or the vascular process as the target, and the remaining two processes as the sources. The assumptions of stationarity and joint Gaussianity that underlie the methodologies presented in this paper are largely exploited in the multivariate analysis of cardiovascular and cardiorespiratory interactions, and are usually supposed to hold when realizations of the cardiac, vascular and respiratory processes are obtained in well-controlled experimental protocols designed to achieve stable physiological and experimental conditions [42,43,44,45,46,47].

4.1. Experimental Protocol and Data Analysis

The study included sixty-one healthy young volunteers (37 females, 24 males, 17.5 ± 2.4 years), who were enrolled in an experiment for which they gave written informed consent, and that was approved by Ethical Committee of the Jessenius Faculty of Medicine, Comenius University, Martin, Slovakia. The protocol consisted of four phases: supine rest in the baseline condition (B, 15 min), head-up tilt (T, during which the subject was tilted to 45 degrees on a motor driven tilt table for 8 min to evoke mild orthostatic stress), a phase of recovery in the resting supine position (R, 10 min), and a mental arithmetic task in the supine position (M, during which the subject was instructed to mentally perform as quickly as possible arithmetic computations under the disturbance of the rhythmic sound of a metronome).

The acquired signals were the electrocardiogram (horizontal bipolar thoracic lead; CardioFax ECG-9620, NihonKohden, Tokyo, Japan), the continuous finger arterial blood pressure collected noninvasively by the photoplethysmographic volume-clamp method (Finometer Pro, FMS, Amsterdam, The Netherlands), and the respiratory signal obtained through respiratory inductive plethysmography (RespiTrace 200, NIMS, Miami Beach, FL, USA) using thoracic and abdominal belts. From these signals recorded with a 1000 Hz sampling rate, the beat-to-beat time series of the heart period (HP), systolic pressure (SP) and respiratory amplitude (RA) were measured respectively as the sequence of the temporal distances between consecutive R peaks of the ECG after detection of QRS complexes and QRS apex location, as the maximum value of the arterial pressure waveform measured inside each detected RR interval, and as the value of the respiratory signal sampled at the time instant of the first R peak denoting each detected RR interval. In all conditions, the occurrences of R-waves peaks was carefully checked to avoid erroneous detections or missed beats, and if isolated ectopic beats affected any of the measured time series, the three were linearly interpolated using the closest values unaffected by ectopic beats. After measurement, segments of consecutive 300 points were selected synchronously for the three series starting at predefined phases of the protocol: 8 min after the beginning of the recording session for B, 3 min after the change of body position for T, 7 min before starting mental arithmetics for R, and 2 min after the start of mental arithmetics for M.

To favor the fulfillment of stationarity criteria, before the analysis all time series were detrended using a zero-phase IIR high-pass filter with cutoff frequency of 0.0107 cycles/beat [48]. Moreover, outliers were detected in each window by the Tukey method [49] and labeled so that they could be excluded from the realizations of the process points to be used for model identification. Then, for each subject and window, realizations of the trivariate process S = {R,S,H} were obtained by normalizing the measured multivariate time series, i.e., subtracting the mean from each series and dividing the result by the standard deviation. The resulting time series {R_n, S_n, H_n} was fitted with a VAR model in the form of Equation (17) where model identification was performed using the standard vector least squares method and the model order was optimized according to the Bayesian Information Criterion [50]. The estimated model coefficients were exploited to derive the covariance matrix of the vector process, and the covariances between the present and the past of the processes were computed as in Equations (18)–(20) used as in Equation (7) to estimate all the partial variances needed to compute the measures of information dynamics. In all computations, the vectors representing the past of the normalized respiratory and vascular processes were incremented with the present variables in order to take into account fast vagal reflexes capable to modify HP in response to within-beat changes of RA and SP (effects R_n→H_n, S_n→H_n) and fast effects capable to modify SP in response to within-beat changes of RA (effect R_n→S_n).

4.2. Results and Discussion

This section presents the results of the decomposition of predictive information (PID), information storage (ISD) and information transfer (ITD) obtained during the four phases of the analyzed protocol (B, T, R, M) using both variance-based and entropy-based information measures when the target of the observed physiological network was either the cardiac process H (Section 4.2.1) or the vascular process S (Section 4.2.2).

In the presentation of results, the distribution of each measure is reported as mean + SD over the 61 considered subjects. The statistical significance of the differences between pairs of distributions is assessed through Kruskall–Wallis ANOVA followed by signed rank post-hoc tests with Bonferroni correction for multiple comparisons. Results are presented reporting and discussing the significant changes induced in the information measures first by the orthostatic stress (comparison B vs. T) and then by the mental stress (comparison R vs. M). Besides statistical significance, the relevance of the observed changes is supported also by the fact that no differences were found for any measure between the two resting state conditions (baseline B and recovery R).

4.2.1. Information Decomposition of Heart Period Variability during Head-Up Tilt

Figure 6 reports the results of information decomposition applied to the variability of the normalized HP (target process H) during the four phases of the protocol.

We start with the analysis of variations induced by head-up tilt, observing that the PID reported in Figure 6a,d documents a significant reduction of the new information produced by the cardiac process, and a significant increase of the information stored in the process, in the upright body position compared to all other conditions (significantly lower $N_H$ and significantly higher $S_H$ during T). Since in this application to normalized series with unit variance the information of the target series is always the same ($H_V(H)=1,H_E(H)=0.5\text{log}(2\pi e)$), the decrease of the new information $N_H$ corresponds to a statistically significant increase of the predictive information $P_H=H_H-N_H$ (see Equation (12)). In turn, this increased predictive information during T is mirrored by the significantly higher information storage not compensated by variations of the information transfer $T_{S,R\to H}$; the latter decreased significantly during T when computed through variance measures (Figure 6d), while it was unchanged when computed through entropy measures (Figure 6a). These results confirm those of a large number of previous studies reporting a reduction of the dynamical complexity (or equivalently an increase of the regularity) of HP variability in the orthostatic position, reflecting the well-known shift of the sympatho-vagal balance towards sympathetic activation and parasympathetic deactivation [40,51,52].

The ISD reported in Figure 6b,e indicates that the higher information stored in the cardiac process H in the upright position is the result of a significant increase of the internal information of H and of the interaction information between H and the vascular process S in this condition (higher $S_{H|S,R}$ and $I_{H;S|R}^H$ during T). Higher internal information in response to an orthostatic stress was previously observed using a measure of conditional self entropy in a protocol of graded head-up tilt [13]. This result documents a larger involvement of mechanisms of regulation of the heart rate which act independently of respiration and arterial pressure, including possibly direct sympathetic influences on the sinus node which are unmediated by the activation of baroreceptors and/or low pressure receptors, and central commands originating from respiratory centres in the brainstem that are independent of afferent inputs [53,54]. The increased interaction information is likely related to the tilt-induced sympathetic activation that affects both cardiac and vascular dynamics [38], thus determining higher redundancy in the contribution of the past history of H and S on the present of H.

The results of ITD reported in Figure 6c,f document a discrepancy between the responses to head-up tilt of the variance-based and entropy-based measures of information transfer. While the information transferred from RA to HP decreased with tilt in both cases (significantly lower $T_{R\to H|S}$ during T in both Figure 6c and Figure 6f), the information transferred from SP to HP and the interaction information transfer showed opposite trends: moving from B to T the variance-based measures of $T_{S\to H|R}$ and $I_{S;R|H}^H$ decreased significantly (Figure 6f), while the entropy-based measures increased or did not change significantly (Figure 6c). The decrease of information transfer from R to H is in agreement with the reduction cardiorespiratory interactions previously observed during orthostatic stress, reflecting the vagal withdrawal and the dampening of respiratory sinus arrhythmia during orthostatic stress [13,55,56]. The other findings are discussed in Section 4.2.3 where the reasons of the discrepancy between variance and entropy measures are investigated and the more plausible physiological interpretation is provided.

4.2.2. Information Decomposition of Heart Period Variability during Mental Arithmetics

The analysis of variations induced by mental stress revealed that the new information produced by the HP series and the information stored in this series are not substantially altered by mental stress (Figure 6a,d). In agreement with previous studies reporting a similar finding [57,58], this result suggests that during mental stress the pattern of alterations in the sympathetic nervous system activity is more complex and interindividually variable than that elicited by orthostatic stress [41]. The only significant variation evidenced by the PID was the decrease of the joint cardiovascular and cardiorespiratory information transferred to the cardiac process during mental arithmetics compared to both resting conditions (significantly lower $T_{S,R\to H}$ during M, Figure 6a,d). This decrease was the result of marked reductions of the information transfer from RA to HP and of the interaction information transfer between RA and SP to HP (lower $T_{R\to H|S}$ and $I_{R;S|H}^H$ during M), not compensated by the statistically significant increase of the information transfer from SP to HP (higher $T_{S\to R|H}$ during M, Figure 6c,f). The decrease of joint, cardiorespiratory and interaction transfers to the cardiac process are all in agreement with withdrawal of vagal neural effects and reduced respiratory sinus arrhythmia observed in conditions of mental stress [59,60,61]. A reduced cardiorespiratory coupling was also previously observed during mental arithmetics using coherence and partial spectrum analysis [62]. The increase in the cardiovascular coupling is likely related to a larger involvement of the baroreflex in a condition of sympathetic activation; interestingly, such an increase could be noticed in the present study where the information transfer from S to H was computed conditionally on R, while a bivariate unconditional analysis could not detect such an increase because of the concomitant decrease of the interaction information transfer. In fact, using a bivariate analysis we did not detect significant changes in the causal interactions from S to H during mental stress [33].

As regards the ISD, we found that the unchanged values of the information storage during mental stress (Figure 6a,d) were the result of unaltered values of all the decomposition terms in the entropy-based analysis (Figure 6b), and of a balance between higher internal information in the cardiac process and lower multivariate interaction information storage in the variance-based analysis (Figure 6e, increase of $S_{H|S,R}$ and decrease of $I_{H;R;S}^H$ during M). These findings confirm those of a previous study indicating that the information storage is unspecific to variations of the complexity induced in the cardiac dynamics by mental stress, and that these variations are better reflected by measures of conditional self-information [58]. Here we find that the detection of stronger internal dynamics of heart period variability is masked, in the measure of information storage, by a weaker interaction among all variables. The stronger internal dynamics reflected by higher internal information are likely attributable to a higher importance of upper brain centers in controlling the cardiac dynamics independently of pressure and respiratory variability. This may also suggest a central origin for the sympathetic activation induced by mental stress. The reduced multivariate interaction is in agreement with the vagal withdrawal [59,60,61] that likely reduces the information shared by RA, SP and HP in this condition.

4.2.3. Information Decomposition of Systolic Arterial Pressure Variability during Head-Up Tilt

Figure 7 reports the results of information decomposition applied to the variability of the normalized SP (target process S) during the four phases of the protocol. We start with the analysis of changes related to head-up tilt, observing that the components of the PID are not significantly affected by the orthostatic stress (Figure 7a,d). In agreement with previous studies, the invariance with head-up tilt of information storage and new information, and that of the joint information transferred to it from H and R, document respectively that the orthostatic stress does not alter the complexity of the vascular dynamics or the capability of cardiac and respiratory dynamics to alter this complexity [33,63]. On the other hand, the decomposition of information storage and transfer evidenced statistically significant variations during T that reveal important physiological reactions to the orthostatic stimulus.

Looking at the ISD, we found that the interaction information terms $I_{S;H|R}^S$ and $I_{S;H;R}^S$ were consistently higher during T than in the other conditions (Figure 7b,e), and the variance-based estimate of the internal information of the systolic pressure process was significantly lower during T (Figure 7e). This result mirrors the increase of cardiovascular interactions contributing to the information stored in HP, suggesting that head-up tilt involves a common mechanism, likely of sympathetic origin, of regulation of both H and S that brings about an overall increase of the redundancy between the past history of these two variables in the prediction of their future state.

The ITD of Figure 7c,f documents that the unchanged amount of information transferred from HP and RA to SP moving from supine to upright (unvaried $T_{H,R\to S}$ during T seen in Figure 7a,d) results from increased vasculo-pulmonary information transfer, unchanged transfer from the cardiac to the vascular process, and decreased cardiorespiratory interaction information transfer to SP (higher $T_{R\to S|H}$, stable $T_{H\to R|S}$, and lower $I_{H;R|S}^S$ during T). The unchanged transfer from H to S supports the view that interactions along this direction are mediated mainly by mechanical effects (Frank–Starling law and Windkessel effect) that are not influenced by the neural sympathetic activation related to tilt [33,56,64]. The increased direct transfer from R to S together with the decreased interaction information can be explained by the fact that respiratory sinus arrhythmia (i.e., the effect of R on H) is known to drive respiration-related oscillations of systolic pressure in the supine position, but also to buffer these oscillations in the upright position [65]. Therefore, in the supine position, respiratory-related effects of H on S are prevalent over the effects of respiration on S unrelated to H (and occurring through effects of R on the stroke volume), also determining high redundancy between R and H causing S; in the upright position the two mechanism are shifted, leading to higher effects of R on S unrelated to H and to lower redundancy.

4.2.4. Information Decomposition of Systolic Arterial Pressure Variability during Mental Arithmetics

As to the analysis of mental arithmetics, the PID revealed an increase of the new information $N_S$ and a corresponding decrease of the information storage $S_S$ relevant to the vascular process during M Figure 7a,d. The ISD applied to the process S documents that the reduction of the information stored in SP during the mental task is the result of a marked decrease of the internal information (lower $S_{S|H,R}$ during M in Figure 7b,e), observed in variance-based analysis together with a decrease of the vasculo-pulmonary information storage (lower $I_{S;R|H}^S$ during M in Figure 7e). These results point out that mental stress induces a remarkable increase of the dynamical complexity of SP variability, intended as a reduction of both the predictability of S given the past of all considered processes (higher new information) and the predictability of S given its own past only (lower information storage). Given that these trends were observed together with a marked decrease of the internal information and in the absence of decrease of the information transfer, we conclude that the higher complexity of the systolic pressure during mental stress is caused by alterations of the mechanisms able to modify its values independently of heart period and respiration. These mechanisms may include an increased modulation of peripheral vascular resistance [41] and an increased influence of higher brain cortical structures exerting “top-down” influence of the control system of blood pressure [66], and possibly manifested as an additional mechanism that limits the predictability of SP given the universe of knowledge that includes also RA and HP.

Similarly to what observed for HP during head-up tilt, the response to mental arithmetics of the information transferred to SP was different when monitored using variance-based or using entropy-based measures. The joint information transfer to the vascular process was significantly higher during M than in all other conditions when assessed by variance measures (Figure 7d), while it was unchanged when assessed by entropy measures (Figure 7a). These two trends were the result of significant increases of the conditional information transferred to SP from RA or from HP in the case of variance measures (higher $T_{H\to S|R}$ and $T_{R\to S|H}$ during M, Figure 7f), and of a balance between higher transfer from heart period to SP and lower interaction transfer in the case of entropy measures (higher $T_{H\to S|R}$ and lower $I_{H;R|S}^S$ during M, Figure 7c). The origin of these different trends is better elucidated and interpreted in the following subsection.

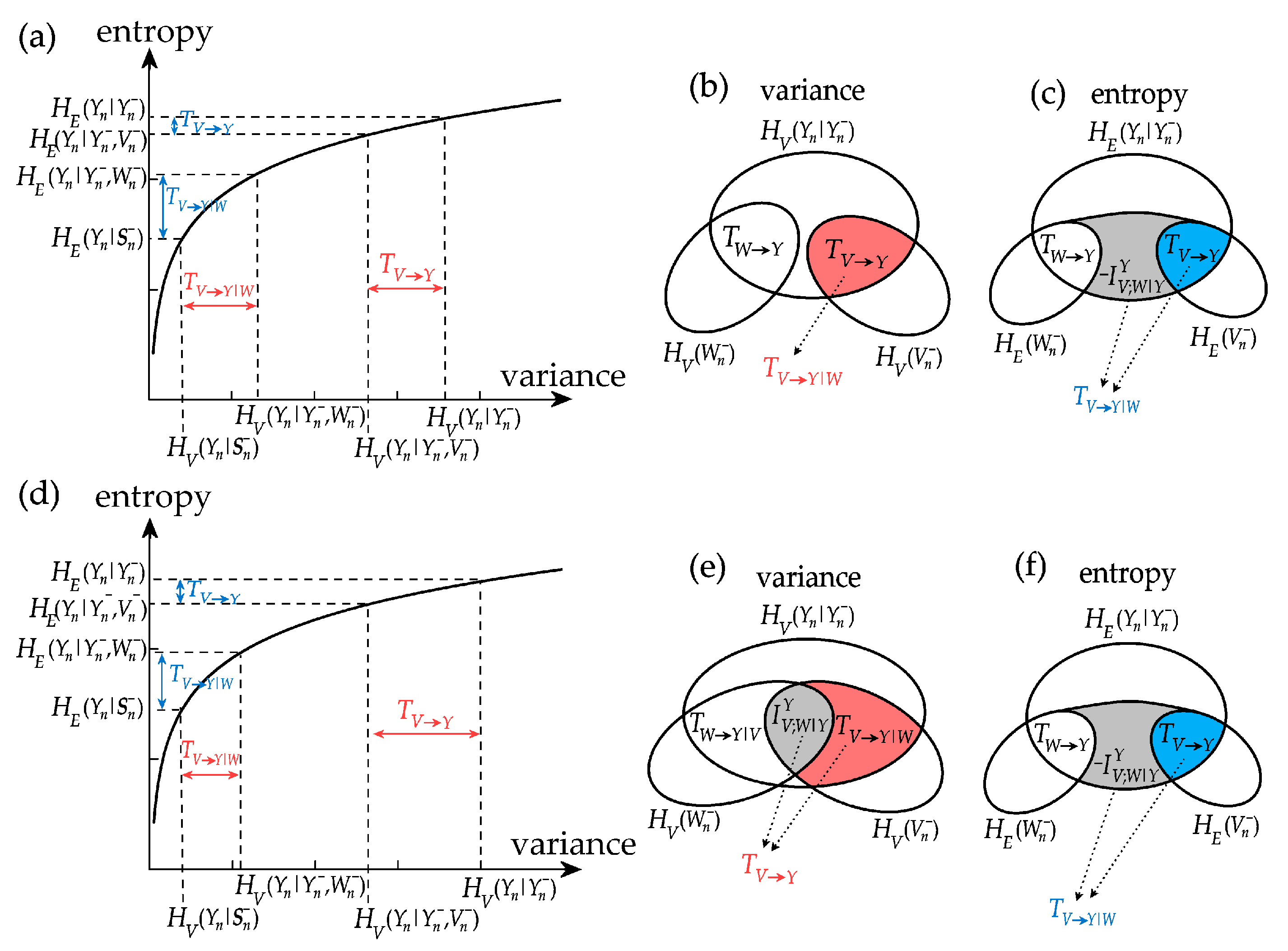
4.2.5. Different Profiles of Variance-Based and Entropy-Based Information Measures

In this subsection we present the results reporting significant variations between conditions of an information measure observed using one of the two formulations of the concept of information but not using the other formulation. These results are typically observed as statistically significant variations of the variance-based expression of a measure in concomitance with absence of significant variations, or even with variations of the opposite sign, of the entropy-based expression of the measure. Similarly to what shown in simulations of Section 3.3, the mathematical explanation of these behaviors lies in the nonlinear transformation of a distribution of values performed by the logarithmic expression that relates conditional variance and conditional entropy. While in Section 3.3 this behavior is explained in terms of its consequences on the sign of interaction information measures for simulations, here we discuss its consequences on the variation of measures of information transfer for physiological time series, also drawing analogies with the findings of [30].

Looking at the decomposition of the information carried by the heart period H, a main result not consistently observed using the two formulations of information is the significant decrease of the variance-based measure of joint information transfer $T_{S,R\to H}$ during head-up tilt (Figure 6d), which is due to significant decreases of the cardiovascular and cardiorespiratory information transfer $T_{S\to H|R}$ and $T_{R\to H|S}$, as well as of the interaction information transfer $I_{S;R|H}^H$ (Figure 6f). Differently, the entropy-based formulation of information transfer indicates unchanged joint transfer $T_{S,R\to H}$ during T (Figure 6a) as a result of a decreased cardiorespiratory transfer $T_{R\to H|S}$, an increased cardiovascular transfer $T_{S\to H|R}$, and an unchanged information transfer $I_{S;R|H}^H$ (Figure 6f). Note that these inconsistent results were obtained in the presence of a marked reduction of the new information and of a marked increase of the information storage in the target process H during T (Figure 6a,d).

Similar but complementary variations were observed looking at the decomposition of the information carried by the vascular process S during mental arithmetics. In this case variance measures evidenced a significant increase of the joint transfer $T_{H,R\to S}$ during M (Figure 7d), due to increases of the decomposition terms $T_{H\to S|R}$ and $T_{R\to S|H}$ (Figure 7f). On the contrary, entropy measures documented unchanged joint transfer (Figure 7a) resulting from a slight increase of $T_{H\to S|R}$ compensated by the decrease of the interaction transfer $I_{H;R|S}^S$ (Figure 7f). These trends were observed in the presence of significant increase of the new information and decrease of the information storage in the target process S during M (Figure 7a,d).

To clarify the apparently inconsistent behaviors described above, we represent in Figure 8 the changes of variance-based and entropy-based information measures relevant to the modifications induced by head-up tilt (transition from B to T) on the cardiac process H (note that complementary descriptions apply to the case of the changes induced by the transition from R to M on the vascular process S). The figure depicts the values of information content of the cardiac process H and conditional information of H given its past and the past of the respiratory and vascular processes R and S computed using variance (horizontal axis) and using entropy (vertical axis) in the resting baseline condition and during head-up tilt; in each condition, the highest and lowest information terms are the information content $H_H$ and the new information $N_H$, while the differences between information terms indicate the information storage $S_H$, the joint information transfer $T_{S,R\to H}$, and the conditional transfers $T_{S\to H|R}$ and $T_{R\to H|S}$. Note that, since the time series are normalized to unit variance, $H_H$ is the same during B and during T. Resembling the physiological results of Figure 6, we see that $N_H$ is much lower during T than during B, and $S_H$ is much higher; this holds for both variance-based and entropy based formulations of the measures. Moreover the figure depicts the decrease from B to T of the variance formulation of $T_{S,R\to H}$ and of $T_{S\to H|R}$; these decreased variance-based values correspond to entropy-based values that are unchanged for $T_{S,R\to H}$, and even increased for $T_{S\to H|R}$. Thus, the discrepancy between the two formulations arises from the shift towards markedly lower values of the conditional variances of H, and from the concave property of the logarithmic transformation that expands the differences between conditional variances producing higher differences in conditional entropy. Note that very similar trends of the information measures were found in a similar protocol in [30] in a different group of healthy subjects, indicating that these behaviours are a typical response of cardiovascular dynamics to head-up tilt. In [30], different formulations of information transfer were compared, observing discrepancies between measures based on the difference in conditional variance and the ratio between the same conditional variances which are consistent with the differences observed here between variance-based and entropy-based measures. The agreement between our findings and those of [30] is confirmed by the fact that measuring the difference of conditional entropies equals to measuring the ratio of conditional variances.

The reported results and the explanation provided above indicate that, working with processes reduced to unit variance as typically recommended in the analysis of real-world time series, if marked variations of the new information produced by the target process occur together with variations of the opposite sign of the information stored in the process, it happens that variance-based measures of the information transferred to the target follow closely the variations of the new information, thus appearing of little use for the evaluation of Granger-causal influences between processes. On the contrary, the intrinsic normalization performed by entropy-based indexes makes them more reliable to assess the magnitude of the information transfer regardless of variations of the complexity of the target. These conclusions are mirrored by our physiological results, which indicate a better physiological interpretability for the variations between conditions of the information transfer measured using entropy rather than using variance. For instance, the greater involvement of the baroreflex that is expected in the upright position to react to circulatory hypovolemia [40,51] is reflected by the entropy based increase of the information transfer from S to H during tilt (Figure 6b), while the variance-based measure showed a hardly interpretable decrease moving from B to T (Figure 6f). Similarly, the increase during mental arithmetics of the information transfer along the directions from R to S and from H to S observed in terms of variance (Figure 7f) seems to reflect more the increased complexity of the target series S rather than physiological mechanisms, and are indeed not captured when entropy is used to measure information (Figure 7c).

We conclude this section mentioning other caveats which may contribute to differences in the estimates of variance-based and entropy-based information measures. Besides distorting the theoretical values of some of the information measures as described above, the logarithm function is also a source of statistical bias in the estimation of entropy-based measures on practical time series of finite length. While this bias was not found to be substantial in realizations of our type-II simulation generated with the same length of the cardiovascular series (see Supplementary Material, Figure S1), an effect of this bias on the significance test results cannot be excluded. Moreover, while the assumption of linear stationary multivariate process should hold reasonably in our data, we cannot exclude that significant differences in measures between conditions may be in part due to confounding factors such as the different goodness of the linear fit to the data (possibly related to a different impact of non-linearities), or the different impact of non-stationarities, in a condition compared to another.

5. Summary of Main Findings

The main theoretical results of the present study can be summarized as follows:

• Information decomposition methods are recommended for the analysis of multivariate processes to dissect the general concepts of predictive information, information storage and information transfer in basic elements of computation that are sensitive to changes in specific network properties;
• The combined evaluation of several information measures is recommended to characterize unambiguously changes of the network across conditions;
• Entropy-based measures are appropriate for the analysis of information transfer thanks to the intrinsic normalization to the complexity of the target dynamics, but are exposed to the detection of net synergy in the analysis of information modification;
• Variance-based measures are recommended for the analysis of information modification since they yield zero synergy/redundancy for uncorrelated sources, but can return estimates of information transfer biased by modifications of the complexity of the target dynamics.

The main experimental results can be summarized as follows:

• The physiological stress induced by head-up tilt brings about a decrease of the complexity of the short-term variability of heart period, reflected by higher information storage and internal information, lower cardiorespiratory and higher cardiovascular information transfer, physiologically associated with sympathetic activation and vagal withdrawal;
• Head-up tilt does not alter the information stored in and transferred to systolic arterial pressure variability, but information decompositions reveal an enhancement during tilt of respiratory effects on systolic pressure independent of heart period dynamics;
• The mental stress induced by the arithmetic task does not alter the complexity of heart period variability, but leads to a decrease of the cardiorespiratory information transfer physiologically associated to vagal withdrawal;
• Mental arithmetics increases the complexity of systolic arterial pressure variability, likely associated with the action of physiological mechanisms unrelated to respiration and heart period variability.

6. Conclusions

This work provides an exhaustive framework to dissect the information carried by the target of a network of interacting dynamical systems in atoms of information that form the building blocks of traditional measures of information dynamics such as predictive information, information storage and information transfer. These basic elements are useful to elucidate the specific contributions of individual systems in the network to the dynamics of the target system, as well as to describe the balance of redundancy and synergy between the sources while they contribute to the information stored in the target and to the information transferred to it. Formulating exact values of these measures for the case of Gaussian systems, our theoretical and real-data results illustrate how information storage, transfer and modification interact with each other to give rise to the predictive information of a target dynamical system connected to multiple source systems. In fact, though confirming that different measures reflect different aspects of information processing (respectively, regularity, causality and synergy/redundancy), we have shown that these measured can undergo concurrent modifications in response to specific system alterations. Therefore, we advocate that the various information dynamics measures should not be computed in isolation, but rather evaluated together as components of the total statistical dependence relevant to target process of a multivariate system. We confirm that “aggregate” measures of information storage and information transfer can be useful to reflect macroscopic phenomena like the overall complexity of the target dynamics or the overall causal effects directed to the target, but are often unspecific to alterations of local network properties such as internal dynamics of the target or causal contributions from an individual source. These alterations are better captured by more specific measures such as the internal information and the conditional information transfer. Moreover, we showed that useful additional inferences about the network dynamics can be made exploring the concept of information modification through measures that point out variations related to how the target interacts with a specific source (interaction information storage), how two sources interact while they send information to the target (interaction information transfer), and how more complex interactions arise between the target and all sources (multivariate interaction information).

We performed an exhaustive exploration of the two implementations of the measures of information dynamics commonly adopted for Gaussian systems, finding that the logarithmic transformation which relates variance-based and entropy-based measures may give rise to non-trivial differences between the two formulations. Specifically, since conditional entropy is proportional to the logarithm of conditional variance, any measure defined as the difference between two conditional entropies can be equally seen as measuring the ratio between two conditional variances. Therefore, given that measures defined as the difference between two variances and as the ratio between the same two variances can change in opposite directions between conditions, situations may arise in which entropy-based measures increase, and variance-based measures decrease, in response to a change in condition. Our simulation results document a general bias of entropy-based measures towards the detection of net synergy, including the case of uncorrelated sources that is reflected by zero interaction transfer if assessed through conditional variance but by negative interaction transfer if assessed through conditional entropy. In the analysis of real data we find that, working with processes normalized to unit variance, when marked variations of the new information produced by the target process occur together with variations of the opposite sign of the information stored in the process, variance-based (un-normalized) measures of the information transferred to the target follow closely the variations of the new information; on the contrary, entropy-based (normalized) are less sensitive to the dynamical structure of the target because of the normalization intrinsically present in their formulation. These results lead to the conclusion that the variance-based formulation should be preferred to compute measures of interaction information, while the entropy-based implementation is more indicated to compute measures of information transfer.

The application to experimental data suggested the importance of adopting information decomposition methods to fully assess the cardiac, vascular and respiratory determinants of short-term heart rate and arterial pressure variability. The analysis confirmed known findings about the variations in the complexity and causality of cardiovascular and cardiorespiratory variability, but also revealed novel interpretations related to how the overall predictability of the dynamics of a target system is modified due to possible interactions between the information sources. Given their high specificity, their efficient implementation via traditional multivariate regression analysis, and their demonstrated link with neural autonomic regulation, the proposed quantities are suitable candidates for large scale applications to clinical databases recorded under uncontrolled conditions.

Future studies should be directed to extend the decompositions to model-free frameworks that assess the role of nonlinear physiological dynamics in information storage, transfer and modification [5,31], to explore novel partial decomposition approaches that separate synergetic and redundant information rather than providing their net balance [3,16,17], and to explore scenarios with more than two source processes [15]. Practical extensions should be devoted to evaluate the importance of these measures for the assessment of cardiovascular and cardiorespiratory interactions in diseased conditions. Moreover, thanks to its generality, the approach might be applied not only to cardiovascular physiology, but also to any field of science in which interactions among realizations, representing the behavior of interacting systems, are under scrutiny.