Abstract
Aging causes foot arches to collapse, possibly leading to foot deformities and falls. This paper proposes a set of measures involving an entropy-based method used for two groups of young adults with dissimilar foot arches to explore and quantize postural stability on a force plate in an upright position. Fifty-four healthy young adults aged 18–30 years participated in this study. These were categorized into two groups: normal (37 participants) and flatfooted (17 participants). We collected the center of pressure (COP) displacement trajectories of participants during upright standing, on a force plate, in a static position, with eyes open (EO), or eyes closed (EC). These nonstationary time-series signals were quantized using entropy-based measures and traditional measures used to assess postural stability, and the results obtained from these measures were compared. The appropriate combinations of entropy-based measures revealed that, with respect to postural stability, the two groups differed significantly (p < 0.05) under both EO and EC conditions. The traditional commonly-used COP-based measures only revealed differences under EO conditions. Entropy-based measures are thus suitable for examining differences in postural stability for flatfooted people, and may be used by clinicians after further refinement.
1. Introduction
Feet can be used as an indicator of the human aging process. Reduced walking and exercise and increasing body weight can lead to retardation of the foot muscles and to foot deformities and falls, as well as increasingly flatfooted structures [1,2,3]. Reduced medial longitudinal arches in adults demonstrate many biomechanical inefficiencies and various gait abnormalities in the feet and ankles [4]. For people with abnormal flat-footed structures, the ability to absorb shock and thus to maintain postural stability is reduced. This may result in inflammation of the plantar fascia, plantar lesions, and body pain, and may even lead to an increased risk of falling [4,5,6,7]. In this way, the structure of the foot arch is important for posture [8], and may be an important variable to assess during pre-participation physical examinations [3,9]. Further study of foot structure, postural control, and the risk of lower extremity musculoskeletal injury may provide appropriate direction for clinical interventions for individuals with abnormal foot structures [10]. Previous studies have examined the use of corrective aids to control abnormal foot gait biomechanics and alleviate the discomfort experienced by people with flat feet [11]. However, the literature suggests that there is currently no set of effective and quantized assessment instruments for post-treatment evaluation [12,13,14]. Clinicians therefore need to consider further evidence when selecting management options for flat feet.
Center of pressure (COP) displacement-based time-series analysis is the measure most often used to examine postural stability during upright standing on a force plate [15,16,17], and has been designed to be a low-cost and portable measurement system for quantifying the dynamic properties of humans’ postural stability [18]. In the real world, humans typically exhibit complex dynamic behavior, and knowledge of system variability is essential for understanding the intrinsic behavior of dynamic systems. Traditional COP-based measures use means of raw data as measurements. However, COP signals analyzed using the complexity index (CI)—calculated using entropy-based measures [19,20]—have recently been considered to be a better measure for analyzing non-stationary human fluctuations in postural sway data.
Entropy concerns system randomness and regularity [21], and has been applied to physiological and biological time-series data to assess the structural dynamics of a system across different time scales [22]. Multiscale entropy (MSE) has potential applications in verifying physiological and physical time-series data [22]. MSE is a univariate method that has the ability to detect intrinsic correlations. It is also used to measure the complexity of single-channel signals. However, only “sufficient” length and “regular” scale are reliably processed with MSE. Empirical mode decomposition (EMD) has been proposed by Huang et al. as a new signal-decomposition method for nonlinear and nonstationary signals [23]. The EMD is data-driven and generates intrinsic multiple data scales from inputs, and it may be used for MSE analysis. Ahmed et al. proposed multivariate EMD (MEMD) as a means to generate intrinsic data scales, and it can be used for the subsequent multivariate MSE (MMSE) analysis of input multichannel data [24,25,26,27]. MMSE offers assessments of multichannel observations. It is characterized with greater freedom in analysis than MSE. Entropy methods can be used in signal processing to separate useful signals from intrusive noise. For example, they can be used to evaluate data such as electroencephalogram (EEG) signals to detect an epileptic attack or to classify the signals as focal or non-focal [28,29,30]. The CIs of the MSE and MMSE methods have been validated for use in postural sway dynamics analysis for both younger and older adults, with and without intervention [18,19,20,25,26,31].
In the present study, differences in postural stability between healthy young adults with flat feet and those with normal feet were observed using both the traditional COP-based measures and the entropy-based measures MSE and MMSE. Different combinations of intrinsic mode functions (IMFs) in the entropy method with different parameters, experimental designs, or force-plate COP signals can generate different postural stability assessment results [18,20,31,32]. We therefore tried to identify combinations of IMFs that could be used to evaluate differences in postural stability between flatfooted and normal foot young adults to identify the appropriate combinations of IMFs.
The aim of this study was to investigate the effectiveness of postural stability measurements for identifying differences between flatfooted and normal-footed participants. The effectiveness of traditional COP-based and entropy-based MSE and MMSE measures was compared based on a quiet-standing task on a force plate.
2. Materials and Methods
2.1. Participants
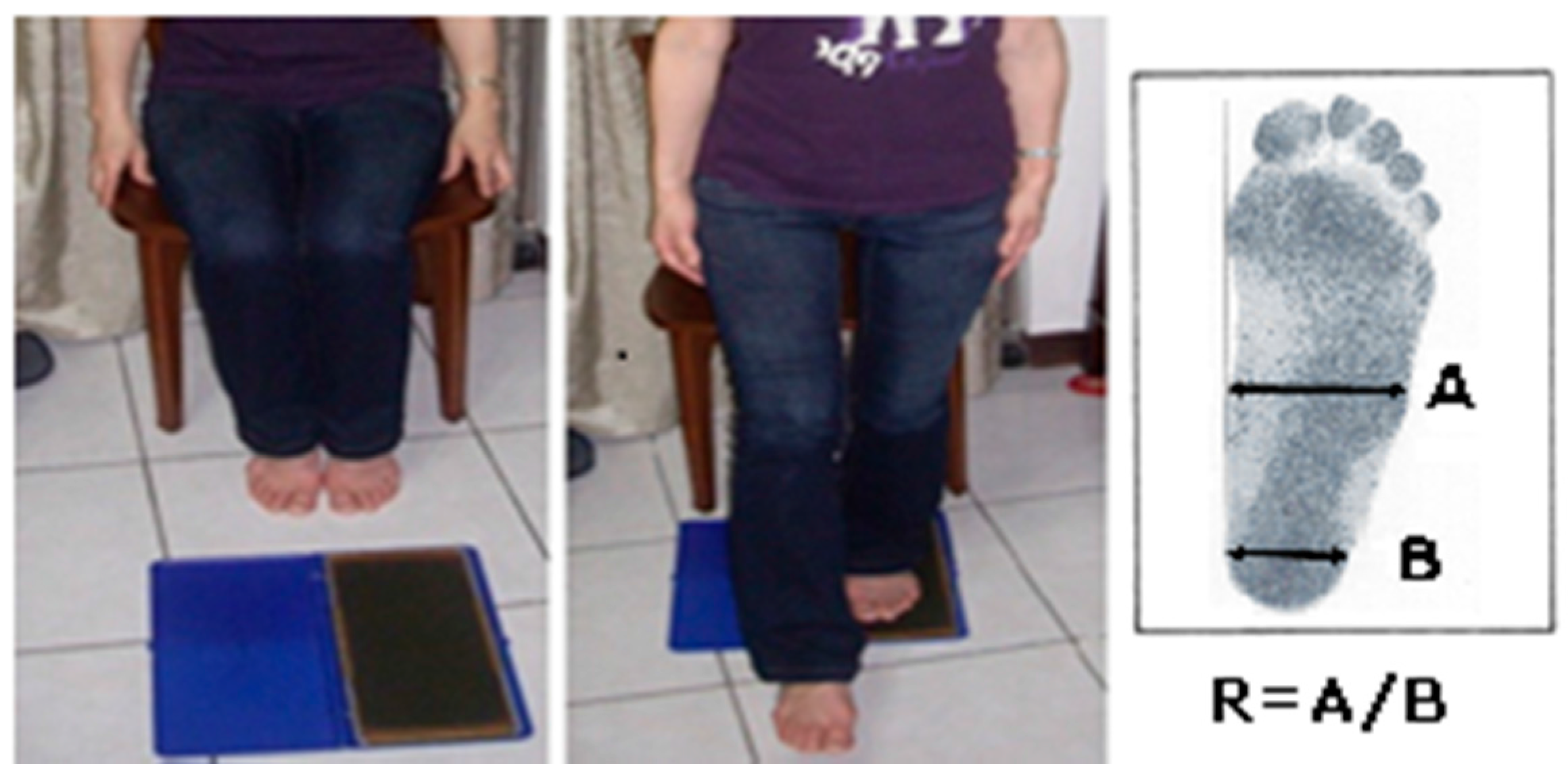
An experiment was conducted to evaluate measurements from 54 (29 males and 25 females) healthy young adults aged 20–30 years (mean: 23.28 ± 2.10 years). None of the participants had mental illness or musculoskeletal or foot disorders, or had undergone foot surgery or other invasive foot treatment procedures. The experiment was approved by the Research Ethics Committee (NTU-REC No. 201206HS011). All participants provided written informed consent before participation, and were requested to provide personal information and footprints before commencing the experiment. They were divided into two groups—flatfooted and normal—using the footprint classification method based on Staheli’s plantar arch index [2]. This static footprint method is used to classify foot types, and is the method most widely used to classify flat feet; it is based on participants standing in a relaxed position [33]. The footprints are used to obtain the arch index ratio (R), which is calculated by dividing the width of the center of the footprint (A) by that of the posterior region (B) (i.e., R = A/B; Figure 1). If R > 1, then the foot is classified as a flat foot. In this study, the flatfoot group comprised 17 participants (mean age: 23.62 ± 2.29 years), and the normal group comprised 37 participants (mean age: 22.53 ± 1.42 years; Table 1).
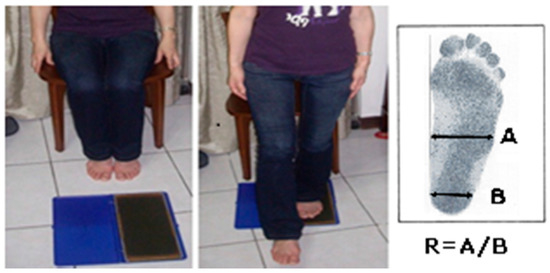
Figure 1.
The participant steps in chalk then takes a step on a sheet of paper. The arch index ratio (R) of the footprint is then calculated [2].

Table 1.
Basic demographic and physiological details of the participants.
2.2. Equipment
The COP movement trajectory data were collected from a force plate (AMTI, Watertown, MA, USA, OR6-7-2000, 50.8 cm × 46.4 cm). The COP-sway time-series data were derived from signals that were continuously recorded for 60 s at a sampling rate of 100 Hz; the length of the time series was 6000 samples. The data were used to investigate the participants’ quantitative postural stability.
2.3. COP-Based Measures
All participants performed the COP-signal-collection task. For signal collection, the participants were requested to stand on the force plate in a static position. Relevant studies have emphasized the importance of the duration of the trial when analyzing COP standing postural stability [34] and the effect of visual input [17,20,35]. The current study therefore proposes a set of COP-based quantitative analysis measures for evaluating differences in postural stability while standing quietly for a short period with eyes open (EO) or eyes closed (EC). Participants were instructed to stand quietly in a natural straight posture with their arms by their sides and to look straight ahead with EO or EC five times, in random order; each trial ran for 60 s (T = 60). The participants rested for approximately 30 s between each trial to avoid fatigue and prevent complicating factors from affecting the results.
The COP signals were collected and divided into anterior–posterior (AP) and medial–lateral (ML) direction signals: and , respectively (t = 1,…,N; N = 6000). These signals were used to describe the COP-based raw data relative to the means of the original data [ and ], and were then transformed to and , as follows:
2.3.1. Traditional COP Methods
This study referenced the traditional COP stabilogram metrics from previous research [15], as follows:
(1) Mean resultant distance (MDIST), MDIST_AP, MDIST_ML:
(2) The root mean square distance (RDIST), RDIST_AP, RDIST_ML:
(3) Total excursion (TOTEX), TOTEX_AP, TOTEX_ML:
(4) Mean displacement velocity (MVELO), MVELO_AP, MVELO_ML:
(5) 95% confidence circle area (AREA-CC), 95% confidence ellipse area (AREA-CE):
AREA-CC and AREA-CE provide estimates of the area of the stabilogram. The others are time-domain distance measures used to estimate either the AP or ML displacement of the COP data.
2.3.2. Entropy Methods
A time-frequency EMD method [23] was used to decompose the signals into signal frequencies; for example, in the ML-direction time-series data, X(t) is composed as follows:
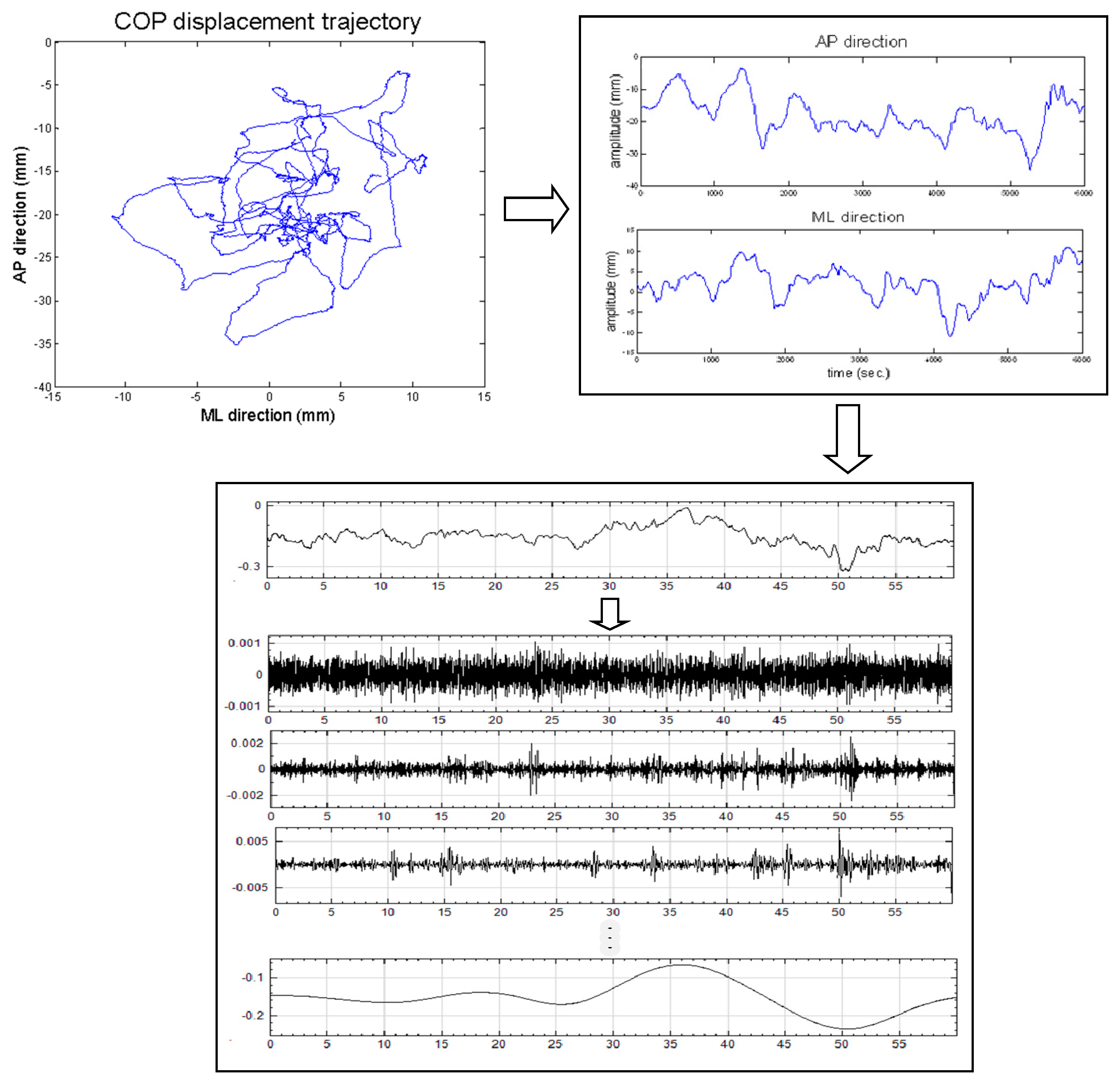
The X(t) signals that contained residuals rn and different modes of oscillation (IMFi, i = 1,…,n). For this analysis, we assumed n = 7 (Figure 2). The detrended signal IMFs were used to derive the CI values of the entropy measures using the formulae above.
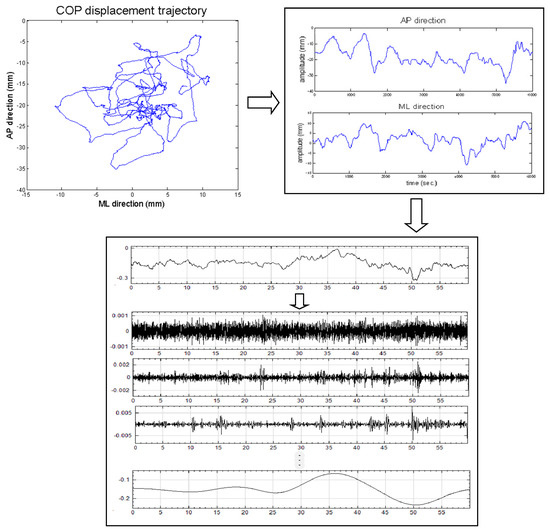
Figure 2.
Center of pressure (COP) displacement trajectories of a participant standing on a force plate were retrieved for the anterior–posterior (AP) and medial–lateral (ML) directions. The time series signal was then detrended into intrinsic mode functions (IMFs) using the empirical mode decomposition (EMD) method.
The MSE method is based on the sample entropy (SampEn) calculation, SampEn(m, r, N), where m is the length of sequences to be compared, r is the tolerance for accepting matches, and N is the length of the time series. The tolerance for accepting matches is r × SD, the standard deviation of the data set [36]. Given a one-dimensional discrete time series, the method then constructs multiple coarse-grained time-series data using the scale factor. The CI of the MSE was defined as the area under the curve for each coarse-grained time series:
Various theoretical and clinical applications have been shown for methods based on the same parameters. We set scale = 20, and based on the literature, set m = 2 and r = 0.15 to analyze the complexity of the COP signals [20].
The MMSE analysis calculates the relative complexity of the multichannel signals by plotting the multivariate sample entropy (MSampEn) for each coarse-grained multivariate. The calculation of MSampEn(m, r, N) uses a combination of different dimensions from the signal group [24,25,26]. For a p-variate time series, , where the multivariate embedding vectors are constructed as:
is the embedding vector, is the time lag vector, and the composite delay vector is , where . Choosing the right IMFs from the original signal is important and challenging when evaluating the postural stability [18,31]. In this study, we used the individual frequency IMF signal to calculate the CI values, then used the different combinations of at least two IMF signals to assess performance in evaluating differences in postural stability between the flatfooted and normal groups.
2.4. Data Analysis
Finally, postural stability was verified by comparing the results with traditional measures based on raw data means with the entropy method, which is based on CI values. These measurement algorithms were implemented using MATLAB R2009.
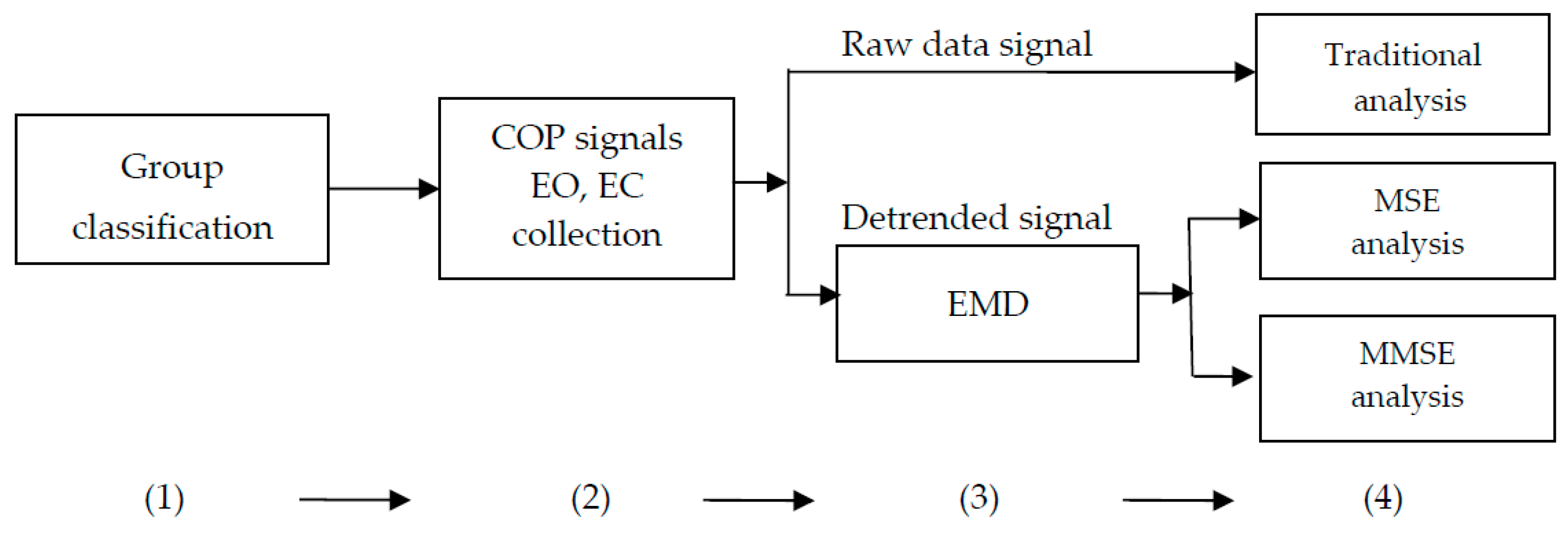
Using the COP signal data to compare postural stability between the normal and flatfooted groups involved the following steps: (1) participants were classified as either normal or flatfooted; (2) the COP signals collected from the force plate, with EO or EC, and were divided into the AP and ML directions; (3) the signals were decomposed and reconstructed using EMD (for MSE analysis) or used raw (for the traditional analysis); and (4) different methods of analyzing the measures were applied. Finally, the results were compared to assess the differences in postural stability as assessed using these data analysis procedures (Figure 3).
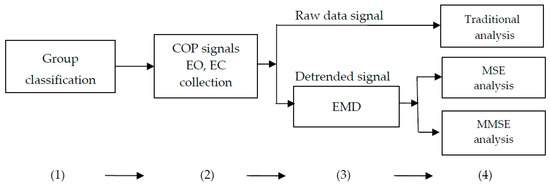
Figure 3.
The overall architecture of assessment procedure for postural stability from the COP displacement trajectory of a participant standing on a force plate in normal foot and flatfooted persons. EC: eyes closed; EO: eyes open; MSE: multiscale entropy; MMSE: multivariate multiscale entropy.
2.5. Statistics
The results of the traditional COP indicators and the CI values from the entropy-based MSE and MMSE methods were statistically evaluated via two-sample t-tests comparing the two groups (means and standard deviations; mean ± SD). An alpha value of 0.05 was used in all statistical tests, which were conducted using Minitab software, to determine whether the difference between the groups was significant.
3. Results
3.1. Traditional COP-Based Measures
In general, the values for the flatfooted group were higher than those for the normal group, although most differences were not significant (Table 2). For the EC test, there were no significant differences, but for the EO test, the differences for the MDIST, MDIST_ML, RDIST, and RDIST_ML measures were significant (p < 0.05). The greatest differences were in the ML direction: (1) the average MDIST_ML values were 1.73 and 1.26 mm for the flatfooted and normal groups, respectively (p = 0.021); and (2) the average RDIST_ML values were 2.17 and 1.57 mm, respectively (p = 0.017).

Table 2.
Descriptive statistics (mean ± SD) for the commonly-used COP-based measures of postural stability with eyes open (EO) and eyes closed (EC) for two groups of participants (flatfooted and normal). MDIST: mean resultant distance; AP: anterior–posterior; ML: medial–lateral; RDIST: root mean square distance; TOTEX: total excursion; MVELO: mean displacement velocity; AREA_CC: 95% confidence circle area; AREA_CE: 95% confidence ellipse area.
3.2. Entropy Measures
We used the individual IMFs to calculate the CI values for the MSE and MMSE analyses, and then calculated the p-values to evaluate the differences in postural stability between the flatfoot and normal groups.
For almost all the MSE and MMSE analyses, there were no significant differences between the groups for either direction or the EO or EC tests (Table 3, Table 4 and Table 5). However, for the MSE analysis in the AP direction, the groups did differ significantly in the EC test (p = 0.036) for the low-frequency signals: IMF6 and IMF7 (0.1–0.3 Hz; Table 3).

Table 3.
MSE analysis results for the AP direction for eyes open (EO) and eyes closed (EC).

Table 4.
MSE analysis results for the ML direction for eyes open (EO) and eyes closed (EC).

Table 5.
MMSE analysis results for eyes open (EO) and eyes closed (EC).
We then combined the IMFs into different signals for further analysis. The high-frequency combinations (IMF2,3, IMF3,4, and IMF2,3,4) revealed no significant differences between the two groups, but the low-frequency combinations (IMF5,6, IMF6,7, and IMF5,6,7) revealed statistically significant differences in complexity between the groups (Table 6). The results were thus similar to those presented in Table 3: a significant difference in the lower-frequency IMFs.

Table 6.
The optimization combination entropy based on MSE and MMSE analysis results for eyes open (EO) and eyes closed (EC).
4. Discussion
Entropy-based data analysis methods have been used to characterize a range of real-world dynamical, non-linear, and non-stationary biomedical time series. We compared MSE and MMSE results with COP-based measures to assess their capacity to identify differences in stability between groups of young adults with dissimilar foot arches. We found that: (1) based on traditional raw-data-based measures from COP signals, MDIST and RDIST exhibited significant differences in the ML direction with EO (Table 2); (2) the CI values (an entropy-based MSE method using the same COP signals) exhibited significant differences in the AP direction with EC in the low-frequency IMF6 and IMF7 signals (Table 3); (3) there were no significant differences in the MMSE (Table 5); and (4) reconstructed combinations of IMFs for the entropy-based measures, IMF5,6, IMF6,7, and IMF5,6,7 revealed significant differences in stability in both directions for both EO and EC between the two groups (Table 6). Thus, the traditional raw-data-based measures only revealed significant differences under EO conditions, whereas the entropy-based measures revealed differences under both EO and EC conditions.
There have been a number of studies that use COP signals to compare postural stability between younger and older adults. Priteo et al. used COP stabilogram metrics to assess postural stability under EO and EC conditions, and showed that there were more differences—which were generally statistically stronger—between these conditions for older adults than for younger adults [15]. However, in the present study (which involved only young participants), differences were only revealed in the lower-frequency measures. Nonstationary COP signals can be decomposed to IMFs by using EMD and MEMD methods, and then evaluated using different combinations of the signals. Costa et al. found significant differences in complexity between older and younger adults by adding together the five highest-frequency IMFs [19]. Yang and Jiang also revealed a difference in complexity for older and younger adults under EO and EC conditions—with or without allocated attention—by using the reconstructed COP signal IMF2,3 [37]. Similarly, Jiang et al. found significant differences in complexity for older adults before and after using vibratory insoles; however, they found no such differences for younger adults [20]. Further, Wei et al. revealed statistically significant differences in complexity between younger and older adults using reconstructed IMF5, IMF4,5, and IMF3,4,5 signals via MSE, and before and after the use of vibratory insoles among older adults using reconstructed IMF4, IMF2,4, IMF3,4, and IMF2,3,4 signals via MMSE [31]. Huang et al. compared different COP systems using entropy measures, and found that IMF5,6 was more sensitive than IMF2,3 in distinguishing among young adults [18]. These studies show that the postural stability of younger adults differs from that of older adults, and that in younger adults it is less likely that changes will be detected after interventions.
Entropy-based measures can be used to distinguish between different types of participants; however, the parameters used with these methods must be set to appropriate values. Examples of such parameters are the length of sequences to be compared, tolerance values, run times, and scale numbers for determining the CI values of the complexity algorithm [20,38,39]. Ramdani et al. [38] assessed postural stability between EO and EC in younger adults using the following parameters: m = 3; and r = 0.3, 0.25, 0.15, or 0.1. They found significant differences between the AP and ML directions, and evaluated the different frequencies taken from the COP signals [38]. Jiang et al. found a significant difference in the AP direction between EO and EC in younger adults using the parameters m = 2 and r = 0.15, with IMF2,4,5 [20]. Previous studies applying entropy-based measures have observed significant differences in postural stability mainly in the higher-frequency signals (~1–30 Hz) [18,19,20,31,32]. One study [40] showed that the frequency range is <2 Hz in human-body COP signals, and another study [41] used COP signals to show that visual input affects the lower frequencies. Further experimentation using appropriate parameters and specific IMF signal frequency ranges is required to verify the analysis results for different groups of participants, to evaluate how human balance control functions.
There are few studies comparing postural stability between flatfooted and normal-footed individuals. Dabholkar et al. [42] compared dynamic balance between flatfooted and normal young females, using the Star Excursion Balance Test (SEBT), and found that the flatfooted individuals’ reach distance was significantly less. Han et al. [43] showed that during walking, the COP pathway of flat feet may be different from that of normal feet, and that the plantar foot pressure of a flat foot was lower than that of a normal foot. Kim et al. [44] examined differences in static and dynamic stability between flexible flat feet and normal feet in young people. They showed that the static stability of both MVELO measurements under single-leg standing (EO or EC) were significantly different between the two groups, and concluded that this might indicate the absence of a relationship between static and dynamic stability. In our study, however, we found no such difference for two-leg standing. Some recent studies have shown that the effects of aging on balance may be accentuated in the ML direction [17,45,46]. Mediolateral balance assessment methods were shown to be reliable and effective for both younger and older adults. As the degree of flatfoot deformity increases, static postural stability decreases [47]. Quantifying postural stability changes in the ML direction would be the next step in exploring the increased risk of falls that is associated with age. In this study, the COP-based measures in the ML direction revealed differences between dissimilar foot arches (Table 6). Previous studies of flat feet have not specifically explored the direction of changes in postural stability [5,12,13,14]. Among the methods used in these studies, COP-based assessments appear to be the easiest for clinicians to conduct and quantify for use in assessing improvements in, or identifying appropriate management for, individuals with flat feet.
There are a few limitations to this study that affect the application of entropy-based methods to COP. (1) The differences between the participant groups (Table 1) with respect to gender, height, weight, and BMI distributions may have influenced the results. (2) We acknowledge that there are many possible combinations of IMFs with different variables for entropy-based analyses. Investigating a wider range of IMF combinations, and the effects of the combinations selected in this study, require further investigation. (3) The meaning of each IMF is currently unclear, and further research is needed to explore this.
In this paper, we used a basic EMD method to decompose nonstationary COP signals into IMFs, and then combined them using a trial-and-error approach to assess postural stability using MSE and MMSE analyses. In future research, we plan to analyze additional EMD methods. Recent studies have suggested that the original EMD method is prone to mode mixing and mode splitting; methods for stabilizing EMD include noise-assisted MEMD [48] or using MEMD instead of EMD [49,50]. The next stage in this investigatory process is therefore to try to verify the effects of treatment of flatfooted individuals using more-developed EMD and entropy-based methods to deepen the analysis of postural stability using COP signals. There are also other types of postural stability assessments that can be used. These COP-based measurements are a simple and effective means of assessing subtle changes in postural stability, which should be utilized in clinical practice in combination with various strategies for alleviating the symptoms of flatfoot.
5. Conclusions
The proposed entropy-based measures exhibited a clear ability to distinguish between flatfooted and normal individuals in terms of postural stability, under both eyes closed and eyes open conditions. In particular, the lower frequencies of the decomposed dynamic-sway COP time-series data collected during quiet standing facilitated the detection of differences in the ML direction.
In the future, we hope to develop strategies to improve the postural stability of flatfooted people. Analysis of entropy-based measures may help clinicians to identify useful strategies in physical exercise, podiatry, orthotics, splints, or shoe modifications, to improve the symptoms of geriatric foot deformities. The results of these studies may also provide directions for clinical interventions that may be effective in improving postural control in individuals with other types of abnormal foot structures.
Acknowledgments
This research was supported by the National Science Council (NSC 100-2221-E-155-065-MY3) and conducted at the laboratory of the Industry of Engineering and Management, Yuan Ze University. The authors thank all of the colleagues and students who contributed to this study. We are grateful to Hsiao-Ching Hsu for her assistance in data collection and collation.
Author Contributions
Tsui-Chiao Chao and Bernard C. Jiang conceived and designed the experiments; Tsui-Chiao Chao performed the experiments, analyzed the data and wrote the paper. Bernard C. Jiang critically revised the manuscript for important intellectual content, and gave final approval for this version to be submitted.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scott, G.; Menz, H.B.; Newcombe, L. Age-related differences in foot structure and function. Gait Posture 2007, 26, 68–75. [Google Scholar] [CrossRef] [PubMed]
- Staheli, L.T.; Chew, D.E.; Corbett, M. The longitudinal arch: A survey of eight hundred and eighty-two feet in normal children and adults. J. Bone Jt. Surg. Am. 1987, 69, 426–428. [Google Scholar]
- Hue, O.; Simoneau, M.; Marcotte, J.; Berrigan, F.; Doré, J.; Marceau, P.; Marceau, S.; Tremblay, A.; Teasdale, N. Body weight is a strong predictor of postural stability. Gait Posture 2007, 26, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Christensen, K. Flat Feet in Adults. Available online: http://www.dynamicchiropractic.com/mpacms/dc/article.php?id=17842 (accessed on 15 February 2017).
- Otman, S.; Basgöze, O.; Gökce-Kutsal, Y. Energy cost of walking with flat feet. Prosthet. Orthot. Int. 1988, 12, 73–76. [Google Scholar] [PubMed]
- Laughton, C.A.; Slavin, M.; Katdare, K.; Nolan, L.; Bean, J.F.; Kerrigan, D.C.; Phillips, E.; Lipsitz, L.A.; Collins, J.J. Aging, muscle activity, and balance control: Physiologic changes. Gait Posture 2003, 18, 101–108. [Google Scholar] [CrossRef]
- Badlissi, F.; Dunn, J.E.; Link, C.L.; Keysor, J.J.; McKinlay, J.B.; Felson, D.T. Foot musculoskeletal disorders, pain, and foot-related functional limitation in older persons. J. Am. Geriatr. Soc. 2005, 53, 1029–1033. [Google Scholar] [CrossRef] [PubMed]
- Anzai, E.; Nakajima, K.; Iwakami, Y.; Sato, M.; Ino, S.; Ifukube, T.; Yamashita, K.; Ohta, Y. Effects of foot arch structure on postural stability. Clin. Res. Foot Ankle 2014. [Google Scholar] [CrossRef]
- Cobb, S.C.; Bazett-Jones, D.M.; Joshi, M.N.; Earl-Boehm, J.E.; James, C.R. The relationship among foot posture, core and lower extremity muscle function, and postural stability. J. Athl. Train. 2014, 49, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Tsai, L.C.; Yu, B.; Mercer, V.S.; Gross, M.T. Comparison of different structural foot types for measures of standing postural control. J. Orthop. Sports Phys. Ther. 2006, 36, 942–953. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Lou, S.Z.; Huang, C.Y.; Su, F.C. Effects of foot orthoses on gait patterns of flat feet patients. Clin. Biomech. 2010, 25, 265–270. [Google Scholar] [CrossRef]
- Evans, A.M.; Rome, K.A. Cochrane review of the evidence for non-surgical interventions for flexible pediatric flat feet. Eur. J. Phys. Rehabil. Med. 2011, 47, 69–89. [Google Scholar] [PubMed]
- MacKenzie, A.J.; Rome, K.; Evans, A.M. The efficacy of nonsurgical interventions for pediatric flexible flat foot: A critical review. J. Pediatr. Orthop. 2012, 32, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Banwell, H.A.; Mackintosh, S.; Thewlis, D. Foot orthoses for adults with flexible pes planus: A systematic review. J. Foot Ankle Res. 2014, 7. [Google Scholar] [CrossRef]
- Prieto, T.E.; Myklebust, J.B.; Hoffmann, R.G.; Lovett, E.G.; Myklebust, B.M. Measures of postural steadiness: differences between healthy young and elderly adults. IEEE Trans. Biomed. Eng. 1996, 43, 956–966. [Google Scholar] [CrossRef]
- Van Emmerik, R.E.A.; van Wegen, E.E.H. On variability and stability in human movement. J. Appl. Biomech. 2000, 16, 394–406. [Google Scholar] [CrossRef]
- Van Wegen, E.E.H.; van Emmerik, R.E.A.; Riccio, G.E. Postural orientation: Age-related changes in variability and time-to-boundary. Hum. Mov. Sci. 2002, 21, 61–84. [Google Scholar] [CrossRef]
- Huang, C.W.; Sue, P.D.; Abbod, M.F.; Jiang, B.C.; Shieh, J.-S. Measuring center of pressure signals to quantify human balance using multivariate multiscale entropy by designing a force platform. Sensors 2013, 13, 10151–10166. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Priplata, A.A.; Lipsitz, L.A.; Wu, Z.; Huang, N.E.; Goldberger, A.L.; Peng, C.K. Noise and poise: Enhancement of postural complexity in the elderly with a stochastic-resonance-based therapy. Europhys. Lett. 2007, 77, 68008. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.C.; Yang, W.H.; Shieh, J.S.; Fan, J.S.Z.; Peng, C.K. Entropy-based method for COP data analysis. Theor. Issues Ergon. Sci. 2013, 14, 227–246. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Rehman, N.; Looney, D.; Rutkowski, T.M.; Mandic, D.P. Dynamical complexity of human responses: A multivariate data-adaptive framework. Bull. Pol. Acad. Sci. Tech. 2012, 60, 433–445. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Looney, D.; Ahmed, M.U.; Mandic, D.P. Human-centred multivariate complexity analysis. Nat. Intell. 2012, 1, 40–43. [Google Scholar]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Bhat, S.; Koh, J.E. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Based Syst. 2015, 88, 85–96. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Huang, J.R.; Fan, S.Z.; Abbod, M.F.; Jen, K.K.; Wu, J.F.; Shieh, J.S. Application of multivariate empirical mode decomposition and sample entropy in EEG signals via artificial neural networks for interpreting depth of anesthesia. Entropy 2013, 15, 3325–3339. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.H.; Wang, K.H.; Liu, Q.; Abbod, M.F.; Jiang, B.C.; Chen, K.P.; Wu, C.; Shieh, J.S. Multivariate multiscale entropy applied to center of pressure signals analysis: An effect of vibration stimulation of shoes. Entropy 2012, 14, 2157–2172. [Google Scholar] [CrossRef]
- Chao, T.C.; Jiang, B.C. Multi-scale entropy analysis for evaluating the balance of the flatfeet. In Advances in Usability Evaluation, 1st ed.; Soarse, M.M., Rebelo, F., Eds.; CRC Press: Boca Raton, FL, USA, 2012; pp. 76–86. [Google Scholar]
- Razeghi, M.; Batt, M.E. Foot type classification: A critical review of current methods. Gait Posture 2002, 15, 282–291. [Google Scholar] [CrossRef]
- Le Clair, K.; Riach, C. Postural stability measures: What to measure and for how long. Clin. Biomech. 1996, 11, 176–178. [Google Scholar] [CrossRef]
- Hafström, A.; Fransson, P.A.; Karlberg, M.; Ledin, T.; Magnusson, M. Visual influence on postural control, with and without visual motion feedback. Acta Oto-laryngol. 2002, 122, 392–397. [Google Scholar] [CrossRef]
- Cost, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.H.; Jiang, B.C. Multi-scale entropy analysis for postural sway signals with attention influence for elderly and young subjects. In Advances in Human Factors and Ergonomics in Healthcare; Duffy, V.G., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 422–431. [Google Scholar]
- Ramdani, S.; Seigle, B.; Lagarde, J.; Bouchara, F.; Bernard, P.L. On the use of sample entropy to analyze human postural sway data. Med. Eng. Phys. 2009, 31, 1023–1031. [Google Scholar] [CrossRef] [PubMed]
- Gow, B.J.; Peng, C.K.; Wayne, P.M.; Ahn, A.C. Multiscale entropy analysis of center-of-pressure dynamics in human postural control: Methodological considerations. Entropy 2015, 17, 7926–7947. [Google Scholar] [CrossRef]
- Freitas, S.M.; Wieczorek, S.A.; Marchetti, P.H.; Duarte, M. Age-related changes in human postural control of prolonged standing. Gait Posture 2005, 22, 322–330. [Google Scholar] [CrossRef] [PubMed]
- Duarte, M.; Zatsiorsky, V.M. Effects of body lean and visual information on the equilibrium maintenance during stance. Exp. Brain Res. 2002, 146, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Dabholkar, A.; Shah, A.; Yardi, S. Comparison of dynamic balance between flat feet and normal individuals using star excursion balance test. Indian J. Physiother. Occup. Ther. 2012, 6, 27–31. [Google Scholar]
- Han, J.T.; Koo, H.M.; Jung, J.M.; Kim, Y.J.; Lee, J.H. Differences in plantar foot pressure and COP between flat and normal feet during walking. J. Phys. Ther. Sci. 2011, 23, 683–685. [Google Scholar] [CrossRef]
- Kim, J.A.; Lim, O.B.; Yi, C.H. Difference in static and dynamic stability between flexible flatfeet and neutral feet. Gait Posture 2015, 41, 546–550. [Google Scholar] [CrossRef] [PubMed]
- Hilliard, M.J.; Martinez, K.M.; Janssen, I.; Edwards, B.; Mille, M.L.; Zhang, Y.; Rogers, M.W. Lateral balance factors predict future falls in community-living older adults. Arch. Phys. Med. Rehabil. 2008, 89, 1708–1713. [Google Scholar] [CrossRef] [PubMed]
- Lizama, L.E.C.; Pijnappels, M.; Reeves, N.P.; Verschueren, S.M.; van Dieën, J.H. Frequency domain mediolateral balance assessment using a center of pressure tracking task. J. Biomech. 2013, 46, 2831–2836. [Google Scholar] [CrossRef] [PubMed]
- Harrison, P.L.; Littlewood, C. Relationship between pes planus foot type and postural stability. Indian J. Physiother. Occup. Ther. 2010, 4, 21–24. [Google Scholar]
- Ur Rehman, N.; Mandic, D.P. Filter bank property of multivariate empirical mode decomposition. IEEE Trans. Signal Proces. 2011, 59, 2421–2426. [Google Scholar] [CrossRef]
- Mandic, D.P.; Ur Rehman, N.; Wu, Z.; Huang, N.E. Empirical mode decomposition-based time-frequency analysis of multivariate signals: The power of adaptive data analysis. IEEE Signal Proc. Mag. 2013, 30, 74–86. [Google Scholar] [CrossRef]
- Ur Rehman, N.; Park, C.; Huang, N.E.; Mandic, D.P. EMD via MEMD: Multivariate noise-aided computation of standard EMD. Adv. Adapt. Data Anal. 2013, 5. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).