Consistency of Learning Bayesian Network Structures with Continuous Variables: An Information Theoretic Approach
Abstract
:1. Introduction

- (1)
- Compute the local scores for the nonempty subsets of ; for example, if , the seven quantities are obtained; and
- (2)
- Find a BN structure that maximizes the global scores among the candidate BN structures; there are at most DAGs in the case of N variables; for example, if , the eleven quantities are computed and a structure with the largest is chosen.
2. Preliminaries
2.1. Learning the Bayesian Structure for Discrete Variables and Its Consistency
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| 1 | * | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | + | * | + | + | + | 0 | 0 | + | + | + | 0 | |
| 3 | + | + | * | + | 0 | + | 0 | + | + | + | 0 | |
| 4 | + | + | + | * | 0 | 0 | + | + | + | + | 0 | |
| 5 | + | + | + | + | * | + | + | + | + | + | 0 | |
| 6 | + | + | + | + | + | * | + | + | + | + | 0 | |
| 7 | + | + | + | + | + | + | * | + | + | + | 0 | |
| 8 | + | + | + | + | + | + | + | * | + | + | 0 | |
| 9 | + | + | + | + | + | + | + | + | * | + | 0 | |
| 10 | + | + | + | + | + | + | + | + | + | * | 0 | |
| 11 | + | + | + | + | + | + | + | + | + | + | * |
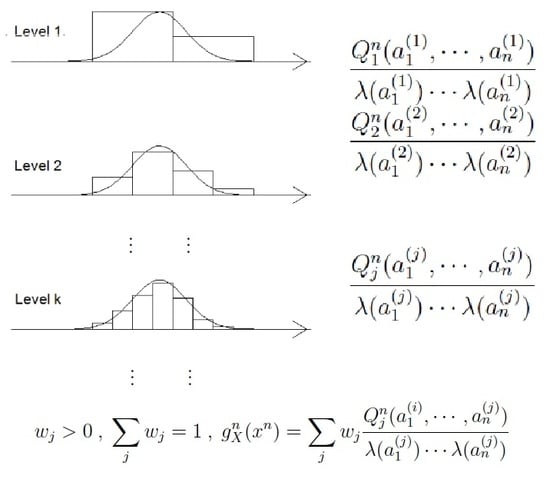
2.2. Universal Measures for Continuous Variables
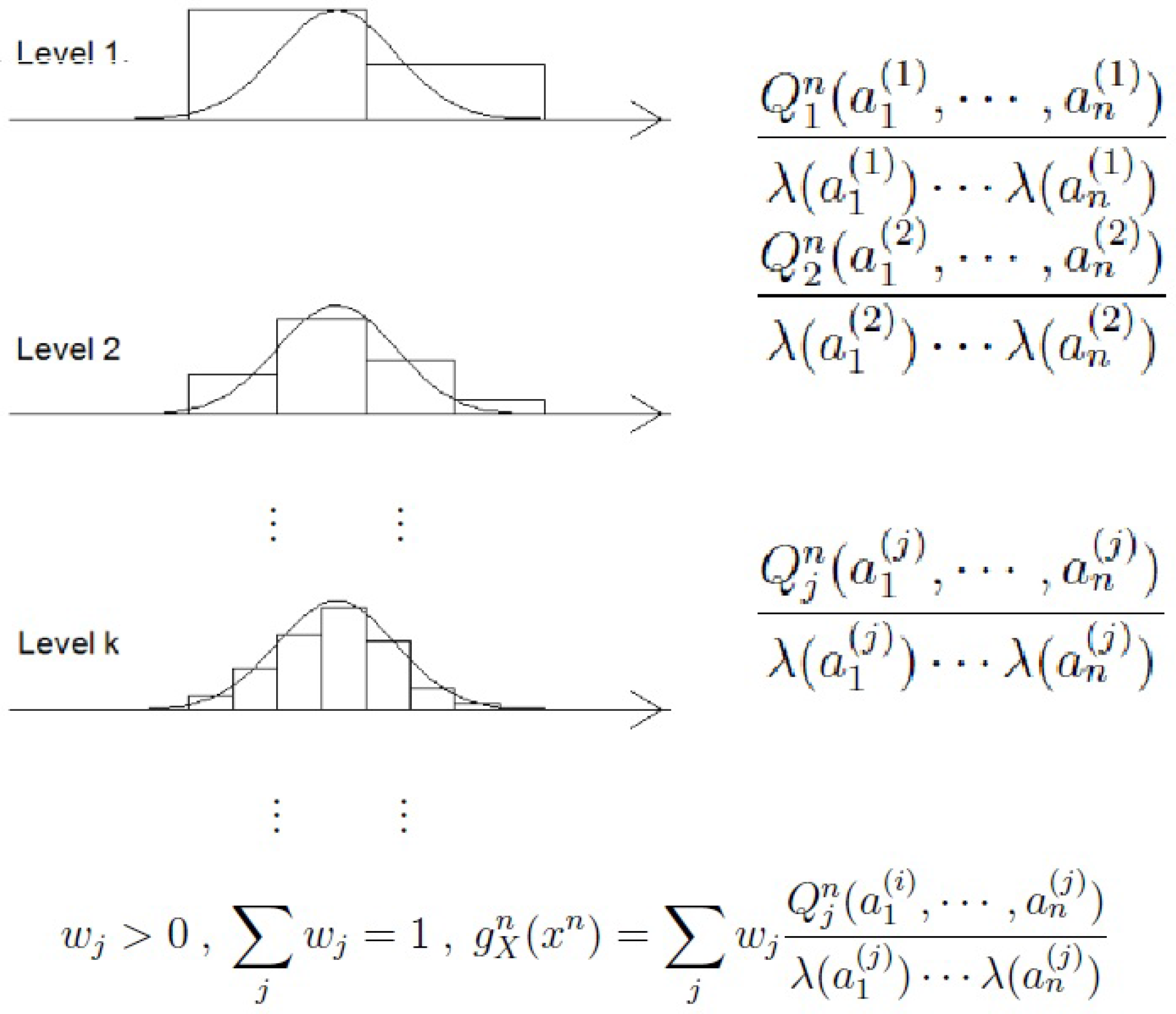
3. Contributions
3.1. The Hannan and Quinn Principle
- is equivalent to (7); and
3.2. Consistency for Continuous Variables
| Algorithm 1 Calculating gn. | |
| (A) Input xn ∈ An, Output | |
| 1. | For each , |
| 2. | For each and each , |
| 3. | For each , |
| (a) , | |
| (b) for each | |
| i. Find from | |
| ii. | |
| iii. | |
| 4. | |
| (B) Input and , Output | |
| 1. | For each , |
| 2. | For each and each and , |
| 3. | For each |
| (a) , , , | |
| (b) for each | |
| i. Find and from and | |
| ii. | |
| iii. | |
| 4. | |
3.3. The Number of Local Scores to be Computed
4. Concluding Remarks
Appendix: Proof of Theorem 1
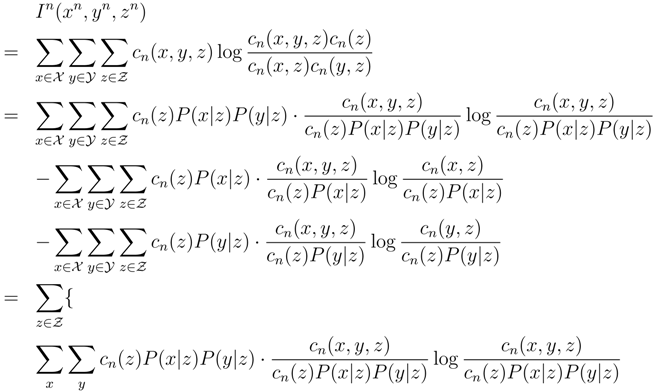


 with:
with:



 and u and v are the column vectors
and u and v are the column vectors  and
and  , respectively. Hereafter, we arbitrarily fix z ∈ Z. Let U = (u[0], u[1], …, u[α − 1]), with u[0] = u and W = (w[0], w[1], …, w[β − 1], with w[0] = w being eigenvectors of
, respectively. Hereafter, we arbitrarily fix z ∈ Z. Let U = (u[0], u[1], …, u[α − 1]), with u[0] = u and W = (w[0], w[1], …, w[β − 1], with w[0] = w being eigenvectors of  and
and  , where Em is the identity matrix of dimension m.
, where Em is the identity matrix of dimension m.









References
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Billingsley, P. Probability & Measure, 3rd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Friedman, N.; Linial, M.; Nachman, I.; Pe'er, D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000, 7, 601–620. [Google Scholar] [CrossRef] [PubMed]
- Imoto, S.; Kim, S.; Goto, T.; Aburatani, S.; Tashiro, K.; Kuhara, S.; Miyano, S. Bayesian network and nonparametric heteroscedastic regression for nonlinear modeling of genetic network. J. Bioinform. Comput. Biol. 2003, 1, 231–252. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Peters, J.; Janzing, D.; Scholkopf, B. Kernel-based Conditional Independence Test and Application in Causal Discovery. In Proceedings of the 2011 Uncertainty in Artificial Intelligence Conference, Barcelona, Spain, 14–17 July 2011; pp. 804–813.
- Silander, T.; Myllymaki, P. A simple approach for finding the globally optimal Bayesian network structure. In Proceedings of the 22nd Conference on Uncertainty in Artificial Intelligence, Arlington, Virginia, 13–16 July 2006; pp. 445–452.
- Hannan, E.J.; Quinn, B.G. The Determination of the Order of an Autoregression. J. R. Stat. Soc. B 1979, 41, 190–195. [Google Scholar]
- Suzuki, J. The Hannan–Quinn Proposition for Linear Regression, Int. J. Stat. Probab. 2012, 1, 2. [Google Scholar]
- Suzuki, J. On Strong Consistency of Model Selection in Classification. IEEE Trans. Inf. Theory 2006, 52, 4767–4774. [Google Scholar] [CrossRef]
- Ryabko, B. Compression-based Methods for Nonparametric Prediction and Estimation of Some Characteristics of Time Series, IEEE Trans. Inform. Theory 2009, 55, 4309–4315. [Google Scholar] [CrossRef]
- Suzuki, J. Universal Bayesian Measures. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 644–648.
- Krichevsky, R.E.; Trofimov, V.K. The Performance of Universal Encoding. IEEE Trans. Inf. Theory 1981, 27, 199–207. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Suzuki, J. Learning Bayesian Network Structures When Discrete and Continuous Variables Are Present. In Proceedings of the 2014 Workshop on Probabilistic Graphical Models, 17–19 September 2014; Springer Lecture Notes on Artificial Intelligence. Volume 8754, pp. 471–486.
- Suzuki, J. Learning Bayesian belief networks based on the minimum description length principle: An efficient algorithm using the B&B technique. In Proceedings of the 13th International Conference on Machine Learning (ICML'96), Bari, Italy, 3–6 July 1996; pp. 462–470.
- De Campos, C.P.; Ji, Q. Efficient Structure Learning of Bayesian Networks using Constraints. JMLR 2011, 12, 663–689. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Judea, P. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan-Kaufmann: San Mateo, CA, USA, 1988. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, J. Consistency of Learning Bayesian Network Structures with Continuous Variables: An Information Theoretic Approach. Entropy 2015, 17, 5752-5770. https://doi.org/10.3390/e17085752
Suzuki J. Consistency of Learning Bayesian Network Structures with Continuous Variables: An Information Theoretic Approach. Entropy. 2015; 17(8):5752-5770. https://doi.org/10.3390/e17085752
Chicago/Turabian StyleSuzuki, Joe. 2015. "Consistency of Learning Bayesian Network Structures with Continuous Variables: An Information Theoretic Approach" Entropy 17, no. 8: 5752-5770. https://doi.org/10.3390/e17085752
APA StyleSuzuki, J. (2015). Consistency of Learning Bayesian Network Structures with Continuous Variables: An Information Theoretic Approach. Entropy, 17(8), 5752-5770. https://doi.org/10.3390/e17085752