The 24-hour bivariate wind vectors are denoted as
in the polar coordinate system, with
ν for wind speed and
θ for wind direction. These vectors can be represented as a bivariate vector as (
) in a Cartesian coordinate system. That is, the magnitude of the vector is the wind speed, and the arrow points in the direction where the wind blows in the global coordinate system. As a daily example shown in
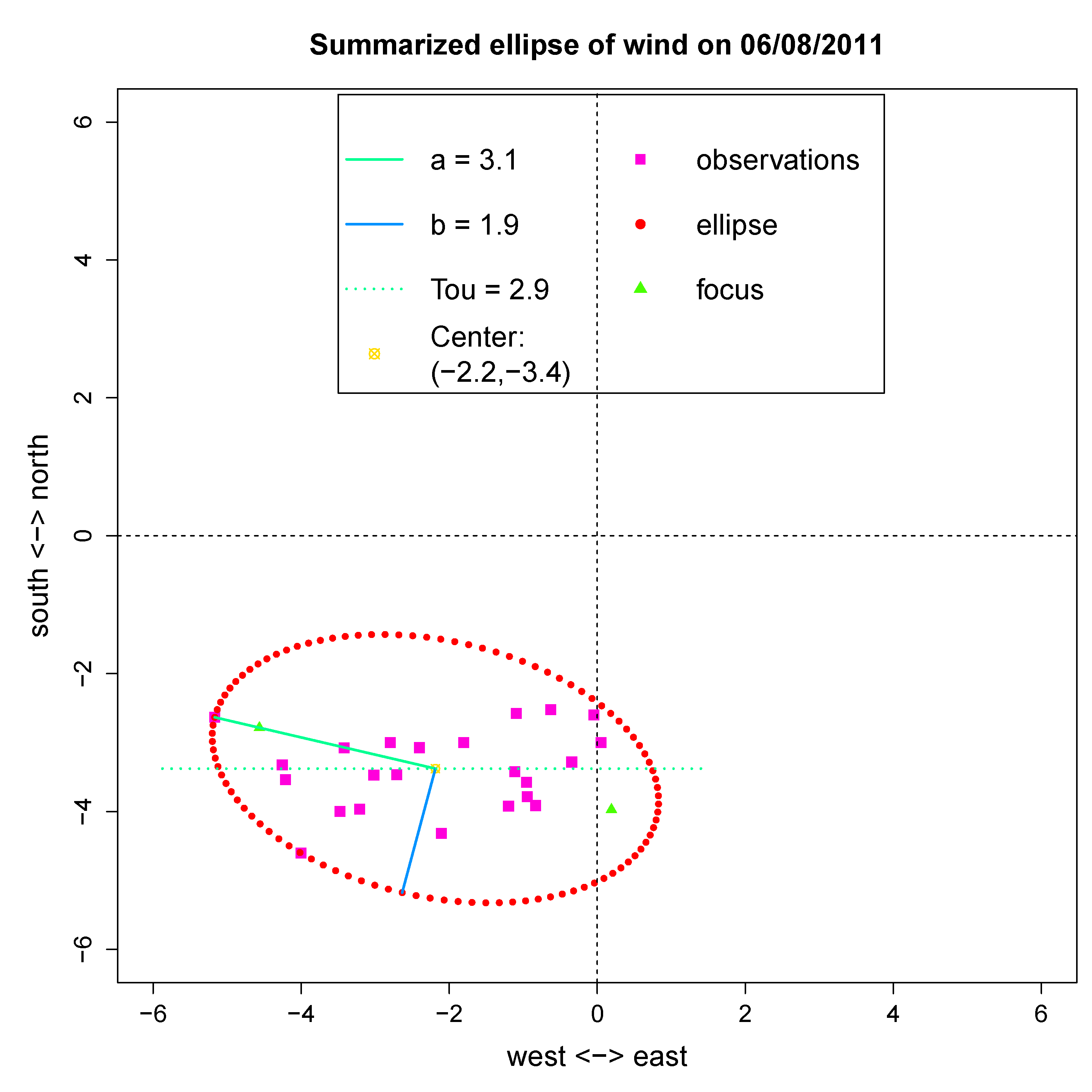
Figure 1, the majority of the wind vector points are located in the 3rd quadrant, which indicates that the wind direction is primarily from south to southwest (a classic summer wind pattern).
Figure 1.
A summarizing ellipse constructed from daily wind speed and direction marked with the (1) 2-dimensional center of mass location, (2) lengths of the two axes and (3) tilt to the horizontal axis.
Figure 2.
Three hundred thirty nine summarizing ellipses from 2011 displayed on 12 monthly panels.
A summary statistic, called the minimum ellipse, is proposed to coherently capture the daily dynamic features of wind, as demonstrated by the ellipse shown in
Figure 1. The minimum ellipse concept is based on the fact that the 24-hour wind speed and direction data indeed contain the aforementioned daily cycle [
5]. The center of mass of such a point cloud relative to the origin of the coordinate system depicts the overall situation of the daily wind characteristics, which represents a large-scale weather pattern. When this center of mass falls within a small vicinity of the origin, the global geostrophic wind might be negligible, and the local daily cycle assumes the primary role in generating the wind pattern of the day. That is, when the point cloud coalesces around the origin with relatively large major axis lengths, it can be inferred that the wind direction changes along the major axes, which might be a land-sea breeze day. By contrast, when the point cloud is located far from the origin, the wind direction is more consistent. It is a day in which geostrophic wind dominates the wind pattern of the day. The average magnitude of wind speed depends on how far the center of mass is located from the origin. The directions of the major axis together with the directions of centers of mass determine the overall direction and direction changes. To compute the minimum ellipse, the following sequential steps are taken: (1) calculate the center of mass of 24 wind bivariate vectors; (2) identify the hourly wind vector that is located farthest away from the center of mass; draw a segment that links the center of mass and the farthest point, and take it as the major axis of the ellipse; (3) mark the angle of the segment of the major axis in the Cartesian coordinate system as the tilt of the ellipse; and (4) perform a recursive search via an ellipse constructed with a minor axis, such that all vectors are enclosed. The defining 5-dimensional parameters of such a computed ellipse include the following: the
and
y-coordinates of its center of mass, the lengths of its major and minor axes and the angle of its major axis. The 5 ellipse parameters are given in the legend of
Figure 1. The area of the ellipse represents the variation of the hourly wind vectors from the mean wind vector. They are not only informative, but also more appropriate than classic daily averages or maximums of wind speed or wind direction.
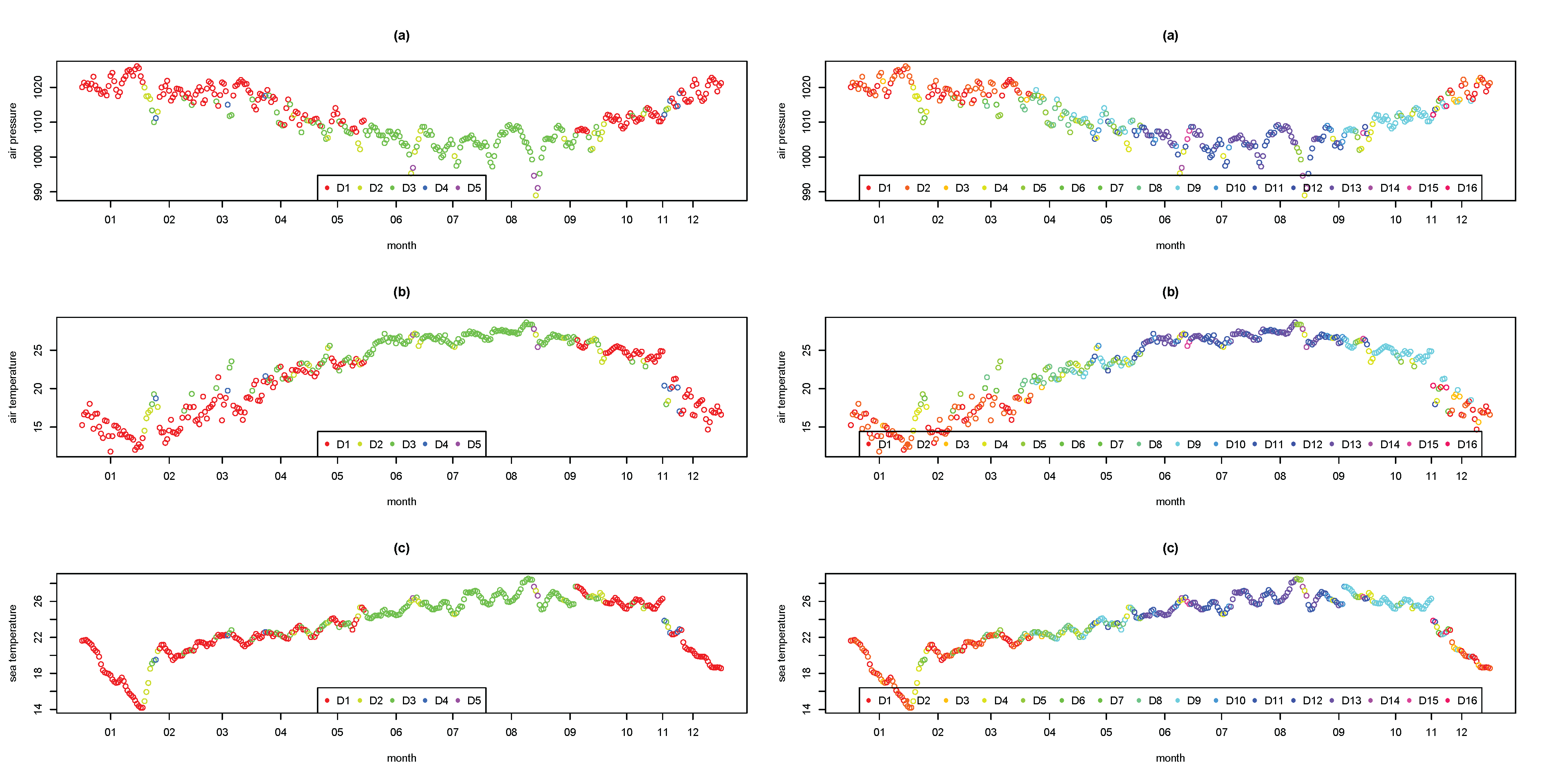
We now demonstrate that such 5-dimensional summary statistics are capable of revealing the informative and dynamic features of Penghu’s daily winds in 2011. The 339 daily summarized ellipses are grouped by month, with the entire year’s ellipses plotted at the center of
Figure 2. This plot shows clear seasonal patterns with most of the ellipses in the upper panels located in the 1st quadrant, which represents the typical north-east monsoon in Penghu. Furthermore, ellipses in the lower panels are observed to move toward the origin. The ellipses moving toward the south-west indicate the classic summer wind patterns. In summary, the dynamic visible features include the following: (1) an evolving trajectory of extreme weather conditions, such as a typhoon’s approach and departure; (2) a new criterion for classifying daytime sea-land breezes; and (3) the yearly cycle of the characteristic northeast (NE)-monsoon.
2.1.1. Computations and Algorithms
The major computational tool is the algorithm, called data cloud geometry (DCG), which produces an ultrametric DCG tree; see Fushing and McAssey (2010) [
8] and Fushing
et al. (2013) [
9]. This DCG tree provides a multiscale clustering configuration on a node space,
, in which an empirical measure of distance,
, is typically derived from knowledge of the subject matter. With this distance measure, an
distance matrix is calculated and denoted as
, with
and
. Rather than directly using the matrix
to arrive at a tree hierarchy of clustering, such as via the hierarchical clustering (HC) algorithm, the DCG algorithm works with a series of similarity matrices
indexed by scalar values
. The scale-tuning parameter
T is specifically called “temperature” because of its statistical mechanics foundation. The concept and function of a temperature (scale) in DCG computing are similar to the concept and function of the “resolution” of a microscope. Under different resolutions, we observe distinct cell structures through a microscope instrument. Similarly, we expect the data to reveal distinct structural pattern information with respect to different temperatures. This temperature-regulated similarity matrix
is very distinct from the “time”-regulated device used in a diffusion map; see Coifman and Lafon (2006) [
6].
Based on
, a trajectory ensemble of node removal-regulated Markov random walks is generated. The random walk, which is defined through a transition probability matrix converted from
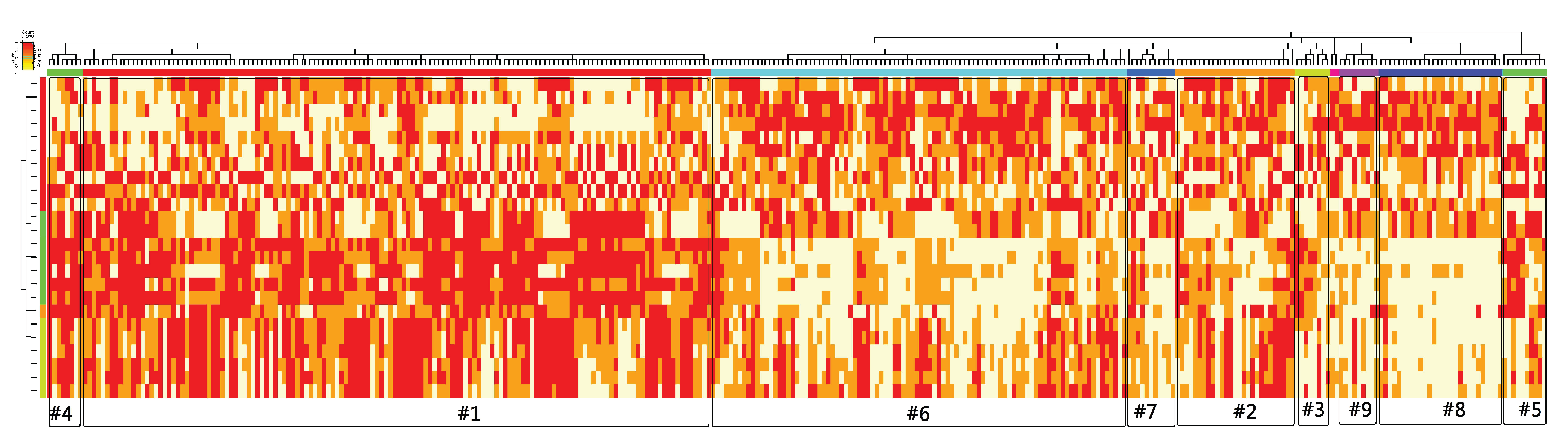
, is a tool for determining the temperature-specific data geometry. To be able to explore the whole landscape without being trapped within a cluster, the design of such a random walk is to remove a node after it has been visited over a threshold number of visits. Thus, with the random traveling among nodes, the number of nodes becomes increasingly smaller. When a random walk explores a landscape of nodes, we also count the number of steps required to remove the next node. A larger number of steps is typically required to remove the first node when it enters into a new cluster. This feature of node removal produces spikes on the node-removal recurrence time process. Thus, a spike indicates that a random walk enters a newly unexplored cluster. Therefore, two pieces of information become available on a node removal recurrence time process: (1) the number of spikes indicates the number of clusters under the temperature
T; and (2) all removed nodes between two successive spikes are likely to be located in the same cluster. Consequently, a node removal-regulated random walk gives rise to a binary connectivity matrix with 1 or 0 at the
entry according to whether nodes
and
are removed between the same pair of successive spikes. An ensemble of random walks gives rise to an ensemble of binary-connected matrices. By averaging such an ensemble of binary-connected matrices, a connectivity or cluster-sharing probability matrix can be obtained. From this connectivity probability matrix, the clustering configuration pertaining to the temperature
T can be extracted. Finally, a subset of temperatures is selected, each of which provides confidence in the extracted temperature-specific clustering configuration. Then, an ultrametric tree algorithm is applied (see Fushing
et al. (2013) [
9] for the detailed construction), for which the Ultrametric DCG-tree on
χ is denoted as
.
For example,
is the space of
daily 5-dimensional summarizing parameters of an ellipse for 2011.
is the weighted Euclidean distance of
with weighted proportional standard deviations of the 5 dimensions. A daily wind ultrametric tree
can then be computed, as presented in the subsequent section. Next, we discuss an algorithm for adapting the Euclidean distance to an ultrametric tree structure. For example, consider the
covariate matrix. Let the node space on the column axis be denoted as
. Therefore,
is a
vector for each
. Then, a new Euclidean distance is defined by adapting the chosen
tree structure on the 339 day nodes. Each covariate is represented by a 339-dimensional vector. On Level 0, the Euclidean distance is computed by summing 339 component-wise discrepancies between two covariate vectors. One level up, for instance, supposes that there exists a known 10-cluster structure among 339 daily nodes. Upon this 10-cluster structure, we can further manifest the degree of discrepancy/concordance between any pair of covariates by separating the 339 dimensions into 10 categories and evaluating their discrepancy/concordance upon the corresponding 10 dimensions. The evaluation involves calculating the difference in pairwise averages within each category and summing them. That is, to a great extent, we accommodate 10 two-sample testing statistics into our new distance measurement. The algorithm is described as follows. Any level of the tree
corresponds to a clustering composition of
χ. Suppose that
levels (including the bottom level) of the tree are chosen to form a multiscale collection of clusters on
χ. This collection is denoted as
, where
is the number of clusters
on the
l-th level. Each cluster size is denoted as
. The updated distance
from the Euclidean distance
on
is defined as follows:
where
is the Euclidean distance and
is the average of components
in
, which is
for
.
This adaptation algorithm comprises the heart of the computational algorithm and is called data mechanics (DM) in Fushing
et al. (2014) [
7]. This algorithm is designed to extract interacting relational patterns between two node spaces, with data being represented as a rectangular matrix, such as the
covariate matrix. This data-driven distance indicates how to operationally couple tree-structural information from a given different node space to a target node space. Two vectors corresponding to two nodes,
and
, which have a relatively small Euclidean distance via
, do not necessarily have a small distance via
. This discrepancy is due to the clustering configuration
; hence, it becomes essential and critical for computing causal and predictive patterns.