Active Control of a Chaotic Fractional Order Economic System
Abstract
:1. Introduction
2. Preliminary Tools
2.1. Fractional Calculus
- .
- .
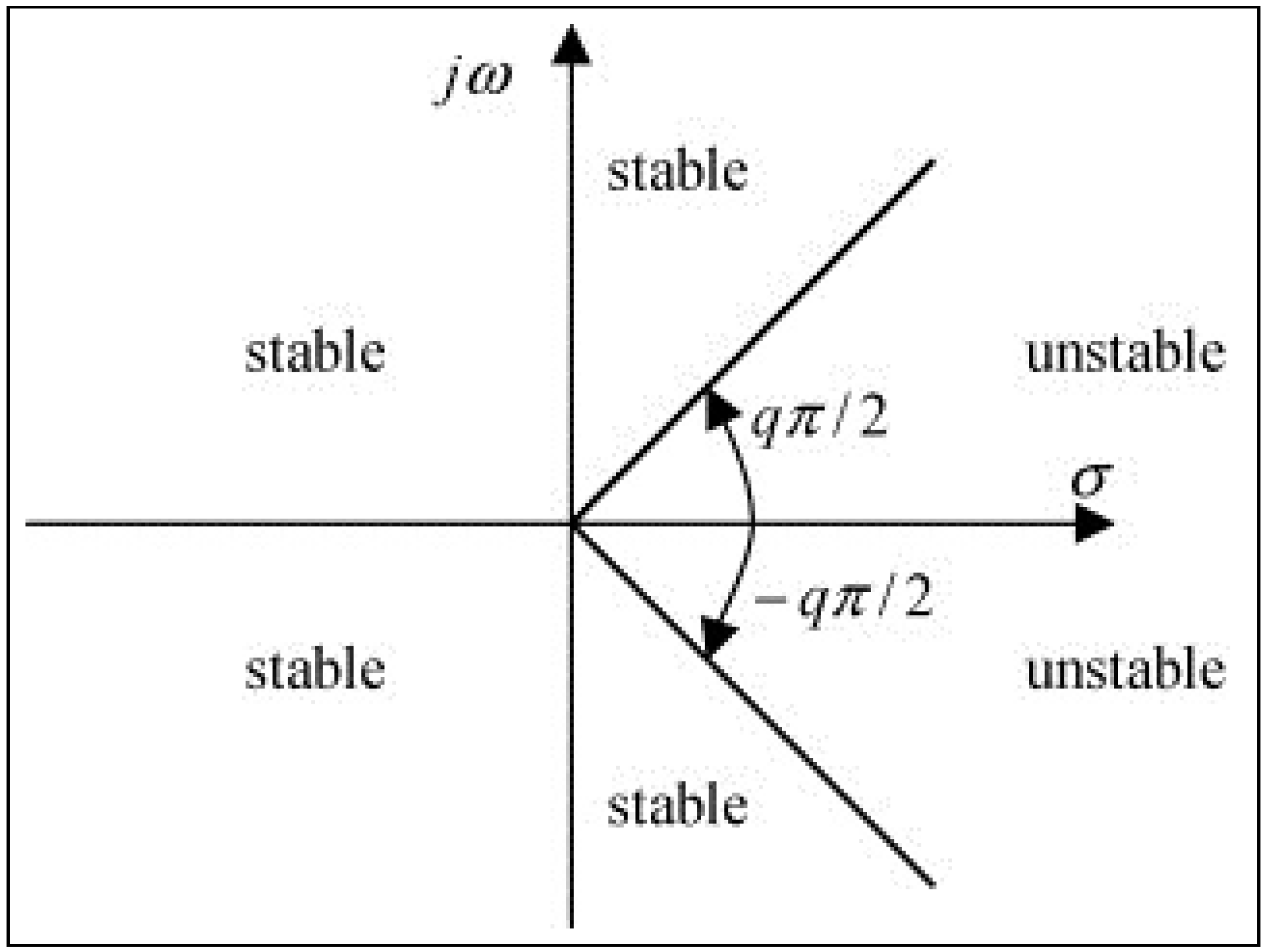
2.2. Stability Criterion
2.3. The Adams–Bashforth–Moulton Algorithm
3. A Fractional Order Economic System
3.1. Dynamical Behavior
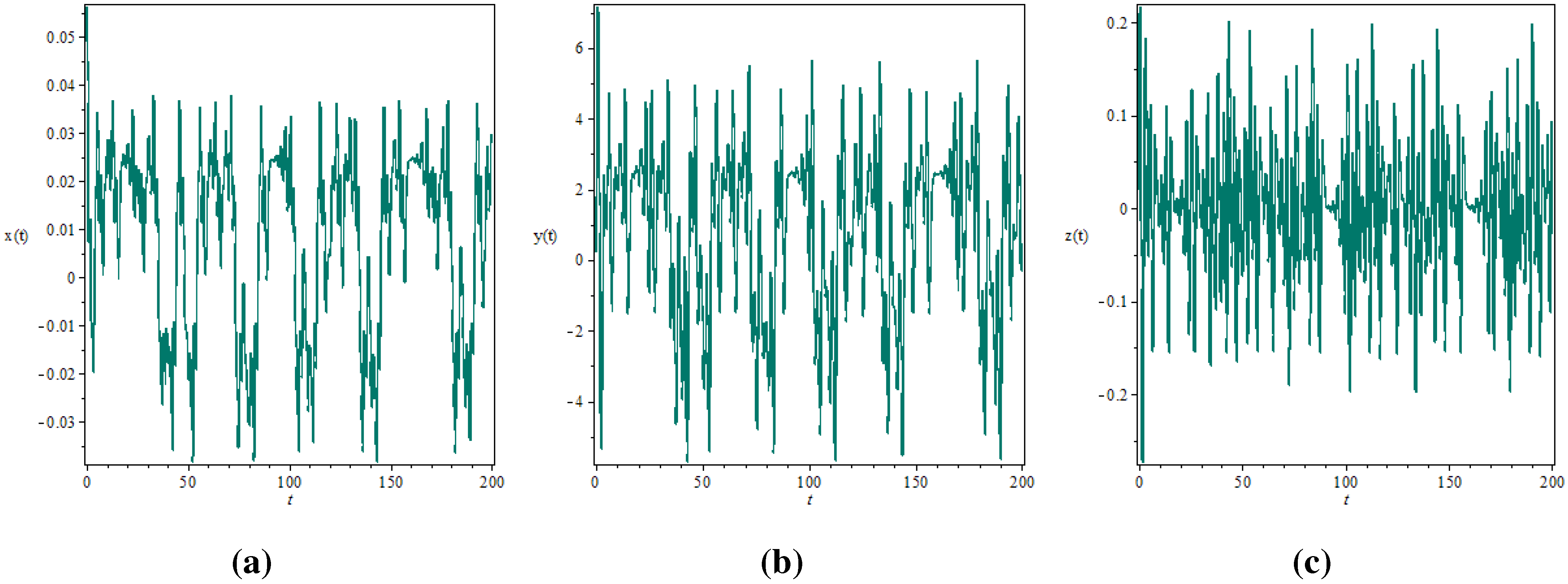
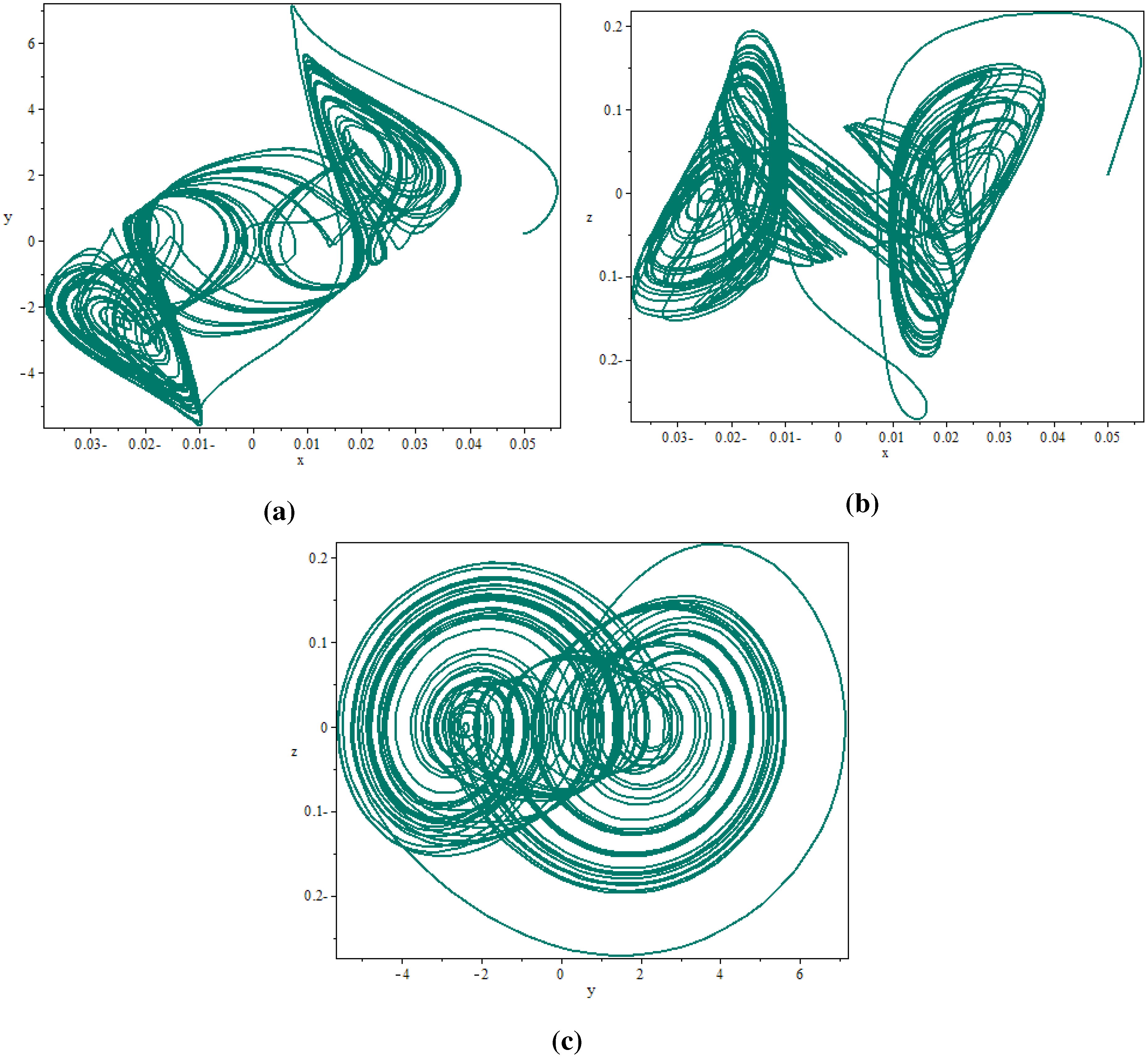
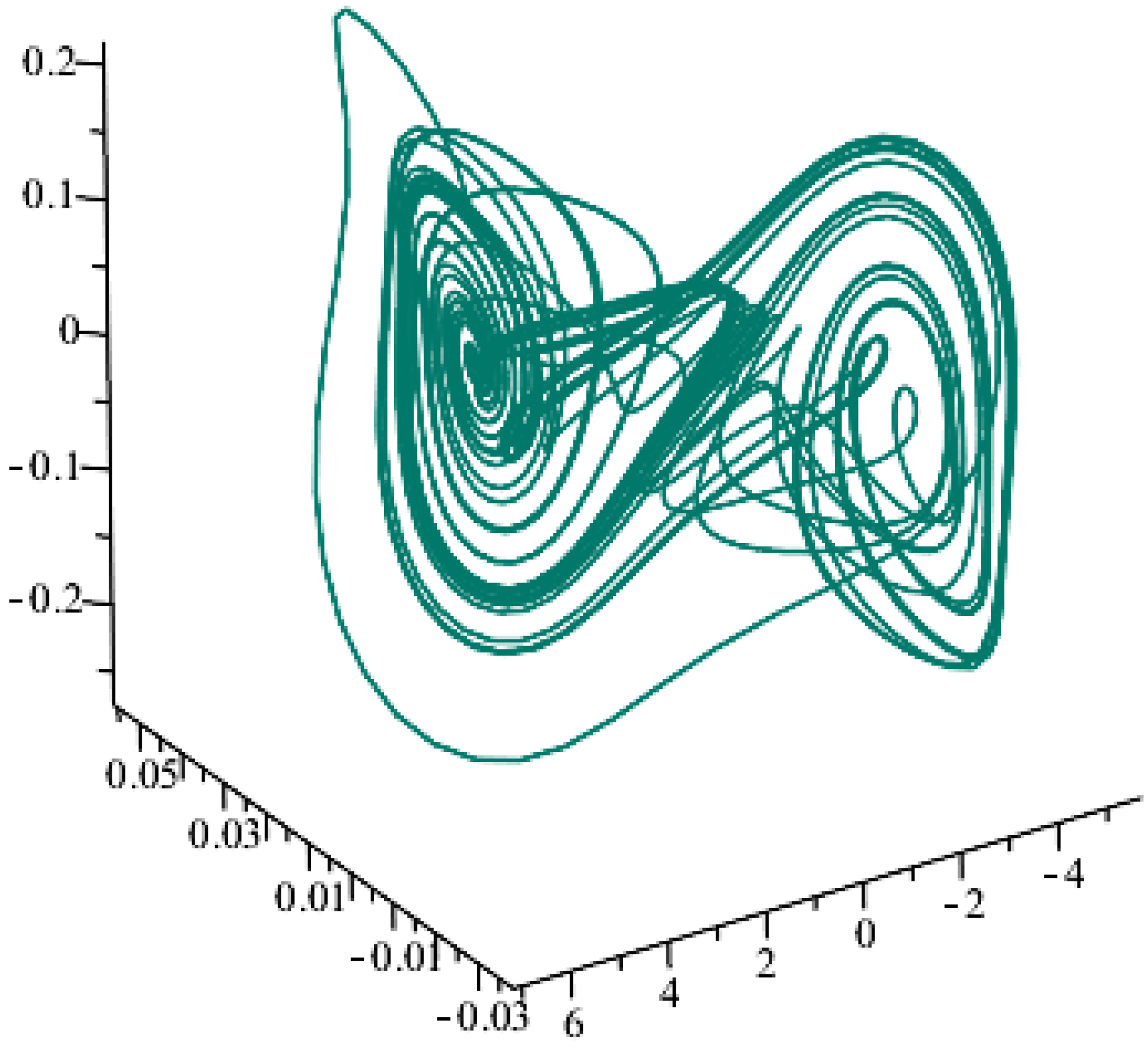
3.2. Numerical Simulations
4. Active Control of the Fractional Order Chaotic System
- For :
- For :
- For :

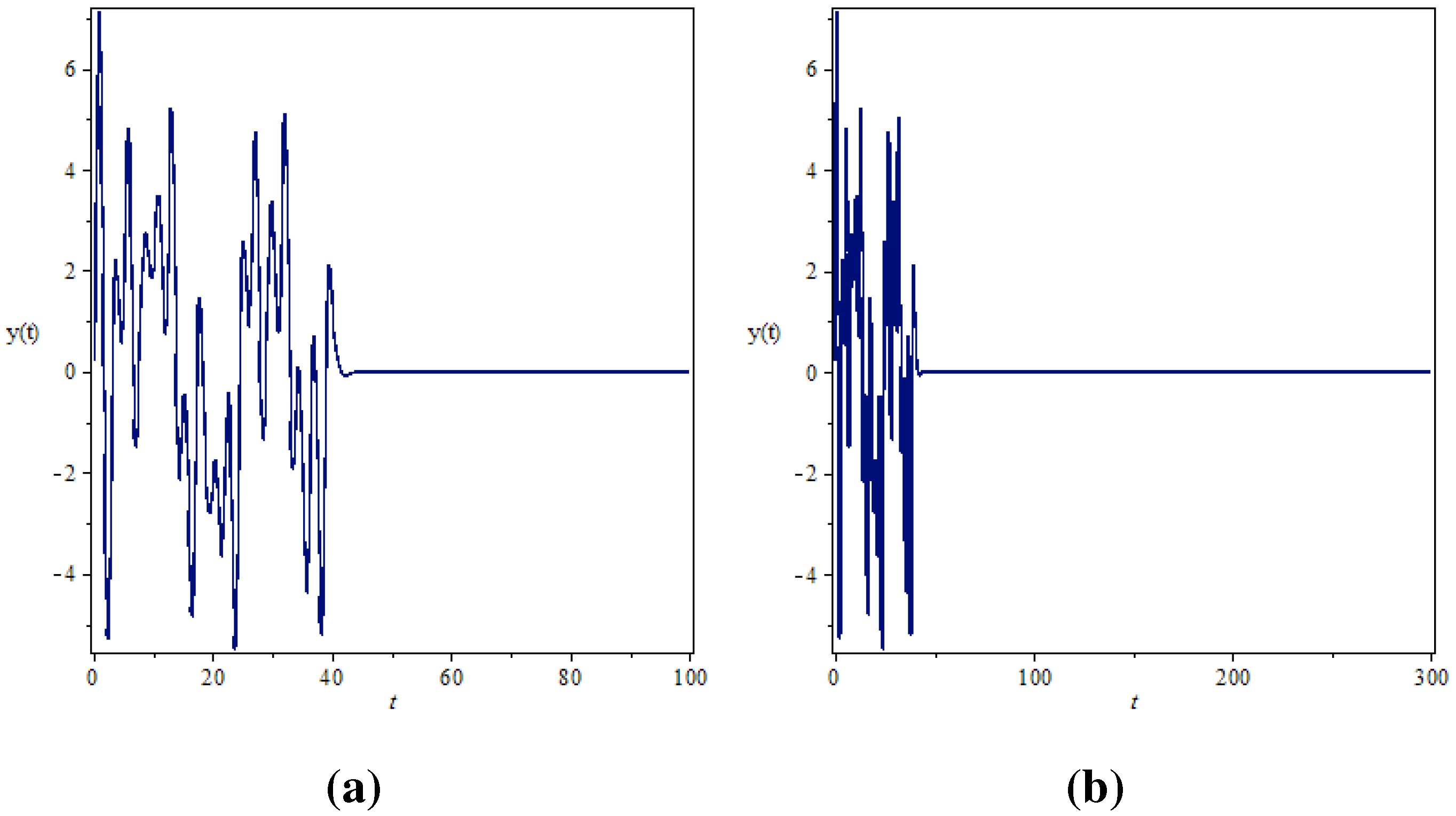
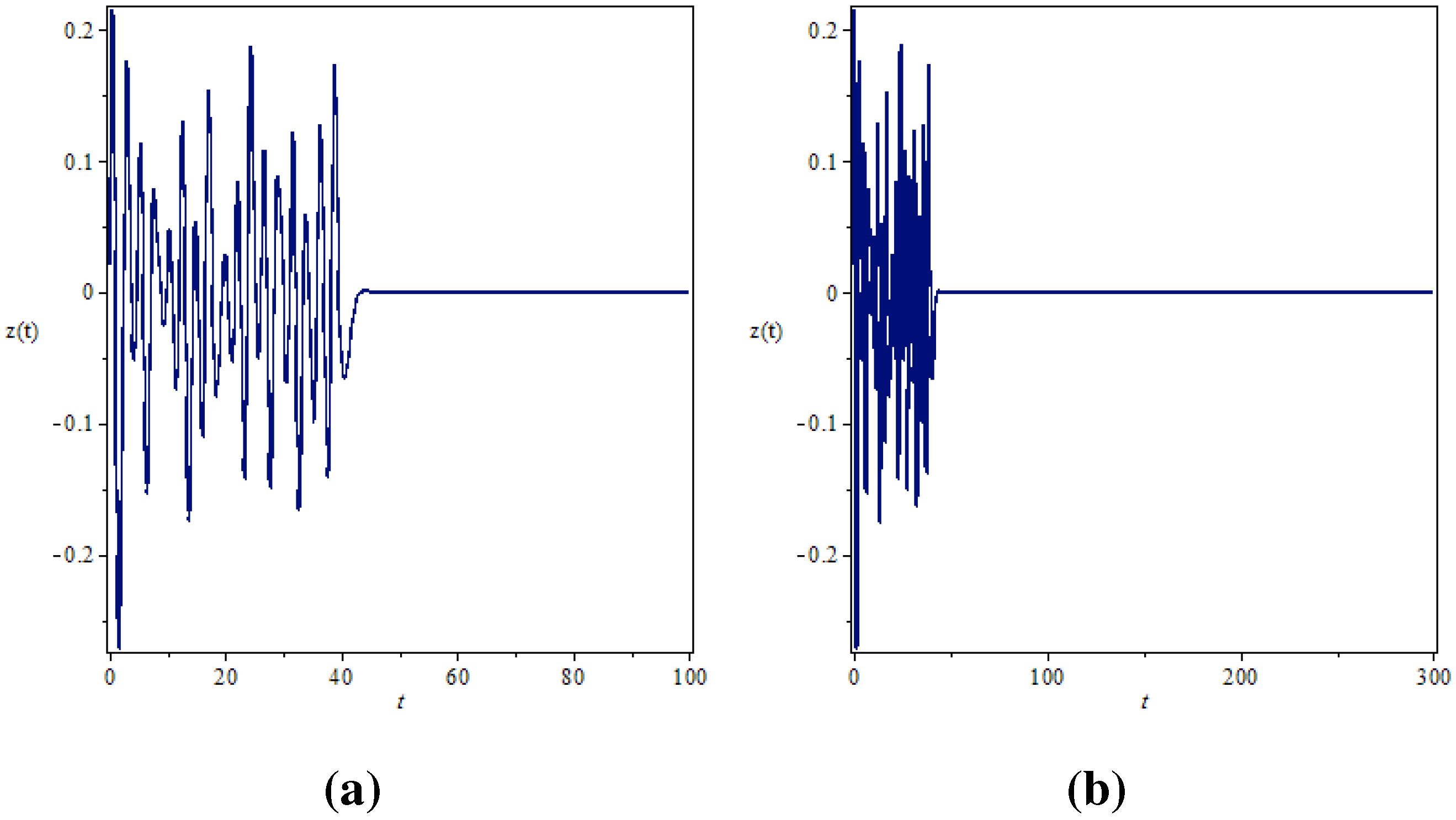
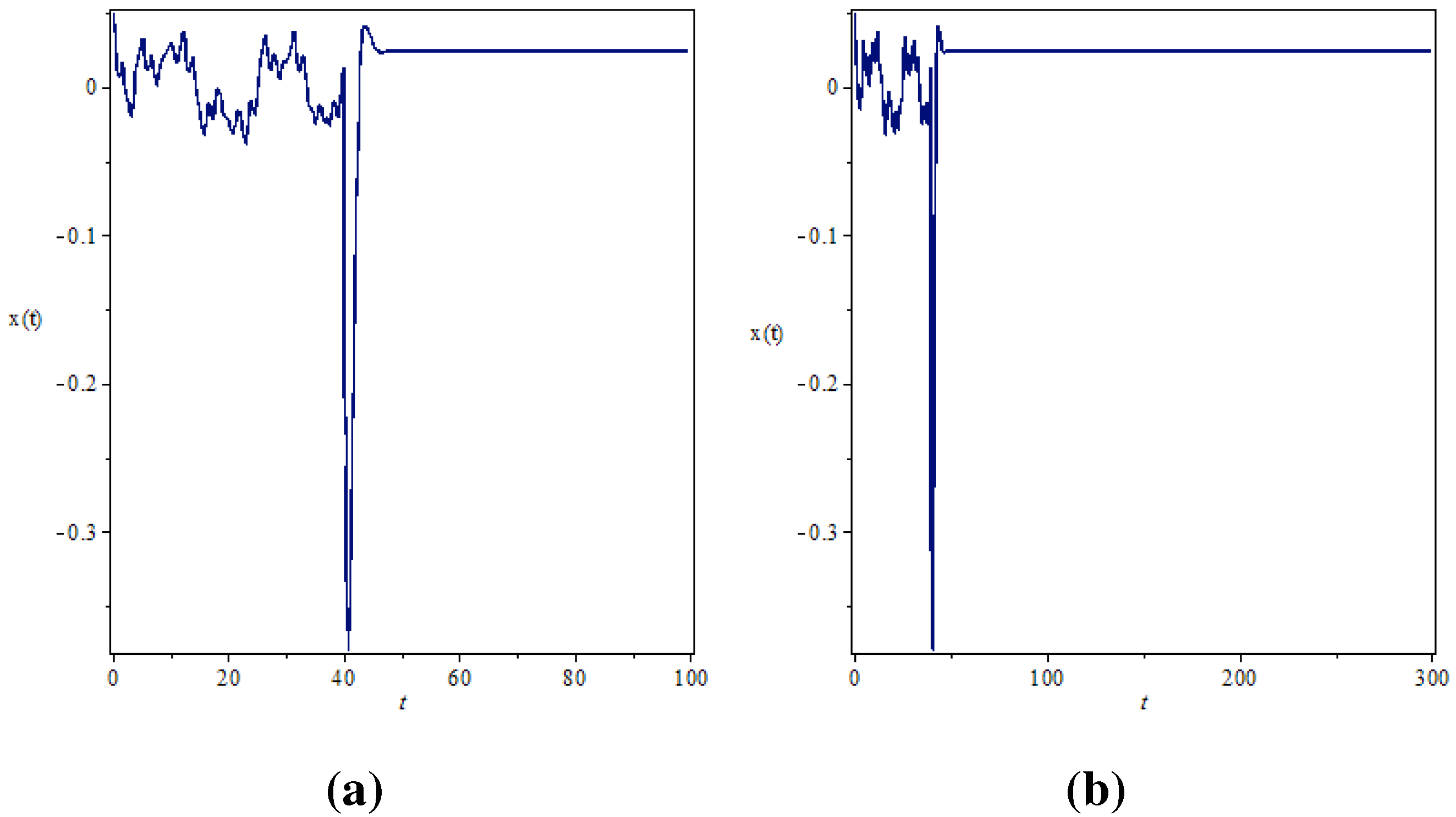
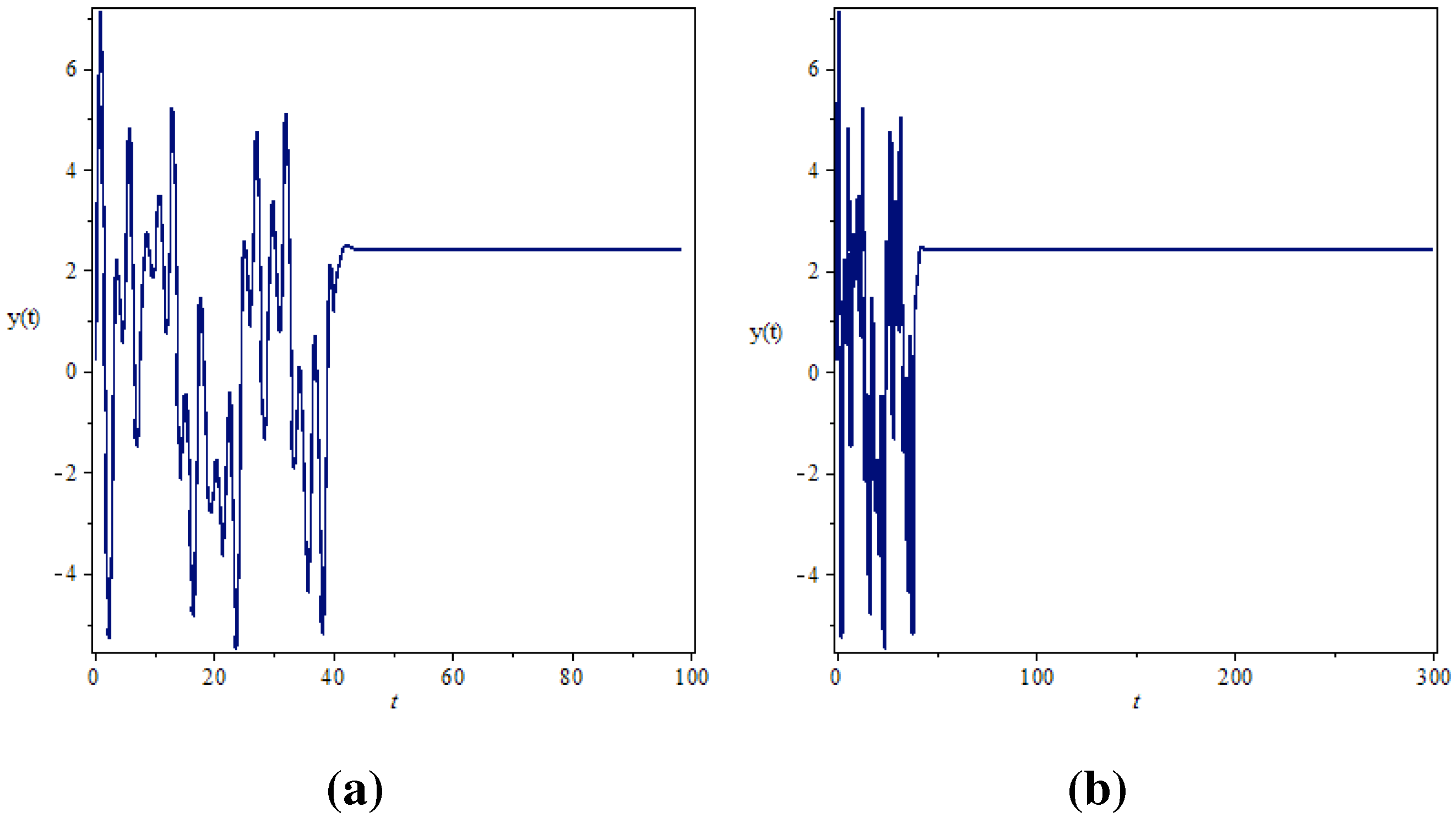
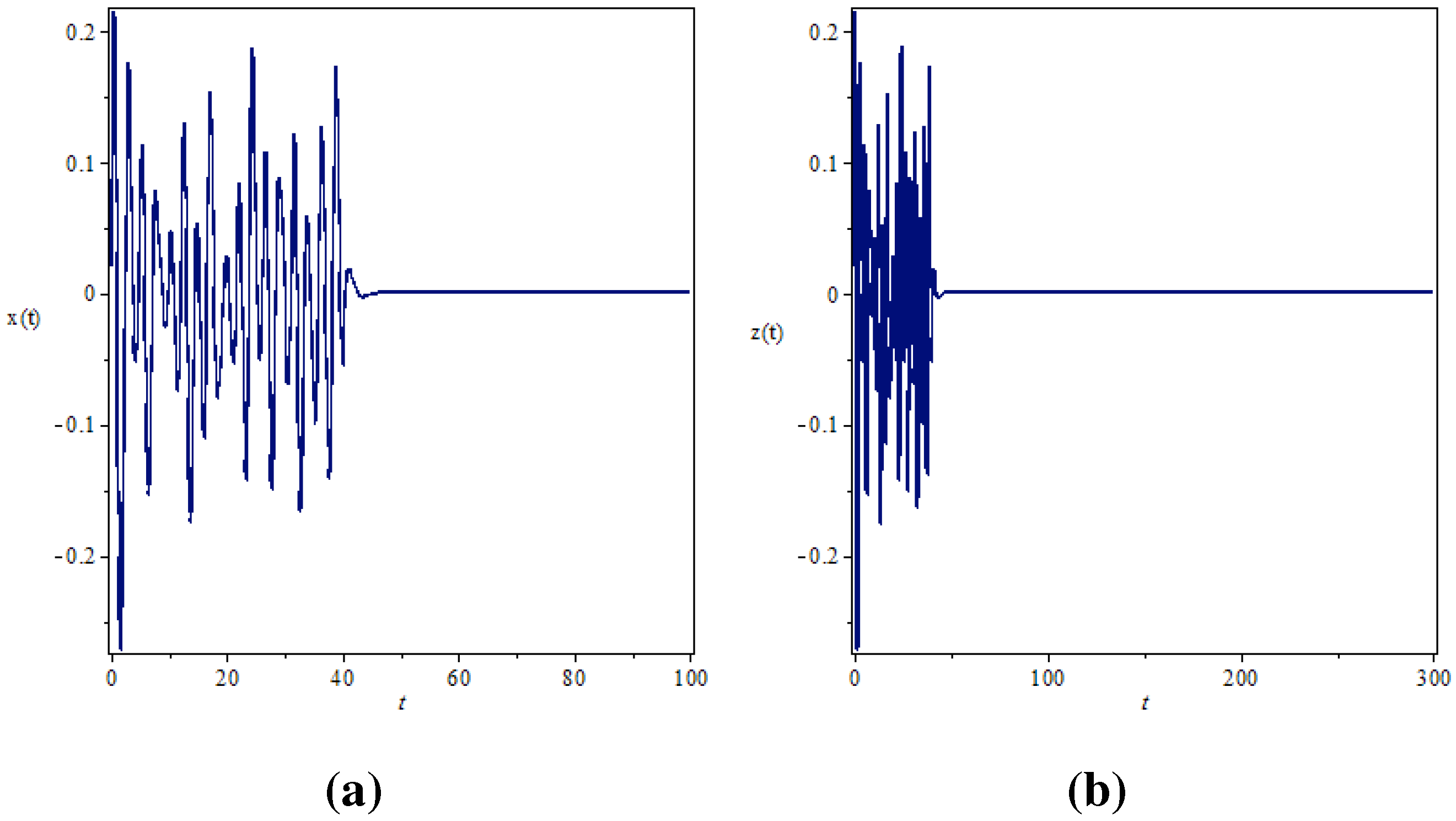
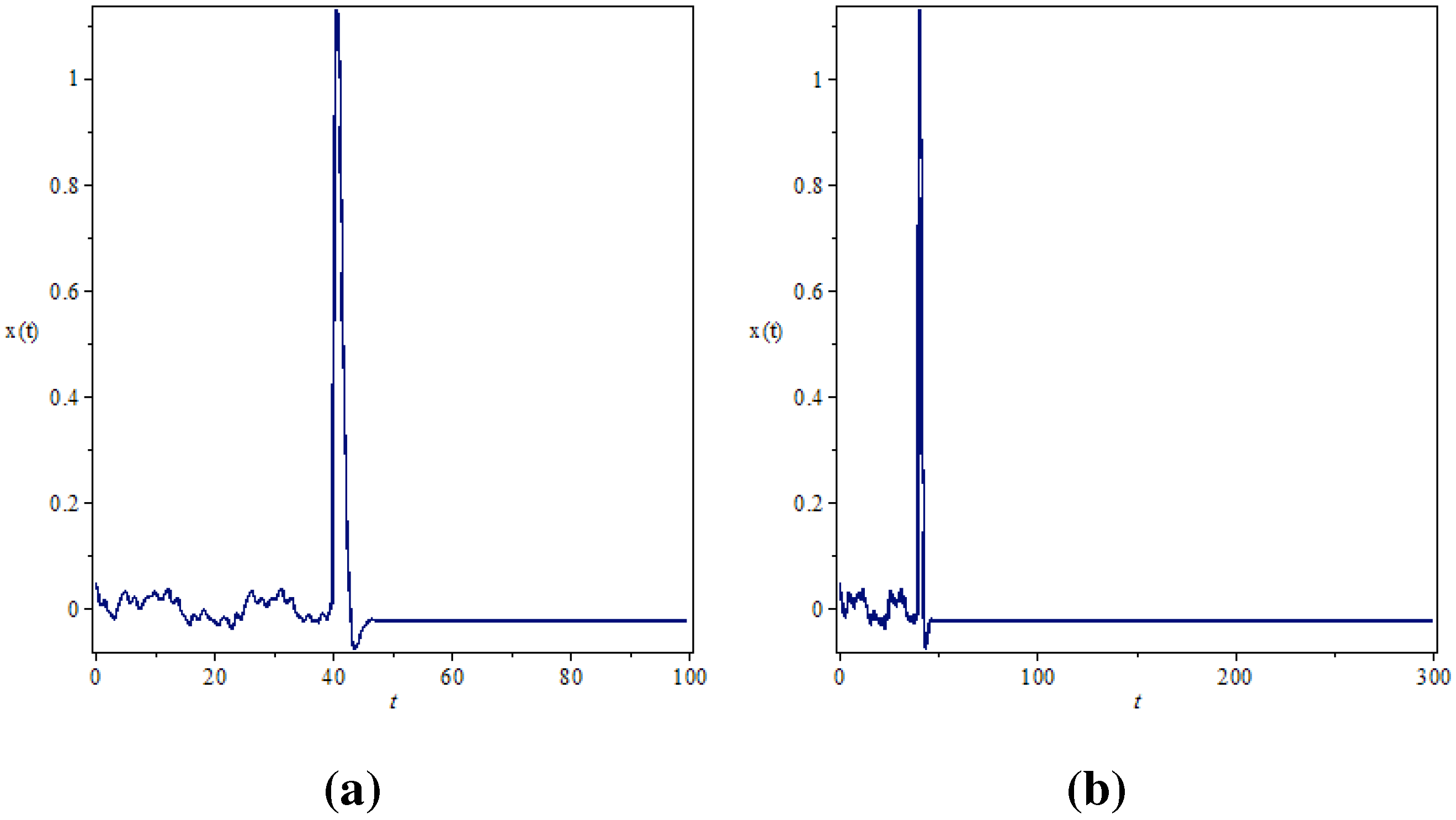

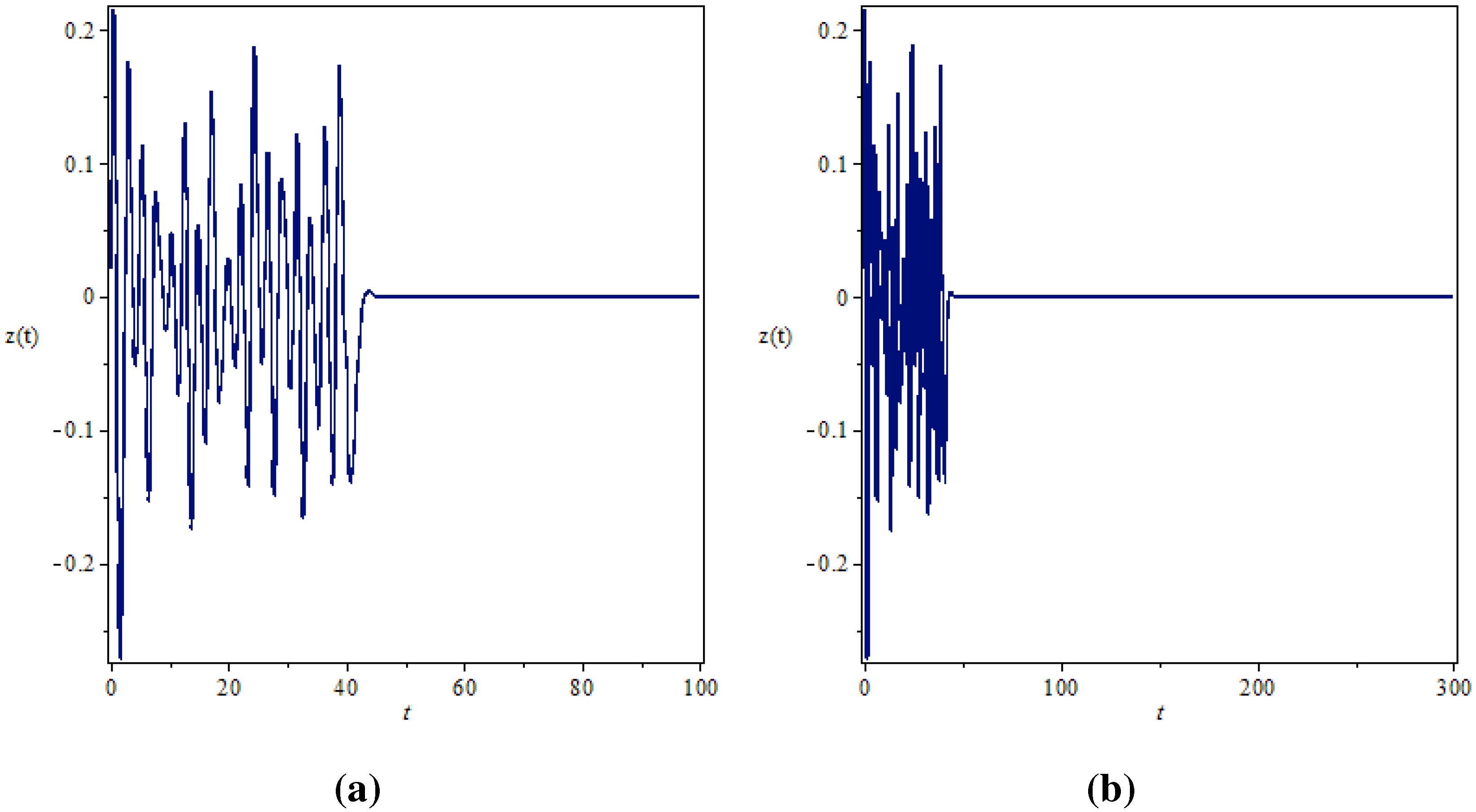
5. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Belgacem, F.B.M.; Baskonus, H.M.; Bulut, H. Variational Iteration Method for Hyperchaotic Nonlinear Fractional Differential Equations Systems. In Advances in Mathematics and Statistical Sciences, Proceedings of the 3rd International Conference on Mathematical, Computational and Statistical Sciences, (MCSS’15), Dubai, United Arab Emirates, 22–24 February 2015; pp. 445–453.
- Miller, K.S.; Rosso, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Nagy, A.M.; Sweilam, N.H. An efficient method for solving fractional Hodgkin–Huxley model. Phys. Lett. A 2014, 378, 1980–1984. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Nagy, A.M.; El-Sayed, A.A. Second kind shifted Chebyshev polynomials for solving space fractional order diffusion equation. Chaos Solitons Fractals 2015, 73, 141–147. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Baleanu, D.; Guvenc, B.; Tenreiro-Machado, J.A. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Bulut, H.; Belgacem, F.B.M.; Baskonus, H.M. Some New Analytical Solutions for the Nonlinear Time-Fractional KdV-Burgers-Kuramoto Equation. In Advances in Mathematics and Statistical Sciences, Proceedings of the 3rd International Conference on Mathematical, Computational and Statistical Sciences, (MCSS’15), Dubai, United Arab Emirates, 22–24 February 2015; pp. 118–129.
- Caponetto, R.; Dongola, G.; Fortuna, L. Fractional Order Systems: Modeling and Control Application; World Scientific: Singapore, Singapore, 2010. [Google Scholar]
- Caponetto, R.; Fazzino, S. An application of Adomian Decomposition Method for analysis of fractional-order chaotic systems. Int. J. Bifurc. Chaos 2013, 23, 1–7. [Google Scholar] [CrossRef]
- Tavazoei, M.; Haeri, M. A necessary condition for double scroll attractor existence in fractional-order systems. Phys. Lett. A 2007, 367, 102–113. [Google Scholar] [CrossRef]
- Wang, S.; Yu, Y. Application of Multistage Homotopy-perturbation Method for the Solutions of theChaotic Fractional Order Systems. Int. J. Nonlinear Sci. 2012, 13, 3–14. [Google Scholar]
- Zaslavsky, G. Hamiltonian Chaos and Fractional Dynamics; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: Mathematics in Science and Engineering; Academic Press: Waltham, MA, USA, 1999. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. J. R. Astral. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of IMACS Multiconference on Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996; pp. 963–968.
- Diethelm, K.; Ford, N.; Freed, A.; Luchko, A. Algorithms for the fractional calculus: A selection of numerical method. Comput. Methods Appl. Mech. Eng. 2005, 94, 743–773. [Google Scholar] [CrossRef]
- Volos, C.K.; Ioannis, M.K.; Ioannis, N.S. Synchronization Phenomena in Coupled Nonlinear Systems Applied in Economic Cycles. WSEAS Trans. Syst. 2012, 11, 681–690. [Google Scholar]
- Hammouch, Z.; Mekkaoui, T. Control of a new chaotic fractional-order system using Mittag-Leffler stability. Nonlinear Stud. 2015. to appear. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baskonus, H.M.; Mekkaoui, T.; Hammouch, Z.; Bulut, H. Active Control of a Chaotic Fractional Order Economic System. Entropy 2015, 17, 5771-5783. https://doi.org/10.3390/e17085771
Baskonus HM, Mekkaoui T, Hammouch Z, Bulut H. Active Control of a Chaotic Fractional Order Economic System. Entropy. 2015; 17(8):5771-5783. https://doi.org/10.3390/e17085771
Chicago/Turabian StyleBaskonus, Haci Mehmet, Toufik Mekkaoui, Zakia Hammouch, and Hasan Bulut. 2015. "Active Control of a Chaotic Fractional Order Economic System" Entropy 17, no. 8: 5771-5783. https://doi.org/10.3390/e17085771
APA StyleBaskonus, H. M., Mekkaoui, T., Hammouch, Z., & Bulut, H. (2015). Active Control of a Chaotic Fractional Order Economic System. Entropy, 17(8), 5771-5783. https://doi.org/10.3390/e17085771







