Experimental Assessment of a 2-D Entropy-Based Model for Velocity Distribution in Open Channel Flow
Abstract
:1. Introduction
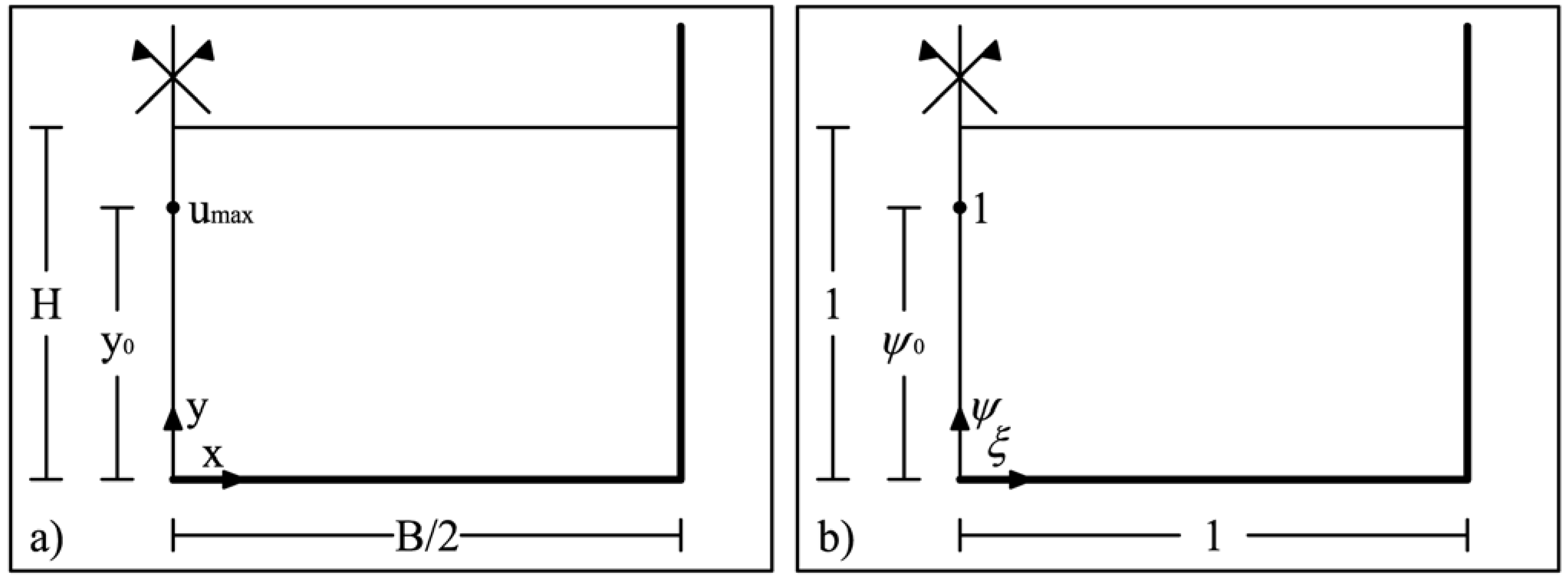
2. 2D Velocity Distribution Model
2.1. Velocity Function Definition in 2D Domain
2.2. Entropic Parameter G
2.3. CDF for Symmetrical Rectangular Domain
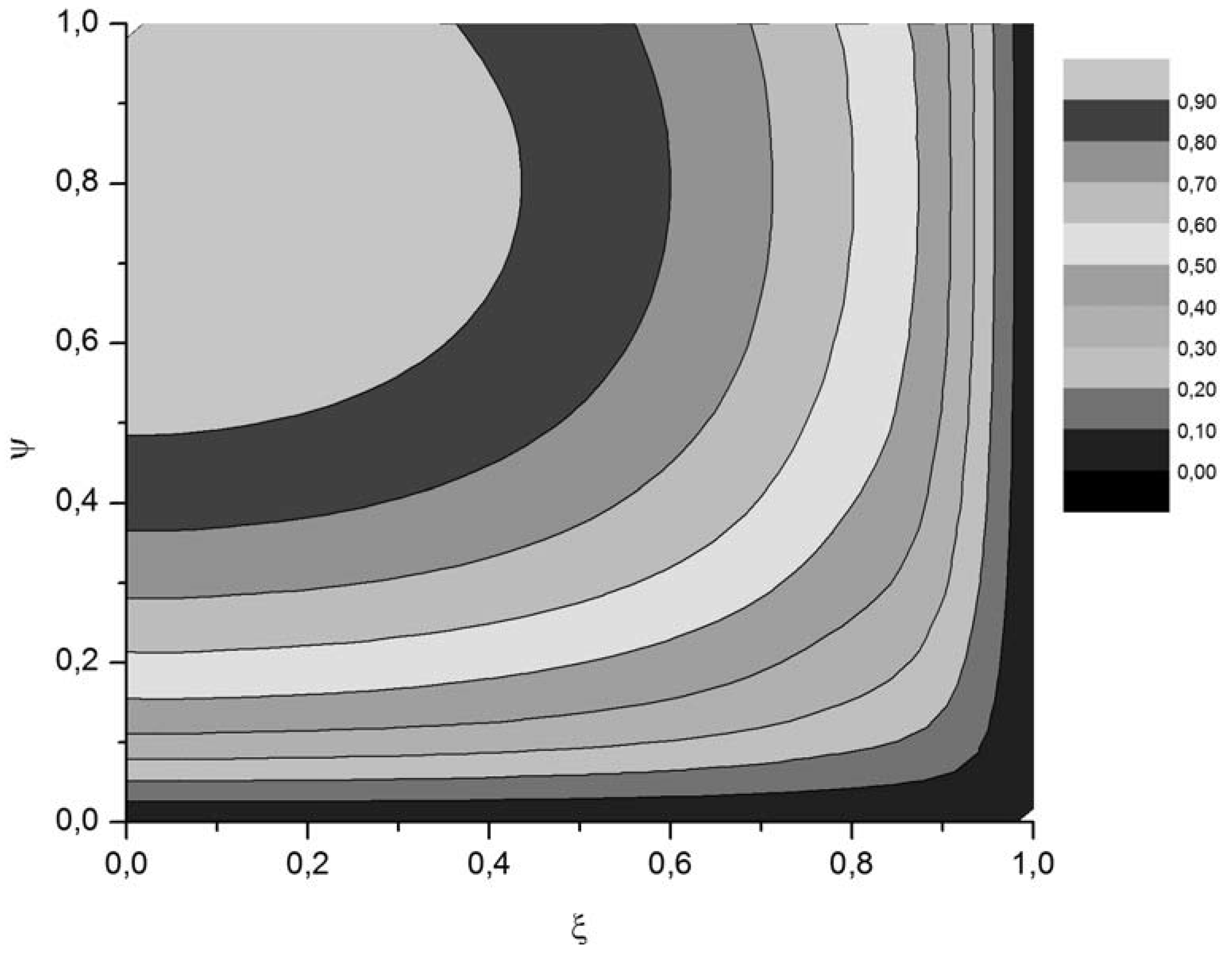
3. Model Validation by Experimental Measurements and Comparison with Chiu’s 2D Distribution

| n° | Number | c | H | Q | uav | umax | G | c22d | c2Chiu | E2D | EChiu | ia2D | iaChiu | d2D | dChiu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| of Data | [cm] | [l/s] | [m/s] | [m/s] | [%] | [%] | [%] | [%] | [%] | [%] | [%] | [%] | |||
| 1 | 54 | 0 | 13.2 | 30.6 | 0.638 | 0.579 | 4.75 | 82.9 | 49.4 | 70.9 | −190.7 | 94.1 | 67.7 | 2.9 | 8.3 |
| 2 | 60 | 0 | 9.4 | 21.6 | 0.647 | 0.574 | 5.25 | 38.7 | 58.8 | −60.7 | −95.1 | 73.2 | 75.6 | 6.3 | 6.9 |
| 3 | 100 | 0 | 9.0 | 19.4 | 0.629 | 0.538 | 4.68 | 52.8 | 62.9 | −56.4 | 1.0 | 77.0 | 84.0 | 6.7 | 5.0 |
| 4 | 70 | 0 | 9.2 | 17.0 | 0.524 | 0.463 | 3.22 | 56.0 | 57.0 | 18.5 | −12.8 | 83.9 | 81.5 | 6.0 | 6.4 |
| 5 | 56 | 0 | 9.3 | 20.2 | 0.598 | 0.543 | 2.10 | 73.8 | 63.8 | −95.0 | −80.0 | 77.4 | 77.4 | 6.9 | 5.9 |
| 6 | 28 | 0 | 5.4 | 20.4 | 1.079 | 0.946 | 5.21 | 93.4 | 91.7 | 84.0 | 83.7 | 95.2 | 95.2 | 2.8 | 2.9 |
| 7 | 35 | 0 | 6.0 | 25.9 | 1.219 | 1.078 | 3.53 | 84.3 | 79.4 | 76.1 | 68.7 | 94.2 | 93.4 | 3.0 | 3.4 |
| 8 | 35 | 0 | 6.5 | 30.9 | 1.423 | 1.188 | 1.61 | 67.7 | 52.6 | 32.7 | −29.2 | 85.8 | 73.2 | 6.7 | 8.9 |
| 9 | 35 | 0 | 5.5 | 26.1 | 1.383 | 1.186 | 2.21 | 61.5 | 56.5 | 20.7 | 1.1 | 83.4 | 79.0 | 6.0 | 6.8 |
| 10 | 28 | 0 | 5.1 | 26.5 | 1.497 | 1.299 | 2.89 | 65.0 | 61.5 | 23.7 | 16.3 | 83.3 | 81.7 | 5.6 | 5.8 |
| 11 | 49 | 1 | 8.2 | 20.2 | 0.715 | 0.615 | 3.75 | 81.3 | 86.6 | 76.8 | 80.2 | 91.5 | 92.8 | 5.1 | 4.3 |
| 12 | 49 | 1 | 8.0 | 20.7 | 0.773 | 0.647 | 2.23 | 90.3 | 89.4 | 89.5 | 75.4 | 97.2 | 92.8 | 3.1 | 4.7 |
| 13 | 49 | 1 | 10.2 | 24.9 | 0.687 | 0.610 | 3.58 | 90.0 | 76.7 | 88.8 | 63.0 | 97.1 | 92.3 | 2.3 | 4.1 |
| 14 | 49 | 1 | 9.6 | 28.6 | 0.878 | 0.745 | 3.01 | 90.4 | 85.0 | 87.2 | 74.0 | 97.1 | 94.0 | 2.9 | 4.0 |
| 15 | 56 | 1 | 9.2 | 26.1 | 0.768 | 0.710 | 3.89 | 84.4 | 35.5 | 79.6 | −50.3 | 93.1 | 69.8 | 3.3 | 8.9 |
| 16 | 56 | 1 | 11.3 | 35.7 | 0.914 | 0.789 | 3.21 | 87.0 | 70.5 | 86.9 | 64.0 | 96.5 | 90.4 | 3.5 | 5.1 |
| 17 | 42 | 1 | 8.5 | 26.7 | 0.949 | 0.785 | 3.79 | 82.8 | 83.4 | 80.8 | −19.9 | 95.2 | 82.8 | 4.6 | 10.6 |
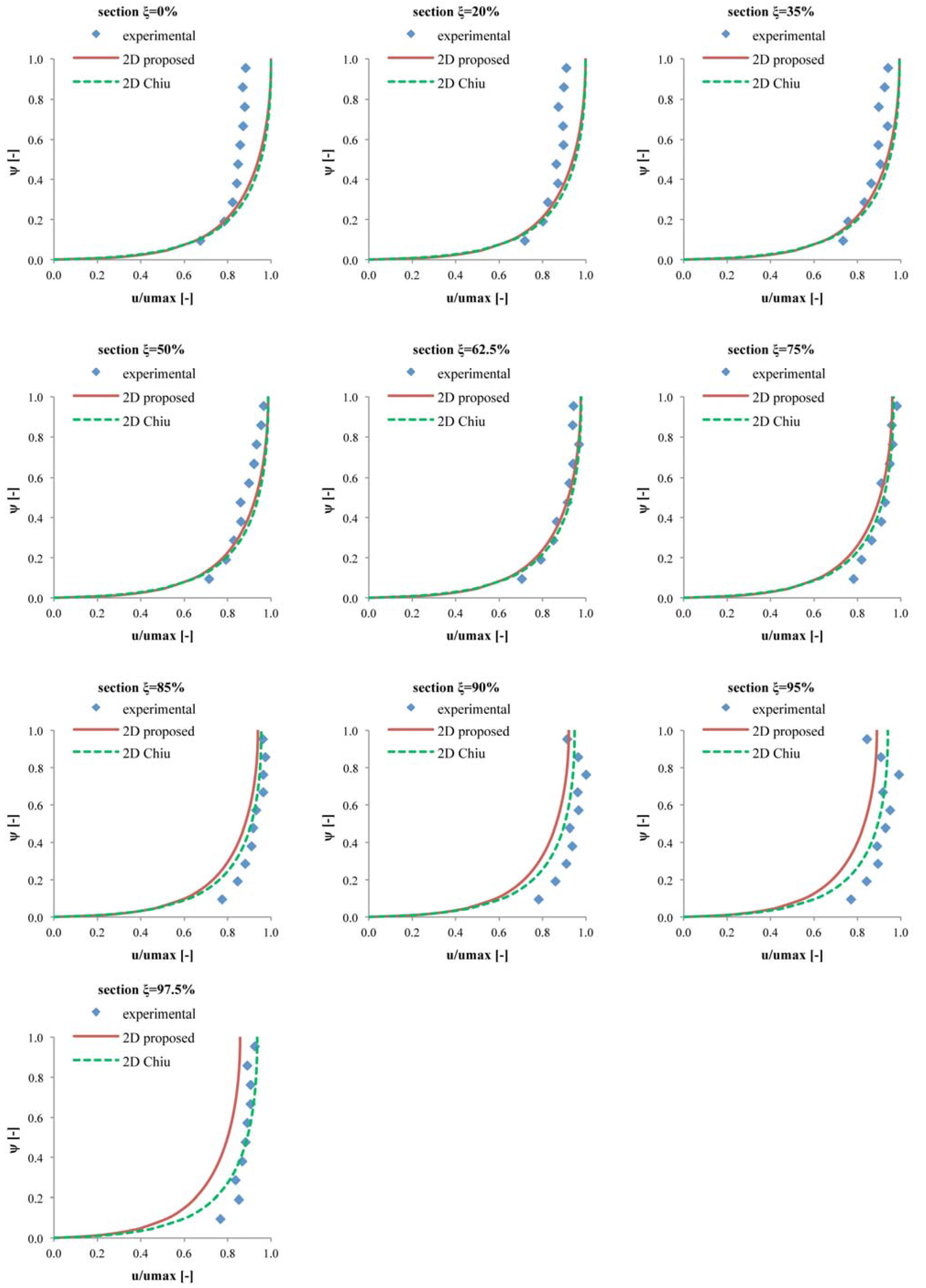
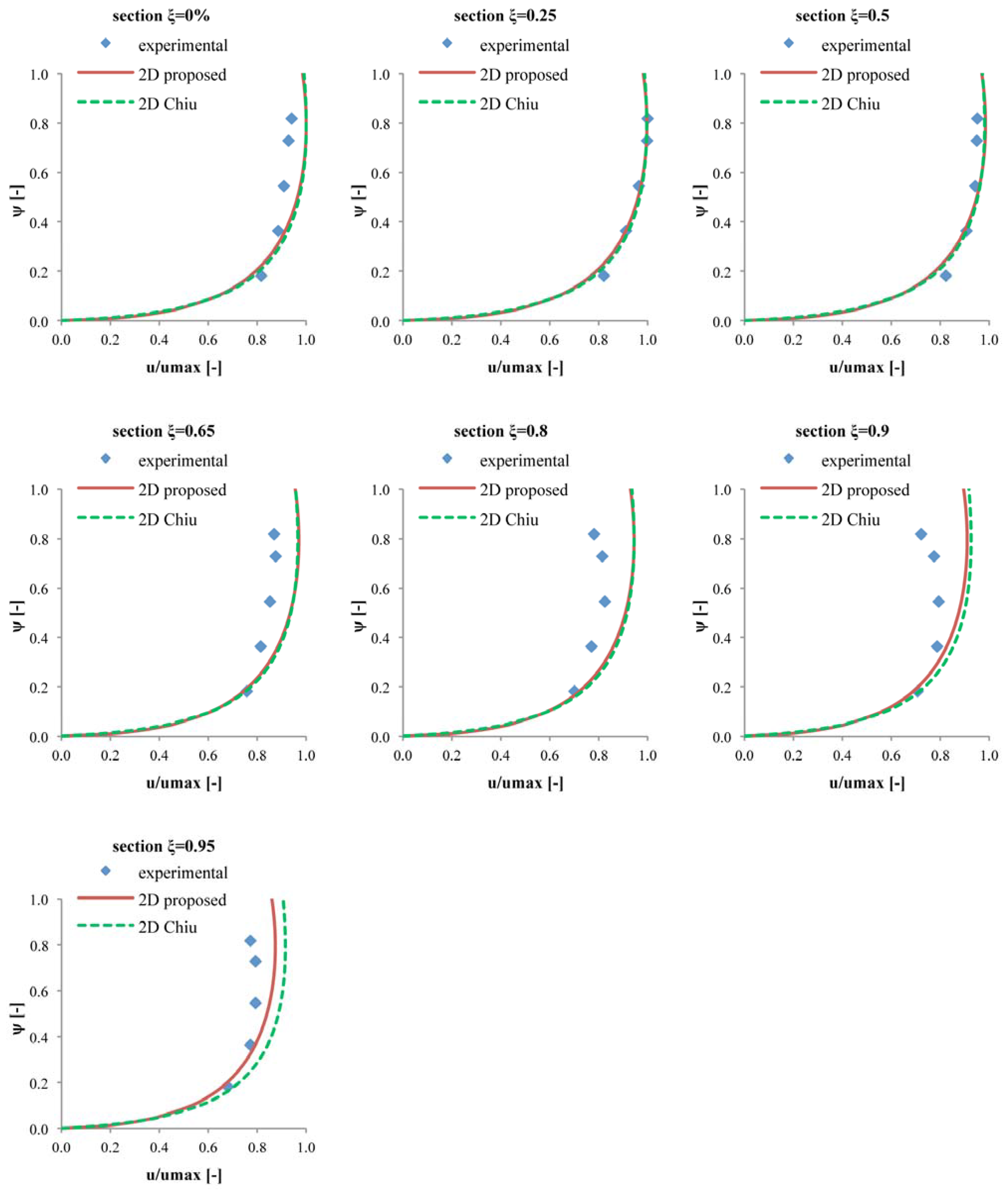
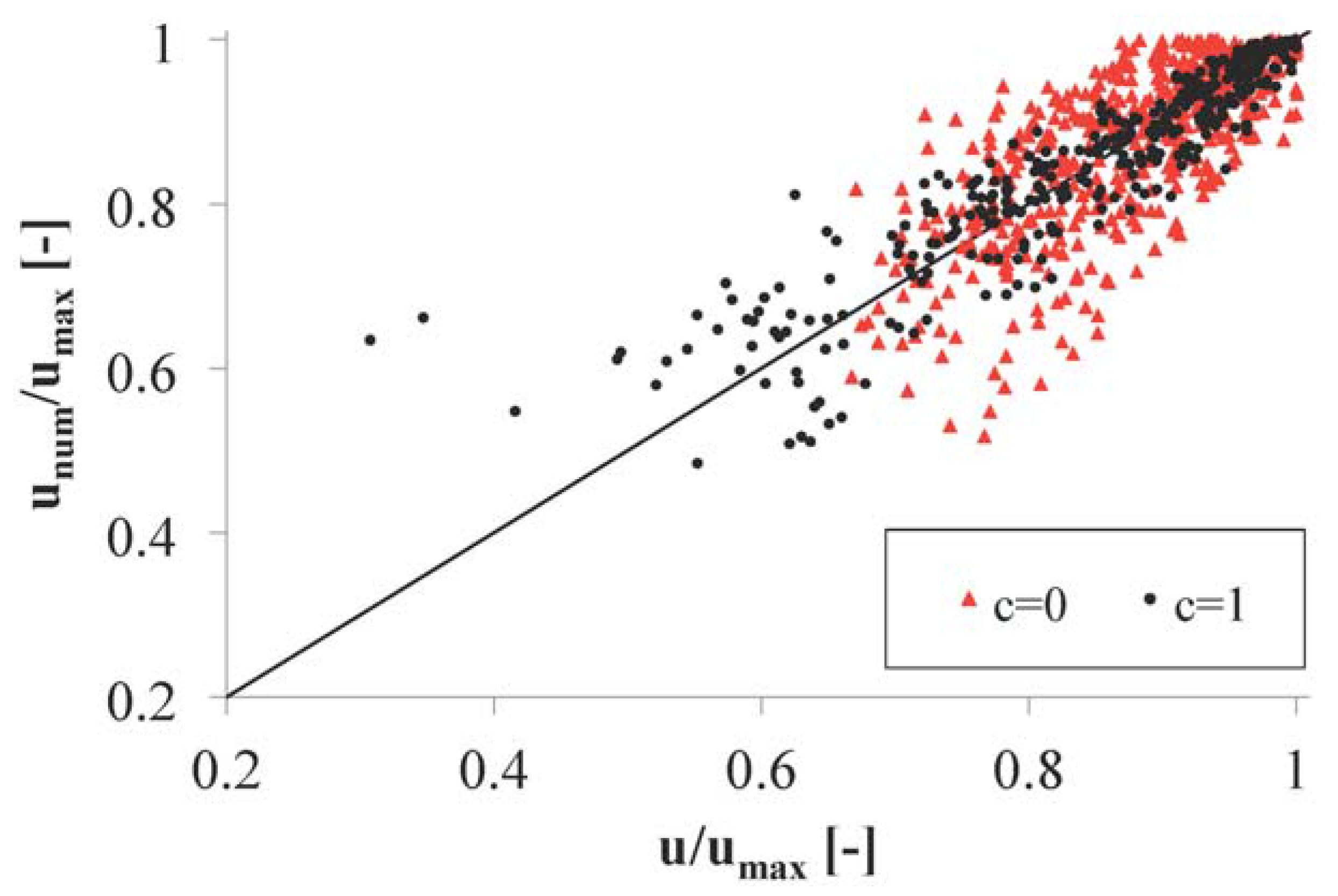
4. Conclusions
Acknowledgement
References
- Singh, V.P. Entropy Theory and Its Applications in Environmental and Water Engineering; John Wiley: New York, 2013; p. 662. [Google Scholar]
- De Martino, G.; Fontana, N.; Marini, G.; Singh, V.P. Variability and trend in seasonal precipitation in the continental United States. J. Hydrol. Eng. 2013. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraulic Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27(7), 379–423, 27(10), 623–656. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Chiu, C.L. Velocity distribution in open channel flow. J. Hydraulic Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Barbé, D.E.; Cruise, J.F.; Singh, V.P. Derivation of a velocity distribution using the principle of maximum entropy. J. Hydraulic Eng. 1991, 117, 1389–1396. [Google Scholar] [CrossRef]
- Chiu, C.L.; Said, C.A. Maximum and mean velocities and entropy in open-channel flow. J. Hydraulic Eng. 1995, 121, 26–35. [Google Scholar] [CrossRef]
- Kirkgoz, M.S.; Akoz, M.S.; Oner, A.A. Numerical modeling of flow over a chute spillway. J. Hydraulic Res. 2009, 47, 790–797. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channel. J. Hydraulic Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C.L.; Hsu, S.H. Probabilistic approach to modeling of velocity distributions in fluid flows. J. Hydrol. 2006, 316, 28–42. [Google Scholar] [CrossRef]
- Singh, V.P.; Marini, G.; Fontana, N. Derivation of 2D power-law velocity distribution using entropy theory. Entropy 2013. submitted. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channels based on Chiu’s velocity distribution equation. J. Hydrologic Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Corato, G.; Melone, F.; Moramarco, T.; and Singh, V.P. Uncertainty analysis of flow velocity estimation by a simplified entropy model. Hydrol. Processes 2012. [Google Scholar] [CrossRef]
- Marini, G.; De Martino, G.; Fontana, N.; Fiorentino, M.; Singh, V.P. Entropy approach for 2D velocity distribution in open channel flow. J. Hydraulic Res. 2011, 49, 784–790. [Google Scholar] [CrossRef]
- Singh, V.P.; Yang, C.T.; Deng, Z.Q. Downstream hydraulic geometry relations 1: Theoretical development. Water Resour. Res. 2003, 39, 1–15. [Google Scholar] [CrossRef]
- Xia, R. Relation between mean and maximum velocities in a natural river. J. Hydraulic Eng. 1997, 123, 720–723. [Google Scholar] [CrossRef]
- Chiu, C.L.; Hsu, S.M.; Tung, N.C. Efficient methods of discharge measurements in rivers and streams based on the probability concept. Hydrol. Processes 2005, 19, 3935–3946. [Google Scholar] [CrossRef]
- Moramarco, T.; Singh, V.P. Formulation of the entropy parameter based on hydraulic and geometric characteristics of river cross sections. J. Hydrologic Eng. 2010, 15, 852–858. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Base, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fontana, N.; Marini, G.; Paola, F.D. Experimental Assessment of a 2-D Entropy-Based Model for Velocity Distribution in Open Channel Flow. Entropy 2013, 15, 988-998. https://doi.org/10.3390/e15030988
Fontana N, Marini G, Paola FD. Experimental Assessment of a 2-D Entropy-Based Model for Velocity Distribution in Open Channel Flow. Entropy. 2013; 15(3):988-998. https://doi.org/10.3390/e15030988
Chicago/Turabian StyleFontana, Nicola, Gustavo Marini, and Francesco De Paola. 2013. "Experimental Assessment of a 2-D Entropy-Based Model for Velocity Distribution in Open Channel Flow" Entropy 15, no. 3: 988-998. https://doi.org/10.3390/e15030988
APA StyleFontana, N., Marini, G., & Paola, F. D. (2013). Experimental Assessment of a 2-D Entropy-Based Model for Velocity Distribution in Open Channel Flow. Entropy, 15(3), 988-998. https://doi.org/10.3390/e15030988







