1. Introduction
According to Shannon’s sampling theorem, a signal
,
et al., a bandlimited signal (see
Section 2 for the exact definition) can be completely reconstructed in terms of samples, equidistantly spaced apart the real axis
. Likewise one can reconstruct the derivatives
or the Hilbert transform
and its derivative
just in terms of samples of
f. Almost immediate applications of these results are Boas-type formulae for arbitrary order derivatives of such signals as well as of their Hilbert transforms, used in numerical analysis for computation of those derivatives.
The essential aim is to extend these results to non-bandlimited signals, in fact to the largest class, denoted by below, for which the Fourier transform, the basic tool of this approach, can be employed effectively. Basic is the fact that by these extensions the exact reconstruction formulae have to be equipped with remainder (error) terms. The errors involved will be measured in terms of the distance of f from the space of bandlimited function, a concept just introduced by the authors for the extensions of basic relations for Bernstein spaces to larger function spaces.
To become familiar with the new approach, the classical Shannon sampling theorem for derivatives of
-signals, namely Theorem 3.1 below, can be extended to the larger space
by adding the remainder term
of (6) to the expansion for bandlimited signals (5). This remainder, the aliasing error, can be estimated (cf. (7)) by:
The integral on the right-hand side is the above mentioned distance of
from the space
. Its behaviour depends on the smoothness properties of
f, and was extensively studied in [
1]. If
f is bandlimited to
, then it vanishes, as to be expected. Otherwise, if
, the largest space to be considered in this context, then this distance tends to zero for
. Furthermore, if one restricts the matter to certain subspaces of
, one can obtain refined estimates, including unusually sharp rates of approximation; see Corollaries 3.5–3.7. In particular, if
f belongs to a Lipschitz or Sobolev space, then
decays like a negative power of
σ, and if
f belongs to a Hardy space, then it decays exponentially.
Similarly, to the sampling reconstruction for the derivatives of the Hilbert transform of -signals, thus for , namely (12), the remainder term of (14), must be added in order to obtain its extension (13) to . The remainder can be estimated in the same way as above.
The paper’s chief point is to generalize the Boas formula for the first derivative, namely (16), to higher order ones, odd order given by (25), even orders by (26). Thus, e.g., the derivative is expressed in terms of the signal values , which depend however on . The proof is unusually simple, one just sets and in Theorem 3.1 and applies the resulting formula to the function .
For the first major result, Theorem 5.1, the extension of (25) to the larger class , formula (25) has to be equipped with the aliasing error term of (38), which can be estimated in the same fashion as the error above, which again tends to zero for .
A basic inequality in the theory of functions of exponential type is Bernstein’s inequality for the derivatives
for bandlimited
f in the finite energy norm or in
,
. This result is generalized in
Section 6 to non-bandlimited signals, the aliasing error being (52) in the case of odd order derivatives and (53) for even ones.
The active field of Landau–Kolmogorov inequalities in our situation is handled in
Section 7. Finally, Boas-type formulae for the Hilbert transform are left to
Section 8.
2. Notation and Preliminary Results
As usual, is the space of all real or complex-valued function f that are Lebesgue integrable to the pth power over the real axis , endowed with the norm , , and is the space of all measurable essentially bounded functions f with the norm . By we denote the class of all functions that are uniformly continuous and bounded on , where .
The Fourier transform
of
,
, is defined by:
where
. If
,
, is such that
, then there holds the Fourier inversion formula:
at each point
where
f is continuous; see [
2, Proposition 5.1.10, 5.2.16].
For
and
, let
the
Bernstein space comprising all entire functions (thus arbitrary often differentiable) of exponential type
σ, (
i.e.,
for
, which belong to
when restricted to the real axis
. There holds:
According to the Paley–Wiener theorem (cf. [
3, p. 103]), a signal
f belongs to
;
, if and only if it is bandlimited to
,
i.e., its Fourier transform vanishes outside
. The same holds true for
, if the Fourier transform is understood in the distributional sense. Note that a bandlimited signal cannot be simultaneously duration limited.
The sinc function is defined by:
where the
rectangle function is given by:
Moreover, there holds by the Fourier inversion formula (
1) (cf. [
2, Section 5.2.4]):
2.1. A Hierarchy of Spaces Extending Bernstein Spaces
In order to extend the Bernstein space
to larger function spaces, we weaken the property of
f being bandlimited,
vanishes outside the compact interval
, to
belonging to
. This still guarantees the reconstructibility of
f from its Fourier transform in terms of the inversion formula (
1). To this end, we introduce the
Fourier inversion classes:
For
, there holds
. In addition to (
1) one has for
that the derivative
exists, belongs to
and has the representation:
see [
2, Proposition 5.1.17 with
replaced by
].
The Fourier inversion classes are in some sense the most general spaces in which our studies can be performed. Spaces between and are also of interest since they will yield smaller errors in the extended formulae.
The modulus of smoothness of
of order
is defined by:
and the associated Lipschitz class for
by:
The Sobolev space is given by:
and Hardy spaces for horizontal strips
,
, by:
There hold the inclusions:
Here we recall some facts concerning the distance functional introduced in [
1]. Let
G be the vector space of all functions
having the representation:
for some
. We define the
distance of two functions having representation (4) with
, respectively, by:
and the
distance of a functions from the Bernstein space by:
If
,
, then the derivative
belongs to
G with
. Hence one has for
with
,
,
Moreover, one has for
,
,
Observe that for and one has in view of the isometry of the Fourier transform that , i.e., is the Euclidean distance.
The following estimates for the distance
can be found in [
1]. In each of the subsequent statements,
c and
γ with attached indices denote positive numbers that depend only on the indices but not on
f and
σ. They may be different at each occurrence.
Proposition 2.1. (a) Let with , , and . One has the derivative free estimate:If also , , then:If , , , then:(b) If and , , , then for each ,the latter holding provided , . Proposition 2.2. Let . Then, for , , and , Proposition 2.3. Let . Then, for , , 3. Extensions of Shannon’s Theorem to Non-Bandlimited Signals and Their Hilbert Transforms; Aliasing Errors
Let us consider the well-known Whittaker–Kotel’nikov–Shannon sampling theorem for reconstructing a bandlimited signal and its derivatives in terms of samples of just
f, namely ((see e.g., [
4,
5], [
6, p. 13], [
7, p. 59]).
Theorem 3.1. Let , then, for each ,the series converging absolutely and uniformly for as well as in -norm. This theorem can be extended to the larger space
by adding a remainder or error term
, to the expansion (
5). This leads to the following extended version of Theorem 3.1.
Theorem 3.2. Let for some , and let be the 2π-periodic signal, defined for by:Then one has the approximate sampling representation:with the remainder given by:In particular, there holds: The remainder
is the so-called aliasing error occurring when a non-bandlimited signal is reconstructed in terms of the sampling theorem; see e.g., [
8].
The case
can be found already in [
9] (see also [
5,
7,
10]), [
6, p. 15 ff]), where the remainder (6) was given in the equivalent form:
Theorem 3.2 for arbitrary
is contained in [
11], where it was deduced as a particular case of a unified approach to various sampling representations. This general approach also covers the following two results on the reconstruction of the Hilbert transform
and its derivatives in terms of samples of f; see [
5,
11].
The Hilbert transform or conjugate function of
, defined by the Cauchy principal value:
plays an important role in electrical engineering (see [
12, p. 267 ff.], [
13]). For the Hilbert transform, also often called “one of the most important operators in analysis”, one may consult [
2, Chap. 8, 9], [
14,
15]. It defines a bounded linear operator from
into itself, and one has:
Furthermore, if
for some
, then by the Fourier inversion formula Equation (
1) for each
,
the latter equality holding provided
. This formula also shows that
; thus derivation and taking Hilbert transform are commutative operations.
Noting (
2) and (8), we see that the Fourier transform of the Hilbert transform of the sinc-function is given by:
and one easily obtains from the case
in (9) that the Hilbert transform of the sinc-function is given by:
Moreover, one has the representation:
Since the Hilbert transform is a bounded linear operator from
into itself, which commutes with differentiation, the following sampling representation follows immediately from (
5) by taking the Hilbert transform of each side.
Theorem 3.3. Let , where . Then, for each ,the series converging absolutely and uniformly for as well as in -norm. This formula enables one to compute
in term of samples of f itself; for the case
see [
5,
6,
7,
16], and for arbitrary s see [
11]. The extended version of this result reads (see [
11]):
Theorem 3.4. Let for some , and let be the 2
t by:Then one has the approximate sampling representation:with the remainder given by:In particular, there holds: The integral on the right-hand side of (7) and (15) is the distance of
from the space
. Its behaviour for
depends on the smoothness properties of f, and was extensively studied in [
1]; recall
Section 2.1. This leads to the following estimates for the remainders
and
.
Corollary 3.5. If , , then for any and ,In particular, if in addition for , then: Corollary 3.6. Let , for some . Then: for ,If moreover , , then Corollary 3.7. If , then for , positive , and , The three corollaries remain true, if is replaced by .
4. Boas-type Formulae for Higher Derivatives
In [
17] (see also [
3]) Boas established a differentiation formula that may be presented as follows.
Let , where . Then, for , we have: When
f is a trigonometric polynomial of degree
n,
i.e.,
, then
and so (16) applies. In this case, by virtue of the periodicity of f, the series in (16) can be condensed to a finite sum. The resulting formula was obtained by M. Riesz in 1914 [
18]. In fact, Riesz’s interpolation formula for trigonometric polynomials reads:
where
and
for
. Since
, (17) implies the classical Bernstein inequality:
Analogously to the proof of (18), Boas’ formula (16), also known as
generalized Riesz interpolation formula (as Isaac Pesenson informed us), can be used to prove the basic Bernstein inequality for functions
, namely
,
, which will be treated extensively in
Section 6.
There exist families of differentiation formulae for higher derivatives holding in Bernstein spaces; see [
6, § 3.2]. Which of them should we consider as a generalization of Boas’ formula? In the applications of (16) the following properties are crucial:
- (a)
The formula applies to all entire functions of exponential type σ that are only bounded on .
- (b)
The sample points are uniformly spaced according to the Nyquist rate and are located relatively to the argument t of the derivative.
- (c)
The coefficients do not depend on t.
- (d)
The coefficients decay like as .
- (e)
When the sample points are arranged in increasing order, then the associated coefficients have alternating signs.
In the case of higher derivatives, a Boas-type formula should also have the properties (a) to (e).
The Boas-type formulae to be established will be deduced as applications of the Whittaker–Kotel’nikov–Shannon sampling theorem for higher order derivatives (Theorem 3.1). Another approach by contour integration methods of complex function theory will be presented in
Section 4.1.
In view of Leibniz’s rule, the basic term
in (5) can be written as follows:
Expressing now
in terms of
and
, we can rewrite
in the more handy form:
where the right hand side is naturally thought to be continuously extended at
by:
This can be easily obtained from (3) or the power series expansion:
Further, it follows easily from (19) that:
In view of (3) there holds the Fourier expansion (cf. [
2, Proposition 4.1.5]):
and, in particular, for
and
,
As an application, we now come to two Boas-type formulae, one for derivatives of odd order and one for those of even order.
Theorem 4.1. Let for some , and define for ,Then there hold the representations: Proof. The identities (23) and (24) follow immediately from (19), noting that and .
For (25) and (26) we will give two proofs. The first one applies only to , which seems to be the more interesting case in engineering applications, whereas the second one also covers the larger space .
First assume that
,
i.e.,
. Setting
in (
5), then by the definition of
,
Now, if
for arbitrary
, then (25) follows by applying (27) to the function
, which belongs to
.
For even order derivatives, one obtains from (
5) for
and
,
The proof can now completed along the same lines as in the case of odd order derivatives.
In order to extend (25) and (26) to
, one may apply the
-result just proved to the function
,
, which belongs to
, and then let
. This density argument can be avoided by the following alternative proof. To this end, let
, and let
be defined by:
By Leibniz’s rule one has:
Since
, we can apply (5) to the terms on the right-hand side to obtain:
Now, we have to distinguish between odd and even order derivatives. Replacing s by
and setting
in (28), we obtain in view of (20),
Further, noting (22) and the definition of
, we end up with:
To complete the proof for odd order derivatives, let now
for arbitrary
and apply (29) to the function
, where
.
For even order derivatives one starts again with (28), replaces
s by
and sets
. In view of (21), (22) and (24), one then obtains:
Finally, apply this equation to the function
. ☐
Representation (25) can also be found in [
19, Corollary 5], where it was proved by contour integral methods.
For
, (25) is the classical Boas formula (16), and (26) reads:
The case
in (25) gives:
It is easily seen that formulae (25) and (26) both have the properties (a) to (d), but it is not immediately clear whether (e) holds. We need to know the signs of the numbers and . For this, we represent these numbers by an integral with an integrand that does not change sign.
Proposition 4.2. (a) For , the numbers of (23) have the representation:In particular,(b) For the numbers of (24) have the representation:In particular, Proof. First we note that the sum on the right-hand side of (23) is the Taylor polynomial of the cosine function of degree
with respect to the origin, evaluated at
. Next we recall Taylor’s formula for a function f with the remainder represented by an integral. It states that:
see, e.g., [20, p. 88, Theorem 6]. Applying this formula to
with
, we see that (23) may be rewritten as:
By a change of variables, we obtain:
Now an integration by parts, taking
as a primitive of
, yields:
for
. From this, (30) follows immediately.
Except for a set of measure zero, the integrand in (30) is positive on the interval of integration if the upper limit of the integral is positive, and is negative if that limit is negative. This shows that the integral in (30) is always positive. Hence (31) holds for , and in view of for as well.
Regarding (32), we note that the sum on the right-hand side of (24) is the Taylor polynomial of degree of the sine function evaluated at . Using again (34) and proceeding as in the proof of (a), we arrive at (32) and (33). ☐
Now (31) and (33) show that formulae (25) and (26) have also the property (e) and so they are Boas-type formulae in our sense.
One may ask, why we started with
in the proof of (25), and with
in the proof of (26). If one begins with
in the case of odd order derivatives, one would end up with formulae, the coefficients of which behave like
for
. Moreover, they are valid in
for
only, but not in
. Hence they are not Boas-type formulae in our sense. For
such a formula can be found in [
7, p. 60 (87)].
4.1. An Alternative Approach by Methods of Complex Analysis
Formulae (25) and (26) of Theorem 4.1 can also be derived by contour integration without employing the sampling theorem and without requiring a process that leads from to .
Denote by
the positively oriented rectangle with vertices at
For
, we first consider the meromorphic function:
It has a simple pole or a removable singularity at
for
, a pole of order at most
at zero and no other singularities. Noting that the sum is a truncated Taylor expansion of
around
, we conclude that:
By a well-known formula for the residue at a pole of order at most
, this implies that:
Furthermore, it is easily verified that:
with
given by (23).
Now, for
, it is readily seen that:
Hence by the residue theorem,
which implies (25) by a transformation of the argument of
f.
Analogously, one considers:
Here
is a pole of order at most
and,
which gives:
while,
with
given by (24). This time, for
, we find that:
which implies (26) by a transformation of the argument of
f.
4.2. Variants
If we abandon property (e) of a Boas-type formula and admit a correction at t by the value of f or that of its first derivative, we can improve upon property (d) by establishing formulae with coefficients that decay like as . Such formulae are of interest in numerical applications since the truncated series will need less terms for achieving certain accuracy.
The following formula (35) was already obtained in [19, Corollary 5] by methods of complex analysis; formula (36) is new.
Corollary 4.3. Let for some and let . Then, in the notation of Theorem 4.1, Proof. Obviously the function
belongs to
and, as is seen by Taylor expansion around 0, we have
Thus applying (25) to
g at
, we obtain
For this formula holds with and yields
Thus,
which gives (35) by shifting the argument of
f.
Analogously, applying (26) to
g at
, we obtain:
For the sinc function, this formula holds with
and yields:
Thus,
which gives (36) by substituting the value of
and shifting the argument of
f. ☐
6. Extended Bernstein Inequalities for Higher Order Derivatives
We now come the matter sketched at the beginning of
Section 4. The well-known Bernstein inequality states:
For , , , there holds: The case
is usually proved with help of Boas’ formula (16), and the general case then by iteration; see [
3, Section 11.3]. Boas’ formulae for higher order derivatives enables us now to prove (48) directly for arbitrary
. Indeed, we have by (25),
The series on the right-hand side can be evaluated as follows. Since
, formula (25) applies to this function. For
it yields that:
where (31) has been used in the last step. Combining this equation with (49), we obtain (48). For derivatives of even order one uses (26) and proceeds analogously.
In this section we employ Theorems 5.1 and 5.2 to extend Bernstein’s inequality for higher derivatives to non-bandlimited functions by adding an “error term”. For this aim, properties (a)–(e) of a Boas-type formula, specified in
Section 4, will be crucial.
Theorem 6.1. Let , , , and suppose that belongs to as a function of v. Then, for any , we have:with defined by (38). Furthermore, Proof. Consider (37) as a function of t and apply
on both sides. Using the triangle inequality on the right-hand side and noting that
does not change under a shift of the argument of
f, we find that:
Inserting (50) for the series on the right-hand side, we obtain (51).
Next we observe that
is the Fourier transform of the function:
The hypotheses imply that
. Thus, using [
2, Prop. 5.2.6] and noting that this book uses the notation
, we conclude that:
where we have used that
. This completes the proof. ☐
By an analogous proof, we deduce from Theorem 5.2 the following result for derivatives of even order.
Theorem 6.2. Let , , , and suppose that belongs to as a function of v. Then, for any , we have:with defined by (45). Furthermore, It should be noted that for derivatives of odd order the bound in terms of the distance function is by a factor
bigger than the corresponding bound for derivatives of even order. However, when
, we can profit from the isometry of the Fourier transform and deduce the same bound in both cases. An obvious modification of the proof in [
1,Theorem 11] leads to the following result.
Theorem 6.3. Let , and suppose that as a function of v. Then, for any , we have 7. Landau–Kolmogorov Inequalities
In this section we consider the case where f belongs to a Sobolev space and deduce Landau–Kolmogorov inequalities, a very popular and still active field. The proof of the following proposition is essentially contained in that of [
1, Proposition 13].
Proposition 7.1. Let , where . Then for with , we haveandfor and , where Proposition 7.1 enables us to deduce from Theorems 6.1–6.3 the following corollaries.
Corollary 7.2. Let and , where . Then, for and any , we have: Corollary 7.3. Let and let , where . Then, for and any , we have Corollary 7.4. Let and let , where . Then, for any , we have: Note that for
Corollary 7.2 reduces to a result in [
1, Corollary 16].
The statements of Corollaries 7.2–7.4 can be interpreted as a linearized equivalent form of a Landau–Kolmogorov inequality [
21,
22]. The equivalence is shown by the following lemma in which
. A more specialized result was mentioned by Stečkin [
23]; also see [
21, pp. 5–6].
Lemma 7.5. Let and Then,for all if and only if,where, Proof. Suppose that (58) holds. Then we may minimize the right-hand side over σ by using standard calculus. This leads us to (59) with α and K given by Equation (60).
Conversely, suppose that (59) holds with
and
. Consider now the function:
Its Hessian shows that it is concave on
. Hence, at any point
the tangent plane of F lies above the graph of F, that is,
Setting
, we find by a straightforward calculation that:
Now, setting
and defining:
we find that:
This shows that:
with
C defined by (60). Since λ may take any value in
, the same is true for σ. Hence (59) implies (58). ☐
Lemma 7.5 can be used to deduce three Landau–Kolmogorov inequalities from (55)–(57). We may state them in a unified form as follows.
Corollary 7.6. Let and , where and For define:and,with given by (54). Then, Unfortunately, the constant in (61) is not the best possible. However, the discussion in [
24, pp. 442–447], does not extend to results for
. For
inequality (61) simplifies to:
Here the term in square brackets can be replaced by 1. For
and
, this is shown in [
25, § 7.9, No. 261]. For general
with
, we may use the isometry of the
-Fourier transform together with Hölder’s inequality and proceed as follows:
Now, employing Lemma 7.5, we may in turn improve upon Corollary 7.4. This way we obtain:
Corollary 7.7. Let and let , where . Then, for any , we have 9. Applications
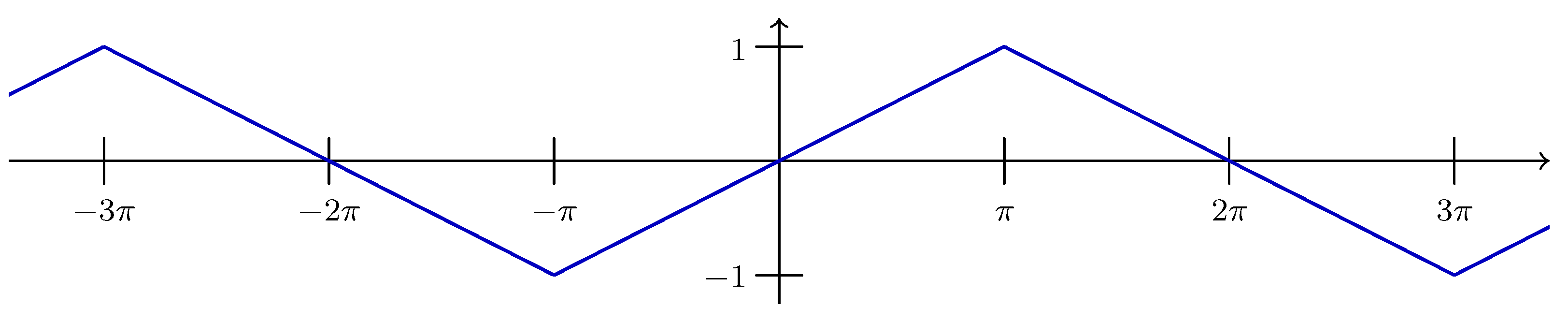
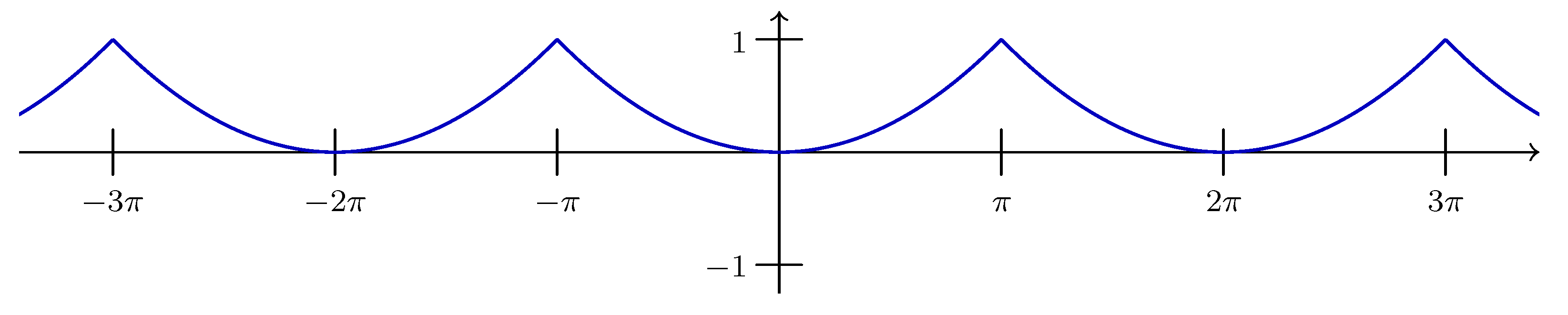
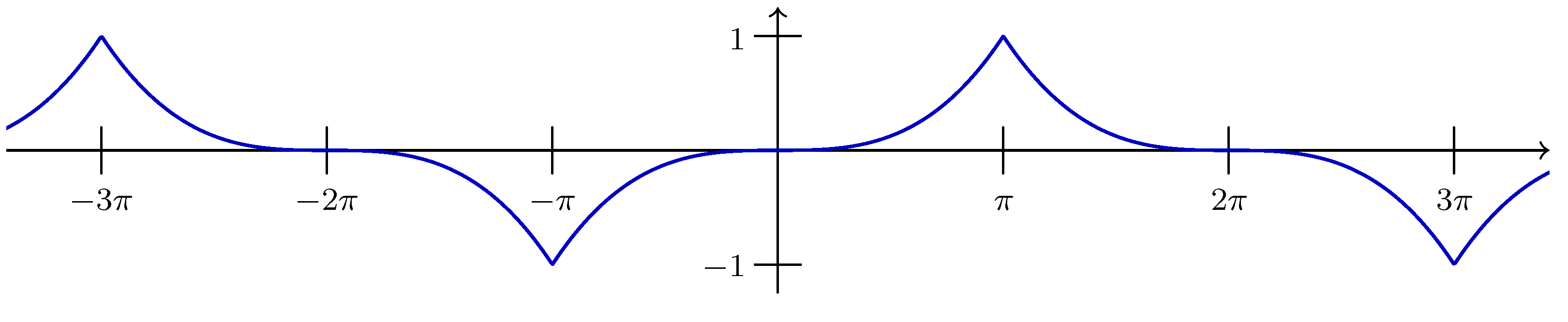
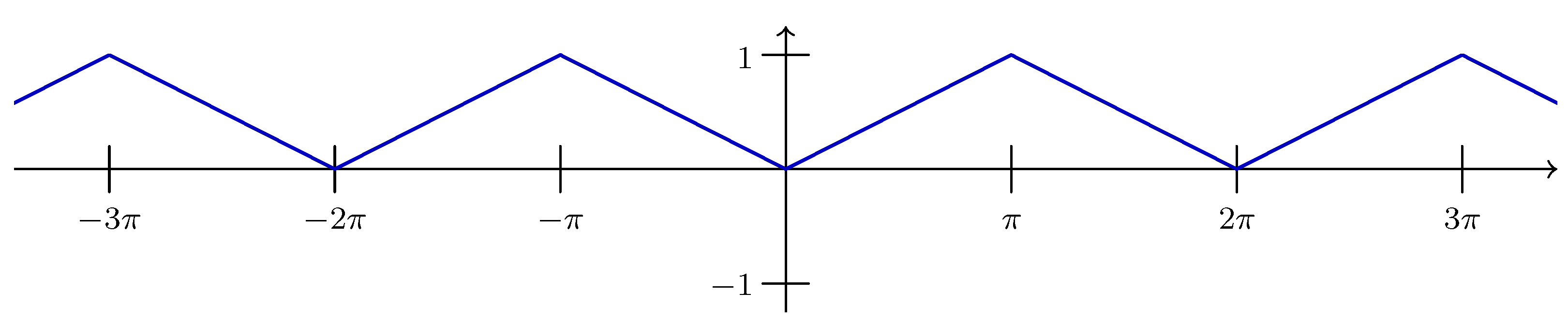
In this section we apply the results of
Section 3 and
Section 8 to the signal function
,
, having Fourier transform
and Hilbert transform
. The extended sampling theorem for the Hilbert transform (Theorem 3.4) takes on the concrete form, first for
,
In practice, one has to deal with a finite sum rather than with the infinite series. This leads to an additional
truncation error, namely,
Assuming
for some constant
, then the terms of the latter series, denoted by
, can be estimated by:
This yields for the truncation error:
Combining the aliasing error in (81) with this estimate for the truncation error, we finally obtain:
Thus, we have a pretty precise and practical estimate for the error occurring when the derivative of the Hilbert transform is reconstructed in terms of the Hilbert version of the sampling theorem. Whereas the first term on the right-hand side covers the aliasing error, the second one is due to truncation.
Similarly, the Boas-type theorem for higher order derivatives (Theorem 8.5) takes the form (recall (67)):
For the second order derivative of
one obtains from Theorem 8.6 for
,
These are the aliasing errors for the reconstruction of derivatives of the Hilbert transform in terms of the Boas-type formulae. In both cases, the truncation errors can be handled in a similar fashion as above.