Abstract
In evolutionary biology, attention to the relationship between stochastic organisms and their stochastic environments has leaned towards the adaptability and learning capabilities of the organisms rather than toward the properties of the environment. This article is devoted to the algorithmic aspects of the environment and its interaction with living organisms. We ask whether one may use the fact of the existence of life to establish how far nature is removed from algorithmic randomness. The paper uses a novel approach to behavioral evolutionary questions, using tools drawn from information theory, algorithmic complexity and the thermodynamics of computation to support an intuitive assumption about the near optimal structure of a physical environment that would prove conducive to the evolution and survival of organisms, and sketches the potential of these tools, at present alien to biology, that could be used in the future to address different and deeper questions. We contribute to the discussion of the algorithmic structure of natural environments and provide statistical and computational arguments for the intuitive claim that living systems would not be able to survive in completely unpredictable environments, even if adaptable and equipped with storage and learning capabilities by natural selection (brain memory or DNA).
1. Why Biology Looks so Different from Physics
Chemical and physical laws are assumed valid anywhere in the universe while biology only describes terrestrial life (even exo- or astrobiology has only DNA-based terrestrial life for an example). In this sense, physics is unrestricted in its domain; anything happening in the universe is always potentially a falsification of a physical theory, which is not only possibly not true for biology, but unlikely [1]. Other sciences, however, are domain specific. We do not assume that life or biology needs to be the same everywhere in the universe. Likewise medicine, insofar as it is a science, is species specific.
Hopfield once asked the very same question we address here [2], and advocated a computational approach of the kind that he himself adopted [3]. In a recent commentary (TWiT, This WEEK in TECH, episode 195 for May 18, 2009: A Series of Tube Tops) Stephen Wolfram advanced a provocative assertion concerning biology and math:
People think of biology as a very accidental science. One where what we have today is a result of a whole series of accidents …But they think of mathematics, for example, as the exact opposite. As a very non-accidental, completely sort of determined-by-higher-principles kind of science …I actually think it’s the opposite way round.
What Wolfram suggests—and this has its basis in [4]—is not too far afield of claims made by other pioneers such as Hopfield [3], viz., that the special features of biology as a field are apparent rather than actual, because rather than being accidental, biological phenomena are more likely subject to informational rather than physical laws. Hopfield underscores the fact that there seems to be no particular reason to believe that biology is ultimately markedly different from physics, insofar as we understand physics as having laws. If this is the case, information and computation may someday describe and provide laws for biological phenomena, just as they are already providing tools to help develop new physical models (e.g., theories of quantum gravity) [5].
1.1. Individuation and the Value of Information
The problem of what makes biology different from physics can be translated into what makes their objects of study different, and differences may be sought not only between the two fields but within each field as well. What makes the objects of study in these fields different? The usual position is that in physics there are laws of increasing accuracy and of a fundamental character describing the world. In biology, by contrast, objects and particular mechanisms seem more important than general laws. General laws have been claimed for biology, such as Fisher’s fundamental theorem [6]. Evolution is in a strong sense a theory of information transfer, describing the process of transmitting messages containing biological information, with mutation a phenomenon of information change and a source of variation. As such, it is very much in line with contemporary developments in physics, where information plays a vital role.
To take an example from physics, entangled particles are indistinguishable from each other. We know that there are two particles only because the system would behave differently were there just one, but there is no way to actually distinguish one particle from the other (some exotic theories even suggest that there is in fact just a single particle, behaving as if it were several. In Feynman’s Nobel Lecture delivered on December 11, 1965 he relates the story of Wheeler, his thesis advisor, calling him by phone to say: “Feynman, I know why all electrons have the same charge and the same mass …Because, they are all the same electron!"). The fact that particles can be treated as identical has important consequences, as they become pure information in statistical mechanics rather than objects, from which probabilities may be calculated.
Biology may be no different. We have always been able to identify different organisms (even of the same species), as they have exclusive particularities that make them distinct. Every organism has a different genome, and even before the discovery of genetic inheritance, taxonomists had established a species classification based on morphological characteristics, which has proved remarkably robust, surviving into the age of the genome. Moreover, natural selection is meaningless if its definition does not encompass fitness, as indexed by the ability of an organism to produce viable offspring—which makes the number of individual organisms (rather than their singular qualities) integral to the reckoning of fitness. For that matter, most of modern biology is about individuation, the shift from the study of a particular entity or collection of entities to the study of indistinguishable objects. Genes, for example, are taken as indistinguishable units, not only within a species but also within an organism. One does not count how many times the same gene occurs in a single organism (this would mean counting at least one per cell). Instead, one gene is taken to represent all others of the same type. Just as with elementary particles, what makes a gene a gene is not the particularities of the physical object but the information about the said object (for particles, their mass, energy, etc.; for genes, the proteins they encode, etc.). What makes a particle a specific particle and a gene a specific gene is nothing but information.
2. Stochastic Environments and Biological Thermodynamics
What can be learned about the relationship between the information content of a stochastic environment and its degree of predictability and structure versus randomness from the way in which organisms gather information from it in order to survive and reproduce?
Stochasticity is a commonly studied property of the environment (e.g., [7]) in which organisms live, and has to do with the constant changes that lead to the modification of the short-term or long-term behavior of individuals or populations (through the DNA).
That information is as essential to the development of modern biology as it has been for physics is borne out by the fact that a central element in living systems turns out to be digital: DNA sequences refined by evolution encode the components and provide complete instructions for producing an organism. It is therefore natural to turn to computer science, with its concepts designed to characterize digital information, and also to computational physics, in order to understand the process of life.
It is our belief that the theory of computation and information may be used to understand fundamental aspects of life, as we have argued before [8,9]. For example, computational thermodynamics provides a new way to study and understand a fundamental property of reality, viz., structure.
Information confers an advantage on living organisms, but organisms must also cope with the cost of information processing. Ultimately the limits are set by thermodynamics, and the link between thermodynamics and information has traditionally been computation [10,11,12] as information processing.
Information processing in organisms should be understood as the process whereby the organism compares its knowledge about the world with the observable state of the world at a given time; in other words, the process whereby an organism weighs possible future outcomes against its present condition. While the larger the number and the more accurate the processed observables from the environment, the better the predictions and decisions, organisms cannot spend more energy than the total return received from information. We will explain how we think organisms can be modeled using instantaneous descriptions written in bits, their states being updated over time as they interact with the environment. Then we will use this argument to show that thermodynamic trade-offs provide clues to the degree of structure and predictability versus randomness in a stochastic natural environment. The sense in which we use the term algorithmic structure throughout this paper is as opposed to randomness (high Kolmogorov complexity, see Section 3.1).
2.1. The Information Content of Life
An organism is an open thermodynamic system, exchanging energy with its environment in the form of heat, work and the energy extracted from biochemical compounds. One can set up an appropriate framework that takes into consideration the dynamics of the interaction of organisms with their environments by using an abstract model of information processing subject to the laws of physics. This model of organisms extracting energy directly from information is really a thought experiment to arrive at the fundamental principles. We do not require or necessarily believe that organisms actually do what the computational framework suggests, only that organisms are subject to the limits of the computational framework just as they are to physical laws.
Classical mechanics is reversible [13] and hence deterministic in a strict sense. One can only find asymmetries of the kind imposed by the second law of thermodynamics in the context of statistical mechanics. Hence the environment in which an organism may live is deterministic in a very strict sense, yet it is often modeled stochastically, because organisms have access only to a finite amount of information and they update their knowledge states dynamically at different rates for different phenomena, making the environment seem apparently random and unpredictable in practice—given the implicit determinism of classical mechanics.
Computation can serve as a framework for investigating issues of thermodynamics. Of course, there are ontological commitments—two, to be precise—but these can be kept simple and reasonable, as they are common. One is that an organism’s behavior is subject to principles of computation just as it is to physical laws, and the other is that an organism has access to only a finite amount of information. In the following sections, we will show how thermodynamics can be employed to explain some of the behavior of living systems.
2.2. Requisite Variety
Cybernetician Ross Ashby proposed the law of requisite variety [14]. This states that an organism, in order to survive in its environment, must possess at least the same degree of differentiation (variety) as that characterizing the environment. For example, if an environment presents seven different situations relevant to the organism, organisms surviving in that environment must possess sufficient differentiation to be able to distinguish at least those seven situations.
The law of requisite variety suggests that less predictable environments will require more algorithmically complex organisms to be able to survive in them. For example, the foraging strategy of organisms depends on the predictability/structure of the environment. Even when there is a degree of randomness, different distributions demand different behaviors. For example, patchy environments are best explored using Lévy flights [15], while homogeneous, unstructured environments are often explored using Brownian motion by simple organisms, while certain other organisms (e.g., some slime moulds or mycelium fungi) may implement strategies close to an exhaustive search. Usually, abundant environments will demand less complexity of organisms compared with environments of scarcity, since less discrimination is required for survival.
Ashby’s Law of Requisite Variety suggests that if the features of an environment E that are evolutionarily relevant to an organism have variety x, then an organism surviving in E must have at least a representation of E that has a variety of x.
2.3. Markov Chains
Markov chains are a common modeling tool in ecology. A Markov chain is a random process (i.e., a set of random variables) where the forthcoming state is only determined by the present state (i.e., the process is memoryless). Note that a random process with memory can be viewed as a Markov chain taking tuples of states as state space. Time may be discrete or continuous. In the case of a Markov chain modeling the real world, the number of random variables of can be unbounded, either because the environment can be regarded as an open system or because one can incorporate more random variables at every possible scale. An organism’s representation of the world, however, is always limited, not only because it has access to limited resources, but also because organisms can only process a finite amount of relevant information in order to make a decision. An example of a Markov chain is shown in Figure 1.
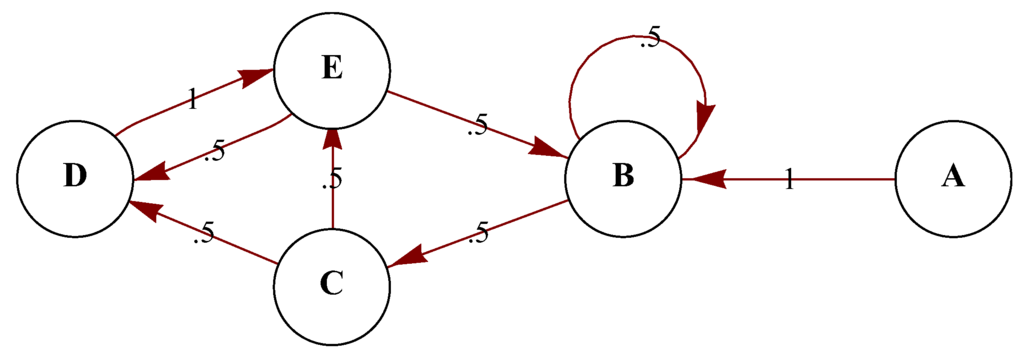
Figure 1.
An example of a simple 5-state Markov chain with simple transition probabilities represented as a stochastic finite-state automaton diagram.
To reduce uncertainty, an organism gathers information from its environment and continually updates its representation of the world. However, this process is subject to a decision as to whether the cost of gathering information exceeds the potential return (in units of energy). For example, as suggested in [16], in an extremely random environment nothing would be known about the location and quantity of food, and a forager would only obtain this information by sampling, which will be more costly on average than the value accruing from finding and ingesting the food. It is also pointed out in [16] that while food represents a short-term benefit, the information accumulated from the experience of finding food is a long-term benefit, because the experience can be used to learn and predict (in the probabilistic algorithmic sense [17,18], as used, for example, in machine learning). Nevertheless, prediction in ecological systems is limited, as discussed in [19], among other reasons because there is only partial access to all the environmental variables.
3. Computation and Life
Among Turing’s most important contributions to science is his definition of universal computation, integral to his attempt to mechanize the concept of a computing machine. A universal (Turing) machine is an abstract device capable of carrying out any computation for which a program can be written. More formally, given a fixed description of Turing machines, we say that a Turing machine U is universal if for any input s and Turing machine M, halts if M halts on s and outputs ; and does not halt if does not. In other words, U is capable of running any Turing machine M with input s.
A digital computer allows us to physically realize this concept, and as suggested in [20], there is no better place in nature where a process similar to the way Turing machines work can be found than in the unfolding of DNA transcription. For DNA is a set of instructions contained in every living organism with a script empowering organisms to self-replicate. In fact, it is today common, even in textbooks, to consider DNA as the digital repository of the organism’s development plan, and the organism’s development itself is not uncommonly thought of as a mechanical, computational process in biology.
Chaitin, one of the founders of algorithmic information theory [21], recently suggested [22,23] that:
Brenner said much the same thing in his recent essay in Nature [20]:DNA is essentially a programming language that computes the organism and its functioning; hence the relevance of the theory of computation for biology.
He continues:The most interesting connection with biology, in my view, is in Turing’s most important paper: ‘On computable numbers with an application to the Entscheidungsproblem’.
Arguably the best examples of Turing’s and von Neumann’s machines are to be found in biology. Nowhere else are there such complicated systems, in which every organism contains an internal description of itself.
Indeed, a central element in living systems turns out to be digital: DNA sequences refined by evolution encode the components and drive the development of all living organisms. All examples of life we know have the same (genomic) information-based biology. Information, in living beings, is maintained one-dimensionally through a double-stranded polymer called DNA. Each polymer strand in the DNA contains exactly the same information, coded in the form of a sequence of four different pairs of bases. In attempting to deepen our understanding of life, it is therefore natural to turn to computer science.
Important concepts in the theory of computation can help us understand aspects of behavior and evolution, in particular concepts drawn from algorithmic complexity and computational thermodynamics. Witness, for instance, the fact that the instructions for life are stored in sequences of DNA, and in identifiable units of information (genes), albeit in a convoluted fashion—full of intricate paths and complicated connections and unpredictable outcomes. Even in the 1960s biologists such as G.C. Williams, for example, made rough calculations of the amount of information an organism’s DNA could contain [24].
Computer simulations performed as part of research into artificial life have reproduced various features of evolution [4,25,26], all of which have turned out to be deeply connected to the concept of (Turing) universal computation [27]. Not taking into account this phenomenon of pervasive computational universality in biology, treating it as a mere technicality with little relevance and consequently avoiding it, is a mistake. As we have claimed before [8], our knowledge of life may be advanced by studying notions at the edge of decidability and uncomputability (e.g., as we define it, algorithmic probability is a non-computable measure, but its importance for us lies in the fact that it can be approximated). The concept of Turing universality (and of a universal Turing machine) should simply be treated as a physical system whose richness allows us to study a low level of basic systems behavior without having to worry about particular causes for particular behaviors. The property that makes a Turing machine Turing universal is its ability to simulate the behavior of any other computer program or specific Turing machine. Hence, its introduction as a tool should not alienate researchers, leading them to treat it as a mere abstract concept with no practical relevance to biology.
To grasp the role of information in biological systems, think of a computer as an idealized information processing system. Today, from a practical point of view it is fairly easy to understand how energy may be converted into information [11,12,28]. Computers may be thought of as engines transforming energy into information (the information may already be there, but without energy one is unable to extract it). One way of looking at this is set forth by Bennett [12], who suggests using a sequence of bits as fuel, relating information on a tape of a Turing machine to the amount of energy one can extract out of it. In [5] there is an explanation of how a binary tape can be used to produce work and how information may therefore be converted into energy.
3.1. Complexity and Algorithmic Structure
The algorithmic complexity of a string s with respect to a universal Turing machine U, measured in bits, is defined as the length in bits of the shortest (prefix-free) Turing machine U that produces the string s and halts [17,18,21,29]. Formally,
This complexity measure clearly seems to depend on U, and one may ask whether there exists a Turing machine that yields different values of for different U. The ability of universal machines to efficiently simulate each other implies a corresponding degree of robustness. The invariance theorem [18,21] states that if and are the shortest programs generating s using the universal Turing machines U and respectively, their difference will be bounded by a constant independent of s. Formally:
Hence it makes sense to talk about without the subscript U. From Equation 1 and based on the robustness provided by Equation 2, one can formally call a string s a Kolmogorov (or algorithmically) random string if where is the length of the binary string s. Hence, an object with high Kolmogorov complexity is an object with low algorithmic structure, because Kolmogorov complexity measures randomness—the higher the Kolmogorov complexity, the more random.
as a function is, however, not computable, which means that no algorithm returns the length of the shortest program that produces s (by reduction to the halting problem). But is semi lower computable (for formal proofs see [30]), meaning that it can be approximated from above, for example, via lossless compression algorithms.
It is also worth mentioning that while the environment is required to have algorithmic structure (hence low Kolmogorov complexity), the type of randomness in the environment that we argue must be surpassed by algorithmic structure is apparent randomness (i.e., not necessarily algorithmic—uncomputable—randomness, given that the question of whether uncomputable randomness occurs in nature is still an open problem with little hope to be answered soon, if someday). Lossless compression algorithms are useful in this approach, as they take advantage of regularities in data in order to compress it, but what compression algorithms detect is precisely apparent randomness. In this sense, there is a parallelism with the way that organisms subjectively perceive their environment. Losslessly compressing a string is, however, a sufficient test of non-randomness, hence of algorithmic structure.
3.2. The Information Content of Organisms and the Extraction of Energy from Strings
The energy (W) reserves in an organism M are fixed at any given time t, and an organism’s description at a given time is assumed to be finite (which in our context means that the information in bits to describe the organism is of finite length). Formally, we can write:
where is a program with input s running on a universal Turing machine U producing M. The maximum information-processing capability of a system is given by , the maximum energy (Feynman calls it fuel [28]) value of the organism from the minimum description length of M. Even if the value of is not computable given that is not (cf. Section 3.1), it represents a theoretical limit, as one can safely assume that an organism cannot deal with more information than it is capable of storing and that can be reflected in its description in bits. Hence supplies a thermodynamic limit on the amount of information that M can convert into energy at a time t. Then the organism cannot process more information than nor can it transform more bits into energy than .
In terms of information, the thermodynamical upper limit of the total information that can be transformed into energy is determined by the minimal description of the organism. A useful representation of how to extract work out of binary sequences using a Turing machine with a piston can be found in [28,31]. When the piston of a machine expands due to its having been set in the correct position—based on accurate knowledge of a bit—one can extract work, but if the piston is not set properly then it contracts, producing negative work, taking the machine back to its initial position on average (assuming positive energy is tantamount to forward movement and negative to backward movement), like a one-dimensional random walk.
This has two immediate consequences. One is that the energy of M is finite, but also that there is in principle a minimum amount of information different from zero, which an organism can trade with when updating its internal representation of the state of the world.
4. Life, Predictability and Structure
In Schrödinger’s What is life? (1944) [32] we read:
In calling the structure of the chromosomes a code-script, we mean that the all-penetrating mind, once conceived by Laplace …could tell from their structure how the egg would develop …
Today, it can be safely said that the code-script has been fully decoded, yet we are incapable of arbitrary prediction. This is not a problem having to do with DNA conceived as a program, but a property of computational irreducibility, as stressed by Wolfram [4]. Wolfram shows that simple computer programs are capable of producing apparently random (not algorithmically random) behavior. Wolfram’s cellular automaton Rule 30 is the classic example, as it is by most standards the simplest possible cellular automaton, yet we know of no way to shortcut its evolution other than by running the rule step by step. This was already known for some mathematical objects, such as the mathematical constant π or , which have simple representations, as they are computable numbers (one can algorithmically produce any arbitrary number of digits) the digits of whose decimal expansions look random. However, a formula has been found to shortcut the digits of π in bases that are powers of , where one does not need to compute the first digits in order to calculate a digit in any position of its -ary expansion [33].
Biological evolution and ecology are intimately linked, because the reproductive success of an organism depends crucially on its reading of the environment. If we assume that the environment is modeled as a Markov chain, we can map the organism’s sensors with a Hidden Markov Model (HMM). In such models, the state of the world is not directly observable. Instead, the sensors are a probabilistic function of the state. HMM techniques can solve a variety of problems: filtering (i.e., estimating the current state of the world), prediction (i.e., estimating future states), smoothing (i.e., estimating past states), and finding the most likely explanation (i.e., estimating the sequence of environmental states that best explains a sequence of observations according to a certain optimality criterion). HMMs have become a popular computational tool for the analysis of sequential data.
Following standard mathematical terminology, let us identify the environment as an HMM denoted by , a sequence of t random variables partially accessed by an organism using the sequence of observables , with corresponding to the hidden states. There are t states of the environment (e.g., “sunny”, “predator nearby”, “cold”, etc.), but organisms can only have partial access to them through . For every state there is a chance that an organism will perform one of a number of possible activities depending on the state of the environment.
In the simulation of a stochastic process, we attempt to generate information about the future based on the observation of the present and eventually of the past. However, implicit in the Markov model is the notion that the past and the future are independent. Particularly from the perspective of an observer, the model is memoryless. In this case it is said that the HMM is of the order , which simply means that , i.e., the probability of the random variable X being x at time t depends only on at time t. If the distribution of the states at time is the same as that at time t, the Markov process is called stationary [34]. The stationary Markov process then has a stationary probability distribution, which we will assume throughout the paper in the interests of mathematical simplicity (without loss of generalization). An m-order HMM is an HMM that allows transitions with probabilities among at most states before the source state, which means that one can take advantage of correlations among these states for learning and predicting. In linguistics, for example, a 0-order HMM allows the description of a single gram distribution of letters (e.g., in several languages “e" is the most common letter), versus a 1-order HMM that provides information about bigrams, determining with a certain probability the letter that precedes or follows another letter (in English, for example, “h" following “t" is among the most common bigrams, so once a “t" is spotted one can expect an “h" to follow, and the probability of its so doing is high compared with, say, the probability of an "h" following a “z".) In a 2-HMM one can rule out the trigram “eee" in English, assigning it a probability 0 because it does not occur, while “ee" can be assigned a reasonable non-zero probability. In what follows we will use the HMM model to discuss potential energy extraction from a string.
4.1. Simulation of Increasingly Predictable Environments
There are distinct binary strings of length n. The probability of picking 1 among the is . We are interested in converting information (bits) into energy, but putting bits together means working with strings. Every bit in a string represents a state in the HMM; it will be 0 or 1 according to a probability value (a belief). So in this example, the organism processes information by comparing every possible outcome to the actual outcome, starting with no prior knowledge (the past is irrelevant). We know that for real organisms, the (evolutionary) past is very relevant, and it is often thought of in terms of a genetic history. This is indeed how we will conceptualize it. We will take advantage of what an HMM allows us to describe in order to model this “past".
Landauer’s Principle [11,12] states that erasing (or resetting) one bit produces joules of heat, where T is the ambient temperature and k is Boltzmann’s constant ( J K). Then it follows that an organism with finite storage memory updates its state according to a series of n observations at time by a process of comparison. And if differs from by j bits, then at least joules will be spent, according to Landauer’s Principle, to reset the bits of to .
Pollination, for example, is the result of honeybees’ ability to remember foraging sites, and is related to the honeybee memory endurance, hence its learning and storing capabilities. Honeybees use landmarks, celestial cues and path integration to forage for pollen and nectar and natural resources like propolis and water [35].
But and can only differ by at most n bits, and they may do so by chance at most on average, in a random environment modeled by a 0-order HMM (a system with no memory). If every bit is equally likely, the probability of occurrence of any string of length n is .
Each of the strings can have different i bits, with . This difference can be measured by the Hamming distance d between strings of the same size.
4.2. Energy Groups
It follows that the number of “energy" groups according to the number of bits is precisely n. This is because if one arbitrarily chooses “1" as a bit that will reconfigure a tape (see Section 3.2) to produce energy, one can extract k bits of energy out of a string of length n given by the binomial formula:
For example, from a one bit binary string, 0 or 1 unit of energy can be extracted, depending on whether the string is 0 or 1 (in the simulations below we will actually assume that 0 returns of energy, which is a fair assumption according to the one-dimensional random walk behavior of a Turing machine equipped with a piston, as described in Section 3.2).
For length we have the possible binary strings 00, 01, 10 and 11. If 1 is the energy returning bit, we have it that 00 returns no energy, 01 and 10 each provides 1 unit of energy, and 11 provides 2 units of energy, that is 1, 2, 1. For , the energy distribution among all the strings is 1, 3, 3, 1, and for , the distribution is 1, 4, 6, 4, 1 (see Figure 2). Evidently the maximum energy return of a binary string is bounded by the length of the string, that is . The minimum energy return is always 0 for any n (the string , that is the repetition of n 0s).
For random strings one would produce on average joules, but to reach thermodynamic equilibrium one can take “0" as a negative return of energy, hence “-1" for these purposes. Thus from a random string one would get 0 units of energy on average. Strings like 01 and 10 are considered energetically equivalent, given that each bit is independent in the stochastic environment, and the organism may expect one or another bit. In other words, if the organism expects a 1 in a string of 2 bits, the position of the bit in the string is irrelevant. It can come in first or second place in the 2 bit string; only when it occurs for the first time will it produce energy (compare again to the piston scenario in Section 3.2).
There are energy groups from the strings of length n (see Figure 2 and Figure 3). One can see then how energy groups can form, each representing the possible amount of energy extracted from a sequence configuration (fixing the expected configuration). In such a case, a string like 0101 produces the same amount of energy as 1010, but also as 110 and 101. In general, for strings of length n, the maximum amount of energy one can extract is n, but with different probabilities (depending on the number of energy groups) one can actually get any integer value in the interval [, n]. Among the strings of length n, there are the energy groups and , each returning a different amount of free energy. For strings of 2 bits we have and , with −1, 0 and 2 as possible energy returns, hence only 3 groups. Therefore, the number of groups is given by the number of different energy returns. This probability can be calculated from C as follows:
which is the probability of extracting i joules out of string s. Better said, it is the probability of getting a string with i joules. If looking to produce negative work out of zeroes, then the probability of getting i joules can be calculated by:
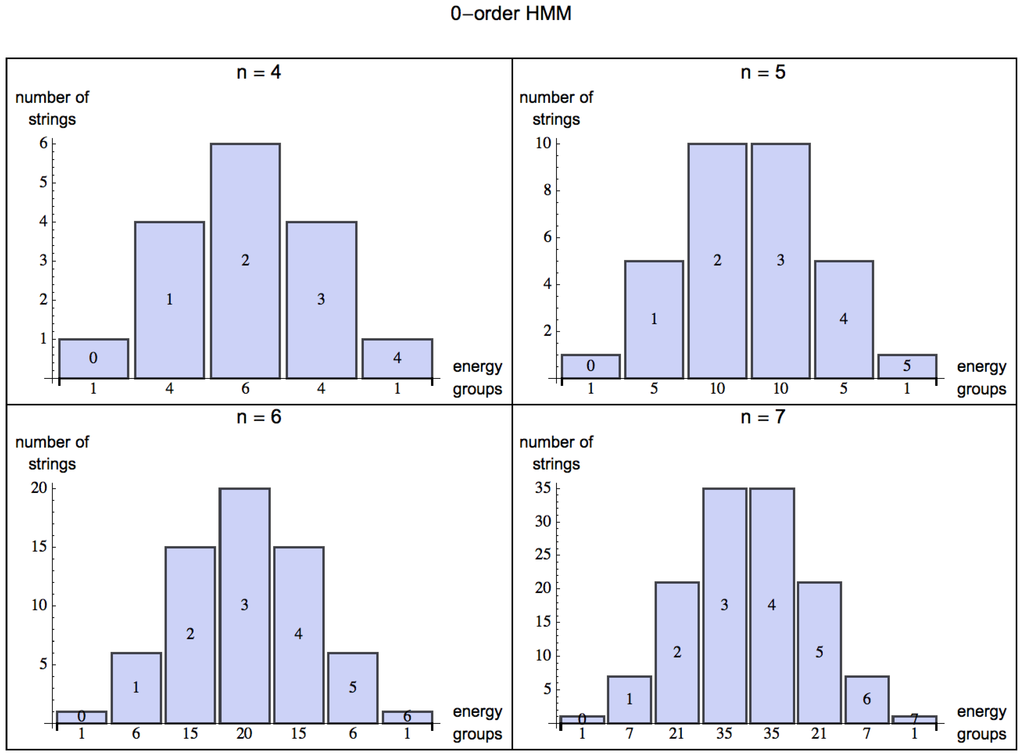
Figure 2.
Energy groups: Possible extraction values from the different energy groups among all the strings of increasing length . Each figure can be read as follows: Taking the first plot (top left), there is 1 string that has an energy return of 0 units of energy (0000); 4 strings that return 1 unit of energy (e.g., 0100); 6 strings that return 2 units of energy (e.g., 1100); 4 other strings that return 3 units of energy (e.g., 0111) and finally 1 string that can return the maximum energy (1111).
By turning from a 0-order (Figure 2) to an m-order HMM, one can model the organism’s ability to capture patterns of up to length (by assigning probabilities based on a distribution of frequencies from experience, or learning). The energy one can extract from the environment is statistically described by the skewness of the probability distribution for energy extraction from strings decreasingly random in nature. For a 0-order HMM, the skewness (the degree of asymmetry of a distribution) of the normal distribution for is evidently 0 (symmetric, evenly distributed, see Figure 2), but as soon as the HMM is of order 1 (see Figure 3) probabilities among states can have values different from , and the skewness is negative for , which means that the bulk of the distribution has shifted to the right and one can have a positive exchange of energy in an environment with some predictability.
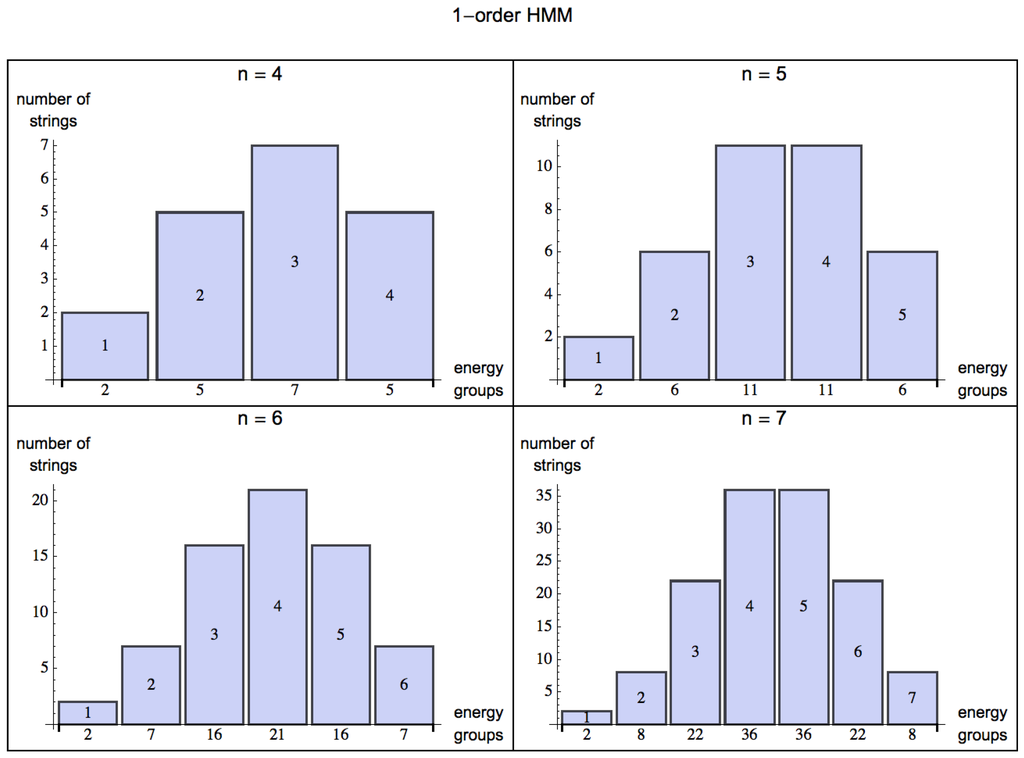
Figure 3.
Shift of the distributions of energy groups for strings of increasing length , modeling a very simple potential predictable environment represented by a 1-order HMM (compared with a 0-order HMM in Figure 2) in a scenario for , where given a state, an organism can potentially make an optimal choice based on the transition value of the next state according to p. The bulk of the values, measured by a negative skewness, clearly lie to the right of the mean, indicating the predictability of the environment (mirrored by the learning capabilities of living organisms) and therefore a possible positive energy extraction.
It is clear that different energy groups grow at different rates for increasing string length n (one way to visualize this is by plotting the Pascal triangle using the binomial formula). The number of strings of length n grows at while the number of strings from which energy can be extracted grows at a slower rate than (for example, the number of strings that provide maximum energy is always 1, and hence remains constant—the strings of n 1s). Thus, one can see how the equilibrium of energy returns pulls the distribution to the mean average, having as a consequence no positive energy return. The possibility of modeling transitions with probability , however, increases the number of strings with a positive energy return.
In other words, if an organism S is a finite state automaton able to make predictions about binary strings of at most length n (hence with memory capacity of length n) and the environment E is another finite-state automaton capable of generating strings of length m, if then S can predict any pattern produced by E. However if then S will be able to predict only patterns of length smaller than n and will miss those greater than m, potentially . Taken to the limit, if n is too short, or m too large compared with n, then S will miss most patterns in E.
4.3. Organisms Survive (only) in Predictable Environments
It is clear how living organisms convert information into energy by using information in locating food, for example, or in figuring out how to navigate within a habitat, in learning how to hunt, in securing a mate, etc. As we argue, however, the extent to which an organism is adapted to or is able to produce offspring in a particular environment depends on a positive exchange ratio between information and energy. For an organism to make use of acquired information (e.g., for learning) it must be able to store it. In the context of biological systems, upon making an observation an organism must record both the stimulus and its appropriate response (e.g., Pavlov’s dog). Memory is a vital characteristic for many organisms (such as honeybees, which develop memory through learning gradually over time [36,37]) and therefore requires the persistence of periodic structures.
The previous rationale allows us to describe how an organism with finite memory will use and convert energy at an abstract fundamental thermodynamic level to keep up with the information from its environment and update its current state. For example, when foraging, honeybees form simple associations between landmarks in order to navigate along their flight path. Honeybees also use the direction of sunlight as an indication when traveling along familiar routes during the process of path integration. For these reasons [38,39], honeybees can fly back to their hives in complicated situations.
Natural selection has equipped organisms to cope with trade-offs involving memory capabilities, time spent and energy return, enabling them to take these into account when deciding whether to undertake certain actions in return for spending resources. Take cheetahs, for example, who spend most of their energy in the very first instants of a hunt. Because they are not able to keep up the speed of pursuit for longer periods, they have to size up a situation and hit upon the near optimal starting point for a chase.
So what does the existence of living organisms tell us about structure versus randomness in nature? That one would need to attribute incredible power to living organisms, power to overcome a random environment having no structure, or alternatively, to accept that a stochastic environment in which living organisms can survive and reproduce needs a degree of structure.
What computational thermodynamics tells us about nature is that organisms cannot survive in a random world, because in order to exchange energy for information about the world, the organism needs a minimum degree of predictability, or else it will not be able to take advantage of the information it has acquired and stored. Hence, an organism in a random world cannot survive due to fundamental thermodynamic limits.
4.4. DNA, Memory in Simple Organisms and Reactive Systems
Our argument might seem to depend on the physical memory of an organism, but it has been shown that reactive systems, for example, can exhibit non-trivial behavior without need of an explicit memory. A classical example is the kind of “vehicle" proposed by Braitenberg [40]. These vehicles make simple, direct connections between sensors and actuators. For example, a vehicle with two photosensors on its sides (left and right) connected to opposing wheel motors (left sensor to right motor, right sensor to left motor) exhibits phototaxis. This is because the sensor closer to the light will cause the opposing motor to spin faster, turning the vehicle towards the light. If the vehicle turns too much, the other sensor will counteract this movement, and both sensors and motors will coordinate until the light source is reached. This behavior does not require an explicit memory, but it does require information stored in the design details of the system, perhaps mirroring what happens in very simple living organisms (such as insects, or simpler organisms such as bacteria), where DNA is the result of the state of the world acting directly on the information stored and codified by genes, as explained by Fisher [6], and hence just another type of memory.
The difference between a reactive system—such as a Braitenberg vehicle—and a representational system (where bits in a memory represent aspects of the environment) is at the level of the location of the relevant information of the system. On the one hand, representational systems can store information in a specific location, generally updated many times during the lifespan of an organism. This is useful when the sensor channel capacity (maximum information that can be transmitted over a communications channel) is low compared with the environmental complexity, since not all of the relevant information can be sensed at once. On the other hand, reactive systems do not store information. Nevertheless, relevant information is required for computation to take place. In principle, a reactive system could perform tasks of the same complexity as a representational system [41], but the reactive system would require a sensor channel capacity equal to or greater than the memory size of the representational system. For example, if an environment requires 4 bits of relevant information to be processed by an organism to survive, this could be achieved by a reactive system with four 1-bit sensors (each sensor having a 1-bit channel capacity), or by a representational system with a single 1-bit sensor and a 4-bit memory. The trade-off is similar to that of storing everything about the environment in the DNA or letting organisms evolve brains capable of storing information that is more volatile.
Given the fact that reactive systems also need to process relevant information from their environment, as stated by Ashby’s law of requisite variety [14], our argument applies to both representational and reactive systems. These are finite, in memory and channel capacity, so the predictability of their environment is also limited. Representational systems are useful for prediction, while reactive systems are useful for adaptation. But computationally, either system requires the same environmental predictability in order to survive, independent of the particular strategy or mechanism used. How to balance memory and channel capacity is certainly an interesting topic, mirrored in the trade-off aforementioned (DNA storage versus brain storage), but it is beyond the scope of this paper.
5. Conclusions
It is interesting to note that some species enhance their fitness by modifying their environments, bringing about an increase in predictability, a clear evolutionary advantage. This seems particularly obvious in the human species’ ability to fashion stable and predictable environments for itself. Using some aspects of information theory, algorithmic complexity and computational thermodynamics, we have captured some of these properties and made explicit their importance for the organism from the standpoint of the environment. In evolutionary terms, it is difficult to justify how biological algorithmic complexity could significantly surpass that of the environment itself. If the organism’s representation of the environment E has algorithmic complexity x, E should have a complexity of no less than x. We have advanced the claim that the algorithmic complexity of biological systems follows the algorithmic complexity of the environment (a similar approach to a related biological question is presented in [42]).
The paper advances an information-theoretic reasoning about the relation of biology to other algorithmic complexity and computational thermodynamics, stresses the applicability of the theory of information and computation to biology (particularly evolutionary theory), and sketches the applicability of the theory of algorithmic complexity to biology and the relevance of the close connections between information theory and thermodynamics to biology.
Using these tools, we have substantiated the intuitively correct assumption that natural environments must have a minimum of algorithmic structure and predictability prevailing over randomness in order for life to evolve. Our argument does not imply that organisms necessarily do things exactly as we have described, nor that in a structured environment life will necessarily evolve, especially because evolution requires a certain variability that is absent in fully predictable environments. But we have advanced the claim that computational principles also apply to biological systems, and can therefore be used to study fundamental limits and tradeoffs as we have done so here and also before (see e.g., [43]). Whether some degree of apparent randomness is necessary, for example, is another interesting question that arises from this analysis. In a fully predictable environment where benefit returns are constant, one would be at a loss to explain why living organisms would evolve. Therefore, paradoxically, the environment seems to require structure and apparent randomness for living systems to evolve. However, our argument justifies the belief that life could only have evolved in an environment where randomness is superseded by algorithmic structure, allowing living organisms to build upon predictable phenomena.
Acknowledgments
The authors would like to thank the anonymous reviewers for their useful comments and suggestions. H.Z. wishes to thank the FQXi for their support (mini-grant No. FQXi-MGA-1212 “Computation and Biology") awarded through the Silicon Valley Foundation. C.G. acknowledges support from SNI membership 47907 of CONACyT, Mexico.
References
- Pinheiro, V.B.; Taylor, A.I.; Cozens, C.; Abramov, M.; Renders, M.; Zhang, S.; Chaput, J.C.; Wengel, J.; Peak-Chew, S.Y.; McLaughlin, S.H.; et al. Synthetic genetic polymers capable of heredity and evolution. Science 2012, 336, 341–344. [Google Scholar] [CrossRef] [PubMed]
- Hopfield, J.J. Brain, neural networks, and computation. Rev. Mod. Phys. 1999, 71, 431–437. [Google Scholar] [CrossRef]
- Hopfield, J.J. Physics, computation, and why biology looks so different. J. Theor. Biol. 1994, 171, 53–60. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Zenil, H. Information theory and computational thermodynamics: Lessons for biology from physics. Information 2012. submitted for publication. [Google Scholar] [CrossRef]
- Fisher, R.A. The Genetical Theory of Natural Selection; Clarendon Press: Oxford, UK, 1930. [Google Scholar]
- Arnoldini, M.; Mostowy, R.; Bonhoeffer, S.; Ackermann, M. Evolution of stress response in the face of unreliable environmental signals. PLoS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef] [PubMed]
- Zenil, H.; Marshall, J.A.R. Some aspects of computation essential to evolution and life. Ubiquity 2012. submitted for publication. [Google Scholar]
- Gershenson, C. The World as Evolving Information. In Proceedings of the International Conference on Complex Systems ICCS2007, Quincy, MA, USA, 28 October – 2 November, 2007; Bar-Yam, Y., Ed.; NECSI: Boston, MA, USA, 2007. Available online: http://arxiv.org/abs/0704.0304 (accessed on 2 November 2012). [Google Scholar]
- Szilárd, L. Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen (On the reduction of entropy in a thermodynamic system by the interference of intelligent beings). Z. Physik 1929, 53, 840–856. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Bennett, C.H. The thermodynamics of computation–a review. Int. J. Theor. Phys. 1982, 21, 905–940. [Google Scholar] [CrossRef]
- Bennett, C.H. Logical reversibility of computation. IBM J. Res. Dev. 1973, 17, 525–532. [Google Scholar] [CrossRef]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall: Milton Keynes, UK, 1956. [Google Scholar]
- Boyer, D.; Ramos-Fernández, G.; Miramontes, O.; Mateos, J.; Cocho, G.; Larralde, H.; Ramos, H.; Rojas, F. Scale-free foraging by primates emerges from their interaction with a complex environment. Proc. Roy. Soc. Lon. B 2006, 273, 1743–1750. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.W.; Mangel, M. Foraging and flocking strategies: Information in an uncertain environment. Am. Nat. 1984, 123, 626–641. [Google Scholar] [CrossRef]
- Levin, L. Laws of information conservation (non-growth) and aspects of the foundation of probability theory. Probl. Inform. Transm. 1974, 10, 206–210. [Google Scholar]
- Solomonoff, R. A Preliminary Report on a General Theory of Inductive Inference; Revision of Report V-131, Contract AF 49(639)-376, Report ZTB–138; Zator Co.: Cambridge, MA, USA, 1960. [Google Scholar]
- Beckage, B.; Gross, L.J.; Kauffman, S. The limits of prediction in ecological systems. Ecosphere 2011, 2. [Google Scholar] [CrossRef]
- Brenner, S. Turing centenary: Life’s code script. Nature 2012, 482. [Google Scholar] [CrossRef] [PubMed]
- Chaitin, G.J. Algorithmic Information Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Chaitin, G.J. Metaphysics, Metamathematics and Metabiology. In Randomness Through Computation; Zenil, H., Ed.; World Scientific: Singapore, 2011; pp. 93–103. [Google Scholar]
- Chaitin, G.J. Life as Evolving Software. In A Computable Universe; Zenil, H., Ed.; World Scientific: Singapore, 2012. [Google Scholar]
- Williams, G.C. Adaptation and Natural Selection: A Critique of Some Current Evolutionary Thought; Princeton University Press: Princeton, NJ, USA, 1966. [Google Scholar]
- Gardner, M. Mathematical Games-The fantastic combinations of John Conway’s new solitaire game “life". Sci. Am. 1970, 223, 120–123. [Google Scholar] [CrossRef]
- Langton, C.G. Studying artificial life with cellular automata. Phys. D: Nonlinear Phenom. 1986, 22, 120–149. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the entscheidungsproblem. Proc. Lon. Math. Soc. 1936, 2, 230–265. [Google Scholar]
- Feynman, R.P.; Hey, A.J.G.; Pines, D. Feynman Lectures on Computation; Westview Press: Boulder, CO, USA, 2000. [Google Scholar]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inform. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Li, M.; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Sethna, J. Statistical Mechanics: Entropy, Order Parameters and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Schrödinger, E. What is Life; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Bailey, D.H.; Borwein, P.B.; Plouffe, S. On the rapid computation of various polylogarithmic constants. Math. Comput. 1997, 66, 903–913. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Blackwell: Hoboken, NJ, USA, 2006. [Google Scholar]
- Srinivasan, M.V. Honeybees as a model for vision, perception, and cognition. Ann. Rev. Entomol. 2010, 55, 267–284. [Google Scholar] [CrossRef] [PubMed]
- Menzel, R.; Müller, U. Learning and memory in honeybees: From behavior to neural substrates. Ann. Rev. Neurosci. 1996, 19, 379–404. [Google Scholar] [CrossRef] [PubMed]
- Menzel, R.; Geiger, K.; Müller, U.; Joerges, J.; Chittka, L. Bees travel novel homeward routes by integrating separately acquired vector memories. Anim. Behav. 1998, 55, 139–152. [Google Scholar] [CrossRef] [PubMed]
- Menzel, R. Searching for the memory trace in a mini-brain: The honeybee. Learn. Mem. 2001, 8, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Menzel, R.; Greggers, U.; Smith, A.; Berger, S.; Brandt, R.; Brunke, S.; Bundrock, G.; Hülse, S.; Plümpe, T.; Schaupp, F.; et al. Honeybees navigate according to a map-like spatial memory. Proc. Natl. Acad. Sci. 2005, 102, 3040–3045. [Google Scholar] [CrossRef] [PubMed]
- Braitenberg, V. Vehicles: Experiments in Synthetic Psychology; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Gershenson, C. Cognitive paradigms: Which one is the best? Cogn. Syst. Res. 2004, 5, 135–156. [Google Scholar] [CrossRef]
- Gershenson, C.; Fernández, N. Complexity and information: Measuring emergence, self-organization, and homeostasis at multiple scales. Complexity 2013. submitted for publication. [Google Scholar] [CrossRef]
- Zenil, H.; Hernandez-Quiroz, F. On the Possible Computational Power of the Human Mind. In Worldviews, Science and Us, Philosophy and Complexity; Gershenson, C., Aerts, D., Edmonds, B., Eds.; World Scientific: Singapore, 2007. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).