Accelerating Universe and the Scalar-Tensor Theory
Abstract
:1. Introduction and Summary
2. Scalar-Tensor Theory Due to Jordan
- The first term with , multiplied with R, is called a nonminimal coupling term, designed to give an effective gravitational “constant” represented by allowing it to be spacetime-dependent, obviously intended to implement Dirac’s idea of the time-dependent gravitational constant [20]. Note the continued use of the Planckian unit system.
- In the sign factor , the positive choice corresponds to a positive kinetic energy of ϕ, though the negative choice is not excluded immediately because ϕ at the level of (7) is not a fully diagonalized field. See Section 2.6 of [11] for details on the mixing interaction between ϕ and the spinless part of the metric, taking place in the nonminimal coupling term.
- We also use the parameter , instead of the original , excluding repulsive gravity.
- We have the ordinary type of the matter Lagrangian , specifically representing the fundamental fields in the microscopic world.
- Also to be added beyond Jordan is the cosmological constant introduced to expect the theory now to provide us with a new way of understanding the accelerating universe. Respecting the arguments on the Unification program, we assume Λ of the order unity in the Planckian unit system, or .
3. Conformal Transformation/Frames
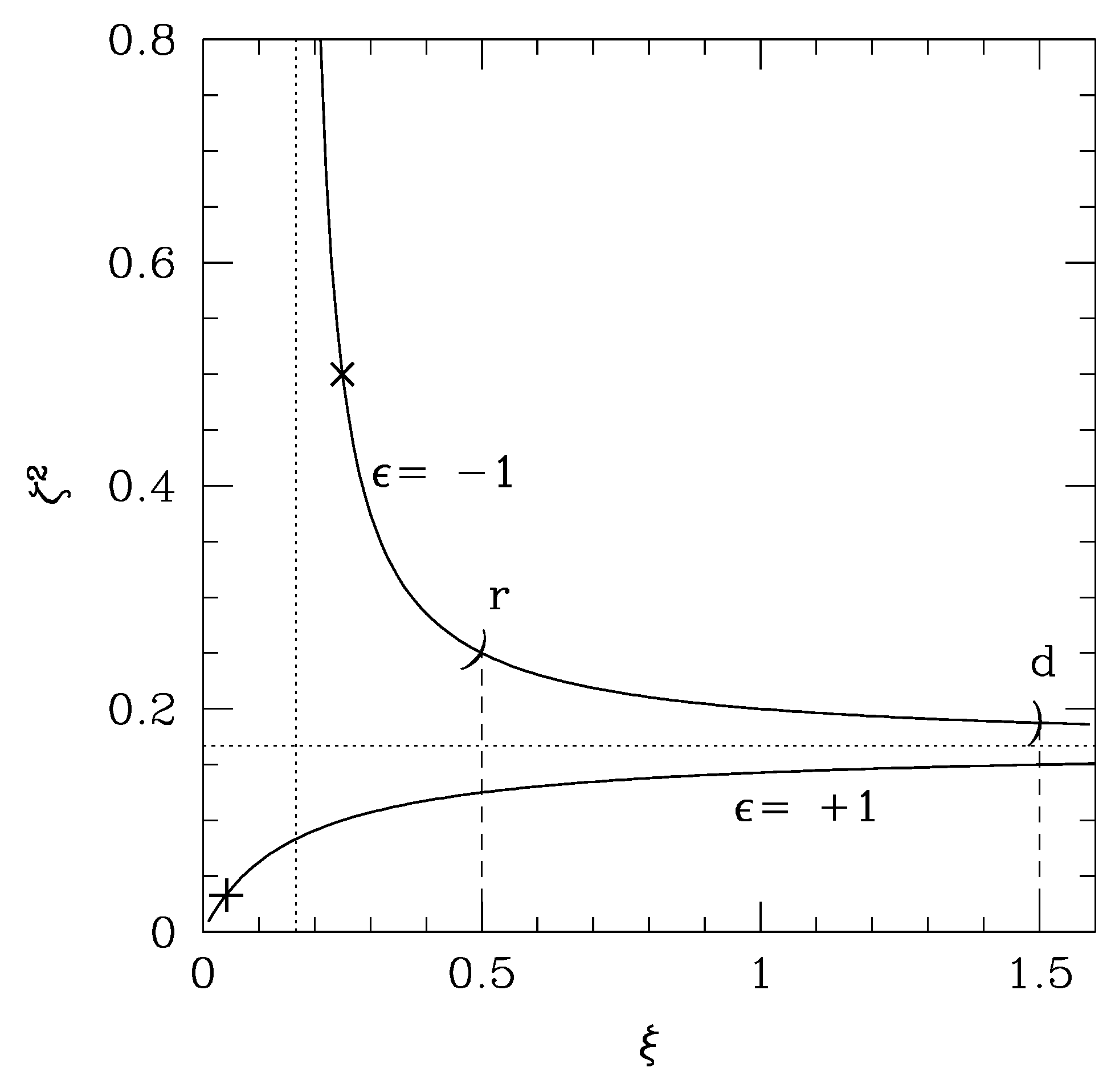
4. Simple Cosmology
4.1. Radiation Dominance in J Frame
4.2. Radiation Dominance in E Frame
- According to (35), the universe not only expands but also does so in conformity with the assumed radiation-dominance.
- Equation (37) can be interpreted as implementing the scenario of a decaying cosmological constant, represented by (6) supposed to apply to quite wide a time span, as a first step toward understanding the numerical relation (4), which we have focused upon as the simplest yet probably the most important achievement arising from the discovery of the acceleration of the universe. As we also add, the behavior of the inverse-square of time is simply a standard result deriving a critical density. As we recall, this nearly desired behavior is a consequence of the exponential potential (15), also traced back to the simplest imaginable choice, Λ, added to (7). We notice, however, that multiplying Λ by results only in replacing ζ in by .
4.3. The Brans–Dicke Requirement
5. Scale-Invariance Model
5.1. Leaving the Brans–Dicke Model
5.2. Spontaneously Broken Scale Invariance
5.3. Quantum Loop Effects

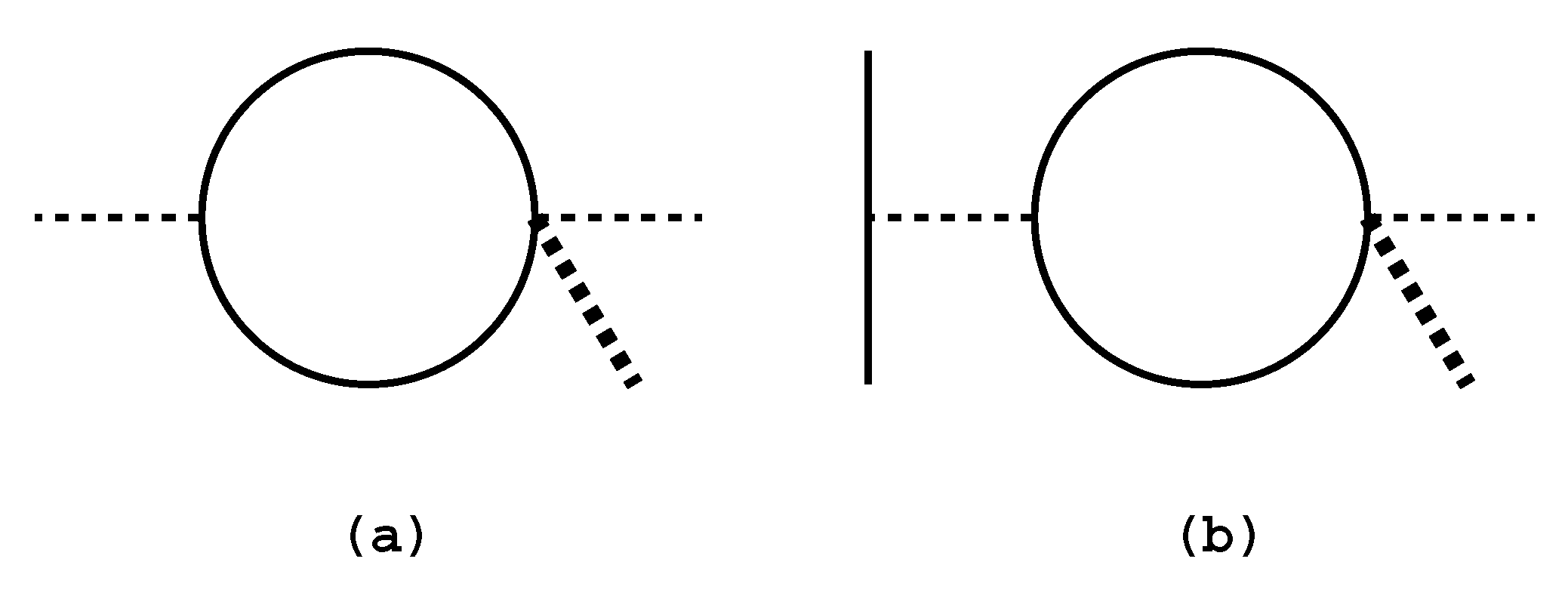
5.4. A Slight Deviation from E Frame
6. Trapping Mechanism
6.1. Hesitation Behavior

6.2. Mini-Inflation(s)
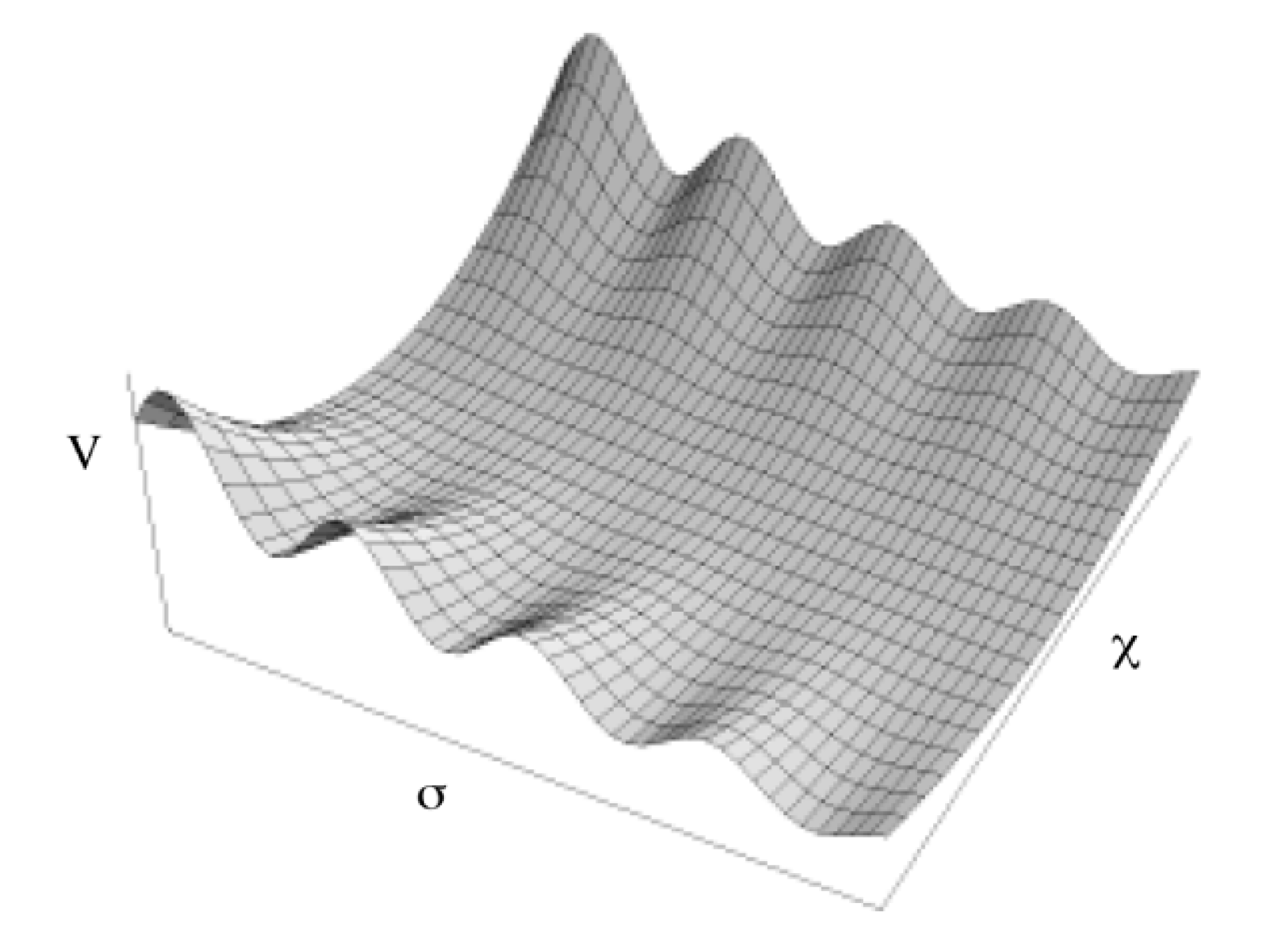
- Generally speaking, the accelerating universe we are now watching might be one of the repeated events, in the past or the future. Due to this feature, we may expect to lessen the weight of the coincidence problem, though by a little bit, not entirely.
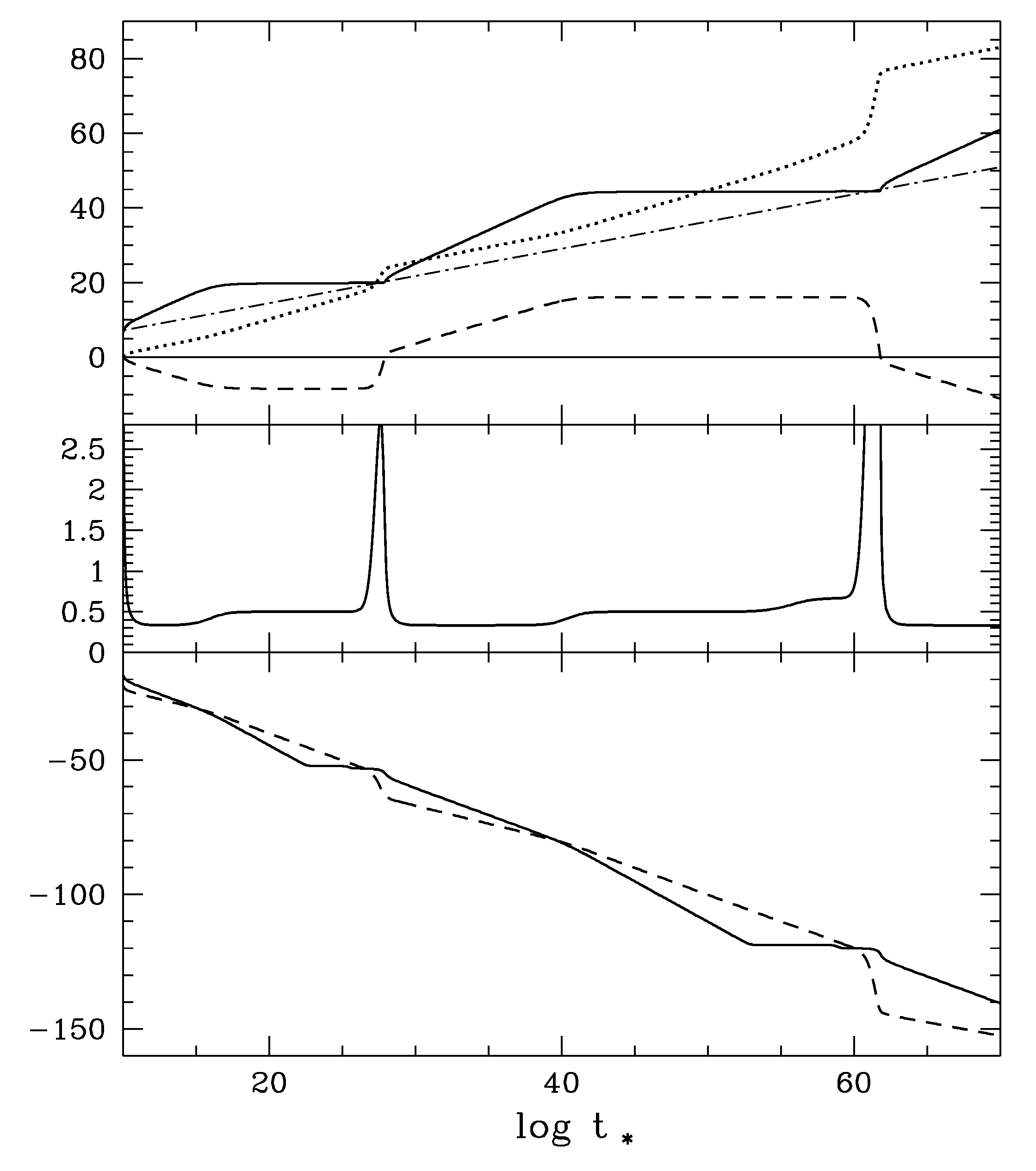
- The mini-inflations do occur as step-like behavior superimposed on the smooth and overall behaviors , as expected. The values of the height of each plateau, essentially for , are given basically by , with the times at which the mini-inflation occurred. This is because and falling off interlacingly with a common overall behavior as . The exact time of a mini-inflation is obviously determined by the height of the plateau, which depends critically on the parameter values at preceding times. For this reason exact timing of mini-inflations are hard to be determined theoretically. But once determined, the relation always follows, no matter when it occurs. This is what is truly meant by (4).
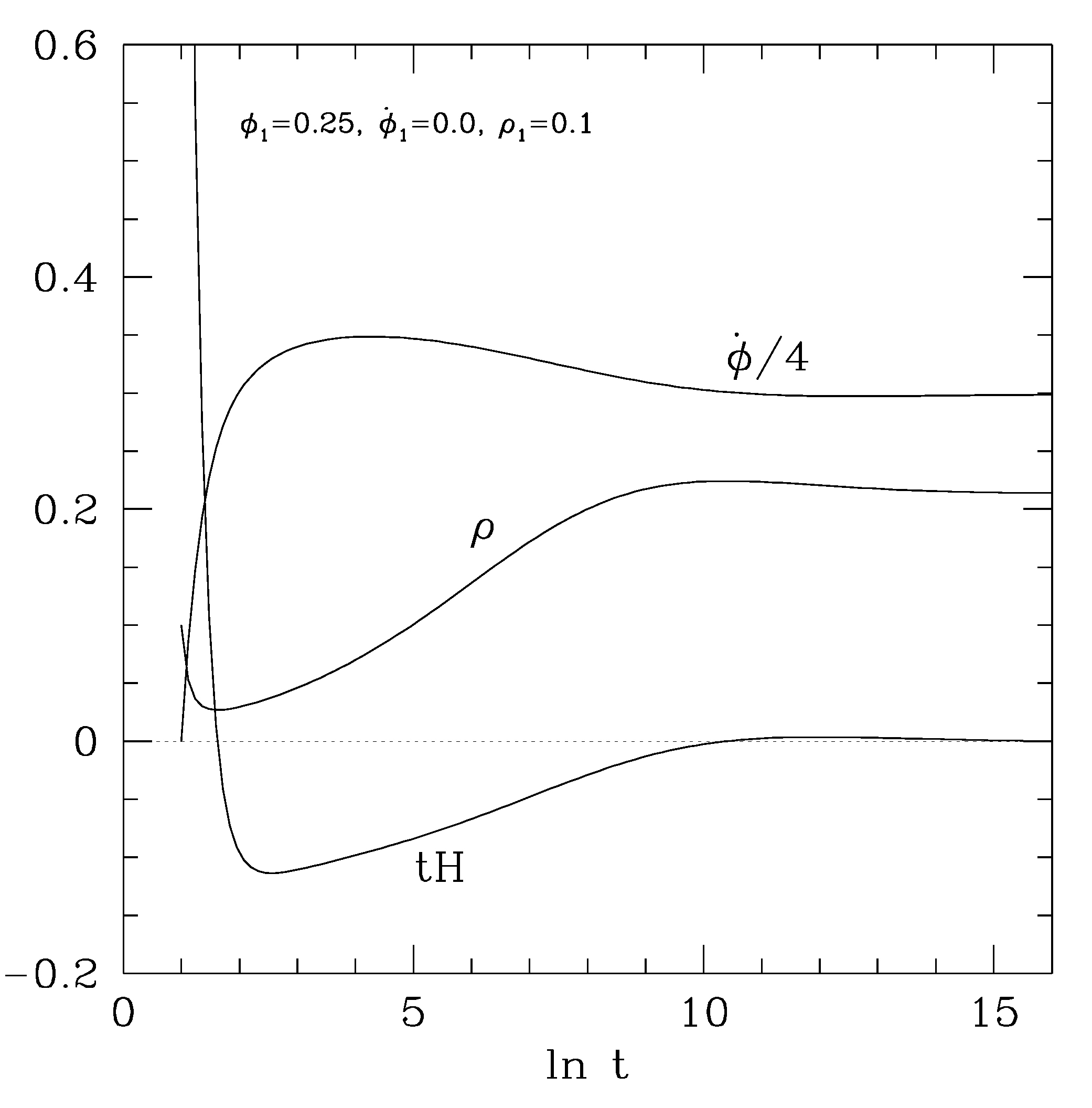
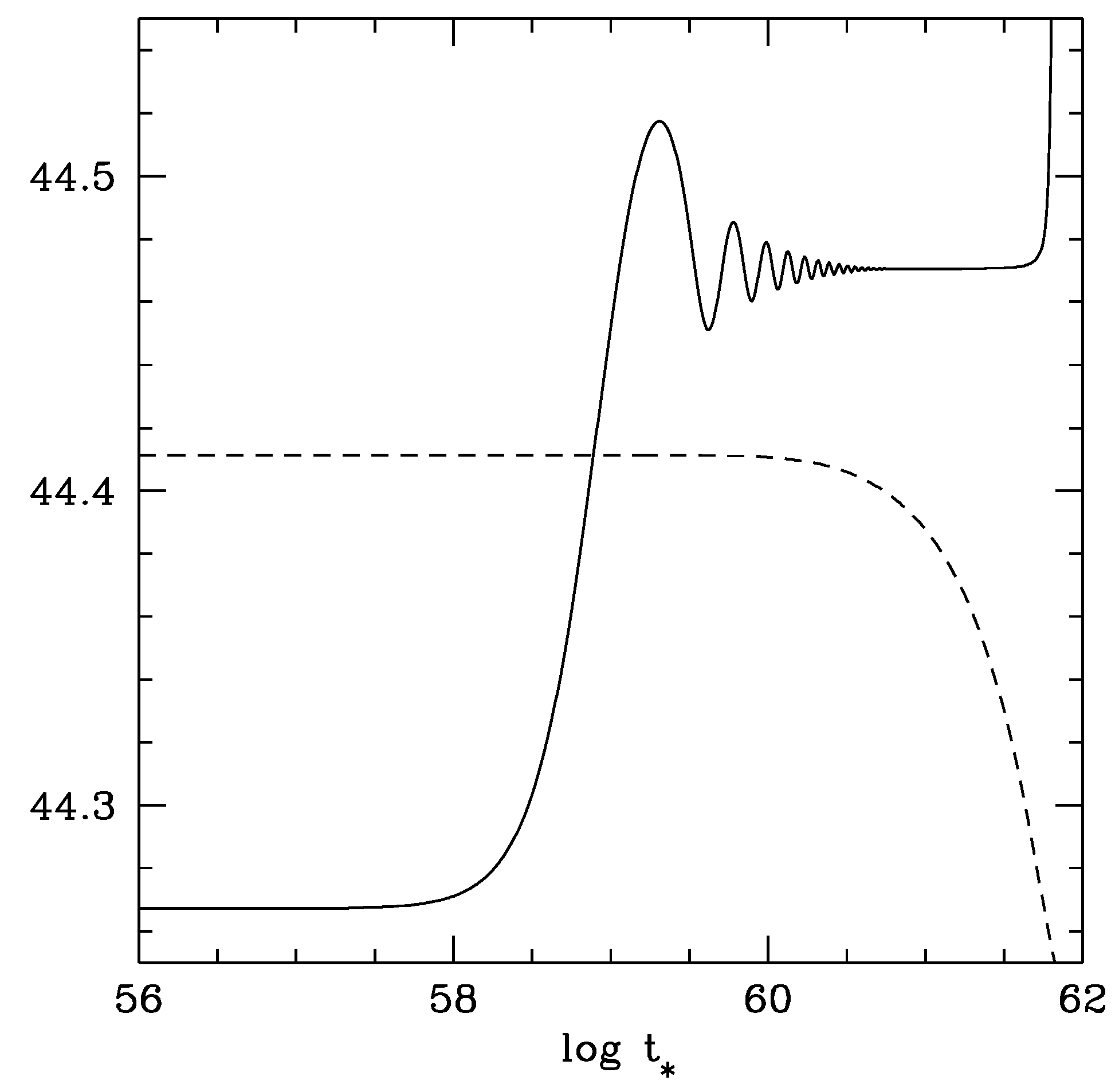
- At this point we take up again the question we asked ourselves toward the end of Section 1: Can we include the presence of a finite-range force between matter objects in a manner consistent with the cosmological evolution in terms of σ, which rolls slowly down the smooth slope of an exponential potential? The key of the points lies in noticing that we found the solution, as in the upper panel of Figure 9 in which σ varies in a range of the order unity in the Planckian units. Even the initial value is overwhelmingly larger than the value corresponding to the resonance; in the Planckian units. This implies that is completely outside the range corresponding to the entire history of the universe. In this sense a massive pseudo dilaton exerts a force nearly independent of the accelerating universe, in conformity with the former phenomenon belonging to the local physics, as we remarked.
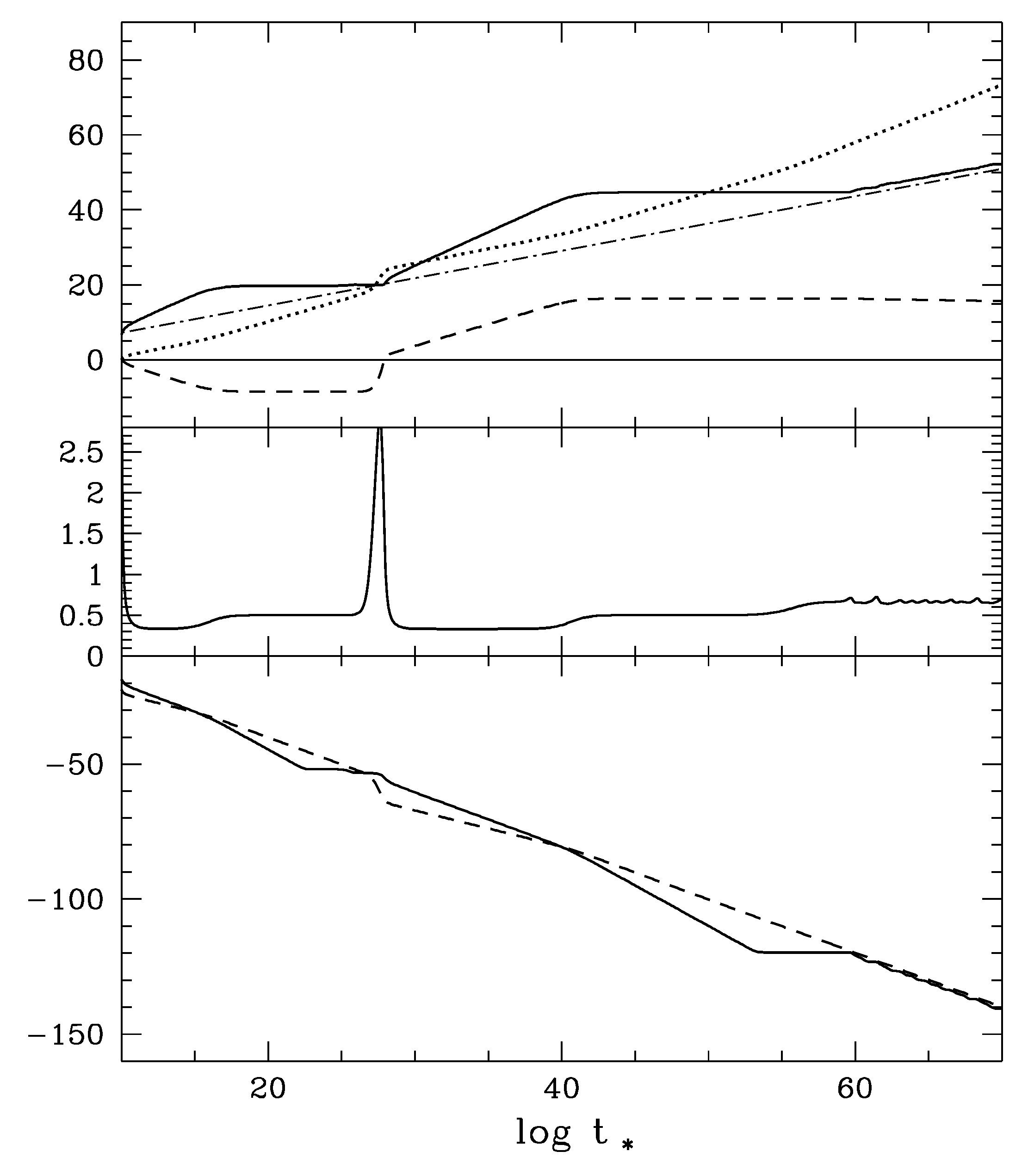
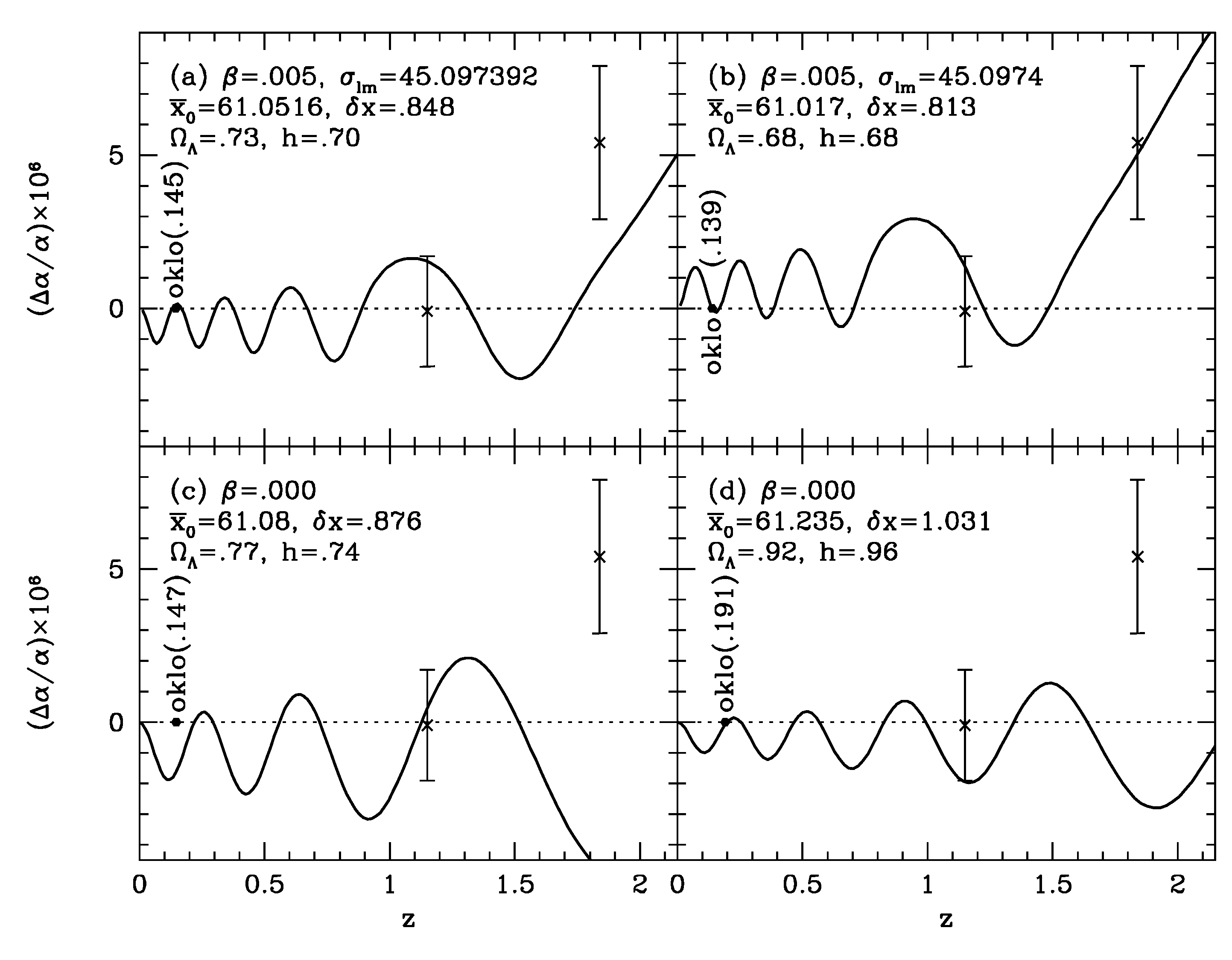
- There are so many different fine details as were discussed in Section 5.4.2. of [11]. We will make a comment particularly on Figure 11, in which the vertical scale is enlarged by more than 300 times of Figure 9, also with the horizontal scale by more than 10 times. Around the present time, what appears to be a little upward kink of σ (solid curve) in the upper panel of Figure 9 is magnified to reveal a small oscillatory structure unique to the trapping dynamics. This small variation of σ may be substituted to the RHS of the second equation of (93) to predict an oscillatory time-variation of the fine-structure constant, to be tested by near-future experiments [40,41,42,43,44]. In order to give an example, we are going to show a set of plots in Figure 12 calculated based on Figure 9 to be compared with the observation [46,47]. We expect that future experiments with improved accuracy will probe the proposed trapping mechanism probably with even better precision than in measuring the way of accelerating universe itself. It seems important to emphasize that we do provide with this way of observational verification, though our trapping mechanism implemented in terms of the potential (98) is not yet necessarily proved unique at present. For more recent observations on the ratio of the electron to the proton masses, see [49,50], and papers cited therein.
- The equations are highly nonlinear, as was discussed in [48] and also in 5.4.3 of [11]. As an example, an apparently repeated occurrence of mini-inflations, particularly its separations, or “frequencies”, are determined by the initial values or the parameters, in the presence of the cosmological friction, but not prepared in the starting Lagrangian like a harmonic oscillator, for example. Consequently, some of the final results may depend sharply on the choice of the initial values or the parameters. This might even be at odds with a traditional attitude that the cosmologically computed results on the present era should be as insensitive as possible to the initial states of the universe. But is anything wrong if certain aspect of the universe is as chaotic as what is happening daily around us? Some of the parameters have been fine-tuned, but not to the extreme extent of 120 orders of magnitude. We have obtained Figure 9, for example, after a few days of working on Mathematica. It might be still worth quoting, among others, that the occurrence of another mini-inflation around was a consequence of requiring none of the significant presence of in the era of primordial nucleo-synthesis around .
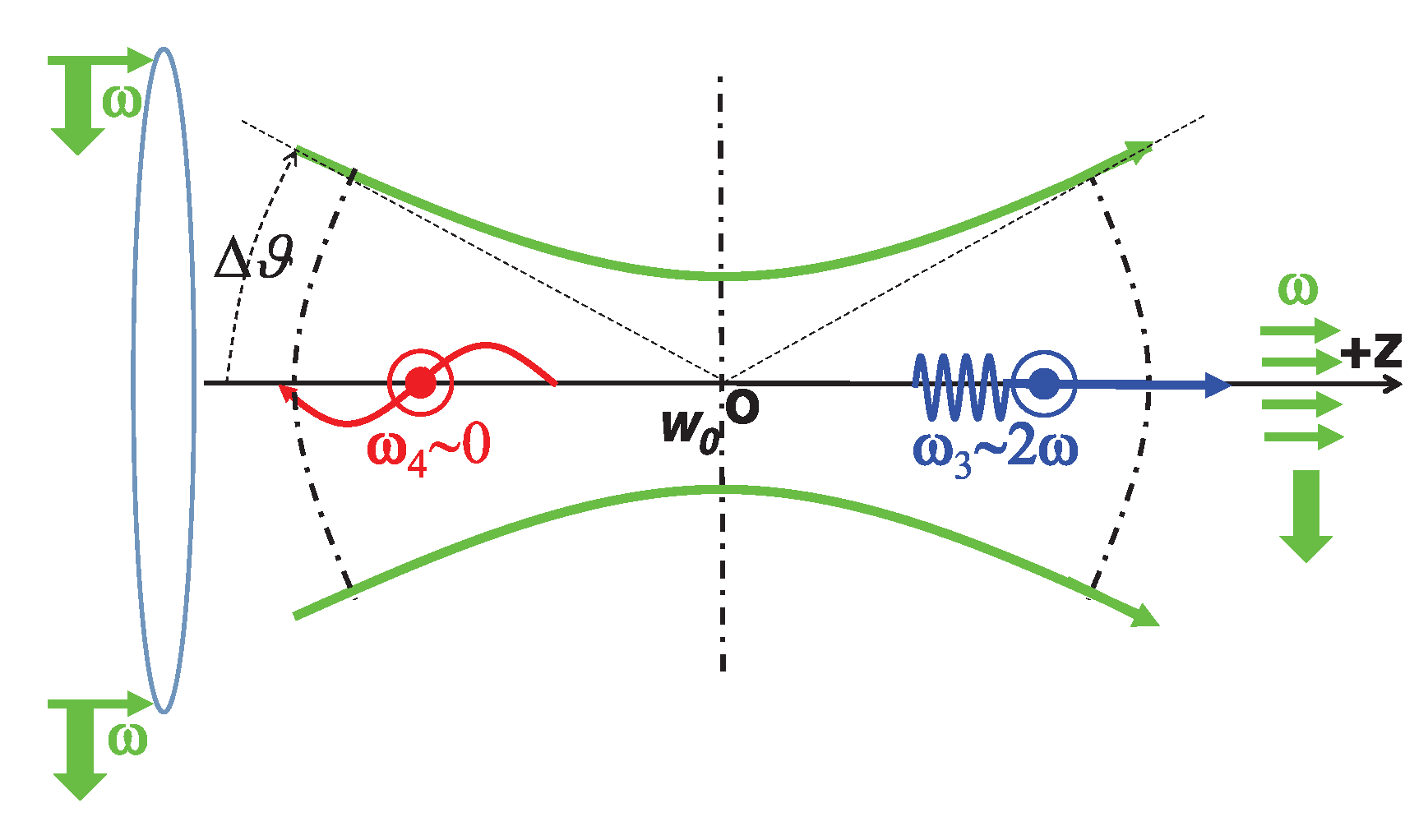
7. Proposed Experimental Search for the Scalar Field
8. Concluding Remarks
- The overall Scenario of a decaying cosmological constant is shown to be implemented naturally in E frame in terms of the simplest version of the scalar-tensor theory with the term of added in J frame, a model much simpler than any of those discussed by [54,55], for example. With the help of a rather phenomenological trapping mechanism, we reproduce a mini-inflation, with , undoubtedly a core of the message of the observed accelerating universe, leaving us free from the fine-tuning problem. This E frame is close to the physical conformal frame in which we have a constant unit of length/time provided by microscopic particles, with reference to which an expansion/acceleration of the universe is measured. We must be ready, however, to leave the long-held idea of the Brans–Dicke requirement, replacing it by another model of global scale invariance, thus allowing WEP violation expected to be somewhere below the directly available observational upper bounds.
- It is crucially important to recognize that the invariance just mentioned is broken spontaneously in which the gravitational scalar field plays a role of a dilaton, a pseudo NG boson, allowing us to understand two vastly different scales of size, cosmological and microscopic, in an entirely new perspective. Remarkably enough, this dilaton mediates a WEP violating force, likely with the finite range around the order of 100 m, or so. In order to search for it, we propose two types of the experiment; photon-photon scattering using strong laser beams, and time-dependent variation of the fine-structure constant and the ratio of the masses of electron and proton. As we also point out, the dilaton is responsible for providing us with the Higgs field in the Standard Model. It then follows that all the masses in the world have their common origin ultimately in the scalar field of the scalar-tensor theory, re-formulated to understand the observed accelerating universe.
- In this connection we recall a comic drawn by Sato [56] in 1983, when he symbolized a then new era of Unification inspired particularly by GUT (Grand Unified Theories), as reproduced in Figure 16. Decades later, we still appreciate the same comic, but this time reminding us of how strongly the cosmology is tied with the microscopic physics, specifically in terms of the choice of the physical conformal frame, a unique concept of the scalar-tensor theory, with the role of a dilaton.
- Also noteworthy is the importance of J frame, although it is not a physical frame. Above-mentioned scale-invariance is made visible in J frame, in which the radiation-dominated universe turns out to be static asymptotically. Obviously, J frame is an indispensable ingredient from a theoretical point of view. In this connection we point out that a string-theory model in higher-dimensional spacetime was shown in J frame, with , as indicated in Figure 1.
- We still know little about how various masses and other coupling constants vary with time beyond the lowest-order perturbation estimates. This might be a problem if we look deeper into the early universe. In the more practical side, on the other hand, we already have examples of “composite” units, like the Rydberg constant, the reduced mass multiplied with the electric charge, as pointed out in Subsection 5.1. Even different reduced masses might depend on time differently, if the leptons and quarks yield different variations. The presence by itself of a number of different units in this sense might be an issue from a more general point of view. The exercises attempted in Subsection 5.4 are expected to provide us with a first step toward possible complications. We should be prepared with other types of complications arising both from theoretical and phenomenological aspects.
- One of the aspects we failed to discuss from a truly more significant view is another possible origin of the cosmological constant; the vacuum energy expected from the relativistic quantum field theory, as was emphasized in [57], for example. In view of our success in understanding the scenario of a decaying cosmological constant as a theoretical goal, probably an entirely different approach appears to be called for. See, however, [58], for example.

Acknowledgments
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurement of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Tegmark, M.; Eisenstein, D.; Strauss, M.; Weinberg, D.; Blanton, M.; Frieman, J.; Fukugita, M.; Gunn, J.; Hamilton, A.; Knapp, G.; et al. Cosmological constraints from SDSS Luminous Red Galaxies. Phys. Rev. 2006, D74, 123507. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy—Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Jordan, P. Schwerkraft und Weltall (in German); Friedrich Vieweg und Sohn: Braunschweig, Germany, 1955. [Google Scholar]
- Fujii, Y. Origin of the gravitational constant and particle masses in a scale-invariant scalar-tensor theory. Phys. Rev. 1982, D26, 2580–2588. [Google Scholar] [CrossRef]
- Bertolami, O. Time dependent cosmological term. Nuovo Cim. 1986, B93, 36–42. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Fujii, Y.; Maeda, K. The Scalar-Tensor Theory of Gravitation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Nambu, Y. Axial vector current conservation in weak interactions. Phys. Rev. Lett. 1960, 4, 380–382. [Google Scholar] [CrossRef]
- Goldstone, J. Field theories with superconductor solutions. Nuovo Cim. 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Mack, G. Partially conserved dilatation current. Nucl. Phys. 1968, B5, 499–507. [Google Scholar] [CrossRef]
- Chiu, C.B.; Fujii, Y.; Wada, W.W. Scale invariance, Goldstone boson and f’ trajectory. Lett. Nuovo Cim. 1971, 1, 110–115. [Google Scholar] [CrossRef]
- Fujii, Y. Dilaton and possible non-Newtonian gravity. Nature Phys. Sci. 1971, 234, 5–7. [Google Scholar] [CrossRef]
- Fujii, Y. How successful can the scalar-tensor theory be in understanding the accelerating universe? In Presented at IPMU international conference Dark Energy, Kashiwa, Japan, 22–26 June 2009. arXiv:0908.4324.
- Fujii, Y.; Homma, K. An approach toward the laboratory search for the scalar field as a candidate of drak energy. Prog. Theor. Phys. 2011, 126, 531–553. [Google Scholar] [CrossRef]
- Fujii, Y.; Homma, K. Probing dark energy with high-intensity laser field. In Proceedings of XLI Int. Symp. Multiparticle Dynamics, Miyajima, Japan, 26–30 September 2011. Prog. Theor. Phys. Suppl. 2012, 193, 230–234. [Google Scholar] [CrossRef]
- Dirac, P.A. A new basis for cosmology. Proc. Roy. Soc. 1938, A165, 199–208. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using a radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Fujii, Y.; Sasaki, M. Gravitational scalar field coupled directly to the Maxwell field and its effect to solar-system experiments. Phys. Rev. 2007, D75, 064028. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equationn of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Wang, L.; Caldwell, R.R.; Ostriker, J.P.; Steinhardt, P.J. Cosmic concordnce of quintessence. Astroph. J. 2000, 530, 17–35. [Google Scholar] [CrossRef]
- Fujii, Y. Conformal transformation in the scalar-tensor theory applied to the acceleraing universe. Prog. Theor. Phys. 2007, 118, 983–1018. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Fujii, Y. Choosing a conformal frame in scalar-tensor theories of gravity with a cosmological constant. Prog. Theor. Phys. 1998, 99, 599–621. [Google Scholar] [CrossRef]
- Maeda, K.; Fujii, Y. Attractor universe in the scalar-tensor theory of gravitation. Phys. Rev. 2009, D79, 084026. [Google Scholar]
- Dolgov, D. An attempt to get rid of the cosmological constant. In The Very Early Universe, Proceedings of Nuffield Workshop; Gibbons, G.W., Siklos, S.T., Eds.; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Srednick, M. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fischbach, E.; Sudarsky, D.; Szafer, A.; Talmadge, C.; Aronson, H. Reanalysis of the Eötvös experiment. Phys. Rev. Lett. 1986, 56, 3–6. [Google Scholar] [CrossRef] [PubMed]
- Fischbach, E.; Talmadge, C. The Search for Non-Newtonian Gravity; AIP Press, Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Nishioka, T.; Fujii, Y. Inflation and the decaying cosmolgical constant. Phys. Rev. 1992, D45, 2140–2143. [Google Scholar]
- Fujii, Y.; Omote, M.; Nishioka, T. Time-dependent coupling constant in unfied theories? Prog. Theor. Phys. 1994, 92, 521–534. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. 1999, D59, 123504. [Google Scholar] [CrossRef]
- Fujii, Y.; Nishioka, T. Reconciling a small density parameter to inflation. Phys. Lett. B 1991, 254, 347–354. [Google Scholar] [CrossRef]
- Fujii, Y. How natural is a small but nonzero cosmological constant? Astropart. Phys. 1996, 5, 133–138. [Google Scholar] [CrossRef]
- Fujii, Y. Two-scalar model for a small but nonzero cosmological constant. Phys. Rev. 2000, D62, 064004. [Google Scholar] [CrossRef]
- Barreiro, T.; Copeland, E.J.; Nunes, N.J. Quintessence arising from exponential potentials. Phys. Rev. 2000, D61, 127301. [Google Scholar] [CrossRef]
- Fujii, Y. Revised fits to Δα/α in consistency with the accelerating universe. Phys. Lett. B 2009, 671, 207–210. [Google Scholar] [CrossRef]
- Fujii, Y.; Mizuno, S. Δα/α from QSO absorption lines. Int. J. Mod. Phys. 2005, D14, 677–885. [Google Scholar] [CrossRef]
- Fujii, Y. A possible new interpretation of the result of Δα/α from QSO absorption lines. Phys. Lett. B 2005, 616, 141–144. [Google Scholar] [CrossRef]
- Fujii, Y. Possible time variability of the fine-structure constant expected from the accelerating universe. Phys. Lett. B 2008, 660, 87–92. [Google Scholar] [CrossRef]
- Fujii, Y. Accelerating universe and the time-dependent fine-structure constant. In Proceedings of IAU General Assembly 2009, JD9 conference, Rio de Janeiro, Brazil, 3–14 August 2009; Molaro, P., Vangioni, E., Eds.; arXiv:0910.5090.
- Fujii, Y.; Iwamoto, A.; Fukahori, T.; Ohnuki, T.; Nakagawa, M.; Hidaka, H.; Oura, Y.; Möller, P. The nuclear interaction at Oklo 2 billion years ago. Nucl. Phys. 2000, B573, 377–401. [Google Scholar] [CrossRef]
- Levshakov, S.A.; Molaro, P.; Lopez, P.; D’Odorico, S.; Centurión, M.; Bonifacio, P.; Agafonova, I.I.; Reimers, D. A new measure of Δα/α at redshift z=1.84 from very high resolution spectra of Q1101-264. Astron. Astrophys. 2007, 466, 1077–1082. [Google Scholar]
- Porsev, S.G.; Koshelef, K.V.; Tupisyn, I.I.; Kozlov, M.G.; Reimers, D.; Levshakov, S.A. Transition frequency shifts with fine structure constant variation for Fe II: Breit and core-valence correlation corrections. Phys. Rev. 2007, A76, 052507. [Google Scholar] [CrossRef]
- Fujii, Y. Nonzero ΩΛ and a new type of the dissipative structure. In Proceedings of XXXIIIrd Rencontre de Moriond, Fundamental Parameters in Cosmology, Les Arcs, France, 17–24 January 1998. arXiv:gr-qc/9806089.
- Beloy, K.; Borschevsky, A.; Flambaum, V.V.; Schwerdfeger, P. Effect of α variation on a prospective experiment to detect variation of me/mp in diatomic molecules. Phys. Rev. 2011, A84, 042117. [Google Scholar] [CrossRef]
- Ilyushin, V.V.; Jansen, P.; Mikhail, J.; Kozlov, G.; Levshakov, S.A.; Kleiner, I.; Ubacks, W.; Bethlem, H.L. Sensitivity to a possible variation of the proton-to-electron mass ratio of torsion-wagging-rotation transition in Methylamine (CH3NH2). Phys. Rev. 2011, A84, 032505. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.-Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the equivalence principle using a rotating torsion balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Coherent and incoherent states of the radiation field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Homma, K. Sensitivity to Dark Energy candidates by searching for four-wave mixing of high-intensity lasers in the vacuum. Prog. Theor. Exp. Phys. 2012. submitted for publication. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Faraoni, V. A bird’s eye view of f(R)-gravity. The open astronomy juournal. arXiv2009. arXiv:0909.0895.
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144, arXiv:1011.0544. [Google Scholar] [CrossRef]
- Sato, F. Observing Universe Through a Microscope (in Japanese); Iwanami: Tokyo, Japan, 1983. [Google Scholar]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Fujii, Y. Mass of the dilaton and the cosmological constant. Prog. Theor. Phys. 2003, 110, 433–439. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fujii, Y. Accelerating Universe and the Scalar-Tensor Theory. Entropy 2012, 14, 1997-2035. https://doi.org/10.3390/e14101997
Fujii Y. Accelerating Universe and the Scalar-Tensor Theory. Entropy. 2012; 14(10):1997-2035. https://doi.org/10.3390/e14101997
Chicago/Turabian StyleFujii, Yasunori. 2012. "Accelerating Universe and the Scalar-Tensor Theory" Entropy 14, no. 10: 1997-2035. https://doi.org/10.3390/e14101997
APA StyleFujii, Y. (2012). Accelerating Universe and the Scalar-Tensor Theory. Entropy, 14(10), 1997-2035. https://doi.org/10.3390/e14101997



