Gibbs’ Paradox and the Definition of Entropy

Abstract

Gibbs’ Paradox is shown to arise from an incorrect traditional definition of the entropy that has unfortunately become entrenched in physics textbooks. Among its flaws, the traditional definition predicts a violation of the second law of thermodynamics when applied to colloids. By adopting Boltzmann’s definition of the entropy, the violation of the second law is eliminated, the properties of colloids are correctly predicted, and Gibbs’ Paradox vanishes.

1. Introduction

Gibbs’ Paradox [1,2,3] is based on a traditional definition of the entropy in statistical mechanics found in most textbooks [4,5,6]. According to this definition, the entropy of a classical system is given by the product of Boltzmann’s constant, k, with the logarithm of a volume in phase space. This is shown in many textbooks to lead to the following equation for the entropy of a classical ideal gas of distinguishable particles,

(1)

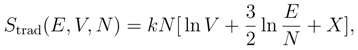where X is a constant. Most versions of Gibbs’ Paradox, including the one I give in this section, rest on the fact that Eq. 1 is not extensive. There is another version of Gibbs’ Paradox that involves the mixing of two gases, which I will discuss in the third section of this paper.

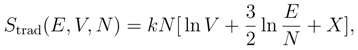
Discussions of Gibbs’ Paradox tend to be fairly abstract. I would like to make my argument concrete by applying the traditional definition of the entropy to a physical system for which Gibb’s Paradox has clear implications. Any colloid would do for this purpose [7]; glue, paint, ink, or blood could be used, but I will choose homogenized milk. The fat globules have a diameter of about one micron, which is large enough to obey classical mechanics. They are distinguishable particles, not only because they obey classical mechanics, but also because different particles generally contain different arrangements of atoms, different impurities, and even different numbers of atoms. The exchange of two particles produces a different microscopic state, so milk (and other colloids) should be described by the classical statistical mechanics of distinguishable particles.

To see why the traditional definition of the entropy is a problem, consider its application to a container of homogenized milk. The entropy of fat globules in the milk should be given by Eq. 1. If we insert a partition into the container so that it is divided into two parts, each with volume V/2, the entropy of each part would be

(2)

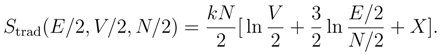The change in entropy upon inserting the partition is then

(3)

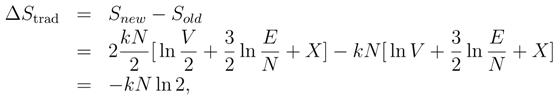which — being negative — would represent a violation of the second law of thermodynamics. This is one aspect of what is known as Gibbs’ Paradox.

However, Eq. 3 does not really present us with a paradox; it presents us with a proof that the traditional definition of the entropy is untenable. Unless we are willing to give up the second law, we must abandon the definition of entropy in terms of a volume in phase space.

2. Boltzmann’s definition of the entropy

Although Boltzmann never addressed Gibbs’ Paradox directly, his approach to statistical mechanics provides a solid basis for its resolution. Boltzmann defined the entropy in terms of the probability of the macroscopic state of a composite system [8,9,10]. Although the traditional definition of the entropy is often attributed to Boltzmann, this attribution is not correct. The equation on Boltzmann’s tombstone, S = k log W , which is sometimes called in evidence, was never written by Boltzmann and does not refer to the logarithm of a volume in phase space. The equation was first written down by Max Planck, who correctly attributed the ideas behind it to Boltzmann [11,12]. Planck also stated explicitly that the symbol “W” stands for the German word “Wahrscheinlichkeit” (which means probability) and refers to the probability of a macroscopic state.

The dependence of Boltzmann’s entropy on the number of particles requires the calculation of the probability of the number of distinguishable particles in the each subsystem of a composite system. The calculation of this probability requires the inclusion of the binomial coefficent, N!/N₁!N₂!, where N₁ and N₂ are the numbers of particles in each subsystem and N = N₁ + N₂. This binomial coefficient is the origin of the missing factor of 1/N! in the traditional definition, and leads to an expression for the entropy that is extensive [9,10].

(4)

Boltzmann’s entropy is consistent with the second law of thermodynamics [8,9,10]. It is easy to see for the example given above that the change in Boltzmann’s entropy is zero when a container of milk is partitioned.

3. Gibbs’ Paradox and the entropy of mixing

The discussion above has concentrated on those versions of Gibbs’ Paradox that rest on the fact that Eq. 1 is not extensive. There is another version that is concerned with the mixing of two gases whose properties are imagined to change continuously from being different to being the same. This “paradox” consists of a discomfort with the entropy of mixing going to zero discontinuously as the properties become the same. Adopting Boltzmann’s definition of entropy also resolves this version of Gibbs’ Paradox.

Since Boltzmann’s definition of the entropy involves probabilities, it must reflect our knowledge (or ignorance) of the microscopic state. This is completely appropriate, since entropy is a description of our knowledge of the properties of a thermodynamic system, rather than a property of the system itself. The dependence of entropy on available information has been most clearly illustrated by Jaynes in his delightful discussion of the properties of the “superkalic elements” Whifnium and Whoofnium, which is too well known to need repetition here [13]. For any given experiment, there either is, or is not, available information on possible differences between types of particles. Since there are only two possibilities for whether or not the particle types are known to be the same, it is neither surprising nor paradoxical that the entropy of mixing changes discontinuously between the two cases [14].

4. Conclusions

If we reject the traditional textbook definition of the entropy in terms of a volume in phase space and adopt Boltzmann’s definition in terms of the probability of the macroscopic state of a composite system, the statistical mechanics of both classical and quantum systems acquire a solid foundation. There is no violation of the second law of thermodynamics. The entropy of colloids is correctly calculated and predicted to be extensive. And Gibbs’ Paradox vanishes.