Prediction of the Non-Reducing Biomineralization of Nuclide–Microbial Interactions by Machine Learning: The Case of Uranium and Bacillus subtilis
Abstract
:1. Introduction
2. Method
2.1. Data Extraction and Dataset Construction
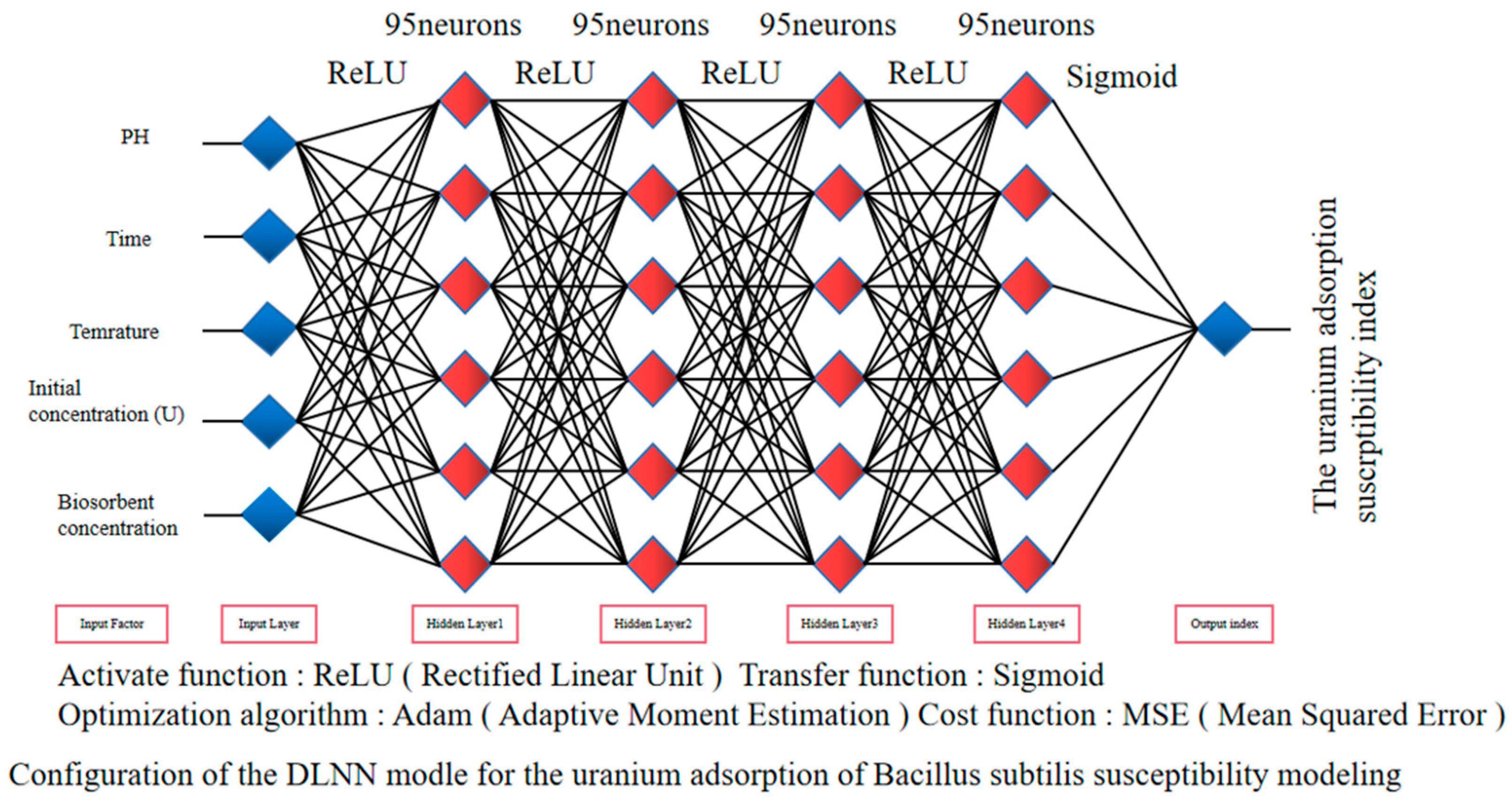
2.2. Fully Connected Deep Neuron Network (DNN)
2.3. Model Validation Analysis
2.4. Loss Function
2.5. Sensitivity Analysis
2.6. Statistical Analysis
3. Results
3.1. Construction of a Database for Machine Learning
3.2. Construction of a DLNN Model for Uranium Adsorption by Bacillus subtilis
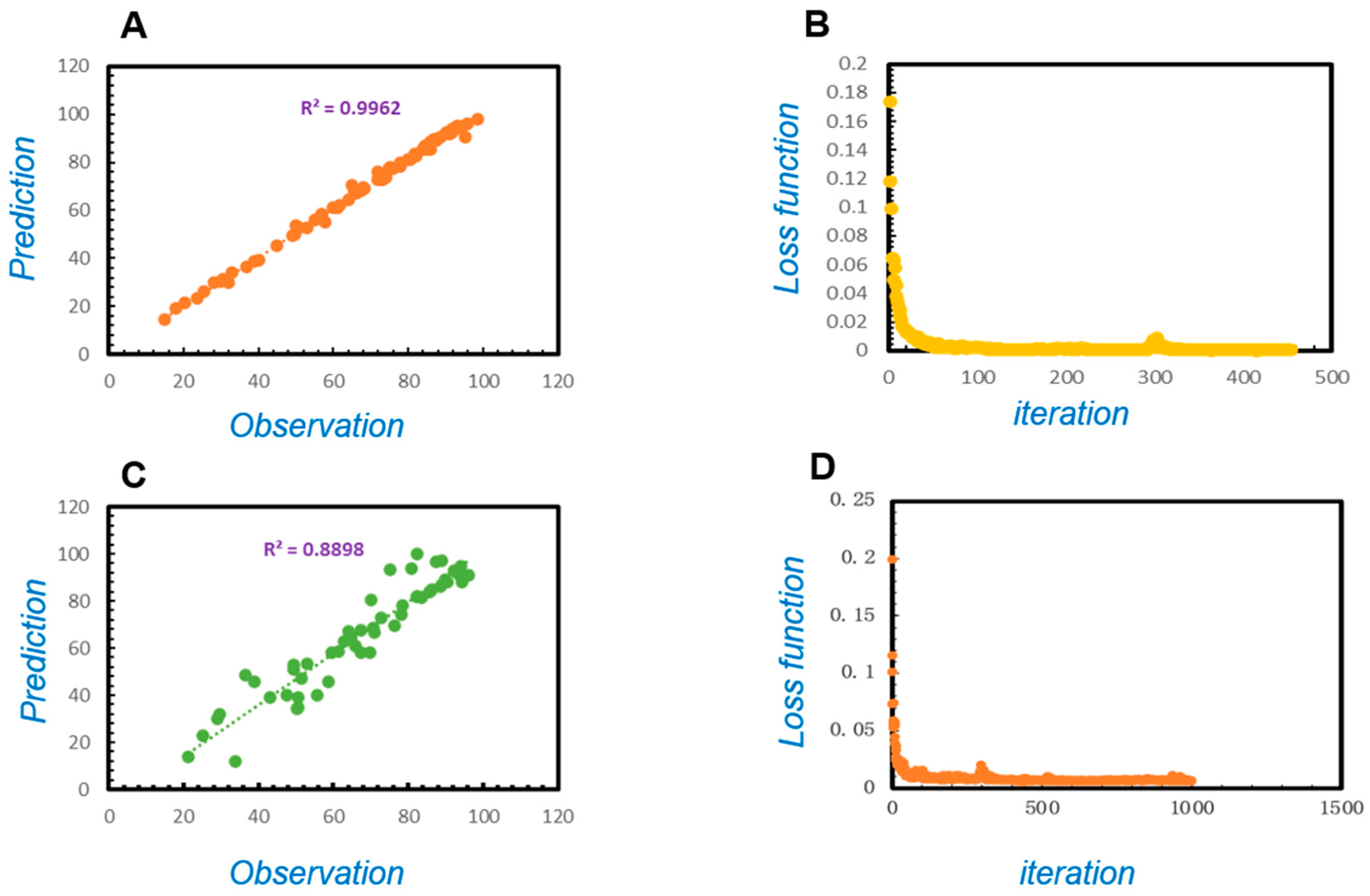
3.3. The Evaluation of the Model Prediction Performance
3.4. Sensitivity Analysis of the Model
3.5. Sensitivity Analysis of the Model at Different pH Values
4. Discussions
4.1. A DLNN Neural Network Model with Good Predictive Performance Is Constructed
4.2. pH Value Is the Main Factor Affecting Non-Reducing Uranium Mineralization
4.3. Sensitivity Analysis Under Different pH Values
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kolhe, N.; Zinjarde, S.; Acharya, C. Responses exhibited by various microbial groups relevant to uranium exposure. Biotechnol. Adv. 2018, 36, 1828–1846. [Google Scholar] [CrossRef]
- Coelho, E.; Reis, T.A.; Cotrim, M.; Mullan, T.K.; Corrêa, B. Resistant fungi isolated from contaminated uranium mine in Brazil shows a high capacity to uptake uranium from water. Chemosphere 2020, 248, 126068. [Google Scholar] [CrossRef]
- Zexin, W.; Hao, S.; Youliang, C.; Jiye, S.; Mingcai, H.; Qi, L.; Qianmin, D.; Huijie, Y. Uranium resource of Europe: Development status, metallogenic provinces and geodynamic setting. Energy Strategy Rev. 2024, 54, 101467. [Google Scholar]
- Xi, X.; Wang, Z.; Zhou, L.; Song, H.; Han, Y.; Dong, F.; Zhou, L. Rapid removal of uranium (VI) by phosphogypsum immobilized sulfate-reducing bacteria microspheres. Chem. Eng. J. 2024, 493, 152676. [Google Scholar] [CrossRef]
- Banala, U.K.; Das, N.P.I.; Padhi, R.K.; Toleti, S.R. Alkaliphilic bacteria retrieved from uranium mining effluent: Characterization, U sequestration and remediation potential. Environ. Technol. Innov. 2021, 24, 101893. [Google Scholar] [CrossRef]
- Luo, M.; Dong, Y.; Kang, C.; Li, X.; Wang, W. Research Progress of Uranium Valence Analysis. Uranium Geol. 2023, 39, 153–162. [Google Scholar]
- Hou, W. Review of study on treatment technology for the radioactive uranium-bearing wastewater. In Proceedings of the National Uranium Mining Base Construction Symposium (Part 2), Haikou, China, 20 December 2012; p. 5. [Google Scholar]
- Guo, Y.; Li, X.; Tu, H.; Zeng, Q.; Chen, S.; Gong, J.; Zeng, J.; Li, F.; Lan, T.; Bian, F.; et al. Insight into the complexation of uranium with Bacillus sp. dwc-2 by multi-spectroscopic approaches: FT-IR, TRLF and XAFS spectroscopies. J. Mol. Struct. 2025, 1321, 140145. [Google Scholar] [CrossRef]
- Munoz, J.A.; Gonzalez, F.; Blazquez, M.L.; Ballester, A. A study of the bioleaching of a Spanish uranium ore. Part I A Rev. Bact. Leaching Treat. Uranium Ores. Hydrometall. 1995, 38, 39–57. [Google Scholar]
- Mumtaz, S.; Streten-Joyce, C.; Parry, D.L.; McGuinness, K.A.; Lu, P.; Gibb, K.S. Fungi outcompete bacteria under increased uranium concentration in culture media. J. Environ. Radioact. 2013, 120, 39–44. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, R.; Ding, C.; Wang, X.; Cheng, W.; Chen, C.; Wang, X. Adsorption of U(VI) on sericite in the presence of Bacillus subtilis: A combined batch, EXAFS and modeling techniques. Geochim. Cosmochim. Acta J. Geochem. Soc. Meteorit. Soc. 2016, 180, 51–65. [Google Scholar] [CrossRef]
- Sboev, A.; Sboeva, S.; Moloshnikov, I.; Gryaznov, A.; Rybka, R.; Naumov, A.; Selivanov, A.; Rylkov, G.; Ilyin, V. Analysis of the Full-Size Russian Corpus of Internet Drug Reviews with Complex NER Labeling Using Deep Learning Neural Networks and Language Models. Appl. Sci. 2022, 12, 491. [Google Scholar] [CrossRef]
- Xia, J. Construction and implementation of music recommendation model utilising deep learning artificial neural network and mobile edge computing. Int. J. Grid Util. Comput. 2022, 13, 183–194. [Google Scholar] [CrossRef]
- Band, S.S.; Janizadeh, S.; Chandra Pal, S.; Saha, A.; Chakrabortty, R.; Shokri, M.; Mosavi, A. Novel ensemble approach of deep learning neural network (DLNN) model and particle swarm optimization (PSO) algorithm for prediction of gully erosion susceptibility. Sensors 2020, 20, 5609. [Google Scholar] [CrossRef]
- Chen, S. Exploration of artistic creation of Chinese ink style painting based on deep learning framework and convolutional neural network model. Soft Comput. 2020, 24, 7873–7884. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Saha, A.; Chakrabortty, R.; Roy, P. Evaluation of different DEMs for gully erosion susceptibility mapping using in-situ field measurement and validation. Ecol. Inform. 2021, 65, 101425. [Google Scholar] [CrossRef]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Gholami, D.M.; Pham, B.T. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. Catena 2020, 188, 104451. [Google Scholar] [CrossRef]
- Fu, J.; Chiba, Y.; Nose, T.; Ito, A. Automatic assessment of English proficiency for Japanese learners without reference sentences based on deep neural network acoustic models. Speech Commun. 2020, 116, 86–97. [Google Scholar] [CrossRef]
- Liu, C.; Kong, D.; Wang, S.; Wang, Z.; Li, J.; Yin, B. Deep3D reconstruction: Methods, data, and challenges. Front. Inf. Technol. Electron. Eng. 2021, 22, 652–672. [Google Scholar] [CrossRef]
- Amerineni, R.; Gupta, R.S.; Gupta, L. CINET: A Brain-Inspired Deep Learning Context-Integrating Neural Network Model for Resolving Ambiguous Stimuli. Brain Sci. 2020, 10, 64. [Google Scholar] [CrossRef]
- Jia, W.; Wei, Z. Short Term Prediction Model of Environmental Parameters in Typical Solar Greenhouse Based on Deep Learning Neural Network. Appl. Sci. 2022, 12, 12529. [Google Scholar] [CrossRef]
- Narayanan, S.N.; Subbian, S. HH model based smart deep brain stimulator to detect, predict and control epilepsy using machine learning algorithm. J. Neurosci. Methods 2023, 389, 109825. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Qiao, K.; Wang, L.; Tong, L.; Hu, G.; Zhang, R.Y.; Yan, B. A visual encoding model based on deep neural networks and transfer learning for brain activity measured by functional magnetic resonance imaging. J. Neurosci. Methods 2019, 325, 108318. [Google Scholar] [CrossRef]
- Li, C. Research on Abnormal Situation Recognition in Ethylene Cracking Process Based on Deep Learning of Multi-Structured Data. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2019. [Google Scholar]
- Zhang, H.; Liu, C.; Hong, Q.; Wang, K.; Wang, H. Research progress of artificial neural network for membrane fouling prediction in MBR. Ind. Water Treat. 2022, 42, 15–23. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, L.; Yan, H.; Fu, P. A deep neural network-based method for on-chip detection of in vivo Symbiodinium. J. Trop. Biol. 2022, 13, 451–456. [Google Scholar]
- Binbin, X.; Jun, W. Protein modeling and design based on deep learning. Chin. J. Biotechnol. (Sheng Wu Gong Cheng Xue Bao) 2021, 37, 3863–3879. [Google Scholar]
- Jiao, S. Research on the Prediction of lncRNA-Protein Interaction Based on Deep Learning of Multiple Type Features. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Wang, X.; Song, X.; Yang, T. Application of Depth Learning Neural Network in Pipeline Fault Diagnosis. Saf. Environ. Eng. 2018, 25, 137–148. [Google Scholar]
- Yan, Y. Research on neural network embedded learning control. Master’s Thesis, Northeast Electric Power University, Jilin, China, 2022. [Google Scholar] [CrossRef]
- Amemiya, A.; Shlok, M.; Miyoshi, T. Application of recurrent neural networks to model bias correction: Idealized experiments with the Lorenz-96 model. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003164. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.-T.; Van Liem, N.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Galeone, A.; Devime, F.; Chapon, V.; Mohamed, L.; Merroun, C.A.; Ravanel, S.; Bourguignon, J. Uranium-tolerant soil bacteria protect Arabidopsis thaliana seedling growth from uranium toxicity. Environ. Exp. Bot. 2024, 225, 105831. [Google Scholar] [CrossRef]
- Song, J.; Han, B.; Song, H.; Yang, J.; Zhang, L.; Ning, P.; Lin, Z. Nonreductive biomineralization of uranium by Bacillus subtilis ATCC–6633 under aerobic conditions. J. Environ. Radioact. 2019, 208–209, 106027. [Google Scholar] [CrossRef]

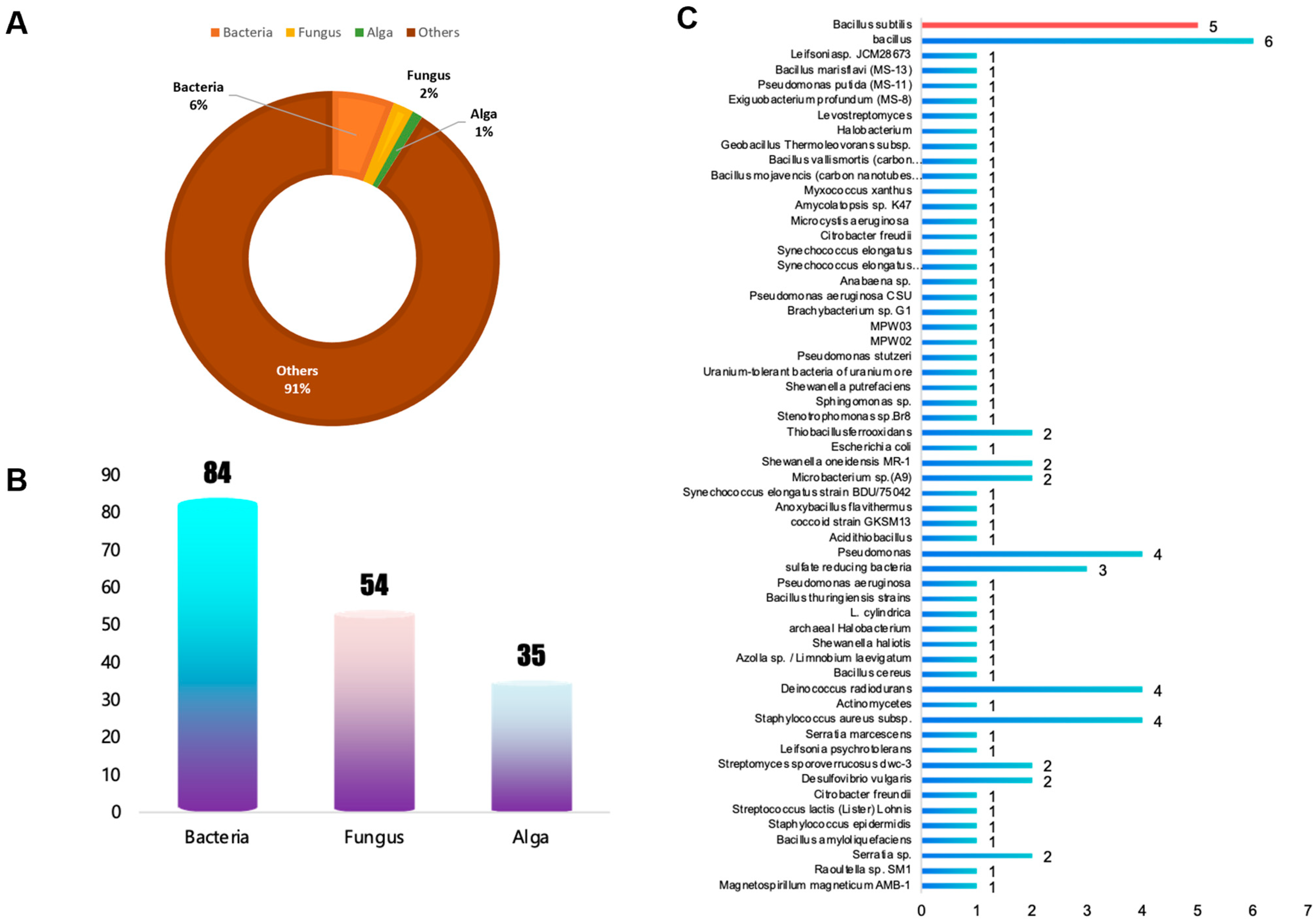


| Variable | Min | Max | Median | Mean | SD |
|---|---|---|---|---|---|
| Temperature/k | 283 | 313 | 298 | 300.1128 | 3.776966 |
| pH | 1.3 | 11 | 4.9 | 5.56391 | 2.319721 |
| Time/h | 0.5 | 3 | 0.5 | 1.097744 | 0.978065 |
| Initial concentration U/(mg/L) | 1 | 300 | 20 | 46.10526 | 70.85008 |
| Biosorbent concentration/(mg/L) | 0.125 | 1.5 | 0.5 | 0.582068 | 0.387437 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, S.; Liu, L.; Li, S.; Wang, S.; Huang, X.; Yang, J.; Song, J.; Zhang, Y.; Huang, Y.; Fan, Q. Prediction of the Non-Reducing Biomineralization of Nuclide–Microbial Interactions by Machine Learning: The Case of Uranium and Bacillus subtilis. Toxics 2025, 13, 305. https://doi.org/10.3390/toxics13040305
Qiang S, Liu L, Li S, Wang S, Huang X, Yang J, Song J, Zhang Y, Huang Y, Fan Q. Prediction of the Non-Reducing Biomineralization of Nuclide–Microbial Interactions by Machine Learning: The Case of Uranium and Bacillus subtilis. Toxics. 2025; 13(4):305. https://doi.org/10.3390/toxics13040305
Chicago/Turabian StyleQiang, Shirong, Leijin Liu, Siqi Li, Shuang Wang, Xinyang Huang, Jiaxin Yang, Jiayu Song, Yue Zhang, Yongxiang Huang, and Qiaohui Fan. 2025. "Prediction of the Non-Reducing Biomineralization of Nuclide–Microbial Interactions by Machine Learning: The Case of Uranium and Bacillus subtilis" Toxics 13, no. 4: 305. https://doi.org/10.3390/toxics13040305
APA StyleQiang, S., Liu, L., Li, S., Wang, S., Huang, X., Yang, J., Song, J., Zhang, Y., Huang, Y., & Fan, Q. (2025). Prediction of the Non-Reducing Biomineralization of Nuclide–Microbial Interactions by Machine Learning: The Case of Uranium and Bacillus subtilis. Toxics, 13(4), 305. https://doi.org/10.3390/toxics13040305






