Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement
Abstract
:1. Introduction
2. Methods
2.1. Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement
2.1.1. Modeling of the Construction Steps and Construction Structure Grouping Principles
2.1.2. Determination of the Value of Temperature Action Based on Staged Measurements
2.1.3. Construction Force Feedback Considering Staged Temperature Action
2.2. Shenzhen Nanshan Science and Technology Innovation Center Project Profile
2.2.1. Project Overview
2.2.2. Construction Program and Difficulties
- (1)
- The steel truss diagonal bracing of the podium goes through the 7–11th floors, as shown in Figure 2. There are many subsections of the components, the node form and stress condition are complicated, and the construction accuracy of the on-site installation must be high.
- (2)
- Temporary supports are used during construction, and the structure undergoes complex force transformations during installation and unloading, making it difficult to assess the mechanical state.
- (3)
- The construction period is long, the temperature change is obvious, and the structure belongs to statically indeterminate large-span continuous steel structures. Furthermore, there is a significant temperature effect.
3. Structural Construction Monitoring Program and Monitoring Data
3.1. Construction Monitoring Program
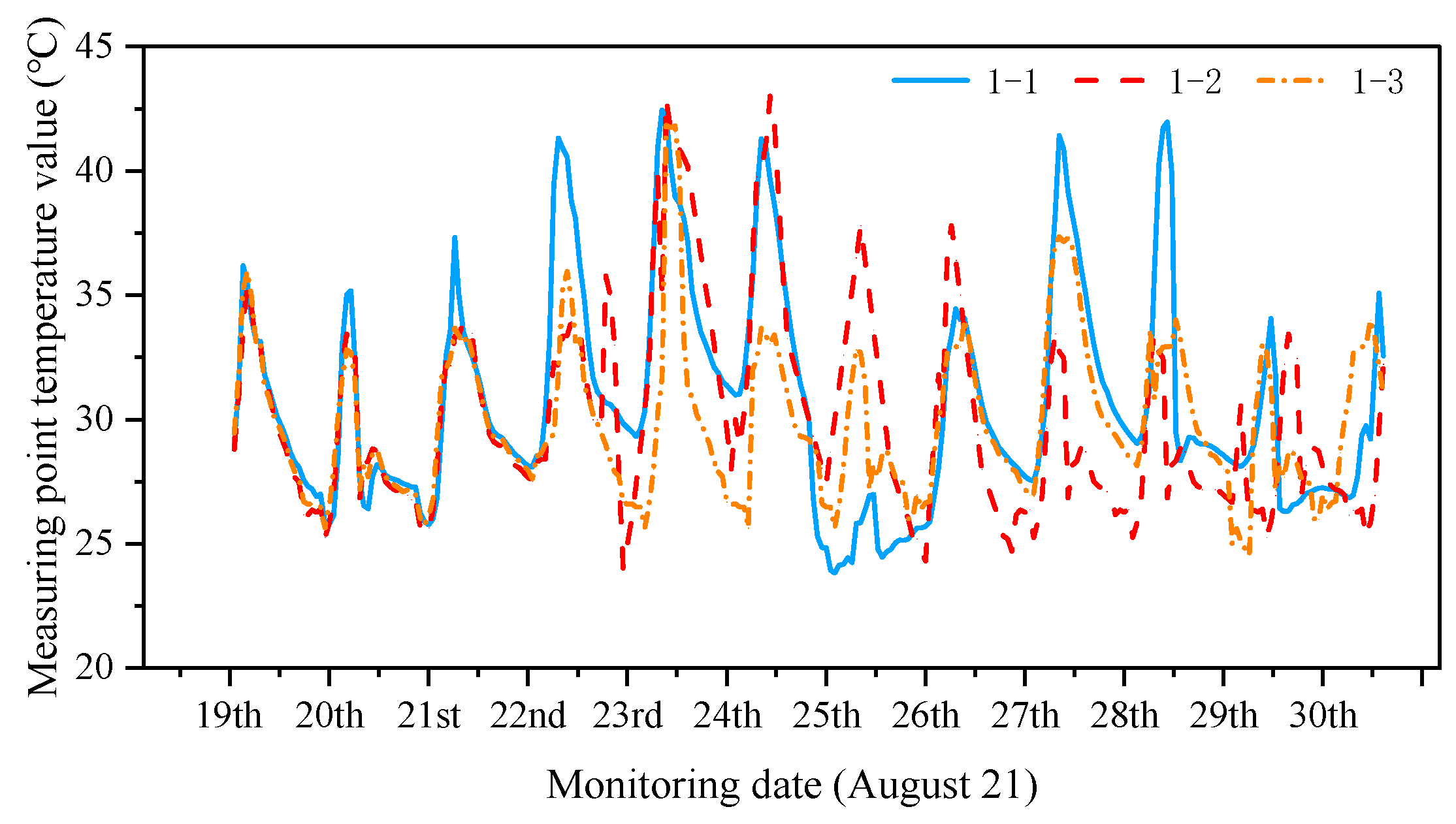
3.2. Temperature Measurement
3.3. Modeling of Structural Construction in Phases
3.4. Structural Grouping
3.5. Temperature-Actuated Condition Control
4. Structural Construction Force Feedback
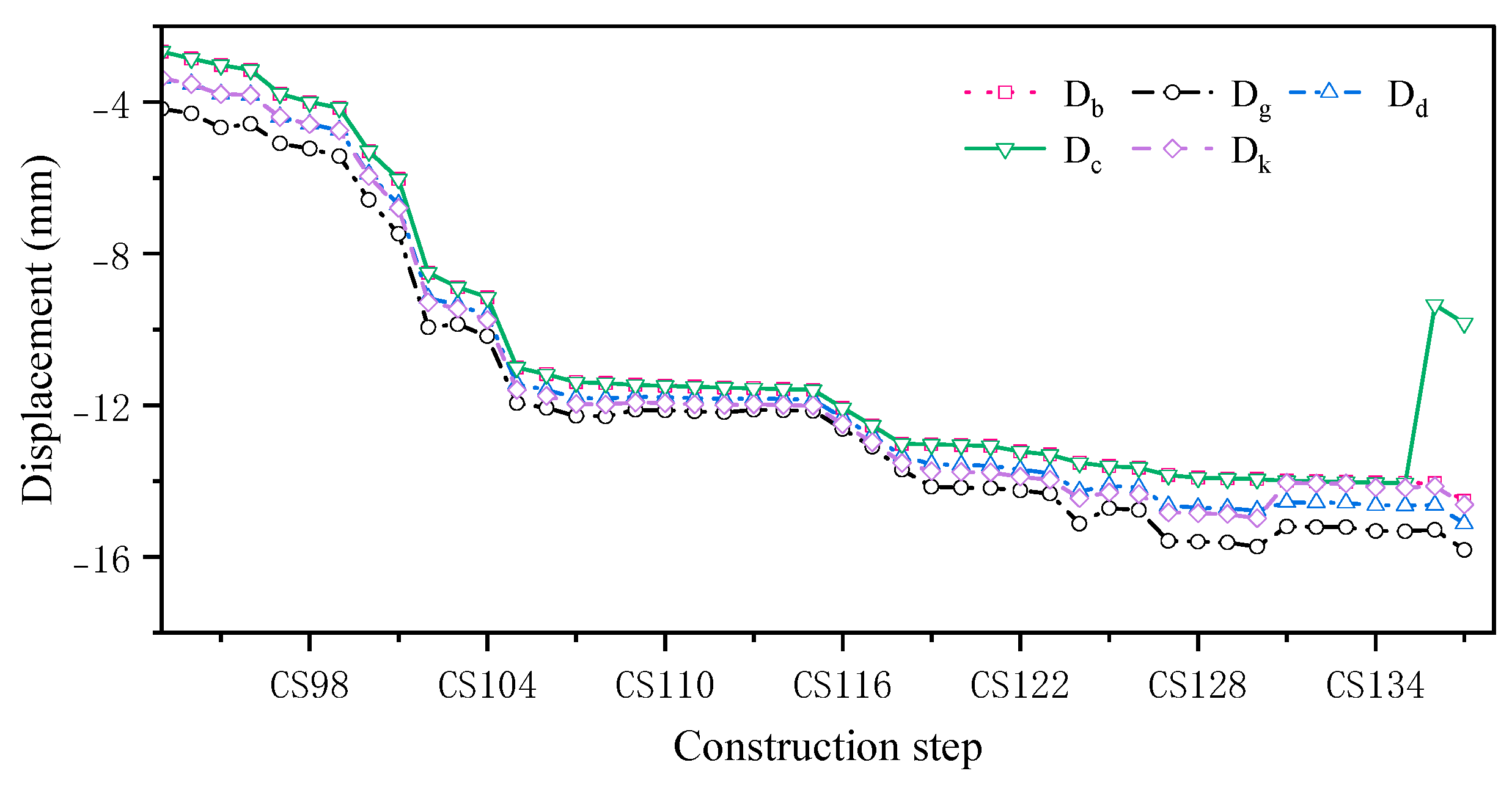
4.1. Displacement Analysis
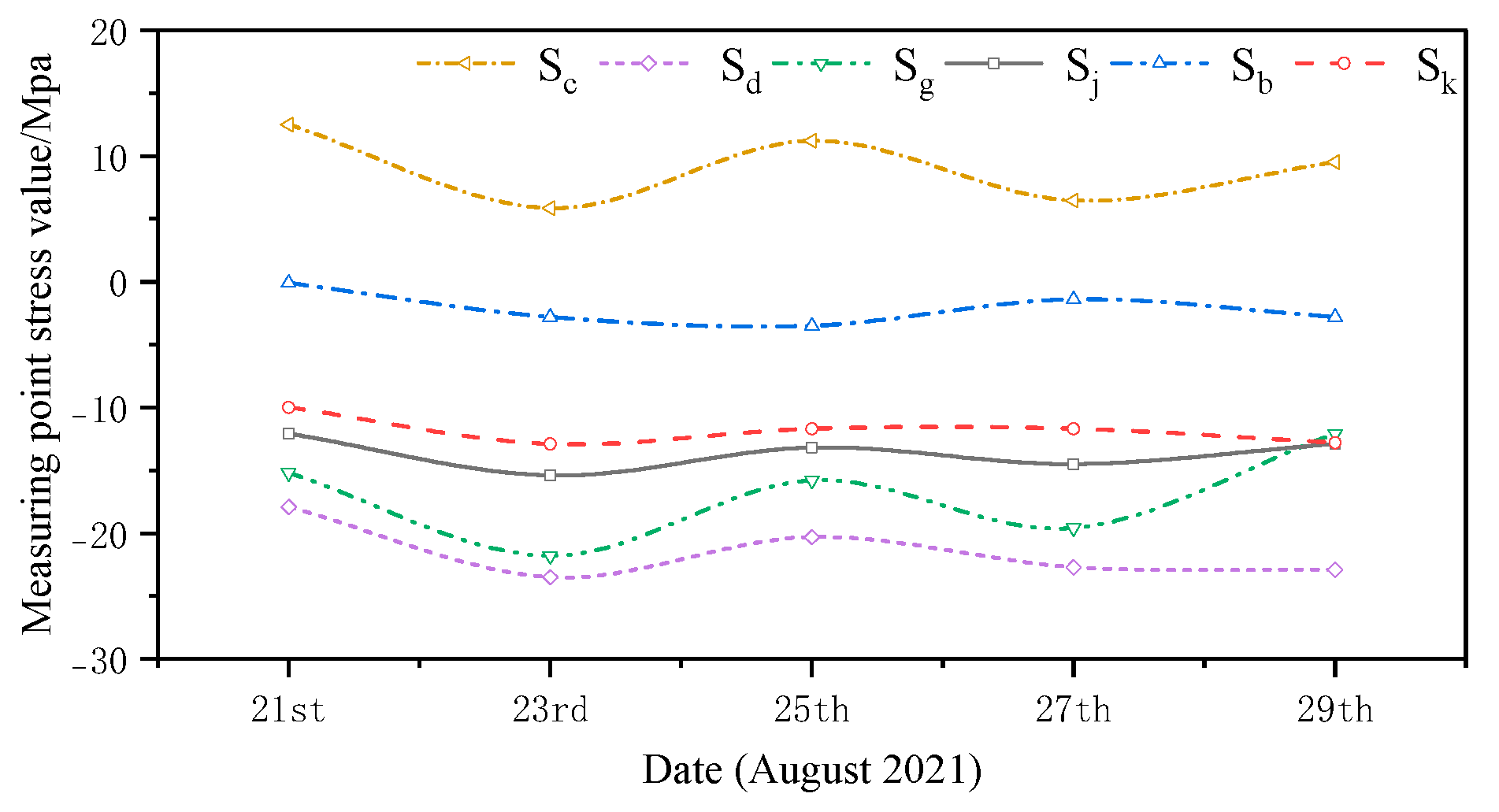
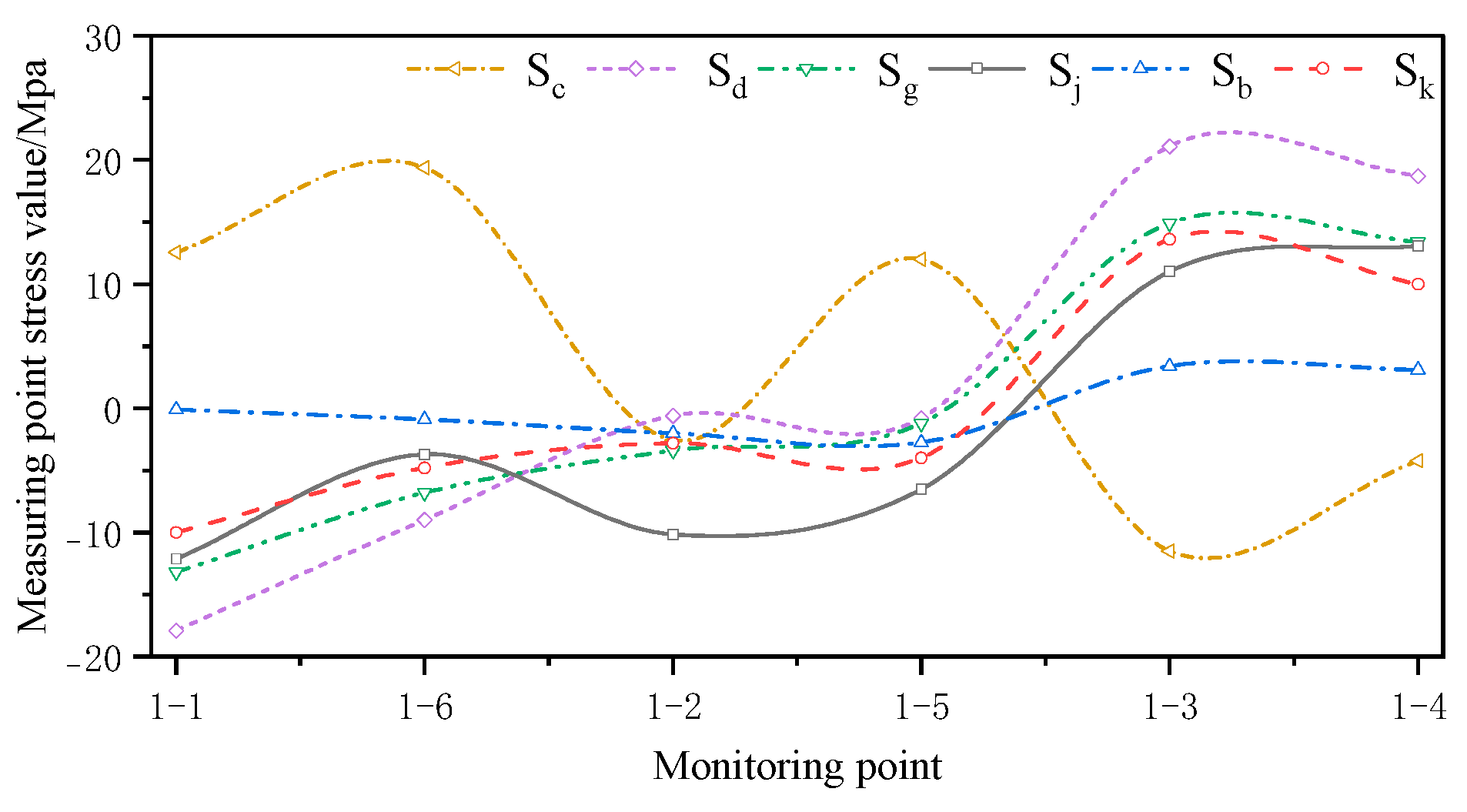
4.2. Stress Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, D.; Wei, D. Simulation method of step-by-step construction of long-span steel structures. Nat. Sci. Educ. 2010, 38, 123–126. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, B.; Zhang, A.; Cao, Y.; Guo, C.; Liu, X. Construction technology of long span steel structure corridor. Constr. Technol. 2022, 51, 21–25. [Google Scholar]
- Fan, Z.; Wang, Z.; Tang, J. Analysis on temperature field and determination of temperature upon healing of large-span steel structure of the National Stadium. J. Build. Struct. 2007, 28, 32–40. [Google Scholar] [CrossRef]
- Liu, H.; Ying, J.; Chen, Z. Progress in the study of nonuniform temperature of space structure solar radiation. J. Build. Struct. 2017, 47, 59–63. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, M.; Liu, T.; Wang, C.; Li, Z. Numerical simulation and construction monitoring the Tianjin Olympic Stadium steel roof structure. J. Build. Struct. 2008, 11, 1–7. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Fan, J.; Zhou, M.; Nie, J.; Qiang, A.; Zhou, Z. Analysis on non-uniform temperature field of large-span steel truss structure with inclined leg. Eng. Mech. 2024, 41, 208–218. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Li, G.; Jing, J.; Liu, P. Temperature stress analysis and countermeasures of long-span steel structure roof of Shanghai National Convention and Exhibition Center. J. Build. Struct. 2020, 50, 40–45. [Google Scholar] [CrossRef]
- Zhou, M.; Fan, J.; Liu, Y.; Zhang, J.; Duan, X.; Lei, S. Analysis on non-uniform temperature field of steel grids of beijing daxing international airport terminal building core area considering solar radiation. Eng. Mech. 2020, 37, 46–54. [Google Scholar] [CrossRef]
- Chen, D.; Xu, W.; Qian, H.; Sun, J.; Li, J. Effects of non-uniform temperature on closure construction of spatial truss structure. J. Build. Eng. 2020, 32. [Google Scholar] [CrossRef]
- Tong, X.; Chen, Z.; Zhao, Z.; Liu, H. Study on temperature effect and sensitivity of long-span steel structure considering construction influence. Ind. Constr. 2018, 48, 141–146. [Google Scholar] [CrossRef]
- Ma, Q.; Shen, W.; Chen, P.; Wan, H. Simulation of sunshine non-uniform temperature effect in National Stadium. J. Civ. Eng. Manag. 2022, 39, 137–144. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X. Construction mechanics problems and analysis methods of large complex steel structures. Ind. Constr. 2007, 37, 1–8. [Google Scholar]
- Tian, L.; Hao, J.; Wang, Y.; Zheng, J. Analysis of temperature effect and determination of temperature upon healing of large-span spatial structures. China Civ. Eng. J. 2012, 45, 1–7. [Google Scholar] [CrossRef]
- Jia, Y.G.; Lu, L.J.; Wu, G.Y.; Liu, Y.; Mo, X. Spatial nonlinear simulation analysis on the temperature shrinkage effect of a super-long frame structure considering the construction process. Processes 2022, 10, 1874. [Google Scholar] [CrossRef]
- Jia, Z.; Zheng, J.; Li, C.; Wang, X. Simulation analysis of temperature effect in construction process of ultra-long, ultra-wide and ultra-rigid multi-layer steel frame workshop. Ind. Constr. 2020, 50, 119–124. [Google Scholar] [CrossRef]
- Liu, M.; Li, X.; Xing, G.; Wu, M.; Li, J. Monitoring and simulation analysis of the construction process of long-span space spoke string truss structure. J. Build. Sci. Eng. 2023, 40, 95–102. [Google Scholar] [CrossRef]
- Zhai, L.; Li, W.; Wang, Y.; Han, Z.; Zhou, S.; Yuan, S.; Wang, H.; Wu, C. Monitoring and analysis of the whole construction process of space string truss of long span steel structure. Constr. Technol. 2022, 51, 77–82. [Google Scholar]



















| Steel Truss Number | Strain Temperature Monitoring Points/Unit | Displacement Monitoring Points/pc |
|---|---|---|
| GHJ1 | 0 | 2 |
| GHJ2 | 13 | 2 |
| GHJ3 | 12 | 3 |
| GHJ6 | 10 | 2 |
| GHJ7 | 12 | 2 |
| GHJ8 | 0 | 2 |
| GHJ9 | 3 | 1 |
| GHJ10 | 20 | 2 |
| GHJ11 | 18 | 4 |
| Total | 88 | 20 |
| Working Condition | Dates | Weather Conditions | Temperature on the Sunny Side/°C | Temperature on the Shady Side/°C |
|---|---|---|---|---|
| 1 | August 21 | Sunny and cloudless | 36 | 32 |
| 2 | August 23 | Sunny and cloudless | 43 | 37 |
| 3 | August 25 | Sunny and cloudless | 36 | 28 |
| 4 | August 27 | Sunny and cloudless | 42 | 34 |
| 5 | August 29 | Rainy | 35 | 35 |
| Working Condition | Dates | Temperature on the Sunny Side/°C | Temperature on the Shady Side/°C |
|---|---|---|---|
| 1 | August 21 | ||
| 2 | August 23 | ||
| 3 | August 25 | ||
| 4 | August 27 | ||
| 5 | August 29 |
| Structure Group Number | Positioning of Rods | Number of Bars/pc |
|---|---|---|
| Structural group 1 | Bottom and diagonal bracing, seventh floor, area B1 | 8 |
| Structural group 2 | Bottom beam, seventh floor, block B1 | 6 |
| …… | …… | |
| Structural group 45 | Bottom secondary beam, seventh floor, area C2 | 2 |
| …… | …… | |
| Structural group 91 | Beam on the west side, eleventh floor, area B3 | 8 |
| Structural group 92 | West inclined beam, eleventh floor, block B3 | 10 |
| Serial Number | Working Condition Name | Working Condition | Displacement Expression | Stress Expression |
|---|---|---|---|---|
| 1 | Disregarding the temperature effect | b | ||
| 2 | Maximum uniform temperature rise | g | ||
| 3 | Minimum uniform temperature rise | d | ||
| 4 | Temperature applied after molding | c | ||
| 5 | Considering the initial temperature difference | k |
| Working Step | CS91 | CS92 | Simulated Value of Displacement Change | Monitored Value of Displacement Change | Absolute Error |
|---|---|---|---|---|---|
| Db/mm | −14.06 | −14.52 | −0.46 | −1.00 | 0.54 |
| Dg/mm | −15.28 | −15.82 | −0.53 | −1.00 | 0.47 |
| Dd/mm | −14.63 | −15.13 | −0.50 | −1.00 | 0.50 |
| Dc/mm | −9.35 | −9.83 | −0.49 | −1.00 | 0.51 |
| Dk/mm | −14.14 | −14.62 | −0.48 | −1.00 | 0.52 |
| Temperature Conditions | 1–1 | 1–6 | 1–2 | 1–5 | 1–3 | 1–4 | Error/% |
|---|---|---|---|---|---|---|---|
| Sj/Mpa | −12.1 | −3.7 | −10.1 | −6.5 | 11.0 | 13.1 | — |
| Sk/Mpa | −10.0 | −4.8 | −2.8 | −4.0 | 13.6 | 10.0 | 34.2 |
| Sb/Mpa | −0.1 | −0.9 | −2.0 | −2.7 | 3.4 | 3.1 | 76.5 |
| Sg/Mpa | −17.9 | −9.0 | −0.6 | −0.8 | 21.1 | 18.7 | 46.3 |
| Sd/Mpa | −13.2 | −6.8 | −3.4 | −1.2 | 14.9 | 13.4 | 84.4 |
| Sc/Mpa | 12.5 | 19.4 | −2.6 | 12.0 | −11.5 | −4.2 | 253.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Fang, X.; Liu, L.; Ao, C.; Hu, W.; Teng, J.; Huo, Z. Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement. Sensors 2024, 24, 8073. https://doi.org/10.3390/s24248073
Lu W, Fang X, Liu L, Ao C, Hu W, Teng J, Huo Z. Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement. Sensors. 2024; 24(24):8073. https://doi.org/10.3390/s24248073
Chicago/Turabian StyleLu, Wei, Xianwei Fang, Liming Liu, Chunfeng Ao, Weihua Hu, Jun Teng, and Zhongcheng Huo. 2024. "Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement" Sensors 24, no. 24: 8073. https://doi.org/10.3390/s24248073
APA StyleLu, W., Fang, X., Liu, L., Ao, C., Hu, W., Teng, J., & Huo, Z. (2024). Force Feedback Method for Statically Indeterminate Steel Structure Construction Based on Staged Temperature Measurement. Sensors, 24(24), 8073. https://doi.org/10.3390/s24248073







