Reanalysis on Performance of Microwave Phase Detector for Multisignals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Traditional Analysis on the MPD
2.1.1. Structure of the MPD
2.1.2. Response Characteristics of the Traditional MPD
2.1.3. Limitations of Traditional Analysis of the MPD
2.2. Multisignal Paradigm and Analysis
2.2.1. Preconditions of Multiple Signal Inputs
2.2.2. The Subprocess of Grade 1
2.2.3. The Subprocess of Grade 2
2.2.4. The Subprocess of Grade 3
2.2.5. The Subprocess of Grade 4
3. Results
3.1. Preconditions of Scenario
3.2. Fixed-Frequency and Linear FM Signals with Only One Frequency Crossing Point
3.3. Fixed-Frequency and Two Linear FM Signals with Three-Frequency Crossings
3.4. Frequency Crossings Cover the Entire Test Band
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rutkowski, A. Single Parallel Stubs as Broadband Microwave Phase Shifters. Metrol. Meas. Syst. 2020, 27, 91–102. [Google Scholar] [CrossRef]
- East, P. Fifty years of instantaneous frequency measurement. IET Radar Sonar Navig. 2012, 6, 112–122. [Google Scholar] [CrossRef]
- Tsui, J.B. Microwave Receiver for Electronic Warfare Applications; Artech House, Inc.: London, UK, 1986. [Google Scholar]
- Sullivan, W.B. Simultaneous signal errors in wideband IFM receivers. Microw. J. 1995, 38, 86–94. [Google Scholar]
- Gruchaila, W.H.; Czyzewski, M.; Slowik, A. The performance of the IFM receiver in a dense signal environment. In Proceedings of the 18-th International Conference on Microwaves, Radar and Wireless Communications, Vilnius, Lithuania, 14–16 June 2010. [Google Scholar]
- Heng, C.; Guan, Z.H.; Shen, Y.T.; Gao, M.Y. A Study on the Influence of Time-frequency Overlapping Electromagnetic Environment on Radar Reconnaissance System. Mod. Radar 2023, 45, 16–20. [Google Scholar]
- Shamim, K.; Nasser, M.; Safieddin, N.S. Reliable, Intelligent, and Design-Independent Digital Frequency Extraction Methodology for High Bit-Count DIFM Receivers. IEEE Trans. Instrumen-Tation Meas. 2021, 70, 6502012. [Google Scholar]
- Shamim, K.; Nasser, M. The Art of Piecewise Linear Approximation in MMSE Estimator for Most Accurate and Fast Frequency Extraction in DIFM Receivers. IEEE Trans. Instrumenta-Tion Meas. 2021, 70, 8004409. [Google Scholar]
- Keshani, S.; Masoumi, N.; Rahimpour, H.; Safavi-Naeini, S. Digital Processing for Accurate Frequency Extraction in IFM Receivers. IEEE Trans. Instrum. Meas. 2020, 69, 6092–6100. [Google Scholar] [CrossRef]
- Rahimpour, H.; Masoumi, N.; Keshani, S.; Safavi-Naeini, S. A High Frequency Resolution Successive-Band Shifted Filters Architecture for a 15-bit IFM Receiver. IEEE Trans. Microw. Theory Tech. 2019, 67, 2028–2035. [Google Scholar] [CrossRef]
- Hirai, A.; Tsutsumi, K.; Nakamizo, H.; Taniguchi, E.; Tajima, K.; Mori, K.; Tsuru, M.; Shimozawa, M. A 0.3-to-5.5 GHz Digital Frequency Discriminator IC with Time to Digital Converter and Edge Counter for Instantaneous Frequency Measurement. IEICE Trans. Electron. 2019, E102.C, 547–557. [Google Scholar] [CrossRef]
- Rahimpour, H.; Masoumi, N. Design and Implementation of a High-Sensitivity and Compact-Size IFM Receiver. IEEE Trans. Instrum. Meas. 2018, 68, 2602–2609. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Z.; Zhang, B.; Li, F.; Li, J.; Guo, X.; Li, Z. Wideband and low-error microwave frequency measurement using degenerate four-wave mixing-based non-linear interferometer. Opt. Lett. 2019, 44, 1848–1851. [Google Scholar] [CrossRef] [PubMed]
- Rutkowski, A.; Kawalec, A. A concept of a microwave seeker designed for an anti-radiation missile. Conf. Reconnaiss. Electron. Warf. Syst. 2019, 11055, 210–215. [Google Scholar]
- Wang, H.X.; Wang, H.W.; Wang, X.; Wang, S.Y. Analysis on Pulses Overlapping of RWR/ESM’s Signal Sensor Channels. Telecommun. Eng. 2013, 53, 1142–1147. [Google Scholar]
- Wang, H.; Wang, L.; Wang, J.; Wang, S.; Wang, H. Analysis of Double Overlapping Signals and Improvement of IFM System. Mod. Def. Technol. 2021, 49, 64–71. [Google Scholar]
- Wang, S.Y.; Wang, L.H.; Wang, J. Instantaneous Frequency Measurement Analysis of Overlapped Signals in Airborne Electronic Countermeasure System. In Proceeding of the 2019 Aviation Equipment Service Support and Maintenance Technology Forum and Annual Conference of China Aviation Industry Technology and Equipment Engineering Association, Nanchang, China, 5–7 December 2019; p. 469. [Google Scholar]
- Tsui, J.B. Digital Techniques for Wideband Receivers; Artech House, Inc.: London, UK, 1995. [Google Scholar]
- Richardson, D. Simultaneous signal detector. US Patent nr 5,574,360, 11 November 1996. [Google Scholar]
- Tsui, J.B. Digital Microwave Receivers. Theory and Concepts; Artech House, Inc.: London, UK, 1989. [Google Scholar]
- Tsui, J.B.; MeCormick, W.S. Instantaneous frequency measurement receiver to measure frequency and angle of arrival of multiple signals. US Patent nr 4,977,365, 11 December 1990. [Google Scholar]
- Gruchałła, W.H.; Czyżewski, M.; Słowik, A. The estimation of simultaneous signals frequencies in the IFM receiver using parametric methods. In Proceedings of the XVII International Conference on Microwaves, Radar and Wireless Communications, Wrocław, Poland, 19–21 May 2008. [Google Scholar]
- Wang, L.; Wang, H.; Wang, H.; Lin, X.; Xiong, Z. Research on Jamming Mechanism of Instantaneous Frequency Measurement. Mod. Def. Technol. 2023, 52, 128. [Google Scholar]
- McCormick, W.; Tsui, J.; Bakkie, V. A noise insensitive solution to an ambiguity problem in spectral estimation. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 729–732. [Google Scholar] [CrossRef]
- Gruchalla, H.; Czyzewski, M.; Slowik, A. The Instantaneous Frequency Measurement Receiver with Simultaneous Signal Capability. In Proceedings of the 2006 International Conference on Microwaves, Radar & Wireless Communications, Krakow, Poland, 22–24 May 2006; pp. 554–557. [Google Scholar]
- Li, P.; Zhang, Q.H. IF Estimation of Overlapped Multicomponent Signals Based on Viterbi Algorithm. Circuits Syst. Signal Process. 2020, 39, 3105–3124. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Chen, H.J. Noise Identification Based on IQ Value in Instantaneous Frequency Measure Receiver. Electron. Inf. Technol. 2021, 36, 105–108. [Google Scholar]





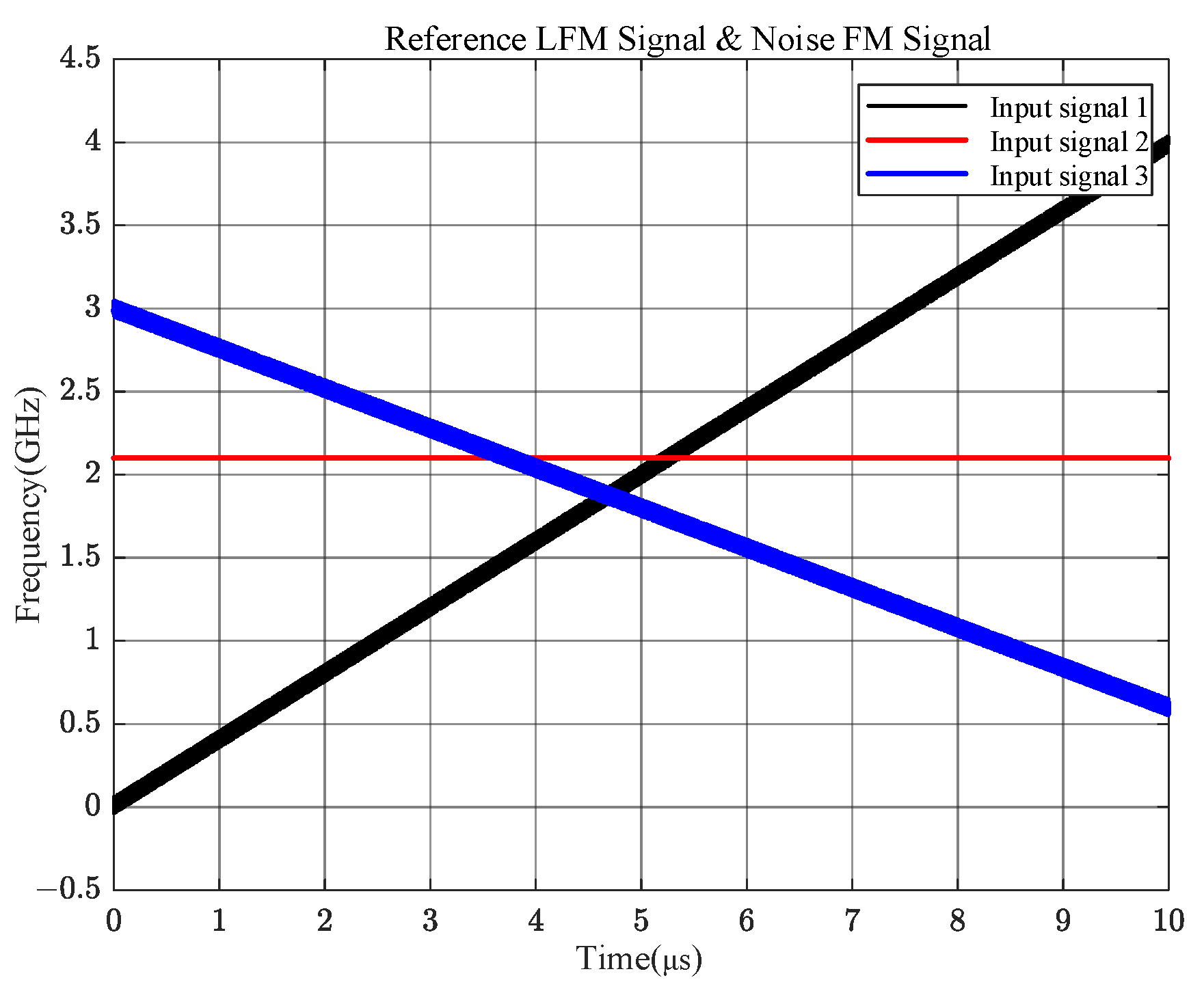
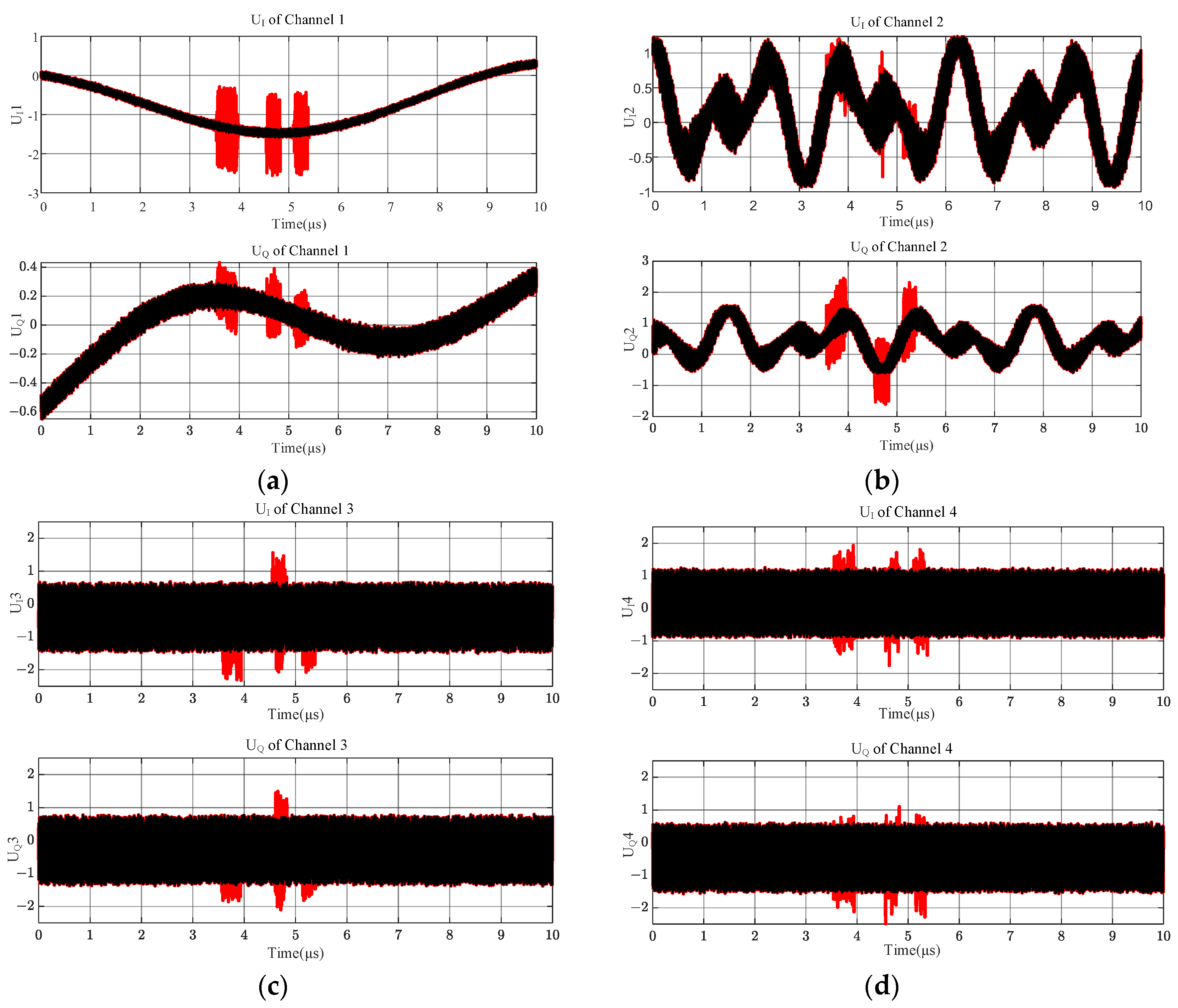



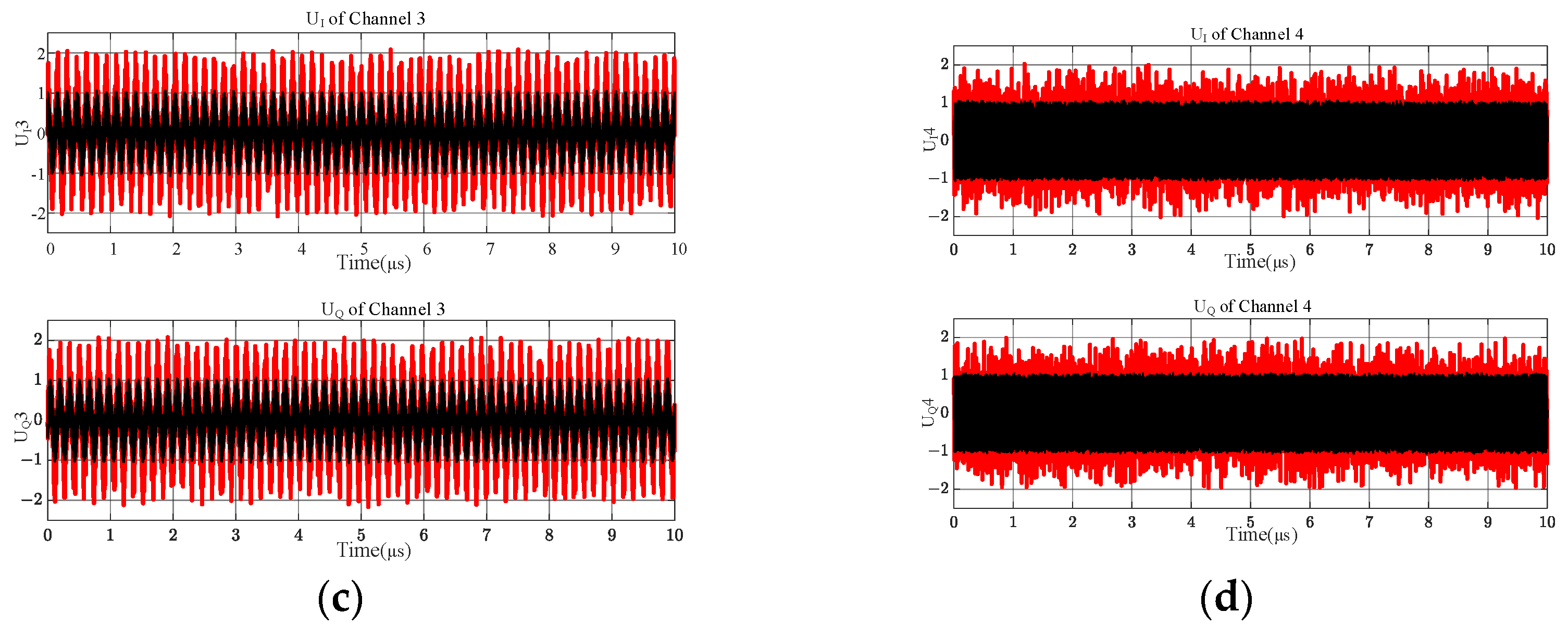

| Input Signal 1 | Input Signal 2 | Frequency Measurements at Signal Frequency Overlaps |
|---|---|---|
| 2~4 GHz LFM signal | 2.5 GHz stabilized signal | 2.5 GHz→3.25 GHz |
| 2~4 GHz LFM signal | 2.7 GHz stabilized signal | 2.7 GHz→3.62 GHz |
| 2~4 GHz LFM signal | 3.0 GHz stabilized signal | 3.0 GHz→3.87 GHz |
| 2~4 GHz LFM signal | 3.5 GHz stabilized signal | 3.5 GHz→4.63 GHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Wang, H.; Xiang, X. Reanalysis on Performance of Microwave Phase Detector for Multisignals. Sensors 2024, 24, 8076. https://doi.org/10.3390/s24248076
Deng J, Wang H, Xiang X. Reanalysis on Performance of Microwave Phase Detector for Multisignals. Sensors. 2024; 24(24):8076. https://doi.org/10.3390/s24248076
Chicago/Turabian StyleDeng, Jing, Hongxun Wang, and Xin Xiang. 2024. "Reanalysis on Performance of Microwave Phase Detector for Multisignals" Sensors 24, no. 24: 8076. https://doi.org/10.3390/s24248076
APA StyleDeng, J., Wang, H., & Xiang, X. (2024). Reanalysis on Performance of Microwave Phase Detector for Multisignals. Sensors, 24(24), 8076. https://doi.org/10.3390/s24248076





