Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure
Abstract
:1. Introduction
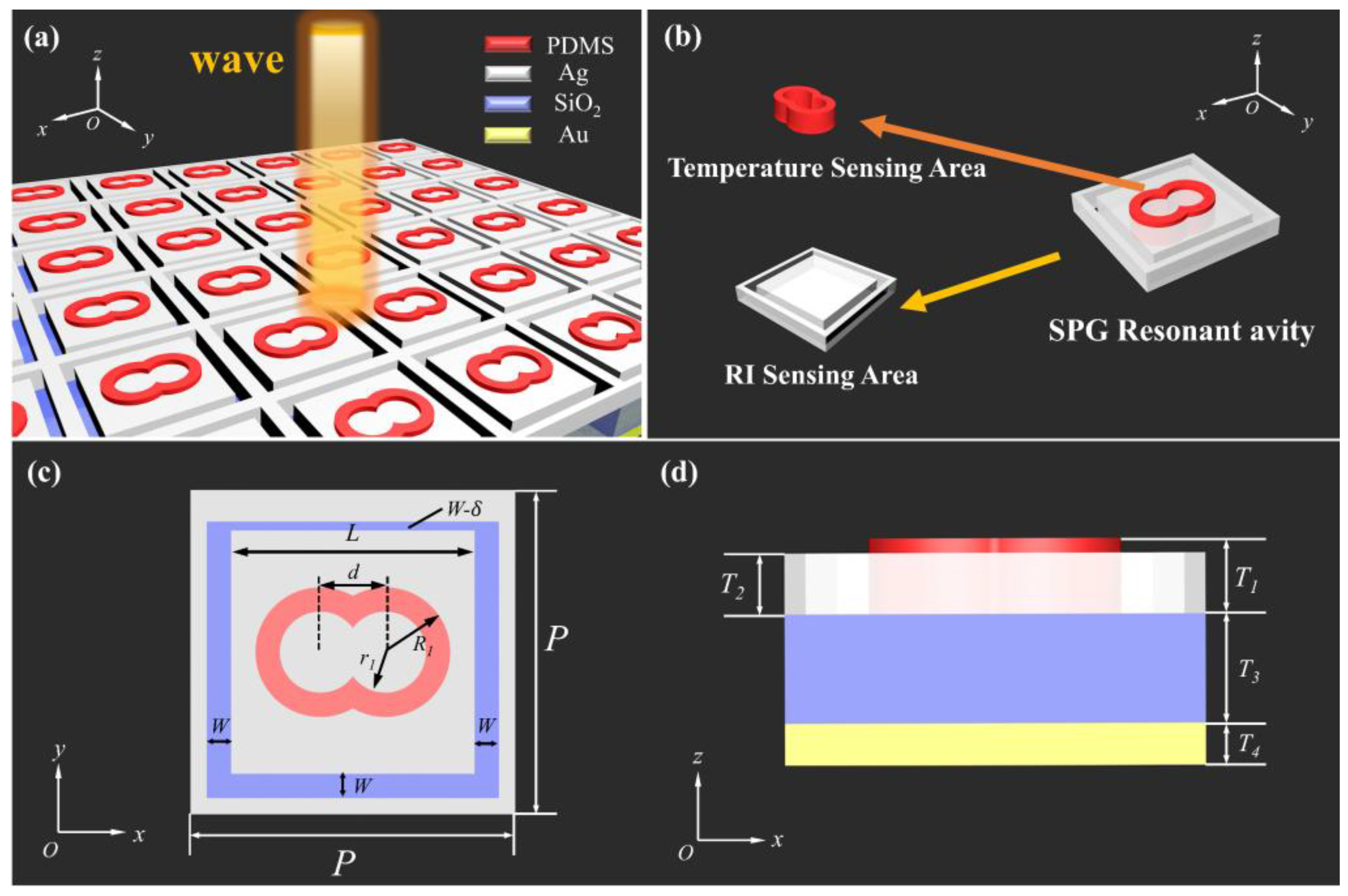
2. Materials and Methods
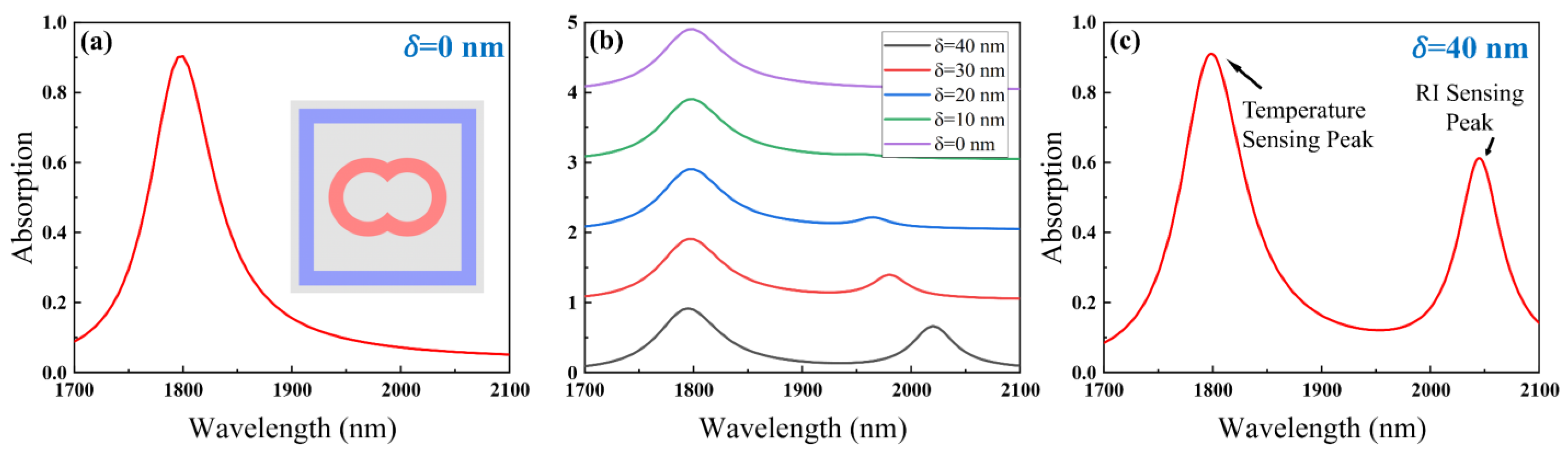
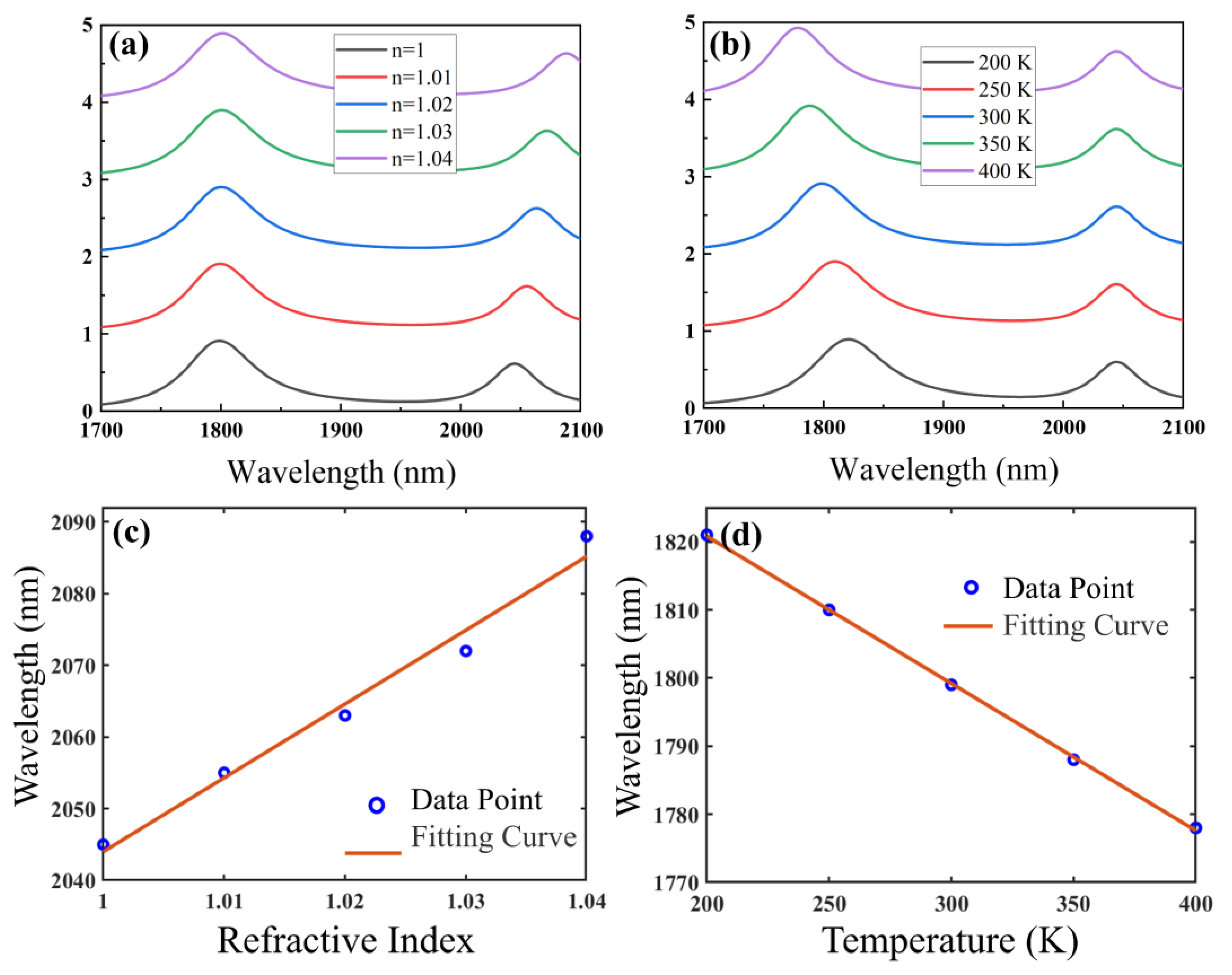
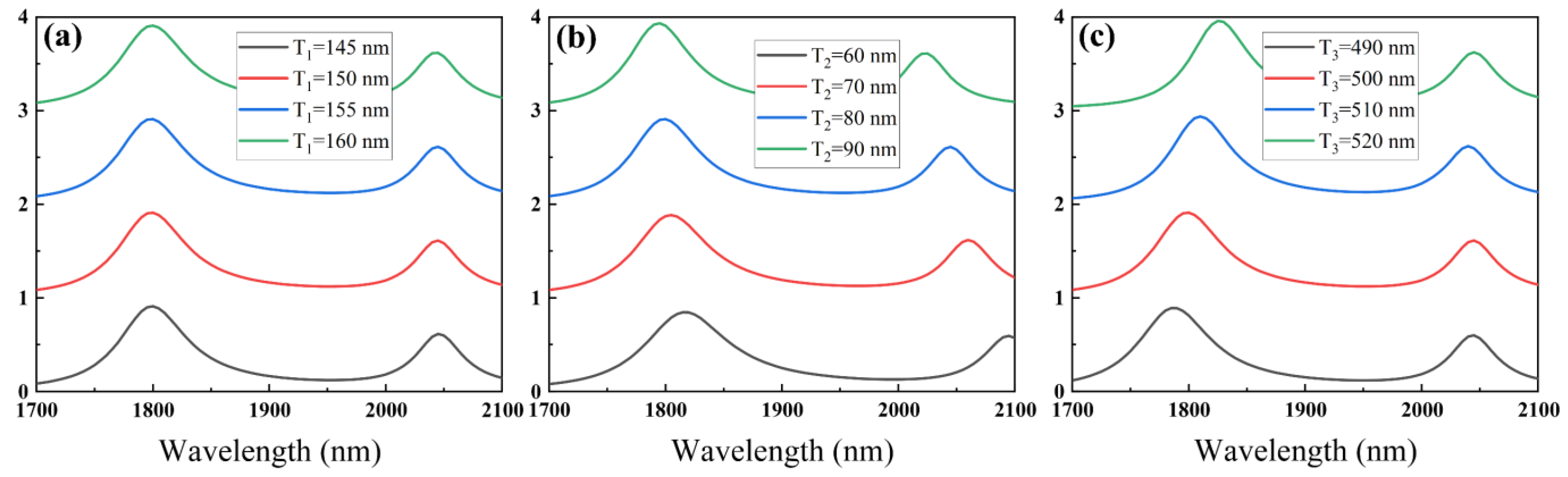
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lakshmiprabha, K.E.; Govindaraju, C.; Mahendran, G. Broadband plus-shaped metasurface absorber based on graphene for visible and ultraviolet regions. Opt. Quantum Electron. 2022, 54, 774. [Google Scholar] [CrossRef]
- Yang, B.; Zou, Y.; Zhou, K.; Liu, H.T.; Wu, X.H. TiN-based metasurface absorber for efficient solar energy harvesting. Int. J. Therm. Sci. 2023, 192, 108428. [Google Scholar] [CrossRef]
- Babu, W.R.; Kumar, P.R.; Murali, L.; Anushkannan, N.K. Broadband graphene and metasurface-loaded solar thermal absorber design for visible and infrared regions. Opt. Quantum Electron. 2023, 55, 68. [Google Scholar] [CrossRef]
- Abramovich, A.; Azoulay, Y.; Rotshild, D. Real-Time Metasurface Sensor for Monitoring Micropoisons in Aqueous Solutions Based on Gold Nanoparticles and Terahertz Spectroscopy. Sensors 2022, 22, 1279. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Xiong, L.; Hu, F.R.; Xiang, Y.J.; Dai, X.Y.; Li, G.Y. Ultrasensitive and Tunable Sensor Based on Plasmon-Induced Transparency in a Black Phosphorus Metasurface. Plasmonics 2021, 16, 1071–1077. [Google Scholar] [CrossRef]
- Ni, B.; Chu, G.H.; Xu, Z.Y.; Hou, L.P.; Liu, X.F.; Xiong, J.C. High Q-Factor, High Contrast, and Multi-Band Optical Sensor Based on Plasmonic Square Bracket Dimer Metasurface. Nanomaterials 2024, 14, 421. [Google Scholar] [CrossRef]
- Wu, S. Physical insight into the terahertz polarization modulator by using Smith chart. Phys. Lett. A 2022, 440, 128143. [Google Scholar] [CrossRef]
- He, J.W.; Xie, Z.W.; Wang, S.; Wang, X.K.; Kan, Q.; Zhang, Y. Terahertz polarization modulator based on metasurface. J. Opt. 2015, 17, 105107. [Google Scholar] [CrossRef]
- Ren, C.; Komatsu, K.; Soma, G.; Nakano, Y.; Tanemura, T. Metasurface-based functional optical splitter for a spatially parallelized dual-polarization coherent modulator. Opt. Lett. 2024, 49, 7238–7241. [Google Scholar] [CrossRef]
- Xiao, Y.Z.; Qian, H.L.; Liu, Z.W. Nonlinear Metasurface Based on Giant Optical Kerr Response of Gold Quantum Wells. ACS Photonics 2018, 5, 1654–1659. [Google Scholar] [CrossRef]
- Wang, M.J.; Li, Y.; Tang, Y.T.; Chen, J.F.; Rong, R.; Li, G.X.; Cao, T.; Chen, S.M. Nonlinear Chiroptical Holography with Pancharatnam-Berry Phase Controlled Plasmonic Metasurface. Laser Photonics Rev. 2022, 16, 2200350. [Google Scholar] [CrossRef]
- Lu, Y.X.; Zheng, J.H.; Zhang, F.L.; Guo, Q.Q.; Song, Y.F.; Dong, J.N.; Chen, Y.H. Broadband and weak-dispersion nonlinear response enhancement in the epsilon-near-zero region of a nano-stepped metasurface. Phys. Chem. Chem. Phys. 2024, 26, 23631–23635. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Olifierczuk, M.; Parka, J. Thermally induced tunability of a terahertz metamaterial by using a specially designed nematic liquid crystal mixture. Opt. Express 2018, 26, 2443–2452. [Google Scholar] [CrossRef]
- Zhu, J.F.; Wang, Z.Y.; Lin, S.W.; Jiang, S.; Liu, X.Y.; Guo, S.S. Low-cost flexible plasmonic nanobump metasurfaces for label-free sensing of serum tumor marker. Biosens. Bioelectron. 2020, 150, 111905. [Google Scholar] [CrossRef]
- Asencios, J.; Moro, R.; Luyo, C.; Talledo, A. High sensitive biosensors based on the coupling between surface plasmon polaritons on titanium nitride and a planar waveguide mode. Sensors 2020, 20, 1784. [Google Scholar] [CrossRef] [PubMed]
- Kovacevic, A.; Potrebic, M.; Tosic, D. Sensitivity Characterization of Multi-Band THz Metamaterial Sensor for Possible Virus Detection. Electronics 2022, 11, 699. [Google Scholar] [CrossRef]
- Aslinezhad, M. High sensitivity refractive index and temperature sensor based on semiconductor metamaterial perfect absorber in the terahertz band. Opt. Commun. 2020, 463, 125411. [Google Scholar] [CrossRef]
- Chao, C.T.C.; Chau, Y.F.C.; Chiang, H.P. Enhancing plasmonic effect in periodic nanometal square prisms with fences and cavities for refractive index and temperature sensing applications. J. Nanopart. Res. 2020, 22, 297. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Li, Z.R.; Cheng, Z.Z. Terahertz perfect absorber based on InSb metasurface for both temperature and refractive index sensing. Opt. Mater. 2021, 117, 111129. [Google Scholar] [CrossRef]
- Gao, W.K.; Chen, F.; Yang, W.X. Temperature and refractive index sensor based on perfect absorber in InSb double rectangular ring resonator metamaterials. Mater. Today Commun. 2024, 40, 109461. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, Y.; Rehman, A.U.; Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Plasmonic Refractive Index and Temperature Sensor Based on Graphene and LiNbO3. Sensors 2022, 22, 7790. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Cai, X.; Dai, W.; Luo, J.; Rao, W.; Fu, H. A Double-Layer Structure SPR Sensor With Temperature Self-Compensation and Ultra-Wide Sensing Range for Refractive index Detection. IEEE Sens. J. 2022, 22, 2309–2316. [Google Scholar] [CrossRef]
- Huang, Z.S.; Wang, J.; Jia, W.; Zhang, S.W.; Zhou, C.H. All-dielectric metasurfaces enabled by quasi-BIC for high-Q near-perfect light absorption. Opt. Lett. 2025, 50, 105–108. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Wang, X.F. Refractive Index, Temperature and Pressure Three-Mode Sensing Design Based on Silver-Nitrogen-Graphene Coupled Resonators. IEEE Sens. J. 2024, 24, 8712–8720. [Google Scholar] [CrossRef]
- Wu, T.S.; Liu, Y.M.; Yu, Z.Y.; Ye, H.; Peng, Y.W.; Shu, C.G.; Yang, C.H.; Zhang, W.; He, H.F. A nanometeric temperature sensor based on plasmonic waveguide with an ethanol-sealed rectangular cavity. Opt. Commun. 2015, 339, 1–6. [Google Scholar] [CrossRef]
- Li, L.; Cui, L.; Zong, X.; Liu, Y. Multinarrowband Perfect Absorption With Bound States in the Continuum for Sensing Application. IEEE Sens. J. 2024, 24, 4400–4406. [Google Scholar] [CrossRef]
- Werner, W.S.M.; Glantschnig, K.; Ambrosch-Draxl, C. Optical Constants and Inelastic Electron-Scattering Data for 17 Elemental Metals. J. Phys. Chem. Ref. Data 2009, 38, 1013–1092. [Google Scholar] [CrossRef]
- Yang, H.U.; D’Archangel, J.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B 2015, 91, 235137. [Google Scholar] [CrossRef]
- Yang, R.D.; Liu, Y.; Wang, X.F. Metamaterial Broadband Absorber Induced by Synergistic Regulation of Temperature and Electric Field and Its Optical Switching Application. Sensors 2024, 24, 5430. [Google Scholar] [CrossRef]
- Reiter, S.; Han, W.J.; Mai, C.; Spirito, D.; Jose, J.; Zöllner, M.; Fursenko, O.; Schubert, M.A.; Stemmler, I.; Wenger, C.; et al. Titanium nitride plasmonic nanohole arrays for CMOS-compatible integrated refractive index sensing: Influence of layer thickness on optical properties. Plasmonics 2023, 18, 831–843. [Google Scholar] [CrossRef]
- Zhu, X.P.; Shi, H.M.; Zhang, S.; Zheng, M.J.; Dai, P.; Huang, R.M.; Liao, J.; Xue, S.W.; Zhang, J. High figure of merit refractive index sensor derived from the axial length ratio of elliptically polarized light of chiral plasmonic structure arrays. Plasmonics 2023, 18, 2365–2373. [Google Scholar] [CrossRef]
- Zhao, H.N.; Fan, X.Y.; Wei, X.; Li, C.C.; Zhao, T.G.; Fang, W.J.; Niu, H.J.; Bai, C.L.; Kumar, S. Highly sensitive multiple Fano resonances excitation on all-dielectric metastructure. Opt. Rev. 2023, 30, 208–216. [Google Scholar] [CrossRef]
- Zhao, J.J.; Fan, X.Y.; Fang, W.J.; Xiao, W.X.; Sun, F.X.; Li, C.C.; Wei, X.; Tao, J.F.; Wang, Y.L.; Kumar, S. High-Performance Refractive Index and Temperature Sensing Based on Toroidal Dipole in All-Dielectric Metasurface. Sensors 2024, 24, 3943. [Google Scholar] [CrossRef]
- Wang, D.D.; Fan, X.Y.; Fang, W.J.; Du, M.C.; Sun, Q.H.; Niu, H.J.; Li, C.C.; Wei, X.; Li, M.X.; Chen, B.X.; et al. High-Performance All-Dielectric Metasurface for Quadruple Fano Resonance-Induced Biosensing Applications in the Near-Infrared Range. IEEE Sens. J. 2024, 24, 12286–12295. [Google Scholar] [CrossRef]
- Verma, S.K.; Srivastava, S.K. Giant Extra-Ordinary Near Infrared Transmission from Seemingly Opaque Plasmonic Metasurface: Sensing Applications. Plasmonics 2021, 17, 653–663. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.K.; Wekalao, J.; Alsalman, O.; Surve, J.; Parmar, J.; Taya, S.A. Development of surface plasmon resonance sensor with enhanced sensitivity for low refractive index detection. Opt. Quantum Electron. 2023, 55, 101. [Google Scholar] [CrossRef]
- Hu, X.; Hu, Y.C.; Zhang, W.H.; Hu, J.; Li, F.; Su, W.; Wu, H. Compact dual-parameter sensor design based on a photonic crystal nanobeam cavity with chirped slotted annular holes. Appl. Opt. 2023, 62, 8593–8599. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L.; Piramidowicz, R. Hybrid metasurface perfect absorbers for temperature and biosensing applications. Opt. Mater. 2022, 123, 111906. [Google Scholar] [CrossRef]
- Butt, M.A. Plasmonic Sensor System Embedded with Orthogonal Mode Couplers for Simultaneous Monitoring of Temperature and Refractive Index. Plasmonics 2024, 20, 459–469. [Google Scholar] [CrossRef]

| Ref. | ST | Sn | Sensing Mode | FOM | Max Q |
|---|---|---|---|---|---|
| [35] | / | 1435.71 nm/RIU | RI | 80 RIU−1 | / |
| [36] | / | 1100 GHz/RIU | RI | 3.832 RIU−1 | / |
| [37] | 78.7 pm/°C | 286.82 nm/RIU | RI and Temperature | / | / |
| [38] | 180 pm/°C | 355 nm/RIU | RI and Temperature | / | / |
| [39] | 336 pm/°C | 737.71 nm/RIU | RI and Temperature | / | 20.5 |
| Our work | 216 pm/K | 1030 nm/RIU | RI and Temperature | 0.0033 K−1, 24.6 RIU−1 | 48.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Dai, M.; Zhao, Y.; Wang, X. Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure. Nanomaterials 2025, 15, 687. https://doi.org/10.3390/nano15090687
Yang R, Dai M, Zhao Y, Wang X. Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure. Nanomaterials. 2025; 15(9):687. https://doi.org/10.3390/nano15090687
Chicago/Turabian StyleYang, Rundong, Minjing Dai, Yihao Zhao, and Xiangfu Wang. 2025. "Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure" Nanomaterials 15, no. 9: 687. https://doi.org/10.3390/nano15090687
APA StyleYang, R., Dai, M., Zhao, Y., & Wang, X. (2025). Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure. Nanomaterials, 15(9), 687. https://doi.org/10.3390/nano15090687







