Diffusion Coefficients and Activation Energies of Diffusion of Organic Molecules in Poly(lactic acid) Films
Abstract
1. Introduction
2. Results
2.1. Film Characterization
2.1.1. Differential Scanning Calorimetry (DSC)
2.1.2. Fourier-Transform Infrared (FTIR) Spectroscopy
2.1.3. Gel Permeation Chromatography
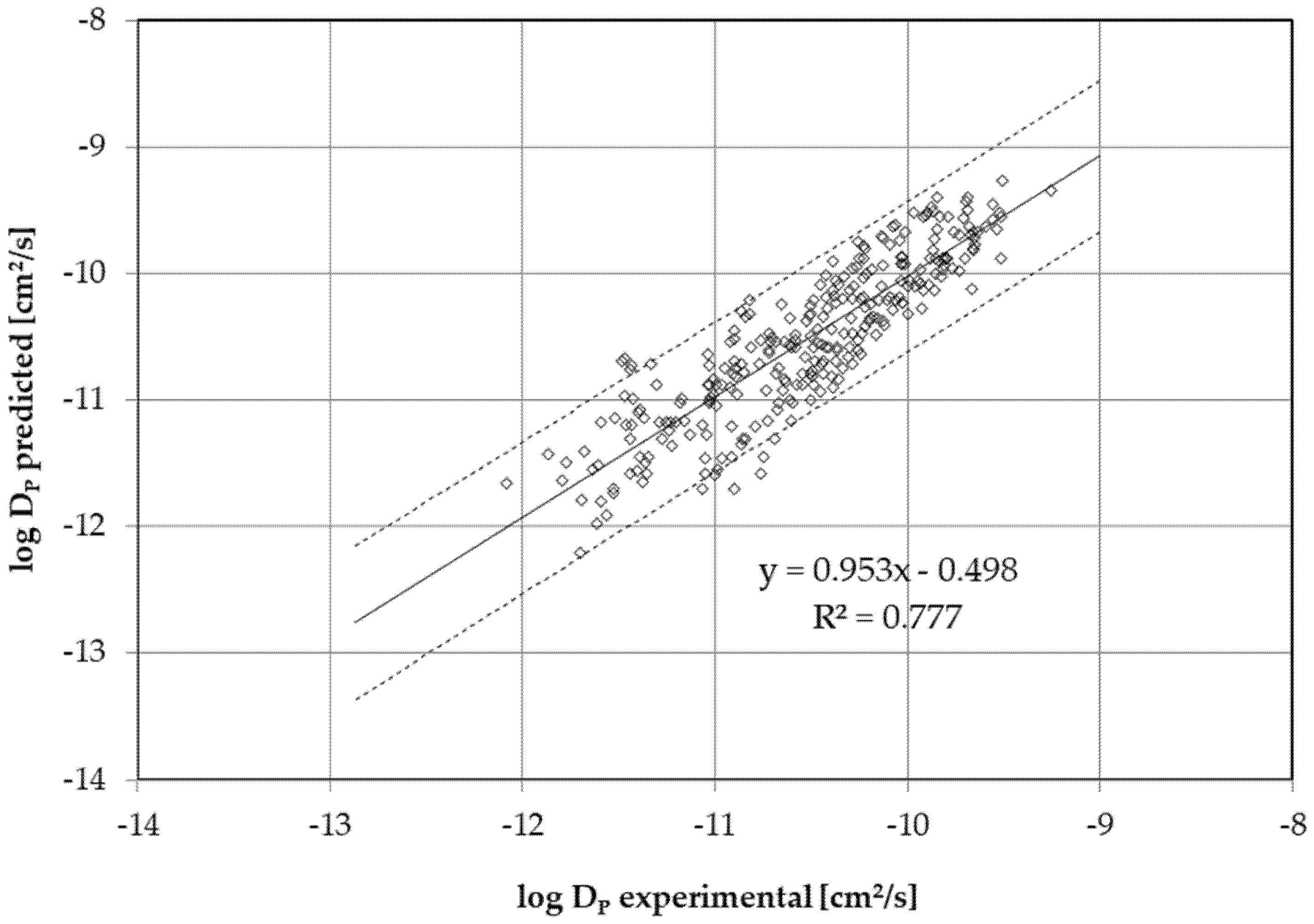
2.2. Diffusion Coefficient Determination
3. Discussion
4. Materials and Methods
4.1. Materials
- PLA-S: A 20-µm biaxially oriented PLA film (Evlon®, BI-AX International Inc., Wingham, ON, Canada).
- PLA-N: A 30-µm biaxially oriented PLA film (Nativia®, Taghleef Industries, Newark, DE, USA).
4.2. Film Characterization
4.2.1. Differential Scanning Calorimetry (DSC)
4.2.2. Fourier-Transform Infrared Spectroscopy
4.2.3. Gel Permeation Chromatography
4.2.4. Statistical Analysis
4.3. Diffusion Coefficient Determination
4.3.1. Permeants
- Liquid permeants: n-alkanes (n-pentane to n-tetradecane), 1-alcohols (1-propanol to 1-octanol), 2-ketones (acetone to 2-octanone), cyclic alkanes, ethers, ketones (tetrahydrofuran, cyclohexane, 4-vinylcyclohexene, 1,3-dioxolane, 2-methyl-1,3-dioxolane, 1,4-dioxane, cyclopentane, cyclopentanone, cyclohexanone), esters (formic acid methyl ester to formic acid heptyl ester), amines (pyridine, pyrrol, 2,6-lutidine, aniline, 2-aminobenzonitrile), and aromatic substances (benzene, toluene, ethylbenzene, n-propylbenzene, n-butylbenzene, naphthalene, 1-methylnaphthalene, 1-ethylnaphthalene, 2,7-di-iso-propylnaphthalene, phenanthrene, anthracene). The respective groups of substances were mixed and measured together.
- Permanent gases: Methane, ethane, n-propane, and n-butane were tested as a mixture of gaseous alkanes.
4.3.2. Permeation Cell
- Liquid permeants: The liquid mixtures were injected into the lower space of the permeation cell through a septum using a syringe. Upon injection, the permeants evaporated immediately at high temperatures (65 °C to 90 °C).
- Permanent gases: The gaseous alkane mixture was flushed through the lower space of the permeation cell with a constant gas flow.
- Liquid permeants: Column: Rxi 624, length: 60 m, internal diameter: 0.32 mm, film thickness: 1.8 µm, carrier gas: 120 kPa helium. Temperature program: 40 °C (2 min), rate 10 °C/min to 200 °C, rate 20 °C/min to 270 °C, and held for 8 min. Pre-trap: substances collected on 20 mm length by 5 mm diameter of Carbopack B, desorbed at 350 °C. Main trap: substances focused at −46 °C on 30 mm length by 1.4 mm diameter of Carbopack B, desorbed at 320 °C.
- Permanent gases: Column: Poraplot Q, length: 30 m, internal diameter: 0.53 mm, film thickness: 20 µm, carrier gas: 120 kPa helium. Temperature program: 70 °C (0.5 min), rate 30 °C/min to 150 °C, and held for 5 min. Pre-trap: substances collected on 20 mm length by 5 mm diameter of Carbopack B, desorbed at 350 °C. Main trap: substances focused at −46 °C on 30 mm length by 1.4 mm diameter of active charcoal 140–280 µm, desorbed at 320 °C.
4.3.3. Diffusion Coefficient Calculation
4.3.4. Molecular Volume Calculations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lim, L.-T.; Auras, R.; Rubino, M. Processing technologies of poly(lactic acid). Prog. Polym. Sci. 2008, 33, 820–852. [Google Scholar] [CrossRef]
- Sonchaeng, U.; Iniguez-Franco, F.; Auras, R.; Selke, S.; Rubino, M.; Lim, L.-T. Poly(lactic acid) mass transfer properties. Prog. Polym. Sci. 2018, 86, 85–121. [Google Scholar] [CrossRef]
- Ewender, J.; Welle, F. Determination and prediction of the lag-times of hydrocarbons through a PET film. Packag. Technol. Sci. 2014, 27, 963–974. [Google Scholar] [CrossRef]
- Macnamara, J.F., Jr.; Vallery, R.; Gidley, D.; Auras, R. Density and crystallinity correlations: Enhancing moisture barrier properties in poly(L-lactic acid), poly(D-lactic acid), and stereocomplex-poly(L,D-lactic acid) films. J. Appl. Polym. Sci. 2025, e56986. [Google Scholar] [CrossRef]
- Bradley, E.L. Biobased Materials Used in Food Contact Applications: An Assessment of the Migration Potential. Report of the Food and Environment Research Agency, York (2010). Available online: https://www.food.gov.uk/sites/default/files/media/document/a03070.pdf (accessed on 6 April 2025).
- Aznar, M.; Ubeda, S.; Dreolin, N.; Nerin, C. Determination of non-volatile components of a biodegradable food packaging material based on polyester and poly-lactic acid (PLA) and its migration to food simulants. J. Chromatogr. A 2019, 1583, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ubeda, S.; Aznar, M.; Alfaro, P.; Nerin, C. Migration of oligomers from a food contact biopolymer based on polylactic acid (PLA) and polyester. Anal. Bioanal. Chem. 2019, 411, 3521–3532. [Google Scholar] [CrossRef] [PubMed]
- Mutsuga, M.; Kawamura, Y.; Tanamoto, K. Migration of lactic acid, lactide and oligomers from polylactide food-contact materials. Food Addit. Contam. Part A 2008, 25, 1283–1290. [Google Scholar] [CrossRef] [PubMed]
- Ubeda, S.; Aznar, M.; Nerin, C. Determination of volatile compounds and their sensory impact in a biopolymer based on polylactic acid (PLA) and polyester. Food Chem. 2019, 294, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Begley, T.; Castle, L.; Feigenbaum, A.; Franz, R.; Hinrichs, K.; Lickley, T.; Mercea, P.; Milana, M.-R.; O’Brien, A.; Rebre, S.; et al. Evaluation of migration models that might be used in support of regulations for food-contact plastics. Food Addit. Contam. 2005, 22, 73–90. [Google Scholar] [CrossRef] [PubMed]
- Practical Guidelines on the Application of Migration Modelling for the Estimation of Specific Migration, EU Report 27529 EN, ISBN 978-92-79-52790-6. 2015. Available online: https://op.europa.eu/de/publication-detail/-/publication/1b79bc61-97f6-11e5-983e-01aa75ed71a1 (accessed on 6 April 2025).
- Bini, F.; Pica, A.; Marinozzi, A.; Marinozzi, F. 3D random walk model of diffusion in human hypo- and hyper-mineralized collagen fibrils. J. Biomech. 2021, 125, 110586. [Google Scholar] [CrossRef] [PubMed]
- Momot, K.I. Diffusion tensor of water in model articular cartilage. Eur. Biophys. J. 2011, 40, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Zador, Z.; Verkman, A.S. Random-walk model of diffusion in three dimensions in brain extracellular space: Comparison with microfiberoptic photobleaching measurements. Biophys. J. 2008, 95, 1785–1794. [Google Scholar] [CrossRef] [PubMed]
- Welle, F. A new method for the prediction of diffusion coefficients in poly(ethylene terephthalate). J. Appl. Polym. Sci. 2013, 129, 1845–1851. [Google Scholar] [CrossRef]
- Ewender, J.; Welle, F. Diffusion coefficients of n-alkanes and 1-alcohols in polyethylene naphthalate (PEN). Int. J. Polym. Sci. 2019, 2019, 2748649. [Google Scholar] [CrossRef]
- Guinault, A.; Sollogoub, C.; Ducruet, V.; Domenek, S. Impact of crystallinity of poly(lactide) on helium and oxygen barrier properties. Eur. Polym. J. 2012, 48, 779–788. [Google Scholar] [CrossRef]
- Piringer, O.G.; Baner, A.L. (Eds.) Plastic Packaging—Interactions with Food and Pharmaceuticals; Wiley-VCH: Weinheim, Germany, 2008; ISBN 978-3-527-31455-3. [Google Scholar]
- Fischer, E.W.; Sterzel, H.J.; Wegner, G. Investigation of the structure of solution grown crystals of lactide copolymers by means of chemical reactions. Kolloid-Z. Z. Polym. 1973, 251, 980–990. [Google Scholar] [CrossRef]
- Magon, A.; Pyda, M. Study of crystalline and amorphous phases of biodegradable poly(lactic acid) by advanced thermal analysis. Polymer 2009, 50, 3967–3973. [Google Scholar] [CrossRef]
- Selke, S.E.M.; Culter, J.D. Plastics Packaging: Properties, Processing, Applications, and Regulations, 3rd ed.; Hanser Publications: Cincinnati, OH, USA, 2016; ISBN 978-1-56990-443-5. [Google Scholar]
- Molinspiration. Available online: www.molinspiration.com (accessed on 30 April 2025).
- Kirchkeszner, C.; Petrovics, N.; Tabi, T.; Magyar, N.; Kovacs, J.; Szabo, B.S.; Nyiri, Z.; Eke, Z. Swelling as a promoter of migration of plastic additives in the interaction of fatty food simulants with polylactic acid and polypropylene-based plastics. Food Control 2022, 132, 108354. [Google Scholar] [CrossRef]
- Dragan, V.K.; Petrovics, N.; Kirchkeszner, C.; Tabi, T.; Szabo, B.S.; Eke, Z. The kinetics of swelling and migration: A case study of plasticized polylactic acid food contact plastics tested with ethanolic food simulants. Express Polym. Lett. 2024, 18, 391–405. [Google Scholar] [CrossRef]
- Regulation No. 10/2011 of 14 January 2011 on Plastic Materials and Articles Intended to Come into Contact with Food. Official Journal of the European Union L12/1. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32011R0010&from=EN (accessed on 6 April 2025).
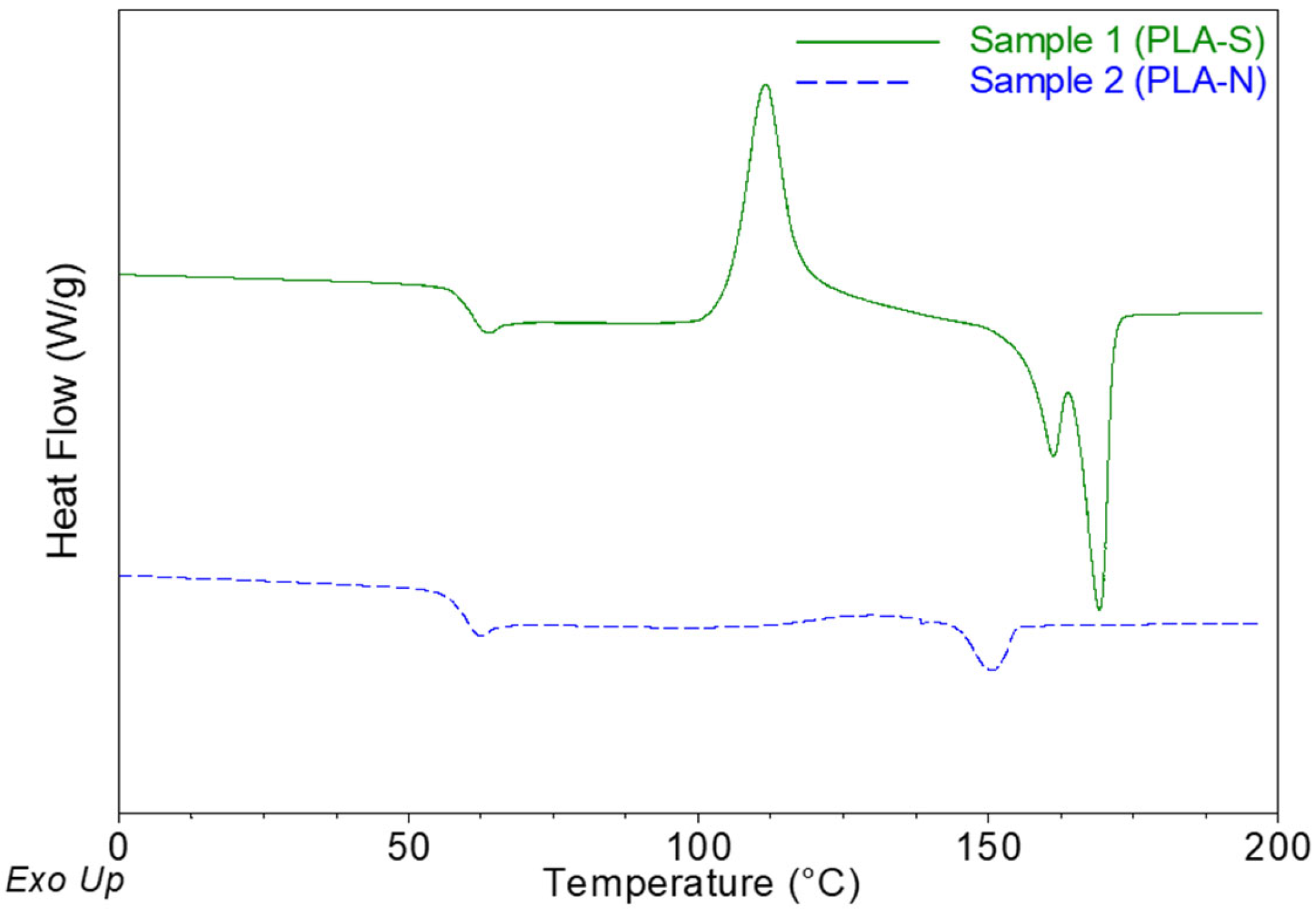

| Sample | Thickness, µm | Tg, °C | Tc, °C | Tm1, °C | Tm2, °C | XC, % | XMAF, % | XRAF, % |
|---|---|---|---|---|---|---|---|---|
| PLA-S | 20.5 ± 0.6 a | 61.3 ± 0.5 a | 110.4 ± 1.4 a | 160.9 ± 0.4 | 169.1 ± 0.1 a | 3.4 ± 1.1 a | 88.3 ± 2.2 a | 8.3 ± 2.6 a |
| PLA-N | 30.0 ± 0.9 b | 60.1 ± 0.2 b | 128.9 ± 1.0 b | n.d. | 151.1 ± 0.3 b | 1.2 ± 0.2 b | 86.6 ± 1.9 a | 12.1 ± 0.8 b |
| Sample | Mn, kDa | Mw, kDa | ĐM |
|---|---|---|---|
| PLA-S | 84.5 ± 1.0 a | 175.3 ± 0.7 a | 2.1 ± 0.02 a |
| PLA-N | 104.4 ± 2.9 b | 171.5 ± 3.9 a | 1.6 ± 0.04 b |
| Substance | Molecular Weight, g/mol | Molecular Volume, Å3 | Temperature Range Tested, °C | Number of DP | Activation Energy EA, kJ/mol | Pre-Exponential Factor D0, cm2/s |
|---|---|---|---|---|---|---|
| 1-propanol | 60.1 | 70.82 | 70–75 | 3 | ||
| n-pentane | 72.2 | 96.16 | 70–85 | 4 | 230.0 | 4.11 × 1023 |
| 1-butanol | 74.1 | 87.62 | 70–85 | 5 | 172.6 | 2.38 × 1015 |
| n-hexane | 86.2 | 112.96 | 75–90 | 4 | 226.8 | 6.88 × 1022 |
| 1-pentanol | 88.2 | 104.42 | 70–85 | 5 | 220.4 | 1.35 × 1022 |
| n-heptane | 100.2 | 129.77 | 75–90 | 4 | 253.9 | 4.32 × 1026 |
| 1-hexanol | 102.2 | 121.22 | 75–85 | 3 | ||
| n-octane | 114.2 | 146.57 | 75–90 | 4 | 279.3 | 1.56 × 1030 |
| 1-heptanol | 116.2 | 138.03 | 75–85 | 3 | ||
| n-nonane | 128.3 | 163.37 | 75–90 | 4 | 304.7 | 6.41 × 1033 |
| 1-octanol | 130.2 | 154.83 | 75–85 | 3 | ||
| n-decane | 142.3 | 180.17 | 80–90 | 3 | ||
| n-undecane | 156.3 | 196.97 | 80–90 | 3 | ||
| n-dodecane | 170.3 | 213.78 | 80–90 | 3 | ||
| n-tridecane | 184.4 | 230.58 | 80–90 | 3 | ||
| n-tetradecane | 198.4 | 247.38 | 80–90 | 3 |
| Substance | Molecular Weight, g/mol | Molecular Volume, Å3 | Temperature Range Tested, °C | Number of DP | Activation Energy EA, kJ/mol | Pre-Exponential Factor D0, cm2/s |
|---|---|---|---|---|---|---|
| methane | 16.0 | 28.64 | 20 | 1 | ||
| ethane | 30.1 | 45.76 | 20–60 | 4 | 60.6 | 1.47 × 100 |
| n-propane | 44.1 | 62.56 | 50–70 | 3 | ||
| acetone | 58.1 | 64.74 | 60–75 | 5 | 114.5 | 3.02 × 107 |
| n-butane | 58.1 | 79.36 | 70 | 1 | ||
| methyl formate | 60.1 | 57.16 | 60–70 | 3 | ||
| 1-propanol | 60.1 | 70.82 | 65–80 | 4 | 162.0 | 2.81 × 1014 |
| pyrrole | 67.1 | 69.03 | 70 | 1 | ||
| cyclopentane | 70.1 | 85.80 | 70–85 | 4 | 247.0 | 1.41 × 1026 |
| tetrahydrofuran | 72.1 | 77.98 | 70–85 | 4 | 191.3 | 1.73 × 1018 |
| 2-butanone | 72.1 | 81.54 | 60–85 | 10 | 160.7 | 9.09 × 1013 |
| n-pentane | 72.2 | 96.16 | 70–85 | 9 | 239.4 | 1.92 × 1025 |
| 1,3-dioxolane | 74.1 | 70.17 | 60–85 | 6 | 141.4 | 1.47 × 1011 |
| ethyl formate | 74.1 | 73.97 | 60–75 | 4 | 128.7 | 3.87 × 109 |
| 1-butanol | 74.1 | 87.62 | 65–85 | 5 | 205.0 | 2.96 × 1020 |
| benzene | 78.1 | 84.04 | 70–85 | 4 | 212.8 | 2.45 × 1021 |
| pyridine | 79.1 | 79.89 | 70 | 1 | ||
| cyclopentanone | 84.1 | 87.98 | 70–85 | 4 | 242.2 | 2.93 × 1025 |
| cyclohexane | 84.2 | 102.60 | 75–85 | 3 | ||
| 2-pentanone | 86.1 | 98.34 | 65–80 | 5 | 256.6 | 1.10 × 1028 |
| n-hexane | 86.2 | 112.96 | 75–85 | 8 | ||
| 2-methyl-1,3-dioxolane | 88.1 | 86.75 | 65–80 | 4 | 228.4 | 5.77 × 1023 |
| 1,4-dioxane | 88.1 | 86.97 | 70–85 | 3 | ||
| n-propyl formate | 88.1 | 90.77 | 60–80 | 5 | 191.9 | 3.60 × 1018 |
| 1-pentanol | 88.2 | 104.42 | 70–85 | 4 | 219.3 | 2.43 × 1022 |
| toluene | 92.1 | 100.61 | 70–85 | 3 | 236.6 | 4.81 × 1024 |
| aniline | 93.1 | 95.33 | 70 | 1 | ||
| cyclohexanone | 98.1 | 104.79 | 75–85 | 3 | ||
| 2-hexanone | 100.2 | 115.15 | 70–85 | 5 | 238.2 | 1.02 × 1025 |
| n-heptane | 100.2 | 129.77 | 75–90 | 9 | 278.9 | 5.12 × 1030 |
| n-butyl formate | 102.1 | 107.57 | 65–80 | 4 | 247.1 | 3.29 × 1026 |
| 1-hexanol | 102.2 | 121.22 | 70–85 | 4 | 241.0 | 2.53 × 1025 |
| ethylbenzene | 106.2 | 117.41 | 70–90 | 5 | 246.0 | 6.78 × 1025 |
| 4-vinyl cyclohexene | 108.2 | 124.17 | 75–90 | 4 | 246.4 | 4.31 × 1025 |
| 2-heptanone | 114.2 | 131.95 | 70–85 | 5 | 261.4 | 2.05 × 1028 |
| n-octane | 114.2 | 146.57 | 80–90 | 6 | ||
| n-pentyl formate | 116.2 | 124.37 | 70–80 | 3 | ||
| 1-heptanol | 116.2 | 138.03 | 70–85 | 4 | 267.5 | 1.66 × 1029 |
| n-propylbenzene | 120.2 | 134.21 | 75–90 | 4 | 230.2 | 2.44 × 1023 |
| naphthalene | 128.2 | 128.03 | 75–90 | 4 | 236.3 | 1.56 × 1024 |
| 2-octanone | 128.2 | 148.75 | 75–85 | 4 | ||
| n-nonane | 128.3 | 163.37 | 80–90 | 6 | ||
| n-hexyl formate | 130.2 | 141.17 | 70–80 | 3 | ||
| 1-octanol | 130.2 | 154.83 | 70–85 | 4 | 279.4 | 7.62 × 1030 |
| n-butylbenzene | 134.2 | 151.01 | 75–90 | 4 | 242.3 | 1.21 × 1025 |
| methyl naphthalene | 142.2 | 144.60 | 75–90 | 4 | 258.0 | 1.35 × 1027 |
| n-decane | 142.3 | 180.17 | 80–90 | 6 | ||
| n-heptyl formate | 144.2 | 157.97 | 75–80 | 2 | ||
| ethyl naphthalene | 156.2 | 161.40 | 75–90 | 4 | 266.2 | 1.75 × 1028 |
| n-undecane | 156.3 | 196.97 | 80–90 | 6 | ||
| n-dodecane | 170.3 | 213.78 | 80–90 | 6 | ||
| n-tridecane | 184.4 | 230.58 | 80–90 | 6 | ||
| n-tetradecane | 198.4 | 247.38 | 80–90 | 6 | ||
| di-iso-propyl naphthalene | 212.3 | 227.94 | 80–90 | 3 |
| Parameter | PLA | PET a | PEN b |
|---|---|---|---|
| a [1/K] | 2.67 × 10−3 | 1.93 × 10−3 | 2.23 × 10−3 |
| b [cm2/s] | 4.46 × 10−9 | 2.37 × 10−6 | 1.12 × 10−9 |
| c [Å3] | 34.4 | 11.1 | 31.1 |
| d [1/K] | 4.14 × 10−5 | 1.50 × 10−4 | 6.74 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ewender, J.; Auras, R.; Sonchaeng, U.; Welle, F. Diffusion Coefficients and Activation Energies of Diffusion of Organic Molecules in Poly(lactic acid) Films. Molecules 2025, 30, 2064. https://doi.org/10.3390/molecules30092064
Ewender J, Auras R, Sonchaeng U, Welle F. Diffusion Coefficients and Activation Energies of Diffusion of Organic Molecules in Poly(lactic acid) Films. Molecules. 2025; 30(9):2064. https://doi.org/10.3390/molecules30092064
Chicago/Turabian StyleEwender, Johann, Rafael Auras, Uruchaya Sonchaeng, and Frank Welle. 2025. "Diffusion Coefficients and Activation Energies of Diffusion of Organic Molecules in Poly(lactic acid) Films" Molecules 30, no. 9: 2064. https://doi.org/10.3390/molecules30092064
APA StyleEwender, J., Auras, R., Sonchaeng, U., & Welle, F. (2025). Diffusion Coefficients and Activation Energies of Diffusion of Organic Molecules in Poly(lactic acid) Films. Molecules, 30(9), 2064. https://doi.org/10.3390/molecules30092064













